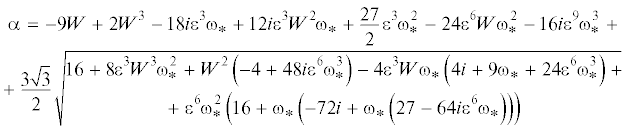1. На главную
  2. Электронные версии
  3. Прикладная математика и механика
  4. T. 87, № 3, 2023

Прикладная математика и механика, 2023, T. 87, № 3, стр. 379-391

Волновое движение в вязкой однородной жидкости с поверхностным электрическим зарядом

А. А. Очиров 1, *, Ю. Д. Чашечкин 1, **

1 Институт проблем механики им. А.Ю. Ишлинского РАН
Москва, Россия

* E-mail: otchirov@mail.ru
** E-mail: yulidch@gmail.com

Поступила в редакцию 13.03.2023
После доработки 15.04.2023
Принята к публикации 24.04.2023

Полный текст (PDF)

Аннотация

Аналитическими асимптотическими методами исследовано влияние поверхностного электрического заряда на характер и свойства волнового движения свободной поверхности вязкой однородной жидкости. Получены выражения, описывающие дисперсионные зависимости компонент волнового движения. Определены фазовые и групповые скорости структур, формирующих волновое движение.

Ключевые слова: жидкость, вязкость, поверхностный электрический заряд

1. Введение. Теоретическим исследованиям волновых движений на свободной поверхности жидкости посвящено множество работ. В качестве примера можно привести классические публикации [1–3], обобщающие монографии [4–7] и трактаты [8–10]. Не ослабевает интерес к изучению поверхностных волн и в XXI веке. Поверхностные волны исследуются в различных теоретических подходах и в приложениях, среди которых можно выделить изучение волнового массопереноса [11, 12], перераспределения газовых пузырьков [13], стоячих гравитационных волн [14–16], общих свойств решений и компонент течений в идеальных [17, 18] или вязких [19] стратифицированных жидкостях. Внимание уделяется описанию поверхностных океанических волн, взаимодействующих с ледовым покрытием [20] и ветром [21]. Активно изучаются капиллярные и гравитационно-капиллярные волновые процессы, возникающие на многих этапах эволюции картины течения, порождаемого в принимающей жидкости падающей каплей [22–25].

Практический интерес представляет изучение влияния электрического заряда на процессы, происходящие на поверхности жидкости. В большинстве исследований внимание уделяется определению критерия устойчивости [26, 27] – условия возникновения на поверхности заряженной жидкости конусообразных выступов (конусов Тейлора), с вершин которых происходит эмиссия заряженных электрических капель [28]. Интерес к изучению влияния электрического заряда на процессы на поверхности жидкости не угасает [29–31]. Актуальными становятся исследования, в которых производится учет трансформации поверхностной энергии [32], включающей дополнительную электрическую энергию заряженной поверхности. В настоящей работе исследуется влияние поверхностного электрического заряда на поверхностные волны в вязкой однородной жидкости и присоединенные к ним лигаменты, возникающие в вязких жидкостях.

2. Математическая формулировка задачи. Рассматривается полубесконечная неограниченная вязкая жидкость с кинематической вязкостью $\nu $, заполняющая нижнее полупространство $z < 0$. Расчеты проводятся в декартовой системе координат $Oxyz$, в которой плоскость $Oxy$ совпадает с равновесным положением поверхности жидкости, а ось $Oz$ направлена вертикально вверх против направления действия поля сил тяжести $\vec {g}$. Жидкость полагается идеально проводящей и считается, что вдоль свободной поверхности распределен поверхностный электрический заряд с равновесной поверхностной плотностью ${{\kappa }_{0}}$. Поверхностная энергия характеризуется коэффициентом поверхностного натяжения $\sigma $ или его нормированным на плотность жидкости $\rho $ значением $\gamma = {\sigma \mathord{\left/ {\vphantom {\sigma \rho }} \right. \kern-0em} \rho }$. Ставится задача об оценке влияния поверхностного электрического заряда на дисперсионные зависимости распространяющейся вдоль свободной заряженной поверхности жидкости синусоидального плоского периодического движения $\zeta = \zeta \left( {x,t} \right)$ с частотой $\omega $, при этом считается, что движение жидкости не зависит от поперечной горизонтальной координаты $y$.

Математическая формулировка задачи состоит из уравнения Навье–Стокса и уравнения неразрывности, которое упрощается, если однородная жидкость несжимаема:

(2.1)
${{\partial }_{t}}\vec {u} + \left( {\vec {u} \cdot \nabla } \right)\vec {u} = \nu \Delta \vec {u} - \frac{1}{\rho }\nabla P + \vec {g}$
(2.2)
$\nabla \cdot \vec {u} = 0$

Здесь $\vec {u} = u{{\vec {e}}_{x}} + {v}{{\vec {e}}_{z}}$ – поле скоростей жидкости, а $P$ – давление, которое представляется в виде суммы атмосферного ${{P}_{0}}$, электрического, гидростатического и волнового $\tilde {P}$ давлений:

(2.3)
$P = {{P}_{0}} + \frac{{E_{0}^{2}}}{{8\pi }} + \rho g\left( {\zeta - z} \right) + \tilde {P}$

Символом ${{E}_{0}} = 4\pi {{\kappa }_{0}}$ обозначен модуль вектора напряженности однородного электрического поля, возникающего над невозмущенной равномерно заряженной плоскостью.

В плоской постановке для несжимаемой жидкости можно ввести функцию тока $\psi $, производные которой задают компоненты скорости жидкости:

(2.4)
$u = {{\partial }_{z}}\psi ,\quad {v} = - {{\partial }_{x}}\psi $

После линеаризации уравнений (2.1)–(2.2) и подстановки (2.3)–(2.4) получим, что уравнение несжимаемости выполняется автоматически, а уравнение Навье–Стокса примет вид:

(2.5)
$z < 0{\kern 1pt} :\quad \left\{ \begin{gathered} g{{\partial }_{x}}\zeta + {{\partial }_{{zt}}}\psi + \frac{{{{\partial }_{x}}\tilde {P}}}{\rho } - \nu {{\partial }_{z}}\Delta \psi = 0 \hfill \\ \frac{{{{\partial }_{z}}\tilde {P}}}{\rho } - {{\partial }_{{xt}}}\psi + \nu {{\partial }_{x}}\Delta \psi = 0 \hfill \\ \end{gathered} \right.$

Избавляясь в (2.5) от волновой части давления получим уравнение на функцию тока:

(2.6)
$z < 0{\kern 1pt} :\quad \Delta \left( {{{\partial }_{t}} - \nu \Delta } \right)\psi = 0$

Уравнение (2.6) описывает периодическое течение в толще жидкости, связанное с распространением поверхностной волны. Помимо возмущения поля скоростей и давления происходит возмущение электрического поля и появляется добавка $\Phi $ к электрическому потенциалу ${{\Phi }_{0}} = - {{E}_{0}}z$ над свободной поверхностью:

(2.7)
$z > 0{\kern 1pt} :\quad \Delta \Phi = 0$

Уравнения необходимо дополнить граничными условиями на свободной поверхности, а также условиями затухания движения жидкости с глубиной и постоянства напряженности электрического поля в бесконечно удаленной от заряженной поверхности точке. Граничные условия после линеаризации и процедуры снесения на равновесную поверхность $z = 0$ [33] выглядят следующим образом:

(2.8)
$z = 0{\kern 1pt} :\quad \left\{ \begin{gathered} \tilde {P} + 2\rho \nu {{\partial }_{{zx}}}\psi + \sigma {{\partial }_{{xx}}}\zeta - \frac{{{{E}_{0}}}}{{4\pi }}{{\partial }_{z}}\Phi = 0 \hfill \\ {{\partial }_{t}}\zeta + {{\partial }_{x}}\psi = 0 \hfill \\ {{\partial }_{{zz}}}\psi - {{\partial }_{{xx}}}\psi = 0 \hfill \\ \Phi - {{E}_{0}}\zeta = 0 \hfill \\ \end{gathered} \right.$
(2.9)
$z \to - \infty {\kern 1pt} :\quad {{\partial }_{z}}\psi \to 0,\quad {{\partial }_{x}}\psi \to 0$
(2.10)
$z \to \infty {\kern 1pt} :\quad \nabla \Phi \to 0$

Стоит отметить, что в такой постановке поверхностный электрический заряд оказывает влияние на дисперсионные соотношения только через динамическое граничное условие на давление.

3. Решение. Будем искать решение линеаризованной задачи для инфинитезимальных отклонений свободной поверхности (2.6)–(2.10) в виде периодических возмущений с положительно определенной частотой и комплексным волновым числом:

(3.1)
$\left( \begin{gathered} \psi \\ \zeta \\ \Phi \\ {\tilde {P}} \\ \end{gathered} \right) = \left( \begin{gathered} A\exp \left( {{{k}_{z}}z} \right) \\ B \\ F\exp \left( {{{k}_{{z\Phi }}}z} \right) \\ C\exp \left( {{{k}_{z}}z} \right) \\ \end{gathered} \right)\exp \left( {i{{k}_{x}}x - i\omega t} \right)$

Погружение задачи в алгебру комплексных чисел приводит к увеличению числа корней. Дополнительные корни традиционно отбраковываются применением физических соображений – в частности, условия затухания решений с удалением от свободной поверхности [8]. Подставляя (3.1) в (2.6)–(2.7) получим дисперсионные соотношения, связывающие компоненты волновых векторов:

(3.2)
$\left( {k_{x}^{2} - k_{z}^{2}} \right)\left( {\nu \left( {k_{x}^{2} - k_{z}^{2}} \right) - i\omega } \right) = 0$
и для добавки к электрическому потенциалу:

(3.3)
$k_{{z\Phi }}^{2} = k_{x}^{2}$

Полный набор решений алгебраического уравнения четвертой степени (3.2) включает корни двух видов:

(3.4)
${{k}_{z}} = \pm {{k}_{x}},\quad {{k}_{l}} = \pm \sqrt {k_{x}^{2} - i\frac{\omega }{\nu }} $

Первые из них описывают волновое движение (обозначены ${{k}_{z}}$). Вторые определяют присоединенный к волновому движению лигамент – тонкую компоненту течения, проявляющуюся в виде тонких струек, сопровождающих волну. Здесь введено обозначение ${{k}_{l}}$ для различия корней.

Математически лигаментные компоненты описываются корнями дисперсионных уравнений, для которых справедливо соотношение $\operatorname{Re} {{k}_{l}} \sim \operatorname{Im} {{k}_{l}}$, тогда как волновые компоненты течения характеризуются корнями, которым свойственно $\operatorname{Re} {{k}_{z}} \gg \operatorname{Im} {{k}_{z}}$.

Вид решения для функции тока с учетом (3.4) запишется следующим образом:

(3.5)
$\psi = A\left( {\exp \left( {{{k}_{z}}z} \right) + \beta \exp \left( {{{k}_{l}}z} \right)} \right)\exp \left( {i{{k}_{x}}x - i\omega t} \right)$

Ротор поля скоростей с учетом (2.4) и (3.5) определяется

(3.6)
$\operatorname{rot} \vec {u} = A\exp \left( {i{{k}_{x}}x - i\omega t} \right)\left( {k_{x}^{2}\left( {{{\operatorname{e} }^{{{{k}_{z}}z}}} + \beta {{\operatorname{e} }^{{{{k}_{l}}z}}}} \right) - \left( {k_{z}^{2}{{\operatorname{e} }^{{{{k}_{z}}z}}} + \beta k_{l}^{2}{{\operatorname{e} }^{{{{k}_{l}}z}}}} \right)} \right)$

И с учетом (3.4) преобразуется в выражение

(3.7)
$\operatorname{rot} \vec {u} = A\beta \exp \left( {i{{k}_{x}}x - i\omega t} \right)\exp \left( {{{k}_{l}}z} \right)\left( {k_{x}^{2} - k_{l}^{2}} \right)$

Из (3.7) видно, что волновая компонента течения ${{k}_{z}}$, в отличие от лигаментной компоненты ${{k}_{l}}$, не участвует в описании вихревой составляющей периодического течения.

Решение уравнения (3.3) записывается в виде:

(3.8)
${{k}_{{z\Phi }}} = \pm {{k}_{x}}$

Выбор корней в (3.4), (3.8) определяется условиями физической реализации (2.9)–(2.10):

(3.9)
$\operatorname{Re} {{k}_{{z,l}}} > 0,\quad \operatorname{Re} {{k}_{{z\Phi }}} < 0$

Условие (3.9) дополняется условием действительности частоты волнового движения $\operatorname{Im} \omega = 0$.

Подставим решение (3.1) с учетом (3.4) в граничные условия (2.8) и получим связь между константами, определяющими физические поля (функцию тока, отклонение свободной поверхности и добавку к электрическому потенциалу):

(3.10)
$\begin{gathered} B = A\frac{{{{k}_{x}}}}{\omega }\left( {1 + \beta } \right),\quad \beta = - \frac{{k_{x}^{2} + k_{z}^{2}}}{{k_{x}^{2} + k_{l}^{2}}} = - \frac{{2k_{x}^{2}}}{{2k_{x}^{2} - {{i\omega } \mathord{\left/ {\vphantom {{i\omega } \nu }} \right. \kern-0em} \nu }}} \\ F = {{E}_{0}}B = {{E}_{0}}A\frac{{{{k}_{x}}}}{\omega }\left( {1 + \beta } \right),\quad C = A{{k}_{x}}\rho \left( {\frac{{k_{x}^{2}\gamma }}{\omega } - \frac{{2i\left( {{{k}_{z}} + {{k}_{l}}\beta } \right)\nu }}{{1 + \beta }} + \frac{{{{k}_{{z\Phi }}}E_{0}^{2}}}{{4\pi \rho \omega }}} \right) \\ \end{gathered} $

Используя (3.10), динамическое граничное условие на давление (2.8) и уравнение Навье–Стокса (2.5) получим уравнение:

(3.11)
$ - {{\partial }_{{ztt}}}\psi + \nu {{\partial }_{{tz}}}\Delta \psi + \left( {g - {{k}_{x}}W\sqrt {g\gamma } } \right){{\partial }_{{xx}}}\psi + 2\nu {{\partial }_{{xxzt}}}\psi - \gamma {{\partial }_{{xxxx}}}\psi = 0,$
которое при подстановке (3.1) и (3.4) приводит к дисперсионному соотношению:

(3.12)
$g{{k}_{x}} - 4k_{x}^{2}{{\nu }^{2}} - k_{x}^{2}W\sqrt {g\gamma } - {{\omega }^{2}} + k_{x}^{3}\left( {\gamma + 4{{\nu }^{2}}\sqrt {k_{x}^{2} - \frac{{i\omega }}{\nu }} } \right) = 0;\quad W = \frac{{E_{0}^{2}}}{{4\pi \sqrt {\rho g\sigma } }}$

Здесь символом $W$ обозначено отношение плотности энергии поля и потенциальной поверхностной энергии (параметр Тонкса–Френкеля). Анализ дисперсионного уравнения (3.12) проведем в безразмерных переменных. В качестве параметров обезразмеривания выберем собственные масштабы задачи: временной – ${{\tau _{\nu }^{\gamma } = \gamma } \mathord{\left/ {\vphantom {{\tau _{\nu }^{\gamma } = \gamma } {\left( {\nu g} \right)}}} \right. \kern-0em} {\left( {\nu g} \right)}}$ и пространственный – $\delta _{g}^{\nu } = \sqrt[3]{{{{{{\nu }^{2}}} \mathord{\left/ {\vphantom {{{{\nu }^{2}}} g}} \right. \kern-0em} g}}}$. При выбранных параметрах естественным образом возникает малый параметр $\varepsilon = \sqrt[6]{{{{g{{\nu }^{4}}} \mathord{\left/ {\vphantom {{g{{\nu }^{4}}} {{{\gamma }^{3}}}}} \right. \kern-0em} {{{\gamma }^{3}}}}}}$ и с точностью до слагаемых, порядка $o\left( {{{\varepsilon }^{6}}} \right)$ дисперсионное уравнение, связывающее безразмерную компоненту волнового вектора ${{k}_{{x*}}}$ и частоту ${{\omega }_{*}}$, принимает вид:

(3.13)
$k_{{x*}}^{3} + {{\varepsilon }^{2}}{{k}_{{x*}}} - \frac{{{{\varepsilon }^{6}}{{\omega }_{*}}}}{2} - \varepsilon k_{{x*}}^{2}\left( {W + 2i{{\varepsilon }^{3}}{{\omega }_{*}}} \right) = 0$

Дисперсионное уравнение (3.11) имеет три корня:

(3.14)
$\begin{gathered} k_{{1x*}}^{{}} = \frac{{\varepsilon {{\alpha }^{{{1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0em} 3}}}}}}{{3 \times {{2}^{{{1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0em} 3}}}}}} + \frac{1}{3}\left( {\varepsilon W + 2i{{\varepsilon }^{4}}{{\omega }_{*}}} \right) - \frac{{{{2}^{{{1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0em} 3}}}}}}{{3\varepsilon {{\alpha }^{{{1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0em} 3}}}}}}\left( {3{{\varepsilon }^{2}} - {{{\left( {\varepsilon W + 2i{{\varepsilon }^{4}}{{\omega }_{*}}} \right)}}^{2}}} \right) \\ k_{{2,3x*}}^{{}} = \frac{{\left( {1 \mp i\sqrt 3 } \right)\varepsilon }}{{6 \times {{2}^{{{1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0em} 3}}}}}}\left[ {{{\alpha }^{{{1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0em} 3}}}} + \frac{{{{2}^{{{2 \mathord{\left/ {\vphantom {2 3}} \right. \kern-0em} 3}}}}}}{{{{\alpha }^{{{1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0em} 3}}}}}}\left( {3 - {{{\left( {W + 2i{{\varepsilon }^{3}}{{\omega }_{*}}} \right)}}^{2}}} \right)} \right] + \frac{\varepsilon }{3}\left( {W + 2i{{\varepsilon }^{3}}{{\omega }_{*}}} \right), \\ \end{gathered} $
где

Анализ корней дисперсионного уравнения (3.14) показывает, что условиям физической реализации (3.9) и определению частоты, как действительной положительной величины, с учетом соотношений (3.4) удовлетворяет только решение $k_{{1x*}}^{{}}$.

Исследуем дисперсионные соотношения. Определим зависимость длины волны $\lambda $ от частоты волнового движения для волнового решения и аналогичную зависимость линейного масштаба лигамента ${{\delta }_{l}}$ от частоты для тонкого неволнового решения:

(3.15)
$\lambda = \frac{{2\pi }}{{\sqrt {\operatorname{Re} {{{\left( {{{k}_{x}}} \right)}}^{2}} + \operatorname{Im} {{{\left( {{{k}_{z}}} \right)}}^{2}}} }},\quad {{\delta }_{l}} = \frac{{2\pi }}{{\sqrt {\operatorname{Re} {{{\left( {{{k}_{x}}} \right)}}^{2}} + \operatorname{Im} {{{\left( {{{k}_{l}}} \right)}}^{2}}} }}$

На рис. 1,а представлены зависимости длины волны от частоты волнового движения при разных значениях параметра Тонкса–Френкеля для жидкости с параметрами воды ($\rho = 1$ г/см3, $\sigma = 72$ дин/см, $\nu = 0.01$ см2/с). На рис. 1,б в более крупном масштабе изображена область, в которой выражено влияние поверхностного электрического заряда.

Рис. 1.

Зависимость длины волны от частоты волнового движения в жидкости с параметрами воды ($\rho = 1$ г/см3, $\sigma = 72$ дин/см, $\nu = 0.01$ см2/с) при различных значениях параметра Тонкса–Френкеля ($W = 0$; 1.0; 1.5) в диапазоне частот а: $\omega = 10{\kern 1pt} - {\kern 1pt} {{10}^{4}}$ с–1, б: $\omega = 20{\kern 1pt} - {\kern 1pt} 400$ с–1.

Анализ показывает, что поверхностный электрический заряд оказывает заметное влияние в области частот, соответствующих капиллярно-гравитационным волнам: увеличение поверхностного заряда, приводит к уменьшению длины волны волновой компоненты движения при выбранной частоте.

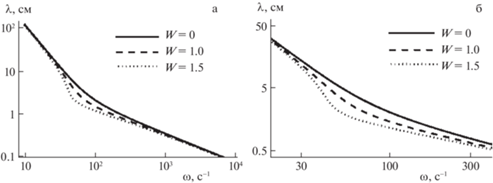
Построим аналогичные зависимости для неволновой компоненты движения. На рис. 2,а представлены зависимости линейного масштаба присоединенного лигамента от частоты волнового движения при разных значениях параметра Тонкса–Френкеля для жидкости с параметрами воды. Из рис. 2 видно, что поверхностный заряд практически не оказывает влияния на лигамент, присоединенный к поверхностной волне (толщина линий на графике не позволяет разрешить разницу между компонентами течения в незаряженной и заряженной жидкости). Из рассмотрения графика зависимости отношения разности масштабов лигаментов в заряженной ${{\delta }_{{lch}}}$ и незаряженной ${{\delta }_{l}}$ жидкости, к их сумме

$\Delta \delta \left( \omega \right) = \frac{{{{\delta }_{{lch}}}\left( \omega \right) - {{\delta }_{l}}\left( \omega \right)}}{{{{\delta }_{{lch}}}\left( \omega \right) + {{\delta }_{l}}\left( \omega \right)}}$
от частоты, приведенного на рис. 2б, следует, что значение $\Delta \delta $ для жидкости с параметрами воды и Тонкса–Френкеля $W = 1.0$, $1.5$ максимально в окрестности частоты $\omega = 100$ с–1, монотонно убывает с отклонением от этого значения и не превышает 0.1%.

Рис. 2.

а: Зависимость линейного размера лигаментной компоненты от частоты в жидкости с параметрами воды ($\rho = 1$ г/см3, $\sigma = 72$ дин/см, $\nu = 0.01$ см2/с) при различных значениях параметра Тонкса–Френкеля ($W = 0$; 1.0; 1.5) в диапазоне частот $\omega = 10{\kern 1pt} - {\kern 1pt} {{10}^{4}}$ с–1; б: зависимость отношения разности масштабов лигаментов в заряженной ${{\delta }_{{lch}}}$ и незаряженной ${{\delta }_{l}}$ жидкости, к их сумме $\Delta \delta $ от частоты волнового движения при различных значениях параметра Тонкса–Френкеля ($W = 1$; $1.5$) в диапазоне частот $\omega = 10{\kern 1pt} - {\kern 1pt} {{10}^{4}}$ с–1.

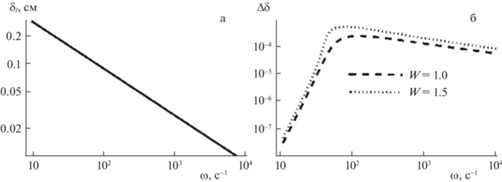
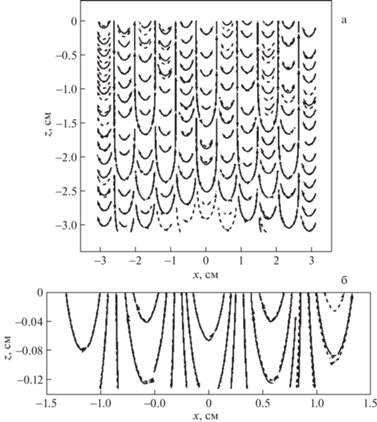
Проследим за линиями тока вблизи свободной поверхности жидкости. Подставим полученные дисперсионные соотношения в решение (3.1) и построим линии тока для жидкости при различных значениях поверхностного электрического заряда. На рис. 3а построены линии тока для незаряженной поверхности воды возникающие при распространении волны с частотой $\omega = 100$ с–1 с учетом (выражения (3.5), кривые изображены сплошными линиями) и без учета (пунктирные линии) лигаментных компонент течения на масштабах нескольких длин волн. Выражение без учета лигаментных компонент построено для функции тока:

$\psi = A\exp \left( {{{k}_{z}}z} \right)\exp \left( {i{{k}_{x}}x - i\omega t} \right)$
Рис. 3.

Линии тока в жидкости с параметрами воды ($\rho = 1$ г/см3, $\sigma = 72$ дин/см, $\nu = 0.01$ см2/с) в начальный момент времени $t = 0\;с$, возникающие при волновом возмущении поверхности с частотой $\omega = 100$ с–1 при отсутствии поверхностного электрического заряда ($W = 0$) с учетом (сплошные линии) и без учета (пунктирные линии) лигаментной компоненты волнового движения на характерных масштабах длины волны – а; и лигамента – б.

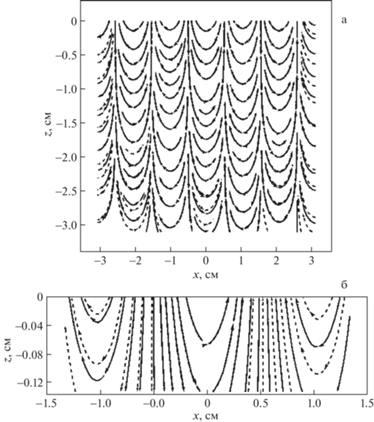
На рис. 3,б изображены те же зависимости, но на масштабах нескольких лигаментов. На рис. 4 и рис. 5 изображены аналогичные зависимости при значении параметра Тонкса–Френкеля $W = 1.0$ и $W = 1.5$ соответственно. Из рисунков видно, что поверхностный электрический заряд оказывает влияние на волновую компоненту течения: его увеличение приводит к уменьшению длины волны – характерного размера волновой компоненты течения. Даже на масштабах длин волн видно, что линии тока, построенные без учета лигаментной компоненты, отличаются от линий тока, построенные с учетом всех компонент течения. Еще более ярко отличия проявляются на малых масштабах, сравнимых с характерными размерами лигаментов ${{\delta }_{l}}$. Учет тонких компонент позволяет строить более точную картину течения. Несмотря на малость абсолютных величин, тонкие течения вносят весомый вклад на малых масштабах за счет большой плотности переносимой энергии.

Рис. 4.

Линии тока в жидкости с параметрами воды ($\rho = 1$ г/см3, $\sigma = 72$ дин/см, $\nu = 0.01$ см2/с) в начальный момент времени $t = 0$ с, возникающие при волновом возмущении поверхности с частотой $\omega = 100$ с–1 при значении параметра Тонкса–Френкеля $W = 1.0$ с учетом (сплошные линии) и без учета (пунктирные линии) лигаментной компоненты волнового движения на характерных масштабах длины волны – а; и лигамента – б.

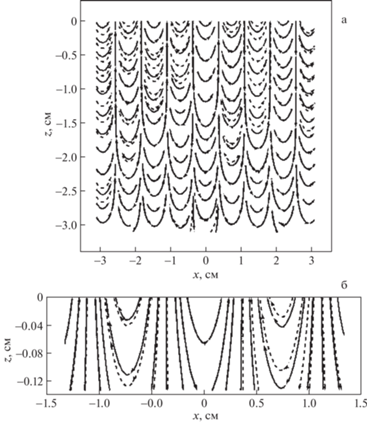
Рис. 5.

Линии тока в жидкости с параметрами воды ($\rho = 1$ г/см3, $\sigma = 72$ дин/см, $\nu = 0.01$ см2/с) в начальный момент времени $t = 0$ с, возникающие при волновом возмущении поверхности с частотой $\omega = 100$ с–1 при значении параметра Тонкса–Френкеля $W = 1.5$ с учетом (сплошные линии) и без учета (пунктирные линии) лигаментной компоненты волнового движения на характерных масштабах длины волны – а; и лигамента – б.

Рассмотрим влияние поверхностного электрического заряда на групповые ${{c}_{{\operatorname{gr} }}}$ и фазовые ${{c}_{{\operatorname{ph} }}}$ скорости волнового и их аналогов ${{c}_{{\operatorname{grl} }}}$, ${{c}_{{\operatorname{phl} }}}$ лигаментной компоненты течения. На рис. 6,а представлены искомые зависимости для волновой компоненты течения от частоты при разных значениях параметра Тонкса–Френкеля для жидкости с параметрами воды, построенные с использованием решений (3.4), (3.14). На рис. 6,б изображена область в диапазоне частот, в котором влияние поверхностного электрического заряда оказывается заметным. На рис. 7,а, б изображены аналогичные зависимости от длины волны.

Рис. 6.

Зависимость фазовой и групповой скорости от частоты в жидкости с параметрами воды ($\rho = 1$ г/см3, $\sigma = 72$ дин/см, $\nu = 0.01$ см2/с) при различных значениях параметра Тонкса–Френкеля ($W = 0;\;1.0;\;1.5$) – а; в более крупном масштабе – б.

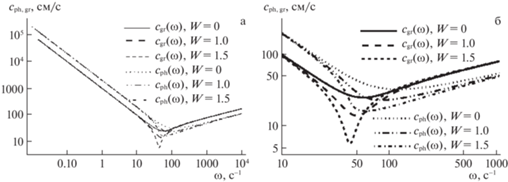
Рис. 7.

Зависимость фазовой и групповой скорости от длины волны в жидкости с параметрами воды ($\rho = 1$ г/см3, $\sigma = 72$ дин/см, $\nu = 0.01$ см2/с) при различных значениях параметра Тонкса–Френкеля ($W = 0;\;1.0;\;1.5$) – а; в более крупном масштабе – б.

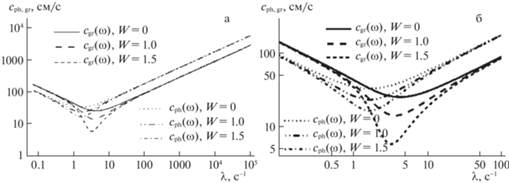
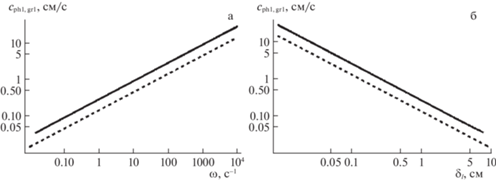
Влияние поверхностного электрического заряда на волновую компоненту течения сказывается в области капиллярно-гравитационных волн. Увеличение поверхностного электрического заряда приводит к уменьшению минимальных значений групповой и фазовой скоростей и смещению экстремумов в область более низких частот (больших длин волн). Аналогичным образом ведет себя значение частоты, при которой происходит резонанс фазовой и групповой скоростей. Анализ показывает, что поверхностный электрический заряд не оказывает значимого влияния на лигаментная компонента течения. На рис. 8,а, б приведены зависимости аналогов групповой и фазовой скоростей лигаментную компоненту от частоты и пространственного масштаба соответственно для незаряженной жидкости ($W = 0$).

Рис. 8.

Зависимость фазовой (пунктирная линия) и групповой (сплошная линия) скорости лигаментной компоненты течения в незаряженной жидкости в жидкости с параметрами воды ($\rho = 1$ г/см3, $\sigma = 72$ дин/см, $\nu = 0.01$ см2/с, $W = 0$) от частоты – а; линейного размера – б.

Заключение. Поверхностный электрический заряд оказывает заметное влияние на волновую компоненту течения в области капиллярно-гравитационных волн. Увеличение поверхностного электрического заряда приводит к уменьшению минимальных значений групповой и фазовой скоростей, при этом наблюдается сдвиг этих значений в область более низких частот. В вязкой жидкости помимо волновой компоненты течения существует неволновая компонента – лигамент, отвечающая за тонкие присоединенные течения. Влияние поверхностного электрического заряда на эту компоненту поверхностного волнового движения незначительно. Учет всех компонент волнового движения позволяет строить корректные картины течения, в частности линии тока.

Работа выполнена при финансовой поддержке Российского научного фонда (проект 19-19-00598-П “Гидродинамика и энергетика капли и капельных струй: формирование, движение, распад, взаимодействие с контактной поверхностью”, https://rscf.ru/project/19-19-00598/).

Список литературы

  1. Rayleigh On waves // Phil. Mag. 1876. V. 1. P. 257–259.

  2. Stokes G.G. On the theory of oscillatory waves // Trans. Cam. Philos. Soc. 1847. V. 8. P. 441–455.

  3. Сретенский Л.Н. О волнах на поверхности вязкой жидкости // Тр. ЦАГИ. 1941. № 541. С. 1–34.

  4. Лэмб Г. Гидродинамика. М.; Л.: ГИТТЛ, 1949. С. 928.

  5. Уизем Д. Линейные и нелинейные волны. М.: Мир, 1977. 624 с.

  6. Лайтхилл Д. Волны в жидкостях М.: Мир, 1981. 598 с.

  7. Chandrasekhar S. Hydrodynamic and Hydromagnetic Stability. Int. Ser. Monographs on Physics. Oxford: Clarendon, 1961. 685 p.

  8. Ландау Л.Д., Лифшиц Е.М. Теоретическая физика. Т. VI. Гидродинамика. М.: Наука, 1986.

  9. Кочин Н.Е., Кибель И.А., Розе И.В. Теоретическая гидромеханика. Ч. I. М.: ГИФМЛ, 1963. 585 c.

  10. Левич В.Г. Физико-химическая гидродинамика. М.: ГИФМЛ, 1959. 700 c.

  11. Чашечкин Ю.Д. Перенос вещества окрашенной капли в слое жидкости с бегущими плоскими гравитационно-капиллярными волнами // Изв. РАН. ФАО. 2022. Т. 58. № 2. С. 218–229.

  12. Grzonka L., Cieślikiewicz W. Mass transport induced by nonlinear surface gravity waves // Copernicus Meetings. 2023. № EGU23-16788.

  13. Druzhinin O.A., Tsai W.T. Numerical simulation of micro-bubbles dispersion by surface waves // Algorithms. 2022. T. 15. № 4. C. 110.

  14. Калиниченко В.А. Регуляризация гравитационных баротропных волн в двухслойной жидкости // Изв. РАН. МЖГ. 2019. № 6. С. 25–37.

  15. Калиниченко В.А. Стоячие гравитационные волны на поверхности вязкой жидкости // ПММ. 2022. Т. 86. Вып. 3. С. 370–380.

  16. Абрашкин А.А., Бодунова Ю.П. Пространственные стоячие волны на поверхности вязкой жидкости // Тр. НГТУ им. Р.Е. Алексеева. МЖГ. 2011. № 2 (87). С. 49–54.

  17. Руденко А.И. Два типа волн в двухслойной стратифицированной жидкости // Акт. пробл. прикл. матем., информ. и мех. 2022. С. 1450–1456.

  18. Чашечкин Ю.Д., Очиров А.А., Лапшина К.Ю. Поверхностные волны вдоль границы раздела устойчиво стратифицированных жидких сред // Физ.-хим. кин. в газ. дин. 2022. Т. 23. Вып. 6.

  19. Chashechkin Yu.D., Ochirov A.A. Periodic waves and ligaments on the surface of a viscous exponentially stratified fluid in a uniform gravity field // Axioms. 2022. V. 11. № 8. P. 402.

  20. Roach L.A. et al. Advances in modeling interactions between sea ice and ocean surface waves // J. Adv. in Modeling Earth Syst. 2019. V. 11. № 12. P. 4167–4181.

  21. Buckley M.P., Veron F. The turbulent airflow over wind generated surface waves // Eur. J. Mech.-B/Fluids. 2019. V. 73. P. 132–143.

  22. Ersoy N.E., Eslamian M. Capillary surface wave formation and mixing of miscible liquids during droplet impact onto a liquid film // Phys. Fluids. 2019. T. 31. № 1. C. 012107.

  23. Ильиных А.Ю., Чашечкин Ю.Д. Тонкая структура картины растекания свободно падающей капли в покоящейся жидкости // Изв. РАН. МЖГ. 2021. № 4. С. 3–8.

  24. Чашечкин Ю.Д. Пакеты капиллярных и акустических волн импакта капли // Вестн. МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2021. № 1 (94). С. 73–91.

  25. Чашечкин Ю.Д. Эволюция тонкой структуры распределения вещества свободно падающей капли в смешивающихся жидкостях // Изв. РАН. ФАО. 2019. Т. 55. № 3. С. 67–77.

  26. Tonks L. A theory of liquid surface rupture by a uniform electric field // Phys. Rev. 1935. T. 48. № 6. C. 562.

  27. Френкель Я.И. К теории Тонкса о разрыве поверхности жидкости постоянным электрическим полем в вакууме // ЖЭТФ. 1936. Т. 6. № 4. С. 348–350.

  28. Taylor G.I. Disintegration of water drops in an electric field // Proc. Roy. Soc. London. 1964. V. A280. P. 383–397.

  29. Григорьев А.И., Колбнева Н.Ю., Ширяева С.О. Нелинейные монопольное и дипольное акустические излучения слабо заряженной капли, осциллирующей в однородном электростатическом поле // ПММ. 2022. Т. 86. Вып. 6. С. 938–957.

  30. Журавлева Е.Н. и др. Новый класс точных решений в плоской нестационарной задаче о движении жидкости со свободной границей // ТМФ. 2020. Т. 202. № 3. С. 393–402.

  31. Белоножко Д.Ф., Григорьев А.И. Нелинейные периодические волны на заряженной поверхности глубокой маловязкой электропроводной жидкости // ЖТФ. 2004. Т. 74. № 3. С. 5–13.

  32. Chashechkin Yu.D. Foundations of engineering mathematics applied for fluid flows // Axioms. 2021. T. 10. № 4. C. 286.

  33. Найфэ А. Введение в методы возмущений М.: Мир, 1984. 535 c.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Прикладная математика и механика

Архивы выпусков Информация о журнале Отправить рукопись в журнал