1. На главную
  2. Электронные версии
  3. Прикладная математика и механика
  4. T. 87, № 3, 2023

Прикладная математика и механика, 2023, T. 87, № 3, стр. 369-378

О критических условиях теплообмена при течении жидкости с немонотонной зависимостью вязкости от температуры в кольцевом канале

В. Н. Киреев 1, *, А. А. Мухутдинова 2, **, С. Ф. Урманчеев 2, ***

1 Уфимский университет науки и технологий
Уфа, Россия

2 Институт механики им. Р.Р. Мавлютова УФИЦ РАН
Уфа, Россия

* E-mail: kireev@anrb.ru
** E-mail: muhutdinova18@gmail.com
*** E-mail: said@anrb.ru

Поступила в редакцию 07.03.2023
После доработки 08.04.2023
Принята к публикации 24.04.2023

Полный текст (PDF)

Аннотация

Работа посвящена математическому моделированию особенностей течения жидкостей с немонотонной зависимостью вязкости от температуры, которая присуща некоторым растворам и расплавам полимеров, а также ряду жидких металлических сплавов. Для заданного перепада давления обнаружены критические условия теплообмена на стенках канала, определяющие расход жидкости в процессе установления потока, связанного с формированием локализованной высоковязкой области.

Ключевые слова: аномально термовязкая жидкость, кольцевой канал, критические условия теплообмена, расход

1. Введение. Решение задач гидродинамики с учётом теплопроводности и процессов теплообмена приводит к необходимости учёта теплофизических свойств жидкостей и в первую очередь зависимости вязкости от температуры. В подавляющем большинстве исследований эти зависимости сводятся к формуле Аррениуса для константы скорости реакции от температуры или к её аппроксимациям [1, 2], которые отражают экспоненциальное убывание вязкости с ростом температуры, характерное для любых капельных жидкостей. Пристальное внимание к вопросам математического моделирования современных технологий в области энергетики, нефтехимии, металлургии, а также медико-биологических исследований требует рассмотрения влияния более сложных зависимостей вязкости от температуры на процесс течения жидкостей. Известно, например, что в жидкой сере в определённом диапазоне температур, происходят процессы полимеризации и распада полимерных цепочек, что приводит к формированию чётко выраженной немонотонной зависимости вязкости от температуры [3]. Весьма интересен и важен для металлообработки факт немонотонной зависимости вязкости в аморфных металлических сплавах, проявляющийся при быстрой закалке [4]. В качестве потокоотклоняющих реагентов при добыче жидких углеводородов применяют термообратимые жидкие реагенты, в основе своей содержащие водный раствор метилцеллюлозы [5]. В этих случаях образования пиковых значений вязкости используются для блокирования высокопроницаемых пропластков для предотвращения прорыва нагнетаемой жидкости.

Можно, также, привести один из первых немногочисленных примеров гидродинамического расчёта течения жидкости с немонотонной зависимостью вязкости от температуры – это работа [6], посвящённая растеканию серосодержащей лавы по поверхности спутника Юпитера Ио. Далее, в работах авторов настоящей статьи были проведены численные исследования по детальному изучению различных аспектов течения аномально термовязких жидкостей в плоских каналах [7–10]. При этом были установлены закономерности распределения гидродинамических параметров потока и температуры, изменения расхода при различных значениях интенсивности теплообмена, влияния теплообмена на гидравлическое сопротивление, а также влияние зависимости вязкости от температуры на изменение критического числа Рейнольдса.

В настоящей работе рассмотрены критические параметры теплообмена, влияющие на скачкообразное изменение расхода аномально термовязкой жидкости.

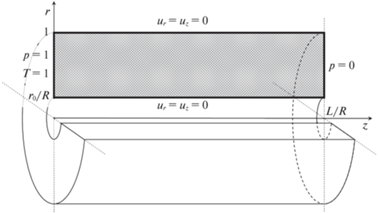
2. Постановка задачи. Рассматривается неизотермическое течение вязкой несжимаемой жидкости в кольцевом канале длины L, образованном двумя соосными цилиндрами радиусов ${{r}_{0}}$ и R, соответственно (${{r}_{0}} < R$). Течение происходит под действием постоянного перепада давления. Уравнения математической модели в цилиндрической системе координат (ось z направлена по оси канала) с учетом осевой симметрии и зависимости вязкости от температуры в безразмерном виде имеют вид:

(2.1)
$\frac{{\partial {{u}_{r}}}}{{\partial r}} + \frac{{\partial {{u}_{z}}}}{{\partial z}} + \frac{{{{u}_{r}}}}{r} = 0$
(2.2)
$\frac{{\partial {{u}_{r}}}}{{\partial t}} + {{u}_{r}}\frac{{\partial {{u}_{r}}}}{{\partial r}} + {{u}_{z}}\frac{{\partial {{u}_{r}}}}{{\partial z}} = - \frac{{\partial p}}{{\partial r}} + \frac{1}{{\operatorname{Re} }}\left[ {\frac{\partial }{{\partial r}}\left( {\mu \frac{{\partial {{u}_{r}}}}{{\partial r}}} \right) + \frac{\partial }{{\partial z}}\left( {\mu \frac{{\partial {{u}_{r}}}}{{\partial z}}} \right) + \frac{\mu }{r}\frac{{\partial {{u}_{r}}}}{{\partial r}} - \frac{\mu }{{{{r}^{2}}}}{{u}_{r}}} \right]$
(2.3)
$\frac{{\partial {{u}_{z}}}}{{\partial t}} + {{u}_{r}}\frac{{\partial {{u}_{z}}}}{{\partial r}} + {{u}_{z}}\frac{{\partial {{u}_{z}}}}{{\partial z}} = - \frac{{\partial p}}{{\partial z}} + \frac{1}{{\operatorname{Re} }}\left[ {\frac{\partial }{{\partial r}}\left( {\mu \frac{{\partial {{u}_{z}}}}{{\partial r}}} \right) + \frac{\partial }{{\partial z}}\left( {\mu \frac{{\partial {{u}_{z}}}}{{\partial z}}} \right) + \frac{\mu }{r}\frac{{\partial {{u}_{z}}}}{{\partial r}}} \right]$
(2.4)
$\frac{{\partial T}}{{\partial t}} + {{u}_{r}}\frac{{\partial T}}{{\partial r}} + {{u}_{z}}\frac{{\partial T}}{{\partial z}} = \frac{1}{{{\text{Pe}}}}\left( {\frac{{{{\partial }^{2}}T}}{{\partial {{r}^{2}}}} + \frac{{{{\partial }^{2}}T}}{{\partial {{z}^{2}}}} + \frac{1}{r}\frac{{\partial T}}{{\partial r}}} \right),$
где ${{u}_{r}}$ и ${{u}_{z}}$ – радиальная и осевая компоненты скорости, p – давление, T – температура.

Безразмерные критерии Рейнольдса Re и Пекле Pe вычисляются по формулам:

$\operatorname{Re} = \frac{{\rho {{u}_{0}}R}}{{{{\mu }_{{\max }}}}},\quad {\text{Pe}} = \frac{{{{u}_{0}}R}}{a},$
где $\rho $ – плотность, ${{u}_{0}} = \sqrt {\Delta p{\text{/}}\rho } $ – характерная скорость, ${{\mu }_{{\max }}}$ – максимальная вязкость жидкости на рассматриваемом температурном интервале, a – коэффициент температуропроводности.

В качестве характерного размера выбран радиус R внешнего цилиндра кольцевого канала, поэтому решение систем уравнений (2.1)–(2.4) ищется внутри прямоугольной области (рис. 1)

(2.5)
$\Omega = \left\{ {\left( {r,z} \right):\;{{{{r}_{0}}} \mathord{\left/ {\vphantom {{{{r}_{0}}} R}} \right. \kern-0em} R} \leqslant r \leqslant 1,\;0 \leqslant z \leqslant {L \mathord{\left/ {\vphantom {L R}} \right. \kern-0em} R}} \right\}$
Рис. 1.

Схема расчетной области и граничные условия.

Во входном (z = 0) и выходном (z = L/R) сечениях кольцевого канала задаются фиксированные значения давления, а на стенках ($r = {{r}_{0}}{\text{/}}R$, $r = 1$) – условия прилипания для скорости, так что граничные условия для давления и компонент вектора скорости имеют вид:

(2.6)
$p(r,0,t) = 1,\quad p(r,{L \mathord{\left/ {\vphantom {L R}} \right. \kern-0em} R},t) = 0$
(2.7)
${{u}_{r}}\left( {{{{{r}_{0}}} \mathord{\left/ {\vphantom {{{{r}_{0}}} R}} \right. \kern-0em} R},z,t} \right) = {{u}_{r}}(1,z,t) = {{u}_{z}}({{{{r}_{0}}} \mathord{\left/ {\vphantom {{{{r}_{0}}} R}} \right. \kern-0em} R},z,t) = {{u}_{z}}(1,z,t) = 0$

Предполагается, что в канал втекает горячая жидкость, которая затем охлаждается за счет конвективного теплообмена на стенках канала. Температура на входе в канал задается постоянной,

(2.8)
$T(r,0,t) = 1,$
а на стенках канала рассматриваются различные виды граничных условий – первого, второго и третьего рода (Ньютона–Рихмана):
(2.9)
$\begin{gathered} T({{{{r}_{0}}} \mathord{\left/ {\vphantom {{{{r}_{0}}} R}} \right. \kern-0em} R},z,t) = T(1,z,t) = 0\quad {\text{или}}\quad {{\left. {\frac{{\partial T}}{{\partial r}}} \right|}_{{r = {{{{r}_{0}}} \mathord{\left/ {\vphantom {{{{r}_{0}}} R}} \right. \kern-0em} R}}}} = {{\left. {\frac{{\partial T}}{{\partial r}}} \right|}_{{r = 1}}} = 0 \\ {\text{или}}\quad {{\left. {\frac{{\partial T}}{{\partial r}}} \right|}_{{r = {{{{r}_{0}}} \mathord{\left/ {\vphantom {{{{r}_{0}}} R}} \right. \kern-0em} R}}}} = {{\left. {\frac{{\partial T}}{{\partial r}}} \right|}_{{r = 1}}} = \alpha T, \\ \end{gathered} $
где $\alpha $ – безразмерный коэффициент теплоотдачи (критерий Нуссельта).

В начальный момент времени жидкость в канале покоится и имеет постоянную температуру:

(2.10)
${{u}_{r}}(r,z,0) = {{u}_{z}}(r,z,0) = 0,\quad p(r,z,0) = 0,\quad T(r,z,0) = 0$

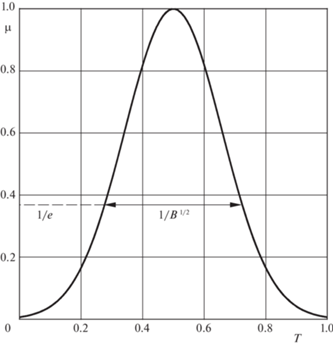
Для замыкания математической модели необходимо задать функцию зависимости вязкости от температуры, которая в настоящей работе принимается в виде следующей немонотонной зависимости (рис. 2):

(2.11)
$\mu (T) = \exp \left( { - \beta {{{(T - {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2})}}^{2}}} \right),$
где $\beta > 0$ – параметр, характеризующий ширину температурного диапазона, на котором происходит увеличение вязкости.

Рис. 2.

Немонотонная зависимость вязкости от температуры.

Таким образом, система дифференциальных уравнений в частных производных (2.1)–(2.4), граничные условия (2.6)–(2.9), начальные условия (2.10) и функция зависимости вязкости от температуры (2.11) представляют собой математическую модель рассматриваемого процесса.

3. Результаты численного моделирования. Поставленная задача решается путем прямого численного моделирования с использованием оригинального компьютерного кода, основанного на методе контрольного объема и алгоритме SIMPLE [11]. Валидация компьютерного кода была проведена путем сравнения результатов численного моделирования с известными аналитическими решениями для задачи о течении жидкости с постоянной вязкостью в кольцевом канале.

При проведении численных экспериментов были зафиксированы безразмерные критерии Рейнольдса (Re = 104) и Пекле (Pe = 940), а также вид функциональной зависимости вязкости от температуры ($\beta = 20$). Отношение длины кольцевого канала к радиусу внешнего цилиндра принято равным L/R = 60. В качестве изменяемых параметров задачи использовались безразмерный геометрический параметр кольцевого канала $\delta = {{\left( {R - {{r}_{0}}} \right)} \mathord{\left/ {\vphantom {{\left( {R - {{r}_{0}}} \right)} {{{r}_{0}}}}} \right. \kern-0em} {{{r}_{0}}}}$ (т.е. отношение величины кольцевого зазора к радиусу внутреннего канала) и безразмерный коэффициент теплоотдачи $\alpha $.

Основной целью численного моделирования в данной работе является определение расхода (мгновенного и установившегося) термовязкой жидкости, вычисляемого по формуле:

(3.1)
$Q(t) = \int\limits_{{{{{r}_{0}}} \mathord{\left/ {\vphantom {{{{r}_{0}}} R}} \right. \kern-0em} R}}^1 {{{u}_{z}}(r,{L \mathord{\left/ {\vphantom {L {R,t)dr}}} \right. \kern-0em} {R,t)dr}}} $

Гидродинамические характеристики течения жидкости с немонотонной зависимостью вязкости от температуры определяются динамикой образующегося в канале сложного неоднородного распределения вязкости. Характерные распределения вязкости в кольцевом канале при различных видах граничных условий для температуры для кольцевого канала с параметром $\delta = 1$ показаны на рис. 3. Для удобства представления результатов введены новые переменные $r{\kern 1pt} '$ и $z{\kern 1pt} '$, принимающие значения от 0 до 1 и связанные с исходными пространственными переменными соотношениями:

(3.2)
$r{\kern 1pt} ' = \frac{{Rr - {{r}_{0}}}}{{R - {{r}_{0}}}},\quad z{\kern 1pt} ' = \frac{{Rz}}{L}$
Рис. 3.

Характерные распределения вязкости в кольцевом канале при граничных условиях для температуры первого (а), второго (б) и третьего (в) рода.

На каждом из графиков на рис. 3 можно выделить залитую более темным цветом область, в которой вязкость жидкости имеет наибольшее значение, получившая в предыдущих работах авторов название “вязкий барьер”.

Формирование вязкого барьера и его эволюция происходят следующим образом. После начала процесса втекания нагретой жидкости в кольцевой канал, заполненный жидкостью с температурой окружающей среды, в зоне контакта благодаря кондуктивной теплопроводности и, в соответствии с принятой зависимостью вязкости от температуры, формируется высоковязкая локализованная область – вязкий барьер. Однако увеличение вязкого барьера приводит к росту вязкого трения в жидкости, вследствие чего средняя скорость потока снижается, соответственно, снижается и расход жидкости. Дальнейшая эволюция вязкого барьера связана с конкуренцией следующих факторов: теплообменом через стенки канала, кондуктивной теплопроводностью и скоростью конвективного переноса жидкости.

В случае, когда температура стенок канала поддерживается при постоянной температуре (граничные условия первого рода), вязкий барьер имеет подковообразную форму и все изолинии вязкости начинаются вблизи угловых точек входного сечения канала, в которых температура и вязкость изменяются скачкообразно (рис. 3,а). При задании на стенках канала нулевого потока тепла (граничные условия второго рода) вязкий барьер выглядит практически как вертикальная полоса, пересекающая все поперечное сечение канала, а изолинии вязкости пересекают стенки канала под прямым углом (рис. 3,б). Если на стенках канала задается теплообмен по закону Ньютона–Рихмана (граничное условие третьего рода) форма и расположение вязкого барьера зависят от значения коэффициента теплоотдачи и изолинии вязкости в этом случае пересекают стенки канала под некоторым углом (рис. 3,в). Следует отметить, что на рис. 3,а и рис. 3,в показаны установившиеся распределения вязкости, тогда как на рис. 3,б показано положение вязкого барьера в некоторый момент времени, поскольку в канале с теплоизолированными стенками стабилизации вязкого барьера не происходит.

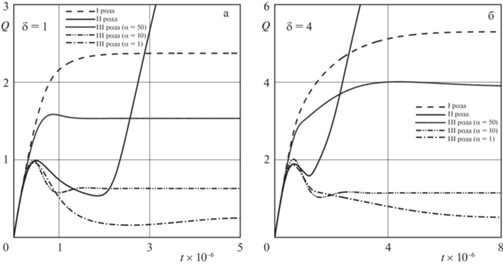
С эволюцией вязкого барьера тесно связана динамика установления расхода аномально-термовязкой жидкости, представленная на рис. 4 для двух значений геометрического параметра ($\delta = 1$ и $\delta = 4$) при различных видах температурных граничных условий и интенсивностях теплообмена. Из рисунка видно, что перед выходом расхода на стационарное значение происходит достаточно сложное его изменение. Так, например, кривые изменения расхода, соответствующие граничным условиям второго и третьего рода, характеризуются наличием локального максимума и минимума.

Рис. 4.

Динамика установления расхода аномально-термовязкой жидкости: (а) δ = 1, (б) δ = 4.

Наиболее простой вид имеют кривые установления расхода при задании на стенках канала граничного условия первого рода (пунктирные кривые на рис. 4). В этом случае вязкий барьер подковообразной формы образуется вблизи входа в канал и затем, по мере протекания процесса конвективного теплообмена, вязкий барьер движется поступательно вдоль канала, область высокой вязкости увеличивается в размере и через некоторое время вязкий барьер занимает установившееся положение (см. также рис. 3,а). Расход при этом монотонно увеличивается и устанавливается на некотором постоянном уровне.

При задании нулевого теплового потока на стенках канала (граничное условие второго рода, сплошные кривые на рис. 4) происходит “поршневое” вытеснение холодной жидкости, заполняющей канал в начальный момент времени, горячей жидкостью, поступающей в канал через входное сечение. Вязкий барьер, характерный вид которого показан на рис. 3,б, формируется на границе областей холодной и горячей жидкости и движется поступательно вместе с потоком вдоль канала. На начальном этапе расход возрастает по мере удаления вязкого барьера от входа в канал. Размер высоковязкой области при этом увеличивается за счет кондуктивной теплопроводности, создается дополнительное гидравлическое сопротивление в результате чего расход, достигнув локального максимума, начинает уменьшаться. Резкое увеличение расхода начинается в момент, когда вязкий барьер достигает выходное сечение канала и устанавливается на высоком уровне после того, как вязкий барьер полностью покидает канал. Таким образом, в стационарном режиме реализуется фактически изотермическое течение маловязкой жидкости, а найденные в результате численного моделирование значения расхода (Q = 9.56 для $\delta = 1$ и Q = 29.42 для $\delta = 4$) совпадают с вычисленными по известным формулам для кольцевого канала.

При использовании граничных условий третьего рода динамика изменения расхода в основном аналогична описанной выше для случая граничных условий второго рода (три кривые с точками на рис. 4). Кривые расхода также имеют локальные максимум и минимум, объясняемые динамикой вязкого барьера, причем их значения зависят от значения коэффициента теплообмена. Отличие заключается в том, что при наличии конечного теплообмена на стенках канала вязкий барьер стабилизируется внутри канала и поэтому установившееся значение расхода гораздо меньше, чем при отсутствии теплообмена: чем меньше безразмерный коэффициент теплоотдачи, тем меньше стационарное значение расхода.

Сравнение результатов для кольцевых каналов, характеризующихся различным геометрическим параметром $\delta $ ($\delta = 1$ на рис. 4,а и $\delta = 4$ на рис. 4,б), показывает качественное совпадение кривых установления расхода. Количественные различия заключаются в том, что для канала с $\delta = 4$ (более “широкий” кольцевой зазор) установившиеся значения расхода примерно в два раза больше соответствующих расходов для канала с $\delta = 1$ и требуется более длительный период времени для достижения стационарного состояния.

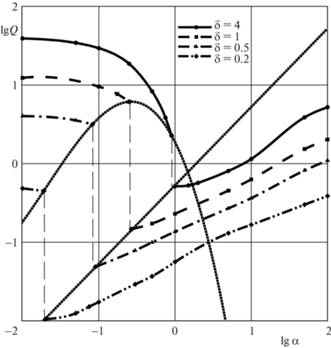
На рис. 5 показаны зависимости установившегося расхода при течении аномально-термовязкой жидкости от коэффициента теплоотдачи при различных значениях геометрического параметра кольцевого канала. Точки соответствуют результатам численных экспериментов, а кривые – интерполяции сплайнами. Видно, что при некотором значении коэффициента теплоотдачи ${{\alpha }_{{\operatorname{cr} }}}$ на каждой из представленных кривых наблюдается скачкообразное уменьшение расхода, которое соответствует явлению стабилизации вязкого барьера внутри канала. При значениях коэффициента теплоотдачи $\alpha < {{\alpha }_{{\operatorname{cr} }}}$ кондуктивный теплообмен со стенок канала гораздо меньше конвективного теплообмена вдоль канала. Поступающая в канал нагретая жидкость практически не охлаждается и незначительное повышение вязкости наблюдается в тонком слое вблизи стенок канала. Толщина этого слоя увеличивается с ростом коэффициента теплоотдачи, что приводит к постепенному уменьшению расхода, наиболее значительному для “широкого” кольцевого зазора с $\delta = 4$.

Рис. 5.

Зависимость установившегося расхода при течении аномально-термовязкой жидкости от коэффициента теплоотдачи при различных значениях геометрического параметра кольцевого канала.

При $\alpha = {{\alpha }_{{\operatorname{cr} }}}$ кондуктивный теплообмен со стенок канала становится сравнимым по величине с конвективным теплообменом вдоль канала, жидкость успевает достаточно охладиться и вблизи выхода из канала формируется вязкий барьер (характерный вид вязкого барьера аналогичен изображенному на рис. 3,б). Расход при этом принимает минимальное значение. При дальнейшем увеличении коэффициента теплоотдачи происходит монотонное увеличение расхода, так как геометрические размеры вязкого барьера уменьшаются, и он постепенно принимает подковообразную форму (см. рис. 3,а). Следует заметить, что при всех значениях геометрического параметра $\delta $ на кривой изменения расхода можно выделить практически линейный участок увеличения расхода, который сменяется нелинейным. Это происходит в тот момент, когда центральная часть подковообразного вязкого барьера выходит за пределы канала и вместо одной высоковязкой области образуются две, расположенные параллельно стенкам канала.

При задании достаточно интенсивного теплообмена на стенках канала ($\alpha \to \infty $) все кривые изменения расхода выходят на стационарное значение, которое несколько меньше, чем расход при малом теплообмене ($\alpha \to 0$), вследствие наличия в первом случае пристеночных слоев с высокой вязкостью.

Из рис. 5 можно также обнаружить следующие закономерности изменения расхода для различных значений геометрического параметра $\delta $ при стремлении коэффициента теплообмена к критическому значению слева и справа: точки на кривых изменения расхода слева от ${{\alpha }_{{{\text{cr}}}}}$ хорошо аппроксимируются полиномом третьей степени, тогда как справа от ${{\alpha }_{{{\text{cr}}}}}$ соответствующие точки лежат практически на одной прямой , т.е.

(3.3)
$\begin{gathered} \lg Q_{{{\text{cr}}}}^{ - } \approx {{с}_{3}}{{\left( {\lg \alpha } \right)}^{3}} + {{с}_{2}}{{\left( {\lg \alpha } \right)}^{2}} + {{с}_{1}}\lg \alpha + {{с}_{0}},\quad {\text{при}}\quad \alpha \to {{\alpha }_{{{\text{cr}}}}} - 0 \\ \lg Q_{{{\text{cr}}}}^{ + } \approx {{a}_{1}}\lg \alpha + {{a}_{2}},\quad {\text{при}}\quad \alpha \to {{\alpha }_{{{\text{cr}}}}} + 0 \\ \end{gathered} $

Справедливость зависимостей (3.3) подтверждается также результатами численного моделирования для других значений геометрического параметра $\delta $, не показанных на рис. 5, чтобы не загромождать рисунок. Полученные полином третьей степени и прямая пересекаются, что дает возможность сделать вывод о том, что для кольцевых каналов с достаточно широким зазором ($\delta > 4$) скачок расхода наблюдаться не будет. Этот теоретически установленный факт также нашел свое подтверждение в вычислительных экспериментах.

Наиболее ясное представление о закономерностях скачкообразного изменения расхода дает рис. 6, на котором показаны зависимости критического коэффициента теплоотдачи и относительного изменения расхода от геометрического параметра кольцевого канала.

Рис. 6.

Зависимость критического коэффициента теплоотдачи (а) и относительного изменения расхода (б) от геометрического параметра кольцевого канала.

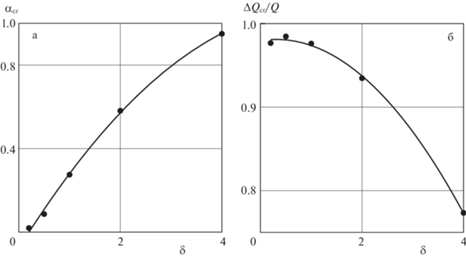
Рис. 6,а свидетельствует о том, что существует квадратичная зависимость между критическим коэффициентом теплообмена и геометрическим параметром кольцевого канала. Квадратичной зависимостью описывается также связь между относительным изменением расхода в точке разрыва, вычисляемым по формуле $\frac{{Q_{{\operatorname{cr} }}^{ - } - Q_{{\operatorname{cr} }}^{ + }}}{{Q_{{\operatorname{cr} }}^{ - }}}$, и геометрическим параметром $\delta $ (рис. 6,б). Интерполируя полученную зависимость, можно сделать вывод, что скачок расхода исчезнет (относительное изменение расхода станет равным нулю) при $\delta \approx 8.3$. Таким образом, для кольцевого канала заданной геометрии можно определить как критический коэффициент теплообмена, так и соответствующую величину относительного изменения расхода.

Заключение. Выполненный цикл расчётов по математической модели течения аномально термовязкой жидкости в кольцевом канале позволяет сделать следующие выводы. Во-первых, обнаружено не только влияние условий теплообмена на закономерности течения жидкости и установление итогового расхода жидкости, аналогично случаю плоского канала, но и влияние отношения зазора кольцевого канала к радиусу внутреннего цилиндра, т.е. геометрического параметра. Во-вторых, при увеличении интенсивности теплообмена в области его малых значений, расход плавно снижается до некоторых критических значений коэффициента теплоотдачи, когда происходит резкий скачок в сторону уменьшения расхода. При дальнейшем увеличении интенсивности теплообмена расход также увеличивается при всех значениях геометрического параметра.

Следует отметить, что логарифм предельных значений расхода слева от точки критической величины теплоотдачи для всей совокупности значений геометрического параметра можно аппроксимировать некоторой кубической параболой в зависимости от логарифма коэффициента теплоотдачи. А справа от критической точки – линейной зависимостью этих параметров. Точка пересечения этих линий свидетельствует об отсутствии скачка расхода и, соответственно, критической величины теплообмена для каналов с достаточно большим значением геометрического параметра, в том числе и для полого цилиндра.

Работа выполнена при поддержке Российского научного фонда (грант № 22-21-00915).

Список литературы

  1. Френкель Я.И. Кинетическая теория жидкостей. Л.: Наука, 1975. 592 с.

  2. Виноградов Г.В., Малкин А.Я. Реология полимеров. М.: Химия, 1977. 438 с.

  3. Bacon R.F., Fanelli R. The viscosity of sulfur // J. Am. Chem. Soc. 1943. V. 65. P. 639–648.

  4. Tabachnikova E.D., Bengus V.Z., Egorov D.V., Tsepelev V.S., Ocelik V. Mechanical properties of amorphous alloys ribbons prepared by rapid quenching of the melt after different thermal treatments before quenching // Mater. Sci. Eng. A, 1997. V. 226–228. P. 887–890.

  5. Алтунина Л.К., Кувшинов В.А., Кувшинов И.В., Стасьева Л.А., Чертенков М.В., Андреев Д.В., Карманов А.Ю. Увеличение нефтеотдачи пермо-карбоновой залежи высоковязкой нефти Усинского месторождения физико-химическими и комплексными технологиями (обзор) // СФУ ж. Химия. 2018. Т. 11. № 3. С. 462–476.

  6. Fink J.H., Park S.O., Greeley R. Cooling and deformation of cooling sulfur flow // Icarus. 1983. V. 56. № 1. P. 38–50.

  7. Урманчеев С.Ф., Киреев В.Н. Установившееся течение жидкости с температурной аномалией вязкости // Докл. РАН. 2004. Т. 396. № 2. С. 204–207.

  8. Urmancheev S., Kireev V.  The transient flow of liquid with non-monotonous temperature dependent viscosity in a plane channel // AIP Conf. Proc. 2017. V. 1906. № 1. P. 200009.

  9. Kireev V.N., Nizamova A.D., Urmancheev S.F. The hydraulic resistance of thermoviscous liquid flow in a plane channel with a variable cross-section // J. Phys. Conf. Ser. 2019. V. 1158. № 3. P. 032014.

  10. Киреев В.Н., Низамова А.Д., Урманчеев С.Ф. Некоторые особенности гидродинамической неустойчивости термовязкой жидкости в плоском канале // ПММ. 2019. № 3. С. 454–459.

  11. Патанкар С. Численные методы решения задач теплообмена и динамики жидкости. М.: Энергоатомиздат, 1984. 152 с.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Прикладная математика и механика

Архивы выпусков Информация о журнале Отправить рукопись в журнал