1. На главную
  2. Электронные версии
  3. Прикладная математика и механика
  4. T. 87, № 3, 2023

Прикладная математика и механика, 2023, T. 87, № 3, стр. 442-453

Прямые и обратные задачи динамики поверхностного волнения, вызванного обтеканием подводного препятствия

Д. Ю. Князьков 1, *, В. Г. Байдулов 1, **, А. С. Савин 2, ***, А. С. Шамаев 1, ****

1 Институт проблем механики им. А.Ю. Ишлинского РАН
Москва, Россия

2 Московский государственный технический университет им. Н.Э. Баумана
Москва, Россия

* E-mail: dmitri.knyazkov@gmail.com
** E-mail: bayd@ipmnet.ru
*** E-mail: assavin@list.ru
**** E-mail: sham@rambler.ru

Поступила в редакцию 01.03.2023
После доработки 15.04.2023
Принята к публикации 24.04.2023

Полный текст (PDF)

Аннотация

В работе представлены алгоритмы и результаты расчетов динамики поверхностного слоя жидкости под действием вышедших из глубины течений. Исследуются несколько подходов к моделированию поля скоростей при обтекании горизонтальным потоком неподвижного подводного препятствия. Предложены формулы для расчета поля скоростей на свободной поверхности идеальной однородной жидкости. Разработана компьютерная программа, позволяющая моделировать взаимодействие потока стратифицированной жидкости с подводным препятствием. Исследована возможность применения асимптотических формул приближения дальней зоны для расчета поля скоростей в равномерно стратифицированной жидкости.

Ключевые слова: стратифицированная жидкость, идеальная жидкость, обтекание, поле скоростей, поверхностные волны

1. Введение. Важным элементом в решении задачи томографии океана [1, 2] является разработка и реализация численных методов моделирования обтекания подводного препятствия. В настоящей работе представлены результаты численного моделирования распространения возмущений в жидкости, возникающих при взаимодействии течения с подводным препятствием, например, элементом рельефа дна или трубопроводом. Возмущения распространяются в толще жидкости вплоть до поверхности океана, где взаимодействуют с ветровой рябью, причем картина этого взаимодействия может быть зафиксирована средствами радиозондирования [3, 4]. Возможны два подхода к решению обратной задачи идентификации параметров течения и препятствия [5]. В первом – эта задача решается на основе данных, полученных средствами активной или пассивной радиометрии океана [6–8]. Во втором – величина и направление скорости течения, размер препятствия определяются на основе анализа показания датчиков, расположенных в толще океана [5, 9].

2. Обтекание подводного препятствия. Рассмотрим задачу моделирования обтекания подводного препятствия потоком идеальной жидкости. Необходимо определить поле скоростей в горизонтальной плоскости, находящейся над препятствием либо на свободной поверхности, находящейся на том же расстоянии от препятствия по вертикали. Подводное препятствие моделируется точечным источником, расположенным в начале координат – точке (0, 0, 0) (рис. 1). Скорость потока на бесконечности равна по величине V и направлена в положительном направлении оси Ox,

${\mathbf{V}} = \left( {V,0,0} \right)$
Рис. 1.

Геометрия задачи.

Горизонтальная плоскость, в которой рассчитывается поле скоростей находится на расстоянии h от источника по вертикали. В работе сравниваются результаты расчетов по четырем моделям: аналитические выражения для поля скоростей в толще или на поверхности идеальной однородной жидкости, приближение дальнего поля и численный расчет поля скоростей в толще идеальной стратифицированной жидкости. Последний подход, в отличие от известных решений (напр., [10]) позволяет моделировать обтекание подводного препятствия течением, имеющим непостоянную скорость и произвольно заданную (вообще говоря, переменную как в вертикальном, так и в горизонтальном направлении) стратификацию. В случае, когда жидкость равномерно стратифицирована, а скорость течения постоянна, для моделирования обтекания подводного препятствия можно применить асимптотические подходы [11–14]. В настоящей работе исследуется возможность использования асимптотики, предложенной в [11].

2.1. Поверхностное волнение при обтекании препятствия потоком однородной жидкости. В первых двух из рассмотренных моделей считается, что жидкость является однородной. При этом в первом случае жидкость считается неограниченной по вертикали, и поле скоростей рассчитывается в толще такой жидкости. Во втором случае жидкость имеет неограниченную глубину, а поле скоростей рассчитывается на свободной поверхности.

Поле скоростей в толще жидкости (в неограниченной области). Запишем сумму потенциалов горизонтального невозмущенного течения идеальной однородной жидкости, имеющего скорость $V$, и точечного источника мощности $Q$ в сферической системе координат $\left( {r,{{\theta }},{{\varepsilon }}} \right)$ [15]:

$\varphi = {{\varphi }_{V}} + {{\varphi }_{Q}} = Vr\cos \left( \theta \right) - \frac{Q}{{4\pi r}}$

Компоненты скорости жидкости могут быть найдены как

${{{v}}_{r}} = \frac{{\partial \varphi }}{{\partial r}},\quad {{{v}}_{\theta }} = \frac{1}{r}\frac{{\partial \varphi }}{{\partial \theta }}$

Отсюда

${{{v}}_{r}} = V\cos ~\theta + \frac{Q}{{4\pi {{r}^{2}}}},\quad {{{v}}_{\theta }} = - V\sin ~\theta $
и компоненты скорости ${{{v}}_{x}}$, ${{{v}}_{y}}$ и ${{{v}}_{z}}$ в декартовой системе координат записываются как
${{{v}}_{x}} = V + \frac{Q}{{4\pi {{r}^{2}}}}\cos ~\theta ,\quad {{{v}}_{y}} = \frac{Q}{{4\pi {{r}^{2}}}}\sin ~\theta ~\cos ~\varepsilon ,\quad {{{v}}_{z}} = \frac{Q}{{4\pi {{r}^{2}}}}\sin ~\theta ~\sin ~\varepsilon ,$
где

$r = \sqrt {{{x}^{2}} + {{y}^{2}} + {{z}^{2}}} ,\quad \theta = \arccos \left( {\frac{x}{r}} \right),\quad \varepsilon = \arccos \left( {\frac{y}{{\sqrt {{{y}^{2}} + {{z}^{2}}} }}} \right)$

Таким образом, в декартовой системе координат в плоскости $z = h$, то есть на расстоянии $h$ от источника по вертикали, имеем:

(2.1)
${{{v}}_{x}} = V + \frac{{Qx}}{{4\pi {{r}^{3}}}},\quad {{{v}}_{y}} = \frac{{Qy}}{{4\pi {{r}^{3}}}},\quad {{{v}}_{z}} = \frac{{Qz}}{{4\pi {{r}^{3}}}},$
где $r = \sqrt {{{x}^{2}} + {{y}^{2}} + {{h}^{2}}} $.

Поле скоростей на свободной поверхности. Пусть поток однородной идеальной жидкости движется со скоростью $V$ вдоль оси Ox, а на глубине $h$ в начале координат находится препятствие, моделируемое точечным источником интенсивности $Q$. Потенциал скорости потока может быть записан следующим образом [16, 17]:

(2.2)
$\Phi \left( {x,y,z} \right) = - Vx + \frac{Q}{{4\pi }}\left( {\frac{1}{{\sqrt {{{x}^{2}} + {{y}^{2}} + {{z}^{2}}} }} - \frac{1}{{\sqrt {{{x}^{2}} + {{y}^{2}} + {{{(z - 2h)}}^{2}}} }} + \varphi \left( {x,y,z} \right)} \right),$
где

$\varphi \left( {x,y,z} \right) = - \frac{{gQ}}{{{{\pi }^{2}}{{V}^{2}}}}\operatorname{Im} \int\limits_0^\infty {\int\limits_0^\infty {\frac{{\cos \left( {\lambda y} \right){{e}^{{i\sigma \left( {z - 2h} \right) + x\sqrt {{{\lambda }^{2}} + {{\sigma }^{2}}} }}}\sigma }}{{\left( {{{\sigma }^{2}} + i\nu \sigma + {{\lambda }^{2}}} \right)\sqrt {{{\lambda }^{2}} + {{\sigma }^{2}}} }}d\sigma d\lambda } } ;\quad x < 0$
$\varphi \left( {x,y,z} \right) = \frac{{gQ}}{{{{\pi }^{2}}{{V}^{2}}}}\operatorname{Im} \int\limits_0^\infty {\int\limits_0^\infty {\frac{{\cos \left( {\lambda y} \right){{e}^{{ - i\sigma \left( {z - 2h} \right) - x\sqrt {{{\lambda }^{2}} + {{\sigma }^{2}}} }}}\sigma }}{{\left( {{{\sigma }^{2}} - i\nu \sigma + {{\lambda }^{2}}} \right)\sqrt {{{\lambda }^{2}} + {{\sigma }^{2}}} }}d\sigma d\lambda } } + $
$ + \;\frac{Q}{\pi }\int\limits_\nu ^\infty {\frac{{\gamma \left( {z - 2h} \right)}}{{\sqrt {\gamma {{\nu }^{{ - 1}}} - 1} }}\sin \left( {x\sqrt {\gamma \nu } } \right)\cos \left( {y\sqrt {{{\gamma }^{2}} - \gamma \nu } } \right)d\gamma } ;\quad x > 0$

Здесь используется обозначение ${{\nu }} = g{\text{/}}{{V}^{2}}$. Горизонтальные компоненты скорости жидкости могут быть найдены как

${{{v}}_{x}} = - \frac{{\partial \Phi }}{{\partial x}},\quad {{{v}}_{y}} = - \frac{{\partial \Phi }}{{\partial y}}$

Тогда поле скоростей $\left( {{{{v}}_{x}}\left( {x,y,h} \right),{{{v}}_{y}}\left( {x,y,h} \right)} \right)$ на свободной поверхности жидкости можно рассчитать по формулам

(2.3)
${{{v}}_{x}}\left( {x,y} \right) = \left\{ \begin{gathered} V - \alpha I\left( {x,y} \right),\quad x < 0 \hfill \\ V + \alpha I\left( {x,y} \right) - \beta J\left( {x,y} \right),\quad x > 0 \hfill \\ \end{gathered} \right.$
(2.4)
${{{v}}_{y}}\left( {x,y} \right) = \left\{ \begin{gathered} \alpha K\left( {x,y} \right),x < 0 \hfill \\ \alpha K\left( {x,y} \right) + \frac{Q}{\pi }M\left( {x,y} \right),x > 0, \hfill \\ \end{gathered} \right.$
где

(2.5)
$I\left( {x,y} \right) = \int\limits_0^\infty {\int\limits_0^\infty {\frac{{\cos \left( {\lambda y} \right){{e}^{{ - \left| x \right|\sqrt {{{\sigma }^{2}} + {{\lambda }^{2}}} }}}\left( {\nu \sigma \cos \left( {\sigma h} \right) + \left( {{{\sigma }^{2}} + {{\lambda }^{2}}} \right)\sin \left( {\sigma h} \right)} \right)\sigma }}{{{{{({{\sigma }^{2}} + {{\lambda }^{2}})}}^{2}} + \nu \sigma }}d\sigma d\lambda } } $
(2.6)
$J\left( {x,y} \right) = \int\limits_\nu ^\infty {\sqrt {\frac{\gamma }{{\gamma - \nu }}} {{e}^{{ - h\gamma }}}\cos \left( {x\sqrt {\nu \gamma } } \right)\cos \left( {y\sqrt {\gamma \left( {\gamma - \nu } \right)} } \right)d\gamma } $
(2.7)
$K\left( {x,y} \right) = \int\limits_0^\infty {\int\limits_0^\infty {\frac{{\sin \left( {\lambda y} \right){{e}^{{ - \left| x \right|\sqrt {{{\sigma }^{2}} + {{\lambda }^{2}}} }}}\left( {\nu \sigma \cos \left( {\sigma h} \right) + \left( {{{\sigma }^{2}} + {{\lambda }^{2}}} \right)\sin \left( {\sigma h} \right)} \right)\sigma \lambda }}{{\left( {{{{({{\sigma }^{2}} + {{\lambda }^{2}})}}^{2}} + (\nu {{\sigma }^{2}})} \right)\sqrt {{{\sigma }^{2}} + {{\lambda }^{2}}} }}d\sigma d\lambda } } $
(2.8)
$\begin{gathered} M\left( {x,y} \right) = \int\limits_\nu ^\infty {\sqrt {\nu \gamma } {{e}^{{ - \gamma h}}}\sin \left( {x\sqrt {\nu \gamma } } \right)\sin \left( {y\sqrt {\gamma \left( {\gamma - \nu } \right)} } \right)d\gamma } \\ \alpha = \frac{{gQ}}{{{{\pi }^{2}}{{V}^{2}}}},\quad \beta = \frac{{gQ}}{{\pi {{V}^{2}}}},\quad \nu = \frac{g}{{{{V}^{2}}}} \\ \end{gathered} $

2.2. Моделирование поля присоединенных внутренних волн. Рассмотрим задачу моделирования пространственного распространения внутренних гравитационных волн, порожденных обтеканием точечного массового источника потоком идеальной стратифицированной жидкости. Поскольку изменения плотности жидкости по отношению к базовой стратификации малы, уравнения движения записываются в приближении Буссинеска. Искомое поле скоростей в некоторой области вблизи подводного препятствия может быть найдено в результате решения уравнения [11, 18]

(2.9)
$\Delta \frac{{{{\partial }^{2}}\psi }}{{\partial {{t}^{2}}}} + N{{(z)}^{2}}{{\Delta }_{{xy}}}\psi = f\left( {{\mathbf{x}} - {{{\mathbf{x}}}_{0}} + {\mathbf{V}}t} \right);\quad {\mathbf{x}} \in {{\Omega }}$
в области $\Omega = [{{x}_{{\min }}},{{x}_{{\max }}}] \times [{{y}_{{\min }}},{{y}_{{\max }}}] \times [ - H,H]$ с граничным условием
(2.10)
${{\psi }} = 0;\quad {\mathbf{x}} \in \partial {{\Omega }},$
где ${{\psi }}\left( {{\mathbf{x}},t} \right)$ – внутренний потенциал, ${\mathbf{V}} = \left( {a,b,c} \right)$ – скорость течения на бесконечности, $N$ – частота плавучести, ${{{{\Delta }}}_{{xy}}} = \partial _{x}^{2} + \partial _{y}^{2}$. В начальный момент времени

(2.11)
${{\left. \psi \right|}_{{t = 0}}} = 0$

Скорость жидкости ${\mathbf{v}} = \left( {{{{v}}_{x}},{{{v}}_{y}},{{{v}}_{z}}} \right)$ может быть найдена как

(2.12)
${\mathbf{v}} = \left( {\frac{{{{\partial }^{2}}}}{{\partial {{t}^{2}}}}\nabla + {{N}^{2}}{{\nabla }_{{xy}}}} \right)\psi ,$
где ${{\nabla }_{{xy}}} = \left( {{{\partial }_{x}},{{\partial }_{y}},0} \right)$. В случае равномерно стратифицированной жидкости (когда $N\left( z \right) \equiv {\text{const}}$), для скорости жидкости, полученной в результате решения уравнения (2.9) с правой частью
$f\left( {x,y,z} \right) = Q{{\delta }}\left( x \right){{\delta }}\left( y \right){{\delta }}\left( z \right)$
в неограниченной области, можно выписать асимптотические формулы. А именно, в приближении дальнего поля, $R \gg V{\text{/}}N$ скорость (2.12) при $x > 0$ может быть найдена как [11]
(2.13)
${\mathbf{v}}\left( {x,y,z} \right) = H\left( x \right)\frac{{NQ}}{{2\pi Vr}}\frac{{\sqrt {{{{\sin }}^{2}}\theta + {{{\cos }}^{2}}\theta ~{{{\cos }}^{2}}\varphi } }}{{\sin ~\theta }}\frac{{\mathbf{W}}}{{\left| {\mathbf{W}} \right|}}\cos \left( {\frac{N}{V}r\left| {\sin \varphi } \right|} \right),$
где

${\mathbf{W}} = \left( { - r\operatorname{tg} \theta \sin \theta ,r\operatorname{tg} \theta \cos \theta \cos \varphi ,r\operatorname{tg} \theta \cos \theta \sin \varphi } \right)$
$r = \sqrt {{{x}^{2}} + {{y}^{2}} + {{z}^{2}}} ,\quad \theta = \arccos \left( {\frac{x}{R}} \right),\quad \varphi = \arccos \left( {\frac{y}{{\sqrt {{{y}^{2}} + {{z}^{2}}} }}} \right)$
$H\left( x \right) = \left\{ \begin{gathered} 0,\quad x < 0 \hfill \\ \frac{1}{2},\quad x = 0 \hfill \\ 1,\quad x > 0 \hfill \\ \end{gathered} \right.$

Рассмотрим задачу (2.9)–(2.11) в случае, когда функция $f$, определяющая массовый источник в правой части (2.9) задана следующим образом:

(2.14)
$f\left( {x,y,z} \right) = \frac{{B{{A}^{3}}}}{{\sqrt {{{\pi }^{3}}} }}{{e}^{{ - {{A}^{2}}\left( {{{x}^{2}} + {{y}^{2}} + {{z}^{2}}} \right)}}}$

Заметим, что $\int_{{{R}^{3}}} {f\left( {\mathbf{x}} \right)d{\mathbf{x}}} = B$. Для решения задачи (2.9)–(2.11), (2.14) на языке программирования С++ была написана компьютерная программа, позволяющая рассчитывать изменение во времени скорости жидкости, вертикального смещения, давления, формы свободной поверхности. В программе используется неявная разностная схема на равномерной по всем трем пространственным переменным сетке. На каждом шаге $s$ по времени решается система

(2.15)
$M{{u}_{s}} = w,$
где $M$ – разреженная матрица. Для осуществления элементарных операций с такой матрицей и решения систем линейных алгебраических уравнений (СЛАУ) в программе используется пакет GNU Scientific Library [19]. Для решения системы (2.15) используется обобщенный метод минимальной невязки (Generalized minimal residual method, GMRES). Это итерационный проекционный метод решения СЛАУ был предложен в [20]. Результаты расчетов качественно согласуются с результатами экспериментов по обтеканию сферы потоком равномерно стратифицированной жидкости [21]. Исходный код программы доступен в интернете по адресу https://bitbucket.org/Jclash/inwaves.

Для написания и отладки программы, для проведения пробных (с увеличенными шагами по пространству и по времени) расчетов использовались персональные компьютеры. Представленные ниже в настоящей работе результаты решения задачи (2.9)–(2.11), (2.14) были получены на суперкомпьютерных кластерах МВС-100К, МВС-10П Broadwell Межведомственного суперкомпьютерного центра Российской академии наук (МСЦ РАН), г. Москва и суперкомпьютере Говорун Лаборатории информационных технологий Объединенного института ядерных исследований (ЛИТ ОИЯИ), г. Дубна.

3. Анализ поля течения. Используя описанные выше подходы, исследовалось обтекание подводного препятствия горизонтальным потоком жидкости. Поток имел на бесконечности скорость $V = 3.13$ м/с, направленную вдоль положительного направления оси $Ox$. Поле скоростей жидкости рассчитывалось в области ${{{{\Omega }}}_{a}}$ = [–30 м, 30 м] × × [–30 м, 30 м], находящейся в горизонтальной плоскости $z = h$ на расстоянии $h = 4$ м над препятствием. При этом подводное препятствие моделировалось массовым источником с интенсивностью $Q = 9.84$. Ускорение свободного падения $g = 9.81$ м/с2. В расчетах по моделям (2.9)–(2.11), (2.14) и (2.13) считалось, что жидкость является равномерно стратифицированной, частота плавучести $N = 1$ с–1.

При таких значениях параметров $V$, $h$, $Q$ в случае обтекания потоком однородной жидкости (2.2), размер подводного препятствия (в данном случае – “радиус” полубесконечного тела) был равен

(3.1)
$R = \sqrt {\frac{Q}{{{{\pi }}V}}} = 1\;{\text{м}}$

Для расчета поля скоростей на свободной поверхности идеальной жидкости (2.3), (2.4) по формулам (2.5)–(2.8), была написана программа на языке программирования Python. Бесконечный интервал интегрирования в этих формулах заменялся конечным, $\left[ {0,M} \right]$. Например, для интеграла $I\left( {x,y} \right)$:

(3.2)
$I\left( {x,y} \right) = \int\limits_0^M {\int\limits_0^M {\frac{{\cos \left( {\lambda y} \right){{e}^{{ - \left| x \right|\sqrt {{{\sigma }^{2}} + {{\lambda }^{2}}} }}}\left( {\nu \sigma \cos \left( {\sigma h} \right) + \left( {{{\sigma }^{2}} + {{\lambda }^{2}}} \right)\sin \left( {\sigma h} \right)} \right)\sigma }}{{{{{({{\sigma }^{2}} + {{\lambda }^{2}})}}^{2}} + \nu \sigma }}d\sigma d\lambda } } $

Суммирование велось на равномерной сетке с шагом ${{h}_{2}} = 0.01$ для интегралов (2.5), (2.7) и с шагом ${{h}_{1}} = 0.0001$ для интегралов (2.6), (2.8). Точность расчета контролировалась сравнением с результатами расчета интегралов в программах компьютерной алгебры (Maple, Wolfram Mathematica) и была приемлемой при достаточном удалении от начала координат (шаги суммирования ${{h}_{1}} = 0.0001$, ${{h}_{2}} = 0.01$, длина отрезка интегрирования $M = 10$). Вблизи начала координат точность расчета по формуле (3.2) ухудшается. В качестве значения скорости в точке (0, 0) был взят результат расчета в среде Wolfram Mathematica, где интеграл $I\left( {x,y} \right)$ рассчитывался по преобразованной формуле

$I\left( {x,y} \right) = \int\limits_0^{\frac{\pi }{2}} {\int\limits_0^M {A\left( {\rho ,\varphi } \right)\cos \left( {y\rho \sin \varphi } \right){{e}^{{ - \left| x \right|\rho }}}\rho d\rho d\varphi ,} } $
на отрезке интегрирования [0, 1000], M = 1000. Расчет поля скоростей на свободной поверхности по формулам (2.5)–(2.8) на сетке $61 \times 61$, то есть в 3721 точке занял 2 часа на персональном компьютере.

При моделировании стратифицированной жидкости задача (2.9)–(2.11), (2.14) численно решалась в области ${{\Omega }}$, заданной значениями параметров ${{x}_{{{\text{min}}}}}$ = ${{y}_{{{\text{min}}}}}$ = –50 м, ${{x}_{{{\text{max}}}}}$ = ${{y}_{{{\text{max}}}}}$ = 50 м, $H = 50$ м. Таким образом, область ${{\Omega }}$ имела размеры 100 м × 100 м × × 100 м. Размеры расчетной сетки составляли 250 × 250 × 250 точек, использовался шаг по пространству $s = 0.4$ м и шаг по времени $q = 0.4$ с. Подводное препятствие моделировалось задающей источник функцией (2.14) с параметрами $A = 5$, $B = 9.84$. Как показал анализ линий тока, получающихся в результате моделирования, такие значения параметров $A$, $B$ определяют подводное препятствие с размером аналогичным (3.1). Расчет одного шага по времени занимал примерно 31 минуту на одном вычислительном узле суперкомпьютера МВС10-П Торнадо МСЦ РАН (Intel(R) Xeon(R) CPU E5-2690 @2.9GHz, 64Gb ОЗУ), время всего расчета составило более 20 часов. При этом на каждом шаге по времени для решения системы (14) осуществлялось 50 итераций метода минимальной невязки. Расчеты выполнялись на одном ядре процессора, параллелизация не применялась.

Результаты расчетов приведены на рис. 2–4. На рис. 2 и 3 показано поле скоростей ${\mathbf{\tilde {v}}} = \left( {{{{v}}_{x}},{{{v}}_{y}}} \right)$ при набегании потока на подводное препятствие. На рис. 2 показана компонента ${{{v}}_{x}}\left( {x,y,h} \right)$ этого поля скоростей. На рис. 2,а показана x-компонента векторного поля ${\mathbf{\tilde {v}}}$ в толще идеальной однородной жидкости, рассчитанная по формулам (2.1). Векторное поле на свободной поверхности идеальной однородной жидкости, рассчитанное по формулам (2.3), (2.4) показано на рис. 2,б. Поле в толще идеальной стратифицированной жидкости показано на рис. 2,в и 2г; на рис. 2,в – результаты расчета по асимптотической формуле (2.13) приближения дальнего поля из [11] и на рис. 2,г – численное решение задачи (2.9)–(2.11), (2.14). Во всех случаях рис. 2,а–г поле ${\mathbf{\tilde {v}}}$ рассчитывалось на расстоянии $h$ над подводным препятствием. На рис. 3 приведены карты компоненты скорости ${{{v}}_{y}}\left( {x,y,h} \right)$.

Рис. 2.

Компонента ${{{v}}_{x}}\left( {x,y} \right)$ скорости жидкости на расстоянии $h$ от подводного препятствия по вертикали в толще идеальной однородной жидкости (а), на свободной поверхности (б), в толще идеальной стратифицированной жидкости, полученная при использовании ассимптотики дальнего поля (в) и в результате численного моделирования (г).

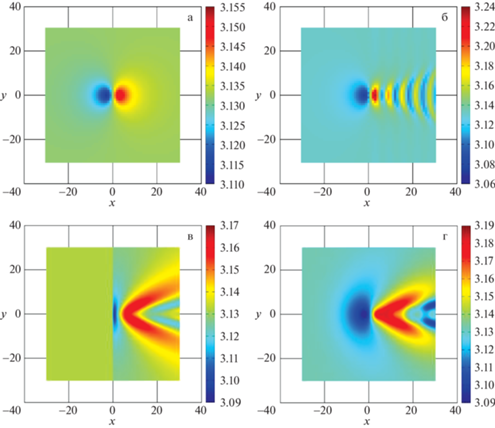
Рис. 3.

Компонента ${{{v}}_{y}}\left( {x,y} \right)$ скорости жидкости на расстоянии $h$ от источника по вертикали в толще идеальной однородной жидкости (а), на свободной поверхности (б), в толще идеальной стратифицированной жидкости, полученная при использовании ассимптотики дальнего поля (в) и в результате численного моделирования (г).

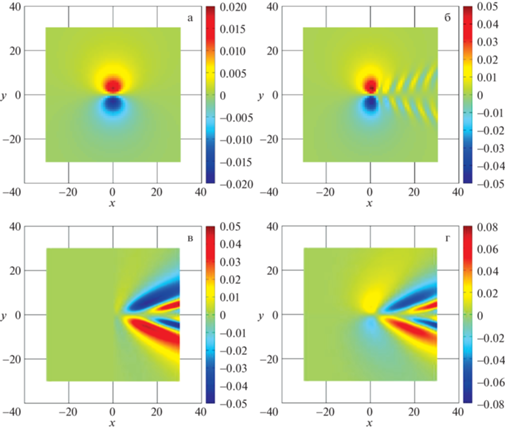
Рис. 4.

Показана компонента скорости жидкости ${{{v}}_{x}}$ вдоль прямой $z = h$, $y = 0$ в толще неограниченной однородной жидкости (кривая 1), на свободной поверхности однородной жидкости (кривая 2), в стратифицированной жидкости при расчете с использованием асимптотических формул (кривая 3). Скорость невозмущенного потока $V$ показана прямой 4.

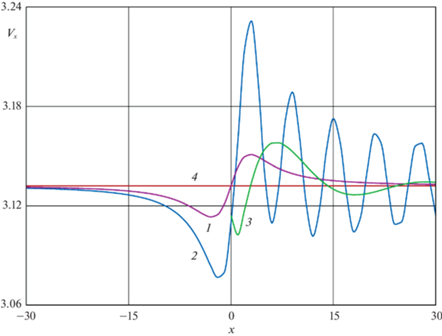
На рис. 4 показано изменение $x$-компоненты скорости, изображенной на рис. 2,а–в вдоль центрального сечения (прямой $z = h$, $y = 0$), то есть ${{{v}}_{x}}\left( {x,0,h} \right)$, $x \in \left[ { - 30,30} \right]$. Амплитуда колебаний изменения скорости течения в стратифицированной жидкости схожа с амплитудой изменения скорости в толще однородной жидкости. Максимум этой амплитуды в 2–3 раза меньше максимума амплитуды для случая изменения поля скоростей на свободной поверхности однородной жидкости. Величина отклонения скорости жидкости от скорости потока на бесконечности монотонно убывает при удалении от начала координат в случае расчета в толще однородной жидкости (кривая 1) и осциллирует для случаев расчета на свободной поверхности (кривая 2) или по модели стратифицированной жидкости (кривая 3). При этом период этих осцилляций в последнем случае примерно в три раза больше.

Поле скоростей, рассчитанное в толще океана по модели однородной жидкости (см. рис. 2 и 3,a) имеет ярко выраженную неоднородность в области, находящейся непосредственно над подводным препятствием, около точки $\left( {0,0,h} \right)$. Такая неоднородность может быть обнаружена в случае непосредственной фиксации поля скоростей в соответствующей горизонтальной плоскости. Однако в поле скоростей, рассчитанном по этой модели отсутствуют осцилляции в области за препятствием (при $x > 0$) в отличие от результатов расчетов на свободной поверхности (см. рис. 2 и 3,б) или по модели стратифицированной жидкости (см. рис. 2 и 3,в и г). Именно осциллирующий характер поля скоростей течения, после взаимодействия с ветровой рябью формирует характерную картину неоднородностей морской поверхности, которая может быть идентифицирована средствами радиозондирования.

В случае, когда жидкость является равномерно стратифицированной ($N = {\text{const}}$), сравнение результатов расчетов по асимптотическим формулам (см. рис. 2 и 3,в) и результатов, полученных в ходе численного моделирования распространения внутренних гравитационных волн в жидкости (см. рис. 2 и 3,г) показало, что расчет по асимптотическим формулам имеет приемлемую точность и может быть использован для определения поля скоростей жидкости в области, где эти асимптотические формулы определены, то есть при $x > 0$. Заметим, что асимптотические формулы неприменимы в случае, если частота плавучести $N$ зависит от вертикальной координаты или изменяется со временем.

Заключение. Рассмотрена задача определения поля скоростей при обтекании потоком идеальной жидкости подводного препятствия. Предложено несколько подходов к определению поля скоростей жидкости в горизонтальной плоскости, находящейся на некотором расстоянии от подводного препятствия. Предложены формулы для точного определения поля скоростей на свободной поверхности однородной жидкости, показано, что рассчитанное по этим формулам поле существенно отличается от поля скоростей в неограниченной области, рассчитанного по классическим формулам. Таким образом, для моделирования поля скоростей следует пользоваться предложенными формулами, несмотря на их существенно более высокую вычислительную сложность.

Проведено моделирование набегания потока стратифицированной жидкости на подводное препятствие с помощью разработанной компьютерной программы и по асимптотическим формулам приближения дальней зоны. Показано, что в случае равномерной стратификации (при постоянной частоте плавучести), при постоянной скорости потока поле скоростей может быть с приемлемой точностью рассчитано по асимптотическим формулам. В прикладных расчетах использование асимптотических формул предпочтительно, так как точное решение трехмерной динамической задачи требует больших вычислительных мощностей, и для вычислений даже с использованием сравнительно небольших расчетных сеток приходится использовать суперкомпьютерные ресурсы.

Рассчитанные в работе поля скоростей жидкости иллюстрируют существенное усложнение картины течений при обтекании подводного препятствия в случае, когда жидкость равномерно стратифицирована по сравнению со случаем отсутствия стратификации. Более того, при моделировании океанических течений следует учитывать неравномерность стратификации жидкости. Частота плавучести меняется с глубиной, эта зависимость частоты плавучести от глубины уникальна для каждого водного объекта, может меняться от сезона к сезону. Применение асимптотических методов для моделирования течений с произвольным профилем стратификации невозможно, тогда как предложенный в настоящей статье подход и разработанная компьютерная программа позволяют моделировать обтекание подводного препятствия потоком, вообще говоря, неравномерно стратифицированной жидкости. При этом возможно моделирование сложного режима обтекания, когда скорость потока непостоянна.

Для повышения точности расчетов требуется усовершенствовать моделирование распространения возмущений в стратифицированной жидкости. Планируется реализовать возможность задания препятствия сложной формы, возможность задания граничных условий свободной поверхности на соответствующей части расчетной области. Для ускорения расчетов и увеличения размеров расчетной области планируется адаптировать компьютерный алгоритм к архитектуре используемых кластерных вычислителей. Рассчитанное поле скоростей на поверхности жидкости может быть использовано для моделирования взаимодействия внутренних волн с ветровой рябью.

Работа выполнена с использованием суперкомпьютерных ресурсов МСЦ РАН и ЛИТ ОИЯИ. Авторы выражает глубокую признательность руководству и сотрудникам МСЦ РАН и ЛИТ ОИЯИ за предоставленную возможность и техническую поддержку расчетов на вычислительных кластерах.

Исследование выполнено за счет гранта Российского научного фонда (проект № 21-11-00151), https://rscf.ru/project/21-11-00151/.

Список литературы

  1. Нестеров С.В., Шамаев А.С., Шамаев С.И. Методы, алгоритмы и средства аэрокосмической компьютерной томографии приповерхностного слоя Земли. М.: Научный мир, 1996. 272 с.

  2. Гавриков А.А., Князьков Д.Ю., Романова А.В. и др. Моделирование влияния волнения поверхности на спектр собственного излучения океана // Прогр. системы: теория и прил. 2016. Т. 7. Вып. 2 (29). С. 73–84.

  3. Булатов М.Г., Кравцов Ю.А., Лаврова О.Ю. и др. Физические механизмы формирования аэрокосмических радиолокационных изображений океана // УФН. 2003. Т. 173. № 1. С. 69–87.

  4. Jackson C.R., da Silva J.C.B., Jeans G. et al. Nonlinear internal waves in synthetic aperture radar imagery // Oceanogr. 2013. V. 26. № 2. P. 68–79.

  5. Baydulov V.G., Knyazkov D., Shamaev A.S. Motion of mass source in stratified fluid // J. Phys.: Conf. Ser. V. 2224. 2021 2nd Int. Symp. on Automation, Information and Computing (ISAIC 2021) 03/12/2021–06/12/2021 Online. P. 012038. 2022.

  6. Ulaby F.T., Moore R.K., Fung A.K. Microwave Remote Sensing. Active and Passive. Massachusetts: Addison-Wesley Pub., 1981. 456 р.

  7. Knyazkov D. Web-interface for HPC computation of a plane wave diffraction on a periodic layer // Lobachevskii J. Math. 2017. V. 38. № 5. P. 936–939.

  8. Knyazkov D. Diffraction of plane wave at 3-dimensional periodic layer // AIP Conf. Proc. 2018. V. 1978. P. 470075-1-4. https://doi.org/10.1063/1.5044145

  9. Байдулов В.Г. О решении обратной задачи движения источника в стратифицированной жидкости // Волны и вихри в сложных средах: 12-я межд. конф. – школа молодых ученых; 01–03 декабря 2021 г. М.: ООО ИСПОпринт, 2021. С. 31–35.

  10. Матюшин П.В. Процесс формирования внутренних волн, инициированный началом движения тела в стратифицированной вязкой жидкости // Изв. РАН. МЖГ. 2019. № 3. С. 83–97.

  11. Voisin B. Internal wave generation in uniformly stratified fluids. Pt. 2. Moving point sources // J. Fluid Mech. 1994. V. 261. P. 333–374.

  12. Voisin B. Lee waves from a sphere in a stratified flow // J. Fluid Mech. 2007. V. 574. P. 273–315.

  13. Scase M.M., Dalziel S.B. Internal wave fields and drag generated by a translating body in a stratified fluid // J. Fluid Mech. 2004. V. 498. P. 289–313.

  14. Scase M.M., Dalziel S.B. Internal wave fields generated by a translating body in a stratified fluid: an experimental comparison // J. Fluid Mech. 2006. V. 564. P. 305–331.

  15. Лойцянский Л.Г. Механика жидкости и газа. М.: Дрофа, 2003. 840 с.

  16. Сретенский Л.Н. Теория волновых движений жидкости. М.: Наука, 1977. 815 с.

  17. Горелов А.М., Носов В.Н., Савин А.С., Савина Е.О. Метод расчета поверхностных возмущений над точечным источником и диполем // Изв. РАН. МЖГ. 2009. № 1. С. 203–207.

  18. Bulatov V.V., Vladimirov Yu.V.  A General Approach to Ocean Wave Dynamics Research: Modelling, Asymptotics, Measurements. M.: OntoPrint, 2019. 587 р.

  19. Galassi M., Davies J., Theiler J. et al. GNU Scientific Library Reference Manual (3rd Ed.). Network Theory Ltd., 2009. 592 р.

  20. Saad Y., Schultz M.H. GMRES: A Generalized Minimal Residual Algorithm for Solving Nonsymmetric Linear Systems // SIAM J. on Sci.&Statist. Comput. 1986. V. 7. № 3. P. 856–869.

  21. Чашечкин Ю.Д., Гуменник Е.В., Сысоева Е.Я. Трансформация плотностного поля трехмерным телом, движущимся в непрерывно стратифицированной жидкости // ПМТФ. 1995. № 1. С. 20–32.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Прикладная математика и механика

Архивы выпусков Информация о журнале Отправить рукопись в журнал