1. На главную
  2. Электронные версии
  3. Журнал общей биологии
  4. T. 83, № 5, 2022

Журнал общей биологии, 2022, T. 83, № 5, стр. 358-368

Что общего между экологией и ядерной физикой: модель случайной матрицы для распределения деревьев в насаждении по таксационным показателям

В. Г. Суховольский 1, *, Ю. Д. Иванова 2, О. В. Тарасова 3

1 Институт леса им. В.Н. Сукачева СО РАН
660036 Красноярск, Академгородок, 50/28, Россия

2 Институт биофизики СО РАН
660036 Красноярск, Академгородок, 50/50, Россия

3 Сибирский федеральный университет
660041 Красноярск, пр. Свободный, 79, Россия

* E-mail: soukhovolsky@yandex.ru

Поступила в редакцию 17.07.2022
После доработки 20.08.2022
Принята к публикации 06.09.2022

Полный текст (PDF)

Аннотация

Взаимодействия деревьев в лесу проявляются в уменьшении прироста фитомассы, ослаблении и отпаде части деревьев. Одним из способов выявления характера взаимоотношений деревьев в лесу является изучение текущих функций распределения деревьев в насаждении по высоте и диаметру ствола. При этом для описания используются различные функции: гамма-функция, нормальная и логарифмически нормальная функции, функция Вейбулла и др. Для теоретического обоснования выбора того или иного распределения для описания диаметров и высот деревьев в насаждении в настоящей работе предложено использовать модель гауссового ортогонального ансамбля (Gaussian orthogonal ensemble – GOE), используемого в ядерной физике для описания распределения энергетических уровней атомных ядер и характеризующего взаимодействия в хаотических системах. Показано, что взаимодействия как в атомной ядре, так и в лесном насаждении могут быть описаны общей моделью. Для описания таксационных показателей деревьев введены характеристики обратных высот и диаметров. Модель GOE для лесного насаждения верифицирована по данным таксационных измерений. Показано, что параметры нормированной GOE-модели не зависят от возраста насаждения.

Давно замечено, что разные научные дисциплины в определенной степени “пересекаются” по своим подходам. Перенос концепций между различными областями наук случается достаточно часто и хорошо известен в теории науки. Достаточно вспомнить взаимоотношения между экономико-социальной концепцией народонаселения Мальтуса (Malthus, 1798) и биологической концепцией естественного отбора Дарвина (Darwin, 1859). Такой объект, как осциллятор, используется в классический и квантовой механике, экологии, экономике. Подход, связанный с представлением о распределении ресурса, широко используется в экономике (Pareto, 1896), лингвистике (Zipf, 1949), науковедении (Bredford, 1948), теории эволюции (Yule, 1924).

Чаще всего такое сходство связано с применением общих математических моделей. Однако иногда сходство подходов (даже в сильно различающихся научных дисциплинах) является более глубоким. В настоящей работе рассмотрена возможность переноса концепции взаимодействия объектов из ядерной физики в лесную экологию на примере сопоставления моделей распределения энергетических уровней атомного ядра и распределения деревьев в насаждении по морфологическим параметрам.

Начнем с ядерной физики. В начале 50-х годов прошлого века Вигнером была рассмотрена задача описания свойств сложных атомных ядер с сильными взаимодействиями между компонентами ядра (Wigner, 1951; Вигнер, 1961). В чем заключаются трудности теоретического описания функций распределения энергетических уровней сложных ядер, состоящих из большого числа взаимодействующих протонов и нейтронов и характеризуемых большим числом взаимодействий неизвестных типов? Как известно, для описания квантовой системы необходимо ввести некоторый матричный оператор – гамильтониан, характеризующий энергию системы, который для сложных физических систем, таких как атомные ядра, можно представить в виде конечномерных матриц (Мета, 2012). Допустимые энергетические уровни системы можно найти, определив собственные значения этого гамильтониана (Зи, 2009). Однако такой подход достаточно сложен: не всегда такой гамильтониан известен, и даже если бы он был из каких-то соображений получен, возникли бы математические трудности с нахождением его собственных значений. Согласно гипотезе, предложенной Вигнером, локальное статистическое распределение энергетических уровней атомного ядра при большом числе различных взаимодействий идентично распределению собственных значений случайных матриц, состоящих из нулей и единиц. В этом случае вместо выбора некоторого гамильтониана можно рассмотреть большие случайные матрицы и изучать распределение собственных значений таких матриц (Wigner, 1951; Dyson, 1962; Дайсон, 1963; Mehta, 2004; Зи, 2009; Мета, 2012). Спектр собственных значений таких случайных матриц можно описать гауссовским ортогональным распределением (Gaussian orthogonal ensemble – GOE) (Dyson, 1962; Stockmann, 2007).

Лесной ценоз как сложную систему можно охарактеризовать через видовой состав и взаимодействия его компонентов – деревьев, кустарников и трав. Определение видового состава растений в насаждении не является проблемой, но достаточно сложно выявить особенности взаимодействий растений в лесной экосистеме. Эти сложности, в частности, связаны с тем, что большинство процессов взаимодействия происходят медленно. Так, характерные времена взаимодействия деревьев в лесу, проявляющиеся в уменьшении прироста фитомассы, ослаблении и отпаде части деревьев, составляют как минимум десятки лет. Проводить столь продолжительные исследования крайне сложно технически. В связи с этим возникает задача поиска “быстрых” индикаторов взаимодействий компонентов лесных ценозов. Одним из способов выявления характера взаимоотношений деревьев в лесу является изучение текущих функций распределения деревьев в насаждении по высоте и диаметру ствола. При этом для описания используются различные функции: гамма-функция, нормальная и логарифмически нормальная функции, функция Вейбулла и др. (Weibull, 1951; Bailey, Dell, 1973; Ek et al., 1975; Ганина, 1984; Shiver, 1988; Лебков, 1990; Maltamo et al., 1995, 2000; Рыжков, 2000; Kangas, Maltamo, 2000; Zhang et al., 2001, 2003; Li et al., 2002; Cao, 2004; Newton et al., 2004; Zasada, Cieszewski, 2005; Mergani, Sterba, 2006; Nord-Larsen, Cao, 2006; Zhang, Liu, 2006; Palahí et al., 2007; Лебков, Каплина, 2008; Lei, 2008; Fonseca et al., 2009; Stankova, Zlatanov, 2010; Zhang, Lei, 2010; Mateus, Tomé, 2011; Jaworski, Podlaski, 2012; Jin et al., 2013; Poudel, Cao, 2013; Gómez-Garcia et al., 2014; Gorgoso-Varela, Rojo-Alboreca, 2014; Liu et al., 2014; Tsogt, Lin, 2014; Lima et al., 2015; Mehtätalo et al., 2015; Gorgoso-Varela et al., 2016; Lin et al., 2016; Podlaski, 2017; Ozcelik et al., 2018; Pogoda et al., 2019; Sharma et al., 2019). При этом тип функции распределения может изменяться на разных стадиях развития насаждения – от симметричного нормального распределения в период от начала интенсивного отпада деревьев до скошенного (skewed) ассиметричного (Laar, Akca, 2007).

Чем, в частности, можно теоретически обосновать выбор того или иного распределения для описания диаметров и высот деревьев в насаждении? Так, известно, что распределение Вейбулла играет значительную роль в ряде прикладных статистических задач, в частности, при исследовании максимально возможных значений (пределов, рекордов) тех или иных показателей, например страховых выплат или потерь из-за коммерческих рисков. Для распределения Вейбулла можно найти аналоги в теории надежности, где этим уравнением описывается распределение времени безотказной работы элементов, времени работы до предельного состояния машин, для описания распределений сроков службы других различных устройств (Острейковский, 2003). Распределение Вейбулла–Гнеденко применяется также в случае построения вероятностных моделей ситуаций, поведение объекта в которых определяется “наиболее слабым звеном” (Гнеденко, 1988). Однако теоретические модели для объяснения функций распределения деревьев не рассматриваются. Обычно выбор функции распределения производится чисто эмпирически – по степени согласия выбранной теоретической функции с таксационными данными (Лебков, 1990).

Отсутствие единой теоретической модели взаимодействий деревьев в насаждении в ходе онтогенеза заставляет рассматривать насаждение как “черный ящик”, в котором большое число частиц (деревьев) взаимодействует между собой неизвестным образом. Сложность описания подобной системы состоит в том, что в ней потенциально могут одновременно реализовываться различные законы взаимодействия компонентов, и неясно, как в этом случае описывать систему с такими взаимодействиями.

Взаимодействия в хаотической системе без указания на тип системы (физической, биологической, экономической и т.п.) описываются теорией случайных матриц (Stockmann, 2007). Используя эту концепцию, в настоящей работе предложена статистическая модель, с помощью которой возможно с высокой точностью описать распределение деревьев в насаждении по высоте и диаметру ствола для различных насаждений в разных возрастах. Используя статистический подход, можно получить полезную информацию относительно взаимодействий в сложной экологической системе в ситуации, когда детальное изучение взаимодействий в экосистеме провести невозможно.

При переносе той или иной концепции в другую научную дисциплину возникают проблемы, связанные с переформулировкой положений концепции на язык новой дисциплины. Поэтому при переносе концепции описания с помощью случайной матрицы энергетических уровней в ядре атома для описания взаимодействия большого числа деревьев в лесном насаждении необходимо трансформировать энергетические представления и принцип минимума энергии в устойчивой физической системе в экологические характеристики.

В качестве аналога энергетических принципов и гамильтониана для экосистемы нами предлагается использовать принцип минимума гибели компонентов устойчивой сложной экосистемы. Будем предполагать, что наблюдаемость такой системы связана с тем, что риск гибели экосистемы минимален. Тогда при описании лесного насаждения можно рассматривать распределения деревьев в насаждении по высоте и диаметру как эквивалент функции риска гибели. Чем выше риск гибели дерева с определенными таксономическими показателями, тем реже такое дерево будет встречаться в насаждении и тем меньше будет “вклад” такого дерева в функцию распределения по таксономическим характеристикам. Если это предположение окажется корректным, то для описания распределения деревьев по таксационным характеристикам в достаточно большом однородном насаждении с большим числом взаимодействий разных типов можно будет использовать гауссовскую ортогональную функцию (GOE) плотности распределения, аналогичную модели, полученной для атомного ядра (Мета, 2012).

Из каких соображений в ядерной физике получена модель GOE? Пусть при наличии уровня энергии Е в системе вероятность появления уровня энергии со значением E + s пропорциональна s при малых значениях s. Будем полагать, что это условие выполняется для всех значений s. Разобьем весь интервал значений s на m равных частей длиной s/m и будем предполагать, что вероятности появления энергетического уровня в каждом интервале s/m независимы. В этом случае общая вероятности будет равна произведению вероятности событий (нахождения уровней) в отдельном интервале (Мета, 2012):

(1)
$\begin{gathered} p{\text{(}}s{\text{)}}ds = \mathop {\lim }\limits_{m \to \infty } \prod\limits_{r = 0}^{m - 1} {\left( {1 - \frac{{{{s}_{r}}}}{m}\frac{s}{m}a} \right)} {\kern 1pt} asds = \\ = as\exp ({{a{{s}^{2}}} \mathord{\left/ {\vphantom {{a{{s}^{2}}} 2}} \right. \kern-0em} 2}). \\ \end{gathered} $

Близкое к (1) выражение, которое будет в дальнейшем нами использоваться, было предложено Вигнером (Wigner, 1951):

(2)
$f(s) = A\frac{{\pi s}}{{2B}}\exp \left( { - \frac{{\pi {{s}^{2}}}}{{4{{B}^{2}}}}} \right),$
где s – моделируемая переменная, А и В – константы модели.

Так как f(s) – функция плотности распределения, то должно выполняться условие $\int_0^\infty {f(s)dx = 1} $. Учитывая это условие, из выражения (2) получим:

(3)
$\int\limits_0^\infty {\frac{{A\pi }}{{2B}}s\exp \left( { - \frac{{\pi {{s}^{2}}}}{{4{{B}^{2}}}}} \right)} ds = 1.$

Интеграл (3) – табличный (Двайт, 1978) и легко вычисляется:

(4)
$\begin{gathered} \int\limits_0^\infty {\frac{{A\pi }}{{2B}}s\exp \left( { - \frac{{\pi {{s}^{2}}}}{{4{{B}^{2}}}}} \right)} ds = \\ = \frac{{A\pi }}{{2B}}\int\limits_0^\infty {s\exp \left( { - \frac{{\pi {{s}^{2}}}}{{4{{B}^{2}}}}} \right)} ds = 2AB = 1. \\ \end{gathered} $

Из (4) следует, что нормировочный множитель А зависит от значения В и фактически функция (2) – однопараметрическая.

Найдем максимум функции (1) из условий $\frac{{df}}{{ds}} = 0,\;\frac{{{{d}^{2}}f}}{{d{{s}^{2}}}} < 0$:

(5)
$\begin{gathered} \frac{{df}}{{ds}} = \frac{{\pi A}}{{2B}}\exp \left( { - \frac{{\pi {{s}^{2}}}}{{4{{B}^{2}}}}} \right) - \frac{{\pi As}}{{2B}}\frac{{2s}}{{4{{B}^{2}}}} \times \\ \times \,\,\exp \left( { - \frac{{\pi {{s}^{2}}}}{{4{{B}^{2}}}}} \right) = 1 - \frac{{{{s}^{2}}}}{{2{{B}^{2}}}} = 0, \\ \end{gathered} $
(6)
$\frac{{{{d}^{2}}f}}{{d{{s}^{2}}}} = - \frac{s}{{{{B}^{2}}}} < 0,$
(7)
$B = {{s}_{m}}\sqrt {\frac{1}{2}} ,$
где sm – значение переменной s, при котором функция плотности распределения f(s) достигает максимума.

Таким образом, параметр В уравнения (2) однозначно связан со значением моды sm распределения f(s).

Далее рассмотрим возможности применения модели случайных матриц для описания распределения деревьев в насаждении по высотам и диаметрам.

ОБЪЕКТЫ И МЕТОДЫ ИССЛЕДОВАНИЙ

Объекты исследований

В качестве объектов исследований использовались данные различных авторов по сплошным перечетам деревьев в насаждениях по диаметрам и высотам. Нами использовались данные перечетов в сосновых древостоях (Pinus sylvestris L.) на территории Иркутской области (Бузыкин и др., 2009) и в лесах Северного Казахстана (Усольцев, 2013).

Данные по Иркутской области (табл. 1) характеризовали одновозрастные сосняки рододендроново-брусничные в возрасте 25, 55 и 90 лет, образовавшиеся после пожаров на слабодерновой среднеподзолистой супесчаной почве, и одновозрастной 35-летний березняк разнотравный, естественно сформировавшийся на старопахотной дерново-лесной суглинистой почве. Древостои расположены в Иркутской области на территории Тангуйского лесхоза, в междуречье рек Ия и Ока, впадающих в Ангару, от 55°10′ с.ш., 101°20′ в.д. до 55°20′ с.ш., 101°30′ в.д. Сосновые древостои принадлежали к одному естественному ряду. Доминирующей породой на пробных площадях является сосна обыкновенная (Pinus sylvestris L.). Единично в сосняках старших возрастов присутствуют деревья лиственницы сибирской (Larix sibirica Ledeb.). Возраст модельных деревьев одного насаждения различался не более чем на два–три года. Пробные площади включали от 379 до 591 дерева.

Таблица 1.  

Таксационная характеристика сосновых древостоев на пробных площадях в Иркутской области

Пробная площадь Возраст Т, лет Число деревьев N Средние показатели
высота, м диаметр, см
S1 25 529 3.9 3.1
S2 25 379 5.7 4.4
S3 55 591 12.8 10.7
S4 90 552 18.7 17.9

Для описания таксационных характеристик сосняков Северного Казахстана (табл. 2) использовались данные перечетов в бору Аман-Карагай (52°30′ с.ш., 63°90′ в.д.) (провинция Тоболо-Убаганской равнинной степной зоны Северного Казахстана) (Усольцев, 2013).

Таблица 2.  

Таксационная характеристика сосновых древостоев на пробных площадях в Северном Казахстане

Пробная площадь Возраст Т, лет Число деревьев N Средние показатели
высота, м диаметр, см
U5 20 311 3.5 2.3
U6 20 83 3.9 3.2
U7 20 259 3.1 2.9
U8 22 158 6.9 7.7
U13 23 101 7.6 8.4
U20 25 128 6.9 6.6
U22 21 102 5.4 7.4
U23 20 133 6.3 6.5
U25 24 110 10.8 10.1
U26 22 101 8.8 12.6
U30 26 106 9.3 8.4
U32 42 173 4.4 2.1
U33 42 156 8.3 4.6
U44 21 235 4.2 2.6
U49 19 147 5.8 7.4
U50 19 137 8.8 8.6
U55 40 120 13.6 14.3
U56 40 124 11.8 14.0

Выбор таксационных показателей деревьев для анализа

В стандартной процедуре расчета эмпирической функции распределения (или плотности распределения) f(Hi) и f(Di) деревьев в насаждении по их морфологическим показателям используется отношение числа n(Hi) или n(Di) деревьев классов высот Нi или диаметров Di стволов деревьев к общему числу деревьев в насаждении:

(8)
$f({{H}_{i}}) = \frac{{n({{H}_{i}})}}{N},\,\,\,\,f({{D}_{i}}) = \frac{{n({{D}_{i}})}}{N}.$

С точки зрения рисков гибели деревьев, различия морфологических показателей между угнетенными деревьями в насаждении важнее различий по этим показателям между господствующими деревьями. Значения высот или диаметров угнетенных деревьев могут быть много меньше значений высот или диаметров больших деревьев. Например, рассмотрим два угнетенных и два господствующих дерева в насаждении с высотами соответственно H1 = 1 м, H2 = 2 м, H3 = 19 м, H4 = 20 м. Безусловно, риск гибели угнетенных деревьев выше, чем риск гибели деревьев, господствующих в насаждении в результате конкуренции. Различия высот между угнетенными и между господствующими деревьями соответственно будут $\Delta {{H}_{{12}}} = 2 - 1 = 1\,{\text{м}}$ и $\Delta {{H}_{{34}}} = 10 - 9 = 1\,\,{\text{м}}$. Однако с экологической точки зрения разница ΔH12 = 1 м между угнетенными деревьями не есть одно и то же, что разница ΔH34 = 1 м между господствующими деревьями. Разницу $\Delta {{H}_{{34}}}$ можно не принимать во внимание. Разница же $\Delta {{H}_{{12}}}$ может быть критической с точки зрения вероятности гибели деревьев.

В связи с этим в модели вместо обычных линейных шкал размеров, в которых высота H деревьев измеряется в метрах, а диаметр D ствола – в сантиметрах, используются шкалы обратных значений высот и диаметров ствола. Пересчет производится по формулам:

(9)
$d = \frac{1}{D},\,\,\,\,h = \frac{1}{H},$
где d – значения диаметров в обратной шкале, h – значения высот в обратной шкале.

В рассматриваемом примере в линейной шкале абсолютные значения различий высот между угнетенными и между господствующими деревьями равны. Однако в шкале обратных значений различия морфологических характеристик между угнетенными $\Delta {{h}_{{12}}} = 1 - 0.5 = 0.5$ будет существенно больше различия между господствующими деревьями $\Delta {{h}_{{34}}} = 0.052632 - 0.05 = 0.002632$. Таким образом, в предлагаемой обратной шкале различия между господствующими в насаждении деревьями окажутся незначительными, тогда как даже достаточно малые различия характеристик угнетенных деревьев будут приводить к существенным различиям показателей этих деревьев в шкале обратных значений.

Для нормализации функций распределения по обратным высотам и диаметрам в различных насаждениях производилась замена переменных. Для нормализованной переменной s запишем

(10)
$s = \frac{{p - {{p}_{{\min }}}}}{{{{p}_{{\max }}} - {{p}_{{\min }}}}},$
где р – данные в шкалах обратных высот h или диаметров d; pmin, pmax – минимальное и максимальное значение p.

Параметр pmin необходим для того, чтобы убрать пустой пробел между нулем и минимальным значением р в данных. Таким образом, после нормализации по формуле (10) значения s изменяются в пределах от 0 до 1 для всех рассматриваемых выборок данных. Изменение исходного моделируемого параметра в одинаковых пределах для всех насаждений обеспечивает возможность сравнения и анализа параметров модели.

Далее переменная s в (10) будет использована для расчетов экологических аналогов выражений (1)–(7). Для расчетов параметров функции (2) использовалась процедура нелинейной регрессии с помощью статистического пакета Statistica 10. Качество приближения к функции (2) оценивалось с помощью коэффициента детерминации R2 и критерия Колмогорова–Смирнова (Поллард, 1982).

РЕЗУЛЬТАТЫ

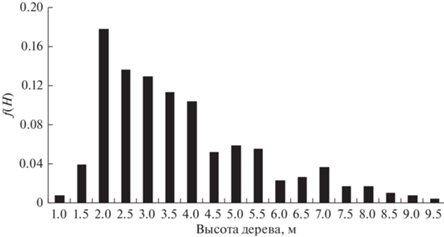
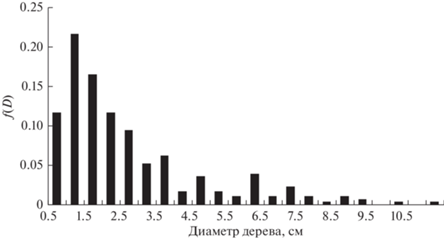
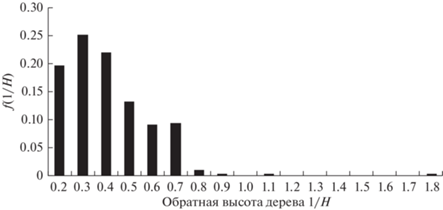
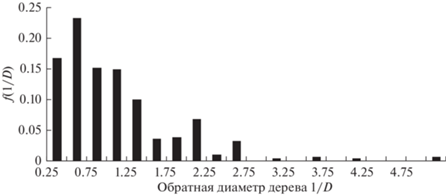
Рассмотрим возможность использования GOE-модели для описания распределения морфологических характеристик деревьев в обратной шкале. На рис. 1–4 приведены эмпирические распределения диаметров и высот деревьев в линейной и обратной шкалах для пробной площади S2 (Бузыкин и др., 2009).

Рис. 1.

Распределение деревьев по высоте в насаждении S2.

Рис. 2.

Распределение деревьев по диаметру в насаждении S2.

Рис. 3.

Типичное распределение деревьев по обратной высоте в насаждении S2.

Рис. 4.

Распределение деревьев по обратному диаметру в насаждении S2.

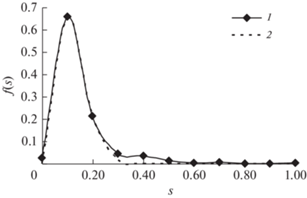
На рис. 5 приведена функция плотности распределения в шкалах нормированных обратных значений s для насаждения S2, для которого функция плотности распределения по высотам приведена на рис. 1, а функция плотности распределения по обратным высотам приведена на рис. 3.

Рис. 5.

Эмпирическая функция плотности распределения (1) и GOE-модель (2) в шкале s обратных значений высот для насаждения S2.

Для сравнения качества приближения с помощью функции Вейбулла $f(x) = \frac{b}{a}{{\left( {\frac{{x - c}}{a}} \right)}^{{b - 1}}}\exp \left( { - {{{\left( {\frac{{x - c}}{a}} \right)}}^{b}}} \right)$ и с помощью GOE-функции можно использовать показатели коэффициента детерминации R2 для приближения с помощью этих уравнений (табл. 3).

Таблица 3.  

Значения коэффициента детерминации R2 для приближения таксационных данных с помощью трехпараметрической функции Вейбулла и обратной GOE-функции

Пробная площадь Модель Вейбулла Обратная GOE-модель
диаметр высота диаметр высота
S1 0.998 0.998 0.987 0.996
S2 0.977 0.760 0.985 0.996
S3 0.986 0.979 0.981 0.996
S4 0.959 0.825 0.985 0.934
S5 0.991 0.844 0.967 0.962

Как видно из табл. 3, значения коэффициентов детерминации для приближения таксационных данных с помощью функции Вейбулла для многих насаждений несколько меньше, чем приближение этих же данных с помощью обратной GOE-функции. Но в любом случае модель с одним параметром предпочтительнее трехпараметрической модели с точки зрения простоты и надежности расчетов.

В табл. 4 приведены результаты расчетов параметров GOE-модели распределения по обратным высотам и диаметрам для изученных насаждений.

Таблица 4.

Характеристики параметров A и B для GOE-приближений в обратных шкалах диаметров и высот для изученных насаждений

Пробная площадь Возраст Т, лет Параметры модели
обратный диаметр обратная высота
Ad Bd Ah Bh
U5 20 1.18 0.18 1.11 0.20
U6 20 1.62 0.13 0.99 0.20
U7 20 1.57 0.13 0.80 0.28
U44 21 3.14 0.09 0.96 0.19
U8 22 2.53 0.11 1.02 0.21
U13 23 1.10 0.17 1.21 0.17
U20 25 1.51 0.15 1.23 0.15
U22 21 2.32 0.11 1.26 0.15
U23 20 2.45 0.11 1.40 0.15
U25 24 0.77 0.28 1.44 0.14
U26 22 0.97 0.26 1.46 0.15
U30 26 1.57 0.15 1.72 0.14
U49 19 1.47 0.15 1.93 0.12
U50 19 1.57 0.15 2.33 0.10
U32 42 1.10 0.20 0.78 0.24
U33 42 2.04 0.11 1.34 0.17
U55 40 1.53 0.14 1.76 0.12
U56 40 0.72 0.29 0.86 0.25
S2 25 1.55 0.45 2.03 0.18
S3 25 0.85 0.26 1.01 0.29
S4 40 0.89 0.24 1.37 0.24
S5 90 0.97 0.25 1.04 0.19

На рис. 6 отражены изменения с возрастом деревьев в насаждениях параметров Ad и Bd GOE распределения деревьев в насаждениях по обратному диаметру d, а на рис. 7 – изменения параметров Ah и Bh GOE распределения деревьев в насаждениях по обратной высоте h.

Рис. 6.

Изменения с возрастом Т параметров Ad (1) и Bd (2) GOE распределения деревьев в насаждениях по обратному диаметру d.

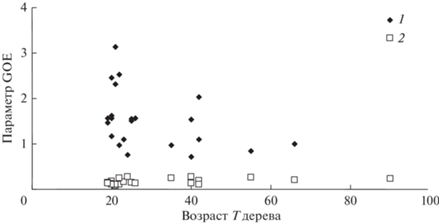
Рис. 7.

Изменения с возрастом Т параметров Ah (1) и Bh (2) GOE распределения деревьев в насаждениях по обратной высоте h.

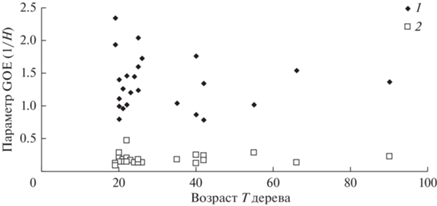
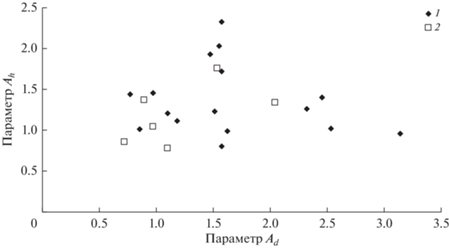
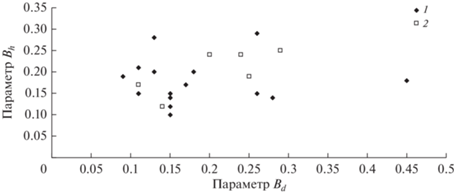
Как видно из рис. 6 и 7, при нормировании характеристик высоты и диаметра с использованием (5) с увеличением возраста параметры функций распределения Bd и Bh не изменяются, тогда как разброс значений Ad и Ah с возрастом уменьшается. При этом значимых связей между параметрами А и В для высот и диаметров не выявлено (рис. 8 и 9).

Рис. 8.

Соотношения между параметрами Ad и Ah для насаждений в возрастах 20–30 лет (1) и свыше 40 лет (2).

Рис. 9.

Соотношения между параметрами Bd и Bh для насаждений в возрастах 20–30 лет (1) и свыше 40 лет (2).

ОБСУЖДЕНИЕ

Таким образом, использование предложенной GOE-модели позволяет с высокой точностью охарактеризовать распределение деревьев в насаждении по высотам и диаметрам стволов. Корректность описания распределений по высотам и диаметрам с помощью GOE-модели может указывать на хаотический характер взаимодействия между деревьями в насаждении. Применимость модели хаоса для описания распределения деревьев в насаждении по таксационным показателям может быть связана с нерегулярностью пространственной структуры насаждения, что приводит к сильному разбросу расстояний между деревьями и, как следствие, к различию в характере конкурентных или кооперативных взаимодействий между деревьями. В этой связи было бы интересно сравнить различия характеристик GOE-модели для естественных древостоев и рядовых посадок с фиксированными расстояниями между деревьями. Отсутствие тренда параметров Bd и Bh можно трактовать как постоянство значений моды обратных значений таксационных параметров h и d для насаждений разных возрастов.

Представляется, что найденные при переходе к обратной шкале с помощью GOE-ансамбля закономерности распределения деревьев в насаждении по высотам и диаметрам носят общий характер для насаждений разных пород и возрастов. По-видимому, найденные при переходе к описанию в экологических шкалах с помощью GOE-ансамбля закономерности распределения деревьев в насаждении по высотам и диаметрам фактически количественно выражают выдвинутый еще Н.В. Третьяковым (1927) принцип единства структуры лесных насаждений.

ЗАКЛЮЧЕНИЕ

Давно замечено, что в разных научных областях имеют место процессы, схожие между собой. Так, ранее нами было показано сходство между процессами в экономике и процессами роста насаждений (Soukhovolsky, Ivanova, 2018), между динамикой численности лесных насекомых, развитием эпидемий и процессами фазовых переходов в физических системах (Суховольский, Ковалев, 2020; Суховольский и др., 2020). При этом сходство между моделями заключается не просто в использовании общих математических моделей (модели, использующие для описания процессов дифференциальные уравнения, встречаются в самых разных областях науки, и это никого не удивляет понятно почему: дифференциальные уравнения – это “язык” науки), а в близости базовых представлений о процессах в этих областях. В настоящей работе показано, что сходными моделями могут быть описаны взаимодействия как в атомном ядре, так и в лесном насаждении. Что это может означать? И в атомном ядре, и в насаждении мы имеем дело c системами сильно взаимодействующих компонентов. Описание таких сильно взаимодействующих систем в науке началось, по-видимому, с описания взаимодействий между молекулами в газах, прямо измерить которые для числа молекул, равного числу Авогадро $6 \times {{10}^{{23}}}\;{\text{мол}}{{{\text{ь}}}^{{ - 1}}}$, невозможно, с помощью таких легко измеряемых макропеременных, как температура, давление и объем. В нашем случае системное сходство между описаниями процессов в атомном ядре и в лесном насаждении заключается в трудностях прямого описания процессов взаимодействия и в возможностях введения макропеременных, описываемых моделью GOE. Пригодность GOE-модели для описания распределения деревьев в насаждении по высотам и диаметрам позволяет говорить о возможности введения функции риска гибели деревьев в насаждении как некоторого аналога гамильтониана для физических систем.

Список литературы

  1. Бузыкин А.И., Секретенко О.П., Хлебопрос Р.Г., 2009. Данные наблюдений и анализ горизонтальной структуры на пяти пробных площадях в одновозрастных древесных ценозах. Красноярск: Ин-т леса им. В.Н. Сукачева СО РАН. 80 с.

  2. Вигнер Ю., 1961. Теория групп и ее приложения к квантовомеханической теории атомных спектров. М.: ИЛ. 452 с.

  3. Ганина Н.В., 1984. Распределение деревьев по диаметру с помощью функции Вейбулла // Лесоведение. № 2. С. 17–19.

  4. Гнеденко Б.В., 1988. Курс теории вероятностей. М.: Наука; Гл. ред. физ.-мат. лит. 448 с.

  5. Дайсон Ф., 1963. Статистическая теория энергетических уровней сложных систем. М.: ИЛ. 121 с.

  6. Двайт Г.Б., 1978. Таблица интегралов и другие математические формулы. М.: Наука. 228 с.

  7. Зи Э., 2009. Квантовая теория поля в двух словах. М.; Ижевск: НИЦ РХД. 632 с.

  8. Лебков В.Ф., 1990. Динамика распределения деревьев сосны по морфометрическим показателям ствола и кроны // Лесоведение. № 5. С. 57–68.

  9. Лебков В.Ф., Каплина Н.Ф., 2008. Закономерности и оценки структуры древостоев сосны // Лесное хозяйство. № 3. С. 39–41.

  10. Мета М.Л., 2012. Случайные матрицы. М.: Изд-во МЦНМО. 648 с.

  11. Острейковский В.А., 2003. Теория надeжности. М.: Высш. шк. 463 с.

  12. Поллард Дж., 1982. Справочник по вычислительным методам статистики. М.: Финансы и статистика. 344 с.

  13. Рыжков О.В., 2000. Особенности распределения деревьев по диаметру в заповедных лесах центральной лесостепи // Лесоведение. № 5. С. 43–52.

  14. Суховольский В.Г., Ковалев А.В., 2020. Моделирование эпидемии коронавируса как фазового перехода // Журн. общ. биологии. Т. 81. № 5. С. 362–373.

  15. Суховольский В.Г., Тарасова О.В., Ковалев А.В., 2020. Моделирование критических явлений в популяциях лесных насекомых // Журн. общ. биологии. Т. 81. № 5. С. 374–386.

  16. Третьяков Н.В., 1927. Закон единства в строении насаждений. М.; Л.: Новая деревня. 113 с.

  17. Усольцев В.А., 2013. Продукционные показатели и конкурентные отношения деревьев. Исследование зависимостей. Екатеринбург: УГЛТУ. 555 с.

  18. Bailey R.L., Dell T.R., 1973. Quantifying diameter distribution with the Weibull function // For. Sci. V. 19. № 2. P. 97–104.

  19. Bredford S.C., 1948. The documentary chaos // Documentation / Ed. Bredford S.C. L.: Crosby Lockwood. P. 106–121.

  20. Cao Q.V., 2004. Predicting parameters of a Weibull function for modelling diameter distribution // For. Sci. V. 50. № 5. P. 682–685.

  21. Darwin Ch., 1859. On the Origin of Species by Means of Natural Selection, or the Preservation of Favoured Races in the Struggle for Life. L.: John Murray. 501 p.

  22. Dyson F.J., 1962. Statistical theory of the energy levels of complex systems // J. Math. Phys. V. 3. P. 140–175.

  23. Ek A.R., Issos J.N., Bailey R.L., 1975. Solving for Weibull diameter distribution parameters to obtain specified mean diameters // For. Sci. V. 21. P. 290–292.

  24. Fonseca T.F., Marques C.P., Parresol B.R., 2009. Describing maritime pine diameter distributions with Johnson’s SB distribution using a new all-parameter recovery approach // For. Sci. V. 55. № 4. P. 367–373.

  25. Gómez-Garcia E., Crecente-Campo F., Tobin B., Hawkins M., Nieuwenhuis M., Diéguez-Arenda U., 2014. A dynamic volume and biomass growth models system for even-aged downy birch stands in south-western Europe // Forestry. V. 87. P. 165–176.

  26. Gorgoso-Varela J.J., Rojo-Alboreca A., 2014. Short communication: A comparison of estimation methods for fitting Weibull and Johnson’s SB functions to pedunculate oak (Quercus robur) and birch (Betula pubescens) stands in northwest Spain // For. Syst. V. 23. № 3. P. 500–505.

  27. Gorgoso-Varela J.J., Garcia-Villabrille J.D., Rojo-Alboreca A., Gadow K., Alvarez-Gonzalez J.G., 2016. Comparing Johnson’s SBB, Weibull and Logit-Logistic bivariate distributions for modeling tree diameters and heights using copulas // For. Syst. V. 25. № 1. https://doi.org/10.5424/fs/2016251-08487

  28. Jaworski A., Podlaski R., 2012. Modelling irregular and multimodal tree diameter distributions by finite mixture models: an approach to stand structure characterization // J. For. Res. V. 17. № 1. P. 79–88.

  29. Jin X., Li F., Jia W., Zhang L., 2013. Modelling and predicting bivariate distributions of tree diameter and height // Sci. Silvae Sin. V. 49. № 6. P. 74–82.

  30. Kangas A., Maltamo M., 2000. Performance of percentile based diameter distribution prediction and Weibull method in independent data sets // Silva Fenn. V. 34. P. 381–398.

  31. Laar A., van, Akca A., 2007. Forest Mensuration. Dordrecht: Springer. 389 p.

  32. Lei Y., 2008. Evaluation of three methods for estimating the Weibull distribution parameters of Chinese pine (Pinus tabulaeformis) // J. For. Sci. V. 54. P. 566–571.

  33. Li F., Zhang L., Davis C.J., 2002. Modelling the joint distribution of tree diameters and heights by bivariate generalized beta distribution // For. Sci. V. 48. № 1. P. 47–58.

  34. Lima R.A.F., de, Batista J.L.F., Prado P.I., 2015. Modeling tree diameter distributions in natural forests: An evaluation of 10 statistical models // For. Sci. V. 61. P. 320–327.

  35. Lin C., Tsogt K., Zandraabal T., 2016. A decompositional stand structure analysis for exploring stand dynamics of multiple attributes of a mixed-species forest // For. Ecol. Manag. V. 378. P. 111–121.

  36. Liu F., Li F., Zhang L., Jin X., 2014. Modelling diameter distributions of mixed-species forest stands // Scand. J. For. Res. V. 28. № 7. P. 653–663.

  37. Maltamo M., Puumalainen J., Päivinen R., 1995. Comparison of beta and Weibull functions for modelling basal area diameter distribution in stands of Pinus sylvestris and Picea abies // Scand. J. For. Res. V. 10. P. 284–295.

  38. Maltamo M., Kangas A., Uuttera J., Torniainen T., Saramäki J., 2000. Comparison of percentile based prediction methods and the Weibull distribution in describing the diameter distribution of heterogeneous Scots pine stands // For. Ecol. Manag. V. 133. P. 263–274.

  39. Malthus T.R., 1798. An Essay on the Principle of Population, As It Affects the Future Improvement of Society. L.: J. Johnson. 396 p.

  40. Mateus A., Tomé M., 2011. Modeling the diameter distribution of Eucalyptus plantations with Johnson’s probability density function: Parameters recovery from a compatible system of equations to predict stand variables // Ann. For. Sci. V. 68. P. 325–335.

  41. Mehta M.L., 2004. Random Matrices. Amsterdam; San Diego: Elsevier/Academic Press. 688 p.

  42. Mehtätalo L., de-Miguel S., Gregoire T.G., 2015. Modelling height-diameter curves for prediction // Can. J. For. Res. V. 45. P. 826–837.

  43. Mergani C.J., Sterba H., 2006. Characterisation of diameter distribution using the Weibull function: Method of moments // Eur. J. For. Res. V. 125. P. 427–439.

  44. Newton P.F., Lei Y., Zhang S.Y., 2004. A parameter recovery model for estimating black spruce diameter distributions within the context of a stand density management diagram // For. Chron. V. 80. P. 349–358.

  45. Nord-Larsen T., Cao Q.V., 2006. A diameter distribution model for even-aged beech in Denmark // For. Ecol. Manag. V. 231. P. 218–225.

  46. Ozcelik R., Cao Q.V., Trincado G., Nilsum G., 2018. Predicting tree height from tree diameter and dominant height using mixed-effect and quantile regression models for two species in Turkey // For. Ecol. Manag. V. 419–420. P. 240–248.

  47. Palahí M., Pukkala T., Blasco E., Trasobares A., 2007. Comparison of beta, Johnson’s SB, Weibull and truncated Weibull functions for modelling the diameter distribution of forest stands in Catalonia (north-east of Spain) // Eur. J. For. Res. V. 126. P. 563–571.

  48. Pareto V., 1896. Cours d’economie politique. Lausanne: F. Rouge. 430 p.

  49. Podlaski R., 2017. Forest modelling: the gamma shape mixture model and simulation of tree diameter distributions // Ann. For. Sci. V. 74. № 2. P. 29–39.

  50. Pogoda P., Ochał W., Orzeł S., 2019. Modeling diameter distribution of black alder (Alnus glutinosa (L.) Gaertn.) stands in Poland // Forests. V. 10. P. 412–428.

  51. Poudel K.P., Cao Q.V., 2013. Evaluation of methods to predict Weibull parameters for characterizing diameter distributions // For. Sci. V. 59. № 2. P. 243–252.

  52. Sharma R.P., Vacek Z., Vacek S., Kucera M., 2019. Modelling individual tree height-diameter relationships for multi-layered and multi-species forests in central Europe // Tree. V. 33. № 1. P. 103–119.

  53. Shiver B.D., 1988. Sample sizes and estimation methods for the Weibull distribution for unthinned slash pine plantation diameter distributions // For. Sci. V. 34. P. 809–814.

  54. Soukhovolsky V., Ivanova Y., 2018. Modeling production processes in forest stands: An adaptation of the Solow growth model // Forests. V. 9. P. 391–403.

  55. Stankova T.V., Zlatanov T.M., 2010. Modelling diameter distribution of Austrian black pine (Pinus nigra Arn.) plantations: A comparison of the Weibull frequency distribution function and percentile-based projection methods // Eur. J. For. Res. V. 129. P. 1169–1179.

  56. Stockmann H.-J., 2007. Quantum Chaos. An Introduction. Cambridge: Cambridge Univ. Press. 386 p.

  57. Tsogt K., Lin C., 2014. A flexible modelling of irregular diameter structure for the volume estimation of forest stands // J. For. Res. V. 19. P. 1–11.

  58. Weibull W., 1951. A statistical distribution function of wide applicability // J. Appl. Mech. V. 18. P. 293–297.

  59. Wigner E.P., 1951. On the statistical distribution of the widths and spacing of nuclear resonance levels // Math. Proc. Camb. Philos. Soc. V. 47. P. 790–798.

  60. Yule G.U., 1924. A mathematical theory of evolutionary based on conclusions of Dr. J.C. Willis, F.R.S. // Philos. Trans. Roy. Soc. B. V. 213. P. 21–87.

  61. Zasada M., Cieszewski C.J., 2005. A finite mixture distribution approach for characterizing tree diameter distributions by natural social class in pure even-aged Scots pine stand in Poland // For. Ecol. Manag. V. 204. P. 145–158.

  62. Zhang L., Liu C., 2006. Fitting irregular diameter distributions of forest stands by Weibull, modified Weibull, and mixture Weibull models // J. For. Res. V. 11. P. 369–372.

  63. Zhang L., Kevin C.P., Chuanmin L., 2003. A comparison of estimation methods for fitting Weibull and Johnson’s SB distributions to mixed spruce-fir stands in north-eastern North America // Can. J. For. Res. V. 33. P. 1340–1347.

  64. Zhang L., Gove J.H., Liu C., Leak W.B., 2001. A finite mixture of two Weibull distributions for modelling the diameter distributions of rotated-sigmoid, uneven-aged stands // Can. J. For. Res. V. 31. P. 1654–1659.

  65. Zhang X., Lei Y., 2010. A linkage among whole-stand model, individual-tree model and diameter-distribution model // J. For. Sci. V. 56. P. 600–608.

  66. Zipf G.K., 1949. Human Behaviour and the Principle of Least Effort. Cambridge: Addison-Wesley. 600 p.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Журнал общей биологии

Архивы выпусков Информация о журнале Отправить рукопись в журнал