1. На главную
  2. Электронные версии
  3. Журнал неорганической химии
  4. T. 67, № 3, 2022

Журнал неорганической химии, 2022, T. 67, № 3, стр. 384-396

Полярность бордипирринов и их строение: полуэмпирический и хемоинформационный анализ

Ф. Ю. Телегин a, *, Ю. С. Марфин a

a Ивановский государственный химико-технологический университет
153000 Иваново, Шереметевский пр-т, 7, Россия

* E-mail: telegin@isuct.ru

Поступила в редакцию 08.09.2021
После доработки 01.11.2021
Принята к публикации 14.11.2021

Полный текст (PDF)

Аннотация

Представлено простое феноменологическое обоснование метода определения полярности бордипирринов на основе спектральных характеристик поглощения и излучения флуорофоров в различных растворителях. Этот метод является новым инструментом экспериментальной оценки влияния растворителя на чувствительность флуорофоров к полярности среды. С использованием фрагментного подхода проведен хемоинформационный анализ библиотеки соединений бордипирринов, собранной из литературных данных и охватывающей широкий спектр сольватохромных эффектов от отрицательных до положительных. Выявлены наиболее значимые фрагменты молекул, ответственные за чувствительность соединений к полярности среды. Установлено, что положительный и отрицательный сольватохромные эффекты усиливаются с повышением молекулярной поляризуемости соединений, что согласуется с параметрами найденных фрагментов BODIPY как цепочек сопряженных ненасыщенных связей. В целом полуэмпирический метод определения полярности флуорофоров и результаты хемоинформационного анализа дают расширенное понимание закономерностей влияния растворителей на спектральное поведение флуоресцентных красителей и дизайн новых соединений.

Ключевые слова: BODIPY, полярность бордипирринов, сольватохромный эффект, хемоинформационный анализ, QSPR

Авторы посвящают свою работу выдающемуся ученому Геннадию Алексеевичу Крестову, чей вклад в развитие представлений о растворах сложно переоценить. Именно Геннадий Алексеевич заложил в Ивановском государственном химико-технологическом университете фундамент исследований по влиянию растворителя на характеристики протекающих процессов и свойства соединений. Частью этих исследований является и настоящая работа по анализу влияния растворителя на спектральные и фотофизические свойства люминофоров на основе борфторидных комплексов дипирринов. Авторы продолжают дело Геннадия Алексеевича на кафедре неорганической химии ИГХТУ.

ВВЕДЕНИЕ

Бордипиррины (BODIPY) находят применение в различных областях науки и в технологиях как в виде индивидуальных соединений, так и в составе функциональных материалов [1–4]. Особенно широко исследуется их аналитическая чувствительность и избирательность к характеристикам полярности окружения и возможности визуализации строения живых клеток и тканей [5–10]. В исследованиях локальной полярности клеток и мембран с использованием флуоресцентных меток на основе бордипирринов наряду с флуорофорами другого химического строения [11–14] достигнуты весьма внушительные результаты в диагностике болезней и изучении физиологии и патологии клеток, визуализации клеточной мембраны, эндоплазматического ретикулума и липидных тел при изучении их строения и реакции клеток на окислительный стресс.

В ряде случаев полярность среды оказывает существенное влияние на функциональные свойства люминофоров. Так, применение флуорофоров для оценки локальной кислотности среды в клетках и биологических тканях осложнено тем, что полярное окружение весьма существенно влияет на флуоресценцию рН-сенсора, переключая его активность в результате изменения дипольного момента в возбужденном состоянии [15–17]. Высокая роль полярности среды проявляется в случае эмиссии, стимулированной агрегацией бордипирринов [18] (aggregation-induced emission, AIE). Последний эффект широко изучается как общее явление для большого числа флуорофоров [19, 20], открывающее новые пути к дизайну биохимических сенсоров и светодиодов. Примерами могут служить мезо-фенил, дифенилзамещенные бордипиррины [21] и многоядерные иод-производные конъюгаты [22].

В настоящее время известно множество химических структур BODIPY, чувствительных к полярному окружению. Примером высокополярных соединений, обладающих положительным сольватохромным эффектом, могут служить стирильные производные [23] и мезо-фторметильные производные с 3-диметиламинофенильной группой [24]. Производные дипирринов с высоким отрицательным сольватохромным эффектом могут быть представлены соединениями, подобными гемицианинам [25, 26]. Некоторые простые производные бордипиррина обладают небольшим стоксовым сдвигом и малой чувствительностью к полярности среды [27]. Таким образом, определение параметров влияния сольватного окружения на спектральные характеристики дипирринов и их производных представляет актуальную задачу не только в дизайне сенсоров полярности, но и при конструировании систем, чувствительных к широкому спектру эффектов молекулярного окружения, где полярность также может влиять на эксплуатационные характеристики молекул.

Спектральные свойства флуорофоров обычно описывают с точки зрения их спектрального поведения в растворителях различной полярности. Применительно к обычным красителям, не проявляющим флуоресцентные свойства, это явление именуется сольватохромизмом. Для изучения люминофоров иногда используется термин сольватофлуорохромизм, следуя фундаментальным работам Теренина [28] и Бахшиева [29–31]. Однако в ранних исследованиях Бахшиева [32] по изучению спектрального поведения флуорофоров этот термин не использовался. В англоязычной литературе термин “solvatofluorochromism” или “solvafluorochromism” также используется нечасто, например, в работах [33–35]. Мы будем придерживаться простого и более традиционного термина “сольватохромизм флуорофора”, принимая во внимание, что понятие цвета (chromo-, χρῶμα, греч.) объединяет несколько путей его формирования: излучение, пропускание и отражение [36].

Сольватохромизм флуоресцентных соединений рассматривается на базе различных теоретических подходов [37, 38] и эмпирических шкал полярности растворителей [39–42]. Последнее, несмотря на подробное рассмотрение механизма сольватации, часто не дает удовлетворительных результатов при количественной характеристике сольватохромизма за счет больших статистических погрешностей сравнительно малого количества применяемых растворителей [43–46]. В литературе накоплены фрагментарные данные об интересующих нас бордипирринах, что затрудняет дальнейший количественный анализ их строения и свойств на единой теоретической или эмпирической основе.

Указанные выше трудности в количественной характеристике BODIPY сдерживают применение современных средств анализа взаимосвязи строение–свойство с использованием методов хемоинформатики, получившей значительное развитие за последние 20 лет [47]. В области анализа строения и свойств исследуемых люминофоров такие подходы также использовались, хотя немногочисленные исследования ограничивались рассмотрением спектральных свойств группы бордипирринов [48], межклеточной локализации производных бордипирринов [49] и их избирательным поглощением органеллами клетки [50].

В нашей работе в качестве предварительного исследования был применен прогрессивный и хорошо адаптированный для физико-химических исследований фрагментный подход, развитый в работах [51, 52] для анализа сенсибилизаторов солнечных батарей на основе бордипирринов и порфиринов, а также для предсказания спектральных свойств жидких кристаллов на основе бордипирринов [53, 54].

Настоящее исследование имеет целью систематический анализ сольватохромизма бордипирринов с помощью нового полуэмпирического подхода для количественной характеристики чувствительности соединений к полярности растворителей, а также применение методов хемоинформационного анализа для обобщения данных большой группы люминофоров.

РЕЗУЛЬТАТЫ И ОБСУЖДЕНИЕ

Физико-химическое обоснование экспериментального определения полярности флуорофоров

Ниже представлено краткое описание полуэмпирического метода, положенного в основу экспериментального определения полярности флуорофоров. Исходные предпосылки найдены в теории Липтэя (Liptay) [55, 56], в которой сформулирована связь волновых чисел для максимумов поглощения и эмиссии флуорофора с физико-химическими свойствами растворителя:

(1)
${{\nu }_{{Abs}}} - {{\nu }_{{Em}}} = {{m}_{f}}f\left( {\varepsilon ,n} \right) + {{\Delta }^{o}},$
(2)
${{\nu }_{{Abs}}} + {{\nu }_{{Em}}} = - {{m}_{\varphi }}\varphi \left( {\varepsilon ,n} \right) + {{{{\Sigma }}}^{o}},$
где коэффициенты наклона ${{m}_{f}}$ и ${{m}_{{{\varphi }}}}$, а также функции растворителя $f\left( {\varepsilon ,n} \right)$ и ${{\varphi }}\left( \varepsilon \right)$ oписываются следующим образом:
(3)
${{m}_{f}} = \frac{{2{{{\left( {{{\mu }_{e}} - {{\mu }_{g}}} \right)}}^{2}}}}{{hc{{a}^{3}}}};\,\,\,\,{{m}_{{{{m}_{\varphi }}}}} = \frac{{2\left( {\mu _{e}^{2} - \mu _{g}^{2}} \right)}}{{hc{{a}^{3}}}},$
(4)
$\begin{gathered} f\left( {\varepsilon ,n} \right) = \frac{{\frac{{\varepsilon - 1}}{{2\varepsilon + 1}} - \frac{{{{n}^{2}} - 1}}{{2{{n}^{2}} + 1}}}}{{\left( {1 - \frac{{2\alpha }}{{{{a}^{3}}}}\frac{{\varepsilon - 1}}{{2\varepsilon + 1}}} \right)\left( {1 - \frac{{2\alpha }}{{{{a}^{3}}}}\frac{{{{n}^{2}} - 1}}{{2{{n}^{2}} + 1}}} \right)}}, \\ \varphi \left( \varepsilon \right) = \frac{{\frac{{\varepsilon - 1}}{{2\varepsilon + 1}}}}{{1 - \frac{{2\alpha }}{{{{a}^{3}}}}\frac{{\varepsilon - 1}}{{2\varepsilon + 1}}}}, \\ \end{gathered} $
${{\Delta }^{o}},~{{{{\Sigma }}}^{o}} = const,$
где ${{\mu }_{g}}$, ${{\mu }_{e}}$ – дипольные моменты молекулы флуорофора в основном и возбужденном состоянии; α – поляризуемость молекулы; $a$ – радиус молекулы согласно определению Онзагера; с – скорость света в вакууме; h – постоянная Планка; ε – относительная диэлектрическая проницаемость; n – показатель преломления. Для простоты записи предполагается, что дипольные моменты параллельны друг другу, поэтому индекс вектора опущен.

В той или иной степени уравнения (1) и (2) обобщают феноменологические подходы, известные как уравнения Липперта–Матаги, Балтера [57] и Коти [58]. В то же время эти уравнения по форме функций растворителя отличаются от уравнений Билота–Кавски и Бахшиева.

Хорошо видно, что названные функции растворителя проявляют линейную зависимость:

(5)
$\begin{gathered} f\left( {\varepsilon ,n} \right) = \frac{{\frac{{\varepsilon - 1}}{{2\varepsilon + 1}} - \frac{{{{n}^{2}} - 1}}{{2{{n}^{2}} + 1}}}}{{\left( {1 - \frac{{2\alpha }}{{{{a}^{3}}}}\frac{{\varepsilon - 1}}{{2\varepsilon + 1}}} \right)\left( {1 - \frac{{2\alpha }}{{{{a}^{3}}}}\frac{{{{n}^{2}} - 1}}{{2{{n}^{2}} + 1}}} \right)}} = \\ = \,\,\frac{{\varphi (\varepsilon )}}{{1 - \frac{{2\alpha }}{{{{a}^{3}}}}\frac{{{{n}^{2}} - 1}}{{2{{n}^{2}} + 1}}}} - \frac{{\frac{{{{n}^{2}} - 1}}{{2{{n}^{2}} + 1}}}}{{\left( {1 - \frac{{2\alpha }}{{{{a}^{3}}}}\frac{{\varepsilon - 1}}{{2\varepsilon + 1}}} \right)\left( {1 - \frac{{2\alpha }}{{{{a}^{3}}}}\frac{{{{n}^{2}} - 1}}{{2{{n}^{2}} + 1}}} \right)}}, \\ \end{gathered} $
(6)
${\text{или }}f\left( {\varepsilon ,n} \right) = P\varphi \left( {\varepsilon ,n} \right) + Q,$
где уравнение (6) является краткой записью уравнения (5), а коэффициенты P и Q можно выразить путем сравнения двух уравнений.

В действительности функции $f\left( {\varepsilon ,n} \right)$ и ${{\varphi }}\left( \varepsilon \right)$ проявляют линейную зависимость для совокупности физико-химических параметров 251 растворителя [40] с практически неизменным коэффициентом наклона $P,~$ равным ~1.02 (R2 = 0.94–0.98), в диапазоне поляризуемости $\alpha {\text{/}}{{a}^{3}}$–0.5. Соответствующие регрессионные уравнения показаны ниже:

(7)
$\begin{gathered} \frac{\alpha }{{{{a}^{3}}}} = 0,\,\,\,\,f\left( {\varepsilon ,n} \right) = \varphi \left( \varepsilon \right) \times 1.0218 \ldots - 0.2174, \\ {{R}^{2}} = 0.9429, \\ \end{gathered} $
(8)
$\begin{gathered} \frac{\alpha }{{{{a}^{3}}}} = 0.25,\,\,\,\,f\left( {\varepsilon ,n} \right) = \varphi \left( \varepsilon \right) \times 1.0205 \ldots - 0.2437, \\ {{R}^{2}} = 0.9587, \\ \end{gathered} $
(9)
$\begin{gathered} \frac{\alpha }{{{{a}^{3}}}} = 0.5,\,\,\,\,f\left( {\varepsilon ,n} \right) = \varphi \left( \varepsilon \right) \times 1.0181 \ldots - 0.2771, \\ {{R}^{2}} = 0.9752. \\ \end{gathered} $

Линейная регрессия на основе уравнений Билота–Кавски дает более низкий коэффициент линейной корреляции (R2 = 0.78), хотя на ограниченной выборке растворителей в широком диапазоне полярности можно получить более плотную корреляцию.

Основываясь на представленном выше анализе, коэффициенты $P$ и Q уравнения (6) можно выразить приближенными соотношениями:

(10)
$P \approx 1,\,\,\,\,~Q \approx - 0.25.$

Совместное рассмотрение уравнений (1) и (2) с учетом найденных упрощений позволяет кратко выразить несколько взаимосвязанных соотношений, удобных для анализа сольватохромного эффекта:

(11)
${{\nu }_{{Abs}}} - {{\nu }_{{Em}}} = - A\left( {{{\nu }_{{Abs}}} + {{\nu }_{{Em}}}} \right) + B,$
(12)
${{\nu }_{{Abs}}} = \frac{{1 - A}}{2}\left( {{{\nu }_{{Abs}}} + {{\nu }_{{Em}}}} \right) + \frac{B}{2},$
(13)
${{\nu }_{{Em}}} = \frac{{1 + A}}{2}\left( {{{\nu }_{{Abs}}} + {{\nu }_{{Em}}}} \right) - \frac{B}{2},$
(14)
${{\nu }_{{Abs}}} = \frac{{1 - A}}{{1 + A}}{{\nu }_{{Em}}} + \frac{B}{{1 + A}},$
(15)
$\begin{gathered} A = P\frac{{{{m}_{f}}}}{{{{m}_{\varphi }}}} \approx \frac{{{{\mu }_{e}} - {{\mu }_{g}}}}{{{{\mu }_{e}} + {{\mu }_{g}}}} = \frac{{{{\mu }_{e}}{\text{/}}{{\mu }_{g}} - 1}}{{{{\mu }_{e}}{\text{/}}{{\mu }_{g}} + 1}} = Const; \\ \frac{{1 - A}}{{1 + A}} = \frac{{{{\mu }_{g}}}}{{{{\mu }_{e}}}}, \\ \end{gathered} $
(16)
$B = {{{{\Sigma }}}^{0}}P\frac{{{{m}_{f}}}}{{{{m}_{\varphi }}}} + Q{{m}_{f}} + {{{{\Delta }}}^{0}} = Const.$

Уравнение (11) представляет собой соотношение двух фундаментальных параметров, характеризующих процесс переноса заряда в флуорофорах с позиций теории Маркуса [59]: общей энергии реорганизации ${{{{\lambda }}}_{r}}$, характеризующей потерю энергии растворенного вещества благодаря реорганизации растворителя и растворенного вещества, и энергии ${{E}_{{00}}} = - {{\Delta }}{{G}^{0}}$, равной изменению свободной энергии при возбуждении молекулы:

(17)
$2{{\lambda }_{r}} = {{\nu }_{{Abs}}} - {{\nu }_{{Em}}},\,\,\,\, - 2{{\Delta }}{{G}^{0}} = 2{{E}_{{00}}} = \left( {{{\nu }_{{Abs}}} + {{\nu }_{{Em}}}} \right).$

Здесь и далее величины волновых чисел выражены в 1000 см–1 в соответствии с длиной волны максимума поглощения или флуоресценции:

(18)
$\nu = {{10}^{4}}{\text{/}}\lambda ,1000\,\,{\text{с}}{{{\text{м}}}^{{--1}}}.$

Параметр A определяется соотношением дипольных моментов флуорофора в основном и возбужденном состоянии согласно формуле (15), что характеризует полярность соединения. С другой стороны, это определяет чувствительность растворенного соединения к полярному окружению и направление этих изменений, т.е. A > 0 для положительного сольватохромного эффекта и A < 0 – для отрицательного.

Главное преимущество предложенного подхода для количественного анализа сольватохромного эффекта люминофоров состоит в том, что зависимость спектральных функций от параметров растворителей “сжата” в коэффициент P, приближенно равный единице, в результате определение величины и знака сольватохромного эффекта сводится к определению наклона одной из функций (11)–(14). Указанные функции являются взаимно коррелированными, поэтому существует возможность проверить установленный параметр по каждой из функций в зависимости от удобства представления данных и наблюдаемого разброса. Остается еще возможность оценки параметра А по известным значениям дипольных моментов, что представляет интерес для предсказания взаимных изменений спектральных характеристик поглощения, флуоресценции и их разности при изменении полярности среды. Это имеет значение для изучения флуоресцентных зондов в полярных и неполярных средах с неизвестными физико-химическими свойствами, такими как биологические среды, смешанные растворители, жидкие кристаллы, ионные жидкости, полимерные среды.

Графическую визуализацию соотношения между поглощением и эмиссией можно определить термином “absorption-emission mapping (AE-mapping)”, используя хемоинформационную терминологию. Элементы такого подхода реализованы при анализе спектральных свойств семейства бордипирринов, соответствующих одному растворителю [48]. В работе [60], напротив, линейная связь волновых чисел поглощения и эмиссии, аналогичная уравнению (14), использована для оценки отношения дипольных моментов флуорофора продан (PRODAN) в серии растворителей.

Физико-химический анализ взаимосвязи между химическим строением и свойствами отдельных соединений

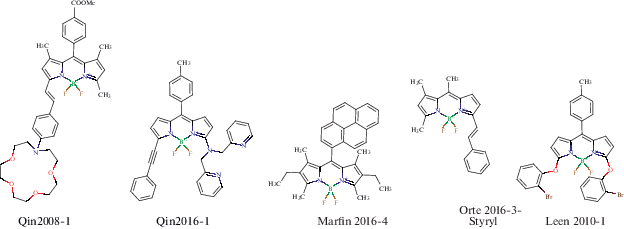
В целях иллюстрации представленного выше полуэмпирического метода были выбраны результаты нескольких работ, предоставляющих достаточно подробные данные по спектральному поведению бордипирринов в больших сериях растворителей. На cхеме 1 показаны структурные формулы соединений в широком диапазоне сольватохромных характеристик, которые проанализированы в данной работе.

Схема 1 . Структурные формулы бордипирринов, построенные с использованием программного обеспечения JChem for Office [61].

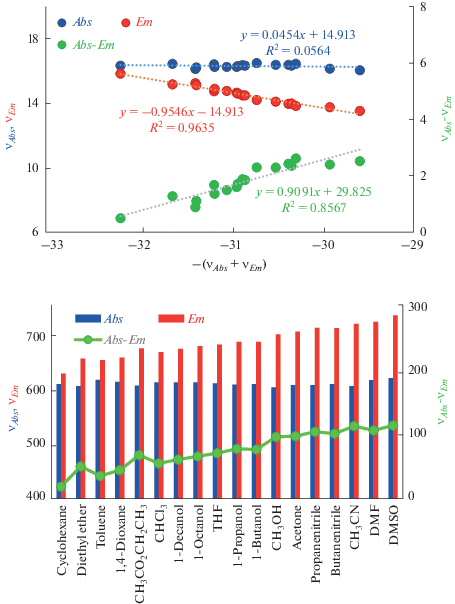
На рис. 1a показана зависимость стоксова сдвига, волновых чисел поглощения и эмиссии соединения Qin2008-1 (схема обозначения соединений, принятая в данной статье, соответствует первому автору, дате публикации и индексу соединения, использованного авторами оригинального исследования). Как следует из уравнения (11), наклон зависимости стоксова сдвига от отрицательного значения суммы волновых чисел непосредственно определяет коэффициент полярности A. Наклоны зависимости значений волновых чисел максимума поглощения и эмиссии определяют этот параметр как функцию коэффициентов уравнений (12) и (13). Наиболее плотную корреляцию в этом случае проявляет кривая для флуоресценции. Несмотря на различие коэффициентов корреляции, каждая кривая дает одинаковое значение параметра A = 0.91, что свидетельствует о взаимной коррелированности всех трех кривых. Для более ясного понимания представленной выше информации рис. 1б иллюстрирует изменение длин волн в названном списке растворителей, расположенных в порядке возрастания отрицательного значения суммарного волнового числа, характеризующего удвоенную свободную энергию возбуждения флуорофора. Очевидно, что порядок растворителей слева направо в этом случае соответствует возрастанию их полярности. Общий характер поведения кривых на рис. 1a, 1б свидетельствует о проявлении положительного сольватохромизма, который характеризуется ярко выраженным смещением полосы флуоресценции в длинноволновую область, что соответствует высокой полярности соединения Qin2008-1 с большим значением параметра A.

Рис. 1.

Корреляция между спектральными параметрами ${{\nu }_{{Abs~}}}$, ${{\nu }_{{Em}}}$ и $\left( {{{\nu }_{{Abs}}} + {{\nu }_{{Em}}}} \right)$ в соответствии с уравнениями (11)–(13) для соединения Qin2008-1 (а), изменение длины волны максимумов поглощения и флуоресценции в различных растворителях в возрастающем порядке величины $ - \left( {{{\nu }_{{Abs}}} + {{\nu }_{{Em}}}} \right)$ для соединения Qin2008-1 (б).

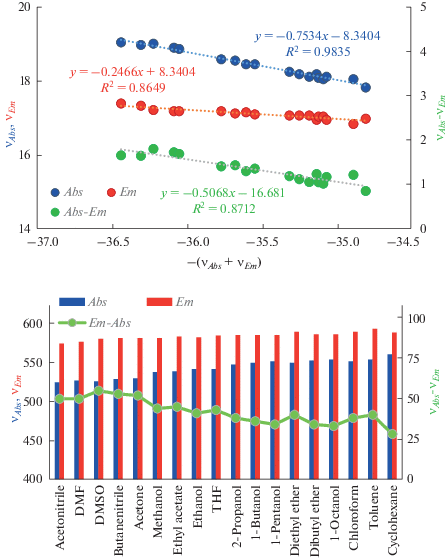
На рис. 2a, 2б представлены серии аналогичных кривых для соединения Qin2016-1. В данном случае производное бордипиррина, имеющее сильные электронодонорные заместители в положениях 3 и 3', проявляет достаточно большой отрицательный сольватохромный эффект, что отражается обратным порядком растворителей на рис. 2б и смещением полос поглощения и флуоресценции в коротковолновую область при повышении полярности растворителя. В отличие от рассмотренных случаев, полоса поглощения более надежна для определения наклона и соответствующего параметра полярности соединения, хотя все три кривые дают одинаковый результат – A = –0.51.

Рис. 2.

Корреляция между спектральными параметрами ${{\nu }_{{Abs~}}}$, ${{\nu }_{{Em}}}$ и $\left( {{{\nu }_{{Abs}}} + {{\nu }_{{Em}}}} \right)$ в соответствии с уравнениями (11)–(13) для соединения Qin2016-1 (а), изменение длины волны максимумов поглощения и флуоресценции в различных растворителях в возрастающем порядке величины $ - \left( {{{\nu }_{{Abs}}} + {{\nu }_{{Em}}}} \right)$ для соединения Qin2016-1 (б).

На рис. 3 представлена AE-диаграмма в координатах длин волн поглощения и эмиссии, позволяющая наглядно увидеть спектральное поведение упомянутых выше соединений Qin2008-1 и Qin2016-1 наряду с другими, указанными на схеме 1 . Анализ диаграммы показывает, что соединение Qin2008-1 обладает значительно большей чувствительностью к полярности среды по сравнению с другими менее полярными соединениями. Следует отметить, что горизонтальный ход кривой для этого соединения на рис. 3, как и на аналогичном графике в координатах волновых чисел, не позволяет надежно определить отношение дипольных моментов. Соединение Qin2016-1, обладающее значительным отрицательным сольватохромным эффектом, не проявляет столь сильного смещения полосы флуоресценции. Для соединений Marfin2016-4, Orte2016-3-styryl и Leen2010-1, представленных на схеме 1 , длина волны максимума флуоресценции также изменяется в узких пределах, что отвечает низким значениям параметра полярности, представленным в табл. 1 для этих флуорофоров. Некоторые расчетные физико-химические параметры соединений приведены в табл. 2.

Рис. 3.

AE-диаграмма: соотношение между длиной волны максимума поглощения и эмиссии для бордипирринов различной полярности.

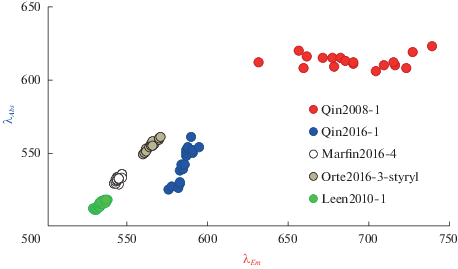
Таблица 1.  

Экспериментальные значения параметра полярности А ряда бордипирринов*

ID N A B R2
Qin2008-1 [62] 20 0.909 29.8 0.96
Qin2016-1 [63] 18 –0.507 –16.7 0.98
Marfin2016-4 [64] 16 –0.0369 –0.975 0.83
Orte2016-3-Styryl [65] 17 –0.0320 –0.847 0.98
Leen2010-1 [66] 20 0.0611 2.99 0.93
Qin2008-1 [62] 20 0.909 29.8 0.96

* ID – идентификационный номер соединения, принятый в данной статье (соответствует первому автору, дате публикации и индексу соединения, использованного авторами оригинального исследования); N – количество растворителей в серии; A, B – коэффициенты уравнений (11)–(14); R – коэффициент корреляции при определении параметров A и B для соединения в серии растворителей.

Таблица 2.  

Расчетные физико-химические свойства ряда бордипирринов*

ID DM lg P MP MV
Qin2008-1 [62] 13.6 1.66 72.3 624
Qin2016-1 [63] 10.5 1.63 63.8 512
Marfin2016-4 [64] 1.92 3.49 61.4 462
Orte2016-3-styryl [65] 5.23 0.82 36.6 300
Leen2010-1 [66] 6.5 3.58 55.6 436

* DM – дипольный момент в основном состоянии (Дебай); lg P – гидрофобность (безразмерная величина), MP – молекулярная поляризуемость (Å3), MV – молекулярный объем (Å3). Оценка молекулярных параметров выполнена с помощью программного обеспечения JСhem for Office [61].

Хемоинформационный анализ взаимосвязи химического строения и полярности бордипирринов

Представленный выше полуэмпирический метод анализа феноменологии сольватохромных эффектов флуорофоров позволяет проводить систематический анализ строения и свойств соединений. В отличие от многих других подходов к описанию сольватохромного эффекта в целом, предложенный параметр полярности соединений содержит информацию о спектральном поведении трех экспериментальных функций: полосы поглощения, флуоресценции и смещения Стокса в зависимости от полярности растворителя. Оценку этого параметра, а также анализ AE-диаграммы можно рассматривать как первый этап обобщения спектральных данных для флуорофоров в целях дальнейшего более глубокого хемоинформационного анализа библиотек соединений.

В настоящем исследовании выполнен хемоинформационный анализ строения и свойств бордипирринов в терминах полярности соединений с помощью фрагментного подхода и программного обеспечения Nasawin [51, 52]. База данных для исследования включает 110 соединений, каждое из которых характеризуется спектральными данными о поглощении и флуоресценции в 8–30 растворителях. Линейная модель множественной регрессии построена с использованием цепных фрагментов, включающих до 15 атомов. Анализ модели, полученной на стадии обучения, привел к выбору 10 фрагментов, показанных в табл. 3, с соответствующими коэффициентами регрессии, представленными в табл. 4.

Таблица 3.  

Фрагменты хемоинформационной модели, иллюстрированные различными BODIPY. Фрагменты соответствуют регрессионным коэффициентам, упомянутым ниже в табл. 4

Уменьшение полярности
Фрагмент 1 –
4 BODIPY 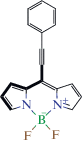		Фрагмент 6 –
4 BODIPY 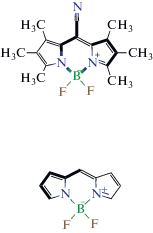		Фрагмент 7 –
3 BODIPY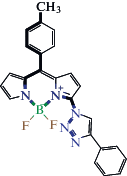
Фрагмент 8 –
5 BODIPY 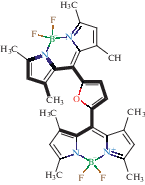		Фрагмент 9 –
8 BODIPY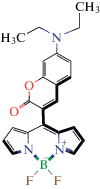 		 
Увеличение полярности
Фрагмент 2 –
9 BODIPY 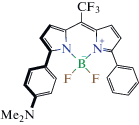		Фрагмент 3 – 22 BODIPY 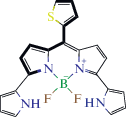Фрагмент 4 –
2 BODIPY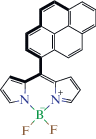
Фрагмент 5 –
7 BODIPY 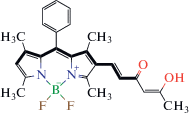		Фрагмент 10 –
3 BODIPY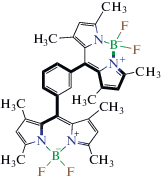
Таблица 4.  

Коэффициенты линейных моделей множественной регрессии статистических параметров для хемоинформационного анализа данных BODIPY

№ Регрессионный коэффициент t-критерий № Регрессионный коэффициент t-критерий
0 1.0494 78.5454 6 0.3036 6.6731
1 –0.3134 –5.1865 7 –0.1316 –4.9308
2 0.3703 19.3745 8 –0.2075 –5.0212
3 0.0549 8.2010 9 –0.0949 –4.6571
4 0.0819 8.8034 10 0.1372 6.7885
5 0.2229 4.3508      
Количество соединений (все) – 144 F = 77.03
Количество соединений для обучения модели – 110 s = 0.1165
R = 0.9413 RMSE (обучение) = 0.1105
R_adj = 0.9346 МАЭ (обучение) = 0.0851

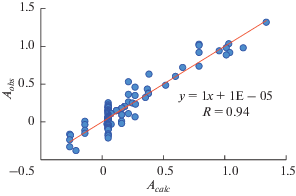
Высокая надежность модели подтверждается значениями параметра Стьюдента для каждого регрессионного коэффициента T-Stat, найденного в диапазоне 4–19, коэффициентом корреляции R = 0.94, числом Фишера F = 77, стандартным отклонением чувствительности к полярности среды s = 0.12 вместе с общей корреляцией между наблюдаемыми и рассчитанными значениями А, показанной на рис. 4.

Рис. 4.

Корреляция между наблюдаемыми и рассчитанными значениями параметра А.

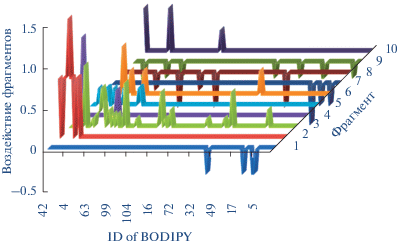
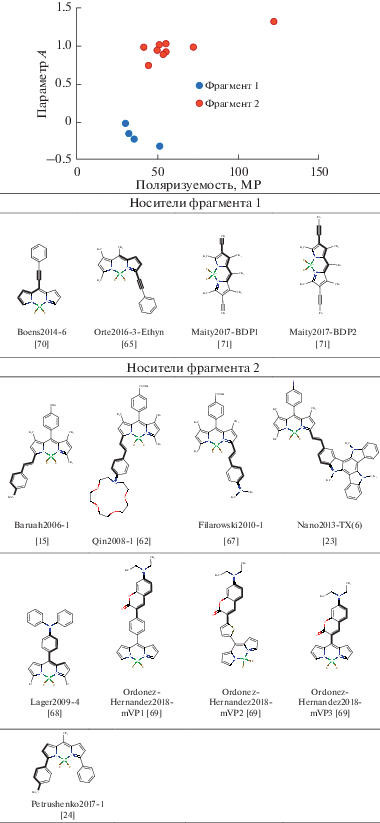
Общее поведение модели отображено на диаграмме рис. 5, иллюстрирующей влияние каждого фрагмента люминофора на параметр А. Наибольший вклад оказывают первые два дескриптора, соответствующие фрагментам 1 и 2 и характеризующие соответственно отрицательное и положительное влияние на параметр полярности флуорофора. Наибольший положительный эффект обусловлен присутствием в молекуле флуорофора цепочки сопряженных двойных неароматических связей и атома азота. Напротив, отрицательное влияние на сольватохромизм оказывает последовательность атомов, содержащих тройную связь и сопряженные двойные неароматические связи внутри или вне ядра дипиррина.

Рис. 5.

Диаграмма вкладов различных фрагментов в величину параметра А.

Возвращаясь к исходным предпосылкам предложенного полуэмпирического подхода для анализа сольватохромного эффекта флуорофоров, необходимо отметить, что параметр полярности A практически не зависит от поляризуемости молекул растворенного вещества, о чем свидетельствуют корреляции (7)–(9). Однако проведенная корреляция параметра A с расчетными значениями молекулярных параметров соединений позволила установить, что влияние растворителя на положительный и отрицательный сольватохромный эффект усиливается при повышении молекулярной поляризуемости соединений (рис. 5). Это наблюдение отвечает найденным выше фрагментам молекул, представленным в табл. 3, которые обладают высокой поляризуемостью как цепочки сопряженных ненасыщенных связей. Таким образом, весь комплекс параметров, характеризующих полярные свойства бордипирринов, – дипольный момент в основном и возбужденном состоянии, молекулярная поляризуемость – отвечает за изменение спектрального поведения флуоресцентных красителей под влиянием полярности внешней среды.

В целом результаты хемоинформационного анализа полярности большой группы бордипирринов наряду с теоретической основой метода определения этого параметра позволят в дальнейшем расширить круг фотофизических и физико-химических параметров для отбора, дизайна и оптимизации сложных конъюгатов бордипирринов.

Рис. 6.

Корреляция между параметром А и молекулярной поляризуемостью MP для групп красителей, соответствующих фрагментам 1 и 2.

ЗАКЛЮЧЕНИЕ

Представлен подход к количественному описанию сольватохромизма флуорофоров на основе бордипирринов с использованием полуэмпирического параметра A полярности соединений, определяющего чувствительность соединений к полярности среды. Это позволяет преодолеть трудности экспериментальных исследований соединений с низкой чувствительностью к растворителям и использовать предложенный метод для систематизации накопленных экспериментальных данных и количественного анализа строения и свойств соединений.

Известные из литературы спектральные данные для бордипирринов в различных растворителях охватывают широкий диапазон сольватохромных эффектов от положительных до отрицательных. Хемоинформационный анализ данных с помощью фрагментного подхода позволил найти дескрипторы, отвечающие наибольшему положительному сольватохромизму бордипирринов и соответствующие цепочке сопряженных двойных неароматических связей и атома азота. Напротив, наибольшее негативное влияние на сольватохромизм оказывает последовательность атомов, содержащих тройную связь и сопряженные двойные неароматические связи внутри или вне ядра дипиррина.

Список литературы

  1. Bañuelos-Prieto J., SolaLlano R. et al. BODIPY Dyes - A Privilege Molecular Scaffold with Tunable Properties. IntechOpen, 2019.

  2. Solomonov A.V., Marfin Y.S., Rumyantsev E.V. // Dyes and Pigments. 2019. V. 162. P. 517. https://doi.org/10.1016/j.dyepig.2018.10.042

  3. Marfin Y.S., Rumyantsev E.V., Yutanova S.L. et al. // Russ. J. Gen. Chem. 2013. V. 83. № 2. P. 381. https://doi.org/10.1134/S1070363213020242

  4. Lu H., Shen Z. et al. BODIPYs and Their Derivatives: The Past, Present and Future. Lausanne: Frontiers Media SA, 2020.

  5. Kowada T., Maeda H., Kikuchi K. // Chem. Soc. Rev. 2015. V. 44. P. 4953. https://doi.org/10.1039/c5cs00030k

  6. Mokrushin A.S., Gorban’ Y.M., Simonenko N.P. et al. // Russ. J. Inorg. Chem. 2021. V. 66. P. 1447. https://doi.org/10.1134/S0036023621090072

  7. Nuraneeva E.N., Guseva G.B., Antina E.V. et al. // Russ. J. Gen. Chem. 2016. V. 86. № 4. P. 840. https://doi.org/10.1134/S1070363216040149

  8. Aleksakhina E.L., Pakhrova O.A., Tomilova I.K. et al. // Chem. Chem. Tech. 2021. V. 64. P. 13. https://doi.org/10.6060/ivkkt.20216403.6355

  9. Bui H.T., Mai D.K., Kim B. et al. // J. Phys. Chem., B. 2019. V. 123. P. 5601. https://doi.org/10.1021/acs.jpcb.9b04782

  10. Collot M., Fam T.K., Ashokkumar P. et al. // J. Am. Chem. Soc. 2018. V. 140. P. 5401. https://doi.org/10.1021/jacs.7b12817

  11. Xiao H., Li P., Tang B. // Coord. Chem. Rev. 2021. V. 427. P. 213582. https://doi.org/10.1016/j.ccr.2020.213582

  12. Collot M., BouS., Fam T.K. et al. // Anal. Chem. 2019. V. 91. P. 1928. https://doi.org/10.1021/acs.analchem.8b04218

  13. Valanciunaite J., Kempf E., Seki H. et al. // Anal. Chem. 2020. V. 92. P. 6512. https://doi.org/10.1021/acs.analchem.0c00023

  14. Ashoka A.H., Ashokkumar P., Kovtun Y.P. et al. // J. Phys. Chem. Lett. 2019. № 10. P. 2414. https://doi.org/10.1021/acs.jpclett.9b00668

  15. Baruah M., Qin W., Flors C. et al. // J. Phys. Chem. A. 2006. V. 110. P. 5998. https://doi.org/10.1021/jp054878u

  16. Boens N., Leen V., Dehaen W. et al. // J. Phys. Chem. A. 2012. V. 116. P. 9621. https://doi.org/10.1021/jp305551w

  17. Li Z., Li L.-J., Sun T. et al. // Dyes and Pigments. 2016. V. 128. P. 165. https://doi.org/10.1016/j.dyepig.2016.01.029

  18. Hu R., Lager E., Aguilar-Aguilar A. et al. // J. Phys. Chem. C. 2009. V. 113. P. 15845. https://doi.org/10.1021/jp902962h

  19. Tang Y., Tang B.Z. Principles and Applications of Aggregation-Induced Emission. Springer, 2019. 518 p.

  20. Suzuki S., Sasaki S., Sairi A.S. et al. // Angew. Chem. Int. Ed. 2020. V. 59. P. 9856. https://doi.org/10.1002/anie.202000940

  21. Banakova E., Bobrov A., Kazak A. et al. // J. Phys. Conf. Series. 2018. V. 951. P. 12017. https://doi.org/10.1088/1742-6596/951/1/012017

  22. Kumar P.P.P., Yadav P., Shanavas A. et al. // Mater. Chem. Frontiers. 2020. № 4. P. 965. https://doi.org/10.1039/D0QM00010H

  23. Nano A., Ziessel R., Stachelek P. et al. // Chem. Eur. J. 2013. № 19. P. 13528. https://doi.org/10.1002/chem.201301045

  24. Petrushenko K.B., Petrushenko I.K., Petrova O.V. et al. // Dyes and Pigments. 2017. 136. P. 488. https://doi.org/10.1016/j.dyepig.2016.09.009

  25. Thakare S.S., Chakraborty G., Kothavale S. et al. // J. Fluorescence. 2017. V. 27. P. 2313. https://doi.org/10.1007/s10895-017-2173-4

  26. González-Vera J.A., Lv F., Escudero D. et al. // Dyes and Pigments. 2020. P. 108510. https://doi.org/10.1016/j.dyepig.2020.108510

  27. Licha K., Resch-Genger U. Comprehensive Biomedical Physics / Ed. Brahme A. Elsevier, 2014. 85 p.

  28. Теренин А.Н. Фотоника молекул красителей. Л.: Наука, 1967. 616 с.

  29. Bakhshiev N.G., Gularyan S.K., Dobretsov G.E. et al. // Opt. Spectrosc. 2006. V. 100. P. 700. https://doi.org/10.1134/S0030400X06050109

  30. Kirillova A.Y., Bakhshiev N.G. // J. Opt. Technol. 2007. V. 74. P. 585. https://doi.org/10.1364/JOT.74.000585

  31. Bakhshiev N.G., Kirillova A.Y., Gularyan S.K. et al. // J. Opt. Technol. 2008. V. 75. P. 407. https://doi.org/10.1364/JOT.75.000407

  32. Бахшиев Н.Г. Сольватохромия: Проблемы и методы. Л.: Изд-во Ленингр. ун-та, 1989.

  33. Aliaga C., Vidal M., Pastenes C. et al. // Dyes and Pigments. 2019. V. 166. P. 395. https://doi.org/10.1016/j.dyepig.2019.03.054

  34. Katayama K., Kawajiri I., Okano Y. et al. // ChemPlusChem. 2019. V. 84. P. 722. https://doi.org/10.1002/cplu.201900067

  35. Ryu H.G., Mayther M.F., Tamayo J. et al. // J. Phys. Chem. C. 2018. V. 122. P. 13424. https://doi.org/10.1021/acs.jpcc.7b11194

  36. Мак-Дональд Р. Цвет в промышленности / Пер. с англ. под ред. Телегина Ф.Ю. М.: Логос, 2002.

  37. Lakowicz J.R. Principles of fluorescence spectroscopy. New York: Springer, 2006. 954 p.

  38. Valeur B., Berberan-Santos M.N. Molecular Fluorescence: principles and applications. Weinheim: Wiley-VCH, 2012.

  39. Reichardt C., Welton T. Solvents and solvent effects in organic chemistry. Weinheim: Wiley-VCH, 2011. 692 p.

  40. Mokrushin A.S., Simonenko N.P., Simonenko T.L. et al. // Russ. J. Inorg. Chem. 2021. V. 66. P. 1425. https://doi.org/10.1134/S0036023621090060

  41. Catalán J. // Handbook of solvents. V. 1. Properties. Toronto: ChemTec Publishing, 2014. 581 p.

  42. Katritzky A.R., Fara D.C., Yang H. et al. // Chem. Rev. 2004. V. 104. P. 175. https://doi.org/10.1021/cr020750m

  43. Sevinç G., Özgür M., Küçüköz B. et al. // J. Lumin. 2019. V. 211. P. 334. https://doi.org/10.1016/j.jlumin.2019.03.058

  44. Bumagina N.A., Antina E.V., Berezin M.B. et al. // Spectrochim. Acta, Part A. 2017. V. 173. P. 228. https://doi.org/10.1016/j.saa.2016.09.026

  45. Leen V., Laine M., Ngongo J.M. et al. // J. Phys. Chem. A. 2018. V. 122. P. 5955. https://doi.org/10.1021/acs.jpca.8b03489

  46. Suhina T., Amirjalayer S., Woutersen S. et al. // Phys. Chem. Chem. Phys. 2017. № 19. P. 19998. https://doi.org/10.1039/c7cp02037f

  47. Баскин И.И., Маджидов Т.И., Варнек А.А. Введение в хемоинформатику. М., 2020. 296 с.

  48. Schüller A., Goh G.B., Kim H. et al. // MolecularInformatics. 2010. V. 29. P. 717. https://doi.org/10.1002/minf.201000089

  49. Uchinomiya S., Horobin R.W., Alvarado-Martínez E. et al. // Combinatorial Chem. High Throughput Screening. 2016. V. 19. P. 378. https://doi.org/10.2174/1386207319666160408150528

  50. Alamudi S.H., Satapathy R., Kim J. et al. // Nature Commun. 2016. № 7. P. 11964. https://doi.org/10.1038/ncomms11964

  51. Baskin I.I., Ait A.O., Halberstam N.M. et al. // Dokl. Phys. Chem. 1997. V. 357. P. 353.

  52. Zhokhova N.I., Baskin I.I., Palyulin V.A. et al. // Russ. J. Appl. Chem. 2005. V. 78. P. 1013. https://doi.org/10.1007/s11167-005-0439-0

  53. Telegin F.Y., Koifman O.I. Third International School-Seminar “From Empirical to Predictive Chemistry”. Kazan: Kazan State University Press, 2018. P. 69.

  54. Telegin F.Y., Marfin Y.S. // Spectrochim Acta., Part A: Mol. Biomol. Spectrosc. 2021. V. 255. P. 119683. https://doi.org/10.1016/j.saa.2021.119683

  55. Liptay W. // Z. Naturforsch. 1965. V. 20a. P. 1441.

  56. Liptay W. Excited states. V. 1. Lim, 1974. 129 p.

  57. Balter A., Nowak W., Pawełkiewicz W., et al. // Chem. Phys. Lett. 1988. V. 143. P. 565. https://doi.org/10.1016/0009-2614(88)87067-2

  58. Koti A., Bhattacharjee B., Haram N. et al. // Photochem. Photobiol. 2000. V. 137. P. 115. https://doi.org/10.1016/S1010-6030(00)00360-9

  59. Marcus R.A. // J. Phys. Chem. 1989. V. 93. P. 3078. https://doi.org/10.1021/j100345a040

  60. Bunker C.E., Bowen T.L., Sun Y.-P. // Photochem. Photobiol. 1993. V. 58. P. 499. https://doi.org/10.1111/j.1751-1097.1993.tb04921.x

  61. ChemAxon. JChem for Office. www.chemaxon.com (last accessed 12 April 2020).

  62. Qin W., Baruah M., Sliwa M. et al. // J. Phys. Chem. A. 2008. V. 112. P. 6104. https://doi.org/10.1021/jp800261v

  63. Qin W., Dou W., Leen V. et al. // RSC Advances. 2016. № 6. P. 7806. https://doi.org/10.1039/C5RA23751C

  64. Marfin Y.S., Vodyanova O.S., Merkushev D.A. et al. // J. Fluor. 2016. V. 26. P. 1975. https://doi.org/10.1007/s10895-016-1891-3

  65. Orte A., Debroye E., Ruedas-Rama M.J. et al. // RSC Advances. 2016. № 6. P. 102899. https://doi.org/10.1039/C6RA22340K

  66. Leen V., Qin W., Yang W. et al. // Chem. Asian J. 2010. № 5. P. 2016. https://doi.org/10.1002/asia.201000248

  67. Filarowski A., Kluba M., Cieślik-Boczula K. et al. // Photochem. Photobiol. Sci. 2010. № 9. P. 996. https://doi.org/10.1039/c0pp00035c

  68. Lager E., Liu J., Aguilar-Aguilar A. et al. // J. Org. Chem. 2009. V. 74. P. 2053. https://doi.org/10.1021/jo802519b

  69. Ordóñez-Hernández J., Jiménez-Sánchez A., García-Ortega H. et al. // Dyes and Pigments. 2018. V. 157. P. 305. https://doi.org/10.1016/j.dyepig.2018.05.009

  70. Boens N., Wang L., Leen V. et al. // J. Phys. Chem. A. 2014. V. 118. P. 1576. https://doi.org/10.1021/jp412132y

  71. Maity A., Sarkar A., Sil A. et al. // New J. Chem. 2017. V. 41. P. 2296. https://doi.org/10.1039/C6NJ03033E

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Журнал неорганической химии

Архивы выпусков Информация о журнале Отправить рукопись в журнал