1. На главную
  2. Электронные версии
  3. Журнал неорганической химии
  4. T. 66, № 2, 2021

Журнал неорганической химии, 2021, T. 66, № 2, стр. 229-241

Мезоструктура композиционных материалов на основе сегментного полиуретанимида, содержащего наночастицы ферритов

В. В. Рунов a, А. Н. Бугров b, c, *, Р. Ю. Смыслов a, b, Г. П. Копица a, d, М. К. Рунова a, Б. В. Васильев b, c, Е. Н. Попова b, С. А. Кириллова c, А. Феоктистов e, В. Пипич e

a Петербургский институт ядерной физики им. Б.П. Константинова, НИЦ “Курчатовский институт”
188300 Ленинградская область, Гатчина, мкр. Орлова роща, 1, Россия

b Институт высокомолекулярных соединений РАН
199004 Санкт-Петербург, В. О. Большой пр., 31, Россия

c Санкт-Петербургский государственный электротехнический университет “ЛЭТИ” им. В.И. Ульянова (Ленина)
197376 Санкт-Петербург, ул. Профессора Попова, 5, Россия

d Институт химии силикатов им. И.В. Гребенщикова РАН
199034 Санкт-Петербург, наб. Макарова, 2, Россия

e Юлихский центр нейтронных исследований GmbH
85748 Гархинг, Германия

* E-mail: alexander.n.bugrov@gmail.com

Поступила в редакцию 06.04.2020
После доработки 23.04.2020
Принята к публикации 30.04.2020

Полный текст (PDF)

Аннотация

Приведены экспериментальные результаты исследования мезоструктуры сегментного полиуретанимида, содержащего 4–10 мас. % наночастиц CoFe2O4 или Al3Fe5O12, методом малоуглового рассеяния поляризованных нейтронов, который позволяет анализировать ядерную и магнитную подсистемы композитов. Цель работы заключалась в изучении трансформации доменной структуры магнитных эластомеров на основе полиуретанимида в зависимости от концентрации, химического состава и локализации наночастиц ферритов в полимерных цепях, а также в оценке динамики изменения сегментальной подвижности гибких блоков в процессе нагрева образцов с помощью методики магнитно-ядерного интерференционного рассеяния. В результате проведенных исследований выявлены изменения в надмолекулярной структуре мультиблочного сополимера в зависимости от процентного содержания и типа наночастиц. Определены корреляционные радиусы в магнитной подсистеме наночастиц ферритов, встроенных в жесткие ароматические блоки полиуретанимида в качестве узлов межмолекулярных сшивок и удлинителей цепи. Проанализированы температурные зависимости интенсивности малоуглового ядерного рассеяния для полиуретанимида и магнитных эластомеров на его основе в условиях перехода гибких алифатических сегментов из стеклообразного в высокоэластическое состояние.

Ключевые слова: малоугловое рассеяние поляризованных нейтронов, мультиблок-сополимеры, доменная структура, магнитные эластомеры

ВВЕДЕНИЕ

В последнее десятилетие стали востребованными так называемые “интеллектуальные” материалы, отличительной особенностью которых является способность контролируемым образом изменять свойства в ответ на внешние воздействия и адаптироваться к ним, снижая возникающие в материале напряжения в результате преобразования одного вида энергии в другой [1, 2]. К таким материалам относятся магнитоактивные эластомеры, способные обратимо изменять свои вязкоупругие характеристики и геометрические размеры под действием внешнего магнитного поля [3, 4]. Данный тип магнитоуправляемых материалов представляет собой полимерную матрицу с относительно невысоким модулем упругости, включающую в свой состав намагничивающиеся микро- или наночастицы [5, 6]. В зависимости от состава и строения магнитоактивные эластомеры способны проявлять различные эффекты: магнитореологический, магнитодеформационный, магнитострикционный, магниторезистивный, а также памяти формы (ЭПФ) [7, 8], что позволяет применять их в качестве магнитных актюаторов, регулируемых мембран, адаптивных вибрационных амортизаторов и других демпфирующих устройств [9–11].

На сегодняшний день известны биодеградируемые магниточувствительные полимерные нанокомпозиты с ЭПФ на основе поликапролактона и наночастиц магнетита, демонстрирующие в переменном магнитном поле высокие значения коэффициента восстановления после деформации (95%) [12]. Для сегментированных полиуретанов на основе полилактида, включающих наночастицы Fe3O4, выявлена высокая скорость отклика на воздействие внешнего магнитного поля [13]. Синтезированы термопластичные полиуретановые эластомеры с 6 мас. % поверхностно-модифицированных суперпарамагнитных наночастиц MnFe2O4, обладающие хорошей управляемостью в слабом магнитном поле 151 < H < 303 Э [14]. Разработаны стабильно работающие в широком диапазоне температур (от –40 до 300°C) магнитоактивные эластомеры с высокой чувствительностью к магнитному полю на основе соединений кремния и частиц карбонильного железа [15]. В ряде теоретических работ предприняты попытки описать взаимодействие магнитных наночастиц в матрице немагнитного эластомера под действием внешнего поля с помощью структурно-механической и дипольной моделей [16, 17], методов фиктивных доменов [18], граничных элементов [19], а также дискретного моделирования [20].

Создание магнитных эластомеров является новым, активно развивающимся направлением, в котором большинство поисковых работ разрознено и требуется больше информации о механизмах формирования магнитной подрешетки в композитах и ее взаимодействии с надмолекулярной структурой полимеров в условиях внешнего магнитного поля [21]. В научной периодике также практически не встречается рекомендаций по выбору и оптимизации химического состава для синтеза магнитно-индуцируемых полимер-неорганических систем с программируемым термомеханическим поведением. Не решены также вопросы определения оптимальной концентрации, типа наночастиц и предпочтительной природы межмолекулярных сшивок в полимерной матрице с точки зрения реализации управляемого магнитным полем ЭПФ и его многократной воспроизводимости.

Поэтому разработка и оптимизация состава магнитоактивных эластомеров требует привлечения химических и физических подходов для синтеза такого рода функциональных материалов, исследования их структуры и свойств, а также анализа полученных данных. Задачи, которые необходимо решить, связаны с распределением наночастиц в композите (магнитная подсистема) и получением нужной надмолекулярной структуры полимерной матрицы. Ответы на эти вопросы могут дать эксперименты по малоугловому рассеянию поляризованных нейтронов.

В данной работе методом малоуглового рассеяния поляризованных нейтронов (МУРПН) изучена мезоструктура сегментных полиуретанимидов, содержащих наночастицы ферритов кобальта и алюминия в диапазоне концентраций 4–10 мас. %. Методика МУРПН позволяет изучать атомарную (ядерную) и магнитную подсистемы, а также анализировать магнитно-ядерное интерференционное рассеяние. В результате в работе определены структурные параметры ядерной и магнитной подсистем, показана степень модификации мезоструктуры и происходящие в ней изменения при релаксационном переходе полиуретанимида из стеклообразного в высокоэластическое состояние. Эти данные получены впервые для таких систем.

ЭКСПЕРИМЕНТАЛЬНАЯ ЧАСТЬ

Методика синтеза наночастиц. Наночастицы ферритов кобальта со структурой шпинели (рис. S1 а) и алюминия со структурой граната (рис. S1 б) получали методом глицин-нитратного горения [22]. Использовали Co(NO3)2 · 6H2O (ч. д. а., ООО “Вектон”, Россия, CAS 10026-22-9), Fe(NO3)3 · 9H2O (ч., ООО “Вектон”, Россия, CAS 7782-61-8), Al(NO3)3 · 9H2O (ч., ООО “Вектон”, Россия, CAS 7784-27-2) и аминоуксусную кислоту (глицин; ч. д. а., ООО “НеваРеактив”, Россия, CAS 56-40-6). Навески глицина и кристаллогидратов металлов брали исходя из заданного количества целевого продукта (2 г) и стехиометрического отношения. Для расчета требуемых стехиометрических соотношений Co : Fe : глицин и Al : Fe : глицин было принято допущение, что реакция взаимодействия нитратов соответствующих металлов с аминоуксусной кислотой протекает до конца с образованием сложных оксидов, азота, углекислого газа и воды по реакциям, приведенным ниже:

$\begin{gathered} {\text{9Co(N}}{{{\text{O}}}_{3}}{{{\text{)}}}_{2}} + {\text{18Fe(N}}{{{\text{O}}}_{3}}{{{\text{)}}}_{3}} + 40{{{\text{C}}}_{2}}{{{\text{H}}}_{5}}{\text{N}}{{{\text{O}}}_{2}} = \\ = 9{\text{CoF}}{{{\text{e}}}_{2}}{{{\text{O}}}_{4}} + 80{\text{C}}{{{\text{O}}}_{2}} + 100{{{\text{H}}}_{2}}{\text{O}} + 56{{{\text{N}}}_{2}}, \\ {\text{15Fe(N}}{{{\text{O}}}_{3}}{{{\text{)}}}_{3}} + {\text{9Al(N}}{{{\text{O}}}_{3}}{{{\text{)}}}_{3}} + 40{{{\text{C}}}_{2}}{{{\text{H}}}_{5}}{\text{N}}{{{\text{O}}}_{2}} = \\ = 3{\text{A}}{{{\text{l}}}_{3}}{\text{F}}{{{\text{e}}}_{5}}{{{\text{O}}}_{{12}}} + 80{\text{C}}{{{\text{O}}}_{2}} + 100{{{\text{H}}}_{2}}{\text{O}} + 56{{{\text{N}}}_{2}}. \\ \end{gathered} $

Объем приготовленного раствора глицина и нитратов соответствующих металлов определялся тем минимальным количеством воды, в котором можно полностью растворить навески используемых компонентов, что составляло порядка 100–150 мл. Раствор помещали в металлическую емкость и подвергали нагреву до кипения. После выкипания воды полученный гелеобразный образец продолжали нагревать до воспламенения. Процесс горения при этом протекал в самоподдерживающемся режиме и завершился, когда топливо полностью закончилось. Полученные в результате глицин-нитратного горения продукты с дендритной структурой перетирали в агатовой ступке. Содержание углерода в полученных образцах наночастиц не превышало 0.5 мас. %, это означало, что реакция прошла практически до конца с образованием сложных оксидов, азота, углекислого газа и воды.

Характеристика наночастиц. Кристаллическую структуру и средний размер областей когерентного рассеяния для полученных наночастиц ферритов определяли методом порошковой рентгеновской дифракции на дифрактометре Rigaku SmatrLab (Токио, Япония), используя CoKα-излучениe. Качественный рентгенофазовый анализ магнитных наночастиц, проведенный в программном пакете PD-Win 4.0, показал их соответствие ферриту кобальта со структурой типа шпинели [23] и алюможелезистому гранату [24, 25] согласно базе данных ASTM (рис. S1 ). Средний размер кристаллитов, вычисленный по формуле Шеррера, составил 37 ± 2 нм в случае CoFe2O4 и 13 ± 2 нм для Al3Fe5O12.

Геометрическую форму и размеры наночастиц оценивали методами электронной микроскопии (рис. S2 ). Микрофотографии, сделанные на просвечивающем JEM-2100 F (JEOL, Токио, Япония) и сканирующем Zeiss SUPRA 55VP (Carl Zeiss AG, Германия) электронных микроскопах, свидетельствуют о том, что наночастицы ферритов кобальта и алюминия имеют квазисферическую форму со средним диаметром 60 ± 10 нм.

Соблюдение стехиометрического соотношения элементов для наночастиц CoFe2O4 и Al3Fe5O12 контролировали методом рентгеноспектрального микроанализа, используя приставку INCA-Energy (Oxford Instruments, Великобритания) (табл. 1).

Таблица 1.  

Элементный состав наночастиц ферритов

Образец Co Al Fe O
ат. %
CoFe2O4 18.2 ± 1.3 – 33.3 ± 2.2 48.5 ± 3.4
Al3Fe5O12 – 16.4 ± 0.2 28.7 ± 1.7 54.9 ± 1.8

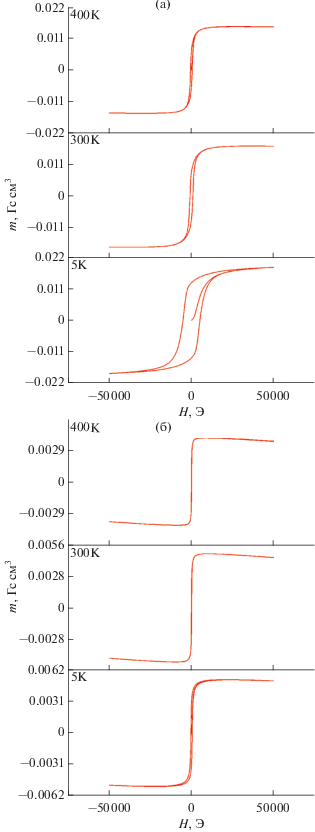
Методом СКВИД-магнитометрии (сверхпроводящий квантовый интерферометр MPMS SQUID VSM компании Quantum Design, США) для синтезированных наночастиц ферритов были установлены магнитные характеристики при температурах 5, 300 и 400 K (рис. 1). В случае СоFe2O4 при комнатной температуре и магнитном поле 1 Тл по петле гистерезиса коэрцитивная сила (Нс) составила 894 Э, намагниченность насыщения (Ms) – 55 (Гс см3)/г, а остаточная намагниченность (Mr) – 31 (Гс см3)/г (рис. 1а). Для наночастиц алюможелезистого граната кривые намагничивания в тех же условиях соответствовали суперпарамагнитному состоянию вещества: Нс = 47 Э, Ms =  15 (Гс см3)/г, Mr = 5 (Гс см3)/г (рис. 1б). На основании анализа температурных зависимостей магнитной индукции насыщения была проведена оценка значений температуры Кюри (Tс) для синтезированных наночастиц. Полученные значения Tс для CoFe2O4 и Al3Fe5O12 составили 660 и 610 K соответственно.

Рис. 1.

Зависимости намагниченности наночастиц CoFe2O4 (а) и Al3Fe5O12 (б) от приложенного поля при разных температурах.

Поверхностная модификация наночастиц, синтез полиуретанимида и магнитных эластомеров на его основе

Функционализацию аминогруппами обоих типов наночастиц ферритов осуществляли с помощью 3-аминопропилтриэтоксисилана (99%, Aldrich, CAS 919-30-2) [26, 27] в соответствии с методикой [28].

В синтезе сегментного полиуретанимида для формирования жестких ароматических блоков использовали 1,3-бис(3′,4-дикарбоксифенокси)бензол (резорциновый диангидрид (Р); ООО “ТехХим-Пром”, Ярославль, Россия), 2,4-толуилендиизоцианат (ТДИ; 95%, tпл = 20–22°C, Aldrich, CAS 584-84-9) и удлинитель цепи – 4,4'-бис(4''-аминофенокси)дифенилсульфон (диамин СОД; >98.0%, tпл = 194–197°С, TCI Europe N.V., CAS 13080-89-2). В качестве гибких алифатических блоков был выбран поли(диэтиленгликоль)адипат (ПДЭГА; tпл < –4°C, Aldrich, CAS 9010-89-3) с молекулярной массой Mn = 2500.

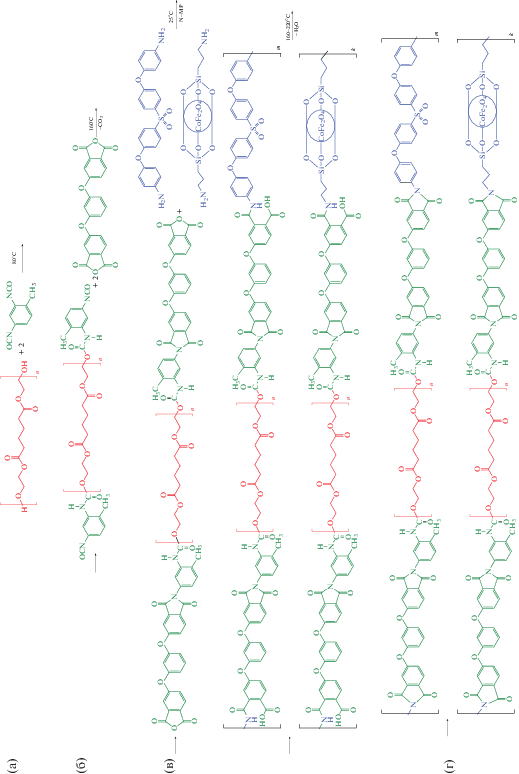
Взятая за основу методика синтеза мультиблочного полиуретанимида (Р-ТДИ-ПДЭГА 2500-ТДИ-P)CОД представлена в работе [29]. Магнитные композиты на основе вышеуказанного сегментного блок-сополимера и наночастиц ферритов были получены в процессе сополиконденсации in situ. На первой стадии в трехгорлую колбу помещали навески ПДЭГА и ТДИ массой 4.28 г (0.0017 моль) и 0.6 г (0.0034 моль) соответственно. Затем содержимое колбы нагревали до 80°С и выдерживали при заданной температуре и непрерывном перемешивании на протяжении часа в токе аргона. К полученному расплаву макродиизоцианата (рис. 2а) добавляли 1.38 г (0.0034 моль) диангидрида Р, после чего температуру в колбе повышали до 160°С и поддерживали постоянной до прекращения выделения СО2 из реакционной смеси (рис. 2б). Образовавшуюся в результате вязкую массу охлаждали до 90°С и разбавляли 5 мл N-метил-2-пирролидона (N-МП; 99.5%, безводный, Aldrich, CAS 872-50-4). После полной гомогенизации системы при интенсивном перемешивании температуру понижали до комнатной и приливали к ней предварительно подготовленную дисперсию магнитных наночастиц в 5 мл N-МП. В качестве магнитных наноразмерных наполнителей использовали CoFe2O4 и Al3Fe5O12 соответственно. В расчете на массу сухого блок-сополимера количество вводимых наночастиц ферритов составляло 1, 4, 7 и 10 мас. %. Далее к реакционной смеси добавляли 5 мл 12.6%-ного раствора диамина СОД в N-МП и перемешивали содержимое колбы при комнатной температуре в течение 4 ч, получили раствор форполимера (сополиэфирамидокислоту) с наночастицами (рис. 2в). Далее, используя насадку Дина–Старка с обратным холодильником, отгоняли выделяющуюся при имидизации воду в виде азеотропной смеси с толуолом, взятым в количестве 1/3 от общего объема реакционной смеси. Процесс проводили в токе аргона при непрерывном перемешивании согласно следующему температурному режиму: 160°С – 3 ч, 180°С – 2 ч, 200°С – 1 ч и 220°С – полчаса (рис. 2г). Образовавшийся в результате термической имидизации сегментный полиуретанимид с магнитными наночастицами высаживали в водно-спиртовой раствор для удаления растворителя (N-МП). Полученную массу магнитного мультиблок-сополимера сутки сушили при 60°С и формовали из нее лопатки в двухшнековом экструдере DSM Xplore (Нидерланды) при 145°С.

Рис. 2.

Схема синтеза магнитных эластомеров на основе мультиблочного полиуретанимида (Р-ТДИ-ПДЭГА2500-ТДИ-P)CОД и наночастиц CoFe2O4.

Методика исследования магнитных эластомеров с помощью МУРПН

Исследование мезоструктуры магнитных эластомеров, синтезированных в данной работе, выполнено на реакторе FRM-2 в Мюнхене на установках малоуглового рассеяния поляризованных нейтронов KWS-1 и KWS-3.

Метод МУРПН позволяет разделять ядерное и магнитное рассеяние, выделять интерференционное магнитно-ядерное рассеяние на контрастирующих областях, которые образуются в образцах с магнитными примесями или возникающими магнитными фазами. Магнитно-ядерное интерференционное рассеяние обладает высокой чувствительностью, которая определяется такими факторами, как линейная зависимость рассеяния от магнитной и ядерной амплитуд и выделение интерференционного рассеяния из общего малоуглового рассеяния, т.е. измерение на “нулевом” физическом фоне. Последнее достигается тем, что интерференционное рассеяние измеряется как разница в рассеянии для двух спиновых состояний нейтронов, по или против приложенного к образцу магнитного поля (up/down) [30].

Прежде всего отметим в самом упрощенном виде в приближении упругого рассеяния и без учета рассеяния на сложных магнитных структурах разницу в информации, получаемой из данных малоуглового рассеяния неполяризованных и поляризованных нейтронов для материалов с магнитными примесями или фазами. Детальная информация о рассеянии поляризованных нейтронов содержится, например, в обзоре [31]. Интенсивность рассеянных нейтронов в зависимости от вектора рассеяния $\overline q = \overline k - \overline k '$, где $\overline k ,\,\,\overline k '$ – волновые векторы падающих и рассеянных нейтронов, определяется как сумма квадратов соответствующих амплитуд рассеяний. Так, ядерное рассеяние In(q) на флуктуациях амплитуды ядерных плотностей рассеяния (A) определяется как In(q) ∼ A2, соответственно, магнитное рассеяние на флуктуациях амплитуды магнитных плотностей рассеяния (B), которая, в свою очередь, пропорциональна локальной магнитной индукции (Bs), – как Im(q) ~ [Bs sinα]2. Здесь q = |$\bar {q}$|, а α – угол между вектором локальной магнитной индукции в образце (Bs) и вектором рассеяния $(\bar {q})$. Измерения рассеяния поляризованных нейтронов с поляризацией P на намагниченном образце во внешнем магнитном поле H, как правило, проводят в геометрии P || H || Bs. Поляризацию нейтронов ориентируют относительно магнитного поля на образце +/– или up/down флиппером, эффективность которого считается равной единице (Bs – индукция в образце). В таком случае магнитную амплитуду можно записать как PBsinα. При этом в рассеянии нужно учесть интерференцию магнитного и ядерного рассеяния, т.е. суммировать амплитуды ядерного и магнитного рассеяния для разных спиновых состояний нейтронов. В результате рассеяние неполяризованных (1) и поляризованных (2) нейтронов запишется как:

(1)
$I(q) = {{I}_{n}}(q) + {{I}_{m}}(q) + {{B}_{{ck}}},$
(2)
$I\left( q \right) = {{I}_{n}}\left( q \right) + {{I}_{m}}\left( q \right) \pm 2P\left[ {AB\sin \alpha } \right] + {{B}_{{ck}}},$
где третий член в уравнении (2) описывает интерференцию ядерного и магнитного рассеяния, а Bck – фон некогерентного рассеяния.

Из выражений (1) и (2) видно, что в рассеянии поляризованных нейтронов появляется интерференционный член, который легко выделить, измеряя (2) с противоположными направлениями поляризации P(up) и P(down) и вычитая одно из другого. В результате получим удвоенное значение интерференционного члена, который определяется магнитно-ядерным кросс-коррелятором, т.е. пропорционален произведению (AB):

(3)
$\begin{gathered} \Delta \left( q \right) = I\left[ {q,P\left( {up} \right)} \right] - I\left[ {q,P\left( {down} \right)} \right] \equiv \\ \equiv {{I}^{ + }}\left( q \right) - {{I}^{ - }}\left( q \right) = 4PAB\sin \alpha , \\ \end{gathered} $
(4)
$I\int {\Delta qdq} = 0,$

Причем выражение (4) следует из закона сохранения числа частиц. В данном случае предполагается, что спин-зависимое сечение поглощения нейтронов пренебрежимо мало. Данная задача аналогична задаче изучения магнитно-ядерных кросс-корреляций на 3d-примесях в немагнитной матрице, рассмотренной нами в работе [32]. Для выделения ядерного рассеяния, согласно (2), надо измерить интенсивность рассеяния на намагниченном образце в узком телесном угле при α ≈ 0, т.е. при q||Bs (в данной работе сектор усреднения составлял ±16°). В свою очередь, магнитное рассеяние можно получить из измерений рассеяния в узком телесном угле при α ≈ 90° (сектор усреднения ±16°), т.е. при q⊥Bs за вычетом изотропного ядерного рассеяния, определенного выше.

РЕЗУЛЬТАТЫ И ОБСУЖДЕНИЕ

Вследствие разной химической природы гибкие алифатические и жесткие ароматические сегменты в составе мультиблочного полиуретанимида (Р-ТДИ-ПДЭГА2500-ТДИ-P)CОД имеют тенденцию к микрофазовому разделению. Образование между N–H уретана и карбонильными группами имидного кольца межмолекулярных водородных связей приводит к формированию областей концентрации жeстких ароматических блоков (доменов), которые действуют как узлы сшивки макромолекул [29]. Введение в состав полимерной матрицы на стадии ее получения магнитных наночастиц, предварительно функционализированных NH2-группами, не оказывает влияния на молекулярную подвижность и упорядочение гибких алифатических блоков согласно данным ДСК (рис. S3 ).

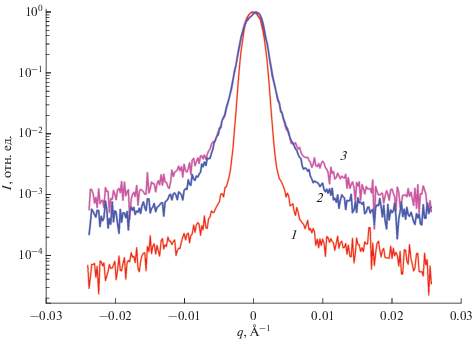
При исследовании с помощью метода МУРПН мезоструктуры магнитных эластомеров на основе полиуретанимида (Р-ТДИ-ПДЭГА2500-ТДИ-P)CОД и наночастиц ферритов наблюдается уширение нейтронного пучка за счет рассеяния на неорганических включениях и доменах, образованных жесткими блоками. На рис. 3 приведены типичные зависимости нормированных интенсивностей малоуглового рассеяния от переданного импульса q, характеризующие уширение нейтронного пучка при рассеянии на ядерных и магнитных неоднородностях.

Рис. 3.

Нормированные интенсивности малоуглового рассеяния в зависимости от переданного импульса q для прямого пучка (1), мультиблочного полиуретанимида (Р-ТДИ-ПДЭГА 2500-ТДИ-P)CОД (2) и магнитного эластомера на его основе с 10 мас. % наночастиц CoFe2O4 (3).

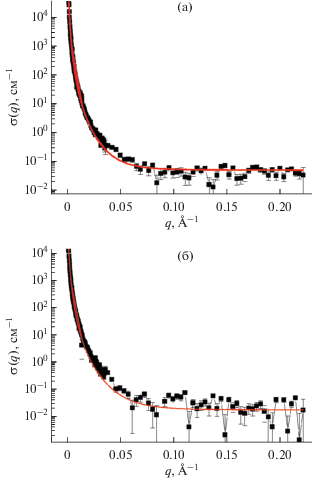
Типичные импульсные зависимости сечения магнитно-ядерного интерференционного рассеяния во внешнем магнитном поле H = 2 Tл на полиуретанимиде (Р-ТДИ-ПДЭГА2500-ТДИ-P)CОД, содержащем 10 мас. % наночастиц CoFe2O4 либо Al3Fe5O12, представлены на рис. 4. Данные обрабатывали по формуле:

(5)
$\sigma (q) = a/{{({{q}^{2}} + {{(1/{{R}_{C}})}^{2}})}^{2}},$
где a – свободный параметр, RC – корреляционный радиус магнитно-ядерной контрастирующей и, соответственно, рассеивающей области.

Рис. 4.

Сечения интерференционного рассеяния на мультиблочном полиуретанимиде (Р-ТДИ-ПДЭГА2500-ТДИ-P)CОД, содержащем 10 мас. % наночастиц CoFe2O4 (а) или Al3Fe5O12 (б) в зависимости от переданного импульса q. Сплошная линия – расчет по формуле (5).

В табл. 2 приведены значения корреляционных радиусов магнитно-ядерного интерференционного рассеяния для образцов мультиблочного полиуретанимида с содержанием наночастиц ферритов от 4 до 10 мас. %. Показано, что магнитно-ядерное интерференционное рассеяние, характеризующее распределение магнитных неоднородностей в полимерной матрице, отчетливо наблюдается для всех синтезированных композитов с содержанием наночастиц CoFe2O4 или Al3Fe5O12 более 1 мас. %. Интерференционное рассеяние хорошо описывается квадрированным лоренцианом (формула 5) с характерными радиусами корреляции RC (табл. 2). В координатном представлении распределение соответствует экспоненциально спадающему с расстоянием r коррелятору exp(–r/RC) с асимптотикой Порода ∝ q–4 при больших q (qRC $ \gg $ 1), это характерно для описания рассеяния на объектах с хорошо выраженными границами. Согласно рассчитанным значениям RC, магнитные неоднородности в матрице (Р-ТДИ-ПДЭГА 2500-ТДИ-P)CОД располагаются примерно на одном и том же расстоянии друг от друга для всех выбранных концентраций наночастиц ферритов. Исключение составляет лишь полиуретанимид с 10 мас. % CoFe2O4, где наблюдается двукратное увеличение расстояния между магнитными включениями, вероятно, вызванное агломерацией наночастиц с образованием устойчивых однодоменных структур большего размера в полимерной матрице [33].

Таблица 2.  

Корреляционные радиусы магнитно-ядерного интерференционного рассеяния для образцов мультиблочного полиуретанимида (Р-ТДИ-ПДЭГА2500-ТДИ-P)CОД с разным содержанием наночастиц ферритов

Образец RC, Å
(Р-ТДИ-ПДЭГА2500-ТДИ-P)CОД + 4 мас. % CoFe2O4 730 ± 10
(Р-ТДИ-ПДЭГА2500-ТДИ-P)CОД + 7 мас. % CoFe2O4 670 ± 10
(Р-ТДИ-ПДЭГА2500-ТДИ-P)CОД + 10 мас. % CoFe2O4 1570 ± 30
(Р-ТДИ-ПДЭГА2500-ТДИ-P)CОД + 4 мас. % Al3Fe5O12 820 ± 12
(Р-ТДИ-ПДЭГА2500-ТДИ-P)CОД + 7 мас. % Al3Fe5O12 775 ± 10
(Р-ТДИ-ПДЭГА2500-ТДИ-P)CОД + 10 мас. % Al3Fe5O12 770 ± 10

Магнитное рассеяние, пропорциональное квадрату магнитной амплитуды (Im(q) ~ [B sin α]2), в исследованных образцах магнитных эластомеров априори мало. Кроме того, традиционное выделение его из общего малоуглового рассеяния, как это обычно делается и описано выше, связано с большими систематическими погрешностями, особенно в области малых переданных импульсов. В данной работе магнитное рассеяние приведено на рис. 5 для сегментного полиуретанимида с максимальным содержанием (10 мас. %) наночастиц CoFe2O4 в импульсном диапазоне, где его масштаб более или менее удовлетворительно определяется. Как оказалось, доля магнитного рассеяния не превышает 10% от интерференционного для всех измеренных магнитных эластомеров и значительно меньше 10% по сравнению с общим малоугловым рассеянием (рис. 5).

Рис. 5.

Зависимости сечения общего малоуглового рассеяния (1), интерференционного рассеяния (2) и магнитного рассеяния (3) от переданного импульса q для мультиблочного полиуретанимида (Р-ТДИ-ПДЭГА2500-ТДИ-P)CОД с 10 мас. % наночастиц CoFe2O4. Сплошная линия – расчет по формуле (5) с RC = 586(14) Å.

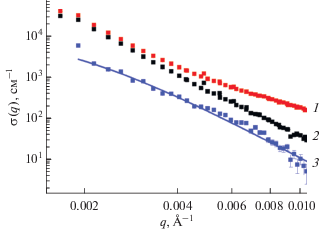
На рис. 6а приведена зависимость сечения ядерного рассеяния на полимерной матрице (Р-ТДИ-ПДЭГА2500-ТДИ-P)CОД от переданного импульса q. Как и ожидалось, сечение ядерного рассеяния в доменной структуре сегментного полиуретанимида имеет непростой вид. Весьма удовлетворительно рассеяние можно описать, введя два масштаба:

(6)
$\begin{gathered} \sigma (q) = a/{{({{q}^{2}} + {{(1/{{R}_{C}})}^{2}})}^{2}} + \\ + \,\,b/[{{(q - {{q}_{0}})}^{2}} + {{(1/{{R}_{{C1}}})}^{2}}] + d, \\ \end{gathered} $
где a, b, d и q0 – свободные параметры, RC и RC1 – характерные ядерные корреляционные радиусы рассеивающих областей. Результаты такой обработки приведены на рис. 6 сплошной линией.

Рис. 6.

Сечения ядерного рассеяния на мультиблочном полиуретанимиде (Р-ТДИ-ПДЭГА2500-ТДИ-P)CОД (а) и его магнитных эластомерах с 10 мас. % наночастиц CoFe2O4 (б) и Al3Fe5O12 (в) в зависимости от переданного импульса q. Сплошная линия – расчет по формуле (6).

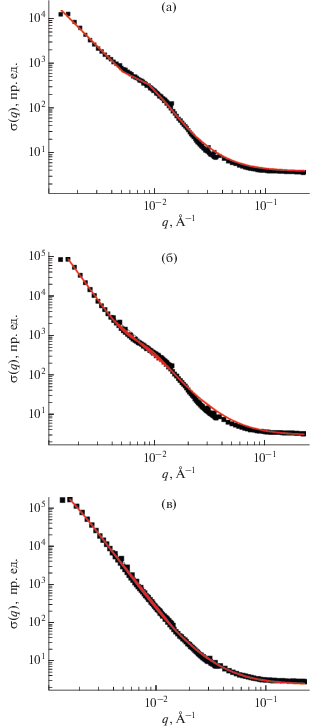
Аналогичный вид имеют зависимости сечения ядерного рассеяния от переданного импульса q для магнитных эластомеров с 10 мас. % наночастиц CoFe2O4 и Al3Fe5O12 (рис. 6б, 6в).

Для наглядности на рис. 7 приведены расчетные зависимости ядерного сечения рассеяния для измеренных образцов без экспериментальных точек, чтобы не загромождать графики, иллюстрирующие влияние магнитных наночастиц на мезоструктуру матрицы полиуретанимида.

Рис. 7.

Расчетные зависимости ядерного сечения рассеяния на образцах мультиблочного полиуретанимида (1) и магнитных эластомеров на его основе с разным содержанием наночастиц CoFe2O4 (а) или Al3Fe5O12 (б): 2 – 4 мас. %; 3 – 7 мас. %; 4 – 10 мас. %.

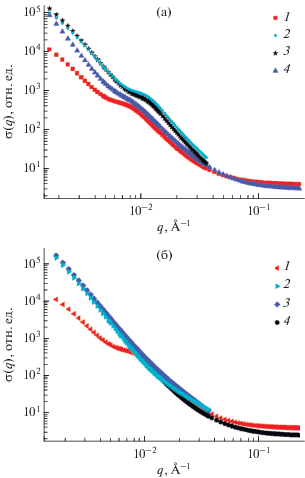
Наибольшие изменения в рассеянии наблюдаются при малых переданных импульсах, т.е. в наибольших пространственных масштабах. Особенно это заметно при введении в структуру мультиблочного полиуретанимида наночастиц Al3Fe5O12 (рис. 7б). Естественно предположить, что наночастицы встраиваются в матрицу избирательно в определенные сегменты.

Определенное в работе ядерное рассеяние имеет весьма сложную импульсную зависимость сечения рассеяния, что предсказуемо для столь негомогенных композиционных материалов. Как уже отмечалось ранее, сечение весьма удовлетворительно можно описать суммой квадрированного лоренциана и лоренциана (формула (6)), взятых со своими корреляционными радиусами (табл. 3). Отметим, что лоренциан (функция Орнштейна–Цернике) соответствует более быстро спадающему с расстоянием r коррелятору, характерному для рассеяния на участках с размытыми границами. В импульсной зависимости для интенсивности ядерного рассеяния на полимерной матрице и композите с наночастицами CoFe2O4 наблюдается перегиб в диапазоне q0 (рис. 6, 7а). Скорее всего, это обусловлено перераспределением интенсивности рассеяния на жестких и гибких сегментах полиурентанимида (Р-ТДИ-ПДЭГА2500-ТДИ-P)CОД, так как рассеяние от более плотных доменов жесткой фазы и флуктуирующих алифатических участков полимерных цепей может иметь разную импульсную зависимость рассеяния [34]. Для магнитных эластомеров на основе мультиблок-сополимера и наночастиц Al3Fe5O12 нет необходимости вводить параметр q0 в подгоночную формулу (6), поскольку данный перегиб выражен слабо (рис. 7б). По-видимому, функционализированные наночастицы алюможелезистого граната при введении in situ в матрицу полиуретанимида оказывают пластифицирующий эффект, встраиваясь в полимерные цепи как удлинители [35], что приводит к ухудшению микрофазового разделения гибкого и жесткого сегментов.

Таблица 3.  

Характерные ядерные корреляционные радиусы рассеивающих областей для образцов мультиблочного полиуретанимида и магнитных эластомеров на его основе

Образец RС, Å RС1, Å q0, Å–1
(Р-ТДИ-ПДЭГА2500-ТДИ-P)CОД 655(7) 255(4) 0.007(1)
(Р-ТДИ-ПДЭГА2500-ТДИ-P)CОД + 4 мас. % CoFe2O4 665(2) 223(3) 0.009(3)
(Р-ТДИ-ПДЭГА2500-ТДИ-P)CОД + 7 мас. % CoFe2O4 794(2) 228(3) 0.009(3)
(Р-ТДИ-ПДЭГА2500-ТДИ-P)CОД + 10 мас. % CoFe2O4 2746(127) 232(4) 0.007(1)
(Р-ТДИ-ПДЭГА2500-ТДИ-P)CОД + 4 мас. % Al3Fe5O12 1239(9) 59(5) –
(Р-ТДИ-ПДЭГА2500-ТДИ-P)CОД + 7 мас. % Al3Fe5O12 1104(9) 181(18) –
(Р-ТДИ-ПДЭГА2500-ТДИ-P)CОД + 10 мас. % Al3Fe5O12 1143(8) 130(22) –

В табл. 3 приведены результаты обработки по формуле (6) импульсных зависимостей сечений ядерного рассеяния для сегментного полиуретанимида и магнитных эластомеров на его основе.

Как в случае ненаполненной матрицы мультиблочного полиуретанимида, так и при низких концентрациях наночастиц феррита кобальта в ее структуре не фиксируется существенных изменений величин корреляционных радиусов для доменов, образованных жесткими ароматическими блоками Rc, и участков между ними Rc1, представленных гибкими алифатическими сегментами (табл. 3). Близкие значения Rc1, вероятно, обусловлены тем, что наночастицы CoFe2O4, встроенные в ароматические блоки полиуретанимида, выступают наряду с доменами жесткой фазы в роли узлов межмолекулярных сшивок и ограничивают подвижность гибких сегментов (рис. 8а) [36]. Повышение содержания в полимерной матрице наночастиц со структурой типа шпинели до 10 мас. % приводит к формированию агломератов и локализации вблизи них жестких ароматических блоков, что отражается в укрупнении доменов (рис. 8б) [37].

Рис. 8.

Схематическое представление мезоструктуры мультиблочного полиуретанимида с низким (а) и высоким (б) содержанием наночастиц CoFe2O4 или Al3Fe5O12 (в).

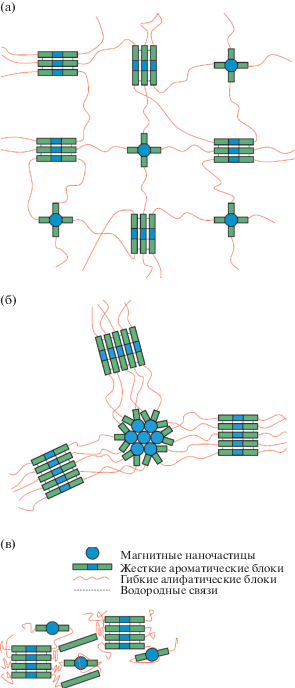
Обратная ситуация наблюдается для магнитных эластомеров на основе мультиблок-сополимера (Р-ТДИ-ПДЭГА2500-ТДИ-P)CОД и суперпарамагнитных наночастиц Al3Fe5O12 (табл. 3). Предполагается, что функционализированные аминогруппами наночастицы алюможелезистого граната встраиваются в структуру ароматических сегментов полиуретанимида как удлинители цепи, не препятствуя компактизации гибких алифатических блоков и их “наматыванию” на домены жесткой фазы (рис. 8в) [38]. В связи с этим размер областей локализации линейных участков макромолекул, ответственных за эластические свойства полиуретанимида, сокращается от 510 до 120–360 Å. В свою очередь, домены жесткой фазы мультиблок-сополимера становятся в два раза больше при введении магнитомягкого наполнителя, что можно объяснить перераспределением ароматических сегментов, которые ввиду стерических затруднений не образуют водородных связей с удлинителями цепи, в составе которых присутствуют наночастицы Al3Fe5O12 (рис. 8в).

В работе также проанализировано изменение мезоструктуры сегментного полиуретанимида (Р-ТДИ-ПДЭГА2500-ТДИ-P)CОД (рис. 9а) и магнитных эластомеров на его основе с 10 мас. % наночастиц CoFe2O4 (рис. 9б) и Al3Fe5O12 (рис. 9в) в зависимости от температуры методом МУРПН. На рис. 9 приведены результаты этих измерений для трех диапазонов волновых векторов: (3 ± 1) × 10–3, (3.5 ± 1.2) × 10–3 и (4.8 ± 1.6) × 10–3 Å–1. По данным ДСК был выбран диапазон температур 230–300 K, перекрывающий релаксационный переход, связанный с “размораживанием” сегментальной подвижности гибких алифатических сегментов в вышеупомянутых структурах (рис. S3 ). Как было показано выше, малоугловое рассеяние, по существу, является ядерным, поскольку доля вклада магнитного рассеяния мала и составляет единицы процентов. Полученные температурные зависимости малоуглового рассеяния на полимерной матрице и композитах с наночастицами ферритов существенно отличаются.

Рис. 9.

Температурные зависимости (охлаждение и нагрев) МУРПН на мультиблочном полиуретанимиде (Р-ТДИ-ПДЭГА2500-ТДИ-P)CОД (а) и его магнитных эластомерах с 10 мас. % наночастиц CoFe2O4 (б) или Al3Fe5O12 (в) для трех диапазонов волновых векторов: 1 – (3 ± 0.8) × 10–3, 2 – (3.5 ± 1.0) × 10–3 и 3 – (4.8 ± 1.3) × 10–3 Å–1.

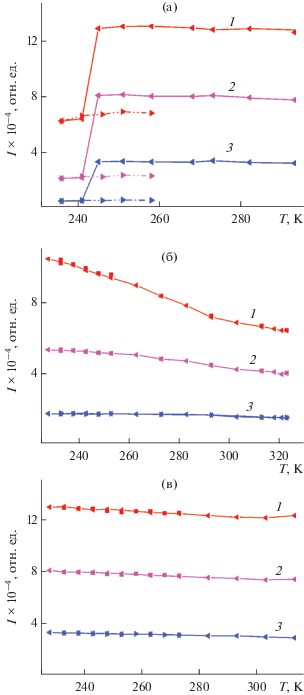
Для мультиблочного полиуретанимида на температурной зависимости МУРПН фиксируется скачoк интенсивности при 243 K, что соответствует температуре стеклования гибких алифатических сегментов по кривым ДСК (рис. S3 ). Введение в структуру полимерной матрицы магнитных наночастиц нивелирует резкий рост интенсивности и температурный гистерезис, регистрируемый в рассеянии при релаксационном переходе алифатических блоков из стеклообразного в высокоэластическое состояние в результате нагрева (рис. 9б, 9в). Этот эффект, вероятно, обусловлен ограничением подвижности гибких сегментов за счет увеличения размера доменов жесткой фазы при включении в их состав наночастиц ферритов в качестве как удлинителей цепи, так и узлов межмолекулярных сшивок (рис. 8б, 8в).

ЗАКЛЮЧЕНИЕ

Выполненные методом МУРПН измерения композитов мультиблочного полиуретанимида с 4–10 мас. % наночастиц CoFe2O4 или Al3Fe5O12 позволили определить характерные мезоскопические параметры ядерной и магнитной подсистем, различные для использованных типов ферритов. Магнитное рассеяние в композитах, как и ожидалось, мало и не превышает 10% интерференционного рассеяния, что составляет единицы процентов по сравнению с ядерным рассеянием.

На основе анализа данных МУРП высказано предположение о формировании трех типов мезоструктуры исследованных композитов, различающихся разными надмолекулярными образованиями. Оказалось, что мезоструктура мультиблочного полиуретанимида с низким содержанием наночастиц CoFe2O4 характеризуется небольшими узлами двух типов. В состав одних входят жесткие ароматические блоки сополимера. Другие узлы в этом случае образованы взаимодействием наночастиц с полимером. Когда концентрация наночастиц CoFe2O4 возрастает, образуются более крупные узлы за счет взаимодействия жестких блоков. При этом наночастицы агрегируют, связывая с собой большее количество полимерных цепей, в то время как в магнитном эластомере, содержащем наночастицы Al3Fe5O12, длина линейных фрагментов между узлами, образованными как жесткими ароматическими блоками, так и наночастицами, укорочена по сравнению с двумя другими случаями.

Данная работа будет полезна для понимания надмолекулярного структурообразования в сегментных полиуретанимидах. Она дает фундаментальные ориентиры для изготовления функциональных магнитных эластомеров с целью их использования в устройствах, где требуются материалы с эффектом памяти формы.

Список литературы

  1. Aguilar M.R., Román J.S. Smart polymers and their applications. Woodhead Publishing, 2014. 584 p.

  2. Meng H., Li G. // Polym. J. 2013. V. 54. № 9. P. 1. https://doi.org/10.1016/j.polymer.2013.02.023

  3. Nguyen V.Q., Ramanujan R.V. // Macromol. Chem. Phys. 2010. V. 211. P. 618. https://doi.org/10.1002/macp.200900478

  4. Soto G.D., Meiorin C., Actis D. et al. // Polym. Test. 2018. V. 65. P. 360. https://doi.org/10.1016/j.polymertesting.2017.12.012

  5. Pelteret J.-P., Steinmann P. Magneto-active polymers: Fabrication, characterization, modelling and simulation at the micro- and macro-scale. De Gruyter, 2020. 379 p. https://doi.org/10.1515/9783110418576

  6. Wang L., Razzaq M.Y., Rudolph T. et al. // Mater. Horiz. 2018. № 5. P. 861. https://doi.org/10.1039/C8MH00266E

  7. Sánchez P.A., Minina E.S., Kantorovich S.S. et al. // Soft Matter. 2019. V. 15. № 2. P. 175. https://doi.org/10.1039/C8SM01850B

  8. Heuchel M., Razzaq M.Y., Kratz K. et al. // Polym. J. 2015. V. 65. P. 215. https://doi.org/10.1016/j.polymer.2015.03.063

  9. Elhajjar R., Law C.-T., Pegoretti A. // Prog. Mater Sci. 2018. V. 97. P. 204. https://doi.org/10.1016/j.pmatsci.2018.02.005

  10. Nguyen V.Q., Ahmed A.S., Ramanujan R.V. // Adv. Mater. 2012. V. 24. № 30. P. 4041. https://doi.org/10.1002/adma.201104994

  11. Dong X. Smart and functional soft materials. Ch. 4: Magnetorheological elastomers: Materials and applications. 2019. https://doi.org/10.5772/intechopen.85083

  12. Gao Y., Zhu G., Xu S. et al. // Inc. J. Appl. Polym. Sci. 2018. V. 135. P. 45652. https://doi.org/10.1002/app.45652

  13. Gu S.-Y., Jin S.-P., Gao X.-F. et al. // Smart Mater. Struct. 2016. V. 25. P. 055036. https://doi.org/10.1088/0964-1726/25/5/055036

  14. Yoonessi M., Peck J.A., Bail J.L. et al. // ACS Appl. Mater. Interfaces. 2011. V. 3. P. 2686. https://doi.org/10.1021/am200468t

  15. Molchanov V.S., Stepanov G.V., Vasiliev V.G. et al. // Macromolekular. 2014. V. 299. P. 1116. https://doi.org/10.1002/mame.201300458

  16. Меленев П.В., Ковров В.Н., Райхер Ю.Л. и др. // Вычислительная механика сплошных сред. 2014. Т. 7. № 4. С. 423. https://doi.org/10.7242/1999-6691/2014.7.4.40

  17. Han K., Feng Y.T., Owen D.R.J. // Int. J. Numer. Methods Eng. 2010. V. 84. № 11. P. 1273. https://doi.org/10.1002/nme.2940

  18. Avci B., Wriggers P. // J. Appl. Mech. 2012. V. 79. № 1. P. 010901. https://doi.org/10.1115/1.4005093

  19. Ravnik J., Hriberˇsek M. // Comput. Mech. 2013. V. 51. № 4. P. 465. https://doi.org/10.1007/s00466-012-0729-3

  20. Vogel F., Pelteret J-P., Kaessmair S. et al. // Eur. J. Mech. A-Solid. 2014. V. 48. P. 23. https://doi.org/10.1016/j.euromechsol.2014.03.007

  21. Roy M., Tran P., Dickens T. et al. // J. Compos. Sci. 2020. V. 4. № 1. P. 1. https://doi.org/10.3390/jcs4010001

  22. Karpov O.N., Tomkovich M.V., Tugova E.A. // Russ. J. Gen. Chem. 2018. V. 88. № 10. P. 2133. https://doi.org/10.1134/S1070363218100171

  23. Natta G., Passerini L. // Gazz. Chim. Ital. 1929. V. 59. P. 286.

  24. Sadhana K., Naina Vinodini S.E., Sandhya R. et al. // Adv. Mater. Lett. 2015. V. 6. № 8. P. 717. https://doi.org/10.5185/amlett.2015.5874

  25. Yahya N., Masoud R.A.H., Daud H. et al. // Am. J. Eng. Appl. Sci. 2009. V. 2. № 1. P. 76.

  26. Olenin A.Yu., Lisichkin G.V. // Russ. J. Gen. Chem. 2019. V. 89. P. 1451. https://doi.org/10.1134/S1070363219070168

  27. Yudin V.E., Bugrov A.N., Didenko A.L. et al. // Polym. Sci. Ser. B. 2014. V. 56. № 6. P. 859. https://doi.org/10.1134/S1560090414060165

  28. Bugrov A.N., Vlasova E.N., Mokeev M.V. et al. // Polym. Sci. Ser. B. 2012. V. 54. № 9, 10. P. 486. https://doi.org/10.1134/S1560090412100041

  29. Sokolova M.P., Bugrov A.N., Smirnov M.A. et al. // Polymers. 2018. V. 10. № 11. P. 1222. https://doi.org/10.3390/polym10111222

  30. Melnyk I.V., Vaclavikova M., Seisenbaeva G.A. et al. Biocompatible hybrid oxide nanoparticles for human health. From synthesis to applications. Ch. 10: Synthesis and study of multiferroic and ferroelectric “core-shell” powders for application in electronic devices for medicine and ecology. Elsevier Inc., 2019. P. 183. https://doi.org/10.1016/B978-0-12-815875-3.00010-2

  31. Maleev S.V. // Phys. Usp. 2002. V. 45. № 6. P. 569. https://doi.org/10.1070/PU2002v045n06ABEH001017

  32. Runov V.V., Ilyn D.S., Runova M.K. et al. // JETP Letters. 2012. V. 95. № 9. P. 467. https://doi.org/10.1134/S0021364012090111

  33. Reichel V., Kovács A., Kumari M. et al. // Sci. Rep. 2017. V. 7. № 1. P. 454. https://doi.org/10.1038/srep45484

  34. Sun Y.-S., Jeng U-S., Huang Y.-S. et al. // Physica B. 2006. V. 385–386. P. 650. https://doi.org/10.1016/j.physb.2006.06.093

  35. Deng F., Zhang Y., Li X. et al. // Polym. Compos. 2017. V. 40. № 1. P. 328. https://doi.org/10.1002/pc.24654

  36. Wu C.-H., Shau S.-M., Liu S.-C. et al. // RSC Adv. 2015. V. 5. № 22. P. 16897. https://doi.org/10.1039/c4ra14277b

  37. Cruz S.M., Viana J.C. // Macromol. Mater. Eng. 2015. V. 300. P. 1153. https://doi.org/10.1002/mame.201500188

  38. Behniafar H., Alimohammadi M., Malekshahinezhad Kh. Prog. Org. Coat. 2015. V. 88. P. 150. https://doi.org/10.1016/j.porgcoat.2015.06.030

Дополнительные материалы

скачать ESM.docx
Дополнительные материалы к статье

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Журнал неорганической химии

Архивы выпусков Информация о журнале Отправить рукопись в журнал