1. На главную
  2. Электронные версии
  3. Микроэлектроника
  4. T. 52, № 2, 2023

Микроэлектроника, 2023, T. 52, № 2, стр. 110-126

Сечения процессов рассеяния при электронно-лучевой литографии

А. Е. Рогожин 1, Ф. А. Сидоров 1, *

1 Физико-технологический институт имени К.А. Валиева Российской академии наук
117218 Москва, Нахимовский проспект, 36, корп. 1, Россия

* E-mail: sidorov@ftian.ru

Поступила в редакцию 14.02.2023
После доработки 27.02.2023
Принята к публикации 27.02.2023

Полный текст (PDF)

Аннотация

Рассмотрены современные модели, использующиеся для описания процессов упругого, квазиупругого и неупругого рассеяния. Для упругого рассеяния приведены различные формы потенциала электростатического взаимодействия, потенциала обменного взаимодействия и корреляционно-поляризационного потенциала. Для квазиупругих процессов, включающих электрон-фононное и электрон-поляронное рассеяние приведена модель на основе теории диэлектриков и эмпирическая модель. Описание неупругого рассеяния проводится на основе функции потерь энергии, для построения которой используются три различных подхода.

Ключевые слова: электронно-лучевая литография, упругое рассеяние, неупругое рассеяние

1. ВВЕДЕНИЕ

Электронно-лучевая литография является одним из наиболее распространенных методов микроструктурирования, обеспечивающим высокое разрешение получаемого изображения. Однако, при уменьшении критических размеров рельефа до величин порядка 1 мкм проявляются так называемые эффекты близости, ограничивающие разрешение метода [1, 2]. Было установлено, что их причиной является рассеяние электронного луча в резисте и подложке, что приводит к уширению области поглощения энергии относительно заданной области экспонирования и искажению получаемого изображения. Вследствие этого уже несколько десятилетий ведется активное изучение метода электронно-лучевой литографии, направленное на улучшение понимания процессов экспонирования и проявления изображения, а также оптимизацию параметров этих процессов. Одной из важных задач, требовавших решения, являлось определение скорости растворения различных участков проэкспонированного резиста. Было установлено, что при дозах экспонирования, характерных для электронно-лучевой литографии, скорость растворения резиста может быть рассчитана на основе распределения выделившейся в нем энергии [3–6]. Для определения последнего использовались различные подходы к описанию взаимодействия электронного луча с резистом и подложкой, что нашло отражение в различных алгоритмах моделирования процесса, как на основе кинетической теории транспорта [4, 7–11], так и на основе метода Монте–Карло [12–17].

В случае моделирования планарных структур с небольшим количеством слоев эффективно применяются алгоритмы на основе кинетической теории транспорта. За счет использования функции распределения для описания процесса распространения всех частиц в структуре они не требует большого вычислительного времени [18–20]. В свою очередь, метод Монте-Карло основан на использовании случайных чисел для описания отдельных параметров моделируемого процесса [21–23], за счет чего является более требовательным к вычислительным мощностям. В основанных на методе Монте-Карло алгоритмах моделирования процессов рассеяния частиц в веществе траектории отдельных частиц моделируются независимо друг от друга, что позволяет использовать их для структур произвольной формы, а также воспроизвести стохастический характер данных процессов [24, 25]. При этом оба этих подхода основываются на одних и тех же данных о веществе – в наиболее простом случае это дифференциальные сечения упругого рассеяния электрона и его потери энергии на единицу длины пути, в которых учитываются все возможные неупругие процессы. Однако, в современных моделях неупругого рассеяния потери энергии сводятся к дискретным процессам, которые также описываются в терминах дифференциальных сечений. Таким образом, сечения упругих и неупругих процессов составляют основу модели взаимодействия электронного луча с веществом, реализацией которой является алгоритм моделирования.

Данная работа является логическим продолжением вышедшей ранее статьи “Моделирование процессов электронно-лучевой литографии” [26], в которой были описаны алгоритмы моделирования на основе кинетической теории транспорта и метода Монте-Карло, а также были приведены базовые модели рассеяния электронного луча в веществе. В настоящей работе рассматриваются подходы к вычислению сечений упругого и неупругого рассеяния электронов в веществе, использующиеся в современных алгоритмах моделирования и обеспечивающие высокую точность результатов. Таким образом, эти две работы предоставляют информацию необходимую для создания алгоритма моделирования взаимодействия электронного луча с веществом, имеющего широкую область применения.

2. УПРУГИЕ ПРОЦЕССЫ

Упругое рассеяние происходит в результате взаимодействия налетающего электрона с ядром атома, частично экранированного электронами. В результате упругого рассеяния изменяется направление движения электрона, его энергия при этом остается практически неизменной. Азимутальный угол рассеяния $\varphi $ имеет равномерное распределение на промежутке (0°, 360°), полярный угол рассеяния $\theta $ распределен неравномерно на промежутке (0°, 180°) с максимумом плотности вероятности в нуле.

Основной характеристикой упругого рассеяния электронов на атомах мишени является дифференциальное сечение рассеяния $\frac{{d{{\sigma }_{{el}}}}}{{d\Omega }}$, определяемое как отношение числа частиц, рассеянных мишенью в элемент телесного угла $d\Omega = d\varphi {\kern 1pt} \sin {\kern 1pt} \theta d\theta $ за единицу времени к плотности потока налетающих частиц. Полное сечение упругого рассеяния находится путем интегрирования дифференциального сечения по полному телесному углу:

(1)
${{\sigma }_{{el}}} = 2\pi \int\limits_0^\pi {\frac{{d{{\sigma }_{{el}}}}}{{d\Omega }}\sin {\kern 1pt} \theta d\theta } .$

Для веществ, имеющих молекулярное строение, дифференциальное сечение упругого рассеяния выражается через сечения рассеяния для отдельных атомов, входящих в состав молекулы, с учетом их стехиометрических индексов. Например, для ПММА (поли(метилметакрилат), (C5O2H8)n) дифференциальное сечение рассеяния электронов на мономерах (метилметакрилат, ММА, C5O2H8) имеет вид:

(2)
$\frac{{d{{\sigma }_{{{\text{MMA}}}}}}}{{d\Omega }} = 5\frac{{d{{\sigma }_{C}}}}{{d\Omega }} + 2\frac{{d{{\sigma }_{{\text{O}}}}}}{{d\Omega }} + 8\frac{{d{{\sigma }_{{\text{H}}}}}}{{d\Omega }}.$

Исторически первые дифференциальные сечения упругого рассеяния вычислялись по формуле Резерфорда, получаемой за счет применения борновского приближения в задаче рассеяния электронов на атомном потенциале [27]:

(3)
$\begin{gathered} \frac{{d{{\sigma }_{{{\text{Ruth}}}}}}}{{d\Omega }} = \frac{{{{Z}^{2}}{{e}^{4}}}}{{4{{E}^{2}}}}\frac{1}{{{{{\left( {1 - \cos {\kern 1pt} \theta + \alpha } \right)}}^{2}}}}, \\ \alpha = \frac{{m{{e}^{4}}{{\pi }^{2}}}}{{{{h}^{2}}}}\frac{{{{Z}^{{2/3}}}}}{E}, \\ \end{gathered} $
где Z – заряд ядра, E – энергия налетающего электрона, m – масса электрона, h – постоянная Планка. Формула Резерфорда позволяет описывать упругое рассеяние электронов на легких атомах, однако, ее точность снижается с ростом зарядового числа атома, особенно в области низких энергий [28–30].

Более точные значения сечений упругого рассеяния (моттовские сечения) могут быть получены за счет решения уравнения Дирака для задачи рассеяния релятивистского электрона в центральном статическом поле атома-мишени [31–34]. В этом подходе дифференциальное сечение упругого рассеяния задается формулой

(4)
$\frac{{d{{\sigma }_{{el}}}}}{{d\Omega }} = {{\left| {f\left( \theta \right)} \right|}^{2}} + {{\left| {g\left( \theta \right)} \right|}^{2}},$
где $f\left( \theta \right)$ и $g\left( \theta \right)$ – амплитуды рассеяния, соответствующими параллельному и антипараллельному направлению спина относительно направления движения электрона, соответственно, и определяемые выражениями
(5)
$\begin{gathered} f\left( \theta \right) = \frac{1}{{2iK}}\sum\limits_{l = 0}^\infty {\left\{ {\left( {l + 1} \right)\left[ {\exp \left( {2i\delta _{l}^{{ - 1}}} \right) - 1} \right] + l\left[ {\exp \left( {2i\delta _{l}^{ + }} \right) - 1} \right]} \right\}} {{P}_{l}}\left( {\cos {\kern 1pt} \theta } \right), \\ g\left( \theta \right) = \frac{1}{{2iK}}\sum\limits_{l = 0}^\infty {\left[ { - \exp \left( {2i\delta _{l}^{ - }} \right) + \exp \left( {2i\delta _{l}^{ + }} \right)} \right]} P_{l}^{1}\left( {\cos {\kern 1pt} \theta } \right). \\ \end{gathered} $
Здесь k – волновое число налетающего релятивистского электрона, ${{P}_{l}}\left( {\cos {\kern 1pt} \theta } \right)$ и $P_{l}^{1}\left( {\cos {\kern 1pt} \theta } \right)$ – полиномы Лежандра и присоединенные полиномы Лежандра соответственно, $\delta _{l}^{ \pm }$ – фазовые сдвиги сферических волн, рассчитываемые по формуле
(6)
${\text{tg}}\left( {\delta _{l}^{ \pm }} \right) = \frac{{K{{j}_{{l + 1}}}\left( {Kr} \right) - {{j}_{l}}\left( {Kr} \right)\left[ {\left( {W + 1} \right){\text{tg}}{\kern 1pt} \phi _{l}^{ \pm } + {{\left( {1 + l + {{k}^{ \pm }}} \right)} \mathord{\left/ {\vphantom {{\left( {1 + l + {{k}^{ \pm }}} \right)} r}} \right. \kern-0em} r}} \right]}}{{K{{n}_{{l + 1}}}\left( {Kr} \right) - {{n}_{l}}\left( {Kr} \right)\left[ {\left( {W + 1} \right){\text{tg}}{\kern 1pt} \phi _{l}^{ \pm } + {{\left( {1 + l + {{k}^{ \pm }}} \right)} \mathord{\left/ {\vphantom {{\left( {1 + l + {{k}^{ \pm }}} \right)} r}} \right. \kern-0em} r}} \right]}},$
где ${{K}^{2}} = {{W}^{2}} - 1$, W – полная энергия электрона в единицах $m{{c}^{2}}$, r – расстояние до рассеивающего центра в единицах ${h \mathord{\left/ {\vphantom {h {2\pi mc}}} \right. \kern-0em} {2\pi mc}}$, индексы “+” и “–” обозначают параллельное и антипараллельное направление спина:
(7)
$\begin{gathered} ^{ + }:{\text{ }}{{k}^{ + }} = - l - 1,{\text{ }}j = l + {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}, \hfill \\ ^{ - }:{\text{ }}{{k}^{ - }} = l,{\text{ }}j = l - {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}, \hfill \\ \end{gathered} $
$\phi _{l}^{ \pm }$ – предел функции $\phi _{l}^{ \pm }\left( r \right)$ ($r \to \infty :{\text{ }}\phi _{l}^{ \pm }\left( r \right) \to \phi _{l}^{ \pm }$), которая находится путем численного интегрирования уравнения Дирака:
(8)
$\frac{{d\phi _{l}^{ \pm }\left( r \right)}}{{dr}} = \frac{{{{k}^{ \pm }}}}{r}\sin \left[ {2\phi _{l}^{ \pm }\left( r \right)} \right] - \cos \left[ {2\phi _{l}^{ \pm }\left( r \right)} \right] + W - V\left( r \right),$
где $V\left( r \right)$ – рассеивающий потенциал.

В настоящей работе в составе рассеивающего потенциала будет рассматриваться потенциал электростатического взаимодействия ${{V}_{{st}}}\left( r \right)$, потенциал обменного взаимодействия ${{V}_{{ex}}}\left( r \right)$ и корреляционно-поляризационный потенциал ${{V}_{{cp}}}\left( r \right)$ (для частиц с энергией ниже ~10 кэВ):

(9)
$V\left( r \right) = {{V}_{{st}}}\left( r \right) + {{V}_{{ex}}}\left( r \right) + {{V}_{{cp}}}\left( r \right),$

2.1 Потенциал электростатического взаимодействия

Для нахождения потенциала электростатического взаимодействия потенциал атома $\varphi \left( r \right)$ рассчитывается на основе потенциалов заряда ядра и электронного облака (${{\varphi }_{n}}\left( r \right)$ и ${{\varphi }_{e}}\left( r \right)$ соответственно):

(10)
${{V}_{{st}}}\left( r \right) = - e\varphi \left( r \right) = - e\left[ {{{\varphi }_{n}}\left( r \right) + {{\varphi }_{e}}\left( r \right)} \right],$
где ${{\rho }_{n}}\left( r \right)$ и ${{\rho }_{e}}\left( r \right)$ – объемные плотности заряда протонов ядра и орбитальных электронов:

(11)
$\begin{gathered} {{\varphi }_{n}}\left( r \right) = e\left( {\frac{1}{r}\int\limits_0^r {{{\rho }_{n}}\left( {r{\kern 1pt} '} \right)4\pi r{\kern 1pt} {{'}^{2}}dr{\kern 1pt} ' + } \int\limits_r^\infty {{{\rho }_{n}}\left( {r{\kern 1pt} '} \right)4\pi r{\kern 1pt} 'dr{\kern 1pt} '} } \right), \hfill \\ {{\varphi }_{e}}\left( r \right) = - e\left( {\frac{1}{r}\int\limits_0^r {{{\rho }_{e}}\left( {r{\kern 1pt} '} \right)4\pi r{\kern 1pt} {{'}^{2}}dr{\kern 1pt} ' + } \int\limits_r^\infty {{{\rho }_{e}}\left( {r{\kern 1pt} '} \right)4\pi r{\kern 1pt} 'dr{\kern 1pt} '} } \right). \hfill \\ \end{gathered} $

Распределение заряда ядра становится существенным для значений энергии налетающего электрона, превышающих 50 МэВ, при которых его длина волны де Бройля

(12)
${{\lambda }_{{dB}}} = \frac{{2\pi }}{k} = \frac{{12.398 \times {{{10}}^{{ - 11}}}{\text{ см}}}}{{\sqrt {\left( {{E \mathord{\left/ {\vphantom {E {{\text{МэВ}}}}} \right. \kern-0em} {{\text{МэВ}}}}} \right)\left[ {\left( {{E \mathord{\left/ {\vphantom {E {{\text{МэВ}}}}} \right. \kern-0em} {{\text{МэВ}}}}} \right) + 1.022} \right]} }}$
становится сопоставима с размерами ядра. Значения энергии электронов в электронно-лучевой литографии обычно много меньше 50 МэВ, поэтому в данной работе интерес представляет только модель точечного ядра (остальные модели могут быть найдены в работе [35]):
(13)
$\begin{gathered} {{\rho }_{{n,P}}}\left( r \right) = Z\delta \left( r \right), \hfill \\ {{\varphi }_{{n,P}}}\left( r \right) = \frac{{Ze}}{r}, \hfill \\ \end{gathered} $
где $\delta \left( r \right)$ – дельта-функция Дирака.

В отличие от моделей распределения заряда ядра, различные модели плотности электронного облака представляют интерес во всем диапазоне энергий, и для количественной оценки эффекта экранирования заряда ядра электронами атома вводится функция экранирования:

(14)
$\phi \left( r \right) \equiv \frac{r}{{Ze}}\varphi \left( r \right).$

При этом потенциал атома и объемные плотности его зарядов связаны уравнением Пуассона, которое, с учетом сферической симметрии системы, имеет вид:

(15)
${{\rho }_{n}}\left( r \right) - {{\rho }_{e}}\left( r \right) = - \frac{1}{{4\pi er}}\frac{{{{d}^{2}}}}{{d{{r}^{2}}}}\left[ {r\varphi \left( r \right)} \right] = - \frac{Z}{{4\pi r}}\frac{{{{d}^{2}}\phi \left( r \right)}}{{d{{r}^{2}}}}.$

В условиях модели точечного ядра это выражение принимает более простой вид:

(16)
${{\rho }_{e}}\left( r \right) = \frac{Z}{{4\pi r}}\frac{{{{d}^{2}}\phi \left( r \right)}}{{d{{r}^{2}}}},$
и в дальнейшем в различных моделях электронной плотности будет приводиться только выражение для функции экранирования.

• Потенциал Томаса–Ферми–Мольера

Наиболее простой метод получения электронной плотности в атоме основывается на модели атома Томаса–Ферми [36, 37], в которой электронное облако рассматривается как однородный электронный газ, удерживаемый полем точечного ядра. В этой модели функция экранирования не зависит от вида атома и задается уравнением Томаса–Ферми [38]:

(17)
$\begin{gathered} \frac{{{{d}^{2}}{{\phi }_{{TF}}}}}{{d{{x}^{2}}}} = \frac{{\phi _{{TF}}^{{3/2}}}}{{\sqrt x }}, \hfill \\ {{\phi }_{{TF}}}\left( 0 \right) = 1, \hfill \\ \end{gathered} $
где $x = {{2r{{Z}^{{1/3}}}} \mathord{\left/ {\vphantom {{2r{{Z}^{{1/3}}}} {{{{\left( {\frac{3}{4}\pi } \right)}}^{{2/3}}}}}} \right. \kern-0em} {{{{\left( {\frac{3}{4}\pi } \right)}}^{{2/3}}}}}$. Обычно это уравнение решается численно, после чего решение приближается эмпирической функцией. Наиболее часто используется приближение Мольера [39]:
(18)
${{\chi }_{{TFM}}}\left( r \right) = \sum\limits_{i = 1}^3 {{{A}_{i}}\exp \left( { - {{a}_{i}}r{\text{/}}b} \right)} ,$
где
(19)
${{A}_{1}} = 0.10,{\text{ }}{{A}_{2}} = 0.55,{\text{ }}{{A}_{3}} = 0.35,{\text{ }}{{a}_{1}} = 6,{\text{ }}{{a}_{2}} = 1.2,{\text{ }}{{a}_{3}} = 0.3$
и $b = \frac{{{{{\left( {3\pi } \right)}}^{{3/2}}}}}{{{{2}^{{7/3}}}}}\frac{{{{\hbar }^{2}}}}{{m{{e}^{2}}}}{{Z}^{{ - 1/3}}}$ – радиус Томаса–Ферми, r – расстояние до рассеивающего центра в атомных единицах Хартри (здесь и в пунктах 1.1.2 и 1.1.3), m – масса электрона (здесь и далее). Такое приближение хорошо согласуется с исходным решением уравнения Томаса–Ферми в большом диапазоне значений r ($r < 6b$).

• Потенциал Томаса—Ферми–Дирака

Модель Томаса–Ферми может быть дополнена с учетом обменного взаимодействия, что приводит к уравнению Томаса–Ферми–Дирака [38]:

(20)
$\begin{gathered} \frac{{{{d}^{2}}{{\phi }_{{TFD}}}}}{{d{{x}^{2}}}} = x{{\left( {\sqrt {\frac{{{{\phi }_{{TFD}}}}}{x}} + \beta } \right)}^{3}}, \hfill \\ \beta = \sqrt {\frac{b}{{{{a}_{0}}Z}}} \frac{1}{{\pi \sqrt 2 }}, \hfill \\ {{\phi }_{{TFD}}}\left( 0 \right) = 1. \hfill \\ \end{gathered} $

Функция экранирования снова получается путем численного интегрирования дифференциального уравнения, однако в этом случае в решении отсутствует зависимость вида ${{Z}^{{ - 1/3}}}$. Таким образом, функция экранирования должна вычисляться для каждого элемента индивидуально, и для нее было получено следующее приближение [40, 41]:

(21)
${{\phi }_{{TFD}}}\left( {\text{r}} \right) = \sum\limits_{i = 1}^3 {{{B}_{i}}{\kern 1pt} \exp \left( { - {{b}_{i}}r} \right)} ,$
в котором параметры Bi и bi плавно меняются с ростом Z и могут быть описаны зависимостями:
(22)
$\begin{gathered} {{B}_{1}} = 0.0126671 - 0.0261047x + 0.0214184{{x}^{2}} - 0.00235686{{x}^{3}} + 0.0000210672{{x}^{4}}, \hfill \\ {{B}_{2}} = 0.0580612 + 0.0293077x + 0.0857135{{x}^{2}} - 0.0223342{{x}^{3}} + 0.00164675{{x}^{4}}, \hfill \\ {{B}_{3}} = 0.927968 - 0.00164643x - 0.107685{{x}^{2}} + 0.0247998{{x}^{3}} - 0.00167822{{x}^{4}}{\text{, }} \hfill \\ {{b}_{1}} = {{\left( {164.564 - 152.192x + 62.3879{{x}^{2}} - 11.5005{{x}^{3}} + 0.808424{{x}^{4}}} \right)} \mathord{\left/ {\vphantom {{\left( {164.564 - 152.192x + 62.3879{{x}^{2}} - 11.5005{{x}^{3}} + 0.808424{{x}^{4}}} \right)} {{{a}_{0}}}}} \right. \kern-0em} {{{a}_{0}}}}, \hfill \\ {{b}_{2}} = {{\left( {11.3060 - 6.31902x + 2.26025{{x}^{2}} - 0.370738{{x}^{4}} + 0.0261151{{x}^{4}}} \right)} \mathord{\left/ {\vphantom {{\left( {11.3060 - 6.31902x + 2.26025{{x}^{2}} - 0.370738{{x}^{4}} + 0.0261151{{x}^{4}}} \right)} {{{a}_{0}}}}} \right. \kern-0em} {{{a}_{0}}}}, \hfill \\ {{b}_{3}} = {{\left( {1.48219 - 0.0557601x + 0.0164387{{x}^{3}} - 0.00439703{{x}^{3}} + 0.000997225{{x}^{4}}} \right)} \mathord{\left/ {\vphantom {{\left( {1.48219 - 0.0557601x + 0.0164387{{x}^{3}} - 0.00439703{{x}^{3}} + 0.000997225{{x}^{4}}} \right)} {{{a}_{0}}}}} \right. \kern-0em} {{{a}_{0}}}}, \hfill \\ \end{gathered} $
где $x = \ln {\kern 1pt} Z$. Однако, такое выражение для функции экранирования уже менее точно согласуется с исходным численным решением уравнения Томаса—Ферми–Дирака, чем в предыдущем случае, особенно, для элементов с низким Z.

• Потенциал Дирака–Хартри—Фока–Слейтера

В модели Дирака–Хартри–Фока–Слейтера [42] N-электронная волновая функция атома представляется в виде детерминанта Слейтера

(23)
$\left| \Psi \right\rangle = \frac{1}{{\sqrt {N!} }}\left| {\begin{array}{*{20}{c}} {{{\psi }_{1}}\left( {{{{\mathbf{r}}}_{1}}} \right)}& \ldots &{{{\psi }_{N}}\left( {{{{\mathbf{r}}}_{1}}} \right)} \\ \vdots & \cdots & \vdots \\ {{{\psi }_{1}}\left( {{{{\mathbf{r}}}_{N}}} \right)}& \ldots &{{{\psi }_{N}}\left( {{{{\mathbf{r}}}_{N}}} \right)} \end{array}} \right|,$
где функции одноэлектронных состояний ${{\psi }_{i}}\left( {\mathbf{r}} \right)$ являются решениями уравнения Дирака
(24)
$\left[ {c\alpha {\mathbf{\hat {p}}} + \beta m{{c}^{2}} + U\left( {\mathbf{r}} \right)} \right]{{\psi }_{i}}\left( {\mathbf{r}} \right) = E{{\psi }_{i}}\left( {\mathbf{r}} \right)$
в стационарном поле $U\left( {\mathbf{r}} \right)$, включающем в себя кулоновское взаимодействие и обменное взаимодействие с потенциалом Слейтера [43]. Как и в двух предыдущих случаях, функция экранирования, полученная таким методом, может быть приближена суммой экспоненциальных функций:

(25)
${{\phi }_{{e,DHFS}}}\left( r \right) = \sum\limits_i {{{C}_{i}}\exp \left( { - {{c}_{i}}r} \right)} .$

Их параметры для большинства элементов (Z = = 1–92) приведены в работе [44], также параметры для элементов, входящих в систему ПММА/Si, приведены в табл. 1.

Таблица 1.  

Параметры функции экранирования, получаемой в модели Дирака—Хартри–Фока–Слейтера для элементов, входящих в систему ПММА/Si

Элемент ${{C}_{1}}$ ${{C}_{2}}$ ${{с}_{1}}$ ${{с}_{2}}$
H –184.39 185.39 2.0027 1.9973
C 0.1537 0.8463 8.0404 1.4913
O 0.0625 0.9375 14.823 2.0403
Si 0.5160 0.4840 5.8492 1.1732

• Потенциал Дирака–Фока

Наиболее точные значения электронной плотности атома могут быть получены многоконфигурационным методом Дирака–Фока [45, 46], являющегося релятивистским аналогом метода Хартри–Фока. Значения электронной плотности атомов, полученные этим методом, могут быть найдены в файлах вида “z_nnn.den”, входящими в состав пакета ELSEPA [35], в котором реализуется решения уравнения Дирака задачи рассеяния электронов и позитронов на свободных атомах и молекулах с различными параметрами рассеивающего потенциала.

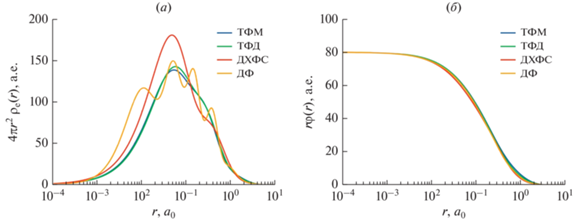
Графики электронной плотности и потенциала, полученные на основе различных моделей, приведены на рис. 1.

Рис. 1.

Графики электронной плотности (а) и потенциала (б), полученные на основе моделей Томаса–Ферми–Мольера (ТФМ), Томаса—Ферми–Дирака (ТФД), Дирака–Хартри—Фока–Слейтера (ДХФС) и Дирака–Фока (ДФ).

2.2. Потенциал обменного взаимодействия

Точное описание обменного взаимодействия налетающего электрона с электронной оболочкой атома-мишени формулируется в терминах детерминантов Слейтера [47]. При этом волновая функция должна удовлетворять уравнениям, аналогичным уравнениям Дирака-Фока с нелокальным обменным членом, решение которых представляет определенные трудности [35]. Более простой с вычислительной точки зрения подход основан на использовании локальной аппроксимации обменного взаимодействия [48]. В данной работе будут приведены три потенциала обменного взаимодействия, полученные с использованием локальной аппроксимации.

• Потенциал Томаса–Ферми

Данный обменный потенциал получается путем вычисления потенциала Слейтера [49] в модели атома Томаса–Ферми (модель свободного электронного газа) [50]:

(26)
$\begin{gathered} {{V}_{{ex,TF}}}\left( r \right) = - \frac{{{{e}^{2}}}}{{\pi {{k}_{L}}}}\left[ {{{k}_{L}}{{k}_{F}} - \frac{1}{2}\left( {k_{L}^{2} - k_{F}^{2}} \right)\ln \left| {\frac{{{{k}_{L}} + {{k}_{F}}}}{{{{k}_{L}} - {{k}_{F}}}}} \right|} \right], \hfill \\ {{k}_{L}} = {{k}^{2}} + k_{F}^{2}, \hfill \\ {{\left( {c\hbar k} \right)}^{2}} = E\left( {E + 2m{{c}^{2}}} \right), \hfill \\ \end{gathered} $
где ${{k}_{F}}\left( r \right) = {{\left[ {3{{\pi }^{2}}{{\rho }_{e}}\left( r \right)} \right]}^{{1/3}}}$ – локальное волновое число Ферми электронного облака, с – скорость света.

• Потенциал Фернесса–МакКарти

Данный потенциал получается за счет применения квазиклассического приближения (метод ВКБ [51]) в задаче с нелокальным обменным потенциалом [52]:

(27)
${{V}_{{ex,FM}}}\left( r \right) = \frac{1}{2}\left[ {E - {{V}_{{st}}}\left( r \right)} \right] - \frac{1}{2}{{\left\{ {{{{\left[ {E - {{V}_{{st}}}\left( r \right)} \right]}}^{2}} + 4\pi {{a}_{0}}{{e}^{4}}{{\rho }_{e}}\left( r \right)} \right\}}^{{1/2}}}.$
Здесь ${{V}_{{st}}}\left( r \right)$ – потенциал электростатического взаимодействия, ${{\rho }_{e}}\left( r \right)$ – электронная плотность, ${{a}_{0}}$ – боровский радиус. Известно, что такой потенциал корректно описывает обменное взаимодействие для атомов водорода и гелия при энергиях налетающего электрона, превышающих 1 Хартри (≈27 эВ) [48].

• Потенциал Рили–Трулара

При высоких энергиях налетающего электрона степенная функция в потенциале Фернесса–МакКарти может быть разложена в ряд, что приводит к потенциалу Рили–Трулара [50]:

(28)
${{V}_{{ex,RT}}}\left( r \right) = - \pi {{a}_{0}}{{e}^{4}}{{\rho }_{e}}\left( r \right){{\left[ {\frac{{{{\hbar }^{2}}}}{{2{{m}_{e}}}}{{k}^{2}} + e\varphi \left( r \right)} \right]}^{{ - 1}}},$
где $\varphi \left( r \right)$ – электростатический потенциал атома-мишени.

2.3. Поляризационно-корреляционный потенциал

Налетающие электроны с низкой энергией могут вызывать поляризацию и появление соответствующего дипольного момента у электронного облака атома-мишени. Это приводит к дополнительному притяжению между электроном и атомом, для описания которого используется поляризационно-корреляционный потенциал.

• Потенциал Букингема

При больших расстояниях между налетающим электроном и атомом-мишенью корреляционно-поляризационный потенциал может быть описан потенциалом Букингема [53]:

(29)
${{V}_{{cp,B}}}\left( r \right) = - \frac{{{{\alpha }_{d}}{{e}^{2}}}}{{2{{{\left( {{{r}^{2}} + {{d}^{2}}} \right)}}^{2}}}},$
где ${{\alpha }_{d}}$ – дипольная поляризуемость атома-мишени, d – феноменологический параметр, предотвращающий расходимость потенциала при $r \to 0$. Экспериментальные значения дипольной поляризуемости атомов приведены в работе [54], а значения параметра d определяются формулой [53]

(30)
${{d}^{4}} = \frac{1}{2}{{\alpha }_{d}}{{a}_{0}}{{Z}^{{ - 1/3}}}b_{{{\text{pol}}}}^{2},$
(31)
$b_{{{\text{pol}}}}^{2} = \max \left\{ {{{\left( {E - 50\,\,{\text{эВ}}} \right)} \mathord{\left/ {\vphantom {{\left( {E - 50\,\,{\text{эВ}}} \right)} {\left( {16\,\,{\text{эВ}}} \right),{\text{ }}1}}} \right. \kern-0em} {\left( {16\,\,{\text{эВ}}} \right),{\text{ }}1}}} \right\}.$

• Потенциал в приближении локальной плотности

Более точный корреляционно-поляризационный потенциал может быть получен путем комбинирования потенциала Букингема (для больших расстояния между налетающим электроном и атомом-мишенью) и поляризационного потенциала, получаемого в приближении локальной плотности [53]. Последнее основывается на предположении о том, что энергия корреляционно-поляризационного взаимодействия атома с налетающим электроном является такой же, как и в случае движения электрона в свободном электронном газе с плотностью ${{\rho }_{e}}\left( r \right)$, равной локальной электронной плотности атома. При этом удобно использовать параметр

(32)
${{r}_{s}} \equiv \frac{1}{{{{a}_{0}}}}{{\left[ {\frac{3}{{4\pi {{\rho }_{e}}\left( r \right)}}} \right]}^{{1/3}}},$
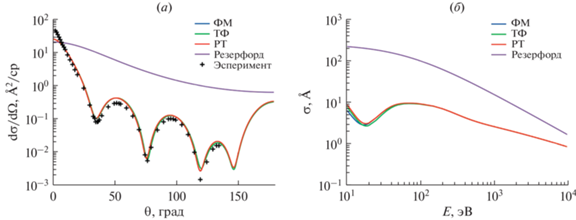
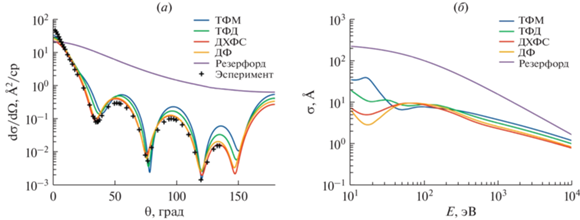
определяемый как радиус сферы (в единицах ${{a}_{0}}$), содержащей в среднем один электрон газа. Параметризация потенциала, полученного в приближении локальной плотности, приводит к следующим выражениям [55]:

(33)
$\begin{gathered} {{V}_{{cp,LDA}}}\left( r \right) = - \frac{{{{e}^{2}}}}{{{{a}_{0}}}}\left( {0.0311{\kern 1pt} \ln {\kern 1pt} {{r}_{s}} - 0.0584 + 0.00133{{r}_{s}}{\kern 1pt} \ln {\kern 1pt} {{r}_{s}} - 0.0084{{r}_{s}}} \right),\,\,\,\,{{r}_{s}} < 1, \hfill \\ {{V}_{{cp,LDA}}}\left( r \right) = - \frac{{{{e}^{2}}}}{{{{a}_{0}}}}{{\beta }_{0}}\frac{{1 + \left( {7{\text{/}}6} \right){{\beta }_{1}}r_{s}^{{1/2}} + \left( {4{\text{/}}3} \right){{\beta }_{2}}{{r}_{s}}}}{{{{{\left( {1 + {{\beta }_{1}}r_{s}^{{1/2}} + {{\beta }_{2}}{{r}_{s}}} \right)}}^{2}}}},\,\,\,\,{{r}_{s}} \geqslant 1, \hfill \\ {{\beta }_{0}} = 0.1423,\,\,\,\,{{\beta }_{1}} = 1.0529,\,\,\,\,{{\beta }_{2}} = 0.3334. \hfill \\ \end{gathered} $

На рис. 2–4 приведены дифференциальные сечения и полные сечения упругого рассеяния, полученные с различными потенциалами электростатического, обменного и корреляционно-поляризационного взаимодействия. Для потенциала электростатического взаимодействия (Vst) используются модели Томаса–Ферми–Мольера (ТФМ), Томаса–Ферми–Дирака (ТФД), Дирака–Хартри-Фока–Слейтера (ДХФС) и Дирака–Фока (ДФ), для потенциала обменного взаимодействия (Vex) – модели Томаса–Ферми (ТФ), Фернесса–МакКарти (ФМ) и Рили–Трулара (РТ), для корреляционно-поляризационного потенциала (Vcp) – модель Букингема (Б) и приближение локальной плотности (ПЛП). При вариации потенциала одного из взаимодействий два других выбираются согласно стандартным настройкам для программы ELSEPA (Vst – ДФ, Vex – ФМ, Vcp = 0) [56]. Также для сравнения приведены сечения, полученные по формуле Резерфорда. Как видно из графиков, дифференциальные и полные сечения упругого рассеяния наиболее чувствительны к изменению модели потенциала электростатического взаимодействия. При этом основные различия наблюдаются в области сверхнизких энергий (ниже 100 эВ), где точность многих моделей (как упругого, так и неупругого рассеяния) вызывает определенные вопросы [57–59].

Рис. 2.

Дифференциальные сечения (а) (для энергии 300 эВ) и полные сечения (б) упругого рассеяния электронов на атомах ртути (Z = 80), полученные с различными потенциалами электростатического взаимодействия.

Рис. 3.

Дифференциальные сечения (а) (для энергии 300 эВ) и полные сечения (б) упругого рассеяния электронов на атомах ртути (Z = 80), полученные с различными потенциалами обменного взаимодействия.

Рис. 4.

Дифференциальные сечения (а) (для энергии 300 эВ) и полные сечения (б) упругого рассеяния электронов на атомах ртути (Z = 80), полученные с различными корреляционно-поляризационными потенциалами.

3. КВАЗИУПРУГИЕ И НЕУПРУГИЕ ПРОЦЕССЫ

Квазиупругие и неупругие процессы включают в себя все процессы взаимодействия между налетающим электроном и веществом мишени, в которых электрон теряет свою энергию. При этом также происходит изменение направления движения электрона, и полярный угол рассеяния $\theta $ задается выражением

(34)
${{\sin }^{2}}\theta = \frac{{\hbar \omega }}{E},$
где E – энергия электрона до акта рассеяния, $\hbar \omega $ – потери энергии [60]. В моделях неупругого рассеяния часто рассматривается взаимодействие налетающего электрона с веществом мишени в целом, и для описания такого взаимодействия используется обратная длина свободного пробега $\lambda _{{{\text{inel}}}}^{{ - 1}}\left( E \right)$ [61–63], связанная с сечением неупругого рассеяния ${{\sigma }_{{{\text{inel}}}}}$ формулой
(35)
$\lambda _{{{\text{inel}}}}^{{ - 1}}\left( E \right) = n\sigma \left( E \right),$
где n – концентрация рассеивающих центров в веществе.

Основной характеристикой упругого рассеяния электронов на атомах мишени является дифференциальная обратная длина свободного пробега $\frac{{d\lambda _{{{\text{inel}}}}^{{ - 1}}}}{{d\hbar \omega }}\left( {E,\hbar \omega } \right)$, позволяющая определить обратную длину свободного пробега по формуле [64]

(36)
$\lambda _{{{\text{inel}}}}^{{ - 1}}\left( E \right) = \int\limits_0^{{E \mathord{\left/ {\vphantom {E 2}} \right. \kern-0em} 2}} {\frac{{d\lambda _{{{\text{inel}}}}^{{ - 1}}\left( {E,\hbar \omega } \right)}}{{d\hbar \omega }}d\hbar \omega } ,$
а также потери энергии электрона на единицу длины пути $S\left( E \right)$ по формуле

(37)
$S\left( E \right) = \int\limits_0^{{E \mathord{\left/ {\vphantom {E 2}} \right. \kern-0em} 2}} {\frac{{d\lambda _{{{\text{inel}}}}^{{ - 1}}\left( {E,\hbar \omega } \right)}}{{d\hbar \omega }}} \hbar \omega d\hbar \omega .$

Потери энергии $\hbar \omega $ при неупругом рассеянии также определяются на основе функции $\frac{{d\lambda _{{{\text{inel}}}}^{{ - 1}}}}{{d\hbar \omega }}$ методом Монте–Карло [60]. Потери энергии на единицу длины пути, вообще говоря, не используются в современных моделях дискретных потерь энергии заряженных частиц в веществе, но эта величина в целом является важной характеристикой функции $\frac{{d\lambda _{{{\text{inel}}}}^{{ - 1}}}}{{d\hbar \omega }}$, используемой, например, при сравнении различных моделей.

3.1. Электрон-фононное взаимодействие

За счет теплового движения атомы кристаллических тел колеблются вблизи своих положений равновесия. С такими колебаниями связывается наличие фононов в кристаллической решетке, и взаимодействие налетающего электрона с оптическими модами колебаний решетки может увеличивать их число [65, 66]. Энергия фононов не превышает значения kBTD, где kB – постоянная Больцмана и TD – температура Дебая. Для большинства твердых тел величина kBTD составляет менее 0.1 эВ, и учет потерь энергии налетающего электрона на генерацию фононов становится целесообразен при энергиях электрона порядка 1 эВ [67].

Согласно существующим работам [65, 66], обратная длина свободного пробега при электрон-фононном рассеянии может быть выражена формулой

(38)
$\lambda _{{{\text{ph}}}}^{{ - 1}} = \frac{1}{{{{a}_{0}}}}\frac{{{{\varepsilon }_{0}} - {{\varepsilon }_{\infty }}}}{{{{\varepsilon }_{0}}{{\varepsilon }_{\infty }}}}\frac{{\hbar \omega }}{E}\frac{{n\left( T \right) + 1}}{2}\ln \left[ {\frac{{1 + \sqrt {1 - {{\hbar \omega } \mathord{\left/ {\vphantom {{\hbar \omega } E}} \right. \kern-0em} E}} }}{{1 - \sqrt {1 - {{\hbar \omega } \mathord{\left/ {\vphantom {{\hbar \omega } E}} \right. \kern-0em} E}} }}} \right],$
где E – энергия налетающего электрона, $\hbar \omega $ – его потери энергии (порядка 0.01–0.1 эВ), ${{\varepsilon }_{0}}$ – статическая диэлектрическая проницаемость, ${{\varepsilon }_{\infty }}$ – высокочастотная диэлектрическая проницаемость, ${{a}_{0}}$ – боровский радиус и $n\left( T \right)$ – число заполнения:

(39)
$n\left( T \right) = \frac{1}{{{{e}^{{{{\hbar \omega } \mathord{\left/ {\vphantom {{\hbar \omega } {{{k}_{B}}T}}} \right. \kern-0em} {{{k}_{B}}T}}}}} - 1}},$

Было установлено, что для ПММА величина $\hbar \omega $ может быть принята равной 0.1 эВ [66, 67], что вкупе с формулой (38) предоставляет все необходимое для моделирования электрон-фононного взаимодействия.

3.2 Электрон-поляронное взаимодействие

Электроны, медленно движущиеся в диэлектриках, приводят к появлению поляризационного поля, которое оказывает на них стабилизирующее воздействие. Такой процесс описывается как генерация квазичастицы – полярона, состоящего из электрона и поляризационного облака вокруг него. Было установлено, что обратная длина свободного пробега для такого взаимодействия может быть описана экспоненциальной функцией [67]

(40)
$\lambda _{{{\text{pol}}}}^{{ - 1}} = C{{e}^{{ - \gamma E}}},$
параметры которой определяются для каждого вещества косвенным методом (например, по энергетическому распределению вторичных электронов [60, 68]). При этом считается, что при генерации полярона налетающий электрон полностью останавливается ($\hbar \omega = E$). Было установлено, что для ПММА параметры C и $\gamma $ могут быть приняты равными 0.1 нм–1 и 0.15 эВ–1, соответственно [69]. Следует отметить, что в силу фиксированных потерь энергии как при электрон-фононном, так и при электрон-поляронном рассеянии допустимо непосредственное использование обратной длины свободного пробега (без предварительного введения дифференциальной обратной длины свободного пробега).

3.3. Электрон-электронное взаимодействие

Электрон-электронное рассеяние, вызываемое взаимодействием налетающего электрона с электронной оболочкой атома-мишени, является доминирующим неупругим процессом при движении электрона в веществе. Если энергия налетающего электрона достаточно высока, он может вызвать переход одного из остовных электронов в свободное состояние выше уровня Ферми. Последующая релаксация атома происходит посредством рентгеновского излучения или испускания другого электрона. Взаимодействие налетающего электрона с валентными электронами атома может происходить одним из двух возможных способов. В первом случае происходит возбуждение одного валентного электрона, что приводит к его переходам внутри зоны или между зонами. При получении большой энергии от налетающего электрона возбужденный электрон также может преодолеть потенциальный барьер между зоной проводимости и вакуумом и в дальнейшем быть зарегистрированным как вторичный электрон. Снятие возбуждения атома при этом происходит за счет излучения света в видимом диапазоне (катодолюминесценция) или за счет безызлучательного переходов с выделением тепла. Во втором случае происходит коллективное возбуждение валентных электронов, описываемое как генерация плазмона. Энергия плазмона, как правило, находится в диапазоне 5–30 эВ, и его распад сопровождается генерацией вторичного электрона и/или выделением тепла [27].

Исторически первые подходы к описанию потерь энергии электрона в веществе основывались на формуле Бете [70, 71]. Эта формула приведена в работе [72], предшествующей настоящей и, в силу своей простоты, имеет существенные недостатки. Формула Бете не может быть применена в области низких энергий, а также она описывает лишь потери энергии на единицу длины пути, не предоставляя информации о длине свободного пробега. Поэтому в настоящей работе будут рассматриваться более точные и детальные подходы на основе функции потерь энергии (Energy Loss Function, ELF):

(41)
$ELF\left( {q,\omega } \right) \equiv \operatorname{Im} \left[ {\frac{{ - 1}}{{\varepsilon \left( {q,\omega } \right)}}} \right],$
где $\varepsilon \left( {q,\omega } \right)$ – комплексная диэлектрическая проницаемость, q и $\hbar \omega $ – передаваемые среде импульс и энергия, соответственно. При известной функции потерь энергии дифференциальная обратная длина свободного пробега может быть найдена по формуле
(42)
$\frac{{d\lambda _{{{\text{inel}}}}^{{ - 1}}}}{{d\hbar \omega }} = \frac{1}{{\pi E{{a}_{0}}}}\int\limits_{{{k}_{ - }}}^{{{k}_{ + }}} {\operatorname{Im} \left[ {\frac{{ - 1}}{{\varepsilon \left( {q,\omega } \right)}}} \right]\frac{{dq}}{q}} ,$
где
(43)
${{q}_{ \pm }} = \frac{{\sqrt {2m} }}{\hbar }\left( {\sqrt E \pm \sqrt {E - \hbar \omega } } \right),$
E – энергия налетающего электрона, m – масса электрона и ${{a}_{0}}$ – боровский радиус.

Поскольку функция $\varepsilon \left( {\omega ,q} \right)$ может быть найдена из первых принципов только в нескольких идеализированных случаях [73, 74], часто используется подход на основе оптической функции потерь энергии, получаемой в пределе $q \to 0$:

(44)
$OELF\left( \omega \right) \equiv ELF\left( {0,\omega } \right) = \operatorname{Im} \left[ {\frac{{ - 1}}{{\varepsilon \left( {0,\omega } \right)}}} \right].$

Оптическая функция потерь энергии может быть рассчитана на основе значений коэффициентов преломления (n) и поглощения (k) [75]:

(45)
$\operatorname{Im} \left[ {\frac{{ - 1}}{{\varepsilon \left( {0,\omega } \right)}}} \right] = \frac{{2nk}}{{{{{\left( {{{n}^{2}} + {{k}^{2}}} \right)}}^{2}}}}.$

Коэффициенты n и k табулированы для низких энергий (примерно до 2 кэВ) [76, 77], для более же высоких энергий они могут быть найдены из компонент атомных факторов рассеяния $f = {{f}_{1}} + i{{f}_{2}}$ (для молекулярных веществ) [78, 79]:

(46)
$\begin{gathered} n = 1 - \frac{{{{e}^{2}}}}{{2\pi m{{c}^{2}}}}{{\lambda }^{2}}N\sum\limits_p {{{x}_{p}}{{f}_{{1p}}},} \hfill \\ k = \frac{e}{{2\pi m{{c}^{2}}}}{{\lambda }^{2}}N\sum\limits_p {{{x}_{p}}{{f}_{{2p}}},} \hfill \\ \end{gathered} $
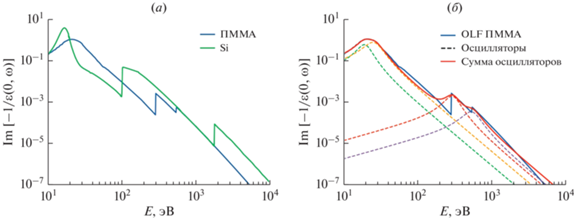
где N – концентрация молекул, содержащих ${{x}_{p}}$ атомов каждого вида, $\lambda $ – длина волны фотона. Для атомарных веществ оптическая функция потерь энергии может быть найдена непосредственно по формуле
(47)
$\operatorname{Im} \left[ {\frac{{ - 1}}{{\varepsilon \left( {0,\omega } \right)}}} \right] = \frac{{{{n}_{m}}c{{\sigma }_{{{\text{phot}}}}}}}{\omega },$
где ${{n}_{m}}$ – концентрация остовных электронов, ${{\sigma }_{{{\text{phot}}}}}$ – сечение фотоионизации [80, 81]. На рис. 5а приведены графики оптической функции потерь энергии для ПММА и кремния, найденные вышеописанными способами.

Рис. 5.

(а) Оптические функции потерь энергии ПММА и Si, (б) оптическая функция потерь энергии ПММА, приближенная суммой осцилляторов Друде.

При известной оптической функции потерь энергии поведение функция потерь энергии в области $q > 0$ учитывается с помощью одного из подходов, описанных ниже.

• Аппроксимация функции потерь энергии эмпирической функцией

Наиболее простым является подход, в котором поведение функции потерь энергии в области $q > 0$ описывается подгоночными функциями $L\left( x \right)$ и $S\left( x \right)$ [82, 83], что позволяет непосредственно рассчитать обратную длину свободного пробега:

(48)
$\begin{gathered} \lambda _{{}}^{{ - 1}}\left( E \right) = \frac{{m{{e}^{2}}}}{{2\pi {{\hbar }^{2}}E}}\int\limits_0^{{{W}_{{\max }}}} {\operatorname{Im} \left[ {\frac{{ - 1}}{{\varepsilon \left( {0,\omega } \right)}}} \right]L\left( {\frac{{\hbar \omega }}{E}} \right)d\hbar \omega ,} \hfill \\ L\left( x \right) = \left( {1 - x} \right)\ln \frac{4}{x} - \frac{7}{4}x + {{x}^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}}}} - \frac{{33}}{{32}}{{x}^{2}}, \hfill \\ \end{gathered} $
а также потери энергии на единицу длины пути:
(49)
$\begin{gathered} - \frac{{dE}}{{ds}} = \frac{{m{{e}^{2}}}}{{\pi {{\hbar }^{2}}E}}\int\limits_0^{{{W}_{{\max }}}} {\operatorname{Im} \left[ {\frac{{ - 1}}{{\varepsilon \left( {0,\omega } \right)}}} \right]S\left( {\frac{{\hbar \omega }}{E}} \right)} \hbar \omega d\hbar \omega , \hfill \\ S\left( x \right) = \ln \frac{{1.166}}{x} - \frac{3}{4}x - \frac{x}{4}\ln \frac{4}{x} + \frac{1}{2}{{x}^{{3/2}}} - \frac{{{{x}^{2}}}}{{16}}\ln \frac{4}{x} - \frac{{31}}{{48}}{{x}^{2}}, \hfill \\ \end{gathered} $
где ${{W}_{{\max }}} = {E \mathord{\left/ {\vphantom {E 2}} \right. \kern-0em} 2}$. В данном подходе сложно говорить о дифференциальной обратной длине свободного пробега, которая может потребоваться, например, для моделирования потерь энергии при электрон-электронном рассеянии. Однако, при необходимости она может быть определена по формуле [60]

(50)
$\frac{{d{{\lambda }^{{ - 1}}}}}{{d\hbar \omega }} = \frac{{m{{e}^{2}}}}{{2\pi {{\hbar }^{2}}E}}\operatorname{Im} \left[ {\frac{{ - 1}}{{\varepsilon \left( {0,\omega } \right)}}} \right]L\left( {\frac{{\hbar \omega }}{E}} \right).$

• Аппроксимация функции потерь энергии суммой осцилляторов Друде

В данном подходе оптическая функция потерь энергии приближается суммой осцилляторов Друде [84]:

(51)
$\operatorname{Im} \left[ {\frac{{ - 1}}{{\varepsilon \left( {0,\omega } \right)}}} \right] = \sum\limits_i {\frac{{{{A}_{i}}{{\Gamma }_{i}}\hbar \omega }}{{{{{\left[ {E_{i}^{2} - {{{\left( {\hbar \omega } \right)}}^{2}}} \right]}}^{2}} + {{{\left( {{{\Gamma }_{i}}\hbar \omega } \right)}}^{2}}}},} $
параметры ${{E}_{i}}$, ${{\Gamma }_{i}}$ и ${{A}_{i}}$ которых определяются путем подгонки [75, 85] (см. рис. 5б, табл. 2). Продолжение оптической функции потерь энергии в область $q > 0$ осуществляется за счет использования квадратичного закон дисперсии:
(52)
${{E}_{i}}\left( q \right) = {{E}_{i}} + \frac{{{{\hbar }^{2}}{{q}^{2}}}}{{2m}},$
что в дальнейшем позволяет построить функцию потерь энергии (см. рис. 6а):
(53)
$\operatorname{Im} \left[ {\frac{{ - 1}}{{\varepsilon \left( {q,\omega } \right)}}} \right] = \sum\limits_i {\frac{{{{A}_{i}}{{\Gamma }_{i}}\hbar \omega }}{{{{{\left[ {{{{\left( {{{E}_{i}} + \frac{{{{\hbar }^{2}}{{q}^{2}}}}{{2m}}} \right)}}^{2}} - {{{\left( {\hbar \omega } \right)}}^{2}}} \right]}}^{2}} + {{{\left( {{{\Gamma }_{i}}\hbar \omega } \right)}}^{2}}}},} $
и получить дифференциальную обратную длину свободного пробега по формуле (42).

Таблица 2.  

Параметры осцилляторов для ПММА в моделях Друде и Мермина [75, 90]

  Осцилляторы Друде Осцилляторы Мермина
$i$ ${{E}_{i}}$, эВ ${{\Gamma }_{i}}$, эВ ${{A}_{i}}$, эВ2 $\hbar {{\omega }_{i}}$, эВ $\hbar {{\gamma }_{i}}$, эВ ${{A}_{i}}$
1 19.46 8.77 100.0 19.13 9.03 2.59 × 10–1
2 25.84 14.75 286.5 25.36 14.34 4.46 × 10–1
3 300.0 140.0 80.0 70.75 48.98 4.44 × 10–3
4 550.0 300.0 55.0 –
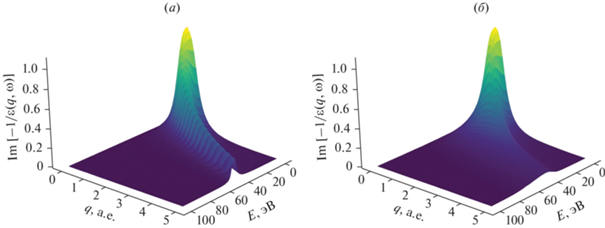
Рис. 6.

(а) Функция потерь энергии ПММА, представленная суммой осцилляторов Друде, (б) функция потерь энергии ПММА, представленная суммой осцилляторов Мермина.

Следует отметить, что именно такой подход к определению дифференциальной обратной длины свободного пробега используется в модуле “MuElec”, входящим в состав пакета Geant4 и предназначенном для моделирования процессов в области микроэлектроники [86, 87]. Для кремния (1s22s22p63s23p2), например, в нем используется функция потерь энергии, включающая в себя шесть осцилляторов: один для K-оболочки (1s), два для L-оболочки (2s и 2p), два для M-оболочки (3s и 3p) и один для описания коллективных колебаний валентных электронов.

• Диэлектрическая функция Мермина

Наиболее точным подходом к построению функции потерь энергии в органических полимерах является подход на основе модели Мермина [69, 88, 89]. В его основе лежит диэлектрическая функция Мермина для столкновительной плазмы,

(54)
${{\varepsilon }_{M}}\left( {q,\omega } \right) = 1 + \frac{{\left( {1 + {{i\gamma } \mathord{\left/ {\vphantom {{i\gamma } \omega }} \right. \kern-0em} \omega }} \right)\left[ {{{\varepsilon }_{L}}\left( {q,\omega + i\gamma } \right) - 1} \right]}}{{1 + \left( {{{i\gamma } \mathord{\left/ {\vphantom {{i\gamma } \omega }} \right. \kern-0em} \omega }} \right){{\left[ {{{\varepsilon }_{L}}\left( {q,\omega + i\gamma } \right) - 1} \right]} \mathord{\left/ {\vphantom {{\left[ {{{\varepsilon }_{L}}\left( {q,\omega + i\gamma } \right) - 1} \right]} {\left[ {{{\varepsilon }_{L}}\left( {q,0} \right) - 1} \right]}}} \right. \kern-0em} {\left[ {{{\varepsilon }_{L}}\left( {q,0} \right) - 1} \right]}}}},$
где $\gamma $ – постоянная затухания, ${{\varepsilon }_{L}}\left( {q,\omega } \right)$ – диэлектрическая функция Линдхарда [73]:
(55)
${{\varepsilon }_{L}}\left( {q,\omega } \right) = 1 + \frac{{{{\chi }^{2}}}}{{{{z}^{2}}}}\left[ {{{f}_{1}}\left( {u,z} \right) + i{{f}_{2}}\left( {u,z} \right)} \right].$
Здесь $u = {\omega \mathord{\left/ {\vphantom {\omega {\left( {q{{v}_{F}}} \right)}}} \right. \kern-0em} {\left( {q{{v}_{F}}} \right)}}$, $z = {q \mathord{\left/ {\vphantom {q {\left( {2{{q}_{F}}} \right)}}} \right. \kern-0em} {\left( {2{{q}_{F}}} \right)}}$ и ${{\chi }^{2}} = {{{{e}^{2}}} \mathord{\left/ {\vphantom {{{{e}^{2}}} {\left( {\pi \hbar {{v}_{F}}} \right)}}} \right. \kern-0em} {\left( {\pi \hbar {{v}_{F}}} \right)}},$ где ${{v}_{F}}$ – скорость Ферми валентных электронов вещества, ${{q}_{F}} = {{m{{v}_{F}}} \mathord{\left/ {\vphantom {{m{{v}_{F}}} \hbar }} \right. \kern-0em} \hbar }$. При этом функции ${{f}_{1}}\left( {u,z} \right)$ и ${{f}_{2}}\left( {u,z} \right)$ определяются формулами
(56)
$\begin{gathered} {{f}_{1}}\left( {u,z} \right) = \frac{1}{2} + \frac{1}{{8z}}\left[ {g\left( {z - u} \right) + g\left( {z + u} \right)} \right], \hfill \\ {{f}_{2}}\left( {u,z} \right) = \left\{ \begin{gathered} \frac{\pi }{2}u,{\text{ }}z + u < 1 \hfill \\ \frac{\pi }{{8z}}\left[ {1 - {{{\left( {z - u} \right)}}^{2}}} \right],{\text{ }}\left| {z - u} \right| < 1 < z + u \hfill \\ 0,{\text{ }}\left| {z - u} \right| > 1. \hfill \\ \end{gathered} \right. \hfill \\ \end{gathered} $
где

(57)
$g\left( x \right) = \left( {1 - {{x}^{2}}} \right)\ln \left| {\frac{{1 + x}}{{1 - x}}} \right|.$

Как и в предыдущем подходе, функция потерь энергии вещества суммой функций потерь отдельных осцилляторов, и ее построение проводится в два этапа. Сначала оптическая функция потерь энергии вещества подгоняется суммой функций потерь энергии Мермина (осцилляторов Мермина) для $q = 0$:

(58)
$\operatorname{Im} \left[ {\frac{{ - 1}}{{\varepsilon \left( {0,\omega } \right)}}} \right] = \sum\limits_i {{{A}_{i}}\operatorname{Im} } \left[ {\frac{{ - 1}}{{{{\varepsilon }_{M}}\left( {{{\omega }_{i}},{{\gamma }_{i}},q = 0,\omega } \right)}}} \right],$
что позволяет получить параметры ${{A}_{i}}$, ${{\omega }_{i}}$ и ${{\gamma }_{i}}$ отдельных осцилляторов (см. табл. 2, рис. 6б). Параметр ${{\omega }_{i}}$ определяет частоту каждого из осцилляторов, что позволяет найти параметр ${{v}_{F}}$, входящий в величины u, z и $\chi $, используемые в диэлектрической функции Линдхарда:
(59)
$\begin{gathered} {{\omega }_{i}} = \sqrt {\frac{{4\pi {{n}_{i}}{{e}^{2}}}}{m}} \Rightarrow {{n}_{i}} = \frac{{\omega _{i}^{2}m}}{{4\pi {{e}^{2}}}}, \hfill \\ {{v}_{{{{F}_{i}}}}} = \frac{\hbar }{m}{{\left( {3{{\pi }^{2}}{{n}_{i}}} \right)}^{{{1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0em} 3}}}}, \hfill \\ \end{gathered} $
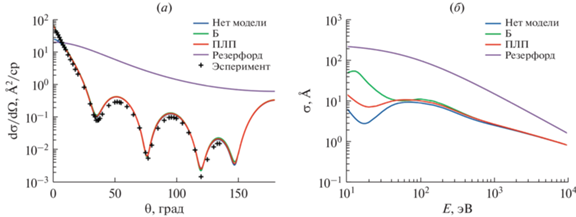
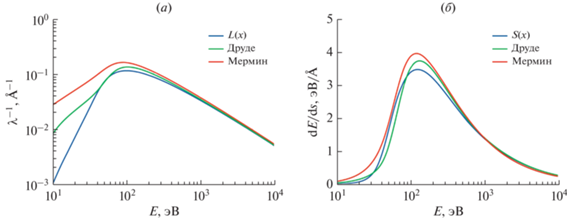
где ${{n}_{i}}$ – концентрация электронов, соответствующая осциллятору с индексом i, m – масса электрона. Далее на основе параметров ${{A}_{i}}$, ${{\omega }_{i}}$ и ${{\gamma }_{i}}$ составляется функция потерь энергии:
(60)
$\operatorname{Im} \left[ {\frac{{ - 1}}{{\varepsilon \left( {q,\omega } \right)}}} \right] = \sum\limits_i {{{A}_{i}}\operatorname{Im} } \left[ {\frac{{ - 1}}{{{{\varepsilon }_{M}}\left( {{{\omega }_{i}},{{\gamma }_{i}},q,\omega } \right)}}} \right]$
и определяется дифференциальная обратная длина свободного пробега.

На рис. 7 приведено сравнение энергетических зависимостей обратной длины свободного пробега и потерь энергии на единицу длины пути, полученные для ПММА с использованием вышеописанных моделей. Как видно из графиков, принципиальное различие между моделями проявляется в области малых энергий налетающего электрона, и при энергиях выше 1 кэВ зависимости, полученные на основе различных моделей, практически совпадают. Таким образом каждая из них может применяться для моделирования выделения энергии в слое резисте толщиной порядка 100 нм при экспонировании электронным лучом с начальной энергией электронов в несколько десятков килоэлектронвольт. В случаях, когда необходимы точные значения длины свободного пробега в области низких энергий (например, при моделировании различных распределений для вторичных электронов), следует использовать подходы на основе осцилляторов Друде и Мермина.

Рис. 7.

Энергетические зависимости обратной длины свободного пробега (а) и потерь энергии на единицу длины пути (б) при неупругом рассеянии, полученные для ПММА с использованием различных моделей.

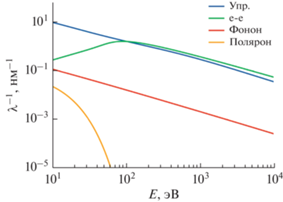
Энергетические зависимости обратной длины свободного пробега электронов в ПММА для упругого и всех видов неупругого рассеяния приведены на рис. 8. Как и следовало ожидать, преобладающими являются процессы упругого и электрон-электронного рассеяния, в то время как вклад процессов электрон-поляронного и электрон-фононного рассеяния проявляется лишь в области сверхнизких энергий (ниже 100 эВ). Такая модель, учитывающая четыре вышеупомянутых механизма взаимодействия налетающего электрона с веществом, изначально была предложена именно для ПММА [60]. Однако, она также может быть применена и для других веществ, для которых были или могут быть проведены необходимые измерения. Так, для построения функции потерь энергии на основе оптической функции потерь энергии необходимы данные о показателях преломления и поглощения вещества, для определения обратной длины пробега при электрон-фононном рассеянии – статическая и высокочастотная диэлектрическая проницаемость вещества. Параметры обратной длины свободного пробега при электрон-фононном рассеянии могут быть определены на основе работы выхода вещества и распределения вторичных электронов аналогично тому, как это было сделано для ПММА [60, 68, 69]. Следует также отметить, что учет электрон-фононного и электрон-поляронного взаимодействия является критичным в основном в случае высоких требований к точности моделирования в области низких энергий. При решении же вышеупомянутой задачи моделирования выделения энергии в слое резиста при экспонировании учет этих двух взаимодействий может быть заменен введением энергии отсечки в несколько десятков электронвольт, что существенно упростит процесс построения модели и сам алгоритм моделирования.

Рис. 8.

Энергетические зависимости обратной длины свободного пробега электронов в ПММА для упругого и всех видов неупругого рассеяния.

ЗАКЛЮЧЕНИЕ

В данной работе рассмотрены современные подходы к вычислению сечений взаимодействия электронного луча с веществом – подход на основе релятивистской квантовой теории рассеяния для вычисления сечений упругого рассеяния и подход на основе функции потерь энергии для вычислений сечений неупругого электрон-электронного рассеяния. Также приведены модели процессов, характерных для сверхнизких энергий электрона – электрон-фононного и электрон-поляронного рассеяния. Вкупе с предыдущей работой, посвященной описанию алгоритмов моделирования рассеяния электронного луча в веществе [72], это предоставляет всю информацию, необходимую для разработки высокоточных алгоритмов моделирования. Такие алгоритмы могут применяться для моделирования распределения энергии, выделившейся в резисте на стадии экспонирования в процессе электронно-лучевой литографии, что позволяет оценить масштабы проявления эффекта близости и скорректировать параметры экспонирования. Следует также отметить, что область применения вышеописанных моделей выходит далеко за пределы электронно-лучевой литографии. К примеру, подходы на основе функции потерь энергии широко применяются для определения характеристик веществ, использующихся в микроэлектронике, космической промышленности, в различных биологических и медицинских отраслях.

Работа выполнена в рамках Государственного задания ФТИАН им. К.А. Валиева РАН Минобрнауки РФ по теме № FFNN-2022-0021.

Список литературы

  1. Chang T.H.P. Proximity effect in electron-beam lithography // J. Vac. Sci. Technol. Nov. 1975. V. 12. № 6. P. 1271–1275.

  2. Nilsson B.A. Experimental evaluation method of point spread functions used for proximity effects correction in electron beam lithography // J. Vac. Sci. Technol. B, Nanotechnol. Microelectron. Mater. Process. Meas. Phenom. 2011. V. 29. № 6. P. 06F311.

  3. Greeneich J.S., T. Van Duzer. Model for Exposure of Electron-Sensitive Resists // J. Vac. Sci. Technol. Nov. 1973. V. 10. № 6. P. 1056–1059.

  4. Greeneich J.S., T. Van Duzer. An Exposure Model For Electron-Sensitive Resists // IEEE Trans. Electron Devices. 1974. V. 21. № 5. P. 286–299.

  5. Greeneich J.S. Solubility Rate of Poly-(Methyl Methacrylate), PMMA, Electron-Resist // J. Electrochem. Soc. 1974. V. 121. № 12. P. 1669.

  6. Greeneich J.S. Developer Characteristics of Poly-(Methyl Methacrylate) Electron Resist // J. Electrochem. Soc. 1975. V. 122. № 7. P. 970.

  7. Glezos N. Application of a new analytical technique of electron distribution calculations to the profile simulation of a high sensitivity negative electron-beam resist // J. Vac. Sci. Technol. B Microelectron. Nanom. Struct. Nov. 1992. V. 10. № 6. P. 2606.

  8. Schmoranzer H., Reisser M. Spatial energy deposition distribution by a keV-electron beam in resist layers for electron-beam lithography // Nucl. Instruments Methods Phys. Res. Sect. B Beam Interact. with Mater. Atoms. 1995. V. 105. № 1–4. P. 35–41.

  9. Paul B.K. An analytical model of the diffusive scattering of low-energy electrons in electron-beam resists // Microelectron. Eng. 1999. V. 49. № 3–4. P. 233–244.

  10. Raptis I., Glezos N., Hatzakis M. Use of the Boltzmann transport equation for the evaluation of energy deposition in the case of electron sensitive resist films over composite substrates // Microelectron. Eng. 1993. V. 21. № 1–4. P. 289–292.

  11. Stepanova M. et al. Simulation of electron beam lithography of nanostructures // J. Vac. Sci. Technol. B, Nanotechnol. Microelectron. Mater. Process. Meas. Phenom. 2010. V. 28. № 6. P. C6C48–C6C57.

  12. Kyser D.F., Viswanathan N.S. Monte Carlo simulation of spatially distributed beams in electron-beam lithography // J. Vac. Sci. Technol. 2002. V. 12. № 6. P. 1305–1308.

  13. Shimizu R., Everhart T.E. A semiempirical stopping-power formula for use in microprobe analysis // Appl. Phys. Lett. 1978. V. 33. № 8. P. 784–786.

  14. Adesida I., Shimizu R., Everhart T.E. A study of electron penetration in solids using a direct Monte Carlo approach // J. Appl. Phys. 1980. V. 51. № 11. P. 5962–5969.

  15. Samoto N., Shimizu R. Theoretical study of the ultimate resolution in electron beam lithography by Monte Carlo simulation, including secondary electron generation: Energy dissipation profile in polymethylmethacrylate // J. Appl. Phys. 1983. V. 54. № 7. P. 3855–3859

  16. Kim S.-H., Ham Y.-M., Lee W., Chun K. New approach of Monte Carlo simulation for low energy electron beam lithography // Microelectron. Eng. 1998. V. 41–42. P. 179–182.

  17. Ivin V.V., Silakov M.V., Vorotnikova N.V., Resnick D.J., Nordquist K.N., Siragusa L. Efficient and robust algorithms for Monte Carlo and e-beam lithography simulation // Microelectron. Eng. 2001. V. 57–58. P. 355–360.

  18. Glezos N., Raptis I. A fast electron beam lithography simulator based on the Boltzmann transport equation // IEEE Trans. Comput. Des. Integr. Circuits Syst., 1996. V. 15. № 1. P. 92–102.

  19. Aktary M., Stepanova M., Dew S.K., Simulation of the spatial distribution and molecular weight of polymethylmethacrylate fragments in electron beam lithography exposures // J. Vac. Sci. Technol. B Microelectron. Nanom. Struct. 2006.V. 24. № 2. PP. 768–779.

  20. Stepanova M. et al. Simulation of electron beam lithography of nanostructures // J. Vac. Sci. Technol. B, Nanotechnol. Microelectron. Mater. Process. Meas. Phenom. Nov. 2010. V. 28. № 6. P. C6C48–C6C57.

  21. Асадов С.М., Мустафаева С.Н., Лукичев В.Ф., Келбалиев К.И. Концентрационные зависимости переноса заряда и кинетика Монте-Карло моделирования роста 2D моно- и нанокристаллов халькогенидов галлия // Микроэлектроника. 2022. V. 51. № 1. P. 48–59.

  22. Пермякова О.О. Рогожин А.Е. Моделирование резистивного переключения в мемристорных структурах на основе оксидов переходных металлов // Микроэлектроника, 2020. Т. 49. № 5. С. 323–333.

  23. Борздов В.М., Борздов А.В., Сперанский Д.С., Вьюрков В.В., Орликовский А.А. Оценка эффективной пороговой энергии межзонной ударной ионизации в глубокосубмикронном кремниевом n-канальном МОП-транзисторе // Микроэлектроника. 2014. Т. 43. № 3. С. 188–192.

  24. Руденко М.К., Мяконьких А.В., Лукичев В.Ф. Моделирование методом Монте-Карло дефектов профиля тренча в процессе глубокого криогенного травления кремния // Микроэлектроника. 2019. Т. 48. № 3. С. 191–200.

  25. Руденко М.К., Мяконьких А.В., Лукичев В.Ф. Численное моделирование криогенного травления: модель с отложенной десорбцией // Микроэлектроника. 2021. Т. 50. № 1. С. 58–67.

  26. Рогожин А.Е., Сидоров Ф.А. Моделирование процессов электронно-лучевой литографии // Микроэлектроника. 2020. Т. 49. № 2. С. 116–132.

  27. Dapor M. Transport of Energetic Electrons in Solids, 2014.V. 257. Cham: Springer International Publishing.

  28. Marrian C.R.K. Modeling of electron elastic and inelastic scattering // J. Vac. Sci. Technol. B Microelectron. Nanom. Struct. 1996. V. 14. № 6. P. 3864.

  29. Ding-Ju J., Zhen-Yu T. A Monte Carlo Study of Low-Energy Electron Transport in Liquid Water: Influence of the Rutherford Formula and the Mott Model // Chinese Phys. Lett. 2010. V. 27. № 3. P. 033401.

  30. Dapor M. Elastic scattering calculations for electrons and positrons in solid targets // J. Appl. Phys. 1996. V. 79. № 11. P. 8406–8411.

  31. Mott N.F., Massey H.S.W. The Theory Of Atomic Collisions. Oxford University Press, London, 1949.

  32. Dapor M. Elastic scattering of electrons and positrons by atoms: differential and transport cross section calculations // Nucl. Instruments Methods Phys. Res. Sect. B Beam Interact. with Mater. Atoms. Apr. 1995. V. 95. № 4. P. 470–476.

  33. Czyżewski Z., MacCallum D.O.N., Romig A., Joy D.C. Calculations of Mott scattering cross section // J. Appl. Phys. Oct. 1990. V. 68. № 7. P. 3066–3072.

  34. Gauvin R., Drouin D. A formula to compute total elastic mott cross-sections // Scanning. 1993. V. 15. № 3. P. 140–150.

  35. Salvat F., Jablonski A., Powell C.J. Elsepa-Dirac partial-wave calculation of elastic scattering of electrons and positrons by atoms, positive ions and molecules // Comput. Phys. Commun. 2005. V. 165. № 2. P. 157–190.

  36. Thomas L.H. The calculation of atomic fields // Math. Proc. Cambridge Philos. Soc. 1927. V. 23. № 5. P. 542–548.

  37. Fermi E. No Un metodo statistico per la determinazione di alcune priorieta dell’atome // Rend. Accad. Naz. Lincei. 1927. V. 6. P. 602–607.

  38. Bethe H., Jackiw R. Intermediate Quantum Mechanics. New York - Amsterdam: CRC Press, 1986.

  39. Molière G. Theorie der Streuung schneller geladener Teilchen // Zeitschrift für Naturforsch. A. Mar. 1955. V. 10. № 3. P. 177–211.

  40. Thomas L.H. Tables of statistical electron distributions for atoms with degree of ionization zero to four and of the corresponding electrostatic potentials // J. Chem. Phys. 1954. V. 22. № 10. P. 1758–1767.

  41. Bonham E.A., Strand T.G. Analytical expressions for potentials of neutral thomas-fermi-dirac atoms and for the corresponding atomic scattering factors for x rays and electrons // J. Chem. Phys. 1963. V. 39. № 9. P. 2200–2204.

  42. Liberman D., Waber J.T., Cromer D.T. Self-consistent-field dirac-slater wave functions for atoms and ions. I. Comparison with previous calculations // Phys. Rev. 1965. V. 137. № 1. P. A27–A34.

  43. Liberman D.A., Cromer D.T., Waber J.T. Relativistic self-consistent field program for atoms and ions // Comput. Phys. Commun. 1971. V. 2. № 2. P. 107–113.

  44. Salvat F., Mart$\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{t} $nez J.D., Mayol R., Parellada J. Analytical Dirac-Hartree-Fock-Slater screening function for atoms (Z = 1–92) // Phys. Rev. A. 1987. V. 36. № 2. P. 467–474.

  45. Desclaux J.P. A multiconfiguration relativistic DIRAC-FOCK program // Comput. Phys. Commun. Jan. 1975. V. 9. № 1. P. 31–45.

  46. Fischer C.F., Godefroid M., Brage T., Jönsson P., Gaigalas G. Advanced multiconfiguration methods for complex atoms: I. Energies and wave functions // J. Phys. B At. Mol. Opt. Phys. 2016. V. 49. № 18. P. 1–35.

  47. Yates A.C. Spin Polarization of Low-Energy Electrons Scattered Elastically from Atoms and Molecules // Phys. Rev. Dec. 1968. V. 176. № 1. P. 173–180.

  48. Bransden B.H., McDowell M.R.C., Noble C.J., Scott T. Equivalent exchange potentials in electron scattering // J. Phys. B At. Mol. Phys. Jun. 1976. V. 9. № 8. P. 1301–1317.

  49. Slater J.C. A simplification of the Hartree-Fock method // Phys. Rev. V. 81. № 3. P. 385–390. 1951.

  50. Riley M.E., Truhlar D.G. Approximations for the exchange potential in electron scattering // J. Chem. Phys. 1975. V. 63. № 5. P. 2182–2191.

  51. Karnakov B.M., Krainov V.P. WKB Approximation in Atomic Physics. Berlin, Heidelberg: Springer Berlin Heidelberg, 2013.

  52. Furness J.B., McCarthy I.E. Semiphenomenological optical model for electron scattering on atoms // J. Phys. B At. Mol. Phys. Nov. 1973. V. 6. № 11. P. 2280–2291.

  53. Salvat F. Optical-model potential for electron and positron elastic scattering by atoms // Phys. Rev. A – At. Mol. Opt. Phys. 2003.V. 68. № 1. P. 17.

  54. Weast R.C., Handbook of chemistry and physics, 49th ed // Am. J. Med. Sci. 1969. V. 257. № 6. P. 423.

  55. Perdew J.P., Wang Y., Erratum: Accurate and simple analytic representation of the electron-gas correlation energy (Physical Review B (1992) 45 (13244) // Phys. Rev. B. 2018. V. 98. № 7. P. 244–249. https://doi.org/10.1103/PhysRevB.45.13244

  56. Salvat F., Jablonski A., Powell C.J. Elsepa—Dirac partial-wave calculation of elastic scattering of electrons and positrons by atoms, positive ions and molecules // Comput. Phys. Commun. Jan. 2005. V. 165. № 2. P. 157–190.

  57. Tan Z., Xia Y., Liu X., Zhao M. Monte-Carlo simulation of low-energy electron scattering in PMMA – Using stopping powers from dielectric formalism // Microelectron. Eng., 2005. V. 77. № 3–4. P. 285–291.

  58. Wang F., Li D.-J., Li X.-J., Cui W.-Z., Hu T.-C., Cao M. Modelling energy deposition in polymethyl methacrylate with low-energy electron irradiation // Micron. 2022.V. 156. P. 103232.

  59. Lee Y., Lee W., Chun K., Kim H. New three dimensional simulator for low energy (∼1 keV) electron beam systems // J. Vac. Sci. Technol. B Microelectron. Nanom. Struct., 2002.V. 17. № 6. P. 2903.

  60. Ciappa M. Monte Carlo modeling in the low-energy domain of the secondary electron emission of polymethylmethacrylate for critical-dimension scanning electron microscopy // J. Micro/Nanolithography, MEMS, MOEMS. 2010.V. 9. № 2. P. 023001.

  61. Tanuma S., Powell C.J., Penn D.R. Calculations of electron inelastic mean free paths. V. Data for 14 organic compounds over the 50-2000 eV range // Surf. Interface Anal. 1994. V. 21. № 3. P. 165–176.

  62. Roberts R.F., Allara D.L., Pryde C.A., Buchanan D.N.E., Hobbins N.D. Mean free path for inelastic scattering of 1.2 kev electrons in thin poly(methylmethacrylate) films // Surf. Interface Anal. 1980. V. 2. № 1. P. 5–10.

  63. Tahir D.and Sari N.H. Stopping powers and inelastic mean free path of 200 eV–50 keV electrons in polymer PMMA, PE, and PVC // Appl. Radiat. Isot. 2015. V. 95. P. 59–62.

  64. Tan Z., Xia Y., Liu X., Zhao M., Zhang L. A new calculation on the stopping power and mean free path for low energy electrons in toluene over energy range of 20–10 000 eV // Appl. Radiat. Isot. 2009. V. 67. № 4. P. 625–629.

  65. Fröhlich H. Electrons in lattice fields // Adv. Phys., Jul. 1954. V. 3. № 11. P. 325–361.

  66. Llacer J., Garwin E.L. Electron-Phonon Interaction in Alkali Halides. I. The Transport of Secondary Electrons with Energies between 0.25 and 7.5 eV // J. Appl. Phys. Jun. 1969. V. 40. № 7. P. 2766–2775.

  67. Ganachaud J.P., Mokrani A. Theoretical study of the secondary electron emission of insulating targets // Surf. Sci. Jul. 1995. V. 334. № 1–3. P. 329–341.

  68. Dapor M. Secondary electron emission yield calculation performed using two different Monte Carlo strategies // Nucl. Instruments Methods Phys. Res. Sect. B Beam Interact. with Mater. Atoms. Jul. 2011. V. 269. № 14. P. 1668–1671.

  69. Dapor M. Role of the tail of high-energy secondary electrons in the Monte Carlo evaluation of the fraction of electrons backscattered from polymethylmethacrylate // Appl. Surf. Sci. Jan. 2017. V. 391. P. 3–11.

  70. Bethe H. Zur Theorie des Durchgangs schneller Korpuskularstrahlen durch Materie // Ann. Phys. 1930. V. 397. № 3. P. 325–400.

  71. Bethe J., Ashkin H. Experimental Nuclear Physics. New York: Wiley, 1953.

  72. Rogozhin A.E., Sidorov F.A. E-Beam Lithography Simulation Techniques // Russ. Microelectron. Mar. 2020. V. 49. № 2. P. 108–122.

  73. Lindhard J. On the properites of a gas of charged particles // Kgl. Danske Vidensk. Selsk. Mat-fys. Medd. 1954. V. 28. P. 8.

  74. Ritchie R.H. Interaction of Charged Particles with a Degenerate Fermi-Dirac Electron Gas // Phys. Rev., May 1959. V. 114. № 3. P. 644–654.

  75. Dapor M. Energy loss of fast electrons impinging upon polymethylmethacrylate // Nucl. Instruments Methods Phys. Res. Sect. B Beam Interact. with Mater. Atoms. 2015. V. 352. P. 190–194.

  76. Palik E.D. Handbook of Optical Constants of Solids. USA: Academic Press, 1998.

  77. Ritsko J.J., Brillson L.J., Bigelow R.W., Fabish T.J. Electron energy loss spectroscopy and the optical properties of polymethylmethacrylate from 1 to 300 eV // J. Chem. Phys. 1978. V. 69. № 9. P. 3931–3939.

  78. Henke B.L., Gullikson E.M., Davis J.C. X-Ray Interactions: Photoabsorption, Scattering, Transmission, and Reflection at E = 50–30 000 eV, Z = 1–92 // At. Data Nucl. Data Tables. Jul. 1993. V. 54. № 2. P. 181–342.

  79. Henke B.L., Lee P., Tanaka T.J., Shimabukuro R.L., Fujikawa B.K. Low-energy x-ray interaction coefficients: Photoabsorption, scattering, and reflection // At. Data Nucl. Data Tables. Jan. 1982. V. 27. № 1. P. 1–144.

  80. Biggs F., Lighthill R. Analytical Approximations for X‑Ray Cross Sections III // Natl. Tech. Inf. Serv. 1988.

  81. Fano U., Cooper J.W. Spectral distribution of atomic oscillator strengths // Rev. Mod. Phys. 1968. V. 40. № 3. P. 441–507.

  82. Ashley J.C. Simple model for electron inelastic mean free paths: Application to condensed organic materials // J. Electron Spectros. Relat. Phenomena, Jan. 1982. V. 28. № 2. P. 177–194.

  83. Ashley J.C. Energy loss rate and inelastic mean free path of low-energy electrons and positrons in condensed matter // J. Electron Spectros. Relat. Phenomena. Jan. 1990. V. 50. № 2. P. 323–334.

  84. Ritchie R.H., Howie A. Electron excitation and the optical potential in electron microscopy // Philos. Mag. 1977. V. 36. № 2. P. 463–481.

  85. Akkerman A., Boutboul T., Breskin A., Chechik R., Gibrekhterman A., Lifshitz Y. Inelastic Electron Interactions in the Energy Range 50 eV to 10 keV in Insulators: Alkali Halides and Metal Oxides // Phys. Status Solidi. Dec. 1996. V. 198. № 2. P. 769–784.

  86. Valentin A., Raine M., Sauvestre J.E. Inelastic cross-sections of low-energy electrons in silicon for the simulation of heavy ion tracks with the GEANT4-DNA toolkit // 2010. № 2. P. 80–85.

  87. Valentin A., Raine M., Sauvestre J.E., Gaillardin M., Paillet P. Geant4 physics processes for microdosimetry simulation: Very low energy electromagnetic models for electrons in silicon // Nucl. Instruments Methods Phys. Res. Sect. B Beam Interact. with Mater. Atoms. 2012. V. 288. P. 66–73.

  88. MerminN.D. Lindhard Dielectric Function in the Relaxation-Time Approximation // Phys. Rev. B. Mar. 1970. V. 1. № 5. P. 2362–2363.

  89. Dapor M. Mermin Differential Inverse Inelastic Mean Free Path of Electrons in Polymethylmethacrylate // Front. Mater. 2015. V. 2. № April. P. 10–12.

  90. Vera P.De, Abril I., Garcia-Molina R. Inelastic scattering of electron and light ion beams in organic polymers // J. Appl. Phys., 2011. V. 109. № 9.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Микроэлектроника

Архивы выпусков Информация о журнале Отправить рукопись в журнал