Известия РАН. Механика жидкости и газа, 2023, № 2, стр. 138-150
СРАВНЕНИЕ ЭЙЛЕРОВА И ЛАГРАНЖЕВА ПОДХОДОВ ДЛЯ НАХОЖДЕНИЯ ОСОБЕННОСТЕЙ РАСПРЕДЕЛЕНИЯ МЕЖЗВЕЗДНОЙ ПЫЛИ В ГЕЛИОСФЕРЕ В РАМКАХ МОДЕЛИ ХОЛОДНОГО ГАЗА
Е. А. Годенко a, b, c, *, В. В. Измоденов a, b, c
a Институт проблем механики им. А.Ю. Ишлинского РАН
Москва, Россия
b Институт космических исследований РАН
Москва, Россия
c Московский государственный университет им. М.В. Ломоносова
Москва, Россия
* E-mail: godenko.egor@yandex.ru
Поступила в редакцию 10.10.2022
После доработки 11.10.2022
Принята к публикации 11.10.2022
- EDN: NTGHJS
- DOI: 10.31857/S0568528122600783
Аннотация
Межзвездные пылевые частицы проникают в гелиосферу, область пространства, занятую солнечным ветром, вследствие относительного движения Солнца и окружающей его межзвездной среды. Внутри гелиосферы на движение частиц действует главным образом электромагнитная сила, которая определяется гелиосферным магнитным полем. Под действием этой силы траектории пылевых частиц могут пересекаться и самопересекаться. В результате возникают области накопления межзвездной пыли, которые представляют большой интерес как с теоретической точки зрения, так и в контексте планирования будущих космических миссий. Целью данной работы является моделирование распределения межзвездной пыли, а также исследование особенностей ее распределения внутри гелиосферы. Для описания пылевой компоненты используется приближение холодной среды, а для нахождения распределения концентрации используются два подхода для описания среды – эйлеров и лагранжев. Для решения уравнения неразрывности в лагранжевых координатах используется полный лагранжев метод, или метод Осипцова. В результате найдены все особенности распределения пылевой компоненты, которые лежат на каустиках (огибающих семейств траекторий частиц пыли), а также регулярные (без сингулярности в концентрации) области повышенной концентрации. Показано, что области накопления пылевой компоненты находятся в окрестности гелиосферного токового слоя, на котором магнитное поле меняет свою полярность, а также в хвостовой части гелиосферы. Проведено сравнение эффективности метода Осипцова решения уравнения неразрывности в лагранжевых координатах с широко используемым в литературе методом Монте-Карло (эйлеров подход). Показано, что по сравнению с методом Осипцова метод Монте-Карло требует чрезвычайно высокого разрешения расчетной сетки для достижения сопоставимого уровня точности расчетов.
ВВЕДЕНИЕ
Окружающая Солнечную систему локальная межзвездная среда состоит из плазменной, нейтральной и пылевой компонент. Из-за относительного движения Солнца и межзвездной среды частицы пыли проникают в гелиосферу – область, занятую плазмой солнечного ветра. Присутствие частиц межзвездной пыли внутри гелиосферы было экспериментально подтверждено измерениями космического аппарата (КА) Улисс [1]. По данным КА Кассини [2] удалось определить химический состав межзвездной пыли в окрестности Сатурна. В рамках миссии КА Стардаст [3] несколько образцов межзвездной пыли было доставлено на Землю. Исследование распределения частиц межзвездной пыли предоставляет уникальную возможность удаленной диагностики межзвездного вещества, окружающего нашу Солнечную систему, поэтому эта область исследований сейчас активно развивается. В настоящее время планируется ряд новых космических экспериментов по изучению пыли. Для анализа полученных экспериментальных данных, а также для планирования будущих миссий по исследованию межзвездной пыли необходимо проводить теоретические исследования распределения этих частиц в гелиосфере.
Первые исследования траекторий межзвездных пылевых частиц [4, 5] были инициированы задолго до их экспериментального обнаружения. Динамика движения пылинок, в основном, определяется действием трех сил: гравитационным притяжением к Солнцу, радиационным давлением со стороны солнечных фотонов, а также электромагнитой силой. В случаях, когда гравитационное притяжение к Солнцу преобладает над радиационным давлением, происходит накопление пылевых частиц за счет гравитационной фокусировки [4]. Однако возможна и обратная ситуация, когда радиационное давление превосходит гравитационное притяжение – в этом случае происходит фильтрация частиц пыли на расстояниях порядка нескольких астрономических единиц [6]. Для пылинок относительно небольшого размера, а также для частиц, для которых гравитационное притяжение и радиационное давление взаимно компенсируются, основной силой, определяющей динамику, является электромагнитная сила.
Рис. 1.
Система координат. Начало координат O совпадает с Солнцем, ось $Oy$ направлена навстречу вектору скорости набегающего потока межзвездной среды, ось $Oz$ – вдоль оси вращения Солнца, ось Ox дополняет систему $Oxyz$ до правильного трехгранника. Плоскость голубого цвета ($Oxy$) соответствует поверхности гелиосферного токового слоя ($HCS$).
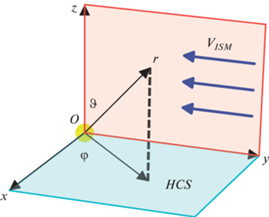
Рис. 2.
Траектории частиц межзвездной пыли в гелиосфере в плоскости X = 0. В малой окрестности гелиосферного токового слоя (прямая Z = 0) формируются каустики – огибающие семейств траекторий частиц пыли. $HCS$ – гелиосферный токовый слой.
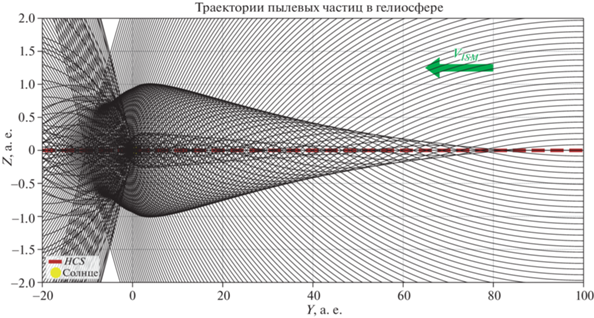
Рис. 3.
Поле направлений результирующей силы, действующей на частицы. Электромагнитная сила в каждой точке направляет пылинки к плоскости токового слоя. Возникают колебания частиц пыли вокруг плоскости токового слоя. Амплитуда этих колебаний уменьшается по ходу движения частиц в гелиосфере.
В работах [7–13] исследовались распределения пылевой компоненты в гелиосфере с учетом различных физических эффектов. При этом использовался метод Монте-Карло, а распределения пылевых частиц по пространству и скоростям определялись на численных сетках с небольшим пространственным разрешением. Такие методы не позволяют эффективно находить и исследовать возможные сингулярности в распределениях, так как для этого требуется чрезвычайно высокое разрешение сетки и, как следствие, большое количество моделируемых частиц.
В данной работе для нахождения распределения пыли мы используем альтернативный лагранжев подход. Пылевая компонента рассматривается в рамках модели холодного газа, а для определения концентрации частиц решается уравнение неразрывности, записанное в лагранжевых координатах. Для решения уравнения неразрывности в лагранжевых переменных используется полный лагранжев метод (ПЛМ), который в литературе часто называют методом Осипцова [14]. ПЛМ был уже неоднократно применен к решению различных задач: взаимодействие гиперзвукового потока и сверхзвукового источника с дисперсной фазой (модель испарения ядра, [15]); неортогональное столкновение двух различных вязких несжимаемых потоков, один из которых содержит твердые инерционные частицы [16]; обтекание запыленным газом каскада турбин [14]; исследование областей накопления частиц в самогравитирующих средах [17] и так далее. Некоторые результаты применения лагранжева метода к вычислению концентрации межзвездной пыли в гелиосфере изложены в [18].
Для сравнения результатов и оценки эффективности ПЛМ проведены вычисления концентрации межзвездной пыли также и в рамках классического эйлерова подхода методом Монте-Карло. Математические постановки задач, используемые при эйлеровом и лагранжевом подходах, представлены в разделе 1. В разделе 2 описаны факторы, влияющие на динамику движения межзвездных пылевых частиц в гелиосфере. Результаты моделирования представлены в разделе 3. В разделе 4 сформулированы выводы о преимуществах и недостатках каждого из представленных методов.
1. МАТЕМАТИЧЕСКАЯ ПОСТАНОВКА ЗАДАЧИ
Для математического описания подходов, используемых для моделирования распределения концентрации пыли, введем декартову и связанную с ней сферическую системы координат (рис. 1). Начало системы координат $O$ совместим с Солнцем, ось $Oy$ направим навстречу вектору скорости набегающего потока межзвездной среды ${{{\mathbf{v}}}_{{ISM}}}$, ось $Oz$ – вдоль оси вращения Солнца, ось $Ox$ дополняет систему $Oxyz$ до правильного трехгранника. Полярный угол $\vartheta $ сферической системы координат будем отсчитывать от оси $Oz$, азимутальный угол $\varphi $ – от оси $Ox$ к оси $Oy$. Будем также предполагать, что гелиосферный токовый слой (поверхность, на которой меняет знак полярность магнитного поля) является плоским, стационарным и лежит в плоскости $Oxy$. Такое предположение позволяет наглядно продемонстрировать эффекты, связанные с сингулярностями распределения концентрации.
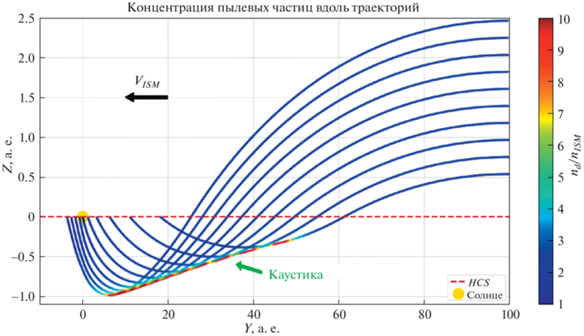
Рис. 4.
Траектории частиц межзвездной пыли и концентрация, вычисленная вдоль этих траекторий с использованием метода Осипцова. Когда траектория касается огибающей, концентрация резко возрастает из-за того, что величина якобиана приближается к нулю.
1.1. Решение кинетического уравнения для пылевой компоненты методом Монте-Карло
Стандартным подходом к описанию движения пылевой компоненты является подход, основанный на кинетической теории. В рамках этого подхода для функции распределения по скоростям fd решается кинетическое уравнение
(1.1)
${\mathbf{v}} \cdot \frac{{\partial {{f}_{d}}}}{{\partial {\mathbf{r}}}} + {\mathbf{F}} \cdot \frac{{\partial {{f}_{d}}}}{{\partial {\mathbf{v}}}} = 0,$Рис. 5.
Каустики траекторий пылевых частиц в гелиосфере. Разные каустики соответствуют разным типам траекторий пылевых частиц по количеству пересечений частицами плоскости токового слоя.
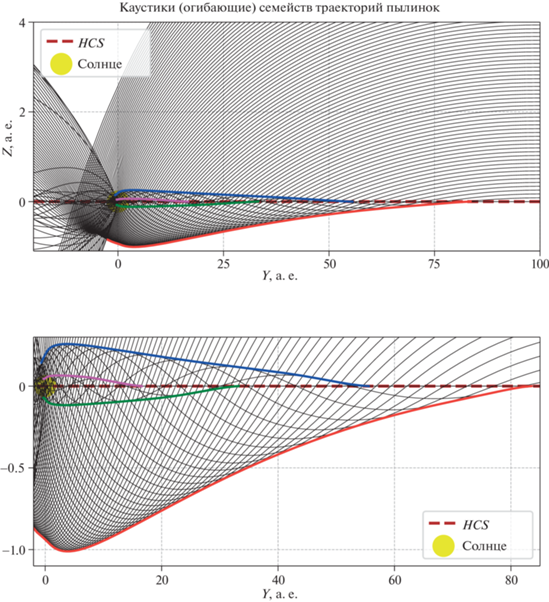
Рис. 6.
Распределение концентрации межзвездной пыли в плоскости X = 0, вычисленное с использованием эйлерова подхода. В окрестности плоскости гелиосферного токового слоя по обе стороны от него образуется область повышенной концентрации пыли. Количество рассмотренных траекторий $N = 2{\kern 1pt} {\kern 1pt} 000{\kern 1pt} {\kern 1pt} 000$, относительная статистическая ошибка не превышает 3% в каждой точке. Размер ячеек сетки расчетной области 0.001 а.е.
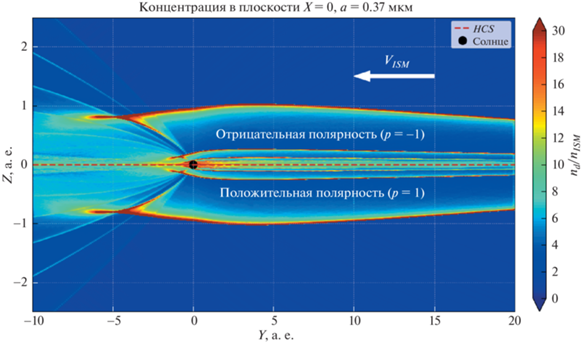
Рис. 7.
Распределение концентрации межзвездной пыли в плоскости $X = 0,\,\;Y = \bar {Y}$ для фиксированных значений $\bar {Y} = - 10,\, - 5,\,0,\,5,\,10,\,15,\,20$ а.е. В окрестности гелиосферного токового слоя наблюдается сложная структура, состоящая из множества тонких слоев резкого повышения концентрации.
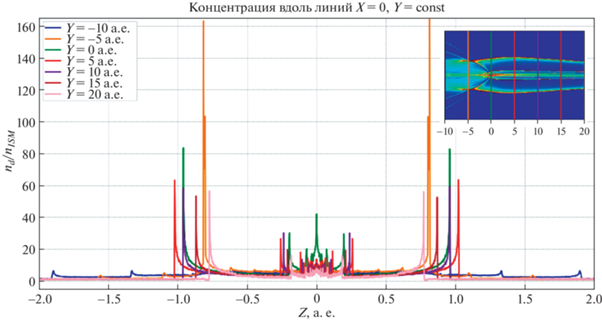
Рис. 8.
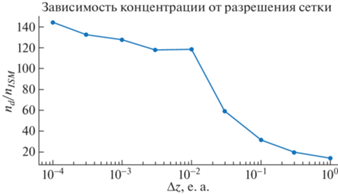
Исследование сходимости концентрации в окрестности каустики от размера ячейки сетки. Численное значение концентрации в ячейке, содержащей каустику, монотонно возрастает с увеличением разрешения сетки, за исключением перехода от сетки с ячейками размера 10–2 а.е. к сетке с ячейками размера 3 × 10–3 а.е.
Несмотря на то что в реальности в распределении пыли по скоростям может присутствовать небольшая дисперсия (до 15%, [19]), будем предполагать, что все частицы начинают свое движение в гелиосфере с одинаковой скоростью, равной ${{{\mathbf{v}}}_{{ISM}}}$. Поэтому в качестве граничного условия будем использовать дельта-функцию
Макроскопические характеристики пылевой компоненты определяются как соответствующие интегралы от функции распределения. Например, для концентрации имеем:
Решение кинетического уравнения (1.1) находится методом Монте-Карло. Вся расчетная область разбивается на ячейки. Начальную плоскость $y = {{y}_{\infty }}$, откуда начинают свое движение пробные частицы пыли, выберем на расстоянии ${{y}_{\infty }} = 100$ астрономических единиц (а.е.) от Солнца, что приблизительно соответствует расстоянию до гелиосферной ударной волны [20, 21]. Положение частиц на начальной плоскости разыгрывается случайным образом. Далее численно решаются уравнения движения частиц и рассчитываются траектории. Вдоль траекторий при прохождении частицами пыли расчетной ячейки вычисляется время нахождения частицы внутри ячейки. Это время является случайной величиной, математическое ожидание которой равно искомой концентрации (с точностью до нормировки). При достаточно большом количестве рассмотренных траекторий выборочное среднее по полученным реализациям случайной величины будет стремиться к математическому ожиданию по закону больших чисел:
1.2. Модель холодного газа. Лагранжев подход
Наряду с кинетическим подходом для описания распределения межзвездной пыли в гелиосфере можно использовать модель холодного газа, которая определяется системой уравнений
(1.2)
$\left( {\begin{array}{*{20}{c}} {\frac{{\partial {{n}_{d}}}}{{\partial t}} + {\text{div}}({{n}_{d}}{\mathbf{v}}) = 0,} \\ {\frac{{\partial {\mathbf{v}}}}{{\partial t}} + ({\mathbf{v}} \cdot \nabla )({\mathbf{v}}) = {\mathbf{F}},} \end{array}} \right.$Характеристики системы уравнений (1.2) совпадают с траекториями частиц пыли, а траектории для заданной электромагнитной силы могут пересекаться, что означает, что в точке пересечения траекторий решения (1.2) не существует. Эту проблему можно устранить, если использовать лагранжев подход к описанию движения сплошной среды.
Уравнение неразрывности в лагранжевых переменных имеет следующий вид:
(1.3)
${{n}_{d}}(t,{{{\mathbf{r}}}_{0}}){\text{|det}}({{J}_{{ij}}}(t,{{{\mathbf{r}}}_{0}})){\text{|}} = {{n}_{d}}(0,{{{\mathbf{r}}}_{0}}),$Рассмотрим радиус-вектор ${\mathbf{r}}$ и вектор скорости ${\mathbf{v}}$ индивидуальной частицы как функции лагранжевых координат и времени: ${\mathbf{r}} = {\mathbf{r}}(t,{{{\mathbf{r}}}_{0}}) = {\mathbf{r}}(t,{{x}_{{1,0}}},{{x}_{{2,0}}},{{x}_{{3,0}}})$, ${\mathbf{v}} = {\mathbf{v}}(t,{{{\mathbf{r}}}_{0}}) = {\mathbf{v}}(t,{{x}_{{1,0}}},{{x}_{{2,0}}},{{x}_{{3,0}}})$. В этом случае уравнения движения примут вид
В рамках полного лагранжева метода вводится еще одна вспомогательная матрица ${{\Omega }_{{ij}}} = \frac{{\partial {{J}_{{ij}}}}}{{\partial t}}$ и проводится следующая цепочка преобразований с учетом достаточной гладкости компонент радиус-вектора и вектора скорости
Поскольку поле результирующей силы F задано (см. разд. 2), то для каждой фиксированной частицы пыли получаем замкнутую систему обыкновенных дифференциальных уравнений [15]
(1.4)
$d\left( {\begin{array}{*{20}{l}} {\frac{{d{{x}_{i}}}}{{dt}} = {{{v}}_{i}},} \\ {\frac{{\partial {{{v}}_{i}}}}{{dt}} = {{F}_{i}},} \\ {\frac{{d{{J}_{{ij}}}}}{{dt}} = {{\Omega }_{{ij}}},} \\ {\frac{{d{{\Omega }_{{ij}}}}}{{dt}} = \sum\limits_{k = 1}^3 \frac{{\partial {{F}_{i}}}}{{\partial {{x}_{k}}}}{{J}_{{kj}}}.} \end{array}} \right.$В качестве начальных условий нужно взять начальные координаты рассматриваемой фиксированной частицы (т.е. в нашем случае просто ее лагранжевы координаты), а скорость положить равной ${{{\mathbf{v}}}_{{ISM}}} = - {{{v}}_{{ISM}}}{{{\mathbf{e}}}_{y}}$. В этом случае компоненты матриц Jij и ${{\Omega }_{{ij}}}$ могут быть вычислены как
(1.5)
$\left( {\begin{array}{*{20}{l}} {{\mathbf{r}}{{{\text{|}}}_{{t = 0}}} = {{{\mathbf{r}}}_{0}},} \\ {{\mathbf{v}}{{{\text{|}}}_{{t = 0}}} = - {{{v}}_{{ISM}}}{{{\mathbf{e}}}_{y}},} \\ {{{J}_{{ij}}}{{{\text{|}}}_{{t = 0}}} = {{{\left. {\left( {\frac{{\partial {{x}_{i}}}}{{\partial {{x}_{{j,0}}}}}} \right)} \right|}}_{{t = 0}}} = {{\delta }_{{ij}}},} \\ {{{\Omega }_{{ij}}}{{{\text{|}}}_{{t = 0}}} = {{{\left. {\left( {\frac{{\partial {{{v}}_{i}}}}{{\partial {{x}_{{j,0}}}}}} \right)} \right|}}_{{t = 0}}} = 0,} \end{array}} \right.$2. ДИНАМИКА ДВИЖЕНИЯ МЕЖЗВЕЗДНЫХ ПЫЛЕВЫХ ЧАСТИЦ
В обоих описанных выше методах вычисления распределения концентрации необходимым шагом является определение характеристик записанных уравнений, которые совпадают с траекториями частиц. На движение частиц межзвездной пыли в гелиосфере основное влияние оказывают три силы: сила гравитационного притяжения, сила радиационного давления и электромагнитная сила. Для простоты будем считать, что пылинки имеют сферическую форму, и их радиус равен a. Силы гравитационного притяжения и радиационного давления обратно пропорциональны квадрату расстояния до Солнца и направлены в противоположные стороны вдоль линии, соединяющей Солнце и частицу пыли. В зависимости от химического состава пылинок и их размера возможен случай, когда эти силы уравновешивают друг друга. В данной работе для удобства демонстрации и анализа особенностей в распределении концентрации пыли будет рассмотрен именно такой случай. Силы гравитационного притяжения и радиационного давления полностью компенсируют друг друга, например, в случае астрономических силикатов (MgFeSiO4, [23]) размера $a = 0.37$ мкм. Следовательно, на такие частицы действует только электромагнитная сила.
Поскольку силовые линии солнечного магнитного поля вморожены в солнечный ветер, выражение для электромагнитной силы имеет следующий вид:
(2.1)
${\mathbf{F}} = \frac{q}{{{{c}_{0}}m}}[({\mathbf{v}} - {{{\mathbf{v}}}_{p}}) \times {\mathbf{B}}],$(2.3)
${{B}_{r}} = p{{B}_{E}}{{\left( {\frac{{{{r}_{E}}}}{r}} \right)}^{2}},\quad {{B}_{\varphi }} = - p\frac{{{{B}_{E}}\Omega {{r}_{E}}}}{{{{{v}}_{{sw}}}}}\left( {\frac{{{{r}_{E}}}}{r}} \right)\sin \theta ,\quad {{B}_{\theta }} = 0,$Такая конфигурация магнитного поля, как будет показано в дальнейшем, создает особые условия в гелиосфере для возникновения сингулярностей в распределении концентрации пылевых частиц.
Если подставить выражения (2.2) и (2.3) для скорости солнечного ветра и индукции магнитного поля в (2.1), а затем провести обезразмеривание на характерные величины $L_{*}^{{}}\, = \,\frac{{G{{M}_{S}}}}{{{v}_{{ISM}}^{2}}}$ и $V_{*}^{{}}\, = \,{{{v}}_{{ISM}}}$, то получим следующее выражение для результирующей силы в безразмерном виде
Для Солнца значения безразмерных параметров $\kappa = {{{v}}_{{ISM}}}{\text{/}}{{{v}}_{{sw}}} \approx 26.4{\text{/}}400.0 \approx 0.07 \ll 1,$ α = = ${{{v}}_{{sw}}}{\text{/}}({{L}_{*}}\Omega ) \approx 0.8$, поэтому всеми членами, содержащими в качестве множителя параметр $\kappa $, можно пренебречь, и выражение для вектора результирующей силы в безразмерном виде принимает упрощенный вид
(2.4)
${\mathbf{\hat {F}}} = - p\varepsilon \frac{{\sin \vartheta }}{{\hat {r}}}{{{\mathbf{e}}}_{\vartheta }},$Можно заметить, что все пылевые частицы, которые в начальный момент находились в плоскости X = 0 (изображена красным на рис. 1), не выходят за ее пределы (вектор ${{{\mathbf{e}}}_{\vartheta }}$ для таких частиц тоже будет лежать в этой плоскости). Для простоты будем рассматривать только частицы, траектории которых лежат в плоскости X = 0.
3. РЕЗУЛЬТАТЫ МОДЕЛИРОВАНИЯ
Для начала на качественном уровне покажем, как происходит движение межзвездных пылевых частиц. На рис. 2 представлены траектории частиц межзвездной пыли в плоскости X = 0. В небольшой окрестности гелиосферного токового слоя (до ~1 а.е.) образуются каустики – огибающие семейств траекторий частиц пыли. По определению, каустики каждым своим конечным сегментом касаются бесконечного числа траекторий из соответствующего семейства, поэтому в их окрестности должны формироваться области резкого повышения концентрации частиц пыли. Формирование каустик происходит из-за того, что полярность межпланетного магнитного поля, а следовательно и направление действующей на частицу силы, меняется при пересечении токового слоя. Поле направлений вектора результирующей силы, действующей на частицы, показано на рис. 3. Полярность гелиосферного магнитного поля такова, что электромагнитная сила в каждой точке направляет пылинки к плоскости токового слоя, поэтому частицы осциллируют вокруг этой плоскости. Более того, из выражения (2.4) следует, что абсолютная величина этой силы обратно пропорциональна расстоянию до Солнца, поэтому амплитуда осцилляций вокруг токового слоя будет уменьшаться вдоль траектории, и, следовательно, общий поток пылинок будет сужаться при приближении к Солнцу, за счет чего и происходит формирование каустик.
3.1. Результаты: лагранжев подход
В лагранжевом подходе концентрация частиц вычисляется вдоль их траекторий. На рис. 4 показаны начальные участки нескольких траекторий пылевых частиц в плоскости X = 0, а концентрация пыли вдоль этих траекторий показана цветом. Когда траектория касается огибающей, концентрация резко возрастает из-за того, что величина якобиана приближается к нулю. Это происходит вследствие того, что трубка тока из траекторий, начинающих свое движение из некоторого конечного участка на границе расчетной области, в окрестности огибающей сужается до нулевой ширины [13] под действием электромагнитной силы, прижимающей пылинки к плоскости токового слоя.
Лагранжев подход позволяет продолжить расчет концентрации вдоль траектории и после прохождения первой каустики. В дальнейшем траектории продолжают осциллировать вокруг гелиосферного токового слоя, образуя множественные вторичные каустики. Эти каустики уже гораздо сложнее увидеть на рисунках с траекториями. Однако полный лагранжев метод позволяет определить точно положения всех вторичных каустик, так как при их пересечении концентрация вдоль траектории неограниченно возрастает. На рис. 5 представлены траектории пылевых частиц и несколько каустик. Каустики были получены на основе точек траекторий, где значение концентрации превышает некоторое предельное (для наглядности визуализации для каждой каустики это значение свое). Разные каустики соответствуют разным типам траекторий: каустика красного цвета огибает траектории, которые один раз пересекли токовый слой, каустики синего цвета соответствуют траекториям, которые два раза пересекли эту плоскость и так далее – чем ближе каустика располагается к плоскости токового слоя, тем больше пересечений этой поверхности испытали траектории пылевых частиц (до пересечения с каустикой), которые эта каустика огибает.
3.2. Эйлеров подход
Для сравнения эффективности эйлерова и лагранжева подходов при определении особенностей в распределении концентрации межзвездной пыли мы провели расчеты методом Монте-Карло. На рис. 6 представлено двумерное распределение концентрации частиц межзвездной пыли в плоскости X = 0, полученное в рамках эйлерова подхода. Видно, что в окрестности плоскости гелиосферного токового слоя по обе стороны от него на расстояниях до 1 а.е. образуется область повышенной концентрации пыли, ограниченная тонкими слоями резкого увеличения концентрации. Данные слои как раз соответствуют упомянутым каустикам, и возникновение области повышенной концентрации связано с особой конфигурацией гелиосферного магнитного поля с отрицательной полярностью над токовым слоем и положительной – под ним.
Одномерные распределения концентрации вдоль линий $X = 0,\,Y = \bar {Y}$ для различных значений $\bar {Y}$ представлены на рис. 7. В малой окрестности токового слоя для всех $Y \geqslant 0$ наблюдается сложная структура, состоящая из нескольких менее ярко выраженных особенностей в распределении концентрации, хотя механизм их образования подобен тому же, что и для особенностей, лежащих на внешних каустиках, ограничивающих область повышенной концентрации. При $Y < 0$ эта структура разрушается, и особенности пропадают, однако на расстоянии ~0.8 а.е. от гелиосферного токового слоя возникают другие особенности, и примечательно, что значение концентрации в этих точках является наибольшим среди всех рассмотренных ($Y = - 5$ а.е. на рис. 7).
На рис. 7 в области $Y > 0$ точки, в которых концентрация принимает наибольшие значения, очевидно, соответствуют положениям внешней каустики при различных $Y$. Исследуем то, как численное значение концентрации в ячейке, содержащей точку каустики, зависит от разрешения сетки. На рис. 8 представлена зависимость соответствующей величины от размера сетки $\Delta Z$ для точки внешней каустики при $Y = 5$ а.е. За исключением перехода от сетки с ячейками размера 10–2 а.е. к сетке с ячейками размера 3 × 10–3 а.е. наблюдается монотонное возрастание значения концентрации в ячейке, содержащей точку каустики, с увеличением разрешения сетки. Такая зависимость указывает на наличие сингулярности в распределении концентрации в этой ячейке, т.е. ожидается, что концентрация будет возрастать до бесконечности при увеличении разрешения сетки. Однако возможность использования сеток еще более высокого разрешения ограничена мощностью имеющихся вычислительных ресурсов. Таким образом, можем заключить, что эйлеров подход не является эффективным при исследовании особенностей распределения концентрации пылевых частиц.
4. ЗАКЛЮЧЕНИЕ
Главным результатом работы является определение областей накопления пылевой компоненты внутри гелиосферы. В рамках лагранжева подхода для модели холодного газа методом Осипцова нами были определены все каустики семейств траекторий частиц межзвездной пыли. Именно на каустиках в рамках холодной модели концентрация частиц становится бесконечной, возникают сингулярности – интегрируемые особенности – в распределении концентрации частиц. Данные особенности были найдены также в рамках эйлерова подхода с использованием метода Монте-Карло. Было показано, что для получения сопоставимой с методом Осипцова точности вычислений требуется чрезвычайно высокое разрешение расчетной сетки, а следовательно, и большое количество рассматриваемых частиц. Так, для приемлемых значений относительной статистической погрешности (до 5%) при использовании метода Монте-Карло в каждую ячейку расчетной сетки должно попадать по 100–200 частиц пыли, в то время как в рамках метода Осипцова достаточно провести вычисления вдоль одной траектории.
Необходимо отметить, что в настоящей работе делался ряд предположений. Самыми существенными из них являются: 1) предположение о стационарности и плоской форме гелиосферного токового слоя, 2) модель холодного газа.
В реальности гелиосферный токовый слой поворачивается в соответствии с 22-летним циклом солнечной активности, и, следовательно, конфигурация магнитного поля, при которой происходит фокусировка пылевых частиц, будет справедлива лишь непродолжительный промежуток времени – в определенные периоды солнечных минимумов. Упрощенная постановка с плоским стационарным гелиосферным токовым слоем позволила получить наглядные результаты, исследовать физическую причину образования областей накопления частиц, а также определить ограничения на параметры вычислительных схем, что, как было показано в работе, особенно важно при использовании эйлерова подхода. Стоит отметить, что описанные в работе численные модели могут быть легко обобщены и на случай нестационарного неплоского токового слоя.
Вторым принятым упрощением является модель холодного газа. В настоящее время данное упрощение используется во всех основных моделях распределения межзвездной пыли в гелиосфере. Тем не менее наличие некоторой тепловой компоненты в скоростях частиц следует ожидать из-за флуктуаций электромагнитного поля в межзвездной среде. Оценки показывают (см., например, [19]), что тепловые скорости межзвездных частиц в среде составляют до 15% от их массовой скорости.
Работа выполнена в рамках гранта РНФ 19-12-00383.
Список литературы
Grun E., Zook H.A., Baguhl M., Balogh A., Fechtig H., Forsyth R., Hanner M.S., Horanyi M., Kissel J., Lindblad B.-A., Linkert D. Linkert G., Mann I., McDonnell J.A.M., Morfill G.E., Phillips J.L., Polanskey C., Schwehm G., Siddique N., Staubach P., Svestka J., Taylor A. Discovery of Jovian dust streams and interstellar grains by the Ulysses spacecraft // Nature. 1993. V. 362. P. 428–430. https://doi.org/10.1038/362428a0
Altobelli N., Postberg F., Fiege K., Trieloff M., Kimura H., Sterken V.J., Hsu H.-W., Hillier J., Khawaja N., Moragas-Klostermeyer G., Blum J., Burton M., Srama R., Kempf S., Grun E. Flux and composition of interstellar dust at Saturn from Cassini’s Cosmic Dust Analyzer // Science. 2016. V. 352. № 6283. P. 312–318. https://doi.org/10.1126/science.aac6397
Westphal A.J., Stroud R.M., Bechtel H.A., Brenker F.E., Butterworth A.L., Flynn G.J., Frank D.R., Gainsforth Z., Hillier J.K., Postberg F., Simionovici A.S., Sterken V.J., Nittler L.R., Allen C., Anderson D., Ansari A., Bajt S., Bastien R.K., Bassim N., Bridges J., Brownlee D.E., Burchell M., Burghammer M., Changela H., Cloetens P., Davis A.M., Doll R., Floss C., Grun E., Heck P.R., Hoppe P., Hudson B., Huth J., Kearsley A., King A.J., Lai B., Leitner J., Lemelle L., Leonard A., Leroux H., Lettieri R., Marchant W., Ogliore R., Ong W.J., Price M.C., Sandford S.A., Tresseras J.-A.S., Schmitz S., Schoonjans T., Schreiber K., Silversmit G. Solé V.A., Srama R., Stadermann F., Stephan T., Stodolna J., Sutton S., Trieloff M., Tsou P., Tyliszczak T., Vekemans B., Vincze L., Von Korff J., Wordsworth N., Zevin D., Zolensky M.E. Evidence for interstellar origin of seven dust particles collected by the Stardust spacecraft // Science. 2014. V. 345. № 6198. P. 786–791. https://doi.org/10.1126/science.1252496
Bertaux J.L., Blamont J.E. Possible evidence for penetration of interstellar dust into the Solar System // Nature. 1976. V. 262. № 5566. P. 263–266. https://doi.org/10.1038/262263a0
Levy E.H., Jokipii J.R. Penetration of interstellar dust into the solar system // Nature. 1976. V. 264. P. 423. https://doi.org/10.1038/264423a0
Sterken V.J., Altobelli N., Kempf S., Kruger H., Srama R., Strub P., Grun E. The filtering of interstellar dust in the solar system // Astronomy and Astrophysics. 2013. V. 552. P. A130. https://doi.org/10.1051/0004-6361/201219609
Morfill G.E., Grun E. The motion of charged dust particles in interplanetary space - II. Interstellar grains // Planetary and Space Science. 1979. V. 27. № 10. P. 1283–1292. https://doi.org/10.1016/0032-0633(79)90106-5
Landgraf M. Modeling the motion and distribution of interstellar dust inside the heliosphere // Journal of Geophysical Research. 2000. V. 105. № A5. P. 10303–10316. https://doi.org/10.1029/1999JA900243
Linde T.J., Gombosi T.I. Interstellar dust filtration at the heliospheric interface // Journal of Geophysical Research. 2000. V. 105. № A5. P. 10411–10418. https://doi.org/10.1029/1999JA900149
Sterken V.J., Altobelli N., Kempf S., Schwehm G., Srama R., Grun E. The flow of interstellar dust into the solar system // Astronomy and Astrophysics. 2012. V. 538. P. A102. https://doi.org/10.1051/0004-6361/201117119
Slavin J.D., Frisch P.C., Muller H.-R., Heerikhuisen J., Pogorelov N.V., Reach W.T., Zank G. Trajectories and Distribution of Interstellar Dust Grains in the Heliosphere // The Astrophysical Journal. 2012. V. 760. № 1. P. 46. https://doi.org/10.1088/0004-637X/760/1/46
Alexashov D.B., Katushkina O.A., Izmodenov V.V., Akaev P.S. Interstellar dust distribution outside the heliopause: deflection at the heliospheric interface // MNRAS. 2016. V. 458. № 3. P. 2553–2564. https://doi.org/10.1093/mnras/stw514
Godenko E.A., Izmodenov V.V. Effects of Dispersion of the Dust Velocity in the LISM on the Interstellar Dust Distribution inside the Heliosphere // Astronomy Letters. 2021. V. 47. № 1. P. 50–60. https://doi.org/10.1134/S1063773721010047
Healy D.P., Young J.B. Full Lagrangian methods for calculating pconcentration fields in dilute gas-pflows // Proceedings of the Royal Society of London Series A. 2005. V. 461. № 2059. P. 2197–2225. https://doi.org/10.1098/rspa.2004.1413
Osiptsov A.N. Full Lagrangian Modelling of Dust Admixture in Gas Flows // Astrophysics and Space Science. 2000. V. 274. P. 377–386. https://doi.org/10.1023/A:1026557603451
Лебедева Н.А., Осипцов А.Н. Течения вблизи критических точек при несимметричном столкновении вязких дисперсных потоков // Изв. РАН. МЖГ. 2007. № 5. С. 85–97.
Ahuja R., Belonoshko A.B., Johansson B., Osiptsov A.N. Inertial phase separation in rotating self-gravitating media // Fluid Dynamics. 2004. V. 39. № 6. P. 920–932. https://doi.org/10.1007/s10697-005-0027-2
Mishchenko A.V., Godenko E.A., Izmodenov V.V. Lagrangian fluid approach for the modelling of peculiarities of the interstellar dust distribution in the astrospheres/heliosphere // MNRAS. 2020. V. 491. № 2. P. 2808–2821. https://doi.org/10.1093/mnras/stz3193
Hoang T., Lazarian A., Schlickeiser R. Revisiting Acceleration of Charged Grains in Magnetohydrodynamic Turbulence // The Astrophysical Journal. 2012. V. 747. № 1. P. 54. https://doi.org/10.1088/0004-637X/747/1/54
Баранов В.Б., Измоденов В.В. Модельные представления о взаимодействии солнечного ветра со сверхзвуковым потоком межзвездной среды. Предсказание и интерпретация экспериментальных данных // Изв. РАН. МЖГ. 2006. № 5. С. 19–40.
Izmodenov V.V., Alexashov D.B. Magnitude and direction of the local interstellar magnetic field inferred from Voyager 1 and 2 interstellar data and global heliospheric model // Astronomy and Astrophysics. 2020. V. 633. P. L12. https://doi.org/10.1051/0004-6361/201937058
van Marle A.J., Meliani Z., Keppens R., Decin L. Computing the Dust Distribution in the Bow Shock of a Fast-moving, Evolved Star // The Astrophysical Journal Letters. 2011. V. 734. № 2. P. L26. https://doi.org/10.1051/0004-6361/201937058
Greenberg J.M., Li A. What are the true astronomical silicates? // Astronomy and Astrophysics. 1996. V. 309. P. 258–266.
Parker E.N. Dynamics of the Interplanetary Gas and Magnetic Fields // The Astrophysical Journal. 1958. V. 128. P. 664. https://doi.org/10.1086/146579
Дополнительные материалы отсутствуют.
Инструменты
Известия РАН. Механика жидкости и газа


