Известия РАН. Механика жидкости и газа, 2022, № 6, стр. 101-115

1. ПОСТАНОВКА ЗАДАЧИ

Рассмотрим клеточный агрегат, первоначально образованный смесью клеток двух разных типов в присутствии внеклеточной жидкости. Будем считать, что клеточный агрегат в начальный и последующие моменты времени имеет правильную сферическую форму и окружен жидкостью с нулевым давлением.

Постановка задачи о перераспределении плотностей двух типов клеток в клеточном сфероиде будет использовать разработанную нами ранее континуальную модель биологической сплошной многофазной среды, образованной двумя активно взаимодействующими клеточными фазами и жидкостью [23]. Схематическое изображение структуры сфероида в разные моменты времени показано на рис. 1. Ниже приведены основные допущения, использованные при построении модели.

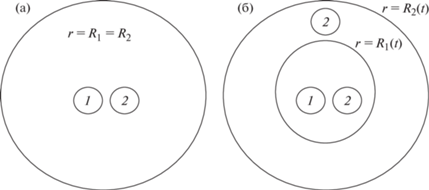
Клеточные фазы различаются параметрами зависимостей, управляющих развитием активных взаимодействий между клетками, и активными перемещениями клеток друг относительно друга. Активные взаимодействия между клетками описываются посредством введения трех дополнительных фаз, две из которых обеспечивают активные взаимодействия между клетками, принадлежащими только к первой или только ко второй клеточной фазе. Третья дополнительная фаза обеспечивает перекрестные активные взаимодействия между клетками разных фаз. Более подробное обсуждение возможных биологических структур, отождествляемых с дополнительными фазами, и физические механизмы, связанные с активными межклеточными взаимодействиями, приводится в [22, 23]. Объемы, занимаемые дополнительными фазами, считаются пренебрежимо малыми в сравнении с объемами основных фаз. В дальнейшем будем предполагать, что активные стягивающие взаимодействия развиваются только между клетками, принадлежащими к одной фазе, а между клетками двух разных фаз отсутствуют. Таким образом, в межфазной перекрестной активной силе будем учитывать только расталкивающую компоненту.

В среде отсутствуют деления и гибель клеток, а также потоки массы между клеточными фазами и жидкостью. Истинные плотности фаз считаются постоянными и равными между собой, поэтому объемные концентрации фаз совпадают с массовыми. Оценка коэффициента межфазного вязкого трения между клеточными фазами и жидкостью [23] позволяет пренебречь в уравнениях импульсов изменением гидростатического давления p во внеклеточной жидкости, поэтому в дальнейшем оно считается пространственно-однородным. Тогда уравнения для клеточных фаз можно решать отдельно от уравнений, описывающих движение жидкости. Будем полагать, что жидкость может свободно перетекать через внешнюю границу сферы, и давление $p$ совпадает с давлением во внешней среде, т.е. p = 0.

Введем сферическую систему координат с началом в центре сферы. Решение задачи о перераспределении плотностей клеток будет выполнено в предположении сферической симметрии всех величин. У всех тензоров смешанные компоненты считаются равными нулю. Будем отмечать компоненты тензоров в направлениях $r$, $\varphi $ и $\theta $ соответствующим буквенным индексом, заменяя повторяющийся индекс однократным. У единственной отличной от нуля компоненты векторов скорости в радиальном направлении индекс $r$ опускается, а нижним индексом будем обозначать номер клеточной фазы. Систему уравнений для физических компонент векторов и тензоров (получаемую из общей модели [12]), относящихся к клеточным фазам, можно записать в следующем виде:

Здесь ${{\phi }_{1}}$ и ${{\phi }_{2}}$ – объемные концентрации первой и второй клеточных фаз соответственно; ${{{v}}_{1}}$ и ${{{v}}_{2}}$ – компоненты векторов скорости клеточных фаз; ${{\sigma }^{{(1)}}}$ и ${{\sigma }^{{(2)}}}$ – тензоры напряжений в клеточных фазах; тензоры ${{\tau }^{{(1)}}}$ и ${{\tau }^{{(2)}}}$ – характеризуют напряжения в дополнительных фазах, обеспечивающих активные межклеточные взаимодействия между клетками только первой и только второй клеточных фаз соответственно; тензор напряжений ${{\tau }^{{(12)}}}$ описывает активные взаимодействия клеток, принадлежащих к разным фазам; индекс $\alpha $ принимает значения $r$, $\varphi $ и $\theta $, при этом ${{r}_{r}}$, ${{r}_{\varphi }}$ и ${{r}_{\theta }}$ – координаты радиус-вектора точек на поверхности сферы $S$ радиуса ${{R}_{s}}$ (радиус дальнодействия) с центром в рассматриваемой точке, в локальном физическом базисе сферической системы координат; $F$ – радиальная компонента силы межфазного взаимодействия между клеточными фазами; $e_{\alpha }^{{(1)}}$ и $e_{\alpha }^{{(2)}}$ – компоненты тензоров скоростей деформаций клеточных фаз; ${{p}_{1}}$ и ${{p}_{2}}$ – давления в первой и второй клеточных фазах соответственно; для первого инварианта любого тензора второго ранга $T$принято обозначение ${{I}_{1}}(T)$.

Уравнения (1.1) являются уравнениями неразрывности для клеточных фаз с учетом сделанных выше предположений. Уравнения баланса импульса для клеточных фаз (1.2) – (1.5), в пренебрежении инерционными эффектами, учитывают силы их взаимодействия с дополнительными фазами (второе и третье слагаемые), а также силу межфазного взаимодействия между двумя клеточными фазами. Уравнения баланса импульса по оси $\theta $ выполнено тождественно.

Выражение (1.6) для силы межфазного взаимодействия F представлено в виде суммы двух составляющих, связанных с действием сил давления (первое и второе слагаемые) и силой вязкого трения (третье слагаемое) на межфазных поверхностях.

Уравнения (1.8) и (1.9) являются определяющими соотношениями для активных напряжений в дополнительных фазах. Они учитывают как хаотическую активность клеток, характеризуемую давлениями ${{\Pi }_{1}}$, ${{\Pi }_{2}}$ и ${{\Pi }_{{12}}}$, проявляющимися в отталкивании клеток, так и стягивающие усилия, определяемые неоднородностью их микроокружения. Интегрирование в соотношениях (1.8) выполняется по сферической поверхности $S$ фиксированного для данной среды радиуса ${{R}_{s}}$ (радиуса дальнодействия) с центром в рассматриваемой точке. Для точек, находящихся на расстоянии, меньшем ${{R}_{s}}$ от поверхности клеточного сфероида, интегрирование ведется по той части поверхности сферы, которая лежит внутри этого объема.

Соотношения (1.10)–(1.11) представляют собой выражения для компонент тензоров скоростей деформаций клеточных фаз. В общем случае тензор скоростей деформаций в клеточной среде учитывает как деформацию клеток, так и их переупаковку [24]. В настоящей работе (как и в [23]) предполагается, что деформация клеточных фаз определяется только переупаковками. Система дополняется кинематическими соотношениями (1.12), (1.13) для компонент тензоров скоростей деформации клеточных фаз.

2. ГРАНИЧНЫЕ УСЛОВИЯ

Рассмотрим две постановки задачи о перераспределении плотностей клеток двух типов в клеточном сфероиде. Постановки задач будут различаться граничными условиями. В первом случае постановка задачи учитывает возможность независимого перемещения поверхностей, ограничивающих клетки каждого типа. Координаты $r = {{R}_{1}}(t)$ и $r = {{R}_{2}}(t)$ являются радиусами сфер, ограничивающих первую и вторую клеточную фазы соответственно (рис. 1б).

Будем считать, что в начальный момент времени клетки обеих фаз заполняют весь объем сферы, и в качестве начальных условий при t = 0 будем задавать положение границ клеточных фаз ${{R}_{1}}(0) = {{R}_{2}}(0) = {{R}_{0}}$ и начальные распределения объемных концентраций фаз ${{\phi }_{1}}(0,x) = {{\phi }_{{10}}}(x)$, ${{\phi }_{2}}(0,x) = {{\phi }_{{20}}}(x)$.

В дальнейшем при решении задачи будет происходить разделение границ областей, занятых клетками разных типов. Последующие рассуждения будут проведены для случая ${{R}_{1}}(t) < {{R}_{2}}(t)$, когда центральная область занята двумя типами клеток, а внешняя – только клетками второго типа. Заранее неизвестно, какая из фаз замыкает другую. Это определяется в процессе решения и зависит от числовых параметров, характеризующих каждую фазу. Во внешней области, где присутствует лишь клеточная фаза 2, ${{\phi }_{1}} = 0$, ${{\sigma }^{{(1)}}} = {{\tau }^{{(1)}}} = {{\tau }^{{(12)}}} = 0$, и уравнения системы (1.1)–(1.13), относящиеся к фазе 1, выполняются тождественно. В случае ${{R}_{1}}(t) > {{R}_{2}}(t)$ рассуждения будут аналогичными.

Сила, действующая на внешней границе со стороны окружающей среды, сводится к давлению жидкости. Будем предполагать, что оно распределено между фазами пропорционально их концентрациям. Тогда в начальный момент времени (и пока ${{R}_{1}}(t) = {{R}_{2}}(t)$) на внешней границе выполнены условия:

После разделения границ, второе условие (2.1) при $r = {{R}_{2}}(t)$ для второй фазы сохраняется. Граница $r = {{R}_{1}}(t)$ делит клеточный сфероид на области, занятые двухфазной и однофазной клеточными средами. Для первой фазы условие при $r = {{R}_{1}}(t)$ теперь должно учитывать силовое воздействие частиц второй фазы, расположенных по другую сторону этой границы. Для второй фазы граница $r = {{R}_{1}}(t)$ является поверхностью разрыва, и на этой границе должны быть сформулированы дополнительные условия непрерывности потока массы и перераспределения нагрузки в результате взаимодействия с частицами первой фазы.

Из уравнения неразрывности (1.1) для второй фазы следует условие непрерывности потока массы на разрыве

Квадратные скобки обозначают разность соответственных величин по разные стороны разрыва, точкой обозначена производная по времени.

Условия для напряжений были получены в [12]. Они имеют следующий вид

Здесь p* является средним давлением на поверхности межфазного контакта при $r = {{R}_{1}}(t)$. Верхний индекс “плюс” или “минус” указывает на значение соответствующей величины справа или слева от разрыва.

Перемещение границ $r = {{R}_{1}}(t)$ и $r = {{R}_{2}}(t)$ определяется движением клеток соответствующих фаз, поэтому считаются выполненными условия ${{\dot {R}}_{1}}(t) = {{{v}}_{1}}$ при $r = {{R}_{1}}(t)$ и ${{\dot {R}}_{2}}(t) = {{{v}}_{2}}$ при $r = {{R}_{2}}(t)$.

Из уравнений неразрывности (1.1) и условия ограниченности скоростей фаз в центре сферы следует, что при r = 0:

Граничные условия для ${{\phi }_{1}}$ при r = 0 и $r = {{R}_{1}}(t)$, а также ${{\phi }_{2}}$ при r = 0 и $r = {{R}_{2}}(t)$ не ставятся, так как границы фаз перемещаются со скоростями, равными скоростям частиц соответствующих фаз на этих границах. То есть, границы r = 0 и $r = {{R}_{1}}(t)$ являются характеристиками для первого уравнения (1.1), а r = 0 и $r = {{R}_{2}}(t)$ – для второго. Соответствующие граничные условия получаются из решения уравнений (1.1), записанных в соответствующих точках.

Система уравнений для определения скоростей фаз при известных распределениях концентраций имеет четвертый порядок. В то время, пока границы фаз совпадают, для нахождения скоростей используются четыре условия, входящие в (2.1) и (2.6). В дальнейшем, при разделении границ областей, занятых клетками разных типов, необходимо шесть граничных условий. К их числу относятся второе соотношение (2.1), соотношение (2.2), а также (2.3), (2.4) и оба соотношения (2.6).

Непрерывность начальных распределений концентраций фаз обеспечивает их дальнейшую непрерывность, в том числе и при прохождении поверхности разрыва по частицам второй фазы. Разрыв испытывает лишь скорость изменения концентрации ${{\phi }_{2}}$. В силу условия (2.2) на этой поверхности остается непрерывной и скорость второй фазы ${{{v}}_{2}}$. Таким образом, при $r = {{R}_{1}}$ скорость и концентрация второй фазы претерпевают слабый разрыв, тогда как разрыв напряжения в этой фазе ${{\sigma }_{2}}$ оказывается сильным, что видно из условия (2.4).

Вторая постановка задачи отличается от первой тем, что скорости клеточных фаз считаются совпадающим на внешней границе сфероида. Таким образом, в каждый момент времени весь объем сфероида считается заполненным обеими фазами. При этом радиус сфероида, как и в предыдущей постановке задачи, меняется со временем. Для нахождения скоростей в этом случае должны быть использованы оба условия (2.6), условия равенства скоростей на внешней границе и условие равенства нулю внешней нагрузки. Тогда при $r = R(t)$ ($R = {{R}_{1}} = {{R}_{2}}$) должны быть выполнены условия

3. ЧИСЛЕННОЕ РЕШЕНИЕ

Преобразуем систему уравнений (1.1)–(1.13). Для этого выразим напряжения в клеточных фазах $\sigma _{r}^{{(1)}}$, $\sigma _{\varphi }^{{(1)}}$ и $\sigma _{r}^{{(2)}}$, $\sigma _{\varphi }^{{(2)}}$ из уравнений (1.10), (1.11) и подставим их в уравнения импульсов (1.2) и (1.4). Напряжения с индексом θ исключим с помощью уравнений (1.3) и (1.5). Компоненты тензоров скоростей деформаций заменим с помощью кинематических соотношений (1.12) и (1.13). Добавив уравнения (1.1), получим полную систему для нахождения ${{\phi }_{1}}$, ${{\phi }_{2}}$ и ${{{v}}_{1}}$, ${{{v}}_{2}}$.

Введем безразмерные величины:

$t{\kern 1pt} * = t\frac{E}{\mu },$ $r{\kern 1pt} * = \frac{r}{{{{R}_{0}}}},$ $R_{s}^{*} = \frac{{{{R}_{s}}}}{{{{R}_{0}}}},$ $R{\kern 1pt} _{k}^{*} = \frac{{{{R}_{k}}}}{{{{R}_{0}}}},$ $\sigma _{\alpha }^{{(k){\kern 1pt} *}} = \frac{{\sigma _{\alpha }^{{(k)}}}}{E},$ $\tau _{\alpha }^{{(k){\kern 1pt} *}} = \frac{{\tau _{\alpha }^{{(k)}}}}{E},$ $\tau _{\alpha }^{{(12){\kern 1pt} *}} = \frac{{\tau _{\alpha }^{{(12)}}}}{E},$ ${v}_{k}^{*} = {{{v}}_{k}}\frac{\mu }{{E{{h}_{0}}}},$ $\Pi _{k}^{*} = \frac{{{{\Pi }_{k}}}}{E},$ $\Pi _{{12}}^{*} = \frac{{{{\Pi }_{{12}}}}}{E},$ $E_{k}^{*} = \frac{{{{E}_{k}}}}{E},$ $E_{{12}}^{*} = \frac{{{{E}_{{12}}}}}{E},$ $\mu _{k}^{*} = \frac{{{{\mu }_{k}}}}{\mu },$ $\mu _{{k\,n}}^{*} = \frac{{{{\mu }_{{kn}}}}}{\mu },$ $m_{k}^{*} = \frac{{{{m}_{k}}}}{E},$ $k_{{12}}^{*} = \frac{{{{k}_{{12}}}h_{0}^{2}}}{\mu }$

($k = 1,\;2$;$n = 1,\;2$;$\alpha = r,\;\varphi ,\;\theta $)

Здесь $E$ и $\mu $ – некоторые характерные значения соответствующих групп коэффициентов. В дальнейшем звездочку при безразмерных параметрах будем опускать.

В обеих постановках задач численное решение полученной системы на каждом шаге по времени начинается с уравнений для ${{{v}}_{1}}$ и ${{{v}}_{2}}$, при этом значения ${{\phi }_{1}}$ и ${{\phi }_{2}}$ берутся с предыдущего временного шага. Затем при найденных скоростях решаются уравнения (1.1), позволяющие найти ${{\phi }_{1}}$ и ${{\phi }_{2}}$.

Рассмотрим схему решения задачи, которая учитывает возможность независимого перемещение внешних границ клеток каждого типа. На каждом шаге сначала находятся значения ${{{v}}_{1}}$ и ${{{v}}_{2}}$ в области $0 \leqslant r \leqslant \;{{R}_{{\,1}}}(t)$, где присутствуют обе клеточные фазы, после чего ${{{v}}_{2}}$ продолжается в область ${{R}_{{\,1}}}(t) \leqslant r \leqslant {{R}_{2}}(t)$, в которой присутствует только вторая клеточная фаза.

При расчете скоростей на отрезке $[0;{{R}_{1}}(t)]$ вводится безразмерная координата ${{\xi }_{1}} = r{\text{/}}{{R}_{1}}(t)$, что позволяет перейти от решения уравнений с подвижной верхней границей к решению уравнений на отрезке [0; 1].

Система уравнений для безразмерных неизвестных ${{{v}}_{1}}$, ${{{v}}_{2}}$ имеет следующий вид:

Здесь $\Delta = 1 - {{\phi }_{1}}{{\phi }_{2}}$,

В качестве граничных условий при решении системы (3.1) используется равенство ${{{v}}_{1}} = {{{v}}_{2}} = 0$ при ${{\xi }_{1}} = 0$, а при ${{\xi }_{1}} = 1$ – соотношения (2.3) и (2.4).

Условие (2.3) при ${{\xi }_{1}} = 1$ после подстановки в него выражений для $\sigma _{r}^{{(1)}}$ и $\sigma _{r}^{{(2)}}$, полученных из (1.10) и (1.11), с учетом выражения для межфазного давления p* (2.5), а также выражений для ${{p}_{1}}$ и ${{p}_{2}}$ (1.7) и кинематических соотношений (1.12) и (1.13) принимает следующий вид (верхний индекс “–”, указывающий на принадлежность к области 12 совместного присутствия обеих фаз опущен)

Второе граничное условие при ${{\xi }_{1}} = 1$ получим аналогично. Условие (2.4) после подстановки выражений для $\sigma _{r}^{{(1)}}$ и $\sigma _{r}^{{(2)}}$ из (1.10) и (1.11), учитывая (2.5), (1.7), (1.12) и (1.13) принимает следующий вид:

Граничные условия (3.2) и (3.3) для решения системы уравнений (3.1) содержат значения скорости ${{{v}}_{2}}$ и ее производную справа от разрыва. Поэтому для того, чтобы найти значения ${{{v}}_{1}}$ и ${{{v}}_{2}}$ во всей внутренней области $[0;{{R}_{1}}(t)]$ необходимо вычислить скорость клеток второй фазы на отрезке $[{{R}_{1}}(t);\;{{R}_{2}}(t)]$ и исключить ${{\left. {{{{v}}_{2}}} \right|}^{ + }}$ и ${{\left. {\frac{{\partial {{{v}}_{2}}}}{{\partial {{\xi }_{1}}}}} \right|}^{ + }}$ из условий (3.2) и (3.3).

Уравнение для ${{{v}}_{2}}$ во внешней области $[{{R}_{1}}(t);\;{{R}_{2}}(t)]$ может быть получено с помощью преобразований системы (1.1)–(1.13) аналогичных тем, которые использовались при получении системы (3.1). При этом следует учитывать присутствие во внешней области лишь второй клеточной фазы (${{\phi }_{1}} = 0$, ${{\sigma }^{{(1)}}} = {{\tau }^{{(1)}}} = {{\tau }^{{(12)}}} = 0$). При расчете скоростей во внешней области введем новую координату ${{\xi }_{2}} = r{\text{/}}{{R}_{2}}(t)$, тогда уравнение для ${{{v}}_{2}}$ будет иметь следующий вид:

Здесь ${{\Phi }_{{22}}} = \frac{2}{{{{\xi }_{1}}}}\left( {{{\phi }_{2}}\frac{{{{\mu }_{2}}}}{{{{\mu }_{{22}}}}} + 1} \right)(\tau _{r}^{{(2)}} - \tau _{\varphi }^{{(2)}})$ и ${{\Sigma }_{{22}}} = \left( {{{\phi }_{2}}\frac{{{{\mu }_{2}}}}{{{{\mu }_{{22}}}}} + 1} \right)\tau _{r}^{{(2)}}$.

Интегрирование уравнения (3.4) выполняется на отрезке ${{\xi }_{2}} \in [{{R}_{{\,1}}}(t){\text{/}}{{R}_{2}}(t);\;1]$. В качестве граничного условия при ${{\xi }_{2}} = 1$ используется второе условие (2.1), которое после подстановки в него выражения для $\sigma _{r}^{{(2)}}$ из (1.11) и кинематического соотношения (1.13) принимает следующий вид:

В качестве граничного условия при ${{\xi }_{2}} = {{R}_{{\,1}}}(t){\text{/}}{{R}_{2}}(t)$ используется условие на разрыве (2.2). Это условие связывает между собой значения скорости второй фазы по разные стороны разрыва.

Решение уравнения (3.4) с граничными условиями (2.2) и (3.5) будем искать в следующем виде ${{{v}}_{2}}({{\xi }_{2}}) = {{U}_{1}}({{\xi }_{2}}) + C \cdot {{U}_{2}}({{\xi }_{2}})$, где U₁ удовлетворяет уравнению (3.4), а U₂ – уравнению, полученному из (3.4) заменой правой части нулем.

В качестве “начальных” условий примем, что $2{{\mu }_{2}}{{\phi }_{2}}\frac{{\partial {{U}_{1}}}}{{\partial {{\xi }_{2}}}} + {{R}_{2}}{{\Sigma }_{{22}}} = 0$, ${{U}_{1}} = 0$ и $\frac{{\partial {{U}_{2}}}}{{\partial {{\xi }_{2}}}} = 0$, ${{U}_{2}} = 1$ при ${{\xi }_{2}} = 1$. Тогда ${{{v}}_{2}} = {{U}_{1}} + C \cdot {{U}_{2}}$ удовлетворяет уравнению (3.4) и граничному условию (3.5) при любых значениях постоянной C. Значение C может быть найдено из условия (2.2) при ξ₂ = = ${{R}_{1}}(t){\text{/}}{{R}_{2}}(t)$.

Важно отметить, что найденное значение C будет зависеть от известных значений U₁ и U₂ при ξ₂ = ${{R}_{1}}(t){\text{/}}{{R}_{2}}(t)$ и значений скоростей клеточных фаз только слева от разрыва. Это позволит выразить ${{\left. {{{{v}}_{2}}} \right|}^{ + }}$ и ${{\left. {\frac{{\partial {{{v}}_{2}}}}{{\partial {{\xi }_{1}}}}} \right|}^{ + }}$ в условиях (3.2) и (3.3) через значения скоростей клеточных фаз только слева от разрыва и решить систему (3.1) с полученными из (3.2) и (3.3) граничными условиями и условиями ${{{v}}_{1}} = {{{v}}_{2}} = 0$ при ${{\xi }_{1}} = 0$. Долее можно вычислить значение постоянной C и значения ${{{v}}_{2}}$ во внешней области.

Вычисление интегралов, присутствующих в выражениях для активных напряжений, выполнено путем разложения подынтегральной функции в ряд по формуле Тейлора второго порядка точности и с помощью пятиточечной квадратуры Гаусса [25], при этом учитывается различие пределов интегрирования для внутренних и граничных точек среды, т.е. точек, удаленных от границы слоя на расстояние, не превышающее радиус дальнодействия.

Разностные схемы для решения системы (3.1) и уравнения (3.4) были получены интегро-интерполяционным методом [26]. Монотонность схемы для (3.1) достигается использованием направленных разностей при аппроксимации производных $\partial (\xi _{1}^{2}{{{v}}_{1}}){\text{/}}\partial {{\xi }_{1}}$ и $\partial (\xi _{1}^{2}{{{v}}_{2}}){\text{/}}\partial {{\xi }_{1}}$ в зависимости от знаков стоящих при них коэффициентов. Полученная система разностных уравнений для (3.1) решалась методом матричной прогонки. Для вычисления U₁ и U₂ решались задачи Коши.

Полученные значения ${{{v}}_{1}}({{\xi }_{1}})$ и ${{{v}}_{2}}({{\xi }_{2}})$ используются при решении уравнений для ${{\phi }_{1}}$ и ${{\phi }_{2}}$. Уравнения (1.1) после введения координаты ${{\xi }_{1}}$ для первого из них и ${{\xi }_{2}}$ для второго приводятся к дивергентному виду:

Эти уравнения решаются по отдельности. Численное решение уравнений (3.6) было выполнено с использованием TVD схемы Хартена с ограничителем minmod [27, 28].

Описание эволюции системы дополняется уравнениями ${{\dot {R}}_{1}} = {{{v}}_{1}}$ при ${{\xi }_{1}} = 1$ и ${{\dot {R}}_{2}} = {{{v}}_{2}}$ при ${{\xi }_{2}} = 1$. Эти уравнения решаются методом Эйлера.

При решении задач используется разбиение отрезков $[0;{{R}_{1}}]$ и $[0;{{R}_{2}}]$ на одинаковое число частей. При переходе от одного разбиения к другому (т.е. при переходе от координаты ${{\xi }_{1}}$ к координате ${{\xi }_{2}}$) используется пересчет соответствующих величин с использованием линейной интерполяции.

Решение задачи, в которой клеточные фазы ограничены одной общей границей, отличается от решения предыдущей задачи только схемой вычисления скоростей ${{{v}}_{1}}$ и ${{{v}}_{2}}$. В этом случае уравнения (3.1) решаются при граничных условиях (2.6), (2.7) и (2.8) с учетом того, что R(t) = = ${{R}_{1}}(t) = {{R}_{2}}(t)$.

4. РЕЗУЛЬТАТЫ РАСЧЕТОВ И ИХ ОБСУЖДЕНИЕ

Исследуем решения задач, описывающих формирование клеточных структур, которые появляются в результате пространственного разделения двух типов клеток в клеточном агрегате сферической формы.

Клеточные фазы отличаются значениями параметров, характеризующих развитие активных взаимодействий между клетками. Числовые параметры, используемые ниже, соответствуют тому, что активные стягивающие взаимодействия внутри первой клеточной фазы превышают таковые внутри второй клеточной фазы ($m_{1}^{{}} > m_{2}^{{}}$). Параметры $E_{1}^{{}}$ и $E_{2}^{{}}$, характеризующие активные давления, проявляющиеся в расталкивании клеток внутри фаз, предполагаются равными. Эволюция плотностей клеток в клеточном сфероиде будет исследована в зависимости от значений безразмерных параметров, принятых в предшествующих работах [12, 23]. Примем следующие значения числовых параметров в качестве стандартных: ${{\mu }_{1}} = {{\mu }_{2}} = {{\mu }_{{11}}} = {{\mu }_{{22}}} = 1$, ${{\mu }_{{12}}} = {{\mu }_{{21}}}$ = = 0.5, ${{E}_{1}} = 0.33$, $E_{2}^{{}} = 0.33$, $E_{{12}}^{{}} = 0.167$, ${{k}_{{12}}} = 0.3$, $R_{s}^{{}} = 0.01$, ${{\phi }_{{10}}}(x) = {{\phi }_{{20}}}(x) = 0.4$. Значения параметров ${{m}_{1}}$ и ${{m}_{2}}$, характеризующих стягивающие активные взаимодействия, будут приведены в каждом случае отдельно.

Рассмотрим результаты решения задачи о сортировке клеток, используя постановку задачи с двумя независимо перемещающимися внешними границами областей, занятых клетками разных типов. Распределения концентраций клеток в разные моменты времени при начальных пространственно-однородных распределениях ${{\phi }_{1}}(0,\;x) = {{\phi }_{{10}}}$ и ${{\phi }_{2}}(0,\;x) = {{\phi }_{{20}}}$, стандартных значениях параметров и ${{m}_{1}} = 12$, ${{m}_{2}} = 11$, а также эволюция границ клеточных фаз при различных комбинациях параметров ${{m}_{1}}$ и ${{m}_{2}}$ (${{m}_{1}} = 7$, ${{m}_{2}} = 6$ и ${{m}_{1}} = 12$, ${{m}_{2}} = 11$), представлены на рис. 2.

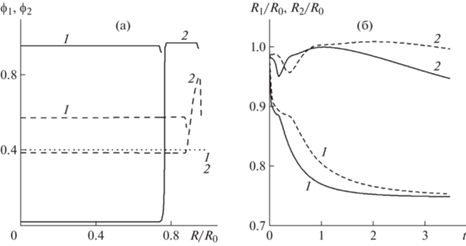
Приведенные на рис. 2а распределения концентраций клеток в разные моменты времени демонстрируют тенденцию к пространственному разделению двух типов клеток, которые первоначально равномерно заполняли сферический клеточный агрегат. Клетки первой фазы, в которой активные стягивающие взаимодействия между клетками сильнее (при этом $E_{1}^{{}} = E_{2}^{{}}$), стремятся занять центральную область, а клетки второй фазы – периферийную. Обрыв сплошных линий 1 соответствует границе области, занятой клетками первой фазы. Эта граница делит клеточный сфероид на две части, первая из которых занята клетками первой и второй фазы. При этом концентрация клеток второй фазы в этой области приближается к нулю, и они имеют тенденцию сосредоточиться во внешней области. Обрыв сплошных линий 2 соответствует внешней границе сфероида.

Эволюция границ клеточных фаз представлена на рис. 2б. На начальном этапе наблюдается быстрое уплотнение среды, проявляющееся в синхронном уменьшении радиусов сферических поверхностей, ограничивающих клеточные фазы. Далее происходит выдавливание наружу первой клеточной фазы, обладающей более слабыми стягивающими межклеточными взаимодействиями. В силу того, что эта фаза остается более рыхлой, чем вторая, происходит незначительное увеличение радиуса сфероида, сменяемое затем монотонным уменьшением.

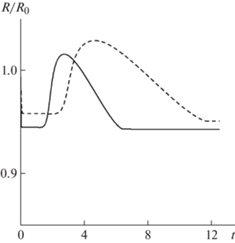
Решение задачи, в которой клеточные фазы имеют общую внешнюю границу, также описывает тенденцию к разделению фаз при пространственно-однородных начальных условиях ${{\phi }_{1}}(0,\;x) = {{\phi }_{{10}}}$, ${{\phi }_{2}}(0,\;x) = {{\phi }_{{20}}}$ в случае использования нелокальных соотношений для активных напряжений ($R_{s}^{{}} \ne 0$). Распределения концентраций клеток в момент времени t = 6, полученные в результате решения задачи с одной общей границей клеточных фаз, имеют вид, практически совпадающий с кривыми на рис. 2а при тех же значениях параметров в момент времени t = 3.5. В данном случае, в отличие от задачи с независимо перемещающимися внешними границами, распределение ${{\phi }_{1}}$ непрерывно во всей области от центра до внешней поверхности сфероида. При этом формируется узкая переходная область, в которой ${{\phi }_{1}}$ падает до очень малых значений. Эволюция радиуса сфероида представлена на рис. 3. На начальной стадии происходит очень быстрое уплотнение агрегата (этот участок зависимости $R{\text{/}}{{R}_{0}}$ от $t$ практически совпадает с осью ординат). Дальнейшее изменение его радиуса – участок плато, последующий всплеск и релаксация к стационарным значениям.

Важно отметить, что использование локальных определяющих соотношений для активных напряжений (получаемых предельным переходом $R_{s}^{{}} \to 0$ в (1.8)) при решении задачи с двумя независимо перемещающимися границами клеточных фаз приводит к распределениям концентраций и эволюции границ клеток, качественно совпадающими с результатами, полученными с использованием нелокальных законов для активных напряжений (рис. 2). Единственное отличие заключается в отсутствии незначительного уменьшения концентраций клеток в узких пограничных областях, примыкающих к наружным границам фаз, которое имеет место вследствие уменьшения активной стягивающей силы из-за сокращения области интегрирования в соотношениях (1.8).

Можно сделать вывод, что основным механизмом сортировки клеток в этой постановке задачи, в отличие от диффузионных моделей [14, 15], является не процесс их самоорганизации, связанный с потерей устойчивости некоторого стационарного решения, обусловленный нелокальностью межклеточных взаимодействий. Формирование новой клеточной структуры происходит в результате несвязанного с потерей устойчивости вытеснения одной клеточной фазы, обладающей более слабыми активными стягивающими взаимодействиями, посредством другой, в которой эти взаимодействия сильней.

Использование локальных определяющих соотношений для активных напряжений в задаче с одной общей границей клеточных фаз не приводит к сортировке клеток при пространственно-однородных начальных условиях: радиус сфероида очень быстро незначительно уменьшается, и далее остается неизменным, а концентрации обеих клеточных фаз совпадают и остаются пространственно-однородными, т.е. происходит только компактизация агрегата.

В отличие от задачи о сортировке клеток в плоском слое [12], используемые зависимости активных давлений Π₁(ϕ₁, ϕ₂), Π₂(ϕ₁, ϕ₂) и Π₁₂(ϕ₁, ϕ₂) от концентраций клеток в данном случае не приводят к значительному расхождению границ клеточных фаз в задаче с двумя границами, и нет необходимости в некотором изменении этих соотношений для устранения этого эффекта, как было сделано в [12]. Развитие тангенциальных напряжений в рассматриваемой задаче приводит к появлению радиальной силы, действующей на частицы среды в направлении к центру сферы. Предельные при $t \to \infty $ значения радиуса внутренней области практически не зависят от параметров ${{m}_{1}}$ и ${{m}_{2}}$, характеризующих стягивающие активные взаимодействия, а предел внешнего радиуса (радиуса сфероида) слабо (нелинейно) зависит ${{m}_{1}}$ и ${{m}_{2}}$.

Вычисления также показали, что в рамках обеих постановок задач толщина переходной области, в которой происходит резкое изменение концентрации клеток второй фазы, уменьшается со временем. Таким образом, происходит формирование четкой границы, разделяющей клетки разных типов. Увеличение значений параметров ${{m}_{1}}$ и ${{m}_{2}}$ также приводит к уменьшению ширины переходной области.

Поведение решений для двух постановок задач также различается при малых возмущениях пространственно-однородных начальных распределений концентраций.

Решение задачи с двумя границами в случае использования как локальных, так и нелокальных соотношений для активных напряжений демонстрирует устойчивость решений по отношению к малым возмущениям начальных распределений. Использование гармонических возмущений начальных пространственно-однородных распределений ${{\phi }_{1}}(0,r) = {{\phi }_{{10}}} + 0.001{\text{cos}}(15,5\pi r)$ и ${{\phi }_{2}}(0,r) = {{\phi }_{{20}}} - 0.001{\text{cos}}(15,5\pi r)$, а также равномерных случайных возмущений ϕ₁(0, r) = ϕ₁₀ + + $0.001\;{\text{random}}(r)$ и ${{\phi }_{2}}(0,r) = {{\phi }_{{20}}} - 0.001\;{\text{random}}(r)$ (функция ${\text{random}}(r)$ генерирует равномерно распределенную на отрезке [–1, 1] случайную величину при каждом значении r) не приводило к заметным изменениям кривых на рис. 2.

Эволюция таких же гармонически возмущенных начальных распределений в задаче с одной общей границей в случае использования нелокальных соотношений для активных напряжений приводит к формированию слоистой структуры, в которой чередуются области с различным соотношением между концентрациями клеточных фаз. На рис. 4а представлены распределения концентраций клеточных фаз в момент времени t = 4 при ${{m}_{1}} = 7$ и ${{m}_{2}} = 6$. Такое же поведение наблюдается и при ${{m}_{1}} = 12$, ${{m}_{2}} = 11$. Можно сказать, что начальные распределения играют роль первоначальной разметки, а в дальнейшем происходит агрегирование клеток разных фаз в местах первоначального их скопления. Использование малых случайных возмущений начальных пространственно-однородных распределений ${{\phi }_{1}}(0,\;x) = {{\phi }_{{10}}} + 0.001\;{\text{random}}(x)$ и ${{\phi }_{2}}(0,\;x) = {{\phi }_{{20}}} - 0.001\;{\text{random}}(x)$ приводит к колебательному характеру концентраций клеток со случайным распределением амплитуд и “периодов”.

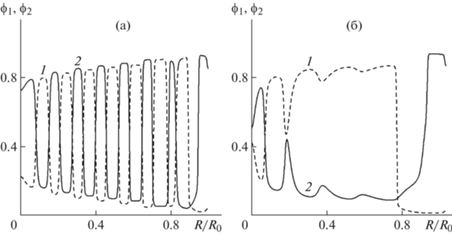
Дополнительные расчеты показали, что скорость развития возмущений значительно уменьшается с уменьшением их амплитуды, и при достаточно малых амплитудах они не успевают развиться. На рис. 4б представлены распределения концентраций клеточных фаз в момент времени t = 4 при уменьшении почти в 10 раз амплитуды гармонических возмущений однородных начальных распределений ${{\phi }_{1}}(0,r) = {{\phi }_{0}} + 0.00012\cos (15.5\pi r)$ и ${{\phi }_{2}}(0,r) = {{\phi }_{0}} - 0.00012\cos (15.5\pi r)$, при ${{m}_{1}} = 7$ и ${{m}_{2}} = 6$. Результатом уменьшения амплитуды начальных возмущений является доминирование формирования типичного для сортировки разделения клеточных фаз.

Решения задачи с одной общей границей и нелокальными активными взаимодействиями устойчивы по отношению к малым возмущениям, поскольку при уменьшении амплитуды возмущений начальных распределений происходит формирование типичной для сортировки клеток структуры, аналогичной рис. 2а. Скорость развития возмущений будет достаточной для переключения с одного режима развития на другой и формирования колебательных распределений только в случае превышения амплитудой начального возмущения некоторого порогового значения.

Дополнительные расчеты также показали, что решения задачи с двумя независимо перемещающимися границами обладают значительно большей устойчивостью по отношению к возмущениям начальных условий. Так, гармонические возмущения с амплитудой до 0.01 полностью затухают к моменту времени $t = 3.5$ при аналогичных значениях параметров (${{m}_{1}} = 7$ и ${{m}_{2}} = 6$). Взаимодействие гармонических возмущений с формированием типичного для сортировки пространственного разделения клеточных фаз становится заметным при возмущениях с амплитудой 0.05 (рис. 5). В этом случае распределение плотностей клеток все еще демонстрирует разделение границ клеточных фаз, где внешняя область характеризуется присутствием клеток только второй фазы (как на рис. 2а). Однако во внутренней области сохраняется присутствие обеих клеточных фаз, а их распределение имеет вид чередования слоев клеток разных фаз (как на рис. 4а).

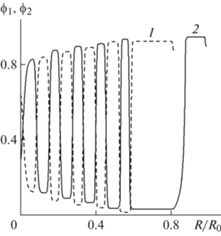
Численное исследование малых гармонических возмущений однородных начальных условий в задаче с одной общей границей при использовании локальных определяющих соотношений для активных напряжений показало, что даже при уменьшении амплитуды возмущений на три порядка происходит формирование колебательных распределений концентраций при всех рассмотренных выше комбинациях ${{m}_{1}}$ и ${{m}_{2}}$. Можно предположить, что пространственно-однородное решение, которое существует в такой постановке задачи, является неустойчивым при рассматриваемых наборах параметров.

В задаче о сортировке клеток в плоском слое [12] была представлена область параметров, при которых эволюция начальных пространственно-однородных распределений различалась при решении задач с одной общей и двумя независимыми внешними границами клеточных фаз. Решение задачи с одной общей границей давало распределения концентраций клеток, качественно отличающиеся от стандартной сортировки: максимум ${{\phi }_{1}}$ и минимум ${{\phi }_{2}}$ достигались на некоторой близкой к внешней границе поверхности. В рассмотренной задаче о сортировке клеток в сферическом агрегате такое поведение не было обнаружено, что является еще одним отличием решения задачи о сортировке клеток в сферическом агрегате от задачи о сортировке в плоском слое [12].

ЗАКЛЮЧЕНИЕ

В работе рассмотрены постановки задачи о сортировке двух разных типов клеток в клеточном агрегате сферической формы. Постановки задач позволяют изучать процессы, обусловленные активным взаимодействием клеток в геометрии, соответствующей большинству экспериментов, в которых изучается сортировка клеток. В решении поставленных задач была использована разработанная нами ранее континуальная модель биологической многоклеточной сплошной среды, образованной двумя активно взаимодействующими клеточными фазами и жидкостью. Предположение о сферической симметрии, используемое при решении задач, вносит определенные ограничения на возможность появления более разнообразных структур, чем те, которые получены в расчетах. Однако целью данной работы является демонстрация возможности разработанной ранее континуальной модели описывать сортировку клеток в объекте с реальной геометрией, а также исследование различных постановок задач с целью выяснения того, какая из них физически более адекватно описывает процесс сортировки клеток.

Исследуемые постановки задач, описывающие перераспределение клеток в сферическом агрегате, различаются граничными условиями. В обеих постановках внешние границы клеточных фаз подвижны, но в одном случае для обеих фаз эти границы совпадают, а в другом перемещаются независимо в соответствии с условиями их нагружения. Таким образом, оказывается возможным описывать образование и перемещение фронтов, разделяющих области с различными объемными концентрациями клеток разных типов. Выполнено сравнение решений для обеих постановок задач. Исследовано участие локального и нелокального законов развития активных межклеточных взаимодействий в процессе сортировки.

Проведенные расчеты показали, что в случае пространственно-однородных начальных распределений концентраций клеток обе постановки задач описывают явление их сортировки в сферическом агрегате при использовании нелокальных определяющих соотношений для активных напряжений: клетки с более сильными стягивающими активными взаимодействиями стремятся занять центральную область, а с более слабыми – периферийную.

При этом только решения задачи с двумя независимо перемещающимися границами описывают сортировку клеток при использовании как нелокальных, так и локальных определяющих соотношений для активных напряжений.

Результаты численного исследования поведения решений двух постановок задач показали, что решения задачи, в которой учитывается возможность независимого перемещения внешних границ клеток разных типов, обладают значительно большей устойчивостью по отношению к возмущениям начальных пространственно-однородных условий.

Продемонстрированы отличия свойств решений в задаче о сортировке клеток в сферическом агрегате и в бесконечном плоском слое. Решение задачи о сортировке в сферическом агрегате, в отличие от задачи о сортировке в плоском слое, не потребовало усложнения вида зависимостей, описывающих хаотическую активность клеток, характеризуемую соответствующими активными давлениями. Также не были обнаружены значения параметров, при которых эволюция начальных пространственно-однородных распределений качественно различалась при решении задач с одной общей и двумя независимыми внешними границами клеточных фаз.

Анализ свойств решений позволяет прийти к заключению, что корректное описание экспериментально наблюдаемой сортировки двух типов клеток должно осуществляться в рамках постановки задачи с независимо перемещающимися границами клеточных фаз.

Работа поддержана РФФИ (проект № 20-01-00329) и Госпрограммой АААА-А19-119012990119-3.