Известия РАН. Механика жидкости и газа, 2022, № 5, стр. 113-118

УСЕЧЕННЫЕ СТЕПЕННЫЕ ТЕЛА КАК РЕЗУЛЬТАТ ПРИБЛИЖЕННОГО РЕШЕНИЯ ЗАДАЧИ НЬЮТОНА О ТЕЛЕ С МИНИМАЛЬНЫМ СОПРОТИВЛЕНИЕМ

С. А. Таковицкий^a, b, *

^a Центральный аэрогидродинамический институт им. проф. Н.Е. Жуковского
Жуковский, Россия

^b Московский авиационный институт (национальный исследовательский университет)
Москва, Россия

^* E-mail: c.a.t@tsagi.ru

Поступила в редакцию 30.03.2022
После доработки 10.05.2022
Принята к публикации 10.05.2022

EDN: OBYZPO
DOI: 10.31857/S0568528122050115

Полный текст (PDF)

Аннотация

Получено приближенное решение задачи Ньютона о теле, движение которого вызывает наименьшее сопротивление со стороны окружающей среды. Решение основано на допущении о тонкости тела и определяет класс оптимальных осесимметричных носовых частей, затупленных по торцу и имеющих образующую со степенной зависимостью радиуса от продольной координаты. Сопоставление с точным решением показало, что отличие по сопротивлению не превышает 1% при удлинении тела выше 1.4.

Ключевые слова: задача Ньютона, аэродинамическое сопротивление, усеченное степенное тело, торец, осесимметричная носовая часть

Одно из важнейших направлений совершенствования сверхзвуковых летательных аппаратов состоит в построении осесимметричных носовых частей фюзеляжей, имеющих близкие к минимальным значения волнового сопротивления (задача Ньютона). Первые результаты решения задачи, отвечающей заданному удлинению носовой части, были получены на основе локальной модели, использующей для связи геометрических параметров и газодинамических функций формулу Ньютона [1, 2]. Установлен ряд особенностей оптимальных форм, которые в значительной мере повлияли на характер дальнейших исследований. Позднее пришло понимание того, что передний торец является участком краевого экстремума, причем как из ограничения на длину носовой части, так и из ограничения по применимости формулы Ньютона для давления [3–6].

Для практических приложений интересным оказалось приближенное решение, обоснованное для носовых частей большого удлинения в предположении стремления к нулю производной r' радиуса по продольной координате. Оптимальная образующая описывается степенной зависимостью радиуса от продольной координаты r ∼ xⁿ с показателем степени, равным n = 3/4 [7, 8]. Численные параметрические исследования и экспериментальные испытания тел со степенной образующей показали, что теоретическое значение n завышено. Экстремальное значение показателя степени увеличивается с ростом числа Маха, но не превосходит n = 0.71 [9]. При использовании высших приближений к точному решению подтверждено возрастание n при увеличении удлинения [10].

Для получения более точных аналитических решений можно использовать усложненные локальные модели взаимодействия тела с окружающей средой. Одной из таких моделей является локальная линеаризация связи между газодинамическими функциями течения и геометрическими параметрами тела. В отличие от стандартного подхода, выполняемого для возмущений, создаваемых телом, помещенным в поток, в случае локальной линеаризации рассматривается окрестность элемента оптимизируемой поверхности с местными параметрами течения. Выделяется плоскость, задаваемая скоростью и нормалью к элементу, и устанавливаются линейные соотношения, связывающие изменение газодинамических функций с изменением геометрических параметров. Таким образом, модель взаимодействия тела с окружающей средой усложняется, оставаясь локальной. При решении задачи Ньютона в рамках локальной линеаризации был установлен класс носовых частей, близких к оптимальным аэродинамическим формам по значениям волнового сопротивления. Эти тела затуплены по торцу и имеют образующую со степенной зависимостью радиуса от продольной координаты [11, 12].

Форма усеченных степенных тел полностью определяется заданием двух параметров – относительного размера переднего торца и показателя степени. На основе полученного аналитического решения проведены параметрические исследования в рамках модели Эйлера в широком диапазоне изменения числа Маха и удлинения и найдены оптимальные значения основных геометрических параметров [13]. В рамках локальной модели Ньютона аэродинамические характеристики усеченных степенных тел исследованы в [14]. Оптимальные значения геометрических параметров определены для случаев, соответствующих невязкому течению, течениям с постоянным коэффициентом трения, ламинарным пограничным слоем, турбулентным пограничным слоем. Результаты исследования в рамках моделей, соответствующих высокоскоростному потоку разреженного газа, представлены в [15]. Теоретический анализ и численные расчеты подтвердили, что усеченные степенные тела незначительно уступают оптимальным телам по значениям волнового сопротивления.

До настоящего момента оставалось неизвестным, что усеченные степенные тела являются приближенным решением задачи Ньютона. Этот результат оказался пропущенным. Данная статья восполняет пробел в теоретическом анализе задачи Ньютона и определяет место усеченных степенных тел посредством сопоставления с известными решениями по геометрическим параметрам и аэродинамическому сопротивлению.

1. ПРИБЛИЖЕННОЕ РЕШЕНИЕ ЗАДАЧИ НЬЮТОНА

Рассматривается задача построения осесимметричной носовой части, имеющей минимальное волновое сопротивление в случае заданного значения удлинения λ = L/(2R) (L и R – длина и радиус основания тела). В общем случае допускается, что тело может быть затуплено по торцу. Образующая тела представляется зависимостью радиуса r от продольной координаты x. Согласно модели Ньютона коэффициент давления на поверхности тела зависит только от угла θ наклона контура тела относительно вектора скорости невозмущенного потока

${{c}_{p}} = 2{{\sin }^{2}}\Theta ,\quad {\text{tg}}\Theta = r'$

Здесь r' – производная радиуса.

Следуя [2], запишем коэффициент сопротивления тела в виде суммы слагаемых, соответствующих переднему торцу и боковой поверхности

(1.1)

${{c}_{x}} = \frac{{8{{\lambda }^{2}}}}{{{{L}^{2}}}}\left[ {r_{0}^{2} + \int\limits_0^L {\frac{{2r{{r}^{{'3}}}}}{{1 + {{r}^{{'2}}}}}dx} } \right]$

Здесь r₀ – радиус переднего торца. При вычислении c_x сопротивление отнесено к скоростному напору и площади основания.

Решением вариационной задачи с_x = min является носовая часть, образующая которой представляется параметрическими зависимостями продольной координаты и радиуса от производной радиуса

(1.2)

$\left\{ \begin{gathered} x = \frac{{{{r}_{0}}}}{4}\left( {\frac{1}{{{{r}^{{'2}}}}} + \frac{3}{{4{{r}^{{'4}}}}} + \ln r{\text{'}} - \frac{7}{4}} \right) \hfill \\ r = \frac{{{{r}_{0}}{{{(1 + r{{'}^{2}})}}^{2}}}}{{4r{{'}^{3}}}} \hfill \\ \end{gathered} \right.$

Неизвестные значения параметров r₀ и r' при x = L однозначно определяются заданным значением удлинения тела. Характерными особенностями оптимальной носовой части являются затупление по торцу, равенство 45° угла наклона образующей в месте стыковки торца и боковой поверхности, формирование элементами единой образующей оптимальных тел для разных значений удлинения, независимость решения от числа Маха.

При увеличении удлинения радиус переднего торца и производная радиуса в плоскости основания предельно уменьшаются. Данная особенность позволила решить задачу Ньютона в упрощенной постановке для тел большого удлинения [7, 8]. В рамках допущений: r₀ = 0 и r' $ \ll $ 1, минимизируемая функция (1.1) представляется следующим интегралом

(1.3)

${{c}_{x}} = \frac{{8{{\lambda }^{2}}}}{{{{L}^{2}}}}\int\limits_0^L {2r{{r}^{{'3}}}dx} $

В этом случае образующая тела с минимальным сопротивлением задается степенной зависимостью радиуса от продольной координаты с показателем степени, равным 3/4

(1.4)

$r = \frac{L}{{2\lambda }}{{\left( {\frac{x}{L}} \right)}^{{0.75}}}$

В данном решении потеряна характерная особенность оптимальной носовой части – затупление по торцу. Поэтому степенные тела (1.4) значительно уступают оптимальным телам (1.2) по значениям волнового сопротивления. Например, при λ = 1 отличие превышает 5%.

Устранить указанный недостаток можно, отказавшись от условия r₀ = 0. Предполагая, что r' $ \ll $ 1, формулируем задачу Ньютона (1.1) в упрощенной постановке

(1.5)

${{c}_{x}} = \frac{{8{{\lambda }^{2}}}}{{{{L}^{2}}}}\left[ {r_{0}^{2} + \int\limits_0^L {2r{{r}^{{'3}}}dx} } \right]$

Функция r(x), минимизирующая функционал (1.5), находится стандартным образом. Поскольку основная функция F = 2rr'³ не содержит в явном виде независимую переменную x, для уравнения Эйлера существует первый интеграл

(1.6)

$ - F + r{\text{'}}{{F}_{{r'}}} = {\text{const}}$

Условие трансверсальности, связанное с варьированием радиуса переднего торца, сводится к равенству

(1.7)

$ - {{F}_{{r'}}} + 2{{r}_{0}} = 0$

Решению дифференциального уравнения (1.6) соответствует зависимость радиуса от продольной координаты с двумя неизвестными константами А и В

(1.8)

$r = {{\left( {Ax + B} \right)}^{{0.75}}}$

Из условия трансверсальности (1.7) устанавливаем значение производной радиуса в сечении х = 0

(1.9)

$r_{0}^{'} = \frac{1}{{\sqrt 3 }}$

Константы А и В в (1.8) определяются из условия (1.9) и заданного значения удлинения тела. Можно представить образующую зависимостью с одним параметром r₀, значение которого определяется решением уравнения четвертой степени

(1.10)

$\left\{ {\begin{array}{*{20}{l}} {r = {{r}_{0}}{{{\left( {1 + \frac{{4x}}{{3\sqrt 3 {{r}_{0}}}}} \right)}}^{{0.75}}}} \\ {{{{\left( {\frac{{{{r}_{0}}}}{R}} \right)}}^{{{4 \mathord{\left/ {\vphantom {4 3}} \right. \kern-0em} 3}}}} + \frac{{8\lambda }}{{3\sqrt 3 }}{{{\left( {\frac{{{{r}_{0}}}}{R}} \right)}}^{{{1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0em} 3}}}} - 1 = 0} \end{array}} \right.$

Для тел большого удлинения справедлива следующая оценка зависимости относительного размера переднего торца от удлинения

$\frac{{{{r}_{0}}}}{R} = {{\left( {\frac{{3\sqrt 3 }}{{8\lambda }}} \right)}^{3}}$

С другой стороны, по аналогии с точным решением (1.2), образующую усеченного степенного тела можно представить параметрическими зависимостями продольной координаты и радиуса от производной радиуса

(1.11)

$\left\{ {\begin{array}{*{20}{l}} {x = \frac{{{{r}_{0}}}}{{4\sqrt 3 }}\left( {\frac{1}{{{{r}^{{'4}}}}} - 9} \right)} \\ {r = \frac{{{{r}_{0}}}}{{3\sqrt 3 {{r}^{{'3}}}}}} \end{array}} \right.$

Как и в случае точного решения, неизвестные значения параметров r₀ и производной r' в сечении x = L однозначно определяются заданным значением удлинения тела. При этом сохраняются все характерные особенности оптимальной носовой части, перечисленные выше.

2. СОПОСТАВЛЕНИЕ ПРИБЛИЖЕННОГО И ТОЧНОГО РЕШЕНИЙ

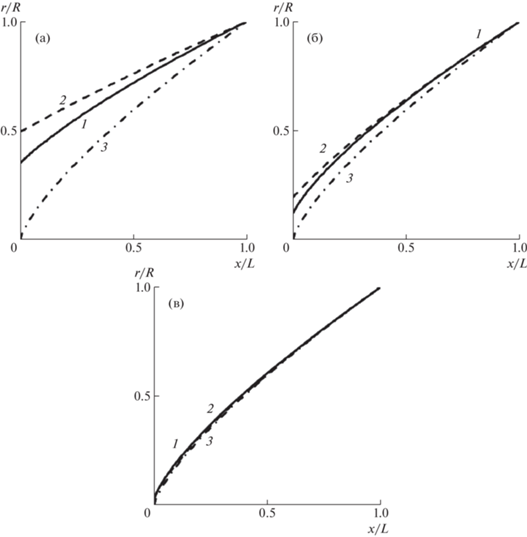
Очевидно, что все три рассмотренных решения сближаются по мере увеличения удлинения носовой части. Поэтому образующие носовой части Ньютона, усеченного степенного тела и степенного тела сопоставлены при умеренных значениях удлинения λ = 0.5, 1, 2 на рис. 1. Видно, что усеченные степенные тела имеют больший размер переднего торца и меньшие значения производной r' в одинаковых поперечных сечениях. Степенное тело характеризуется наибольшим углом наклона образующей в месте стыковки с донным торцом. Согласование с точным решением полностью нарушается при λ < 1.

Рис. 1.

Сопоставление образующих при (а–в) λ = 0.5, 1, 2: 1 – носовая часть Ньютона; 2 – усеченное степенное тело; 3 – степенное тело.

Для степенных тел известна аналитическая зависимость коэффициента сопротивления от удлинения, определенная по соотношению (1.3) и справедливая в диапазоне средних и больших значений удлинения

${{c}_{x}} = \frac{{27}}{{64{{\lambda }^{2}}}}$

Получим точный результат для коэффициента сопротивления степенного тела на основе соотношения (1.1). В данном случае

$r{\text{'}} = \frac{3}{{8\lambda }}{{\left( {\frac{L}{x}} \right)}^{{0.25}}},\quad r{{r}^{{'3}}} = \frac{{27}}{{512{{\lambda }^{3}}}}R,\quad {{c}_{x}} = \frac{{27}}{{64{{\lambda }^{2}}L}}\int\limits_0^L {\frac{1}{{1 + {{r}^{{'2}}}}}dx} $

После интегрирования приходим к окончательному результату

(2.1)

${{c}_{x}} = \frac{{27}}{{64{{\lambda }^{2}}}}\left\{ {1 - \frac{9}{{32{{\lambda }^{2}}}} + \frac{{81}}{{2048{{\lambda }^{4}}}}\ln \left( {1 + \frac{{64{{\lambda }^{2}}}}{9}} \right)} \right\}$

Нулевому значению удлинения соответствует значение c_x = 2.

Для носовой части Ньютона и усеченного степенного тела явные зависимости коэффициента сопротивления от удлинения записать невозможно. Однако, следуя параметрическим представлениям (1.2) и (1.11), на основе соотношения (1.1) можно выразить c_x через производную радиуса в плоскости основания тела.

Для носовой части Ньютона получено

(2.2)

${{c}_{x}} = \frac{{{{r}^{{'6}}}}}{{{{{(1 + r{\kern 1pt} {{'}^{2}})}}^{4}}}}\left\{ {\frac{3}{{r{{'}^{4}}}} + \frac{{10}}{{r{\kern 1pt} {{'}^{2}}}} + 17 - 4\ln r{\text{'}} + 2{{r}^{{'2}}}} \right\}$

В случае усеченного степенного тела коэффициент сопротивления определяется следующим соотношением

(2.3)

${{c}_{x}} = 3{{r}^{{'6}}}\left\{ {\frac{1}{{{{r}^{{'4}}}}} - \frac{2}{{{{r}^{{'2}}}}} + 15 + 2\ln \frac{{1 + {{r}^{{'2}}}}}{{4{{r}^{{'2}}}}}} \right\}$

Соотношения (2.2) и (2.3) дополняют соотношения (1.2) и (1.11) соответственно. Приняв радиус переднего торца равным единице, и постепенно уменьшая значения производной, находим значение коэффициента сопротивления и удлинения, которое вычисляется по соотношению между x (длина тела) и y (радиус основания).

Нулевому значению удлинения соответствуют значения производной r' = 1 (носовая часть Ньютона) и r' = 1/3^0.5 (усеченное степенное тело). В этом предельном случае оба решения, (2.2) и (2.3), совпадают и дают значение c_x = 2. Оптимальным телом является диск.

Сопоставление построенных носовых частей по величине сопротивления, рассчитанного по соотношениям (2.1), (2.2) и (2.3), продемонстрировано на рис. 2. Аэродинамическое сопротивление тел, соответствующих приближенным решениям оптимизационной задачи, отнесено к сопротивлению носовой части Ньютона равного удлинения.

Рис. 2.

Превышение волнового сопротивления по отношению к носовой части Ньютона (c_{x N}): 1 – усеченное степенное тело; 2 – степенное тело.

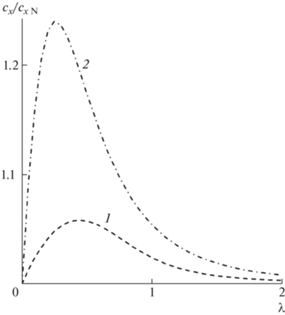
По мере уменьшения удлинения коэффициент сопротивления степенных тел монотонно возрастает (2.1). Уже при λ = 0.7 степенные тела уступают оптимальным телам более 11%. Наибольший проигрыш по сопротивлению составляет больше 24% и достигается при λ ≈ 0.25.

Усеченные степенные тела имеют заметно лучшие характеристики. При λ ≥ 1.4 отличие по волновому сопротивлению от носовой части Ньютона меньше 1%. Максимальное отличие не превышает 5.9% и получается при λ ≈ 0.45. Ограниченное возрастание погрешности обусловлено тем, что полученные в точной и приближенной постановках задачи предельные решения, соответствующие телу нулевого и бесконечно большого удлинения, совпадают. Следует добавить, что найденное двухпараметрическое представление приближенного решения позволяет выполнять прямую численную оптимизацию в рамках более точных моделей течения и таким образом учесть дополнительные условия (например, влияние числа Маха). Для точного решения задачи Ньютона такая возможность отсутствует.

Таким образом, можно заключить, что усеченные степенные тела незначительно уступают носовой части Ньютона по значениям волнового сопротивления во всем диапазоне удлинений. Это подтверждает важность найденного приближенного решения задачи Ньютона как дополнительного обоснования целесообразности исследования и использования в практических приложениях усеченных степенных тел.

Список литературы

Eggers A.J.Jr., Resnikoff M.M., Dennis D.H. Bodies of revolution having minimum drag at high supersonic air speeds // NACA. Report N 1306. 1957. 12 p.
Эггерс А. Нетонкие тела вращения минимального волнового сопротивления // Теория оптимальных аэродинамических форм. М.: Мир, 1969. С. 260–274.
Крайко А.Н. Об определении тел минимального сопротивления при использовании законов сопротивления Ньютона и Буземана // ПММ. 1963. Т. 27. Вып. 3. С. 484–495.
Гонор А.Л., Черный Г.Г. Формы нетонких тел минимального волнового сопротивления // Теория оптимальных аэродинамических форм. М.: Мир, 1969. С. 379–395.
Крайко А.Н., Пудовиков Д.Е., Пьянков К.С., Тилляева Н.И. Осесимметричные головные части заданного удлинения, оптимальные или близкие к оптимальным по волновому сопротивлению // ПММ. 2003. Т. 67. Вып. 5. С. 795–828.
Крайко А.Н. Задача Ньютона о построении оптимальной головной части обтекаемого тела. История решения // ПММ. 2019. Т. 83. Вып. 5–6. С. 734–748.
Miele A. Slender shapes of minimum drag in Newtonian flow. ZFW. 1963. V. 11. № 5.
Миеле А. Тонкие тела минимального волнового сопротивления // Теория оптимальных аэродинамических форм. М.: Мир, 1969. С. 203–215.
Аэромеханика сверхзвукового обтекания тел вращения степенной формы / Под ред. Г.Л. Гродзовского. М.: Машиностроение, 1975. 183 с.
Васильченко В.И., Притуло М.Ф. Высшие приближения к точному решению задачи обтекания тела вращения сверхзвуковым потоком газа // Тр. ЦАГИ. 1975. Вып. 1666. С. 29–41.
Таковицкий С.А. Аналитическое решение в задаче построения осесимметричных носовых частей минимального волнового сопротивления // Изв. РАН. МЖГ. 2006. № 2. С. 157–162.
Таковицкий С.А. Оптимизационные задачи сверхзвуковой аэродинамики. М.: Наука, 2015. 236 с.
Иванюшкин Д.С., Таковицкий С.А. Носовые части минимального волнового сопротивления с передним торцом и степенной образующей // Уч. зап. ЦАГИ. 2009. Т. XL. № 5. С. 35–40.
Takovitskii S.A. Axisymmetric forebodies having minimum drag in supersonic flow // AIAA AVIATION Forum. June 15–19, 2020. https://doi.org/10.2514/6.2020-3120.
Горелов С.Л., Нгуен В.Л. Затупленное осесимметричное тело минимального сопротивления в гиперзвуковом потоке разреженного газа // Тр. МФТИ. 2021. Т. 13. № 1. С. 96–107.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Известия РАН. Механика жидкости и газа

Архивы выпусков Информация о журнале Отправить рукопись в журнал