Известия РАН. Механика жидкости и газа, 2022, № 5, стр. 119-128
ОЦЕНКА ВЛИЯНИЯ ЭФФЕКТА РАЗРЕЖЕНИЯ НА ЧИСЛО ПУАЗЕЙЛЯ В ДЛИННОМ КОЛЬЦЕВОМ КАНАЛЕ ПРИ НЕПОЛНОЙ АККОМОДАЦИИ МОЛЕКУЛ ГАЗА
О. В. Гермидер a, *, В. Н. Попов a, **
a Северный (Арктический) федеральный университет им. М.В. Ломоносова
Архангельск, Россия
* E-mail: o.germider@narfu.ru
** E-mail: v.popov@narfu.ru
Поступила в редакцию 12.04.2022
После доработки 15.05.2022
Принята к публикации 15.05.2022
- EDN: AFGYIH
- DOI: 10.31857/S056852812205005X
Аннотация
В зависимости от значений параметра разрежения, отношений радиусов цилиндров, образующих длинный кольцевой канал, и коэффициентов аккомодации тангенциального импульса молекул газа на стенках канала предложен метод вычислений значений числа Пуазейля. В промежуточном режиме течения газа данные значения получены с использованием полиномиальной аппроксимации Чебышева на основе линеаризованного модельного кинетического уравнения Шахова с зеркально-диффузными граничными условиями Максвелла. Приведен анализ полученных результатов в окрестности гидродинамического режима течения газа со скольжением и проведено их сравнение с аналогичными результатами, найденных в рамках БГК модели.
Развитие методов математического моделирования процессов, протекающих в прямых микро- и наноканалах, является одним из главных направлений исследований, проводимых в последнее время в области динамики разреженного газа [1–4]. Гидравлические диаметры этих каналов могут варьироваться от десятков нанометров до десятков миллиметров, что приводит к тому, что течение газа в условиях, когда средняя длина свободного пробега молекул газа сравнима с характерным размером поперечного сечения канала ( в частности, с гидравлическим диаметром) не может быть описано на основе уравнений динамики слошных сред [5]. Для исследования гидродинамических закономерностей течения газа в длинном канале, образованном двумя коаксиальными цилиндрами, введем число Пуазейля P0, определяемое как произведение коэффициента трения Дарси fd на число Рейнольдса Re [6, 7]. Как отмечено в [8], выбранная конфигурация сечения канала представляет интерес как с прикладной, так и с теоретической точек зрения. В постановочной части работа близка к [8] и [9]. Течение газа в канале обусловлено градиентом давления в продольном направлении. В представленной работе в отличие от [8] и [9] в качестве основного уравнения, описывающего кинетику массопереноса, используется линеаризованная S модель (уравнение Шахова) [10], которая при переходе к гидродинамическому режиму дает корректное значение числа Прандтля в отличие от модели БГК. Граничные условия обобщены на случай с несовпадающими значениями коэффициентов аккомодации тангенциального импульса молекул газа на стенках канала. Проводится сравнительный анализ с результатами из [9] и результатами в режиме течения со скольжением, которые получены в явном виде с использованием уравнения Навье–Стокса. Значения числа Пуазейля находятся с применением полиномиальной аппроксимации Чебышева [11, 12] в широком диапазоне изменения параметра разрежения в зависимости от значений коэффициентов аккомодации тангенциального импульса молекул газа на цилиндрах и гидравлического диаметра канала. Модификация метода коллокации [12] выполнена путем использования свойств конечных сумм полиномов Чебышева, произведения Кронекера при построении матрицы системы алгебраических уравнений.
1. ПОСТАНОВКА ЗАДАЧИ. КИНЕТИЧЕСКОЕ УРАВНЕНИЕ
Рассмотрим течение разреженного газа в длинном канале, образованном двумя коаксиальными цилиндрами с радиусами $R_{1}^{'}$ и $R_{2}^{'}$ ($R_{1}^{'} < R_{2}^{'}$), под действием заданного градиента давления, направленного вдоль оси канала $z{\text{'}}$. Считаем, что цилиндры поддерживаются при постоянной температуре. Коэффициенты аккомодации тангенциального импульса молекул газа на внутреннем и внешнем цилиндрах обозначим соответственно ${{\alpha }_{1}}$ и ${{\alpha }_{2}}$. Канал соединяет два резервуара, давления в которых обозначим $p_{1}^{'}$ и $p_{2}^{'}$ соответственно. Полагаем, что $p_{2}^{'} < p_{1}^{'}$ и длина канала $L{\text{'}} \gg D_{h}^{'}$, где $D_{h}^{'} = 2(R_{2}^{'} - R_{1}^{'})$ – гидравлический диаметр [7]. Состояние газа в точке ${\mathbf{r}}{\text{'}}$ определяем функцией распределения молекул газа $f{\text{'}}({\mathbf{r}}{\text{'}},{\mathbf{v}})$, где ${\mathbf{v}}$ – молекулярная скорость газа. В качестве масштабов длины, скорости, вектора потока тепла, концентрации, температуры, функции распределения выберем соответственно величины: $D_{h}^{'}$, ${{\beta }^{{ - 1/2}}}$, $p_{0}^{'}{{\beta }^{{ - 1/2}}}$, $n_{0}^{'}$, $T_{0}^{'}$, $n_{0}^{'}{{\beta }^{{3/2}}}$, где $\beta = m{\text{'/}}(2{{k}_{{\text{B}}}}T_{0}^{'})$, ${{k}_{{\text{B}}}}$ – постоянная Больцмана, $m{\text{'}}$ – масса молекул газа, $n_{0}^{'}$, $T_{0}^{'}$ – концентрация, температура газа в некоторой точке, принятой за начало координат; $p{\text{'}} = n{\text{'}}{{k}_{{\text{B}}}}T{\text{'}}$. Тогда для безразмерных величин имеем следующие соотношения
Число Пуазейля P0 определяем как произведение коэффициента трения Дарси ${{f}_{d}}$ на число Рейнольдса Re [6, 7]
(1.1)
${{{\text{P}}}_{0}} = {{f}_{d}}{\text{Re}} = - \frac{{2{{G}_{p}}p_{0}^{'}D_{р}^{'}{{\beta }^{{1/2}}}}}{{\mu {{{\bar {u}}}_{z}}}}$Полагаем, что модуль безразмерного градиента давления Gp является малым по величине. Учитывая осесимметричный характер течения газа в канале, введем цилиндрические координаты ${\mathbf{r}} = (\rho ,{{r}_{\varphi }},{{r}_{z}})$ в конфигурационном пространстве и ${\mathbf{C}} = ({{C}_{ \bot }},{{C}_{\psi }},{{C}_{z}})$ в пространстве скоростей. В линейном приближении получим
(1.2)
$f({\mathbf{r}},{\mathbf{C}}) = {{f}_{0}}(C)\left( {1 + {{G}_{p}}(z + h(\rho ,{\mathbf{C}}))} \right),\quad {{f}_{0}}(C) = {{\pi }^{{ - 3/2}}}\exp ( - {{C}^{2}})$Здесь f0 – безразмерный абсолютный максвеллиан. Используя (1.2), представляем ${{\bar {u}}_{z}}$ в виде разложения по Gp
(1.3)
${{\bar {u}}_{z}} = - {{G}_{p}}{{\bar {U}}_{z}},\quad {{\bar {U}}_{z}} = - \frac{2}{{R_{2}^{2} - R_{1}^{2}}}\int\limits_{{{R}_{1}}}^{{{R}_{2}}} {{{U}_{z}}} (\rho )\rho d\rho $Подставляя (1.3) в (1.1) и учитывая, что в случае модели жестких сфер для параметра разреженности $\delta $ выполняется соотношение [5]:
получаемВведем функции ${{Z}_{1}} = {{Z}_{1}}(\rho ,\zeta ,{{C}_{ \bot }})\bar {\tau }$ и ${{Z}_{2}} = {{Z}_{2}}(\rho ,\zeta ,{{C}_{ \bot }})$
Компоненты ${{U}_{z}}$ и ${{q}_{z}}$ записываем через функции ${{Z}_{1}}$ и ${{Z}_{2}}$ как
Функцию ${{Z}_{1}}$ находим из линеаризованной модели кинетического уравнения Шахова [12]
(1.4)
$\begin{gathered} \left( {\frac{{\partial {{Z}_{1}}}}{{\partial \rho }}\zeta + \frac{{\partial {{Z}_{1}}}}{{\partial \zeta }}\frac{{(1 - {{\zeta }^{2}})}}{\rho }} \right){{C}_{ \bot }} + \delta {{Z}_{1}}(\rho ,\zeta ,{{C}_{ \bot }}) + \frac{1}{2} = \\ = \;\delta \left( {{{U}_{z}}(\rho ) + \frac{{2(1 - {\text{Pr}})}}{5}{{q}_{z}}(\rho )(C_{ \bot }^{2} - 1)} \right) \\ \end{gathered} $(1.5)
$\left( {\frac{{\partial {{Z}_{2}}}}{{\partial \rho }}\zeta + \frac{{\partial {{Z}_{2}}}}{{\partial \zeta }}\frac{{(1 - {{\zeta }^{2}})}}{\rho }} \right){{C}_{ \bot }} + \delta {{Z}_{2}}(\rho ,\zeta ,{{C}_{ \bot }}) + \frac{3}{4} = \delta \left( {\frac{3}{2}{{U}_{z}}(\rho ) + \frac{{3(1 - {\text{Pr}})}}{5}{{q}_{z}}(\rho )C_{ \bot }^{2}} \right)$В качестве граничного условия на цилиндрах используем модель зеркально-диффузного отражения Максвелла [5]. В этом случае имеем
2. РЕШЕНИЕ КРАЕВОЙ ЗАДАЧИ
Неизвестные функции ${{Z}_{1}}(\rho ,\zeta ,{{C}_{ \bot }})$ и ${{Z}_{2}}(\rho ,\zeta ,{{C}_{ \bot }})$, где $\rho \in [{{R}_{1}},{{R}_{2}}]$, ${{C}_{ \bot }} \in [0, + \infty )$ и $\zeta \in [ - 1,\;1]$, раскладываем в ряды по полиномам Чебышева первого рода ${{T}_{{{{k}_{i}}}}}$ и ограничиваясь в этих рядах членами с номерами ${{k}_{i}} \leqslant {{n}_{i}}$ ($i = \overline {1,\;3} $) [11], получаем
(2.1)
${{Z}_{j}}(\rho ,\zeta ,{{C}_{ \bot }}) = {{{\mathbf{T}}}_{1}}({{x}_{1}}) \otimes {{{\mathbf{T}}}_{2}}({{x}_{2}}) \otimes {{{\mathbf{T}}}_{3}}({{x}_{3}}){{{\mathbf{A}}}_{{\mathbf{j}}}},\quad j = 1,\;2$В качестве точек коллокации в (1.4) и (1.5) для xi выберем нули ${{T}_{{n_{i}^{'}}}}({{x}_{i}})$ на отрезке [–1, 1] [11]:
(2.2)
${{x}_{{i,{{k}_{i}}}}} = \cos {{\xi }_{i}},\quad {{\xi }_{i}} = \frac{{\pi (2{{n}_{i}} - 2{{k}_{i}} + 1)}}{{2({{n}_{i}} + 1)}},\quad {{k}_{i}} = \overline {0,\;{{n}_{i}}} ,\quad i = \overline {1,\;3} $Для нахождения значений полиномов Чебышева и производных от полиномов Чебышева в точках (2.2) воспользуемся геометрическим определением ${{T}_{{{{j}_{i}}}}}({{x}_{i}}) = \cos ({{j}_{i}}\arccos {{x}_{i}})$, где ${{x}_{i}} \in [ - 1$, 1] [11]. Тогда
(2.3)
${{T}_{{{{j}_{i}}}}}({{x}_{{i,{{k}_{i}}}}}) = \cos {{j}_{i}}{{\xi }_{i}},\quad \frac{{d{{T}_{{{{j}_{i}}}}}({{x}_{{i,{{k}_{i}}}}})}}{{d{{x}_{i}}}} = \frac{{{{j}_{i}}\sin {{j}_{i}}{{\xi }_{i}}}}{{\left| {\sin {{\xi }_{i}}} \right|}},\quad {{j}_{i}},\quad {{k}_{i}} = \overline {0,\;{{n}_{i}}} ,\quad i = 1,\;2$Подставляя (2.1)–(2.3) в (1.4), приходим к системе $n_{1}^{'}n_{2}^{'}n_{3}^{'}$-уравнений, в которой заменяем уравнения с x1, 0, ${{x}_{{2,{{k}_{2}}}}}$ (${{k}_{2}} = \overline {n_{2}^{'}{\text{/}}2,{{n}_{2}}} $) на уравнения, вытекающие из граничного условия (1.6) для функции Z1 при ${{x}_{2}} > 0$:
Здесь и ниже считаем, что ${{n}_{2}}$ – нечетное число. Аналогично в системе $n_{1}^{'}n_{2}^{'}n_{3}^{'}$-уравнений, полученной подстановкой точек (2.3) в (1.5), на уравнения, вытекающие из граничного условия (1.6) для функции Z2.
Учитывая, что в точках (2.3) имеют место равенства [11]:
(2.4)
$\frac{2}{{n_{i}^{'}}}\sum\limits_{{{k}_{i}} = 0}^{{{n}_{i}}} {{\text{'}}{{T}_{{{{k}_{i}}}}}} ({{x}_{{{{l}_{i}}}}}){{T}_{{{{k}_{i}}}}}({{x}_{{{{j}_{i}}}}}) = {{\delta }_{{{{l}_{i}},{{j}_{i}}}}},\quad {{l}_{i}},{{j}_{i}} = \overline {0,\;{{n}_{i}}} ,\quad i = \overline {1,\;3} $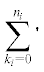 понимаем конечную сумму, в которой первое слагаемое умножается на 1/2, выразим коэффициенты
в (2.1) через значения функций ${{Z}_{1}}$ и ${{Z}_{2}}$, вычисленные в точках (2.3). Обозначая
понимаем конечную сумму, в которой первое слагаемое умножается на 1/2, выразим коэффициенты
в (2.1) через значения функций ${{Z}_{1}}$ и ${{Z}_{2}}$, вычисленные в точках (2.3). Обозначая
На основе полученных элементов матрицы Z1 восстанавливаем ${{U}_{z}}(\rho )$
(2.5)
${\mathbf{K}} = 2\int\limits_{ - 1}^1 {\frac{{1 + {{x}_{3}}}}{{{{{(1 - {{x}_{3}})}}^{3}}}}} {{{\mathbf{T}}}_{3}}({{x}_{3}})\exp \left( { - \frac{{{{{(1 + {{x}_{3}})}}^{2}}}}{{{{{(1 - {{x}_{3}})}}^{2}}}}} \right)d{{x}_{3}}$Для вычисления интеграла (2.5) применяем рекуррентные соотношения [11]
Находим значение ${{\bar {U}}_{z}}$ по формуле (1.3) и подставляем его в (1.1). Таким образом, число Пуазейля P0 зависит от параметра разрежения газа $\delta $, отношения радиусов цилиндров $r = R_{1}^{'}{\text{/}}R_{2}^{'}$ и коэффициентов аккомодации тангенциального импульса молекул газа на стенках канала ${{\alpha }_{1}}$ и ${{\alpha }_{2}}$. Здесь выразили безразмерные радиусы цилиндров ${{R}_{1}}$ и ${{R}_{2}}$ через r
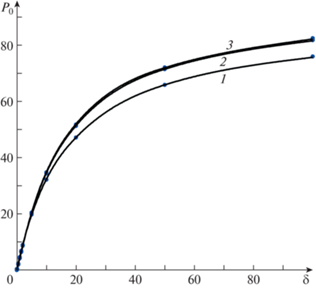
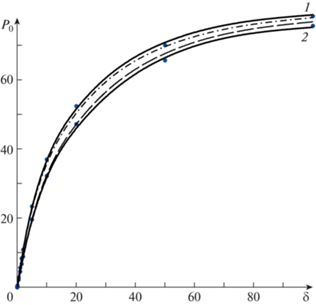
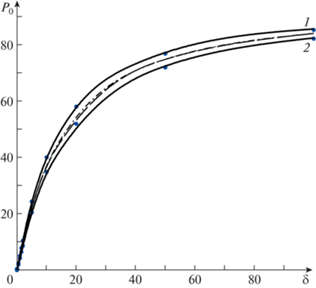
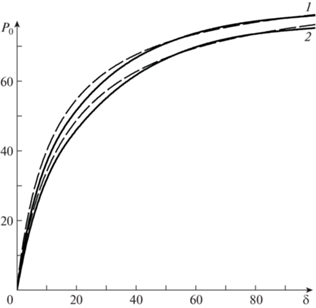
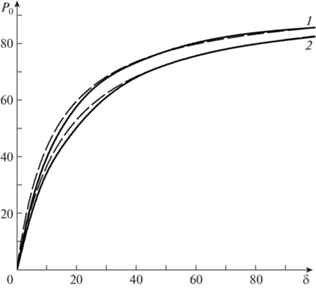
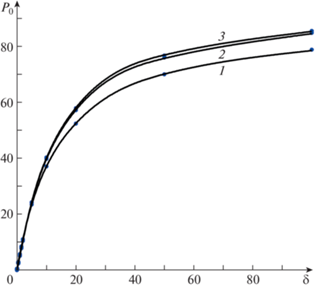
Полученные результаты вычислений P0 представлены графически на рис. 1–4. В случае ${\text{Pr}} = 1$ на рис. 1 и 2 кривые 1, 2 и 3 построены с применением кубической сплайн-интерполяции для отношения радиусов цилиндров 0.1, 0.5, 0.9 при совпадающих коэффициентах аккомодации тангенциального импульса молекул газа на внешнем и внутреннем цилиндрах $\alpha = {{\alpha }_{{1,2}}} = 1$ (рис. 1) и $\alpha = 0.85$ (рис. 2). Наблюдается возрастание числа Пуазейля с ростом отношения радиусов цилиндров и параметра разряжения. Существенное сближение c кривой 3 происходит при уменьшении значения $\alpha $. Точками показаны значения P0 из [9]. Наблюдается хорошее согласие полученных результатов в настоящей работе с [9] (погрешность менее 2%). На рис. 3 и 4 сплошными линиями 1 (α = 1) и 2 ($\alpha = 0.85$) проиллюстрирована зависимость ${{{\text{P}}}_{0}}(\delta )$ для $r = 0.1$ и $r = 0.9$ при Pr = 2/3. Кривая, построенная штриховой линией, соответствует значениям ${{\alpha }_{1}} = 1$ и ${{\alpha }_{2}} = 0.85$, штрихпунктирной – ${{\alpha }_{1}} = 0.85$ и ${{\alpha }_{2}} = 1$. С увеличением значений $\delta > 20$ наблюдается сближение этих кривых. Точками на рис. 3 и 4 показаны значения P0 при Pr = 1. Видно, что результаты, основанные на решении уравнения БГК и S-модели, согласуются между собой.
Рис. 1.
Графики функции ${{{\text{P}}}_{0}}(\delta )$: $\alpha = 1$, Pr = 1, $r = 0.1,\;0.5,\;0.9$ (1–3).
3. АНАЛИЗ ПОЛУЧЕННЫХ РЕЗУЛЬТАТОВ
В гидродинамическом режиме течения (${{\delta }^{{ - 1}}} \ll 1$) массовую скорость газа можно восстановить на основе решения уравнения Навье–Стокса для одноатомного газа
(3.1)
$\frac{1}{\rho }\frac{d}{{d\rho }}\left( {\rho \frac{{d{{U}_{z}}(\rho )}}{{d\rho }}} \right) = - \delta $(3.2)
${{U}_{z}}(\rho ) = \frac{\delta }{4}\left( {R_{1}^{2}\ln \frac{{{{R}_{2}}}}{\rho } + R_{2}^{2}\ln \frac{\rho }{{{{R}_{1}}}} - {{\rho }^{2}}} \right){{\left( {\ln \frac{{{{R}_{2}}}}{{{{R}_{1}}}}} \right)}^{{ - 1}}}$В этом случае, подставляя (3.2) в (1.3) и используя (1.1), имеем
При $r \to 0$ получаем ${{{\text{P}}}_{0}} = 64$, которое соответствует цилиндрическому каналу [7]. При $r \to 1$ приходим к значению ${{P}_{0}} = 96$, которое имеет место при течении газа в плоском канале [7].
Покажем, что в пределе (${{\delta }^{{ - 1}}} \ll 1$) массовая скорость газа ${{U}_{z}}(\rho )$, полученная на основе уравнения (1.4), принимает вид (3.2). Действительно, в этом случае, ограничиваясь нулевым приближением относительно ${{\delta }^{{ - 1}}}$ в уравнении (1.4), имеем
(3.3)
${{Z}_{1}}(\rho ,\zeta ,{{C}_{ \bot }}) = {{U}_{z}}(\rho ) + \frac{{2(1 - {\text{Pr}})}}{5}{{q}_{z}}(\rho )(C_{ \bot }^{2} - 1)$Умножим левую и правую части уравнения (3.3) на ${{C}_{ \bot }}\exp ( - C_{ \bot }^{2})$ и проинтегрируем в пределах от 0 до $ + \infty $. В результате получаем
(3.4)
$2\int\limits_0^{ + \infty } {{{Z}_{1}}} (\rho ,\zeta ,{{C}_{ \bot }}){{C}_{ \bot }}\exp ( - C_{ \bot }^{2})d{{C}_{ \bot }} = {{U}_{z}}(\rho )$Откуда следует, что функция ${{Z}_{1}} = {{U}_{z}}$, определяемая выражением (3.2), является решением уравнения (3.4) и удовлетворяет граничным условиям (1.5). При фиксированных значениях $r$ максимум функции ${{{\text{P}}}_{0}}(\delta )$ достигается в гидродинамическом пределе. Для отношения радиусов цилиндров 0.1 и 0.9 максимальные значения ${{{\text{P}}}_{0}}(\delta )$ равны соответственно 89.4 и 96, т.е. происходит существенный сдвиг значений ${{{\text{P}}}_{0}}(\delta )$ от 64, которое определяет течение газа в цилиндрическом канале, в сторону плоского течения.
В режиме течения со скольжением тангенциальная массовая скорость газа пропорциональна ее нормальному градиенту вблизи стенок канала [5]. Следуя [9] и [5], запишем граничные условия скольжения в виде
(3.5)
${{U}_{z}}({{R}_{i}}) = ( - {{1)}^{{i + 1}}}\frac{{{{\sigma }_{p}}}}{\delta }\frac{{d{{U}_{z}}}}{{d\rho }}({{R}_{i}}),\quad i = 1,\;2$Здесь ${{\sigma }_{p}}$ – безразмерный коэффициент вязкого скольжения. Для диффузного рассеяния (${{\alpha }_{{1,2}}} = 1$) в рамках модели S коэффициент σp равен 1.018 [15] и 1.06 в рамках модели БГК [5], для зеркально-диффузного отражения Максвелла при $\alpha = {{\alpha }_{{1,2}}}$ коэффициент ${{\sigma }_{p}}$ может быть получен по формуле [15]:
Решение уравнение Навье–Стокса (3.1) с граничными условиями скольжения (3.5) находим аналитически
(3.6)
$\begin{gathered} {{U}_{z}}(\rho ) = \frac{1}{4}\left( {\left( {{{\rho }^{2}}\ln r - R_{1}^{2}\ln \frac{\rho }{{{{R}_{2}}}} - R_{2}^{2}\ln \frac{{{{R}_{1}}}}{\rho }} \right)} \right.{{R}_{1}}{{R}_{2}}{{\delta }^{2}} + \\ + \;({{R}_{1}} + {{R}_{2}}){{\rho }^{2}}{{\sigma }_{p}}\delta + 2(R_{2}^{2} - R_{1}^{2})\sigma _{p}^{2} + \\ + \;\left. {\left( {R_{1}^{3} + R_{2}^{3} - R_{1}^{2}{{R}_{2}}\ln \frac{{R_{2}^{2}}}{{{{\rho }^{2}}}} - {{R}_{1}}R_{2}^{2}\ln \frac{{R_{1}^{2}}}{{{{\rho }^{2}}}}} \right){{\sigma }_{p}}\delta } \right){{({{\sigma }_{p}}({{R}_{1}} + {{R}_{2}}) - \delta {{R}_{1}}{{R}_{2}}\ln r)}^{{ - 1}}} \\ \end{gathered} $Подставляя (3.6) в (1.3), согласно (1.1) получаем
(3.7)
${{{\text{P}}}_{0}} = \frac{{64\delta (\delta r\ln r + (2{{r}^{2}} - 2){{\sigma }_{p}}){{{(1 - r)}}^{2}}}}{\beta }$(3.8)
$\begin{gathered} \beta = r\delta (\delta + 8{{\sigma }_{p}})(({{r}^{2}} + 1)\ln r - {{r}^{2}} + 1) + \\ + \;2{{\sigma }_{p}}\delta ({{r}^{4}} - 4{{r}^{2}}\ln r - 1) + 16({{r}^{4}} - 2{{r}^{3}} + 2r - 1)\sigma _{p}^{2} \\ \end{gathered} $На рис. 5 и 6 сплошными линиями 1 (α = 1) и 2 (α = 0.85) показаны результаты вычислений ${{{\text{P}}}_{0}}(\delta )$ для $r = 0.1$ и $r = 0.9$ в рамках линеаризованной S модели. Штриховыми линиями построены кривые по формуле (3.7) при ${{\sigma }_{p}} = 1.018$. Видно, что результаты вычислений числа Пуазейля для отношения радиусов цилиндров 0.1 (кривая 1) и 0.9 (кривая 2) в представленной работе приближаются к результатам гидродинамики со скольжением при $\delta > 20$. Отклонение не превосходит 5.6% при $\delta $ и 1.5% при δ = 40.
ЗАКЛЮЧЕНИЕ
Разработан алгоритм вычисления значений числа Пуазейля в промежуточном режиме течения газа между двумя длинными цилиндрами на основе решения линеаризованного кинетического уравнения Шахова с использованием полиномиальной аппроксимации Чебышева. Проведен анализ влияния отношения радиусов цилиндров, параметра разрежения и коэффициентов аккомодации тангенциального импульса молекул газа на стенках канала на значения числа Пуазейля. Установлено, что с ростом отношения радиусов цилиндров, параметра разрежения и значений коэффициентов аккомодации тангенциального импульса молекул газа на стенках канала происходит монотонное возрастание числа Пуазейля. Максимальное значение этого числа характеризует свойства плоского течения газа, обусловленного действием постоянного продольного градиента давления, в гидродинамическом пределе. Полученные результаты могут быть использованы для численного моделирования массопереноса при течении газа в канале, образованного двумя коаксиальными цилиндрами, и для объяснения особенностей этого процесса.
Список литературы
Ambrus V.E., Sharipov F., Sofonea V. Comparison of the Shakhov and ellipsoidal models for the Boltzmann equation and DSMC for ab initio -based particle interactions // Computers and Fluids. 2020. V. 211. 104637.
Boscarino S., Cho S.Y. On the order reduction of semi-Lagrangian methods for BGKmodel of Boltzmann equation // Applied Mathematics Letters. 2022. V. 123. 107488.
Rovenskaya O.I. Numerical analysis of surface roughness effects on the Poiseuille flow caused by a small pressure drop // International Journal of Heat and Mass Transfer. 2017. V. 110. P. 817–826.
Valougeorgis D., Vasileiadis N., Titarev V. Validity range of linear kinetic modeling in rarefied pressure driven single gas flows through circular capillaries // European Journal of Mechanics / B Fluids, Special Issue on Nonequilibrium Gas Flows. 2017. V. 64. P. 2–7.
Шарипов Ф.М., Селезнев В.Д. Движение разреженных газов в каналах и микроканалах. Екатеринбург: УрО РАН, 2008.
Liu C., Yanga J., Ni Yu. A multiplicative decomposition of Poiseuille number on rarefaction and roughness by lattice Boltzmann simulation // Computers and Mathematics with Applications. 2011. V. 61. P. 3528–3536.
Kandlikar S.G., Garimella S., Li D., Colin S., King M.R. Heat Transfer and Fluid Flow in Minichannels and Microchannels. Oxford: Elsevier Ltd., 2006.
Шахов Е.М. Течение разреженного газа между коаксиальными цилиндрами под действием градиента давления // Ж. вычисл. матем. и матем. физ. 2003. Т. 43. № 7. С. 1107–1116.
Breyiannis G., Varoutis S., Valougeorgis D. Rarefied gas flow in concentric annular tube: Estimation of the Poiseuille number and the exact hydraulic diameter // European Journal of Mechanics B/Fluids. 2008. V. 27. P. 609–622.
Шахов Е.М. Об обобщении релаксационного кинетического уравнения Крука // Изв. АН СССР, МЖГ. 1968. № 5. С. 142–145.
Mason J., Handscomb D. Chebyshev polynomials. Florida: CRC Press, 2003.
Гермидер О.В., Попов В.Н. Неизотермическое течение разреженного газа в длинном цилиндрическом канале при произвольных перепадах давления и температуры // Изв. РАН. МЖГ. 2020. № 3. С. 125–140.
Liu S., Trenkler G. Hadamard, Khatri-Rao, Kronecker and Other Matrix Products // International Journal of Information and Systems Sciences. 2008. V. 4 № 1. P. 160–177.
Landau L.D., Lifshitz E.M. Fluid Mechanics. New York: Pergamon. 1989.
Graur I., Sharipov F. Non-isothermal flow of rarefied gas through a long pipe with elliptic cross section // Microfluid Nanofluid. 2009. V. 6. P. 267–275.
Дополнительные материалы отсутствуют.
Инструменты
Известия РАН. Механика жидкости и газа