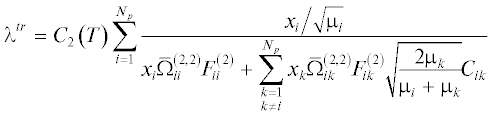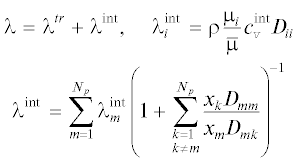1. На главную
  2. Электронные версии
  3. Известия РАН. Механика жидкости и газа
  4. № 5, 2022

Известия РАН. Механика жидкости и газа, 2022, № 5, стр. 94-112

ТЕПЛООБМЕН ЦИЛИНДРИЧЕСКОГО ТЕЛА С КАТАЛИТИЧЕСКОЙ ПОВЕРХНОСТЬЮ ПРИ ОБТЕКАНИИ ПОТОКОМ ДОЗВУКОВОЙ НЕРАВНОВЕСНОЙ ВОЗДУШНОЙ ПЛАЗМЫ

А. И. Брызгалов a, С. А. Васильевский a, А. Ф. Колесников a, С. Е. Якуш a, *

a Институт проблем механики им. А.Ю. Ишлинского РАН
Москва, Россия

* E-mail: yakush@ipmnet.ru

Поступила в редакцию 11.05.2022
После доработки 20.05.2022
Принята к публикации 20.05.2022

Полный текст (PDF)

Аннотация

Исследованы стационарные дозвуковые течения неравновесной воздушной плазмы около цилиндрического тела с плоским торцом и теплообмен в условиях, характерных для испытаний материалов в ВЧ-плазмотроне ВГУ-4 ИПМех РАН. Представлена двумерная вычислительная модель, позволяющая производить расчеты осесимметричного обтекания тел с учетом детальной кинетики частично ионизованного и диссоциированного воздуха. Проведены численные расчеты стационарных обтеканий и тепловых потоков к водоохлаждаемому цилиндрическому телу диаметром 50 мм, на переднем торце которого установлен проточный калориметр. Расчеты проведены для серии экспериментов на установке ВГУ-4 с различными металлическими тепловоспринимающими стенками калориметров (медь, серебро, золото, ниобий, тантал, бериллий, молибден). Получены характеристики течения и распределения концентраций компонент в расчетной области и вблизи поверхностей с различной каталитичностью по отношению к гетерогенной рекомбинации атомов кислорода и азота. Рассчитаны радиальные распределения кондуктивной и рекомбинационной составляющих теплового потока, а также суммарного теплового потока на поверхности обтекаемого тела. Продемонстрирован эффект сверхравновесного нагрева, приводящий к возникновению высоких тепловых потоков вблизи границы раздела материалов с сильно различающейся каталитической активностью. Сравнение с экспериментальными данными показало, что вычислительная модель позволяет предсказывать тепловые потоки на обтекаемых каталитических поверхностях с точностью не хуже 10%.

Ключевые слова: ВЧ-плазмотрон, воздушная плазма, каталитическая поверхность, дозвуковой поток, теплообмен, численная модель, валидация

Термохимическая стойкость, каталитические свойства материалов и покрытий в условиях аэродинамического нагрева определяются в потоках плазмы, создаваемых при помощи высокочастотных индукционных плазмотронов [1–3], в разрядном канале которых плазма создается за счет высокочастотного разряда мощностью от нескольких киловатт до сотен киловатт [4–6]. Преимущества индукционных плазмотронов по сравнению с дуговыми включают возможность получения плазмы высокой чистоты в широком диапазоне расходов газа, при этом вкладываемая в плазму мощность может достигать сотен киловатт. В последнее время, наряду с традиционной схемой организации газового разряда с коаксиальным индуктором, реализованы также тандемные схемы, применяются схемы с модуляцией индукционных токов, а область применения индукционных плазмотронов, наряду с испытаниями теплозащитных материалов, включает синтез наночастиц, алмазов, модификацию поверхностей и другие технологические приложения [4].

Неотъемлемой частью изучения взаимодействия плазмы с веществами и материалами на современном этапе служит численное моделирование, позволяющее восстановить детальную картину процесса и получить многие характеристики, недоступные для прямого экспериментального измерения. Примерами численного моделирования течений плазмы в разрядных каналах ВЧ-плазмотронов и струйного обтекания моделей служат работы [7–13]. В зависимости от режима работы плазмотрона применяются как равновесные [9], так и неравновесные [10, 12] модели плазмы, учитывающие конечную скорость реакций и термическую неравновесность. Достаточно эффективным оказался подход [7, 8], при котором течение в индукционном канале и обтекание тела рассчитываются на основе моделей равновесной плазмы, а эффекты неравновесности учитываются в пограничном слое вблизи передней критической точки тела путем решения соответствующей одномерной задачи.

Одной из важных характеристик теплозащитных покрытий является их каталитическая активность по отношению к рекомбинации атомов, кардинально влияющая на тепловые потоки к поверхности. Для определения коэффициентов каталитической рекомбинации требуются проведение численных расчетов для условий экспериментов на ВЧ-плазмотронах и подбор значений этих коэффициентов, обеспечивающих наилучшее согласие рассчитанных и измеренных тепловых потоков [14].

Несмотря на достаточно длительную историю развития вычислительных моделей и экспериментальных методов в области взаимодействия плазмы с материалами, многие аспекты до сих пор остаются недостаточно изученными. Примером может служить эффект сверхравновесного нагрева вблизи скачка каталитической активности, приводящий к значительному возрастанию тепловых потоков на высококаталитичных участках поверхности тела [16–18].

В настоящей работе представлена вычислительная модель течения химически неравновесной воздушной плазмы, реализованная в двумерном программном коде IPG2D. Адекватность математической модели и ее программной реализации подтверждена результатами валидационных расчетов обтеканий медной водоохлаждаемой модели диаметром 50 мм, имеющей на переднем торце датчик теплового потока с лицевой поверхностью, выполненной из ряда металлов с различной каталитической активностью. Показано хорошее совпадение с результатами недавних экспериментов, проведенных в плазмотроне ВГУ-4 ИПМех РАН [14] для четырех режимов работы плазмотрона и семи типов датчиков теплового потока с охлаждаемой металлической поверхностью.

1. МАТЕМАТИЧЕСКАЯ МОДЕЛЬ

1.1. Определяющие уравнения

Рассматривается течение воздушной плазмы, содержащей Np компонент (включая атомы, молекулы, ионы и электроны). Система определяющих уравнений имеет вид

(1.1)
$\frac{{\partial \rho {{y}_{i}}}}{{\partial t}} + \nabla \left( {\rho {{y}_{i}}({\mathbf{U}} + {{{\mathbf{V}}}_{i}})} \right) = {{\dot {\omega }}_{i}},\quad i = 1,\; \ldots ,\;{{N}_{p}}$
(1.2)
$\frac{{\partial \rho {\mathbf{U}}}}{{\partial t}} + \nabla \left( {\rho {\mathbf{U}} \otimes {\mathbf{U}}} \right) = - \nabla P + \nabla {\mathbf{\Pi }}$
(1.3)
$\frac{{\partial E}}{{\partial t}} + \nabla \left( {(E + P){\mathbf{U}}} \right) = \nabla {{{\mathbf{q}}}_{T}}$

Здесь $t$ – время, $\rho $ – плотность, ${{y}_{i}}$ – массовые доли компонент ($\sum\nolimits_{i = 1}^{{{N}_{p}}} {{{y}_{i}}} = 1$), ${\mathbf{U}}$ – скорость, $P$ – давление, ${{{\mathbf{V}}}_{i}}$ – диффузионная скорость $i$-й компоненты, ${{\dot {\omega }}_{i}}$ – массовая скорость ее производства в единице объема, ${\mathbf{\Pi }}$ – тензор вязких напряжений, E – плотность полной энергии, ${{{\mathbf{q}}}_{T}}$ – вектор теплового потока.

Замыкание системы уравнений (1.1)–(1.3) осуществляется на основе уравнения состояния идеального газа

(1.4)
$P = \rho {{R}^{0}}T\sum\limits_{i = 1}^{{{N}_{p}}} {\frac{{{{y}_{i}}}}{{{{\mu }_{i}}}}} $
где $T$ – температура, ${{R}^{0}} = 8.314$ Дж/моль·K – универсальная газовая постоянная, ${{\mu }_{i}}$ – молярная масса i-й компоненты. Для каждой компоненты заданы температурные зависимости удельной энтальпии (включающей теплоту образования компоненты) ${{h}_{i}}(T)$ и теплоемкости ${{c}_{{p,}}}_{i}(T)$ по табличным данным [19].

Соответствующие характеристики газовой смеси находятся как

$h(T) = \sum\limits_{i = 1}^{{{N}_{p}}} {{{y}_{i}}{{h}_{i}}(T)} ,\quad {{c}_{p}}(T) = \sum\limits_{i = 1}^{{{N}_{p}}} {{{y}_{i}}{{c}_{{p,i}}}(T)} ,\quad {{e}^{{\operatorname{int} }}} = h - \frac{P}{\rho }$
где ${{e}^{{\operatorname{int} }}}$ – удельная внутренняя энергия смеси. Плотность полной энергии смеси, входящая в уравнение (1.3), определяется как

$E = \rho \left( {{{e}^{{\operatorname{int} }}} + \frac{1}{2}{{{\left| {\mathbf{U}} \right|}}^{2}}} \right)$

Тензор вязких напряжений в уравнении импульса (1.2) имеет ньютоновский вид

(1.5)
${\mathbf{\Pi }} = \eta \left( {\nabla {\mathbf{U}} + \nabla {{{\mathbf{U}}}^{T}} - \frac{2}{3}{\mathbf{I}}\left( {\nabla \times {\mathbf{U}}} \right)} \right)$
где $\eta $ – коэффициент динамической вязкости, ${\mathbf{I}}$ – единичный тензор.

Диффузионные потоки компонент в уравнениях (1.1) выражены через диффузионные скорости ${{{\mathbf{V}}}_{i}}$, которые находятся из соотношений Стефана–Максвелла с учетом амбиполярного поля в ионизованном газе. Используется однотемпературное приближение (температуры электронов и тяжелых частиц равны между собой); эффектами бародиффузии и термодиффузии пренебрегается. Система уравнений для определения диффузионных скоростей имеет вид [20]

(1.6)
$\sum\limits_{j = 1,j \ne e}^{{{N}_{p}}} {\frac{{{{x}_{i}}{{x}_{j}}}}{{{{D}_{{ij}}}}}\left( {{{{\mathbf{V}}}_{j}} - {{{\mathbf{V}}}_{i}}} \right)} + \frac{{{{x}_{i}}{{x}_{e}}}}{{{{D}_{{iе}}}}}{{{\mathbf{V}}}_{e}} = {{{\mathbf{d}}}_{i}}$
(1.7)
$ - \sum\limits_{j = 1,j \ne e}^{{{N}_{p}}} {\frac{{{{x}_{e}}{{x}_{j}}}}{{{{D}_{{ej}}}}}{{{\mathbf{V}}}_{e}}} = {{{\mathbf{d}}}_{e}}$
где ${{x}_{i}}$ – мольные доли компонент, ${{D}_{{ij}}}$ – бинарные коэффициенты диффузии, здесь и ниже индекс e относится к электрону. В правой части (1.6) и (1.7) стоят диффузионные термодинамические силы, имеющие вид

(1.8)
${{{\mathbf{d}}}_{i}} = \nabla {{x}_{i}} + \left( {{{x}_{i}} - {{y}_{i}}} \right)\nabla \ln P - e{{x}_{i}}\frac{{{{{\mathbf{E}}}_{{amb}}}}}{{{{k}_{{\text{B}}}}T}}$
(1.9)
${{{\mathbf{d}}}_{e}} = \nabla {{x}_{e}} + {{x}_{e}}\nabla \ln P + e{{x}_{e}}\frac{{{{{\mathbf{E}}}_{{amb}}}}}{{{{k}_{{\text{B}}}}T}}$

Здесь ${{{\mathbf{E}}}_{{amb}}}$ – амбиполярное электрическое поле, ${{k}_{{\text{B}}}}$ – постоянная Больцмана, $e$ – заряд электрона. Система уравнений (1.6)–(1.9) дополняется условиями электрической нейтральности плазмы, амбиполярности (отсутствия электрического тока) и равенства нулю суммы диффузионных потоков всех компонент

$\sum\limits_{j = 1,j \ne e}^{{{N}_{p}}} {{{e}_{j}}{{x}_{j}} - e} {{x}_{e}} = 0$
$\sum\limits_{j = 1,j \ne e}^{{{N}_{p}}} {{{e}_{j}}{{x}_{j}}{{{\mathbf{V}}}_{j}} - e} {{x}_{e}}{{{\mathbf{V}}}_{e}} = 0$
$\rho \sum\limits_{i = 1}^{{{N}_{p}}} {{{y}_{i}}{{{\mathbf{V}}}_{i}}} = 0$
(ej – заряд тяжелых компонент, отличный от нуля только для ионов).

Тепловой поток ${{{\mathbf{q}}}_{T}}$ в уравнении энергии (1.3) включает в себя кондуктивную и рекомбинационную составляющие

(1.10)
${{{\mathbf{q}}}_{T}} = {{{\mathbf{q}}}_{C}} + {{{\mathbf{q}}}_{R}} = - \lambda \nabla T + \rho \sum\limits_{i = 1}^{{{N}_{p}}} {{{y}_{i}}{{h}_{i}}{{{\mathbf{V}}}_{i}}} $

В настоящей работе расчеты проводятся для плазмы с температурой не выше 9100 К, что позволяет не учитывать перенос тепла излучением [21–23].

1.2. Коэффициенты переноса

Расчет коэффициентов вязкости $\eta $ и теплопроводности λ многокомпонентной осуществляется по полуэмпирическим формулам, полученным на основе минимизации функционала квадратов отклонений приближенных значений от коэффициентов переноса, вычисляемых по формулам молекулярно-кинетической теории Чепмена–Энскога во втором приближении для вязкости и в третьем – для теплопроводности [24]

(1.11)
(1.12)
где

${{C}_{1}}\left( T \right) = 8.387 \times {{10}^{{ - 6}}}\sqrt T ,\quad {{C}_{2}}\left( T \right) = 0.2615\sqrt T ,\quad {{C}_{{ik}}} = \frac{{3.75\mu _{i}^{2} + 5{{\mu }_{i}}{{\mu }_{k}} + 1.25\mu _{k}^{2}}}{{{{{\left( {{{\mu }_{i}} + {{\mu }_{k}}} \right)}}^{2}}}}$

Здесь ${{\lambda }^{{tr}}}$ – теплопроводность, обусловленная поступательными степенями свободы, $F_{{ij}}^{{\left( 1 \right)}}$, $F_{{ij}}^{{\left( 2 \right)}}$ – матрицы размером ${{N}_{p}} \times {{N}_{p}}$ постоянных коэффициентов порядка единицы [24]. При наличии в газе молекул вклад внутренних степеней свободы в коэффициент теплопроводности $\lambda $ учитывается введением поправки Эйкена

Здесь $c_{{v}}^{{\operatorname{int} }}$ – теплоемкость, обусловленная внутренней энергией молекул, $\bar {\mu } = \sum\nolimits_{i = 1}^{{{N}_{p}}} {{{x}_{i}}{{\mu }_{i}}} $ – средняя молярная масса смеси, Dij – бинарные коэффициенты диффузии, которые вычисляются согласно молекулярно-кинетической теории [25]

(1.13)
${{D}_{{ij}}} = \frac{3}{{16}}\frac{{\sqrt {2\pi k_{{\text{B}}}^{3}{{T}^{3}}{\text{/}}{{\mu }_{{ij}}}} }}{{P\pi \sigma _{{ij}}^{2}{{{\bar {\Omega }}}^{{(1,1)}}}}}$
где ${{\mu }_{{ij}}} = {{\mu }_{i}}{{\mu }_{j}}{\text{/}}({{\mu }_{i}} + {{\mu }_{j}})$ – приведенная молярная масса, ${{\sigma }_{{ij}}}$ – эффективный диаметр столкновения.

Интегралы столкновений $\bar {\Omega }_{{ij}}^{{\left( {1,1} \right)}}$ и $\bar {\Omega }_{{ij}}^{{\left( {2,2} \right)}}$, входящие в формулы (1.11)–(1.13), вычислялись по аппроксимирующим формулам из работы [26].

1.3. Кинетическая схема

Массовые скорости обратимых химических реакций для компонент газовой смеси, входящие в правые части уравнений сохранения (1.1), вычисляются как

(1.14)
${{\dot {\omega }}_{i}} = {{\mu }_{i}}\sum\limits_{r = 1}^{{{N}_{r}}} {\nu _{i}^{r}} \left( {k_{r}^{f}\prod\limits_{j \in rea} {c_{j}^{{\nu _{j}^{r}}}} - k_{r}^{r}\prod\limits_{j \in prod} {c_{j}^{{\nu _{j}^{r}}}} } \right)$
где ${{c}_{i}} = \rho {{y}_{i}}{\text{/}}{{\mu }_{i}}$ – мольные концентрации компонент, $\nu _{i}^{r}$ – стехиометрический коэффициент i-й компоненты в r-й реакции, ${{N}_{r}}$ – общее число реакций, $k_{r}^{f}$ и $k_{r}^{r}$ – константы скорости прямой и обратной реакций, соответственно, произведения концентраций в (1.14) берутся по исходным реагентам (rea) и по продуктам (prod) в r-й обратимой реакции соответственно. Константа скорости прямой реакции записывается в аррениусовском виде ${{k}_{f}} = A{{T}^{b}}\exp ( - {{E}_{a}}{\text{/}}{{R}^{0}}T)$, где A – предэкспоненциальный множитель, b – показатель степени в температурном факторе, ${{E}_{a}}$ – энергия активации. Константа скорости обратной реакции находится через константу равновесия, включающую термохимические данные компонент.

Для диссоциированного и однократно ионизованного воздуха использовалась кинетическая схема [27], предложенная для моделирования кинетики плазмы у поверхности космических аппаратов. Другие кинетические схемы, также применимые в данной задаче, можно найти в [28].

Рассматриваются следующие Np = 11 компонент: O2, N2, O, N, NO, O$_{2}^{ + }$, N$_{2}^{ + }$, O+, N+, NO+, e–. Протекающие между ними 32 реакции представлены в табл. 1, где предэкспоненциальный множитель A приведен для мольных концентраций ci, выраженных в моль/см3, для энергии активации отношение Ea/R0 измеряется в градусах Кельвина.

Таблица 1
№ Реакция $A$ $b$ ${{E}_{a}}{\kern 1pt} /{\kern 1pt} {{R}^{0}}$
Реакции диссоциации
1 O2 + N = 2O + N $3.600 \times {{10}^{{18}}}$ –1 $59500$
2 O2 + NO = 2O + NO $3.600 \times {{10}^{{18}}}$ –1 $59500$
3 O2 + O = 2O + O $9.000 \times {{10}^{{19}}}$ –1 $59500$
4 O2 + O2 = 2O + O2 $3.240 \times {{10}^{{19}}}$ –1 $59500$
5 O2 + N2 = 2O + N2 $7.200 \times {{10}^{{18}}}$ –1 $59500$
6 N2 + N = 2N + N $4.085 \times {{10}^{{22}}}$ –1.5 $113000$
7 N2 + NO = 2N + NO $1.900 \times {{10}^{{17}}}$ –0.5 $113000$
8 N2 + O = 2N + O $1.900 \times {{10}^{{17}}}$ –0.5 $113000$
9 N2 + O2 = 2N + O2 $1.900 \times {{10}^{{17}}}$ –0.5 $113000$
10 N2 + N2 = 2N + N2 $4.700 \times {{10}^{{17}}}$ –0.5 $113000$
11 NO + N = 2N + O $7.800 \times {{10}^{{21}}}$ –1.5 $75500$
12 NO + NO = N + O + NO $7.800 \times {{10}^{{21}}}$ –1.5 $75500$
13 NO + O = N + 2O $7.800 \times {{10}^{{21}}}$ –1.5 $75500$
14 NO + O2 = N + O + O2 $3.900 \times {{10}^{{20}}}$ –1.5 $75500$
15 NO + N2 = N + O + N2 $3.900 \times {{10}^{{20}}}$ –1.5 $75500$
Реакции Зельдовича
16 NO + O = O2 + N $3.200 \times {{10}^{9}}$ 1 $19700$
17 N2 + O = NO + N $7.000 \times {{10}^{{13}}}$ 0.0 $38000$
Ионные реакции
18 O + ${\text{O}}_{2}^{ + }$ = O2 + O+ $2.920 \times {{10}^{{18}}}$ –1.1 $28000$
19 N2 + N+= N$_{2}^{ + }$ + N $2.020 \times {{10}^{{11}}}$ 0.81 $13000$
20 O + NO+= NO + O+ $3.630 \times {{10}^{{15}}}$ –0.6 $50800$
21 N2 + O+= N$_{2}^{ + }$+O $3.400 \times {{10}^{{19}}}$ –2.0 $23000$
22 O2 + NO+ = NO + O$_{2}^{ + }$ $1.800 \times {{10}^{{15}}}$ 0.17 $33000$
23 N + NO+= NO + N+ $1.000 \times {{10}^{{19}}}$ –0.93 $61000$
Реакции ассоциативной ионизации
24 N + O = NO+ + e– $1.400 \times {{10}^{6}}$ 1.5 $31900$
25 O + O = O$_{2}^{ + }$ + e– $1.600 \times {{10}^{{17}}}$ –0.98 $80800$
26 N + N = N + e– $1.400 \times {{10}^{{13}}}$ 0.0 $67800$
Реакции ионизации электронным ударом
27 O + e–= O++ e– + e– $3.600 \times {{10}^{{31}}}$ –2.91 $158000$
28 N + e–= N++ e– + e– $1.100 \times {{10}^{{32}}}$ –3.14 $169000$
Реакции ионизации ударом тяжелых частиц
29 O2 + N2 = NO + NO+ + e– $1.380 \times {{10}^{{20}}}$ –1.84 $141000$
30 NO + N2 = N2 + NO+ + e– $2.200 \times {{10}^{{15}}}$ –0.35 $108000$
Ионно-молекулярные реакции
31 O + NO+= O2 + N+ $1.340 \times {{10}^{{13}}}$ 0.31 $77270$
32 O2 + NO = NO+ + O2 + e– $8.800 \times {{10}^{{16}}}$ –0.35 $108000$

1.4. Граничные условия

Постановка граничных условий соответствует условиям экспериментов по теплообмену в плазмотроне ВГУ-4 ИПМех РАН, включая испытания [14], используемые ниже для валидационных расчетов.

Рассматривается обтекание цилиндрической водоохлаждаемой модели потоком низкотемпературной плазмы, создаваемой в разрядном канале плазмотрона при помощи высокочастотного газового разряда. Из канала плазма поступает в барокамеру через круглое отверстие диаметром ${{D}_{{in}}}$. На переднем торце модели, находящемся на расстоянии ${{z}_{m}} = 60$ мм от входного отверстия, закреплен круглый датчик теплового потока диаметром Ds, внешняя поверхность которого выполнена из испытываемого материала. В экспериментах [14] передняя кромка модели имела скругление (т.н. евромодель), которое не учитывалось в настоящих численных расчетах.

На входном участке нижней границы расчетной области, $0 \leqslant r \leqslant {{R}_{{in}}} = {{D}_{{in}}}{\text{/}}2$, z = 0, задается поток плазмы с известными радиальными распределениями продольной скорости ${{{v}}_{{in}}}(r)$ и температуры ${{T}_{{in}}}(r)$, рассчитанными программой Alpha (см. [14]) для заданного массового расхода газа Q, статического давления Ps и мощности ${{N}_{{ap}}}$ ВЧ-генератора (считается, что вкладываемая в плазму мощность составляет 60% от этой величины). Радиальная компонента скорости на входе принималась нулевой, ${{u}_{{in}}}(r) = 0$. Химический состав плазмы ${{x}_{{i,in}}}(r)$ во входном сечении считается равновесным и соответствующим статическому давлению в барокамере Ps и локальной температуре плазмы ${{T}_{{in}}}(r)$.

Граничные условия на выходной границе задаются методом характеристик, обеспечивая свободный выход потока с постоянным давлением на бесконечности [29]. При возникновении обратных токов, направленных внутрь расчетной области, втекающий газ соответствует равновесному воздуху при температуре T = 300 K.

На боковой ($r = {{R}_{b}} = {{D}_{b}}{\text{/}}2$) и нижней (вне входного отверстия, ${{R}_{{in}}} < r \leqslant {{R}_{b}}$) границах расчетной области, соответствующих твердым границам барокамеры, ставятся граничные условия прилипания $u = {v} = 0$ и задается постоянная температура ${{T}_{b}}$. Стенки барокамеры считаются химически нейтральными, поэтому для всех компонент смеси на них задаются нулевые диффузионные потоки.

На поверхности водоохлаждаемой модели температура считается заданной и равной ${{T}_{w}}$, для скорости выполняются условия прилипания ${{u}_{w}} = {{{v}}_{w}} = 0$. Поверхность считается каталитической, выполненной из двух разных материалов: на плоском переднем торце модели центральную часть занимает круглый датчик теплового потока диаметром ${{D}_{s}}$, поверхность которого характеризуется эффективным коэффициентом каталитической рекомбинации ${{\gamma }_{w}}$, вне датчика поверхность характеризуется эффективным коэффициентом ${{\gamma }_{{w0}}} = 1$ (что соответствует медной охлаждаемой поверхности модели, используемой в экспериментах [14]).

Боковая поверхность модели, с целью упрощения вычислений, считается суперкаталитической, химический состав газа на ней постоянен и соответствует недиссоциированному воздуху (тепловые потоки к такой стенке приблизительно на 10% больше, чем потоки к полностью каталитической стенке).

Таким образом, эффективный коэффициент каталитической рекомбинации ${{\gamma }_{w}}$ терпит разрыв на торце модели при $r = {{R}_{s}} = {{D}_{s}}{\text{/}}2$. Отметим, что в экспериментах и расчетах [14] определялся эффективный коэффициент каталитической рекомбинации ${{\gamma }_{w}}$, который принимался одинаковым для атомов кислорода и азота. Такой же подход использован и в настоящих расчетах.

Постановка граничных условий на каталитических поверхностях осуществляется следующим образом. Диффузионная скорость атомов i-го типа (кислород, азот), участвующих в каталитических реакциях ${\text{O}} + {\text{O}} \to {{{\text{O}}}_{2}}$ и ${\text{N}} + {\text{N}} \to {{{\text{N}}}_{2}}$ на стенке, определяются как

(1.15)
$V_{i}^{w} = \frac{{2{{\gamma }_{w}}}}{{2 - {{\gamma }_{w}}}}\sqrt {\frac{{{{R}^{0}}{{T}_{w}}}}{{2\pi {{\mu }_{i}}}}} $

Диффузионные скорости молекулярных компонент, направленные от стенки, находятся из равенства нулю суммарного мольного потока каждого элемента: $x_{{{{{\text{O}}}_{2}}}}^{w}V_{{{{{\text{O}}}_{2}}}}^{w} = - \tfrac{1}{2}x_{{\text{O}}}^{w}V_{{\text{O}}}^{w}$, $x_{{{{{\text{N}}}_{2}}}}^{w}V_{{{{{\text{N}}}_{2}}}}^{w} = - \tfrac{1}{2}x_{{\text{N}}}^{w}V_{{\text{N}}}^{w}$ (знак плюс означает направление диффузионного потока компоненты к стенке, минус – от стенки). Для остальных компонент, не участвующих в гетерогенных реакциях, диффузионная скорость на стенке равна нулю.

Химический состав газа на стенке можно найти, подставляя выражения для диффузионных скоростей $V_{i}^{w}$ в уравнения Стефана–Максвелла, при этом считается, что газ на стенке не ионизованный (отсутствуют ионы и электроны). Тогда задача сводится к решению системы уравнений (1.6) в следующем виде

(1.16)
${{\left. { - \frac{{\partial {{x}_{i}}}}{{\partial \xi }}} \right|}_{w}} = \sum\limits_{j = 1}^{{{N}_{p}}} {\frac{{x_{i}^{w}x_{j}^{w}(V_{j}^{w} - V_{i}^{w})}}{{{{D}_{{ij}}}}}} $
где $\xi $ – координата, отсчитываемая вдоль нормали к поверхности, направленной от границы в газовый поток. Производная по нормали от мольной концентрации, стоящая в левой части (1.16), находится путем аппроксимации по схеме заданного порядка точности (например, схема первого порядка точности имеет вид ${{\left. {\partial {{x}_{i}}{\text{/}}\partial \xi } \right|}_{w}} \approx {{(x_{i}^{f} - x_{i}^{w})} \mathord{\left/ {\vphantom {{(x_{i}^{f} - x_{i}^{w})} \delta }} \right. \kern-0em} \delta }$, где $x_{i}^{f}$ – мольная доля i-й компоненты в потоке на расстоянии $\delta $ от стенки). В отличие от решения системы Стефана–Максвелла (1.6) здесь диффузионные скорости считаются известными из (1.15), а мольные доли на поверхности находятся как решение системы нелинейных уравнений (1.16), квадратичной по искомым переменным.

После вычисления $x_{i}^{w}$ можно определить массовые доли $y_{i}^{w}$ на стенке, из (1.4) найти плотность ${{\rho }_{w}}$, затем вычислить теплопроводность ${{\lambda }_{w}}$ и найти по (1.10) полный тепловой поток на стенке qw, включая его кондуктивную $q_{w}^{C}$ и рекомбинационную $q_{w}^{R}$ составляющие. В скалярной записи тепловой поток имеет вид

(1.17)
${{q}_{w}} = q_{w}^{C} + q_{w}^{R} = {{\lambda }_{w}}{{\left. {\frac{{\partial T}}{{\partial \xi }}} \right|}_{w}} + {{\rho }_{w}}\sum\limits_{i = 1}^{{{N}_{p}}} {y_{i}^{w}{{h}_{i}}\left( {{{T}_{w}}} \right)V_{i}^{w}} $

Здесь положительный знак теплового потока означает передачу тепла от газа к поверхности (напомним, что координата $\xi $ отсчитывается вдоль нормали от поверхности тела в область газового потока).

2. ЧИСЛЕННАЯ РЕАЛИЗАЦИЯ

Аппроксимация системы уравнений (1.1)–(1.3) осуществляется на декартовой сетке с переменным шагом по каждому направлению, задаваемым по закону геометрической прогрессии со знаменателем ∼0.9. Сетка строится так, что границы цилиндрического образца, датчика теплового потока и входного отверстия точно совпадают с одной из сеточных линий, что позволяет поставить граничные условия, не рассматривая пересечения границ разного типа.

Для конвективных потоков использована схема HR-SLAU [30, 31], принадлежащая семейству AUSM+ [32, 33], в котором используется масштабирование стабилизирующих членов в потоках импульса по локальному числу Маха. Это позволяет избежать внесения чрезмерной схемной вязкости при переходе от сверхзвуковых течений к существенно дозвуковым, что делает схему пригодной для расчета течений с произвольными числами Маха. Достоинство схемы HR-SLAU2 [30, 31] состоит в отсутствии необходимости задавать некоторое характерное число Маха, выбор которого может влиять на результаты и быть неочевидным для многих течений.

Аппроксимация тензора вязких напряжений (1.5) осуществлялась по стандартной центрально-разностной схеме второго порядка точности, градиенты температуры и концентраций на границах ячеек аппроксимировались по двухточечной схеме. В пристеночных ячейках градиенты температуры и скорости на стенке аппроксимировались без использования фиктивных ячеек, как разность граничного значения и значения в центре ячейки, деленная на половину размера ячейки.

Для получения стационарного решения уравнений (1.1)–(1.3) использовался метод установления, состоящий в интегрировании по псевдовремени до достижения сходимости с заданной точностью. Для повышения эффективности расчета реализована неявная схема интегрирования, состоящая в линеаризации уравнений и решении возникающей системы линейных алгебраических уравнений методом Гаусса–Зейделя с приближенной факторизацией матрицы коэффициентов на нижнюю и верхнюю треугольные матрицы для ее эффективного обращения (LU-SGS). Для обеспечения высокой эффективности метода вычисление якобианов потоков производится приближенно, путем замены их диагональными матрицами, элементы которых представляют собой сумму максимальных собственных числа “невязких” и “вязких” потоков [34]. В результате удается полностью исключить матричные операции, обеспечив абсолютную устойчивость линейного этапа решения уравнений и возможность проведения расчетов с числом Куранта порядка 102–104 [30, 35].

Важную роль для обеспечения устойчивости схемы играет неявная аппроксимация источниковых членов (1.14) в уравнениях неразрывности компонент (1.1). Как показано в [36], для устойчивой аппроксимации скоростей реакции ${{\dot {\omega }}_{i}}$ достаточно использовать лишь диагональные элементы якобиана, представив источниковый член в линеаризованном виде как $\dot {\omega }_{i}^{{(n + 1)}} = \dot {\omega }_{i}^{{(n)}} + {{\left( {\partial {{{\dot {\omega }}}_{i}}{\text{/}}\partial {{q}_{i}}} \right)}^{{(n)}}}\Delta {{q}_{i}}$. Здесь верхний индекс означает номер итерации, ${{q}_{i}} = \rho {{y}_{i}}$, $\Delta {{q}_{i}} = q_{i}^{{(n + 1)}} - q_{i}^{{(n)}}$, причем частные производные скорости i-й реакции по qi практически всегда неотрицательны (за исключением автокаталитических реакций, отсутствующих в используемой здесь кинетической схеме). Таким образом, неявная аппроксимация скоростей реакций сводится к добавлению неотрицательной величины $ - {{\left( {\partial {{{\dot {\omega }}}_{i}}{\text{/}}\partial {{q}_{i}}} \right)}^{{(n)}}}$ к диагональному элементу матрицы коэффициентов при $\Delta {{q}_{i}}$, что обеспечивает устойчивость решения даже с большим шагом по времени.

Отметим, что описанная процедура численного решения стационарных уравнений может быть также использована в качестве метода получения решения на одном шаге по физическому времени при решении истинно нестационарных задач методом двойных шагов по времени [29]. В этом случае более точное решение может быть получено методом расщепления по времени с выделением в отдельный подшаг решения системы обыкновенных дифференциальных уравнений химической кинетики, для которых применяется метод интегрирования жестких систем обыкновенных дифференциальных уравнений. Эта возможность реализована в разработанной программе с применением известного метода VODE [37].

Вычислительная модель реализована в программе IPG2D на языке программирования FORTRAN-95. Верификация кода осуществлялась решением ряда тестовых задач газовой динамики и вязких течений (распад газодинамического разрыва, сверхзвуковое обтекание прямоугольного выступа в канале), подтвердивших возможность проведения расчетов в широком диапазоне чисел Маха единым вычислительным модулем. Результаты валидации модуля расчета неравновесной химической кинетики представлены в работе [38].

3. ГЕОМЕТРИЯ И ПАРАМЕТРЫ РАСЧЕТОВ

В работе [14] на плазмотроне ВГУ-4 ИПМех РАН в потоках диссоциированного воздуха получены экспериментальные данные по тепловым потокам на водоохлаждаемых датчиках с тепловоспринимающими поверхностями из семи металлов (меди, серебра, тантала, бериллия, ниобия, золота, молибдена). В этой же работе на основе известной методики ИПМех РАН [7, 8] были определены эффективные коэффициенты каталитической рекомбинации ${{\gamma }_{w}}$.

В настоящей работе проведено численное моделирование осесимметричного обтекания цилиндрической модели с плоским носком неравновесной воздушной плазмой для четырех режимов работы плазмотрона ВГУ-4, представленных в табл. 2. При этом расчеты проведены для перечисленных выше семи металлических поверхностей датчиков, используя полученные в [14] значения ${{\gamma }_{w}}$. В табл. 2 также приведены экспериментальные значения теплового потока $q_{w}^{{\exp }}$ [14], остальные колонки табл. 2 содержат рассчитанные значения тепловых потоков, которые анализируются ниже.

Таблица 2
№ Ps, гПа ${{N}_{{ap}}}$, кВт Материал γw $q_{w}^{{\exp }}$, Вт/см2 $q_{w}^{{\max }}$, Вт/см2 $q_{w}^{{{\text{av}}}}$, Вт/см2 χ, % εmax, % εav, %
1 50 45 Ag 1.0 158.96 153.72 152.34 0.9 –3.3 –4.2
2 Cu 0.52 158.54 153.20 151.58 1.1 –3.4 –4.4
3 Nb $8.0 \times {{10}^{{ - 3}}}$ 109.95 106.85 103.14 3.6 –2.8 –6.2
4 Au $7.6 \times {{10}^{{ - 3}}}$ 108.74 105.82 102.14 3.6 –2.7 –6.1
5 Ta $4.5 \times {{10}^{{ - 3}}}$ 94.76 96.82 93.22 3.9 2.2 –1.6
6 Be $4.4 \times {{10}^{{ - 3}}}$ 94.46 96.49 92.89 3.9 2.1 –1.7
7 Mo $2.2 \times {{10}^{{ - 3}}}$ 80.72 88.37 84.97 4.0 9.5 5.3
8 64 Ag 1.0 221.00 203.84 203.22 0.3 –7.8 –8.0
9 Cu 0.47 220.05 202.76 201.79 0.5 –7.9 –8.3
10 Nb $1.0 \times {{10}^{{ - 2}}}$ 153.94 142.27 137.81 3.2 –7.6 –10.5
11 Au $9.4 \times {{10}^{{ - 3}}}$ 149.75 140.46 136.02 3.3 –6.2 –9.2
12 Ta $6.1 \times {{10}^{{ - 3}}}$ 131.83 128.91 124.75 3.3 –2.2 –5.4
13 Be $5.0 \times {{10}^{{ - 3}}}$ 125.40 124.36 120.34 3.3 –0.8 –4.0
14 Mo $2.6 \times {{10}^{{ - 3}}}$ 104.68 112.85 109.27 3.3 7.8 4.4
15 100 45 Ag 0.11 145.74 154.13 150.98 2.1 5.8 3.6
16 Cu 1.0 147.37 156.60 154.16 1.6 6.3 4.6
17 Nb $4.1 \times {{10}^{{ - 3}}}$ 121.40 117.36 112.28 4.5 –3.3 –7.5
18 Au $3.0 \times {{10}^{{ - 3}}}$ 118.63 113.32 108.28 4.6 –4.5 –8.7
19 Ta 0 106.65 98.42 93.67 5.1 –7.7 –12.2
20 Be 0 105.45 98.39 93.67 5.0 –6.7 –11.2
21 Mo 0 99.70 98.38 93.67 5.0 –1.3 –6.0
22 64 Ag 0.17 217.15 209.78 206.47 1.6 –3.4 –4.9
23 Cu 1.0 218.95 212.16 209.54 1.3 –3.1 –4.3
24 Nb $6.8 \times {{10}^{{ - 3}}}$ 179.01 162.42 155.715 4.3 –9.3 –13.0
25 Au $4.8 \times {{10}^{{ - 3}}}$ 171.35 154.63 147.86 4.6 –9.8 –13.7
26 Ta $1.9 \times {{10}^{{ - 4}}}$ 143.19 126.18 120.19 5.0 –11.9 –16.1
27 Be $5.1 \times {{10}^{{ - 5}}}$ 142.06 124.96 119.03 5.0 –12.0 –16.2
28 Mo 0 133.61 124.49 118.58 5.0 –6.8 –11.2

Расчеты проведены для геометрических характеристик, соответствующих экспериментам [14]. Диаметр барокамеры составлял ${{D}_{b}} = 800$ мм, в продольном направлении расчетная область занимала длину ${{H}_{b}} = 200$ мм. Воздушная плазма вытекала из разрядного канала диаметром ${{D}_{{in}}} = 80$ мм, цилиндрическая модель имела диаметр ${{D}_{m}} = 50$ мм (в экспериментах использовалась евромодель, имеющая радиус скругления кромки 11.5 мм, это скругление не учитывалось в расчетах). Расстояние от источника плазмы до модели составляло ${{H}_{m}} = 60$ мм, датчик теплового потока имел диаметр ${{D}_{s}} = 13.8$ мм.

Параметры плазмы во входном сечении рассчитывались по равновесной модели на основе программы Alpha [14], при этом массовый расход воздуха соответствовал экспериментальному значению Q = 2.4 г/с. На рис. 1 показаны радиальные распределения температуры, скорости и мольной доли отдельных компонент на выходе из разрядного канала при четырех режимах работы плазмотрона, представленных в табл. 2, эти распределения использовались в качестве граничных условий на входной границе при расчете программой IPG2D.

Рис. 1.

Радиальные распределения во входном сечении источника, расчет программой Alpha [14]: (а) – температура; (б) – входная скорость; (в) – мольные доли компонент для ${{P}_{s}} = 50$ гПа, ${{N}_{{ap}}} = 64$ кВт.

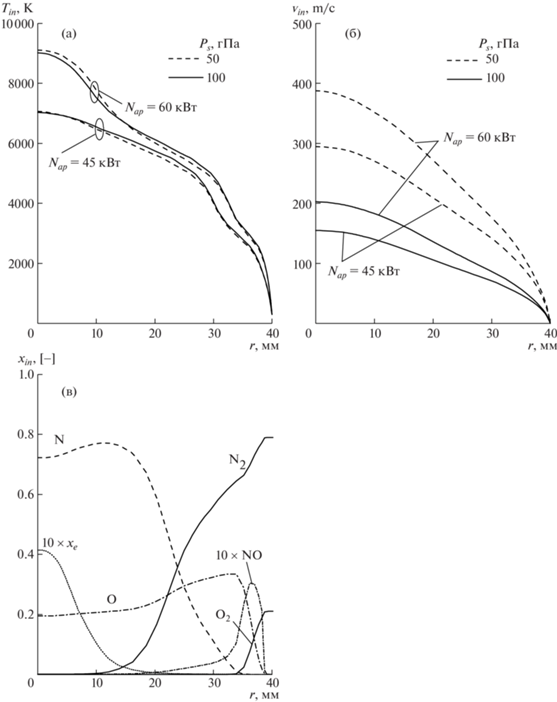
Температура поверхности водоохлаждаемой модели и датчика теплового потока составляла ${{T}_{w}} = 300$ K, температура стенок барокамеры считалась равной ${{T}_{b}} = 300$ K. Эффективный коэффициент каталитической рекомбинации ${{\gamma }_{w}}$ на тепловоспринимающей поверхности датчика в каждом расчете задавался в соответствии с табл. 2, на остальной поверхности медной водоохлаждаемой модели он был постоянным и равным ${{\gamma }_{{w0}}} = 1$.

Расчеты проводились в прямоугольной области размером 400 × 200 мм на неравномерных расчетных сетках, содержащих 136 × 156 ячеек. Сетка сгущалась в радиальном направлении к границе датчика теплового потока (минимальный радиальный размер ячейки у границы $r = {{R}_{s}}$ составлял 10–4 м), к границе входного отверстия $r = {{R}_{{in}}}$ ($1.6 \times {{10}^{{ - 4}}}$ м) и к боковой поверхности образца $r = {{R}_{m}}$ ($2.5 \times {{10}^{{ - 4}}}$ м). В осевом направлении сетка сгущалась к переднему торцу образца, минимальный размер ячейки у поверхности составлял $5 \times {{10}^{{ - 5}}}$ м. Типичное число Куранта в расчетах составляло 2000.

4. РЕЗУЛЬТАТЫ

4.1. Обтекание образца

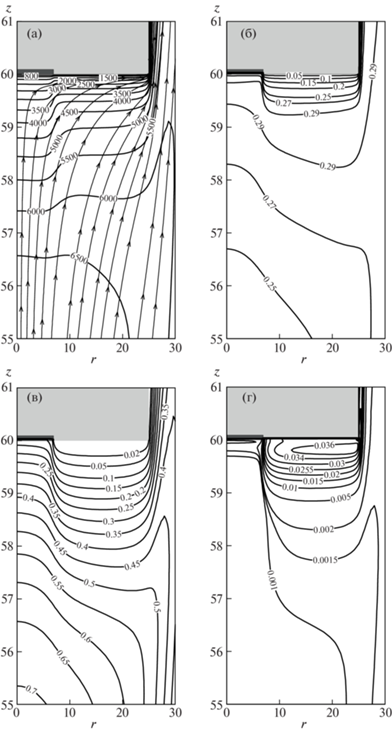
Рассмотрим сначала общую картину обтекания образца, используя в качестве примера вариант 24 из табл. 2, соответствующий датчику теплового потока, выполненному из ниобия, давление в барокамере 100 гПа, мощность ВЧ-генератора ${{N}_{{ap}}} = 64$ кВт.

На рис. 2а–г приведены поля температуры $T$ и линии тока, мольные доли атомарного кислорода xO, атомарного азота xN и окиси азота xNO, демонстрирующие натекание струи плазмы на модель, растекание вдоль лобовой поверхности, дальнейшее течение вдоль цилиндрической образующей модели. Хорошо видна более быстрая рекомбинация атомов азота по сравнению с атомами кислорода. Окись азота образуется в основном на внешней границе струи плазмы, а также в погранслое вблизи холодной поверхности тела.

Рис. 2.

Обтекание образца потоком плазмы: (а) – температура и линии тока; (б) – мольная доля O; (в) мольная доля N; (г) – мольная доля NO.

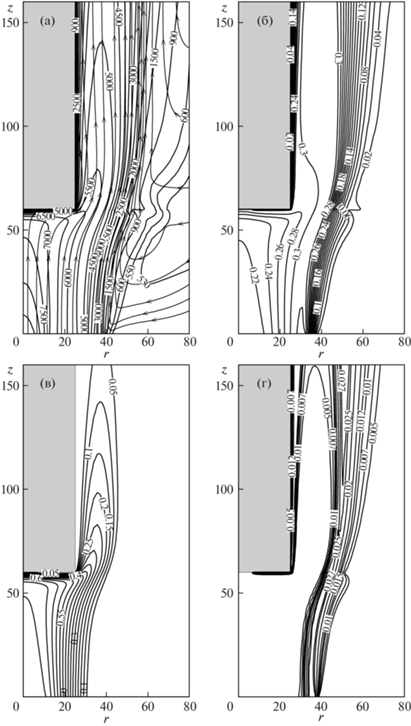
Наиболее значительные проявления неравновесных физико-химических процессов в плазме происходят вблизи поверхности модели и датчика теплового потока, как вследствие резкого охлаждения газа, так и вследствие влияния гетерогенных каталитических реакций. Эти процессы протекают в тонком погранслое на поверхности модели, причем наибольший интерес представляют распределения концентраций и температуры вдоль переднего торца.

На рис. 3а–г укрупненно показаны распределения температуры и мольных долей О, О2 и NO вблизи передней поверхности модели, при этом для ясности масштаб по осевой координате выбран значительно большим, чем по радиальной. Видна сильная неравномерность концентраций, обусловленная большой разницей в каталитических свойствах материала датчика (в пределах до радиуса ${{R}_{s}} = 6.9$ мм) и медной поверхности модели.

Рис. 3.

Характеристики плазмы вблизи переднего торца модели (укрупненный масштаб по оси $z$): (а) температура и линии тока; (б) мольная доля O; (в) мольная доля N; (г) мольная доля NO. На поверхности модели обозначено положение датчика теплового потока.

4.2. Тепловой поток на поверхности образца

Рассмотрим теперь рассчитанные тепловые потоки на поверхности медной модели и датчиков, использованных в экспериментах. На рис. 4а,б построены радиальные распределения теплового потока ${{q}_{w}}(r)$ для двух режимов работы плазмотрона, соответствующих мощности ${{N}_{{ap}}} = 64$ кВт и давлениям в барокамере ${{P}_{s}} = 50$ гПа (варианты 8–14 из табл. 2) и 100 гПа (варианты 22–28). Область радиусом ${{R}_{s}}$ соответствует тепловоспринимающей поверхности датчика теплового потока из соответствующего металла, граница c поверхностью медной модели обозначена вертикальной штриховой линией. На обоих графиках выделяются гладкие кривые (Ag для 50 гПа и Cu для 100 гПа), соответствующие постоянному значению ${{\gamma }_{w}} = 1$ вдоль всей поверхности, они соответствуют обтекаемому телу с однородной высококаталитичной поверхностью (референсный случай).

Рис. 4.

Распределения теплового потока по переднему торцу модели при ${{N}_{{ap}}} = 64$ кВт: (а) – давление 50 гПа; (б) – 100 гПа.

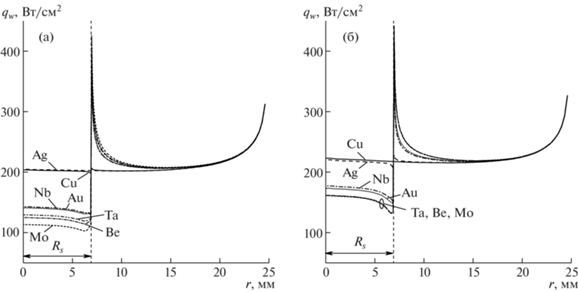
Распределения тепловых потоков, представленные на рис. 4, показывают, что для низкокаталитичных образцов тепловой поток ${{q}_{w}}$ терпит разрыв в точке ${{R}_{s}}$ (на границе раздела материалов поверхности), при этом со стороны испытываемого материала тепловой поток уменьшается к границе, а при переходе к высококаталитичной поверхности – резко возрастает, при этом значительно превышая референсный поток для однородной высококаталитичной поверхности. Данный эффект, известный как сверхравновесный нагрев [16–18], требует внимания при создании теплозащитных покрытий, поскольку его результатом является интенсивный локальный разогрев высококаталитичных участков поверхности на границе с низкокаталитичными. Причиной резкого локального увеличения теплового потока является вынос атомарного кислорода и азота из пограничного слоя, примыкающего к низкокаталитичной поверхности, как за счет течения газа, так и за счет продольных диффузионных потоков.

Более детальный анализ сверхравновесного нагрева у границы раздела поверхностей приведен на рис. 5, где для режима ${{N}_{{ap}}} = 64$ кВт, ${{P}_{s}} = 100$ гПа (варианты 22–28) построены радиальные распределения кондуктивной (а) и рекомбинационной (б) составляющих теплового потока, см. (1.17). Можно выделить следующие особенности поведения тепловых потоков.

Рис. 5.

Кондуктивная (а) и рекомбинационная (б) составляющие теплового потока на переднем торце модели при различной каталитичности образца, ${{N}_{{ap}}} = 64$ кВт, ${{P}_{s}} = 100$ гПа.

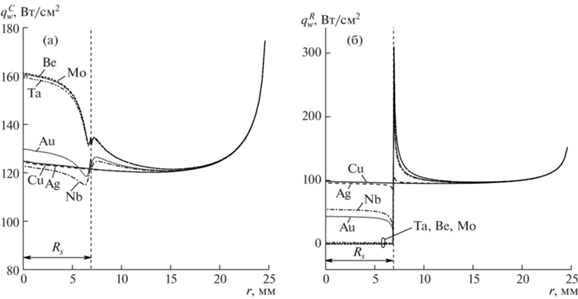
Для случая равномерной высококаталитичной поверхности ${{\gamma }_{w}} = 1$ (Cu) кондуктивная и рекомбинационная составляющие дают сравнимый вклад в суммарный тепловой поток (порядка 120 и 100 Вт/см2 соответственно). Понижение каталитичности образца до значения ${{\gamma }_{w}} = 0.17$ (Ag) практически не сказывается на $q_{w}^{C}$: в передней критической точке кондуктивный тепловой поток снижается со 124.7 до 124.2 Вт/см2. Рекомбинационный тепловой поток $q_{w}^{R}$ в передней критической точке снижается с 98.4 до 96.0 Вт/см2, при этом вблизи границы раздела он падает до 84.9 Вт/см2 со стороны образца, вырастая до 107.3 Вт/см2 со стороны медной модели (референсный поток $q_{w}^{R}$ на границе раздела поверхностей равен 95.8 Вт/см2).

При более сильном уменьшении каталитичности поверхности датчика обе компоненты теплового потока меняются более существенно. Так, в случае ниобиевого покрытия (${{\gamma }_{w}} = 6.8 \times {{10}^{{ - 3}}}$) $q_{w}^{C}$ в передней критической точке уменьшается до 122.7 Вт/см2, затем он падает по направлению к границе раздела до 115.0 Вт/см2, возрастая по другую сторону границы до 124.8 Вт/см2. Для золота (${{\gamma }_{w}} = 4.8 \times {{10}^{{ - 3}}}$) наблюдается рост кондуктивного теплового потока в передней критической точке по сравнению с референсным случаем до 129.8 Вт/см2, минимальное и максимальное значения $q_{w}^{C}$ вблизи границы раздела составляют 118.5 и 126.5 Вт/см2 соответственно. Более существенное возрастание $q_{w}^{C}$ отмечается для трех покрытий с наименьшей каталитичностью (тантал, бериллий, молибден): кондуктивные потоки для этих покрытий практически совпадают, достигая в передней критической точке 159.3–161.0 Вт/см2, вблизи границы раздела имеется слабая немонотонность, однако по всей поверхности кондуктивный тепловой поток превышает поток для референсного случая.

Значительно большее влияние каталитичность поверхности датчика оказывает на рекомбинационный тепловой поток $q_{w}^{R}$, см. рис. 5б. Этот поток, ожидаемо, уменьшается на поверхности материала с уменьшением ${{\gamma }_{w}}$: так, в передней критической точке рекомбинационная составляющая теплового потока составляет 54.5 (Nb), 43.5 (Au), 23.9 (Ta), 6.5 (Be) и 0 (Mo) Вт/см2. Вблизи границы раздела поверхностей тепловой поток $q_{w}^{R}$ достигает минимума со стороны низкокаталитичного покрытия, составляя 27.3 (Nb), 21.4 (Au), 11.1 (Ta), 3.9 (Be) и 0 (Mo) Вт/см2. Однако по другую сторону границы раздела наблюдается обратная зависимость: рекомбинационный тепловой поток $q_{w}^{R}$ резко возрастает за счет выделения тепла при рекомбинации атомов, поступающих со стороны низкокаталитичного участка поверхности, достигая в максимуме 233.3 (Nb), 250.4 (Au), 307.6 (Ta), 310.0 (Be) и 310.7(Mo) Вт/см2.

Таким образом, расчеты демонстрируют существенные различия в поведении тепловых потоков к поверхностям использованных датчиков из различных металлов. Следует отметить, что высокие значения тепловых потоков вследствие сверхравновесного нагрева реализуются локализованно (в расчетах острый максимум наблюдается в пределах одной сеточной ячейки с радиальным размером 0.1 мм), далее тепловой поток спадает на характерных размерах порядка 1–2 мм (см. рис. 4).

При определении каталитической активности материалов по результатам испытаний в ВЧ-плазмотронах важную роль играет вопрос о равномерности распределения теплового потока по поверхности датчика. Экспериментальная процедура, основанная на измерении теплоотвода от водоохлаждаемого датчика по нагреву протекающей через него воды, по сути, является методом определения среднего теплового потока $q_{w}^{{{\text{av}}}}$, связанного с локальным потоком qw соотношением

(4.1)
$q_{w}^{{{\text{av}}}} = \frac{1}{{\pi R_{s}^{2}}}2\pi \int\limits_0^{{{R}_{s}}} {{{q}_{w}}\left( r \right)rdr} $

С другой стороны, применяемый в [14] метод нахождения эффективного коэффициента каталитической рекомбинации γw путем решения одномерных уравнений для неравновесного пограничного слоя конечной толщины вдоль оси симметрии (программа Gamma) обеспечивает соответствие экспериментальному значению (4.1) теплового потока в передней критической точке при заданных параметрах на внешней границе пограничного слоя. Точность такого подхода можно оценить по результатам проведенных в настоящей работе двумерных расчетов.

Неравномерность потока по площади датчика можно охарактеризовать количественно, сравнивая средний поток $q_{w}^{{{\text{av}}}}$ с максимальным тепловым потоком $q_{w}^{{\max }}$, достигаемым в передней критической точке r = 0. Количественной мерой степени неравномерности теплового потока служит величина $\chi = {{(q_{w}^{{\max }} - q_{w}^{{{\text{av}}}})} \mathord{\left/ {\vphantom {{(q_{w}^{{\max }} - q_{w}^{{{\text{av}}}})} {q_{w}^{{{\text{av}}}}}}} \right. \kern-0em} {q_{w}^{{{\text{av}}}}}}$ (поскольку тепловой поток уменьшается к границе образца, эта величина положительна).

Рассчитанные значения максимального и среднего теплового потока приведены для каждого варианта в табл. 2, здесь же рассчитана степень неравномерности потока $\chi $ (в процентах). Видно, неравномерность теплового потока возрастает с уменьшением каталитической активности поверхности, т.е. с ростом скачка в каталитических свойствах между испытываемым образцом материала и медной моделью. Однако даже в предельном случае некаталитического материала степень неравномерности не превышает 5%. Это свидетельствует в пользу правомерности использования интегрального теплового потока, измеряемого в экспериментах, для характеристики локального аэродинамического нагрева тела. Приведенные в табл. 2 оценки степени неравномерности теплового потока могут быть учтены в дальнейшем для более точной интерпретации экспериментальных результатов и определения эффективного коэффициента каталитической рекомбинации γw.

Отметим, что приведенные выше результаты по неравномерности теплового потока вблизи скачка каталитической активности материала получены для случая постоянной температуры поверхности (водоохлаждаемая модель). Для неохлаждаемых моделей сверхравновесный нагрев будет приводить также к возникновению локальных областей с повышенной температурой. Для адекватного расчета температуры поверхности при этом требуется учет не только радиационных теплопотерь, но и теплопередачи в твердом теле, т.е. решение сопряженной задачи. Примером решения сопряженных задач тепломассобмена при аэродинамическом нагреве тел в высокоскоростных потоках служат работы [39, 40].

4.3. Сравнение с экспериментом

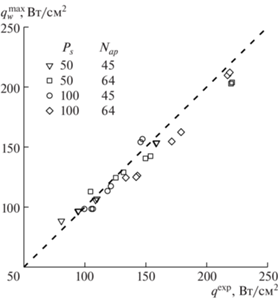
Для валидации разработанной вычислительной модели сравним полученные в расчетах для разных материалов и режимов работы плазмотрона тепловые потоки с экспериментальными данными (табл. 2). Следует отметить, что использованные в расчетах эффективные коэффициенты каталитической рекомбинации γw взяты из [14], где они находились при помощи одномерной вычислительной программы Gamma, осуществляющей расчет течения неравновесного диссоциированного воздуха вдоль оси симметрии от внешней границы пограничного слоя до передней критической точки. В настоящей работе аналогом соответствующего значения теплового потока является максимальный тепловой поток $q_{w}^{{{\text{max}}}}$, который и используется ниже для сравнения с экспериментом. Количественной мерой согласования рассчитанных и измеренных значений является относительное отклонение расчета от эксперимента ${{\varepsilon }^{{\max }}} = {{(q_{w}^{{\max }} - q_{w}^{{\exp }})} \mathord{\left/ {\vphantom {{(q_{w}^{{\max }} - q_{w}^{{\exp }})} {q_{w}^{{\exp }}}}} \right. \kern-0em} {q_{w}^{{\exp }}}}$. В то же время более адекватным по физическому смыслу является сопоставление с $q_{w}^{{\exp }}$ рассчитанного среднего теплового потока $q_{w}^{{{\text{av}}}}$, соответствующее относительное отклонение имеет вид ${{\varepsilon }^{{{\text{av}}}}} = {{(q_{w}^{{{\text{av}}}} - q_{w}^{{\exp }})} \mathord{\left/ {\vphantom {{(q_{w}^{{{\text{av}}}} - q_{w}^{{\exp }})} {q_{w}^{{\exp }}}}} \right. \kern-0em} {q_{w}^{{\exp }}}}$.

В табл. 2 для каждого варианта приведены значения относительных отклонений ${{\varepsilon }^{{\max }}}$ и ${{\varepsilon }^{{{\text{av}}}}}$. Среднеквадратичное значение для этих εmax составляет $\langle {{\varepsilon }^{{\max }}}\rangle = {{({{N}^{{ - 1}}}\sum\nolimits_{i = 1}^N {{{{(\varepsilon _{i}^{{\max }})}}^{2}}} )}^{{1/2}}} = 6.5\% $ (здесь N = 28 – число вариантов в табл. 2). Аналогично вычисленное среднеквадратичное значение для ${{\varepsilon }^{{{\text{av}}}}}$ составляет $\langle {{\varepsilon }^{{{\text{av}}}}}\rangle = 8.6\% $.

Для более наглядного представления полученных результатов на рис. 6 показано сопоставление данных на графике, где каждая точка отвечает одному из вариантов табл. 2. По оси абсцисс отложено экспериментальное значение теплового потока, по оси ординат – рассчитанное значение $q_{w}^{{{\text{max}}}}$. При таком представлении идеальное совпадение с экспериментом достигается на диагонали (штриховая прямая), тогда как разброс точек характеризует их случайное и систематическое отклонение.

Рис. 6.

Сравнение рассчитанных тепловых потоков с экспериментальными данными [14].

Из рис. 6 следует, что в целом достигнуто хорошее согласие результатов расчетов с данными экспериментальных измерений. Точки сконцентрированы вдоль штриховой прямой без видимого систематического отклонения. Для более высоких тепловых потоков (свыше 150 Вт/см2) точки идут ниже диагонали, что означает превышение измеренных тепловых потоков над рассчитанными. Эти отличия могут быть обусловлены влиянием обсуждавшейся выше неравномерности распределения теплового потока по поверхности датчика и вкладом излучения плазмы в теплообмен [21–23]. Кроме того, они могут свидетельствовать о необходимости корректировки рассчитанных значений эффективного коэффициента каталитической рекомбинации для соответствующих режимов работы ВЧ-плазмотрона.

ЗАКЛЮЧЕНИЕ

Представленные результаты валидационных расчетов теплообмена дозвуковых потоков воздушной плазмы с металлами, имеющими различную каталитическую активность по отношению к поверхностной рекомбинации атомов кислорода и азота, подтверждают, что разработанный компьютерный код IPG2D обеспечивает высокую точность предсказания тепловых потоков на каталитических поверхностях, обтекаемых потоком неравновесной плазмы. Среднеквадратичное отклонение рассчитанных тепловых потоков от экспериментальных данных составляет 6.5–8.6%.

Отличительной чертой настоящей вычислительной модели является учет химической неравновесности в дозвуковых потоках многокомпонентной плазмы воздуха. Это позволило изучить сверхравновесный нагрев на границе участков с различной каталитической активностью датчиков тепловых потоков и водоохлаждаемой модели, используемых в ИПМех РАН для исследований теплообмена. Кроме того, полученные в двумерных расчетах результаты позволили оценить неравномерность распределения теплового потока на поверхности датчика, которая не превышает 5%, что подтверждает правомерность используемой в ИПМех РАН методики определения эффективного коэффициента каталитической рекомбинации.

Проведение дальнейших экспериментальных исследований теплообмена на высокотемпературных материалах позволит расширить валидационную базу для кода IPG2D. В дальнейшем представленная вычислительная модель будет использована для расчета тепловых потоков к неохлаждаемым образцам и моделям, а также для определения каталитических характеристик новых материалов при высоких температурах поверхности.

Работа выполнена в рамках Госзадания № АААА-А20-120011690135-5 при частичной поддержке гранта РФФИ № 19-31-90114.

Список литературы

  1. Gordeev A.N., Kolesnikov A.F., Yakushin M.I. An induction plasma application to “Buran’s” heat protection tiles ground tests // SAMPE J. 1992. V. 28. № 3. P. 27–31.

  2. Конвективный теплообмен летательных аппаратов / Под ред. Землянского Б.А. М.: Физматлит, 2014, 377 с.

  3. Власов В.И., Залогин Г.Н., Землянский Б.А., Кнотько В.Б. Методика и результаты экспериментального определения каталитической активности материалов при высоких температурах // Изв. РАН. МЖГ. 2003. № 5. С. 178.

  4. Tanaka Y. Recent development of new inductively coupled thermal plasmas for materials processing // Adv. Phys. X. 2021. V. 6. № 1. P. 1867637.

  5. Massuti-Ballester B., Pidan S., Herdrich G., Fertig M. Recent catalysis measurements at IRS // Advances in Space Research. 2015. V. 56. Iss.4. P. 742.

  6. Massuti-Ballester B., Marynowski T., Herdrich G. New inductively heated plasma source IPG7 // Front. Appl. Plasma Technol. 2013. V. 6. P. 2–6.

  7. Васильевский С.А., Колесников А.Ф. Численное исследование течений и теплообмена в индукционной плазме высокочастотного плазмотрона. Энциклопедия низкотемпературной плазмы. Сер. Б. Т. VII-1. Математическое моделирование в низкотемпературной плазме. Ч. 2 / Под ред. Ю.П. Попова. М.: ЯНУС-К, 2008. С. 220–234.

  8. Васильевский С.А., Гордеев А.Н., Колесников А.Ф. Локальное моделирование аэродинамического нагрева поверхности затупленного тела в дозвуковых высокоэнтальпийных потоках воздуха: теория и эксперимент на ВЧ-плазмотроне // Изв. РАН. МЖГ. 2017. № 1. С. 160–167.

  9. Onda K., Tanaka Y., Akashi K., Nakano Y., Ishijima T., Uesugi Y., Sueyasu S., Watanabe S., Nakamura K. Numerical thermofluid simulation on tandem type of induction thermal plasmas with and without current modulation in a lower coil // J. Phys. D. Appl. Phys. 2020. V. 53. P. 165201.

  10. Сахаров В.И. Численное моделирование термически и химически неравновесных течений и теплообмена в недорасширенных струях индукционного плазмотрона // Изв. РАН. МЖГ. 2007. № 6. С. 157–168.

  11. Гордеев А.Н., Колесников А.Ф., Сахаров В.И. Экспериментальное и численное исследование теплообмена высокоэнтальпийных недорасширенных струй воздуха с цилиндрическими моделями // Изв. РАН. МЖГ. 2018. № 5. С. 125–133.

  12. Yu M., Takahashi Y., Kihara H., Abe K., Yamada K., Abe T. Numerical investigation of flow fields in inductively coupled plasma wind tunnels // Plasma Sci. Technol. 2014. V. 16. P. 930–940.

  13. Власов В.И., Залогин Г.Н., Ковалев Р.В. Численное моделирование течения различных плазмообразующих газов в тракте ВЧ-плазмотрона // Физико-химическая кинетика в газовой динамике. 2018. Т. 19. № 4. С. 2–23.

  14. Васильевский С.А., Гордеев А.Н., Колесников А.Ф., Чаплыгин А.В. Тепловой эффект поверхностного катализа в дозвуковых струях диссоциированного воздуха: эксперимент на ВЧ-плазмотроне и численное моделирование // Изв. РАН. МЖГ. 2020. № 5. С. 137–150.

  15. Баронец П.Н., Колесников А.Ф., Кубарев С.Н., Першин И.С., Труханов А.С., Якушин М.И. Сверхравновесный нагрев поверхности теплозащитной плитки в дозвуковой струе диссоциированного воздуха. // Изв. РАН. МЖГ. 1991. № 3. С. 144–150.

  16. Stewart D., Gokcen T., Sepka S., Leiser D., Resin M. Development of a catalytic coating for a Shuttle flight experiment // 10th AIAA/ASME Joint Thermophysics and Heat Transfer Conference. AIAA Paper. 2010. P. 4321.

  17. Chazot O., Panerai F., Muylaert J. M., Thoemel J. Catalysis phenomena determination in plasmatron facility for flight experiment design // 48th AIAA Aerospace Sciences Meeting Including the New Horizons Forum and Aerospace Exposition, AIAA Paper. 2010. P. 1248.

  18. Чаплыгин А.В. Экспериментальное исследование эффекта сверхравновесного нагрева поверхности в дозвуковой струе диссоциированного воздуха // Физико-химическая кинетика в газовой динамике. 2021. Т. 22. № 2. http://chemphys.edu.ru/issues/2021-22-2/articles/929/

  19. Термодинамические свойства индивидуальных веществ. Спр. изд. в 4-х т. / Под ред. Глушко В.П. М.: Наука, 1979.

  20. Колесников А.Ф. Соотношения Стефана–Максвелла для амбиполярной диффузии в двухтемпературной плазме с приложением к задаче об ионно-звуковой волне // Изв. РАН. МЖГ. 2015. № 1. С. 170–181.

  21. Суржиков С.Т., Шувалов М.П. Анализ радиационно-конвективного нагрева четырех типов спускаемых космических аппаратов // Физико-химическая кинетика в газовой динамике. 2014. Т. 15. № 4. http://chemphys.edu.ru/issues/2014-15-4/articles/237/

  22. Суржиков С.Т. Пространственная задача радиационной газовой динамики командного модуля Аполлон-4 при сверхорбитальном входе в атмосферу. // Изв. РАН. МЖГ. 2018. № 2. С. 149–160.

  23. Суржиков С.Т. Тепловое излучение газов и плазмы. М.: Изд-во МГТУ им. Н.Э. Баумана, 2004. 544 с.

  24. Андриатис А.В., Жлуктов С.А., Соколова И.А. Транспортные коэффициенты смеси воздуха химически неравновесного состава // Математическое моделирование. 1992. Т. 4, № 1. С. 44–64.

  25. Гиршфельдер Дж., Кертисс Ч., Берд Р. Молекулярная теория газов и жидкостей. Пер. с англ. М.: Изд-во Ин. лит., 1961. 929 с.

  26. Laricchiuta A., Bruno D., Capitelli M. High temperature Mars atmosphere. Part I: Transport cross sections // The European Physical Journal D. 2009. V. 54. P. 607–612.

  27. Dunn M.G., Kang S.W. Theoretical and Experimental Studies of Reentry Plasmas. NASA Contract. Reports., NASA CR-2232, 1973.

  28. Суржиков С.Т. Компьютерная аэрофизика спускаемых космических аппаратов. Двухмерные модели. 2018. М.: Физматлит. 543 с.

  29. Blazek J. Computational Fluid Dynamics: Principles and Applications. 3rd ed. Amsterdam, London, New York, Oxford, Paris, Shannon, Tokyo: Elsevier, 2015.

  30. Kitamura K., Hashimoto A. Reduced dissipation AUSM-family fluxes: HR-SLAU2 and HR-AUSM+-up for high resolution unsteady flow simulations // Comput. Fluids. 2016. V. 126. P. 41–57.

  31. Kitamura K., Shima E., Fujimoto K., Wang Z.J. Performance of low-dissipation Euler fluxes and preconditioned LU-SGS at low speeds // Commun. Comput. Phys. 2011. V. 10. P. 90–119.

  32. Liou M.S. A sequel to AUSM, Part II: AUSM+-up for all speeds // J. Comput. Phys. 2006. V. 214. P. 137–170.

  33. Liou M.S. The evolution of AUSM schemes // Def. Sci. J. 2010. V. 60. P. 606–613.

  34. Jameson A., Turkel E. Implicit schemes and LU decompositions // Math. Comput. 1981. V. 37. P. 385–397.

  35. Борисов В.Е., Давыдов А.А., Кудряшов И.Ю. Параллельная реализация неявной схемы на основе метода LU-SGS для моделирования трехмерных турбулентных течений // Математическое моделирование. 2014. Т. 26. № 10. С. 64–78.

  36. Peles O., Turkel E. Acceleration methods for multi-physics compressible flow // J. Comput. Phys. 2018. V. 358. P. 201–234.

  37. Brown P.N., Byrne G.D., Hindmarsh A.C. VODE: A variable-coefficient ODE solver // SIAM J. Sci. Stat. Comput. 1989. V. 10. P. 1038–1051.

  38. Брызгалов А.И. Численное моделирование течения термически и химически неравновесного воздуха за фронтом ударной волны // Вестник МГТУ им. Баумана. 2021. Т. 96. № 3. С. 94–111.

  39. Зинченко В.И., Гольдин В.Д., Зверев В.Г. Численное моделирование влияния материалов тепловой защиты на характеристики сопряженного тепломассообмена при пространственном обтекании затупленных тел // Теплофизика высоких температур. 2018. Т. 56. № 5. С. 747–755.

  40. Зинченко В.И., Гольдин В.Д. Решение задачи о сопряженном нестационарном теплообмене при сверхзвуковом обтекании затупленного по сфере конуса под углом атаки // Инженерно-физический журнал. 2020. Т. 93. № 2. С. 431–442.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Известия РАН. Механика жидкости и газа

Архивы выпусков Информация о журнале Отправить рукопись в журнал