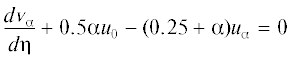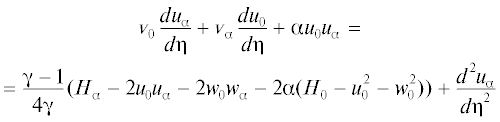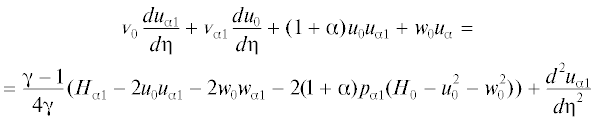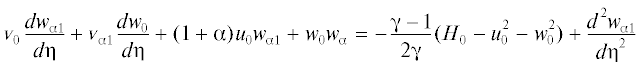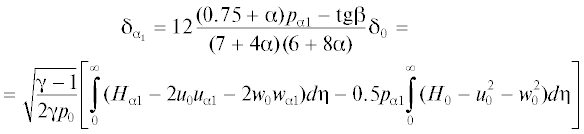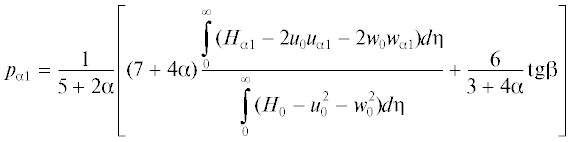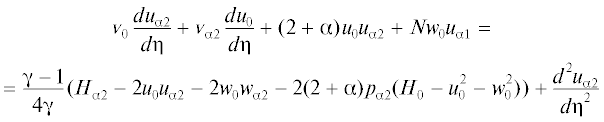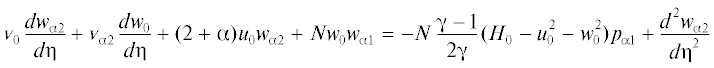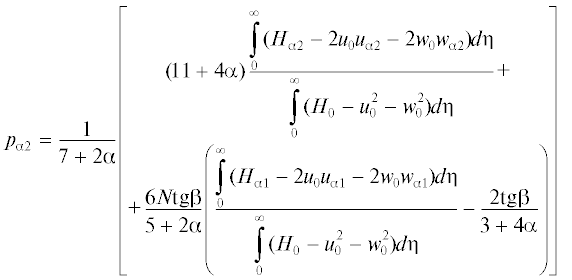1. На главную
  2. Электронные версии
  3. Известия РАН. Механика жидкости и газа
  4. № 3, 2022

Известия РАН. Механика жидкости и газа, 2022, № 3, стр. 30-43

ИССЛЕДОВАНИЕ ВЛИЯНИЯ ВДУВА НА СКОЛЬЗЯЩЕЙ ПЛАСТИНЕ, С ИЗМЕНЯЮЩИМСЯ ПО РАЗМАХУ ДОННЫМ ДАВЛЕНИЕМ, НА РАСПРОСТРАНЕНИЕ ВОЗМУЩЕНИЙ НА РЕЖИМЕ СИЛЬНОГО ВЗАИМОДЕЙСТВИЯ

Г. Н. Дудин a, *

a Центральный аэрогидродинамический институт им. проф. Н.Е. Жуковского
Жуковский, Московская обл., Россия

* E-mail: gndudin@yandex.ru

Поступила в редакцию 06.10.2021
После доработки 20.11.2021
Принята к публикации 21.12.2021

Полный текст (PDF)

Аннотация

Для режима сильного вязко-невязкого взаимодействия рассмотрено течение в трехмерном пограничном слое на скользящей пластине конечной длины, по нормали к которой вдувается газ. Для исследования распространения возмущений против потока, в окрестности передней кромки пластины проведены четырехчленные разложения функций течения в ряды, в предположении, что на задней кромке пластины задается донное давление, величина которого зависит от поперечной координаты. Показано, что в эти разложения входит неопределенная функция, а также ее первая и вторая производные по поперечной координате. Сформулированы и численно решены соответствующие краевые задачи, найдены собственные числа. Показано, что при увеличении, как угла скольжения, так и интенсивности вдуваемого газа, существенно усиливается возможность передачи возмущений вверх против потока. Исследовано влияние определяющих параметров на характеристики течения в пространственном пограничном слое.

Ключевые слова: трехмерный пограничный слой, скользящая пластина, сильное взаимодействие, вдув, температурный фактор

На режиме сильного взаимодействия пограничного слоя с гиперзвуковым потоком автомодельное решение для течения около полубесконечной пластины было получено в [1, 2]. Однако исследования двумерных течений в пограничном слое на пластине, оканчивающейся донным срезом, показали, что в этом случае разложение функций течения в окрестности передней кромки не является единственным, а содержит некоторую константу [3–5]. При этом считалось, что давление на задней кромке пластины постоянно. Существование неединственности решения в окрестности передней кромки объясняет возможность распространения возмущений против потока на всю длину пластины [3]. Влияние определяющих параметров на значение собственного числа в случае двумерных течений достаточно подробно изучено в [6]. В [7, 8] исследовано течение в пограничном слое на пластине в случае, когда дополнительное условие на задней кромке зависит от поперечной координаты. Показано, что в этом случае разложения для давления, энтальпии, продольной и нормальной компонент скорости в ряды зависят от некоторой произвольной функции поперечной координаты. Краевые задачи для определения членов разложения для поперечной компоненты скорости отделяются от основных систем уравнений, так как показатель степени для первого члена разложения равен собственному числу плюс единица, а для второго – удвоенному собственному числу плюс единица. При этом поперечный компонент скорости оказывается пропорциональным производной от указанной выше произвольной функции по поперечной координате. Показано, что в этом случае происходит перестройка двумерного пограничного слоя в трехмерный, но, важно отметить, что образующееся поперечное течение не оказывает влияние на индуцированное давление, энтальпию, продольный и нормальный компоненты скорости.

Совершенно иная картина течения в пограничном слое реализуется при обтекании скользящей пластины конечной длины, когда течение изначально является трехмерным. Для полубесконечной скользящей пластины автомодельное решение впервые найдено в [9]. В [10] было показано, что решение задачи вблизи передней кромки скользящей пластины также может быть не единственным. Результаты исследования обтекания скользящей пластины, когда дополнительное условие на ее задней кромке не является постоянным, а изменяется по размаху, представлены в [11–13], где сформулированы и решены краевые задачи (максимально до трех членов разложения) и исследовано влияние угла скольжения на характеристики течения на пластине.

Еще одним способом изменять “эффективную форму” поверхности пластины, обтекаемой гиперзвуковым потоком вязкого газа, и влиять на распространение возмущений против потока является вдув газа по нормали к поверхности. В [14] рассмотрено течение вблизи верхней стороны клина, через поверхность которого по нормали к ней производится вдувание газа. Индуцированное давление определялось по формуле “касательного клина”. Построены автомодельные решения, как в общем случае, когда возникает невязкая область около поверхности тела (отсоединение пограничного слоя), так и при ее отсутствии. Подробно рассмотрен случай, когда параметр, характеризующий квадрат отношения характерных толщин образовавшегося отсоединенного невязкого течения к толщине вязкого слоя равен N = O(1), а значение функции тока на поверхности клина постоянно. Показано, что краевая задача, кроме автомодельного решения, имеет однопараметрическое семейство решений, если давление на задней кромке отличается от значения, соответствующего автомодельному. Результаты численных расчетов, проведенных для предельного случая N → ∞, показали, что существует одно собственное число α ≈ 0.23, т.е. влияние краевых условий на течение в области, лежащей выше по потоку, может быть очень сильным.

В [15, 16] неавтомодельные краевые задачи решались численно и поэтому разложение функций в ряды в окрестности передней кромки не проводилось. В [15] рассмотрено влияние величины донного давления на обтекание плоской поверхности клина гиперзвуковым потоком вязкого газа, в предположении, что поверхность пластины проницаема и по нормали к ней вдувается газ того же состава, что и в набегающем потоке. В [16] исследовано течение, возникающее при вдуве газа через проницаемую поверхность треугольной пластины, на режиме сильного взаимодействия. Установлено, что увеличение температуры обтекаемой поверхности, при заданной безразмерной величине скорости вдува, приводит как к количественному, так и качественному изменению характеристик течения в пограничном слое, особенно в окрестности линии симметрии треугольной пластины. В [17] исследовано двумерное обтекание пластины гиперзвуковым потоком при наличии массообмена, причем в отличие от [14], для описания течения в невязком ударном слое использовалась гиперзвуковая теория малых возмущений, как и в [5]. Показано, что увеличение скорости вдува приводит к существенному уменьшению собственных чисел, т.е. к усилению интенсивности передачи возмущений против потока. В [18] исследовано влияние вдува на поверхности пластины конечной длины в случае, когда на задней кромке задавалось донное давление, зависящее от поперечной координаты. В окрестности передней кромки построены разложения для функций течения. Показано, что краевые задачи для поперечной компоненты скорости отделяются от основных систем, так как их порядок разложения на единицу больше, чем собственное число. Выявлено сильное влияние скорости вдува на образование пространственного течения в пограничном слое в рассматриваемом случае и на значительное увеличение интенсивности распространения возмущений против потока. Показано, что влияние третьего члена разложения на функции течения увеличивается при усилении интенсивности вдува. Вышеизложенное показывает, что увеличение угла скольжения или интенсивности вдува газа по нормали к поверхности может приводить к уменьшению собственных чисел, а следовательно, и к усилению интенсивности распространения возмущений против потока.

В данной работе исследуется влияние распределенного вдува на течение в ламинарном пограничном слое на скользящей пластине, когда на ее задней кромке давление зависит от поперечной координаты. Рассматривается режим сильного вязко-невязкого взаимодействия. Проведено разложение функций течения в окрестности передней кромки, сформулированы и решены краевые задачи для четырех членов разложения. Определены собственные числа, которые характеризуют интенсивность передачи возмущений против потока. Установлено, что в третью и четвертую систему уравнений входят параметры, которые однозначно определяются из интегральных условий, полученных в результате разложений индуцированного давления и толщины вытеснения. Решение этих систем позволяет учесть влияние, соответственно, первой и второй производных от функции распределения давления на задней кромке пластины. Основное внимание уделено исследованию влияния интенсивности вдувания на изменения характеристик пространственного течения в пограничном слое на скользящей пластине и на распространение возмущений от задней кромки.

1. ПОСТАНОВКА ЗАДАЧИ

Рассматривается обтекание бесконечной по размаху пластины заданной длины L при наличии угла скольжения на режиме сильного вязко-невязкого взаимодействия, через поверхность температура, которой Tw − постоянна, производится распределенный вдув газа. Вдуваемый газ имеет тот же состав, что и в набегающем потоке. Газ считается совершенным с отношением удельных теплоемкостей γ = cp/${{c}_{{v}}}$ и коэффициентом вязкости, линейно зависящим от температуры µ0/µ∞ = c∞T0/T∞, где c∞ = const, а индекс ∞ обозначает параметры в невозмущенном потоке. Компоненты вектора скорости u0, ${{{v}}^{0}}$, w0 в трехмерном ламинарном пограничном слое направлены соответственно вдоль осей x0, y0, z0 декартовой системы координат, начало которой расположено на передней кромке пластины. Ось x0 направлена перпендикулярно передней кромки, а ось z0 – вдоль нее. Угол скольжения β – это угол между направлением невозмущенного потока и осью x0. Считается, что на задней кромке пластины при x0 = L задано распределение донного давления $p_{d}^{0}$(z0), которое зависит от поперечной координаты z0, причем характерный размер области изменения давления по поперечной координате порядка Lz. Отношение характерных линейных масштабов N = L/Lz. Считается, что для проекции числа Маха на нормаль к передней кромке выполняется условие Mn = M∞cosβ $ \gg $ 1. Рассматривается предельный случай, когда в невозмущенном потоке V∞ – скорость, ρ∞ – плотность и H∞ – энтальпия стремятся к постоянным значениям, а число Маха M∞ → ∞. В этом случае параметры: p∞ – давление, a∞ – скорость звука и T∞ – температура стремятся к нулю.

В соответствии с гиперзвуковой теорией малых возмущений [19] при Mn $ \gg $ 1 и характерной безразмерной толщиной ламинарного пограничного слоя δ = $\operatorname{Re} _{0}^{{ - 1/4}}$ $ \ll $ 1 при выполнении предположения о сильном взаимодействии Mnδ $ \gg $ 1 индуцированное давление, создаваемое толщиной вытеснения, имеет порядок p0 ∼ p∞$M_{n}^{2}$δ2, а плотностъ газа − ρ0 ∼ ρ∞δ2. Здесь Re0 = ρ∞V∞L/µ0 − число Рейнольдса, µ0 – динамический коэффициент вязкости при температуре торможения. При обтекании скользящей пластины характерный масштаб поперечного компонента скорости: w0 ∼ V∞sinβ. Заметим, что при отсутствии угла скольжения (β = 0) скорость поперечного течения будет определяться градиентом индуцированного давления по размаху пластины [7, 8].

Через проницаемую верхнюю поверхность пластины по нормали к ней производится непрерывный распределенный вдув газа с заданной скоростью ${v}_{w}^{0}$(x0, z0) = ${{{v}}^{0}}$(x0, z0, y0 = 0), по порядку величины, равной О(δ), что соответствует характерному нормальному компоненту скорости в пограничном слое при отсутствии массообмена. При этом предполагается, что интенсивность вдуваемого газа такова, что около этой поверхности область невязкого течения не образуется [14]. В результате около верхней стороны пластины гиперзвуковой поток обтекает “эффективное тело”, образованное с учетом влияния вязкости и вдува [14]. Для исследования распространения возмущений против потока в пограничном слое в данной работе скорость вдувания задается в следующем специальном виде:

(1.1)
${v}_{w}^{0}({{x}^{0}},{\text{ }}{{z}^{0}}) = \sqrt {\frac{{2{{\gamma }}{{{{\mu }}}_{0}}}}{{\left( {{{\gamma }} - 1} \right){{x}^{0}}{{u}_{\infty }}{{p}^{0}}({{x}^{0}},{{z}^{0}})}}} RT_{w}^{0}{{{v}}_{w}}$

Здесь R − газовая постоянная, p0 (x0, z0) − величина индуцированного давления на верхней поверхности пластины, а безразмерный параметр ${{{v}}_{w}}$ является постоянным по величине и определяет нормальный компонент вектора скорости на поверхности клина в краевой задаче, записанной в безразмерных переменных и с учетом особенностей поведения функций течения в окрестности передней кромки пластины. Следует отметить, что распределение давления p0(x0, z0), входящее в выражение (1.1), заранее не известно, а определяется только в результате решения краевой задачи. Заметим, что при ${{{v}}_{w}}$ = const, в случае обтекания полубесконечной (L → ∞) скользящей пластины, для ${v}_{w}^{0}$(x0, z0) получается фактически автомодельный вдув.

Рассматриваются режимы, для которых характерная толщина “эффективного тела” имеет порядок характерной безразмерной толщины вытеснения пограничного слоя δ $ \ll $ 1. Тогда образующийся невязкий ударный слой в первом приближении описывается гиперзвуковой теорией малых возмущений. При рассмотрении режима сильного вязко-невязкого взаимодействия Mnδ $ \gg $ 1 для определения давления, создаваемого толщиной вытеснения пограничного слоя, в который вдувается газ, можно использовать формулу “касательного клина” [19, 20]. В соответствии с оценками для пространственного ламинарного пограничного слоя в гиперзвуковом потоке [4, 19] вводятся следующие безразмерные переменные:

(1.2)
${{x}^{0}} = Lx,\quad {\text{ }}{{y}^{0}} = {{\delta }}Ly,\quad {{z}^{0}} = {{L}_{z}}z,\quad {{{{\mu }}}^{0}} = {{{{\mu }}}_{0}}{{\mu ,}}\quad {{\delta }}_{e}^{0} = L{{\delta \delta }}_{e}^{*},\quad {{{{\rho }}}^{0}} = {{{{\rho }}}_{\infty }}{{{{\delta }}}^{2}}{{\rho }}$
${\text{ }}{{p}^{0}} = {{{{\rho }}}_{\infty }}V_{\infty }^{2}{{{{\delta }}}^{2}}{{p}_{*}},\quad {\text{ }}p_{{^{d}}}^{0}({{z}^{0}}) = {{{{\rho }}}_{\infty }}V_{\infty }^{2}{{{{\delta }}}^{2}}{{p}_{d}}\left( z \right),\quad {{u}^{0}} = {{V}_{\infty }}u,\quad {{w}^{0}} = {{V}_{\infty }}w$
$\begin{gathered} {{{v}}^{0}} = {{V}_{\infty }}\delta {{{v}}_{*}},\quad {v}_{w}^{0} = {{V}_{\infty }}\delta \sqrt {\frac{{{{\gamma }} - 1}}{{2{{\gamma }}x{{p}_{*}}\left( {x,z} \right)}}} {{H}_{w}}{{{v}}_{w}}, \\ {{H}^{0}} = 0.5V_{\infty }^{2}H,\quad H_{w}^{0} = 0.5V_{\infty }^{2}{{H}_{w}} = \frac{{{\gamma }}}{{{{\gamma }} - 1}}RT_{w}^{0} \\ \end{gathered} $

Здесь H0 – полная энтальпия. Далее используется преобразование А.А. Дородницына

(1.3)
${{\lambda }} = \int\limits_0^y {{{\rho }}dy} ,\quad {{{v}}_{{{\delta }}}} = {{\rho }}{{{v}}_{*}} + u\frac{{\partial {{\lambda }}}}{{\partial x}} + Nw\frac{{\partial {{\lambda }}}}{{\partial z}}$

Учитывая, что на поверхности пластины плотность вдуваемого газа ρw = 2γ${{p}_{*}}$/(γ –1)Hw, то для величины, характеризующей интенсивность вдува в переменных (1.3), получаем ${{{v}}_{{\delta w}}}$(x, z) = = (2γ${{p}_{*}}$(x, z)/(γ – 1)x)1/2${{{v}}_{w}}$.

Для учета особенности поведения функций течения в окрестности передней кромки вводится преобразование переменных

(1.4)
${{\lambda }} = {{x}^{{{1 \mathord{\left/ {\vphantom {1 4}} \right. \kern-0em} 4}}}}{{\lambda *}},\quad {{p}_{*}} = {{x}^{{ - {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}p\left( {x,z} \right),\quad {{\rho }} = {{x}^{{ - {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}\rho {\text{*}}\left( {x,{{\lambda *}},z} \right)$
${{\delta }}_{e}^{*} = {{x}^{{{3 \mathord{\left/ {\vphantom {3 4}} \right. \kern-0em} 4}}}}{{{{\delta }}}_{e}}(x,z),\quad {{{v}}_{\delta }} = {{x}^{{{{ - 3} \mathord{\left/ {\vphantom {{ - 3} 4}} \right. \kern-0em} 4}}}}\left( {{v}{\text{*}} - xu\frac{{\partial {{\lambda *}}}}{{\partial x}}} \right),\quad {\text{ }}{v}_{w}^{*}\left( {x,z} \right) = \sqrt {\frac{{2{{\gamma }}{{p}_{*}}\left( {x,z} \right)}}{{\left( {{{\gamma }} - 1} \right)x}}} {{{v}}_{w}}$

В переменных (1.1)–(1.4) система уравнений пространственного пограничного слоя принимает вид

(1.5)
$x\frac{{\partial u}}{{\partial x}} + \frac{{\partial {v}{\text{*}}}}{{\partial {{\lambda *}}}} + Nx\frac{{\partial w}}{{\partial z}} + \frac{u}{4} = 0$
$xu\frac{{\partial u}}{{\partial x}} + {v}{\text{*}}\frac{{\partial u}}{{\partial {{\lambda *}}}} + Nxw\frac{{\partial u}}{{\partial z}} = \frac{{{{\gamma }} - 1}}{{2{{\gamma }}}}(H - {{u}^{2}} - {{w}^{2}})\left( {\frac{1}{2} - \frac{x}{p}\frac{{\partial p}}{{\partial x}}} \right) + \frac{{2{{\gamma }}p}}{{{{\gamma }} - 1}}\frac{{{{\partial }^{2}}u}}{{\partial {{{{\lambda }}}^{{*2}}}}}$
$xu\frac{{\partial w}}{{\partial x}} + {v}{\text{*}}\frac{{\partial w}}{{\partial {{\lambda *}}}} + Nxw\frac{{\partial w}}{{\partial z}} = - N\frac{{{{\gamma }} - 1}}{{2{{\gamma }}}}(H - {{u}^{2}} - {{w}^{2}})\frac{x}{p}\frac{{\partial p}}{{\partial z}} + \frac{{2{{\gamma }}p}}{{{{\gamma }} - 1}}\frac{{{{\partial }^{2}}w}}{{\partial {{{{\lambda }}}^{{*2}}}}}$
$xu\frac{{\partial H}}{{\partial x}} + {v}{\text{*}}\frac{{\partial H}}{{\partial {{\lambda *}}}} + Nxw\frac{{\partial H}}{{\partial z}} = \frac{{2{{\gamma }}p}}{{{{\gamma }} - 1}}\left[ {\frac{1}{{{\sigma }}}\frac{{{{\partial }^{2}}H}}{{\partial {{{{\lambda }}}^{{*2}}}}} - \frac{{1 - {{\sigma }}}}{{{\sigma }}}\frac{{{{\partial }^{2}}({{u}^{2}} + {{w}^{2}})}}{{\partial {{{{\lambda }}}^{{*2}}}}}} \right]$
$p = \frac{{{{\gamma }} + 1}}{2}{{\left[ {\left( {\frac{3}{4}{{{{\delta }}}_{e}} + x\frac{{\partial {{{{\delta }}}_{e}}}}{{\partial x}}} \right)\cos {{\beta }} + Nx\frac{{\partial {{{{\delta }}}_{e}}}}{{\partial z}}\sin {{\beta }}} \right]}^{2}}$
${{{{\delta }}}_{e}} = \frac{{{{\gamma }} - 1}}{{2{{\gamma }}p}}\int\limits_0^\infty {(H - {{u}^{2}} - {{w}^{2}})} {\text{ }}d{{\lambda *}},\quad p\left( {x = 1,z} \right) = {{p}_{d}}\left( z \right)$
$\begin{gathered} {{ \lambda *}} = 0{\text{:}}\quad u = w = 0,\quad {v}* = {\text{ }}\sqrt {\frac{{2{{\gamma }}p}}{{{{\gamma }} - 1}}} {{{v}}_{w}},\quad H = {{H}_{w}} \hfill \\ {{\lambda *}} \to \infty {\text{:}}\quad u \to \cos {{\beta }},\quad w \to \sin {{\beta }},\quad H \to 1\quad \left( {0 \leqslant x \leqslant 1,\left| z \right| < \infty } \right) \hfill \\ \end{gathered} $

Здесь σ – число Прандтля, Hw – полная энтальпия на поверхности пластины, а pd(z) – безразмерное давление на задней кромке пластины. На передней кромке при x = 0 данная система трехмерных уравнений в частных производных вырождается в систему обыкновенных дифференциальных уравнений и ее решение позволяет найти начальные условия для системы (1.5), а фактически это автомодельное решение на полубесконечной скользящей пластине с автомодельным вдувом. Заметим, что если дополнительно наложить условие ${{{v}}_{w}}$ = 0, то получаем систему для нахождения автомодельного решения на полубесконечной скользящей пластине [9]. Входящее в систему (1.5) распределение индуцированного давления p(x, z) заранее неизвестно и должно быть определено в результате решения задачи. Следует отметить, что в краевую задачу (1.5), учитывая выражение для давления p(x, z), фактически входят вторые производные ∂2δe/∂x2 и ∂2δe/∂z2, а следовательно, данная система уравнений не относится к параболическому типу. Наличие индуцированного градиента давления придает ей новые свойства, связанные с передачей возмущений вверх по потоку и появлением соответствующей неединственности решения [14].

2. РАЗЛОЖЕНИЕ В ОКРЕСТНОСТИ ПЕРЕДНЕЙ КРОМКИ ПЛАСТИНЫ

Для исследования поведения функций течения в окрестности передней кромки следует преобразовать краевую задачу (1.5) и ввести переменные

(2.1)
${{\lambda *}} = \sqrt {\frac{{2{{\gamma }}}}{{{{\gamma }} - 1}}p\left( {x,z} \right)} {{ \eta }},\quad {v}* = \sqrt {\frac{{2{{\gamma }}}}{{{{\gamma }} - 1}}p\left( {x,z} \right)} \left[ {{v} + \frac{{x{{\eta }}}}{{2p}}\left( {u\frac{{\partial p}}{{\partial x}} + Nw\frac{{\partial p}}{{\partial z}}} \right)} \right]$

В результате в уравнениях переноса и неразрывности давление в знаменателе останется только при производных от индуцированного давления, что будет удобно при проведении в дальнейшем разложений. После подстановки (2.1) в краевую задачу (1.5) она приводится к виду

(2.2)
$x\frac{{\partial u}}{{\partial x}} + \frac{{\partial {v}}}{{\partial {{\eta }}}} + Nx\frac{{\partial w}}{{\partial z}} + \frac{x}{2}\left( {\frac{u}{p}\frac{{\partial p}}{{\partial x}} + N\frac{w}{p}\frac{{\partial p}}{{\partial z}}} \right) + \frac{u}{4} = 0$
$xu\frac{{\partial u}}{{\partial x}} + {v}\frac{{\partial u}}{{\partial {{\eta }}}} + Nxw\frac{{\partial u}}{{\partial z}} = \frac{{{{\gamma }} - 1}}{{2{{\gamma }}}}(H - {{u}^{2}} - {{w}^{2}})\left( {\frac{1}{2} - \frac{x}{p}\frac{{\partial p}}{{\partial x}}} \right) + \frac{{{{\partial }^{2}}u}}{{\partial {{{{\eta }}}^{2}}}}$
$xu\frac{{\partial w}}{{\partial x}} + {v}\frac{{\partial w}}{{\partial {{\eta }}}} + Nxw\frac{{\partial w}}{{\partial z}} = - N\frac{{{{\gamma }} - 1}}{{2{{\gamma }}}}(H - {{u}^{2}} - {{w}^{2}})\frac{x}{p}\frac{{\partial p}}{{\partial z}} + \frac{{{{\partial }^{2}}w}}{{\partial {{{{\eta }}}^{2}}}}$
$xu\frac{{\partial H}}{{\partial x}} + {v}\frac{{\partial H}}{{\partial {{\eta }}}} + Nxw\frac{{\partial H}}{{\partial z}} = \frac{1}{{{\sigma }}}\frac{{{{\partial }^{2}}H}}{{\partial {{{{\eta }}}^{2}}}} - \frac{{1 - {{\sigma }}}}{{{\sigma }}}\frac{{{{\partial }^{2}}({{u}^{2}} + {{w}^{2}})}}{{\partial {{{{\eta }}}^{2}}}}$
$p = \frac{{{{\gamma }} + 1}}{2}{{\left[ {\left( {\frac{3}{4}{{{{\delta }}}_{e}} + x\frac{{\partial {{{{\delta }}}_{e}}}}{{\partial x}}} \right)\cos {{\beta }} + Nx\frac{{\partial {{{{\delta }}}_{e}}}}{{\partial z}}\sin {{\beta }}} \right]}^{2}}$
${{{{\delta }}}_{e}} = \sqrt {\frac{{{{\gamma }} - 1}}{{2{{\gamma }}p}}} \int\limits_0^\infty {(H - {{u}^{2}} - {{w}^{2}})} {\text{ }}d{{\eta ,}}\quad p\left( {x = 1,z} \right) = {{p}_{d}}\left( z \right)$
$\begin{gathered} {{ \eta }} = 0{\text{:}}\,\,u = w = {\text{0,}}\quad {v} = {{{v}}_{w}},\quad H = {{H}_{w}} \hfill \\ {{\eta }} \to \infty {\text{:}}\,\,u \to \cos {{\beta }},\quad w \to \sin {{\beta }},\quad H \to 1\quad \left( {0 \leqslant x \leqslant 1,\left| z \right| < \infty } \right) \hfill \\ \end{gathered} $

Краевая задача (2.2), определяющая течение на всей пластине и зависящая от определяющих параметров N, Hw, σ, γ, β, ${{{v}}_{w}}$, может быть решена численно конечно-разностным методом [21]. Как отмечалось выше, при задании скорости вдува в соответствии с соотношением (1.1), в граничных условиях в краевой задаче (2.2) появляется безразмерный параметр ${{{v}}_{w}}$ = const по всей верхней поверхности пластины. Заметим, что при увеличении значений параметра ${{{v}}_{w}}$ поверхностное трение может уменьшиться до нуля, а это означает, что около поверхности может образоваться область невязкого пристеночного течения (происходит отсоединение пограничного слоя), вызванного распределенным вдувом. Дальнейшее увеличение параметра ${{{v}}_{w}}$ в данной постановке задачи становится не правомерным, так как в этом случае необходимо вводить третий невязкий слой около поверхности клина [14]. После решения краевой задачи (2.2) при заданных параметрах и определения индуцированного давления p(x, z), скорость вдувания ${v}_{w}^{0}$ (в размерном виде) может быть определена следующим образом:

(2.3)
${v}_{w}^{0}({{x}^{0}},{{z}^{0}}) = \sqrt {\frac{{{{\gamma }} - 1}}{{2{{\gamma }}}}} {{x}^{{ - {1 \mathord{\left/ {\vphantom {1 4}} \right. \kern-0em} 4}}}}{{p}^{{ - {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}{{\delta }}{{H}_{w}}{{u}_{\infty }}{{{v}}_{w}}$

Заметим, что если поверхность представляет собой полубесконечную пластину или на ее задней кромке задается соответствующее автомодельное значение давления pd, то величина индуцированного давления p = const, а скорость вдува ${v}_{w}^{0}$(x0) ~ x–1/4δHwu∞${v}_{w}^{{}}$, что соответствует автомодельному массообмену [14]. Важно отметить, что в общем случае, когда дополнительное условие на задней кромке пластины p(x = 1, z) = pd(z) отличается от автомодельного, то только после решения краевой задачи (2.2), при заданных значениях определяющих параметров N, Hw, σ, γ, β, ${v}_{w}^{{}}$ с помощью соотношения (2.3) определяется фактическое распределение скорости вдува по нормали к верхней поверхности пластины, при котором и реализуется данное течение.

Так как поперечное течение в пространственном пограничном слое при угле скольжения β ≠ 0 существует изначально, то, как показали детальные предварительные исследования, для того, чтобы учесть еще и возможное влияние второй производной от индуцированного давления на задней кромке пластины, решение в окрестности передней кромки можно искать в виде

(2.4)
$p\left( {x,z} \right) = {{p}_{0}} + {{p}_{{{\alpha }}}}\left( z \right){{x}^{{{\alpha }}}} + {{p}_{{{{\alpha 1}}}}}N\frac{{d{{p}_{{{\alpha }}}}\left( z \right)}}{{dz}}{{x}^{{{{\alpha }} + 1}}} + {{p}_{{{{\alpha 2}}}}}N\frac{{{{d}^{2}}{{p}_{{{\alpha }}}}\left( z \right)}}{{d{{z}^{2}}}}{{x}^{{{{\alpha }} + 2}}} + \; \ldots $
${{{{\delta }}}_{e}}\left( {x,z} \right) = {{{{\delta }}}_{0}} + {{{{\delta }}}_{{{\alpha }}}}\frac{{{{p}_{{{\alpha }}}}\left( z \right)}}{{{{p}_{0}}}}{{x}^{{{\alpha }}}} + {{\delta }_{{{{\alpha 1}}}}}\frac{N}{{{{p}_{0}}}}\frac{{d{{p}_{{{\alpha }}}}\left( z \right)}}{{dz}}{{x}^{{{{\alpha }} + 1}}} + {{\delta }_{{{{\alpha 2}}}}}\frac{N}{{{{p}_{0}}}}\frac{{{{d}^{2}}{{p}_{{{\alpha }}}}\left( z \right)}}{{d{{z}^{2}}}}{{x}^{{{{\alpha }} + 2}}} + \; \ldots $
$\begin{gathered} f(x,{{\eta }},z) = {{f}_{0}}({{\eta }}) + {{f}_{{{\alpha }}}}\left( {{\eta }} \right)\frac{{{{p}_{{{\alpha }}}}\left( z \right)}}{{{{p}_{0}}}}{{x}^{{{\alpha }}}} + \\ + \;{{f}_{{{{\alpha 1}}}}}\left( {{\eta }} \right)\frac{N}{{{{p}_{0}}}}\frac{{d{{p}_{{{\alpha }}}}\left( z \right)}}{{dz}}{{x}^{{{{\alpha }} + 1}}} + {{f}_{{{{\alpha 2}}}}}\left( {{\eta }} \right)\frac{N}{{{{p}_{0}}}}\frac{{{{d}^{2}}{{p}_{{{\alpha }}}}\left( z \right)}}{{d{{z}^{2}}}}{{x}^{{{{\alpha }} + 2}}} + \; \ldots \\ \end{gathered} $
где f(x, η, z) = {u(x, η, z), w(x, η, z), ${v}$(x, η, z), H(x, η, z)}. Индексом 0 обозначены члены разложений, соответствующие автомодельному решению для полубесконечной скользящей пластины с автомодельным вдувом. Предполагается, что показатель степени (собственное число) α > 0. Заметим, что опущенные члены разложений имеют порядки О(xα + 3), О(xα + 4) и т.д., а также – О(x2α), О(x2α + 1) и т.д., т.е. данный вид разложений справедлив, если α > 2. При значениях α ≤ 2 необходимо в разложениях обязательно учитывать член порядка О(x2α). Это обстоятельство необходимо иметь в виду при решении соответствующих краевых задач на нахождение собственных чисел, так как достаточно интенсивный вдув может существенно уменьшить величину α. Важно отметить, что при угле скольжения β = 0 вид разложений (2.4) принципиально изменяется. Как было отмечено уже в [7, 8], в разложении для поперечной компоненты скорости w(x, η, z) в этом случае первые два коэффициента разложения (2.4) оказываются тождественно равными нулю (w0(η) = wα(η) = 0). Ниже проведенные расчеты показали, что при β = 0: pα1 = δα1 = uα1 = Hα1 = = vα1 = 0 и wα2 = 0. Следовательно, при наличии угла скольжения, третьи члены разложения (2.4) пропорциональные xα + 1dpα(z)/dz могут существенно влиять на передачу возмущений против потока, особенно в тех сечениях z = const, где pα(z) достаточно мало, а четвертые члены ∼xα + 2d2pα(z)/dz2 − тех сечениях z, где одновременно pα(z) и dpα(z)/dz малы. Заметим также, что величина собственного числа α уменьшается с увеличением угла скольжения [11–13]. В общем случае, при поиске вида разложений (2.4), предполагалось, что коэффициенты для всех функций течения при членах, содержащих собственное число α и в следующих членах, являются функциями от двух переменных η и z. Но оказалось, что эти коэффициенты зависят только от координаты η и краевые задачи для определения собственного числа, а также для третьих и четвертых членов разложения представляют собой системы обыкновенных дифференциальных уравнений.

Подставляя разложения (2.4) в систему уравнений и граничные условия (2.2) и собирая члены одинакового порядка, получаем соответствующие краевые задачи. Для первых членов разложения получается следующая система (автомодельная часть):

(2.5)
${{{v}}_{0}}\frac{{d{{u}_{0}}}}{{d{{\eta }}}} = \frac{{{{\gamma }} - 1}}{{4{{\gamma }}}}({{H}_{0}} - u_{0}^{2} - w_{0}^{2}) + \frac{{{{d}^{2}}{{u}_{0}}}}{{d{{{{\eta }}}^{2}}}}$
${{{v}}_{0}}\frac{{d{{H}_{0}}}}{{d{{\eta }}}} = \frac{1}{{{\sigma }}}\frac{{{{d}^{2}}{{H}_{0}}}}{{d{{{{\eta }}}^{2}}}} - \frac{{1 - {{\sigma }}}}{{{\sigma }}}\frac{{{{d}^{2}}(u_{0}^{2} + w_{0}^{2})}}{{d{{{{\eta }}}^{2}}}}$
${{{v}}_{0}}\frac{{d{{w}_{0}}}}{{d{{\eta }}}} = \frac{{{{d}^{2}}{{w}_{0}}}}{{d{{{{\eta }}}^{2}}}},\quad \frac{{d{{{v}}_{0}}}}{{d{{\eta }}}} + 0.25{{u}_{0}} = 0$
${{p}_{0}} = \frac{3}{8}\sqrt {\frac{{({{\gamma }} + 1)({{\gamma }} - 1)}}{{{\gamma }}}} \cos {{\beta }}\int\limits_0^\infty {({{H}_{0}} - u_{0}^{2} - w_{0}^{2})} d{{\eta }}$
${{{{\delta }}}_{0}} = 2\sqrt[4]{{\frac{{{{\gamma }} - 1}}{{{{\gamma (\gamma }} + 1{\text{)}}}}}}\sqrt {\frac{1}{{3\cos {{\beta }}}}\int\limits_0^\infty {({{H}_{0}} - u_{0}^{2})} d{{\eta }}} $
$\begin{gathered} {{\eta }} = 0{\text{:}}\,\,{{u}_{0}} = {{w}_{0}} = {\text{ 0,}}\quad {{{v}}_{0}} = {{{v}}_{w}},\quad {{H}_{0}} = {{H}_{w}}{\text{;}} \\ {{\eta }} \to \infty {\text{:}}\,\,{{u}_{0}} \to \cos {{\beta ,}}\quad {{w}_{0}} \to \sin {{\beta }},\quad {{H}_{0}} \to 1 \\ \end{gathered} $

Решением краевой задачи (2.5) является автомодельное решение, которое описывает течение при автомодельном массообмене на полубесконечной скользязщей пластине на режиме сильного взаимодействия или на скользящей пластине конечной длины, если на ее задней кромке задано донное давление, соответствующее местному давлению для автомодельного решения.

Для вторых членов разложения получается краевая задача, решение которой позволяет найти и собственное число α (неавтомодельная часть)

(2.6)
${{{v}}_{0}}\frac{{d{{H}_{{{\alpha }}}}}}{{d{{\eta }}}} + {{{v}}_{{{\alpha }}}}\frac{{d{{H}_{0}}}}{{d{{\eta }}}} + {{\alpha }}{{u}_{0}}{{H}_{{{\alpha }}}} = \frac{1}{{{\sigma }}}\frac{{{{d}^{2}}{{H}_{{{\alpha }}}}}}{{d{{{{\eta }}}^{2}}}} - 2\frac{{1 - {{\sigma }}}}{{{\sigma }}}\frac{{{{d}^{2}}({{u}_{0}}{{u}_{{{\alpha }}}} + {{w}_{0}}{{w}_{{{\alpha }}}})}}{{d{{{{\eta }}}^{2}}}}$
${{{v}}_{0}}\frac{{d{{w}_{{{\alpha }}}}}}{{d{{\eta }}}} + {{{v}}_{{{\alpha }}}}\frac{{d{{w}_{0}}}}{{d{{\eta }}}} + {{\alpha }}{{u}_{0}}{{w}_{{{\alpha }}}} = \frac{{{{d}^{2}}{{w}_{{{\alpha }}}}}}{{d{{{{\eta }}}^{2}}}},\quad {{{{\delta }}}_{{{\alpha }}}} = \frac{3}{{6 + 8{{\alpha }}}}{{{{\delta }}}_{0}}$
$\frac{{\left( {3 + 2{{\alpha }}} \right)}}{{\left( {3 + 4{{\alpha }}} \right)}}\int\limits_0^\infty {({{H}_{0}} - u_{0}^{2} - w_{0}^{2})} d{{\eta }} = \int\limits_0^\infty {({{H}_{{{\alpha }}}} - 2{{u}_{0}}{{u}_{{{\alpha }}}} - 2{{w}_{0}}{{w}_{{{\alpha }}}})d{{\eta }}} $
${{\eta }} = 0{\text{:}}\,\,{{u}_{{{\alpha }}}} = {{w}_{{{\alpha }}}} = {{{v}}_{{{\alpha }}}} = {{H}_{{{\alpha }}}} = 0;\quad {{\eta }} \to \infty {\text{:}}\quad {{u}_{{{\alpha }}}} \to 0,\quad {{w}_{{{\alpha }}}} \to 0,\quad {{H}_{{{\alpha }}}} \to 0$

В системе (2.6) интегральное соотношение для определения собственного числа α получено из разложений (2.4) для индуцированного давления p и толщины вытеснения δe. При заданных значениях параметров Hw, σ, γ, β и ${{{v}}_{w}}$ решение краевой задачи (2.5) позволяет найти все функции течения u0(η), w0(η), ${{{v}}_{0}}$(η), H0(η), p0, δ0 на передней кромке пластины. Затем из решения (2.5) с тривиальными граничными условиями определяется собственное число α, если оно существует, и соответствующие ему коэффициенты разложений uα(η), wα(η), ${{{v}}_{\alpha }}$(η), Hα(η), δα. Важно отметить, что так как праметр pα(z) в разложениях (2.4) оказывается произвольным, то решение в окрестности передней кромки не является единственным. В каждом сечении z = const имеется свое однопараметрическое семейство решений. Подбор параметра pα(z), в принципе, позволяет (в рассматриваемом пока двухчленном разложении) удовлетворить дополнительному условию на задней кромке пластины, или прийти в особую точку на ней, если имеет место отрыв, а трение обращается в ноль. В данном случае для течения в пространственном пограничном на поверхности пластины конечной длины с заданным дополнительным условием на задней кромке pd(z) справедлива теория полос вдоль оси x, перпендикулярной передней кромке пластины.

Собирая члены для третьих членов разложения, получаем краевую задачу

(2.7)
$\frac{{d{{{v}}_{{{{\alpha 1}}}}}}}{{d{{\eta }}}} + ({\text{1}}{\text{.25}} + \alpha ){{u}_{{{{\alpha 1}}}}} + {{w}_{{{\alpha }}}} + {\text{0}}{\text{.5(}}{{w}_{0}} + ({\text{1}} + {{\alpha }}){{p}_{{{{\alpha 1}}}}}{{u}_{0}}{\text{)}} = 0$
${{{v}}_{0}}\frac{{d{{H}_{{{{\alpha 1}}}}}}}{{d{{\eta }}}} + {{{v}}_{{{{\alpha 1}}}}}\frac{{d{{H}_{0}}}}{{d{{\eta }}}} + {\text{(1}} + {{\alpha )}}{{u}_{0}}{{H}_{{{{\alpha 1}}}}} + {{w}_{0}}{{H}_{{{\alpha }}}} = \frac{1}{{{\sigma }}}\frac{{{{d}^{2}}{{H}_{{{{\alpha 1}}}}}}}{{d{{{{\eta }}}^{2}}}} - 2\frac{{1 - {{\sigma }}}}{{{\sigma }}}\frac{{{{d}^{2}}({{u}_{0}}{{u}_{{{{\alpha 1}}}}} + {{w}_{0}}{{w}_{{{{\alpha 1}}}}})}}{{d{{{{\eta }}}^{2}}}}$
${{\eta }} = 0{\text{:}}\,\,{{u}_{{{{\alpha 1}}}}} = {{w}_{{{{\alpha 1}}}}} = {{{v}}_{{{{\alpha 1}}}}} = {{H}_{{{{\alpha 1}}}}} = 0;\quad {{\eta }} \to \infty {\text{:}}\,\,{{u}_{{{{\alpha 1}}}}} \to 0,\quad {{w}_{{{{\alpha 1}}}}} \to 0,\quad {{H}_{{{{\alpha 1}}}}} \to 0$

Краевая задача (2.7) является линейной и неоднородной с нулевыми граничными условиями. Система зависит от параметра pα1, величина которого определяется из интегрального соотношения, полученного в результате разложения в ряды индуцированного давления и толщины вытеснения, причем коэффициент pα1 не зависит от координаты z. Следует отметить, что сформулированные краевые задачи (2.5), (2.6) и (2.7) принципиально отличаются от соответствующих краевых задач для случая обтекания пластины при отсутствии угла скольжения [8], в которых уравнения для определения коэффициентов разложения для поперечной компоненты скорости отделялись от основной системы уравнений. Учитывая, что и сами разложения (2.4) принципиально отличаются от случая, когда скольжение отсутствует, возникает вопрос, что происходит, если в краевых задачах (2.5)–(2.7) считать β = 0. Если в краевых условиях системы (2.5) положить β = 0, то уравнение для определения первого члена разложения для поперечной компоненты скорости имеет единственное решение w0(η) = 0, а следовательно dw0(η)/dη = 0. Тогда уравнение для определения второго члена разложения для поперечной компоненты скорости в системе (2.6) станет однородным, а его решение wα(η) = 0. Заметим, что система (2.5), за исключением граничного условия для ${{{v}}_{w}}$, и (2.6) после этого совпадут с соответствующими краевыми задачами, приведенными в [7]. Рассматривая систему (2.7) при условиях, что β = 0, w0(η) = 0 и wα(η) = 0, то в этой системе только уравнение для определения wα1(η) останется неоднородным и совпадающим с уравнением [7]. Остальные уравнения станут однородными, а их решения соответственно: uα1(η) = 0, ${{{v}}_{{\alpha 1}}}$(η) = 0, Hα1(η) = 0, δα1 = 0 и pα1 = 0. Заметим, что при этом и вид разложений (2.4) (учитывая пока трехчленное представление) изменится и точно совпадет с разложениями [7].

Для четвертых членов разложения получаем краевую задачу

(2.8)
$\frac{{d{{{v}}_{{{{\alpha 2}}}}}}}{{d{{\eta }}}} + ({\text{2}}{\text{.25}} + {{\alpha }}){{u}_{{{{\alpha 2}}}}} + N{{w}_{{{{\alpha 1}}}}} + {\text{0}}{\text{.5(}}N{{p}_{{\alpha 1}}}{{w}_{0}} + ({\text{2}} + {{\alpha }}){{p}_{{{{\alpha 2}}}}}{{u}_{0}}{\text{)}} = 0$
${{{v}}_{0}}\frac{{d{{H}_{{{{\alpha 2}}}}}}}{{d{{\eta }}}} + {{{v}}_{{{{\alpha 2}}}}}\frac{{d{{H}_{0}}}}{{d{{\eta }}}} + {\text{(2}} + {{\alpha )}}{{u}_{0}}{{H}_{{{{\alpha 2}}}}} + N{{w}_{0}}{{H}_{{{{\alpha 1}}}}} = \frac{1}{{{\sigma }}}\frac{{{{d}^{2}}{{H}_{{{{\alpha 2}}}}}}}{{d{{{{\eta }}}^{2}}}} - 2\frac{{1 - {{\sigma }}}}{{{\sigma }}}\frac{{{{d}^{2}}({{u}_{0}}{{u}_{{{{\alpha 2}}}}} + {{w}_{0}}{{w}_{{{{\alpha 2}}}}})}}{{d{{{{\eta }}}^{2}}}}$
${{{{\delta }}}_{{{{\alpha }}2}}} = \sqrt {\frac{{{{\gamma }} - {\text{1}}}}{{2{{\gamma }}{{p}_{0}}}}} \left[ {\int\limits_0^\infty {\left( {{{H}_{{{{\alpha 2}}}}} - 2{{u}_{0}}{{u}_{{{{\alpha 2}}}}} - 2{{w}_{0}}{{w}_{{{{\alpha 2}}}}}} \right)d{{\eta }} - {\text{0}}{\text{.5}}{{p}_{{{{\alpha 2}}}}}\int\limits_0^\infty {({{H}_{0}} - u_{0}^{2} - w_{0}^{2})d{{\eta }}} } } \right]$
${{\eta }} = 0{\text{:}}\,\,{{u}_{{{{\alpha 2}}}}} = {{w}_{{{{\alpha 2}}}}} = {{{v}}_{{{{\alpha 2}}}}} = {{H}_{{{{\alpha 2}}}}} = 0;\quad {{\eta }} \to \infty {\text{:}}\,\,{{u}_{{{{\alpha 2}}}}} \to 0,\quad {{w}_{{{{\alpha 2}}}}} \to 0,\quad {{H}_{{{{\alpha 2}}}}} \to 0$

Система уравнений (2.8), как и (2.7), является линейной и неоднородной с нулевыми граничными условиями. Вид этой системы подтверждает, что коэффициенты разложений uα2(η), wα2(η), ${{{v}}_{{\alpha 2}}}$(η), Hα2(η), δα2 действительно не зависят от поперечной координаты z. В данную систему входит параметр pα2, значение которого определяется из интегрального соотношения, полученного в результате разложения в ряды индуцированного давления и толщины вытеснения, причем коэффициент pα2 также не зависит от координаты z. При решении краевой задачи (2.8) для β = 0 следует иметь в виду, что т.к. в этом случае wα1(η) не равняется нулю, а pα1 = 0, то, следовательно, ${{{v}}_{{\alpha 2}}}$(η), uα2(η), Hα2(η) (за исключением теплоизолированной пластины и числе Прандтля σ = 1), pα2 также не равны нулю, но wα2(η) = 0.

3. РЕЗУЛЬТАТЫ ЧИСЛЕННЫХ РАСЧЕТОВ

В силу ограничений на количество рисунков в данной работе результаты приведены только для теплоизолированной пластины (Hw = 1) при значениях числа Прандтля σ = 1, показателя адиабаты γ = 1.4 и параметра N = 1. В этом случае профиль энтальпии H(η) = 1, а профили коэффициентов Hα(η) = Hα1(η) = Hα2(η) = 0. Основное внимание уделено изучению влияния параметра интенсивности вдува ${{{v}}_{w}}$ и угла скольжения β на характеристики течения. Краевые задачи (2.5)–(2.8) решались численно с помощью метода прогонки. Для вычисления определенных интегралов использовалась формула Симпсона. Размер ячейки по нормальной координате равнялся Δη = 0.01, а количество узлов по нормали к поверхности пластины увеличивалось от Nη = 1501 до Nη = 2801, по мере увеличения интенсивности вдува, в связи с ростом тольщины пограничного слоя. Проводились также контрольные расчеты с шагом Δη = 0.0025 и увеличенным количеством узлов по нормали в 4 раза. Значение собственного числа считалось вычисленным, если интегральное условие в краевой задаче (2.6) выполнялось с точностью |ε| ≤ 0.00002. Такое же требование ставилось при вычислении интегралов для определения параметров pα1 и pα2 при решении краевых задач (2.7) и (2.8).

В результате решения систем уравнений (2.5) и (2.6) определены зависимости собственного числа α (кривые 1–4) от угла скольжения β при значениях параметра интенсивности вдува ${{{v}}_{w}}$ = = 0(1), 0.25 (2), 0.5 (3), 0.9 (4), которые представлены на рис. 1. Наиболее сильно увеличение угла скольжения β влияет на величину α при отсутствии массообмена (кривая 1). В этом случае при изменении β от 0 до 75° значение собственного числа уменьшается почти в 5 раз, а следовательно, значительно возрастает интенсивность распространения возмущений в пограничном слое по нормали к передней кромке против потока (2.4). Еще сильнее на усиление распространения возмущений влияет вдув при обтекании пластины при β = 0. При увеличении ${{{v}}_{w}}$ от 0 до 0.9 число α уменьшается более чем в 11 раз. Важно отметить, что для значения ${{{v}}_{w}}$ = 0.9 собственное число практически не зависит от угла скольжения. Точнее оно даже растет на 10% при увеличении угла скольжения (кривая 4). Интенсивности вдува большие, чем ${{{v}}_{w}}$ = 0.9 в этой работе не рассматривались, так как в этом случае собственные числа становятся меньше двух, а следовательно, необходимо дополнительно учитывать члены порядка О(x2α) в разложения (2.4). Далее приведены результаты численных расчетов, полученных при решении всех четырех краевых задач. Зависимости коэффициентов разложения для индуцированного давления: p0 (1–3) и параметров pα1 (4–6), pα2 (7–9) от угла скольжения β при значениях интенсивности вдува ${{{v}}_{w}}$ = 0 (кривые 1, 4, 7), 0.5 (2, 5, 8), 0.9 (3, 6, 9) представлены на рис. 2. Увеличение ${{{v}}_{w}}$ от 0 до 0.9 приводит к существенному возрастанию значений автомодельного давления p0 особенно при не очень больших углах скольжения β (кривые 1–3). Увеличение β приводит к монотонному уменьшению величины давления p0. Наиболее сильно с увеличением угла скольжения растут коэффициенты pα1 (4), pα2 (7) при отсутствии массообмена. При вдуве с ${{{v}}_{w}}$ = 0.9 их изменения существенно меньше (кривые 6, 9). Следует отметить, что при β = 0 коэффициент pα1 обращается в ноль (кривые 4–6). Зависимости коэффициентов разложения δ0 (1, 2), δα (3, 4), δα1 (5, 6), δα2 (7, 8) от угла скольжения β при значениях параметра интенсивности вдува ${{{v}}_{w}}$ = 0 (кривые 1, 3, 5, 7), 0.9 (2, 4, 6, 8) приведены на рис. 3. Автомодельная толщина вытеснения δ0 (кривые 1, 2) возрастает с увеличением угла скольжения, причем при ${{{v}}_{w}}$ = 0.9 она примерно в полтора раза больше, чем при отсутствии вдува (кривые 1, 2). Изменения остальных коэффициентов при изменении величины интенсивности вдува и/или угла скольжения существенно меньше. Зависимости профилей коэффициентов разложения u0(η) (кривые 1, 5), uα (η) (2, 6), uα1 (η) (3, 7), uα2 (η) (4, 8) от параметра интенсивности вдува ${{{v}}_{w}}$ = 0 (кривые 1–4), 0.9 (5–8) при β = 45° приведены на рис. 4. Толщина автомодельного профиля компоненты скорости нормальной к передней кромке u0(η) существенно увеличивается с ростом скорости вдува ${{{v}}_{w}}$ (кривые 1, 5) и при этом значительно уменьшается коэффициент напряжения ∂u0/∂η(η = 0). Профили коэффициентов uα(η) (кривые 2, 6) являются отрицательными по величине, причем максимумы по модулю значений uα(η) практически близки. Принципиально иной характер поведения профилей uα1(η) (3, 4) и uα2(η) (7, 8) – они противоположны по знаку и при ${{{v}}_{w}}$ = 0.9 (7, 8) на порядок меньше по модулю. Зависимости профилей коэффициентов разложения w0(η) (1, 5), wα(η) (2, 6), wα1(η) (3, 7), wα2(η) (4, 8) от параметра интенсивности вдува ${{{v}}_{w}}$ = 0 (1–4), 0.9 (5–8) при β = 45° представлены на рис. 5. Автомодельные профили компоненты скорости вдоль передней кромки пластины w0(η) (1, 5) существенно различаются. При вдуве с ${{{v}}_{w}}$ = = 0.9 (5) этот профиль имеет вид “предотрывного”, так как для него ∂w0/∂η(η = 0) = 0.00476. Коэффициенты профилей wα(η) (2, 6), полученные в результате решения системы (2.6), более, чем в два раза различаются максимальными значениями. Следует отметить принципиально разный характер профилей wα1(η) (7) и wα2(η) (8) при ${{{v}}_{w}}$ = 0.9.

Рис. 1.

Зависимости собственного числа α(1–4) от угла скольжения β при значениях параметра интенсивности вдува ${{{v}}_{w}}$ = 0 (1), 0.25 (2), 0.5 (3), 0.9 (4).

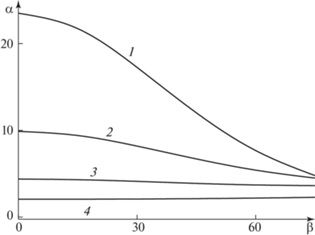
Рис. 2.

Зависимости коэффициентов разложения p0 (1–3), pα1 (4–6), pα2 (7–9) от угла скольжения β при значениях параметра интенсивности вдува ${{{v}}_{w}}$ = 0 (1, 4, 7), 0.5 (2, 5, 8), 0.9 (3, 6, 9).

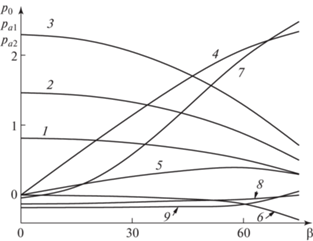
Рис. 3.

Зависимости коэффициентов разложения δ0 (1, 2), δα (3, 4), δα1 (5, 6), δα2 (7, 8) от угла скольжения β при значениях параметра интенсивности вдува ${{{v}}_{w}}$ = 0 (1, 3, 5, 7), 0.9 (2, 4, 6, 8).

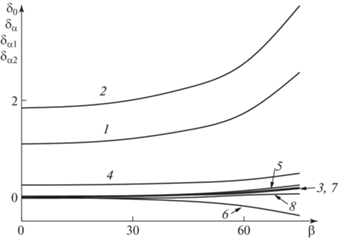
Рис. 4.

Зависимости профилей коэффициентов разложения u0(η) (1, 5), uα(η) (2, 6), uα1(η) (3, 7), uα2(η) (4, 8) от параметра интенсивности вдува ${{{v}}_{w}}$ = 0 (1–4), 0.9 (5–8): β = 45°.

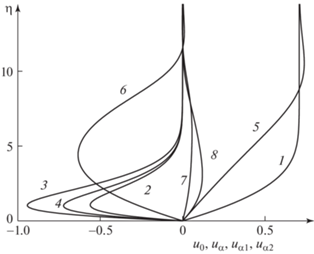
Рис. 5.

Зависимости профилей коэффициентов разложения w0(η) (1, 5), wα(η) (2, 6), wα1(η) (3, 7), wα2(η) (4, 8) от параметра интенсивности вдува ${{{v}}_{w}}$ = 0 (1–4), 0.9 (5–8): β = 45°.

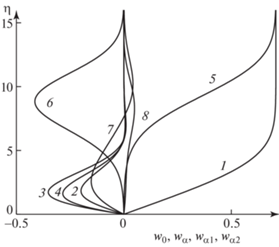
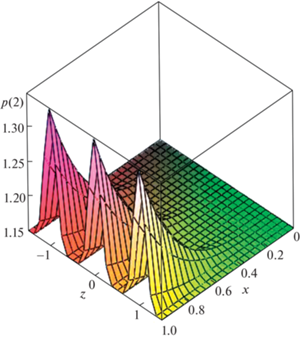
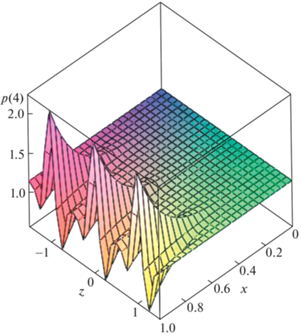
Используя полученные данные, для рассмотренных определяющих параметров, и задавая произвольную функцию pα(z) можно с помощью разложений (2.4) построить возмущенное течение на пластине. Далее, только в качестве примера, рассматривается случай, когда произвольная функция, входящая в разложения (2.4), имеет вид pα(z) = 0.2cos6(πz) (можно взять и любую другу непрерывную дважды дифференцируемую функцию). При значениях параметров β = 45° и ${{{v}}_{w}}$ = = 0.5 в результате решения систем уравнений (2.5)–(2.8) получены: собственное число α = = 3.8848, p0 = 1.1481, pα1 = 0.353, pα2 = –0.081. На рис. 6 приведено распределение индуцированного давления p(2) = p(x, z) = 1.1481 + pα(z)x3.8848 (двухчленное разложение) на части поверхности пластины (0 ≤ x ≤ 1, –1.5 ≤ z ≤ 1.5). В этом случае на задней кромке пластины минимальные значения давления равны ∼1.15, а максимальные ∼1.34, т.е. разница между ними составляет ∆p = 0.19. Учитывая, что собственное число α = 3.8848 не очень большое, то в сечениях z = const, где давление максимально, возмущения в пограничном слое действительно распространяются против потока на 80% от длины пластины. Совершенно иное распределение давления получается, если учесть третий и четвертый члены разложения. На рис. 7 приведено распределение p(4) = p(x, z) = = 1.1481 + pα(z)x3.8848 + 0.353dpα(z)/dzx4.8848 – 0.081d2pα(z)/dz2x5.8848, (четырехчленное разложение) на поверхности пластины при тех же определяющих параметрах. Теперь на задней кромке пластины минимальные значения давления равны ∼0.58, а максимальные ∼2.2, т.е. разница между ними составляет ∆p = 1.62. Таким образом, не только изменился характер распределения давления на задней кромке, но и его перепад увеличился более чем в 8 раз. Используя полученные распределения давления, с помощью выражения (2.3) можно рассчитать скорость вдувания ${v}_{w}^{0}$(x0, z0) (в размерном виде), которую необходимо обеспечить, чтобы получить данное распределение индуцированного давления.

Рис. 6.

Индуцированное давление p(2) на поверхности пластины: β = 45°, ${{{v}}_{w}}$ = 0.5; pα(z) = 0.2cos6(πz).

Рис. 7.

Индуцированное давление p(4) на поверхности пластины: β = 45°, ${{{v}}_{w}}$ = 0.5; pα(z) = 0.2cos6(πz).

ЗАКЛЮЧЕНИЕ

Построены четырехчленные разложения для функций течения в пространственном пограничном слое в окрестности передней кромки скользящей пластины конечной длины, по нормали к которой вдувается газ, в случае, когда на ее задней кромке задается распределение давления, зависящее от поперечной координаты. В результате решения краевой задачи для второго члена разложения определены собственные числа. Показано, что при решении систем уравнений для третьего и четвертого членов разложения однозначно определяются сомножители в этих членах для индуцированного давления. Выявлено сильное влияние угла скольжения и интенсивности вдува на характеристики течения в пространственном пограничном слое. Впервые обнаружено, что при определенной интенсивности вдува возможна ситуация, когда собственные числа практически перестают зависеть от угла скольжения пластины. Установлено, что при наличии угла скольжения и/или вдува необходимо обязательно учитывать третий и четвертый члены разложения, если на задней кромке пластины появляются достаточно большие первые и вторые производные от давления по поперечной координате.

Список литературы

  1. Lees L. On the boundary-layer equations in hypersonic flow and their approximate solutions // J. Aeronaut. Sci. 1953. № 20 (20). P. 143–145.

  2. Stewartson K. On the motion of a flat plate at high speed in a viscous compressible fluid. II Steady motion // J. Aeronaut. Sci. 1955. № 22 (5). P. 303–309.

  3. Нейланд В.Я. Распространение возмущений вверх по течению при взаимодействии гиперзвукового потока с пограничным слоем // Изв. АН СССР. МЖГ. 1970. № 4. С. 40–49.

  4. Нейланд В.Я., Боголепов В.В., Дудин Г.Н., Липатов И.И. Асимптотическая теория сверхзвуковых течений вязкого газа. М.: Физматлит, 2003, 456 с.

  5. Brown S.N., Stewartson K. A non-uniqueness of the hypersonic boundary layer // Q. J. Mech. Appl. Math. 1975. V. XXVIII. Pt. 1. P. 75–90.

  6. Коваленко А.А. Исследование отрыва пограничного слоя при сильном взаимодействии с гиперзвуковым потоком газа // Уч. зап. ЦАГИ. 1974. Т. V. № 6. С. 39–47.

  7. Дудин Г.Н., Нейланд В.Я. Об индуцировании трехмерных возмущений в пограничном слое при сильном взаимодействии с гиперзвуковым потоком // Изв. РАН. МЖГ. 2018. № 1. С. 89–96.

  8. Дудин Г.Н., Нейланд В.Я. Влияние температуры поверхности пластины на распространение возмущений при гиперзвуковом обтекании // Уч. зап. ЦАГИ. 2018. Т. XLIX. № 5. С. 3–16.

  9. Whalen R.J. Boundary-layer interaction on a yawed infinit wing in hypersonic flow // JASS. 1959. V. 26, № 12. P. 839–841.

  10. Козлова И.Г., Михайлов В.В. О сильном вязком взаимодействии на треугольном и скользящем крыльях // Изв. АН СССР. МЖГ. 1970. № 4. С. 94–99.

  11. Дудин Г.Н., Нейланд В.Я. О распространении возмущений на скользящей пластине на режиме сильного взаимодействия // ДАН 2018. Т. 483. № 1. С. 33–36.

  12. Дудин Г.Н., Нейланд В.Я. Об особенностях гиперзвукового обтекания скользящей пластины // ДАН 2019. Т. 487. № 1. С. 23–26.

  13. Дудин Г.Н., Нейланд В.Я. О влиянии температурного фактора на распространение возмущений при гиперзвуковом обтекании скользящей пластины // Изв. РАН. МЖГ. 2019. № 5. С. 59–69.

  14. Нейланд В.Я. Вдувание газа в гиперзвуковой поток // Уч. зап. ЦАГИ. 1972. Т. 3. № 6. С. 32–39.

  15. Липатов И.И. Распределенный вдув газа в гиперзвуковой поток // ПМТФ. 1987. № 6. С. 57–61.

  16. Дудин Г.Н. Вдув газа на поверхности треугольной пластины в гиперзвуковом потоке // Изв. РАН. МЖГ. 2000. № 1. С. 125–133.

  17. Балашов А.А., Дудин Г.Н. Обтекание пластины на режиме сильного взаимодействия при наличии массообмена // Труды МФТИ. 2015. Т. 7. № 1. С. 16–27.

  18. Дудин Г.Н., Нейланд В.Я. Влияние вдува на поверхности клина на распространение возмущений при гиперзвуковом обтекании // Уч. зап. ЦАГИ. 2019. Т. L. № 6. С. 17–32.

  19. Hayes W.D., Probstein R.F. Hypersonic flow theory. N.Y.; L.: Acad. Press, 1959.

  20. Stollery J.L. Laminar and turbulent boundary layer studies at hypersonic speeds // ICAS Paper. 1972. N 72−09.

  21. Дудин Г.Н. Треугольные крылья в вязком гиперзвуковом потоке. М.: МФТИ, 2011. 258 с.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Известия РАН. Механика жидкости и газа

Архивы выпусков Информация о журнале Отправить рукопись в журнал