1. На главную
  2. Электронные версии
  3. Известия РАН. Механика жидкости и газа
  4. № 3, 2022

Известия РАН. Механика жидкости и газа, 2022, № 3, стр. 44-55

ВОЛНЫ УПЛОТНЕНИЯ С ЧАСТИЧНОЙ И ПОЛНОЙ ДИСПЕРСИЕЙ В ГАЗОКАПЕЛЬНОЙ СРЕДЕ С ФАЗОВЫМИ ПЕРЕХОДАМИ

И. В. Голубкина a, *, А. Н. Осипцов a, **

a МГУ им. М.В. Ломоносова, Научно-исследовательский институт механики
Москва, Россия

* E-mail: giv-mm@mail.ru
** E-mail: osiptsov@imec.msu.ru

Поступила в редакцию 21.11.2021
После доработки 21.12.2021
Принята к публикации 21.12.2021

Полный текст (PDF)

Аннотация

Рассматриваются задачи о структуре прямой и косой волн уплотнения в газокапельной среде при наличии испарения на поверхности капель, а также симметричное взаимодействие (или отражение от стенки) косых скачков уплотнения в такой среде. Основное внимание уделено малоисследованным вопросам нахождения границ существования волн качественно различной структуры в пространстве безразмерных определяющих параметров. С использованием обобщенных соотношений Рэнкина–Гюгонио определены условия существования волн с частичной и полной дисперсией при полном и неполном испарении дисперсной фазы. Проведены численные расчеты, иллюстрирующие распределения параметров фаз в волнах различной структуры. Впервые найдены диапазоны параметров двухфазного потока и характеристик пересекающихся косых скачков уплотнения в газокапельной среде с испаряющимися каплями, при которых отраженные скачки вырождаются в волны с полной дисперсией либо полностью исчезают.

Ключевые слова: газокапельный поток, капли, испарение, скачки уплотнения, волны с полной дисперсией, обобщенные соотношения Рэнкина–Гюгонио, структура волны, взаимодействие скачков уплотнения, регулярное отражение волн

Паро- и газокапельные потоки широко распространены в природе и технике (теплоэнергетические и химикотехнологические аппараты, паровые турбины, камеры сгорания, системы охлаждения, движение летательных аппаратов в облаках и др.), что стимулирует непрерывное развитие механики аэродисперсных систем. В высокоскоростных газокапельных течениях существенную роль играет массо- и теплообмен между фазами, обусловленный наличием фазовых переходов (испарения и конденсации). Исследования волновых процессов в газокапельных средах имеют уже значительную историю (например, [1–10]). Подробно изучены задачи о распространении акустических возмущений в газо- и парокапельных средах в отсутствие и при наличии фазовых переходов [2]. Имеются экспериментальные исследования и численные расчеты структуры зон скоростной и тепловой релаксации фаз за ударными волнами в таких средах [1, 3, 4, 7, 8], в том числе, с учетом дробления крупных капель и образования мелкодисперcной фазы [10]. В литературе можно найти и отдельные численные расчеты нестационарных задач о распространении ударных волн и их отражении от препятствий в нестационарном потоке [9]. Опубликованные исследования посвящены, в основном, двухфазным потокам с крупными инерционными каплями. В то же время ряд вопросов фундаментального характера остался малоизученным. К таким вопросам относятся условия существования так называемых “волн с полной дисперсией” при наличии испарения капель, а также структура волн уплотнения в туманообразных средах с мелкими каплями при полном испарении капель. В литературе имеются лишь отдельные публикации на эту тему [4–6], где отмечены трудности исследования структуры волн с полностью испаряющимися каплями. Анализу условий существования волн уплотнения различной структуры в туманообразной среде с испаряющимися каплями посвящена первая часть настоящей статьи.

Авторам неизвестны публикации, в которых бы рассматривались задачи о пересечении ударных волн и отражении косых скачков от твердых стенок в стационарных газокапельных потоках с фазовыми переходами. Современной мотивацией для рассмотрения таких задач является продолжающийся поиск новых способов “безмашинного газодинамического энергоразделения”, т.е. поиск таких схем течения, при которых происходит разделение исходного однородного газового потока на два потока, имеющих существенно различающиеся температуры торможения, без совершения работы и в отсутствие внешнего теплообмена. Одной из таких схем течения, представляющих альтернативу хорошо известным вихревым трубкам Ранка–Хилша, является так называемая “труба Леонтьева”, в которой энергоразделение осуществляется за счет теплообмена между сверх- и дозвуковым газовыми потоками, разделенными тонкой теплопроводной перегородкой [11]. В последние годы проводятся исследования различных способов повышения эффективности этой схемы энергоразделения, в том числе – за счет добавления в поток мелких жидких капель, позволяющих снизить температуру восстановления стенки со стороны сверхзвукового потока [12]. В недавней экспериментальной работе [13] сделана попытка использования центрального тела в сверхзвуком газокапельном потоке для создания коcой ударной волны, приходящей на стенку, с целью активизации осаждения капель и интенсификации теплоотдачи стенки. Интерпретация полученных результатов ставит вопросы о структуре течения, формирующегося при отражении косой ударной волны от стенки в газокапельном потоке, о параметрах отраженной волны, условиях отсутствия отраженной волны и др. Эти вопросы обсуждаются в заключительной части данной статьи.

1. О МОДЕЛИ ГАЗОКАПЕЛЬНОЙ СРЕДЫ С ИСПАРЯЮЩИМИСЯ КАПЛЯМИ

В качестве базовой модели газокапельной среды при наличии фазовых переходов на поверхности капель используется классическая двухжидкостная модель [14], в которой объемная концентрация дисперсной фазы считается малой, пренебрегается столкновениями капель и различием термодинамических свойств пара вещества капель и несущей газовой среды. Считается, что несущая фаза – сжимаемый совершенный газ с постоянными теплоемкостями, вязкость и теплопроводность которого зависят от температуры по степенному закону: λ/λ0 = μ/μ0 = (T/T0)ω; индекс 0 относится к параметрам невозмущенного потока. Дисперсная фаза – мелкие монодисперсные сферические капли. Масса m и радиус $\sigma $ капель изменяются в процессе их движения из-за испарения. Стационарное течение среды капель описывается уравнениями континуума, лишенного собственных напряжений:

(1.1)
$\begin{gathered} {\text{div}}({{n}_{s}}{{{\mathbf{V}}}_{s}}) = 0,\quad m({{{\mathbf{V}}}_{s}}\nabla ){{{\mathbf{V}}}_{s}} = {{{\mathbf{f}}}_{s}},\quad ({{{\mathbf{V}}}_{s}}\nabla )m = - J \\ {{c}_{s}}m({{{\mathbf{V}}}_{s}}\nabla )\left\langle {{{T}_{s}}} \right\rangle = {{q}_{{in}}},\quad {{q}_{{in}}} = {{q}_{s}} - JH \\ \end{gathered} $

Здесь ns – числовая плотность капель, Vs – их скорость, cs – теплоемкость вещества капель, J – поток массы с поверхности капли за счет испарения в единицу времени, $\left\langle {{{T}_{s}}} \right\rangle $ – температура вещества капли, осредненная по ее объему, fs – сила аэродинамического сопротивления капли, qs – приток тепла к поверхности капли со стороны газовой фазы, qin – отток тепла от поверхности внутрь капли, H – скрытая удельная теплота парообразования. Последнее уравнение в (1.1) есть условие баланса энергии на поверхности капли. Предполагается, что в большей части области течения капли обтекаются при малых числах Рейнольдса, испарение происходит радиально симметрично и с очень малой скоростью, поэтому можно использовать выражения для fs и qs как для стационарного обтекания сферы с мгновенным значением радиуса σ:

(1.2)
${{{\mathbf{f}}}_{s}} = 6\pi \sigma \mu ({\mathbf{V}} - {{{\mathbf{V}}}_{s}}),\quad {{q}_{s}} = 4\pi \sigma \lambda (T - {{T}_{{sw}}})G$

Здесь V и T – скорость и температура несущей фазы, Tsw – температура поверхности капли. Завершающая фаза испарения капель проходит в переходном и свободномолекулярном режиме, при этом в законах силового и теплового взаимодействия фаз следует учитывать поправки на конечность чисел Кнудсена обтекания капель. Однако на этой стадии скорости газа и мелких капель уже практически совпадают, поэтому влияние поправки в выражении для силы сопротивления на распределения параметров фаз в зоне релаксации оказывается несущественным. В то же время поправка G(Kn) в выражении для межфазного потока тепла может заметно повлиять на распределения параметров фаз в поле течения, поскольку при некоторых значениях параметров задачи после завершения релаксации скоростей фаз рассогласование их температур может оставаться конечным еще на значительном расстоянии. Для поправки G в выражении для теплового потока в расчетах использованы формулы, часто используемые в литературе [5]:

$\begin{gathered} G = \frac{1}{{1 + 4.5{{{\text{Kn}}} \mathord{\left/ {\vphantom {{{\text{Kn}}} {\Pr }}} \right. \kern-0em} {\Pr }}}},\quad {\text{Kn}} = \frac{\delta }{{2\sigma }} \\ \delta = \frac{\mu }{p}\sqrt {0.5\pi RT} = \mu \sqrt {\frac{\pi }{{2p\rho }}} \\ \end{gathered} $

Здесь δ – средняя длина свободного пробега молекул несущей фазы, ρ и p – плотность и давление несущей фазы, R – газовая постоянная, Pr – число Прандтля.

Уравнения стационарного течения несущей фазы с учетом обмена массой, импульсом и энергией с дисперсной фазой записываются в следующем виде (вязкость и теплопроводность несущей фазы учитываются лишь при описании межфазного взаимодействия) [14]:

(1.3)
$\begin{gathered} {\text{div}}(\rho {\mathbf{V}}) = {{n}_{s}}J \\ ({\mathbf{V}}\nabla ){\mathbf{V}} = - \nabla p - {{n}_{s}}{{{\mathbf{f}}}_{s}} + {{n}_{s}}J({{{\mathbf{V}}}_{s}} - {\mathbf{V}}) \\ {{c}_{p}}\rho ({\mathbf{V}}\nabla )T = ({\mathbf{V}}\nabla )p - {{n}_{s}}{{q}_{s}} + {{n}_{s}}{{{\mathbf{f}}}_{s}}({\mathbf{V}} - {{{\mathbf{V}}}_{s}}) + {{n}_{s}}J[{{({\mathbf{V}} - {{{\mathbf{V}}}_{s}})}^{2}}{\text{/}}2 + {{c}_{p}}({{T}_{{sw}}} - T)] \\ p = \rho RT \\ \end{gathered} $

Здесь cp – теплоемкость газа при постоянном давлении.

Для замыкания постановок задач для уравнений (1.1)–(1.3) необходимо задать связь между средней температурой капли $\left\langle {{{T}_{s}}} \right\rangle $ и температурой ее поверхности Tsw, определить способ вычисления потока массы с поверхности испаряющейся капли J, а также сформулировать граничные условия.

Для простоты принимается, что в невозмущенном потоке имеет место скоростное (V = Vs = V0), температурное T = Ts = T0 и термодинамическое равновесие фаз (радиус σ0 и числовая плотность капель ns0 постоянны). Используется наиболее простая модель испарения капли, согласно которой весь тепловой поток, приходящий к поверхности капли со стороны газовой фазы, тратится на испарение, т.е. qin = 0 и

(1.4)
$J = 4\pi \sigma \lambda (T--{{T}_{0}})G{\text{/}}H$

Эта модель реализуется, если при внедрении капли, имеющей температуру невозмущенного потока, в область горячего газа за ударной волной, температура поверхности капли изменяется очень мало (Tsw ≈ T0). Естественно считать, что на поверхности капли имеют место условия равновесного испарения, описываемые уравнением Клапейрона–Клаузиуса. В случае испарения капель в инородный газ (например, в смеси “воздух–водяные капли”), когда скорость испарения лимитируется диффузией, имеющиеся в литературе решения для температуры капли показывают приближенную справедливость предположения о постоянстве температуры капли при ее внедрении в область нагретого газа при не слишком больших изменениях давления [15]. Этот факт объясняется очевидной оценкой для относительного изменения равновесной температуры поверхности испаряющейся капли, следующей из условия Клапейрона–Клаузиуса

$\frac{{{{T}_{{sw}}} - {{T}_{0}}}}{{{{T}_{{sw}}}}} = \frac{{{{R}_{{v}}}{{T}_{0}}}}{H}\ln \left( {\frac{{{{p}_{{{v}w}}}}}{{{{p}_{{{v}0}}}}}} \right)$

Здесь ${{p}_{{{v}w}}}$ и ${{p}_{{{v}0}}}$ – текущее (в окрестности капли) и начальное (в невозмущенном потоке) значения давления насыщенных паров вещества капли вблизи ее поверхности, ${{R}_{{v}}}$ – газовая постоянная паров вещества капель. Даже когда давление насыщенных паров вблизи поверхности капли увеличивается на порядок при ее движении в неоднородном горячем газе, логарифм отношения ${{p}_{{{v}w}}}$/${{p}_{{{v}0}}}$ остается величиной порядка единицы. Например, для капель воды в воздухе при T0 = 300 K имеем ${{R}_{{v}}}$ ≈ 0.4 Дж/(г град), H ≈ 2.4 × 103 Дж/г, коэффициент перед логарифмом равен 0.05, и, следовательно, даже при изменении на порядок величины ${{p}_{{v}}}$/${{p}_{{{v}0}}}$ относительное изменение температуры капли не превысит единиц процентов. При испарении капель в собственный пар вместо парциальных давлений в соотношении Клапейрона–Клаузиуса следует взять значения истинных давлений в паре. В качестве еще одного примера можно рассмотреть прохождение капель через фронт ударной волны с числом Маха М = 2. При этом давление за волной увеличивается приблизительно в 4.5 раза, а значение логарифма приблизительно равно 1.5. Таким образом, использование упрощенной модели для вычисления скорости испарения (1.4) в рассматриваемых ниже задачах о структуре волн уплотнения вполне оправдано, тем более что такое приближение кардинально упрощает всю процедуру построения и анализа решений. В противном случае потребовалось бы решать уравнение теплопроводности внутри капель одновременно с решением макроуравнений двухконтинуальной среды, как это сделано в [16]. В рамках принятой упрощенной модели испарения средняя по объему температура капли равна температуре ее поверхности и температуре невозмущенного потока: 〈Ts〉 = Tsw = T0.

Следует отметить, что при движении испаряющихся капель в инородном газе игнорируется зависимость теплофизических параметров и коэффициентов переноса смеси от концентрации паров вещества капель. Это оправдано лишь в рассматриваемом случае небольших массовых концентраций примеси.

2. ОБОБЩЕННЫЕ СООТНОШЕНИЯ РЭНКИНА–ГЮГОНИО НА СКАЧКАХ В ГАЗЕ С ИСПАРЯЮЩИМИСЯ КАПЛЯМИ

Ниже рассматриваются задачи о существовании и структуре волн уплотнения в газокапельных средах с фазовыми переходами, т.е. одномерные течения в релаксационной зоне, соединяющей два равновесных состояния газокапельной смеси.

Прямая волна уплотнения в газокапельной среде, как правило, представляет собой ударную волну в газе (поверхность сильного разрыва параметров газа), за которой следует зона неравновесного по скоростям и температурам фаз течения. Капли проходят через скачок в несущей фазе, сохраняя исходные значения всех своих параметров. Далее, в релаксационной зоне, происходит выравнивание скоростей фаз и испарение капель, поскольку температура газа сразу за скачком уплотнения увеличивается. Зона неравновесного течения заканчивается, когда: а) капли полностью испарятся, т.е. за зоной релаксации течение становится однофазным, или б) скорости и температуры фаз выравниваются, и достигается новое равновесное состояние. Ударная волна вместе с зоной релаксации параметров фаз в литературе иногда называется “волной с частичной дисперсией”, поскольку параметры несущей фазы имеют разрыв, а параметры дисперсной фазы непрерывны. В газокапельных средах возможно также возникновение “волн с полной дисперсией” параметров. В такой волне отсутствует газодинамический разрыв, а изменение параметров обеих фаз происходит непрерывно. Такие волны возможны, когда двухфазный поток является эффективно сверхзвуковым, т.е. число Маха, посчитанное по параметрам смеси, Mef > 1, а число Маха по параметрам несущей газовой фазы M0 < 1. Состояния двухфазной среды до волны и в зоне, расположенной далеко вниз по течению, описываются уравнениями односкоростной и однотемпературной модели “эффективного газа” с суммарной плотностью и эффективными термодинамическими параметрами смеси [14]. Для двухфазной смеси суммарная плотность и безразмерные эффективные параметры определяются так [14]:

(2.1)
${{{{\rho }}}_{{ef}}} = (1 + {{\alpha }}){{\rho }},\quad {{{{\gamma }}}_{{ef}}} = {{\gamma }}\frac{{{\text{1}} + {{\alpha \chi }}}}{{{\text{1}} + {{\alpha \gamma \chi }}}},\quad {\text{M}}_{{ef}}^{2} = {\text{M}}_{{\text{0}}}^{{\text{2}}}\frac{{({\text{1}} + {{\alpha }})({\text{1}} + {{\alpha \gamma \chi }})}}{{({\text{1}} + {{\alpha \chi }})}}$

Здесь α = mns/ρ – относительная массовая концентрация капель, γ – показатель адиабаты, χ = cs/cp – отношение теплоемкости вещества капель к теплоемкости газа при постоянном давлении. На масштабе, много большем ширины зоны неравновесного течения, волну с полной и частичной дисперсией можно рассматривать как газодинамический разрыв в “эффективном газе” (в общем случае, с изменением уравнений состояния и теплоотводом за счет фазового перехода).

Чтобы вывести обобщенные соотношения Рэнкина–Гюгонио, связывающие параметры равновесного невозмущенного потока и равновесного потока в дальней области вниз по течению, запишем уравнения баланса массы, импульса и энергии для среды в целом. В системе координат, начало отсчета которой лежит в невозмущенном потоке, складывая попарно уравнения балансов массы, импульса и энергии фаз из (1.1), получаем дивергентную форму уравнений баланса массы, импульса и энергии для среды в целом:

(2.2)
$\begin{gathered} \frac{d}{{dx}}(\rho u + m{{n}_{s}}{{u}_{s}}) = 0 \\ \frac{d}{{dx}}(p + \rho {{u}^{2}} + m{{n}_{s}}u_{s}^{2}) = 0 \\ \frac{d}{{dx}}\left[ {\rho u\left( {{{c}_{p}}T + \frac{{{{u}^{2}}}}{2}} \right) + m{{n}_{s}}{{u}_{s}}\left( {{{c}_{p}}{{T}_{s}} - H + \frac{{u_{s}^{2}}}{2}} \right)} \right] = 0 \\ \end{gathered} $

При выводе последнего соотношения в (2.2) использовано определение скрытой теплоты парообразования как разности энтальпий в жидкой фазе и паре на границе испаряющейся капли: H = cpTs – csTs + H0, где H0 = const.

В случае волны с полной дисперсией все параметры обеих фаз остаются непрерывными. В случае волны с частичной дисперсией имеется фронт сильного разрыва для параметров несущей фазы, однако на этом разрыве потоки массы, импульса и энергии несущей фазы непрерывны и все параметры среды частиц сохраняются. Поэтому в обоих случаях из (2.2) следует очевидная связь параметров среды в невозмущенном потоке (индекс 0) и в области равновесного течения далеко вниз по потоку (индекс 1)

(2.3)
$\begin{gathered} {{{{\rho }}}_{0}}{{u}_{0}}(1 + {{{{\alpha }}}_{0}}) = {{{{\rho }}}_{1}}{{u}_{1}}(1 + {{{{\alpha }}}_{1}}),\quad {{{{\alpha }}}_{i}} = {{m}_{i}}{{n}_{{si}}}{\text{/}}{{{{\rho }}}_{i}} \\ {{p}_{0}} + (1 + {{{{\alpha }}}_{0}}){{{{\rho }}}_{0}}u_{0}^{2} = {{p}_{1}} + (1 + {{{{\alpha }}}_{1}}){{{{\rho }}}_{1}}u_{1}^{2} \\ \frac{{u_{0}^{2}}}{2} + {{c}_{p}}{{T}_{0}} - \frac{{{{{{\alpha }}}_{0}}H}}{{1 + {{{{\alpha }}}_{0}}}} = \frac{{u_{1}^{2}}}{2} + {{c}_{p}}{{T}_{1}} - \frac{{{{{{\alpha }}}_{1}}H}}{{1 + {{{{\alpha }}}_{1}}}} \\ \end{gathered} $

Здесь учтено, что Ts = T0. Формулы (2.3), совместно с уравнением состояния совершенного газа, можно считать обобщенными соотношениями Рэнкина–Гюгонио для скачков уплотнения в газокапельных средах с испаряющимися каплями в рамках принятой модели. Ранее соотношения на разрывах в эффективной среде без фазовых переходов использовались в [17] для анализа границ существования различных волновых структур в газах с твердыми частицами.

Если капли полностью испаряются в зоне релаксации, то к соотношениям (2.2) добавляется условие α1 = 0. Если к наступлению нового состояния равновесия капли не успевают полностью испариться, то реализуется дополнительное условие T1 = T0.

Для несущей среды, описываемой моделью совершенного газа с постоянными теплоемкостями, из (2.3) все параметры за волной, отнесенные к соответствующим параметрам до волны, можно выразить аналитически через безразмерные определяющие параметры M0, α0, γ, Pr и a. В случае полного испарения капель за волной (α1 = 0) параметры газа далеко вниз по потоку выражаются следующим образом:

(2.4)
$\begin{gathered} \frac{{{{\rho }_{1}}}}{{{{\rho }_{0}}}} = (1 + {{\alpha }_{0}})\frac{{{{u}_{0}}}}{{{{u}_{1}}}} = \frac{{{{{(1 + {{\alpha }_{0}})}}^{2}}{\text{(1}} + \gamma {\text{)M}}_{0}^{2}}}{{1 + (1 + {{\alpha }_{0}})\gamma {\text{M}}_{0}^{2} - \sqrt D }} \\ \frac{{{{p}_{1}}}}{{{{p}_{0}}}} = 1 + \frac{\gamma }{{1 + \gamma }}[(1 + {{\alpha }_{0}}){\text{M}}_{0}^{2} - 1 + \sqrt D ] \\ \frac{{{{T}_{1}}}}{{{{T}_{0}}}} = \frac{{{{p}_{1}}}}{{{{p}_{0}}}}\frac{{{{\rho }_{0}}}}{{{{\rho }_{1}}}} \\ D = {{[(1 + {{\alpha }_{0}}){\text{M}}_{0}^{2} - 1]}^{2}} + 2{{\alpha }_{0}}(1 + {{\alpha }_{0}})(1 + \gamma ){\text{M}}_{0}^{2}(E - 1) \\ E = \frac{2}{{3a\Pr }} = \frac{H}{{{{c}_{p}}{{T}_{0}}}},\quad a = \frac{{2{{c}_{p}}{{T}_{0}}}}{{3H\Pr }} \\ \end{gathered} $

Здесь a – безразмерный параметр, характеризующий скорость испарения капель. В случае неполного испарения капель за волной (α1 ≠ 0, T1 = T0) выражения для равновесных параметров за волной принимают следующий вид:

(2.5)
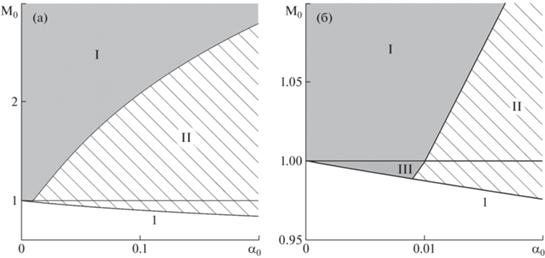
$\begin{gathered} \frac{{{{u}_{1}}}}{{{{u}_{0}}}} = \frac{{2E + (1 + {{\alpha }_{0}}){\text{(}}\gamma - {\text{1)M}}_{0}^{2}}}{{(1 + {{\alpha }_{0}}){\text{M}}_{0}^{2}\left( {2\gamma E - \left( {\gamma - 1} \right)} \right)}} \\ \frac{{{{\rho }_{1}}}}{{{{\rho }_{0}}}} = \frac{{{{p}_{1}}}}{{{{p}_{0}}}} = \frac{{2(1 + {{\alpha }_{0}})\gamma {\text{M}}_{0}^{2}\left( {\kappa E - 1} \right) - 1}}{{2\kappa E - 1}},\quad \kappa = \frac{\gamma }{{\gamma - 1}} \\ {{{{\alpha }}}_{1}} = (1 + {{{{\alpha }}}_{0}})\frac{{{{{{\rho }}}_{0}}}}{{{{{{\rho }}}_{1}}}}\frac{{{{u}_{0}}}}{{{{u}_{1}}}} - 1 \\ \end{gathered} $

Для установления границ существования волн различной структуры были проведены численные расчеты, в которых варьировались в основном два параметра: число Маха M0, посчитанное по параметрам несущей фазы в невозмущенном потоке, и исходная массовая доля капель α0. Остальные параметры были приняты следующими: γ = 1.4, Pr = 0.72 и a = 0.1, что по порядку величины соответствует случаям, наиболее интересным для приложений. Сначала для каждого рассматриваемого набора параметров M0 и α0 анализируется существование решения (2.5) с α1 > 0 и p1/p0 > 1. Если такое решение существует, то при таких параметрах реализуется волна, в которой капли не испаряются полностью. В противном случае находится решение (2.4) и определяются параметры, соответствующие полному испарению капель. Волнам с полной дисперсией соответствуют решения, когда M0 < 1, но Mef > 1. На рис. 1а показаны рассчитанные области параметров M0, α0, отвечающие полному (I) и неполному (II) испарению капель. Область выше линии M0 = 1 соответствует волнам с частичной дисперсией, а ниже – волнам с полной дисперсией. Кривая 1, соответствующая условию Mef = 1, ограничивает снизу области существования волн уплотнения в газокапельном потоке. На рис. 1б более подробно показана сравнительно малая область (III), соответствующая волнам с полной дисперсией и полным испарением капель.

Рис. 1.

Области существования прямой волны с частичной и полной дисперсией в случае полного (I, III) и неполного (II) испарения капель за волной.

Все полученные выше результаты легко обобщаются на случай косых волн уплотнения. Поскольку на косом скачке касательные скорости обеих фаз (${v}$, ${{{v}}_{s}}$) непрерывны, и в зоне релаксации ${v}$ = ${{{v}}_{s}}$ = ${{{v}}_{0}}$, течения в направлениях нормали и касательной к волне могут быть рассмотрены независимо. Таким образом, в случае косой волны полученные обобщенные соотношения Рэнкина–Гюгонио (2.3) и формулы (2.4)–(2.5) справедливы для нормальных к косой волне компонент скорости фаз. Число Маха M0 в этом случае также следует считать по нормальной к волне компоненте скорости.

3. СТРУКТУРА ВОЛН С ЧАСТИЧНОЙ И ПОЛНОЙ ДИСПЕРСИЕЙ В ГАЗОКАПЕЛЬНОЙ СРЕДЕ

Для численного исследования структуры зоны релаксации в волне уплотнения запишем уравнения модели (1.1) для нормальных к скачку компонент скорости в безразмерном виде, отнеся все параметры к их значениям в невозмущенном потоке:

$x = \frac{{x{\text{*}}}}{{l_{{v}}^{*}}},\quad u = \frac{{u{\text{*}}}}{{u_{0}^{*}}},\quad \rho = \frac{{\rho {\text{*}}}}{{\rho _{0}^{*}}},\quad T = \frac{{T{\text{*}}}}{{T_{0}^{*}}},\quad p = \frac{{p{\text{*}}}}{{\rho _{0}^{*}RT_{0}^{*}}},\quad \mu = \frac{{\mu {\text{*}}}}{{\mu _{0}^{*}}},\quad \lambda = \frac{{\lambda {\text{*}}}}{{\lambda _{0}^{*}}}$
${{u}_{s}} = \frac{{u_{s}^{*}}}{{u_{0}^{*}}},\quad {{T}_{s}} = \frac{{T_{s}^{*}}}{{T_{0}^{*}}},\quad {{n}_{s}} = \frac{{n_{s}^{*}}}{{n_{{s0}}^{*}}},\quad \sigma = \frac{{\sigma {\text{*}}}}{{\sigma _{0}^{*}}},\quad \delta = \frac{{\delta {\text{*}}}}{{\delta _{0}^{*}}},\quad l_{{v}}^{*} = \frac{{m_{0}^{*}u_{0}^{*}}}{{6\pi \sigma _{0}^{*}\mu _{0}^{*}}}$
(3.1)
$\frac{d}{{dx}}(\rho u) = \alpha a\lambda {{n}_{s}}\sigma (T - 1)G,\quad {{n}_{s}}{{u}_{s}} = 1,\quad {{\sigma }^{2}}{{u}_{s}}\frac{{d{{u}_{s}}}}{{dx}} = \mu \left( {u - {{u}_{s}}} \right)$
$\sigma {{u}_{s}}\frac{{d\sigma }}{{dx}} = \frac{{a\mu (1 - T)G}}{3},\quad G = \frac{1}{{1 + 4.5{\text{Kn/}}\Pr }},\quad {\text{Kn}} = {\text{K}}{{{\text{n}}}_{0}}\frac{\mu }{{\sqrt {p\rho } }}$
${{\rho }}u\frac{{du}}{{dx}} = - \frac{1}{{{{\gamma }}{{\operatorname{M} }^{2}}}}\frac{{dp}}{{dx}} + \alpha {{\mu }}{{n}_{s}}{{\sigma }}\left( {{{u}_{s}} - u} \right) + \alpha a{{\lambda }}{{n}_{s}}{{\sigma }}(T - 1)G({{u}_{s}} - u)$
$\begin{gathered} \rho u\frac{{dT}}{{dx}} = u\frac{{\gamma - 1}}{\gamma }\frac{{dp}}{{dx}} + \frac{{2\alpha }}{{3\Pr }}{{n}_{s}}\sigma \lambda \left( {1 - T} \right)G + \alpha (\gamma - 1){\text{M}}_{0}^{2}{{n}_{s}}\mu \sigma {{(u - {{u}_{s}})}^{2}} - \\ - \;\alpha a\sigma \lambda {{n}_{s}}{{(T - 1)}^{2}}G + \frac{1}{2}\alpha a(\gamma - 1){\text{M}}_{0}^{2}\lambda {{n}_{s}}\sigma (T - 1)G{{(u - {{u}_{s}})}^{2}} \\ \end{gathered} $
$\begin{gathered} {{T}_{s}} = 1,\quad p = \rho T,\quad \lambda = \mu = {{T}^{\omega }} \\ \alpha = \frac{{m_{0}^{*}n_{{s0}}^{*}}}{{\rho _{0}^{*}}},\quad a = \frac{{2{{c}_{p}}T_{0}^{*}}}{{3H\Pr }},\quad \Pr = \frac{{{{c}_{p}}\mu _{0}^{*}}}{{\lambda _{0}^{*}}},\quad {{{\text{M}}}_{0}} = \frac{{u_{0}^{*}}}{{\sqrt {\gamma RT_{0}^{*}} }},\quad {\text{K}}{{{\text{n}}}_{0}} = \frac{{\delta _{0}^{*}}}{{2\sigma _{0}^{*}}} \\ \end{gathered} $

В этом параграфе все переменные величины, кроме отмеченных звездочками, являются безразмерными. Система уравнений (3.1) содержит следующие независимые параметры подобия: показатель адиабаты газовой фазы γ, число Маха М0, посчитанное по нормальной к волне компоненте скорости несущей фазы в невозмущенном потоке, число Прандтля газа Pr, относительную массовую концентрацию капель в невозмущенном потоке α, параметр a, характеризующий скорость испарения капель, и степенной показатель ω.

В невозмущенном потоке имеем

(3.2)
$x = 0{\text{:}}\,\,u = T = \rho = {{u}_{s}} = {{n}_{s}} = \sigma = 1$

Постановки и методы численного решения задач о структуре волн с частичной и полной дисперсией отличаются.

При расчете структуры волн с частичной дисперсией (M0 > 1) безразмерные параметры несущей фазы сразу за газодинамическим разрывом находятся из стандартных соотношений Рэнкина–Гюгонио для газа

(3.3)
$\begin{gathered} {{\rho }_{ + }} = \frac{{(\gamma + 1){\text{M}}_{0}^{2}}}{{2 + (\gamma - 1){\text{M}}_{0}^{2}}},\quad {{u}_{ + }} = \frac{{2 + (\gamma - 1){\text{M}}_{0}^{2}}}{{(\gamma + 1){\text{M}}_{0}^{2}}} \\ {{T}_{ + }} = \frac{{[2\gamma {\text{M}}_{0}^{2} - (\gamma - 1)][(\gamma - 1){\text{M}}_{0}^{2} + 2]}}{{{{{(\gamma + 1)}}^{2}}{\text{M}}_{0}^{2}}} \\ \end{gathered} $

Здесь индекс “плюс” отмечает безразмерные значения параметров среды сразу за фронтом газодинамического разрыва. Частицы пересекают фронт ударной волны в газе без изменения значений своих параметров

(3.4)
${{u}_{{s + }}} = {{n}_{{s + }}} = {{\sigma }_{ + }} = 1$

Таким образом, имеем задачу Коши для системы обыкновенных дифференциальных уравнений (3.1) с граничными условиями (3.3)–(3.4). Указанная задача решалась численно методом Рунге–Кутты.

При расчете структуры волн с полной дисперсией (M0 < 1, но Mef > 1) соотношения (3.2) являются граничными условиями на левой границе расчетной области, а условия на правой границе находятся из обобщенных условий Рэнкина–Гюгонио, полученных в предыдущем разделе. Таким образом, в этом случае для системы (3.1) получаем краевую задачу. Левые и правые граничные условия заданы в особых точках дифференциальных уравнений, что затрудняет непосредственный расчет искомого решения, поэтому был использован следующий численный алгоритм. Система уравнений (3.1) была дополнена производными искомых параметров по фиктивному времени. Полученная система в частных производных решалась методом установления с использованием конечно-разностной схемы Мак-Кормака. Точность всех расчетов контролировалась последовательным увеличением числа расчетных узлов сетки.

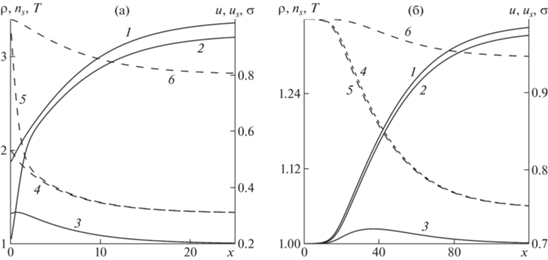
На рис. 2 показаны типичные рассчитанные распределения параметров двухфазного потока в зоне релаксации для волн с частичной (рис. 2а) и полной (2б) дисперсией. Расчеты приведены для значений параметров α = 0.1, M0 = 1.5, a = 0.1 (рис. 2а) и α = 0.1, M0 = 0.95, a = 0.1 (рис. 2б), которые соответствуют неполному испарению капель за волной (рис. 1). Значения остальных безразмерных параметров здесь и далее имеют фиксированные значения: γ = 1.4, Pr = 0.72, ω = 0.5, Kn0 = 0.1. В обоих случаях температура газа изменяется немонотонно, что обусловлено конкуренцией двух различных процессов: диссипации механической энергии в тепловую из-за разности скоростей фаз и расходования тепла на испарение капель жидкости. Расчеты показали, что при всех рассмотренных значениях параметров α и M0 существует локальный максимум температуры, после чего ее значение уменьшается и, если капли “внутри” волны испаряются не полностью, температура газа приближается к температуре потока до волны.

Рис. 2.

Структура волны с частичной (а) и полной (б) дисперсией в случае частичного испарения капель за волной: плотность несущей фазы ρ, числовая концентрация капель ns, температура газа T, скорости фаз u, us, радиус капель σ (кривые 1–6); α = 0.1, Kn0 = 0.1, a = 0.1, M0 = 1.5 (а) и 0.95 (б).

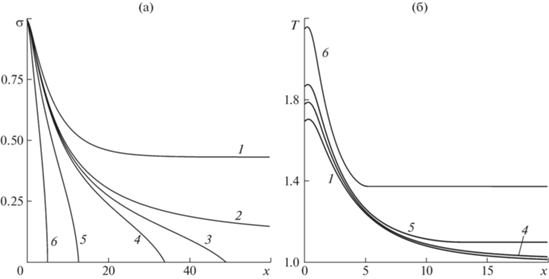
Изменение характера распределения радиуса капель и температуры газа вдоль оси x при увеличении числа Маха, когда происходит переход от частичного к полному испарению капель, показано на рис. 3а,б. Существенно изменяется вид кривых σ(x), а также резко снижается ширина области неравновесного течения, в которой происходит испарение капель, т.е. ширина волны.

Рис. 3.

Изменение безразмерных радиуса капель (а) и температуры газа (б) в волне с частичной дисперсией при α0 = 0.1, Kn0 = 0.1, a = 0.1 для различных значений числа Маха: M0 = 2, 2.08, 2.09, 2.1, 2.2, 2.5 (кривые 1–6).

На рис. 4 показано, как зависит ширина волны с частичной дисперсией от параметров M0 и α0. При полном испарении капель безразмерная (отнесенная к длине скоростной релаксации) ширина волны lw – это значение x, при котором радиус капель обращается в ноль; при неполном испарении считается, что новое состояние равновесия наступает, когда рассогласование температур фаз становится меньше 1%. Локальные пики на рис. 4 отвечают значениям параметров, при которых происходит переход от неполного к полному испарению капель. С приближением к этим значениям размер капель “внутри” волны быстро становится достаточно малым, проскальзывание капель отсутствует, остается только тепловое рассогласование, которое сохраняется на довольно длительном расстоянии, за счет чего ширина волны резко возрастает. В случае малых значений концентрации (α0 ≤ 0.01) всегда происходит полное испарение капель. Ширина волны монотонно снижается с увеличением числа Маха волны и увеличением параметра a, характеризующего скорость испарения капель (рис. 4).

Рис. 4.

Зависимость безразмерной ширины волны с частичной дисперсией от числа Маха волны при а = 0.05, 0.1, 0.15 (а–в) для различных значений массовой концентрации капель: α0 = 0.01, 0.05, 0.1, 0.2 (кривые 1–4).

4. ГРАНИЦЫ СУЩЕСТВОВАНИЯ РАЗЛИЧНЫХ ВОЛНОВЫХ СТРУКТУР В ГАЗЕ С ИCПАРЯЮЩИМИСЯ КАПЛЯМИ ПРИ СИММЕТРИЧНОМ СТОЛКНОВЕНИИ (ОТРАЖЕНИИ ОТ СТЕНКИ) КОСЫХ СКАЧКОВ УПЛОТНЕНИЯ

При симметричном столкновении косых ударных волн в газокапельном потоке или отражении косой волны от плоской стенки в такой среде возможно формирование различных волновых структур. Ниже анализируются границы существования различных волновых структур для случая регулярного отражения волн от стенки при условии, что обе волны (падающая и отраженная) существуют и являются волнами с полной или частичной дисперсией. Анализ проводится с использованием обобщенных соотношений Рэнкина–Гюгонио для косых волн, при этом рассматриваются лишь “макротечения”, т.е. течения на масштабах, много больших ширины зон неравновесного течения, когда внутренняя структура волн уплотнения не существенна.

Приведенные ниже результаты основаны на решении громоздких систем нелинейных алгебраических уравнений (обобщенных соотношений Рэнкина–Гюгонио типа (2.4) или (2.5) для падающей и отраженной волны), выписывание которых для каждого случая занимает много места, хотя формулировки этих уравнений для каждого случая однотипны. Поэтому ниже эти соотношения не приводятся, а будут описаны лишь основные идеи и этапы построения решений.

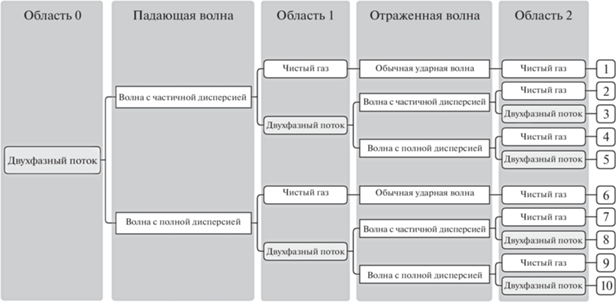
На рис. 5 изображена схема течения газокапельного потока в области взаимодействия косого скачка уплотнения с плоской стенкой (или плоскостью симметрии). Возможные варианты регулярного отражения волны от стенки с различными типами волн и различным состоянием среды в областях 0, 1 и 2 приведены в виде таблицы на рис. 6. Всего обнаружено десять таких режимов. Если в падающей волне происходит полное испарение капель, то в области 1 течение однофазное, а значит, отраженной волной может быть только обычная ударная волна. Если в области 1 поток остается двухфазным, то отраженной волной может быть волна либо с полной, либо с частичной дисперсией. При этом за отраженной волной поток также может оставаться двухфазным либо становиться однофазным.

Рис. 5.

Схема течения в области взаимодействия волны с плоской стенкой: I – падающая волна, II – отраженная волна.

Рис. 6.

Возможные режимы регулярного взаимодействия волны уплотнения с плоской стенкой.

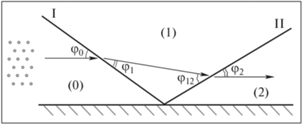
Для анализа существования того или иного типа сначала рассчитываются параметры потока в области 1 между падающей и отраженной волной. Для вычисления параметров газа можно использовать выражения (2.4) и (2.5), если под скоростями потока и числами Маха в областях 0 и 1 понимать нормальные к падающей волне компоненты скорости и числа Маха, посчитанные по нормальной компоненте скорости. Для расчета параметров в области 2 нужно разрешить соотношения (2.3) на отраженной волне, заменив скорость на нормальную к отраженной волне компоненту скорости и добавив геометрическое условие φ0 – φ1 = φ12 – φ2, где φ0, φ1 – углы между падающей волной и направлением потока в областях 0 и 1, φ12, φ2 – углы между отраженной волной и направлением потока в областях 1 и 2 (рис. 5). В зависимости от режима полного или неполного испарения капель в областях 1 и 2 получаются различные системы алгебраических уравнений, которые во всех случаях можно свести к кубическому уравнению относительно ζ = ctgφ12. Во всех трех случаях физическим смыслом обладает лишь одно из трех решений этого уравнения. После нахождения угла φ12 вычисляются угол φ2 и остальные параметры в области 2.

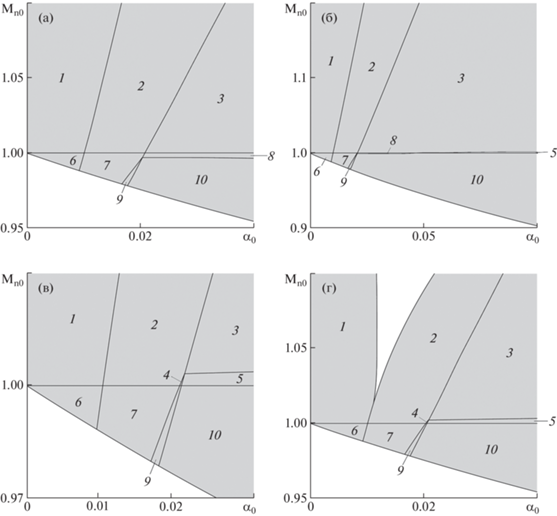
В результате анализа трех различных систем уравнений и дополнительных условий для чисел Маха Mn0 и Mn1, посчитанных по нормальной к волне скорости газа и определяющих наличие либо отсутствие газодинамического разрыва в падающей и отраженной волне, было установлено, что при определенных наборах параметров M0, φ0, α0 возможна реализация всех десяти типов отражения волны от стенки.

На рис. 7а–г приведены области существования различных вариантов в плоскости параметров Mn0, α0 для четырех различных значений угла φ0. Для режимов, в которых падающая волна является волной с полной дисперсией, а в области 2 поток становится однофазным (типы 6, 7, 9), диапазоны существования в плоскости параметров M0, α0 ограничены и относительно малы, тогда как области существования режимов 1, 2, 3, 10 не ограничены и расширяются при увеличении M0 или α0. Режимы 5 и 8 реализуются при значениях нормальных чисел Маха Mn0, близких к 1. Типы отражения 4 и 5 не возможны при небольших значениях угла φ0 (рис. 7а). Незакрашенные области на рис. 7а–г соответствуют параметрам, для которых не существует решений в рассмотренном виде комбинации падающей и отраженной волны, но возможны более сложные двумерные течения или маховское отражение ударной волны от стенки.

Рис. 7.

Области существования режимов 1–10 (по классификации на рис. 6) для различных углов между потоком и падающей волной: φ0 = 10, 20, 30, 40° (а–г), a = 0.1.

ЗАКЛЮЧЕНИЕ

В рамках двухконтинуальной модели получены обобщенные соотношения Рэнкина–Гюгонио для прямых и косых волн уплотнения в газокапельных средах с испаряющимися каплями. Эти соотношения учитывают поглощение тепла из несущей фазы за счет фазового перехода внутри структуры волны. На основе проведенного параметрического исследования найдены диапазоны безразмерных определяющих параметров, соответствующие существованию волн с полной и частичной дисперсией в газокапельных средах с испаряющимися каплями. Определены условия полного и частичного испарения капель в зоне релаксации параметров фаз в волнах уплотнения. На основе численных расчетов исследованы распределения параметров фаз в волнах с полной и частичной дисперсией, а также зависимость ширины волны от определяющих параметров. Установлено, что для всех рассмотренных значений параметров внутри зоны релаксации имеется локальный максимум температуры. Ширина волны имеет локальный максимум для параметров, соответствующих переходу от неполного к полному испарению капель. С увеличением числа Маха и параметра, характеризующего скорость испарения капель, ширина волны монотонно уменьшается. Показано, что при симметричном столкновении косых ударных волн в газокапельных средах или отражении косых волн от плоской стенки возможно формирование десяти различных волновых структур и определены границы существования каждой из возможных структур. Впервые найдены условия, при которых отраженные волны вырождаются в волны с полной дисперсией или полностью исчезают, а также условия полного испарения капель за падающей волной.

Работа выполнена при финансовой поддержке гранта РНФ № 19-19-00234.

Список литературы

  1. Нигматулин P.И. Уравнения гидромеханики и волны уплотнения в двухскоростной и двухтемпературной среде при наличии фазовых превращений // Изв. АН СССР. Механика жидкости и газа. 1967. № 5. С. 33–47.

  2. Gumerov N.A., Ivandaev A.I., Nigmatulin R.I. Sound waves in monodisperse gas-particle or vapour-droplet mixtures // J. Fluid Mech. 1988. V. 193. P. 53–74. https://doi.org/10.1017/S0022112088002058

  3. Goossens H.W.J., Cleijne J.W., Smolders H.J., Van Dongen M.E.H. Shock wave induced evaporation of water droplets in a gas-droplet mixture // Exp. Fluids. V. 6. P. 561–568 (1988). https://doi.org/10.1007/BF00196603

  4. Аманбаев Т.Р., Ивандаев А.И. Влияние фазовых превращений на структуру ударных волн в парокапельной смеси // Вестн. Моск. ун-та. Сер. 1. Матем. мех. 1988. № 3. С. 81–85.

  5. Young J.B., Guha A. Normal shock-wave structure in two-phase vapor-droplet flow // J. Fluid Mech. 1991. V. 228. P. 243–274. https://doi.org/10.1017/S0022112091002690

  6. Guha A. Structure of partly dispersed normal shock waves in vapor-droplet flows// Phys. Fluids A. 1992. V. 4. № 7. P. 1566–1578. https://doi.org/10.1063/1.858429

  7. Smolders H.J., Van Dongen M.E.H. Shock wave structure in a mixture of gas, vapour and droplets // Shock Waves. 1992. V. 2. P. 255–267. https://doi.org/10.1007/BF01414761

  8. Chang E.J., Kailasanath K. Shock wave interactions with particles and liquid fuel droplets // Shock Waves. 2003. V. 12. P. 333–341. https://doi.org/10.1007/s00193-002-0170-1

  9. Yeom G.S., Chang K.S. Shock wave diffraction about a wedge in a gas-microdroplet mixture // Int. J. Heat Mass Transfer. 2010. V. 53. P. 5073–5088. https://doi.org/10.1016/j.ijheatmasstransfer.2010.07.056

  10. Chauvin A., Daniel E., Houas L., Tosello R. Experimental investigation of the propagation of a planar shock wave through a two-phase gas-liquid medium // Phys. Fluids. 2011. V. 23. P. 113301. https://doi.org/10.1063/1.3657083

  11. Леонтьев А.И. Газодинамический метод энергоразделения газовых потоков // Теплофизика высоких температур. 1997. Т. 35. № 1. С. 157–159.

  12. Azanov G.M., Osiptsov A.N. The efficiency of one method of machineless gasdynamic temperature stratification in a gas flow // Int. J. Heat Mass Transfer. 2017. V. 106. P. 1125–1133. https://doi.org/10.1016/j.ijheatmasstransfer.2016.10.090

  13. Виноградов Ю.А., Здитовец А.Г., Киселев Н.А., Медвецкая Н.В., Попович С.С. Измерение адиабатической температуры стенки плоской пластины, обтекаемой сверхзвуковым воздушно-капельным потоком // Изв. РАН. Механика жидкости и газа. 2020. № 5. С. 130–136. https://doi.org/10.31857/S056852812005014X

  14. Marble F.E. Dynamics of dusty gases // Annu. Rev. Fluid Mech. 1970. V. 2. P. 397–446. https://doi.org/10.1146/annurev.fl.02.010170.002145

  15. Sazhin S. Droplets and Sprays. Springer, London, 2014. 345 p.

  16. Голубкина И.В., Осипцов А.Н. Влияние примеси неиспаряющихся капель на структуру течения и температуру адиабатической стенки в сжимаемом двухфазном пограничном слое // Изв. РАН. Механика жидкости и газа. 2019. № 2. С. 58–69. https://doi.org/10.1134/S0568528119030046

  17. Голубкина И.В., Осипцов А.Н. Взаимодействие скачков уплотнения в запыленном газе и возникновение волн с полной дисперсией // Изв. РАН. Механика жидкости и газа. 2010. № 1. С. 70–83.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Известия РАН. Механика жидкости и газа

Архивы выпусков Информация о журнале Отправить рукопись в журнал