Известия РАН. Механика жидкости и газа, 2021, № 6, стр. 62-65
О ПОГРАНИЧНОМ СЛОЕ ПРИ ОБТЕКАНИИ ПОЛУТЕЛА РЭНКИНА
Г. Л. Королев a, *, Вик. В. Сычёв a
a Центральный аэрогидродинамический институт им. проф. Н.Е. Жуковского
Жуковский, Московская обл., Россия
* E-mail: glk7776@mail.ru
Поступила в редакцию 07.06.2021
После доработки 22.06.2021
Принята к публикации 22.06.2021
Аннотация
Получено численное решение задачи для уравнения пограничного слоя Прандтля для плоского стационарного течения несжимаемой жидкости при заданном градиенте давления. Этот градиент определяется известным решением Рэнкина, которое описывает обтекание полутела. Контур последнего получается путем наложения однородного потока на течение от точечного источника. Установлено, что в решении задачи для уравнения пограничного слоя точки нулевого поверхностного трения не возникает – рассмотренное течение является безотрывным.
При изучении обтекания тонких тел при больших числах Рейнольдса ($\operatorname{Re} \to \infty $) решения в целом даются на основе теории малых возмущений (см. [1]). Однако эти решения становятся несправедливыми вблизи точек торможения [2]. Данная работа посвящена анализу течения в пограничном слое в малой окрестности такой точки для сильно затупленного тела.
1. ПОСТАНОВКА ЗАДАЧИ
Рассмотрим плоское установившееся течение несжимаемой жидкости около тонкого тела, установленного под нулевым углом атаки к однородному набегающему потоку.
Пусть $\ell x$, $\ell y$ − оси прямоугольной декартовой системы координат с началом в малой окрестности передней критической точки; ${{u}_{\infty }}\,u$, ${{u}_{\infty }}{v}$ − соответствующие проекции вектора скорости; ${{p}_{\infty }} + \rho u_{\infty }^{2}p$ − давление; $\ell {{u}_{\infty }}\psi $ − функция тока; $\operatorname{Re} = {{u}_{\infty }}\ell {\text{/}}\nu $ − число Рейнольдса. Здесь $\ell $ − продольный размер тела; ${{u}_{\infty }}$ и ${{p}_{\infty }}$ − абсолютная величина вектора скорости и давление в набегающем потоке, направленном вдоль оси $Ox$; $\rho $ − плотность, $\nu $ − кинематический коэффициент вязкости.
Обозначим через $\tau $ малый параметр, определяющий толщину тела: $\tau = \tau (\operatorname{Re} ) \to 0$ при Re → ∞. Тогда в масштабах тела ($x = O(1)$, $y = O(1)$) согласно теории малых возмущений (см. [1, 3])
и относительно искомых функций известно, что где ${{f}_{1}}(z)$ – аналитическая функция комплексного переменного. (В силу симметрии речь всюду идет о течении в верхней полуплоскости.)Пусть $y = \tau F(x)$, $0 < x < 1$ и $F(x)$ определяет форму обтекаемой поверхности. Если параметр $\tau $ не слишком мал, то течение сопровождается отрывом потока. Основополагающие результаты исследования для таких течений при гладких $F(x)$, $F(0) = F(1)$ = 0 были получены в [4]. (О последующих работах в этом направлении см. в [5].)
Предположим, что передняя кромка имеет степенную форму
при $x \to + 0$, ${{a}_{0}} > 0$ и $0 < \alpha < 1$. В работах [4, 6] основное внимание было уделено изучению течений при $\alpha = 1{\text{/}}2$.Известно [3], что при $z \to 0$:
(1.4)
${{f}_{1}} = {{A}_{1}}{{z}^{\beta }} + o({{z}^{\beta }}),\quad \beta = \alpha - 1,\quad {{A}_{1}} = \alpha {{a}_{0}}({\text{ctg}}\beta \pi - i)$Нетрудно видеть, что асимптотическое представление (1.1), согласно (1.4), теряет равномерную пригодность при $z = O({{\tau }^{{ - 1/\beta }}})$. Для рассмотрения течения в этой области следует ввести внутренние переменные
Решение здесь на основании (1.1), (1.4) может быть представлено в виде
В дальнейшем речь будет идти о течении для предельного случая, когда в (1.3) значение α = 0. (Прямоугольная передняя кромка.) При этом в (1.4) постоянная${{A}_{1}} = {{a}_{0}}{\text{/}}\pi $ и в (1.5) $\beta = - 1$.
Для искомых функций из (1.6), при условии, что $\tau \operatorname{Re} \to \infty $ при $\operatorname{Re} \to \infty $ и в соответствии с (1.2), приходим к уравнениям, описывающим потенциальное течение идеальной жидкости
(1.7)
$\begin{gathered} \frac{{dW}}{{dZ}} = U - iV,\quad Z = X + iY,\quad W = \Phi + i\Psi \\ Z \to \infty {\text{:}}\;\frac{{dW}}{{dZ}} = 1 + \frac{{{{a}_{0}}}}{\pi }{{Z}^{{ - 1}}} + O({{Z}^{{ - 2}}}) \\ \end{gathered} $Здесь W(Z) − комплексный потенциал, $\Psi (X,Y)$ − функция тока, $\Phi (X,Y)$ − потенциал для течения в этой области и также выписано условие сращивания с разложением (1.1).
Предположим, что в рассматриваемой области течение описывается решением Рэнкина [7]. Это решение есть сумма комплексных потенциалов для однородного потока и источника, помещенного, скажем, в точку Z = 0:
(1.8)
$W = Z + \frac{{{{Q}_{0}}}}{{2\pi }}{\text{lnZ,}}\quad \frac{{dW}}{{dZ}} = 1 + \frac{{{{Q}_{0}}}}{{2\pi Z}}$Дадим краткое описание этого решения. В плоскости симметрии лежит точка торможения
Из (1.7), (1.8) следует, что
(1.9)
$\Psi = Y + \frac{{{{Q}_{0}}}}{{2\pi }}\theta ,\quad \theta = {\text{arctg}}\left( {\frac{Y}{X}} \right),\quad Z = r{{e}^{{i\theta }}},\quad r = {{\left( {{{X}^{2}} + {{Y}^{2}}} \right)}^{{1/2}}}$Линия тока, проходящая через точку торможения, в которой $\theta = \pi $ и $Y = 0$, есть
Пусть эта кривая есть контур обтекаемого тела, и она определена функцией $Y = G(x)$:
(1.11)
$G + \frac{{{{Q}_{0}}}}{{2\pi }}{\text{arctg}}\left( {\frac{G}{X}} \right) = \frac{{{{Q}_{0}}}}{2}$Параметрическое представление кривой, согласно (1.10), (1.9), имеет вид
(1.12)
$\begin{gathered} X = x_{0}^{{}}(t) = - \frac{{{{Q}_{0}}}}{{2\pi }}t{\text{ctg}}t \\ \,Y\,\, = \,\,{{y}_{0}}(t)\,\, = \,\,\,\frac{{{{Q}_{0}}}}{{2\pi \,}}\,\,t,\,\,\,\,t\,\, = \,\,\pi \,\, - \,\,\theta ,\,\,\,0 \leqslant \,t\, < \pi \\ \end{gathered} $Наконец из (1.7)–(1.10) следует (см. [8]), что скорость ${{U}_{0}}(t)$ вдоль линии тока $\Psi = {{Q}_{0}}{\text{/}}2$ выражается следующей формулой:
(1.13)
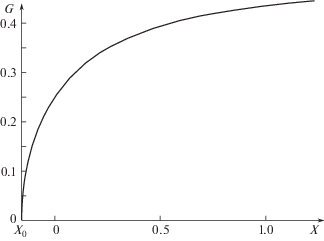
${{U}_{0}} = {{\left[ {1 - \frac{{\sin 2t}}{t} + {{{\left( {\frac{{\sin t}}{t}} \right)}}^{2}}} \right]}^{{1.2}}}$При $X \to \infty $, согласно (1.11), $G \to {{Q}_{0}}{\text{/}}2$, т.е. ${{a}_{0}} = {{Q}_{0}}{\text{/}}2$ (см. (1.7), (1.8)).
Заметим, что замена
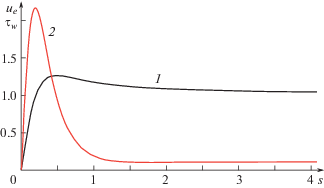
График функции $G(X)$, построенный в [7], представлен на рис. 1. На рис. 2 дана функция ${{u}_{e}}(s) = {{U}_{0}}(t)$ из (1.13), где $s$ – длина дуги, отсчитываемая от точки торможения вдоль контура тела
2. РЕШЕНИЕ ЗАДАЧИ ДЛЯ УРАВНЕНИЯ ПОГРАНИЧНОГО СЛОЯ
Рассмотрим течение в пограничном слое, который развивается вдоль поверхности обтекаемого тела в области $z = O(\tau )$ при $R = \tau \operatorname{Re} \to \infty ,R$ − локальное число Рейнольдса. Введем здесь ($Z = O(1)$) ортогональную криволинейную систему координат s, $n$, связанную с этой поверхностью, и на которой $\Psi = {{Q}_{0}}{\text{/}}2$, $\psi = \tau \Psi $. В пограничном слое, как обычно [3]
Для ${{\Psi }_{0}}(s,N)$ приходим к уравнению Прандтля
(2.1)
$\begin{gathered} \frac{{\partial {{\Psi }_{0}}}}{{\partial N}}\frac{{{{\partial }^{2}}{{\Psi }_{0}}}}{{\partial s\partial N}} - \frac{{\partial {{\Psi }_{0}}}}{{\partial s}}\frac{{{{\partial }^{2}}{{\Psi }_{0}}}}{{\partial \;{{N}^{2}}}} - {{u}_{e}}\frac{{d{{u}_{e}}}}{{ds}} = \frac{{{{\partial }^{3}}{{\Psi }_{0}}}}{{\partial {{N}^{3}}}} \\ N = 0{\text{:}}\;{{\Psi }_{0}} = \frac{{\partial {{\Psi }_{0}}}}{{\partial N}} = 0,\quad N \to \infty {\text{:}}\;\frac{{\partial {{\Psi }_{0}}}}{{\partial N}} \to {{u}_{e}}(s) \\ \end{gathered} $Здесь также приведены краевые условия, обеспечивающие прилипание на поверхности и сращивание с решением во внешней области, где $Z = O(1)$.
В результате численного решения задачи (2.1) было найдено распределение поверхностного трения ${{\tau }_{W}}(s) = {{\left. {\partial {{\Psi }_{0}}{\text{/}}\partial N} \right|}_{{N = 0}}}$ (рис. 2). Оказалось, что действие заданного неблагоприятного градиента давления, связанного с уменьшением скорости на внешней границе пограничного слоя (см. рис. 2), не приводит к появлению точки нулевого поверхностного трения. Функция ${{\tau }_{W}}(s)$ всюду положительна, а $s = 1.77$ и $s = 3.63$ являются для нее точками слабо выраженных минимума и максимума. При $s = \to \infty $ решение имеет автомодельную асимптотику Прандтля–Блазиуса: ${{\tau }_{W}} = O({{s}^{{ - 1/2}}})$.
ЗАКЛЮЧЕНИЕ
Проведенный анализ показал, что при обтекании сильно затупленных тонких тел в малой окрестности их передней части возможно безотрывное течение. Такой вывод соответствует сказанному в [4] (с. 157) относительно решения при $0 < \alpha < 1{\text{/}}2$ (см. 1.3)). В то же время, как было установлено в [6], при этом возможно и течение с развитой областью возвратных токов, где точка отрыва находится вблизи передней кромки.
Список литературы
Van Dyke M.D. Second-order subsonic airfoil theory including edge effects // NACA Rep. 1956. № 1274. 23 p.
Jones R.T. Leading-edge singularities in thin-airfoil theory // J. Aeronaut. Sci. 1950. V. 17. № 5. P. 307–310.
Van Dyke M. Perturbation methods in fluid mechanics. Stanford: Parabolic Press, 1975. 271 p.
Cheng H.K., Smith F.T. The influence of airfoil thickness and Reynolds number on separation // ZAMP. 1982. V. 33. № 2. P. 151–180.
Сычев В.В. О течении при больших числах Рейнольдса около пластины, установленной под малым углом атаки // Изв. РАН. МЖГ. 2001. № 2. С. 85–104.
Тимошин С.Н. Отрывное обтекание тонкого профиля с параболической передней кромкой при больших числах Рейнольдса // Учен. зап. ЦАГИ. 1985. Т. 16. № 2. С. 24–32.
Rankine W.J.M. On plane water-lines in two dimensions // Phil. Trans. Roy. Soc. London. 1864. V. 154. P. 369–391.
Башкин В.А., Егоров И.В. Семинары по теоретической гидродинамике. Ч. I. Учебное пособие. М.: МФТИ, 2003. 194 с.
Дополнительные материалы отсутствуют.
Инструменты
Известия РАН. Механика жидкости и газа