Известия РАН. Механика жидкости и газа, 2021, № 6, стр. 51-61

ДАЛЬНЕЕ ПОЛЕ ТРЕХМЕРНОЙ ПРИСТЕННОЙ ЛАМИНАРНОЙ СТРУИ

И. И. Бут^a, *, А. М. Гайфуллин^a, **, В. В. Жвик^a, ***

^a Центральный аэрогидродинамический институт им. проф. Н.Е. Жуковского
Жуковский, Московская область, Россия

^* E-mail: Ivan.But@skoltech.ru
^** E-mail: gaifullin@tsagi.ru
^*** E-mail: VladZhvick@yandex.ru

Поступила в редакцию 19.05.2021
После доработки 27.06.2021
Принята к публикации 27.06.2021

DOI: 10.31857/S0568528121060025

Аннотация

Рассматривается затопленная стационарная ламинарная струя вязкой несжимаемой жидкости, вытекающая из трубы и распространяющаяся вдоль твердой плоскости. Получено численное решение уравнений Навье–Стокса в трехмерной стационарной постановке. Подтверждена гипотеза, что поле течения на большом расстоянии от выходного сечения трубы описывается автомодельным решением параболизованных уравнений Навье–Стокса. Получены асимптотические разложения автомодельного решения при больших и малых значениях координаты в поперечном сечении струи. С помощью численного решения определен показатель автомодельности. Найдена явная зависимость автомодельного решения от числа Рейнольдса и условий в источнике струи.

Ключевые слова: пристенная струя, затопленная струя, автомодельные решения первого и второго рода, закон сохранения, асимптотика, инвариант

Хорошо известно решение плоской задачи о затопленной струе, выдуваемой вдоль пластины из бесконечно тонкой щели [1, 2]. В приближении пограничного слоя данное течение является автомодельным. Показатель автомодельности определяется с помощью инварианта струи, размерность которого равна произведению потока импульса на расход.

При этом мало что известно о затопленной струе, которая вытекает из трубки параллельно бесконечной твердой плоскости. Основы математической модели данного течения заложены в [3]. При стремлении вязкости к нулю область течения, в которой вязкие и инерционные члены в уравнениях Навье–Стокса одного порядка, становится узкой. В этой области течение описывается параболизованными уравнениями Навье–Стокса, у которых существует однопараметрический класс автомодельных по продольной координате решений. Высказана гипотеза [3], что дальнее поле струи является решением из этого класса. Для используемых уравнений вычислены локальные законы сохранения массы, импульса и момента импульса. Однако потоки указанных величин через поперечное сечение пристенной струи не сохраняются, что привело к неверному определению показателя автомодельности в [3].

Автомодельные решения являются асимптотиками решений для неавтомодельных струй на большом расстоянии от источника. Дальнее автомодельное поле струи зависит от интегральных характеристик источника, которые обычно определяются из законов сохранения. Существование сохраняющейся величины позволяет рассматривать предельный переход к точечному источнику. В этом случае автомодельное решение является точным решением задачи истечения струи из точечного источника.

Решения, в которых показатель автомодельности определяется при помощи интегрального закона сохранения, принято называть автомодельными решениями первого рода [4]. Таковыми являются решение для плоской пристенной струи [1, 2], а также решения для свободных затопленных струй [5–7], в которых сохраняется поток импульса. На сегодняшний день решение для трехмерной пристенной струи следует отнести к автомодельным решениям второго рода, поскольку не установлен интегральный инвариант данной задачи.

Согласно обзорам [8, 9] расчетные и экспериментальные работы по трехмерной пристенной струе направлены в основном на исследование турбулентной струи. Ламинарная струя исследовалась в небольшом количестве работ [10–12]. Во всех работах декларируется автомодельность дальнего поля струи. При этом отсутствует тщательное сравнение численного решения или эксперимента с автомодельным решением [3], позволяющее определить показатель автомодельности и детально изучить свойства автомодельного решения. Настоящая работа заполняет имеющийся пробел.

1. АВТОМОДЕЛЬНОЕ РЕШЕНИЕ

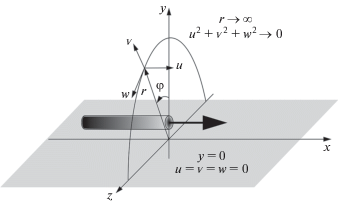
Будем рассматривать стационарную ламинарную струю вязкой несжимаемой жидкости, которая вытекает в затопленное той же жидкостью пространство из трубы с характерным размером поперечного сечения $a$ параллельно безграничной твердой плоскости. Пусть ${{u}_{0}}$ – среднерасходная скорость в трубе. Определим безразмерные переменные:

${\mathbf{r}} = \frac{{{\mathbf{r}}{\text{*}}}}{a},\quad {\mathbf{V}} = \frac{{{\mathbf{V}}{\text{*}}}}{{{{u}_{0}}}},\quad p = \frac{{p{\text{*}} - p_{\infty }^{ * }}}{{\rho u_{0}^{2}}},\quad {\text{Re}} = \frac{{{{u}_{0}}a}}{\nu }$

где ${\mathbf{r}}$ – радиус-вектор точки поля течения с координатами (x, r, $\varphi $) в цилиндрической системе координат (рис. 1); ${\mathbf{V}} = (u,{v},w)$ – вектор скорости и его компоненты в цилиндрической системе координат; $\rho $ – постоянная плотность жидкости; $p$ – давление; $p_{\infty }^{ * }$ – давление в невозмущенной области; ${\text{Re}}$ – число Рейнольдса; $\nu $ – кинематический коэффициент вязкости. Звездочкой отмечены размерные переменные. Струя распространяется вдоль оси x. Угол $\varphi $ отсчитывается от плоскости симметрии. Твердой плоскости соответствует $\varphi = \pm \pi {\text{/}}2$. Начало координат находится в плоскости выходного отверстия трубы.

Рис. 1.

Цилиндрическая система координат и граничные условия.

Функции ${\mathbf{V}}({\mathbf{r}})$, $p({\mathbf{r}})$ удовлетворяют уравнениям Навье–Стокса:

(1.1)

$\nabla \cdot {\mathbf{V}} = 0,\quad ({\mathbf{V}}\nabla ){\mathbf{V}} = - \nabla p + \mathop {{\text{Re}}}\nolimits^{ - 1} \Delta {\mathbf{V}}$

Граничные условия определяются распределением скорости во входном сечении трубы ($x = - L$, где L – длина трубы), прилипанием на твердых поверхностях и затуханием всех компонент скорости на большом расстоянии от трубы. На плоскости симметрии выполняются условия ${{u}_{\varphi }} = {{{v}}_{\varphi }} = w = 0$. Здесь и далее нижним индексом обозначается частная производная.

Известно [3], что в приближении пограничного слоя трехмерная пристенная струя описывается параболизованными уравнениями Навье–Стокса, которые отличаются от уравнений (1) отсутствием слагаемых ${{p}_{x}}$, ${{u}_{{xx}}}$, ${{{v}}_{{xx}}}$, ${{w}_{{xx}}}$:

(1.2)

${{(ur)}_{x}} + {{({v}r)}_{r}} + {{w}_{\varphi }} = 0$

(1.3)

$u{{u}_{x}} + {v}{{u}_{r}} + \frac{{w{{u}_{\varphi }}}}{r} = \mathop {{\text{Re}}}\nolimits^{ - 1} \left( {{{u}_{{rr}}} + \frac{{{{u}_{r}}}}{r} + \frac{{{{u}_{{\varphi \varphi }}}}}{{{{r}^{2}}}}} \right)$

(1.4)

$u{{{v}}_{x}} + {v}{{{v}}_{r}} + \frac{{w{{{v}}_{\varphi }}}}{r} - \frac{{{{w}^{2}}}}{r} = - {{p}_{r}} + {{\operatorname{Re} }^{{ - 1}}}\left( {{{{v}}_{{rr}}} + \frac{{{{{v}}_{r}}}}{r} + \frac{{{{{v}}_{{\varphi \varphi }}}}}{{{{r}^{2}}}} - \frac{{v}}{{{{r}^{2}}}} - \frac{{2{{w}_{\varphi }}}}{{{{r}^{2}}}}} \right)$

(1.5)

$u{{w}_{x}} + {v}{{w}_{r}} + \frac{{w{{w}_{\varphi }}}}{r} + \frac{{{v}w}}{r} = - \frac{{{{p}_{\varphi }}}}{r} + {{\operatorname{Re} }^{{ - 1}}}\left( {{{w}_{{rr}}} + \frac{{{{w}_{r}}}}{r} + \frac{{{{w}_{{\varphi \varphi }}}}}{{{{r}^{2}}}} - \frac{w}{{{{r}^{2}}}} + \frac{{2{{{v}}_{\varphi }}}}{{{{r}^{2}}}}} \right)$

Приведем общий вид автомодельного по продольной координате решения системы (1.2)–(1.5):

(1.6)

$u(x,r,\varphi ) = {{\operatorname{Re} }^{{2\alpha - 1}}}{{x}^{{ - (2k - 1)}}}U(\eta ,\varphi )$

(1.7)

${v}(x,r,\varphi ) = {{\operatorname{Re} }^{{\alpha - 1}}}{{x}^{{ - k}}}V(\eta ,\varphi )$

(1.8)

$w(x,r,\varphi ) = {{\operatorname{Re} }^{{\alpha - 1}}}{{x}^{{ - k}}}W(\eta ,\varphi )$

(1.9)

$p(x,r,\varphi ) = {{\operatorname{Re} }^{{2\alpha - 2}}}{{x}^{{ - 2k}}}P(\eta ,\varphi )$

(1.10)

$\eta = r{\text{/}}({{\operatorname{Re} }^{{ - \alpha }}}{{x}^{k}})$

где α, k – вещественные параметры.

Функции $U$, $V$, $W$, $P$ удовлетворяют уравнениям:

(1.11)

$(1 - 2k)U - k\eta {{U}_{\eta }} + {{V}_{\eta }} + {{\eta }^{{ - 1}}}V + {{\eta }^{{ - 1}}}{{W}_{\varphi }} = 0$

(1.12)

$\left( {(1 - 2k)U - k\eta {{U}_{\eta }}} \right)U + V{{U}_{\eta }} + {{\eta }^{{ - 1}}}W{{U}_{\varphi }} - ({{U}_{{\eta \eta }}} + {{\eta }^{{ - 1}}}{{U}_{\eta }} + {{\eta }^{{ - 2}}}{{U}_{{\varphi \varphi }}}) = 0$

(1.13)

$\begin{gathered} - k(V + \eta {{V}_{\eta }})U + V{{V}_{\eta }} + {{\eta }^{{ - 1}}}W{{V}_{\varphi }} - {{\eta }^{{ - 1}}}{{W}^{2}} + \\ + {{P}_{\eta }} - ({{V}_{{\eta \eta }}} + {{\eta }^{{ - 1}}}{{V}_{\eta }} + {{\eta }^{{ - 2}}}{{V}_{{\varphi \varphi }}} - {{\eta }^{{ - 2}}}V - 2{{\eta }^{{ - 2}}}{{W}_{\varphi }}) = 0 \\ \end{gathered} $

(1.14)

$\begin{gathered} - k(W + \eta {{W}_{\eta }})U + V{{W}_{\eta }} + {{\eta }^{{ - 1}}}W{{W}_{\varphi }} + {{\eta }^{{ - 1}}}VW + \\ + \;{{\eta }^{{ - 1}}}{{P}_{\varphi }} - ({{W}_{{\eta \eta }}} + {{\eta }^{{ - 1}}}{{W}_{\eta }} + {{\eta }^{{ - 2}}}{{W}_{{\varphi \varphi }}} + 2{{\eta }^{{ - 2}}}{{V}_{\varphi }} - {{\eta }^{{ - 2}}}W) = 0 \\ \end{gathered} $

Примем гипотезу [3], что поле течения на большом расстоянии от выходного сечения трубы $x \to + \infty $ описывается автомодельным решением (1.6)–(1.10) уравнений (1.2)–(1.5).

2. КООРДИНАТНОЕ РАЗЛОЖЕНИЕ ПРИ $\eta \to 0$

Из анализа численного решения, который будет дан в разделе 4, следует, что азимутальная скорость в рассматриваемой струе много меньше продольной и радиальной. Построим асимптотическое разложение по малой радиальной координате решения уравнений (1.11)–(1.14), имея в виду условие симметрии при φ = 0 и условия прилипания при $\varphi = \pm \pi {\text{/}}2$:

(2.1)

$U = \eta {{U}_{1}}(\varphi ) + {{\eta }^{4}}{{U}_{2}}(\varphi ) + {{\eta }^{7}}{{U}_{3}}(\varphi ) + o({{\eta }^{7}})$

(2.2)

$V = {{\eta }^{2}}{{V}_{1}}(\varphi ) + {{\eta }^{5}}{{V}_{2}}(\varphi ) + O({{\eta }^{8}})$

(2.3)

$W = {{\eta }^{5}}{{W}_{2}}(\varphi ) + O({{\eta }^{8}})$

(2.4)

$P = {{P}_{0}} + \eta {{P}_{1}}(\varphi ) + {{\eta }^{4}}{{P}_{2}}(\varphi ) + O({{\eta }^{7}})$

${{U}_{1}}(\varphi ) = Acos\varphi $

${{U}_{2}}(\varphi ) = - \frac{1}{{24}}{{A}^{2}}\left( {k - \frac{1}{3}} \right){{(cos2\varphi + 1)}^{2}}$

${{U}_{3}}(\varphi ) = Ccos7\varphi + \left( {\left( {\frac{{13}}{{840}}{{A}^{2}}\left( {k - \frac{1}{3}} \right)\left( {k - \frac{4}{{39}}} \right) - \frac{8}{{21}}B} \right)co{{s}^{2}}\varphi + \frac{1}{3}B} \right)Aco{{s}^{5}}\varphi $

${{V}_{1}}(\varphi ) = A\left( {k - \frac{1}{3}} \right)cos\varphi $

$\begin{gathered} {{V}_{2}}(\varphi ) = - \frac{1}{{24}}{{A}^{2}}\left( {k - \frac{1}{3}} \right)\left( {k - \frac{1}{6}} \right){{(cos2\varphi + 1)}^{2}} - \\ - \;\frac{1}{{24}}{{A}^{2}}(k - 1)\left( {k - \frac{1}{3}} \right)\left( {\frac{1}{8}cos2\varphi + \frac{1}{5}cos4\varphi + \frac{3}{{40}}cos6\varphi } \right) - \frac{2}{3}Bcos4\varphi - \frac{2}{3}Bcos6\varphi \\ \end{gathered} $

${{W}_{2}}(\varphi ) = \frac{1}{{16}}{{A}^{2}}(k - 1)\left( {k - \frac{1}{3}} \right)\left( {\frac{1}{4}{\text{sin}}2\varphi + \frac{1}{5}{\text{sin}}4\varphi + \frac{1}{{20}}{\text{sin}}6\varphi } \right) + B{\text{sin}}4\varphi + \frac{2}{3}B{\text{sin}}6\varphi $

${{P}_{1}}(\varphi ) = 2A\left( {k - \frac{1}{3}} \right)cos\varphi $

${{P}_{2}}(\varphi ) = - \frac{2}{3}\left( {\left( {k - \frac{1}{3}} \right)\left( {k - \frac{7}{{12}}} \right){{A}^{2}} + 40B} \right)co{{s}^{4}}\varphi + \frac{{80}}{3}Bco{{s}^{2}}\varphi - \frac{{10}}{3}B$

Полученное разложение зависит от четырех неизвестных констант: A, P₀, B, C. Константы, P₀, B связаны с распределением давления на стенке при $\eta \to 0$ следующим образом:

(2.5)

$P = {{P}_{0}} - \frac{{10}}{3}B{{\eta }^{4}},\quad \varphi = \pm \frac{\pi }{2}$

Заметим, что в первом приближении азимутальная скорость отсутствует, а продольная и радиальная скорости зависят от азимутального угла одинаковым образом.

3. КООРДИНАТНОЕ РАЗЛОЖЕНИЕ ПРИ $\eta \to + \infty $

Предположим, чтo при больших значениях радиальной координаты $\eta \to + \infty $ продольная и азимутальная составляющие скорости затухают сильнее, чем радиальная скорость. Тогда уравнения (1.11), (1.13), (1.14) принимают вид:

${{V}_{\eta }} + {{\eta }^{{ - 1}}}V = 0$

$V{{V}_{\eta }} + {{P}_{\eta }} - ({{V}_{{\eta \eta }}} + {{\eta }^{{ - 1}}}{{V}_{\eta }} + {{\eta }^{{ - 2}}}{{V}_{{\varphi \varphi }}} - {{\eta }^{{ - 2}}}V) = 0$

$2{{V}_{\varphi }} - \eta {{P}_{\varphi }} = 0$

Полученные уравнения, дополненные граничным условием V = 0 при $\varphi = \pm \pi {\text{/}}2$, соответствуют задаче Гамеля [13] о течении в конфузоре с углом полураствора π/2.

Решение имеет вид:

(3.1)

$V = {{\eta }^{{ - 1}}}F(\varphi )$

$P = 2{{\eta }^{{ - 2}}}F(\varphi ) + {{\eta }^{{ - 2}}}E$

где E – константа, а $F(\varphi )$ удовлетворяет уравнению:

(3.2)

$F{\kern 1pt} {\text{''}} + 4F + {{F}^{2}} + 2E = 0$

при $F( \pm \pi {\text{/}}2) = 0$.

Понизим порядок уравнения (3.2):

(3.3)

$F{\kern 1pt} {\text{'}} = \pm \mathop {\left( { - 4{{F}^{2}} - \frac{{2{{F}^{3}}}}{3} - 4EF + {{C}_{1}}} \right)}\nolimits^{1/2} $

Будем искать симметричное решение $F(\varphi ) < 0$ с минимумом на плоскости симметрии F(0) = = $ - {{F}_{0}}$. Из условия $F{\kern 1pt} '(0) = 0$ следует, что ${{C}_{1}} = 4F_{0}^{2} - 2F_{0}^{3}{\text{/}}3 - 4E{{F}_{0}}$. Тогда $ - 4{{F}^{2}} - 2{{F}^{3}}{\text{/}}3 - 4EF$ + C₁ = = $(F + {{F}_{0}})(4({{F}_{0}} - F) - 2({{F}^{2}} - {{F}_{0}}F + F_{0}^{2}){\text{/}}3 - 4E)$.

Для произвольной величины ${{F}_{0}} > 0$ решение имеет вид:

$\varphi = {\text{sign}}(\varphi )\int\limits_{ - {{F}_{0}}}^{F(\varphi )} \mathop {\left[ {(F + {{F}_{0}})\left( {4({{F}_{0}} - F) - \frac{{2({{F}^{2}} - {{F}_{0}}F + F_{0}^{2})}}{3} - 4E} \right)} \right]}\nolimits^{ - 1/2} dF$

Константа $E$ находится из итегрального соотношения:

$\frac{\pi }{2} = \int\limits_{ - {{F}_{0}}}^0 \mathop {\left[ {(F + {{F}_{0}})\left( {4({{F}_{0}} - F) - \frac{{2({{F}^{2}} - {{F}_{0}}F + F_{0}^{2})}}{3} - 4E} \right)} \right]}\nolimits^{ - 1/2} dF$

Получим предельное решение при ${{F}_{0}} \to + \infty $. В этом случае внешнее решение является константой $F(\varphi ) = - {{F}_{0}}$. Из уравнения (3.2) находим $E = - F_{0}^{2}{\text{/}}2$.

Будем отсчитывать угол $\theta $ от стенки:

$\begin{gathered} \varepsilon \theta = \frac{\pi }{2} - \varphi \\ F = {{F}_{0}}f(\theta ) \\ \end{gathered} $

где $\varepsilon $ – малый угол, ограничивающий пограничный слой. Переменные $\theta $ и f порядка единицы.

Запишем уравнение (3.3) в новых переменных при ${{F}_{0}} \to + \infty $:

${{\varepsilon }^{{ - 1}}}{{F}_{0}}\frac{{df}}{{d\theta }} = - F_{0}^{{3/2}}\mathop {\left[ {(f + 1)\left( { - \frac{{2({{f}^{2}} - f + 1)}}{3} + 2} \right)} \right]}\nolimits^{1/2} $

откуда определяем угловой размер пограничного слоя $\varepsilon = 1{\text{/}}\sqrt {{{F}_{0}}} $. Имеем

$\frac{{df}}{{d\theta }} = - \sqrt {\frac{2}{3}} (f + 1)\sqrt {2 - f} $

Полученное уравнение можно проинтегрировать:

$f = 2 - 3tan{{h}^{2}}\left( {{\text{arctanh}}\left( {\sqrt {\frac{2}{3}} } \right) + \frac{\theta }{{\sqrt 2 }}} \right)$

Решение зависит от одной неизвестной константы F₀.

4. АНАЛИЗ ЧИСЛЕННОГО РЕШЕНИЯ

Получены численные решения уравнений Навье–Стокса (1.1) для задач распространения ламинарной струи вдоль твердой стенки при истечении из трубы прямоугольного или кругового поперечного сечения при разных числах Рейнольдса. Использовался метод конечных объемов. Аппроксимация конвективных членов проводилась по схеме второго порядка точности с разностями против потока. Аппроксимация диффузионных членов и давления – по схеме с центральными разностями второго порядка точности. Стационарное решение строилось методом установления. Критерий сходимости – установление постоянного расхода через дальнее поперечное сечение расчетной области при максимальном значении невязок менее 10^–5.

Расчет истечения струи из трубы кругового сечения проводился на сетке, использованной в работе [14]. Продольный размер расчетной области составляет 550 диаметров, размеры прямоугольного поперечного сечения расчетной области изменяются линейно с ростом продольной координаты от 60 × 30 до 536 × 266, где первый размер задан в направлении z на рис. 1, а второй – в направлении y. Длина трубы равна 10. Расстояние от оси трубы до твердой плоскости равно двум диаметрам. Количество ячеек сетки 10.3 × 10⁶. Задача решалась при числах Рейнольдса 100, 150 и 200. Число Рейнольдса определено по диаметру трубы и среднерасходной скорости в ней. Условие симметрии течения не использовалось, что позволило проконтролировать реализацию во всех рассмотренных случаях симметричного течения.

Задача истечения струи из трубы прямоугольного сечения с размерами 1 × 0.5, где меньший размер задан в направлении нормали к твердой плоскости, рассматривалась с плоскостью симметрии. Продольный размер расчетной области составляет 700, размеры квадратного поперечного сечения расчетной области изменяются линейно с ростом продольной координаты от 50 × 50 до 1750 × 1750. Труба имеет длину 14 и лежит на твердой плоскости. Количество ячеек сетки $5.7 \times {{10}^{6}}$. Размер сетки в продольном направлении составляет 600 ячеек, из них 100 ячеек вдоль трубы. В поперечном сечении размер сетки 100 × 100 ячеек, причем на струю приходится область 50 × 50 ячеек. Сетка в поперечном сечении трубы содержит 30 × 30 ячеек. Течение исследовалось при числе Рейнольдса 200, которое определялось по среднерасходной скорости и большой стороне прямоугольного поперечного сечения.

В обоих вариантах расчета на входе в трубу задавалось однородное распределение продольной скорости. На всех границах расчетной области кроме входного сечения трубы и плоскости симметрии задавались нулевые нормальные производные всех компонент скорости.

Чувствительность численного решения по отношению к измельчению сетки исследовалась с помощью расчетов на более грубой сетке с удвоенными размерами ячеек во всех направлениях. Проведено сравнение профилей продольной и радиальной скорости в поперечном сечении $x = 400$ при $\varphi = 0$ и $\varphi = \pi {\text{/}}4$. Отличие профилей, рассчитанных на разных сетках, менее 1% в высоконапорной части струи $r \leqslant 100$.

На рис. 2 приведены графики зависимостей максимальных при $x = {\text{const}}$ значений продольной и радиальной составляющих скорости от координаты x. Можно видеть, что при $x > 100$ данные зависимости хорошо аппроксимируются степенными функциями:

(4.1)

${{u}_{{\max }}}(x) = 108.771{{x}^{{ - 5/3}}}$

(4.2)

${{{v}}_{{\max }}}(x) = 1.195{{x}^{{ - 4/3}}}$

Рис. 2.

Труба прямоугольного сечения, ${\text{Re}} = 200$. Зависимость максимальных в поперечном сечении струи продольной (a) и радиальной (б) составляющих скорости от продольной координаты; сплошные линии – аппроксимации (4.1), (4.2).

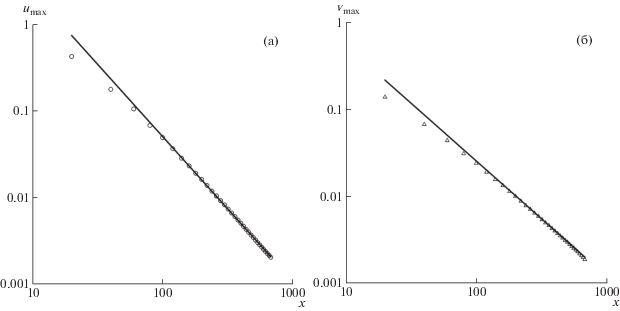
Отличие численного решения от формул (4.1), (4.2) менее 2% при $160 \leqslant x \leqslant 640$.

Функциям (4.1), (4.2) соответствует показатель автомодельности $k = 4{\text{/}}3$ в решении (1.6)–(1.10). Погрешность определения данной величины по численным данным порядка 1%.

Покажем, что зависимость решения (1.6)–(1.10) от числа Рейнольдса соответствует $\alpha = k$. На рис. 3 представлены графики функций $U(\eta ,0)$, $V(\eta ,0)$, построенных при $\alpha = k$ для поперечного сечения x = 390 при числах Рейнольдса 100, 150, 200. Их согласование указывает на правильность определения показателя $\alpha $.

Рис. 3.

Труба кругового сечения. Автомодельные профили продольной (а) и радиальной (б) скорости в плоскости симметрии сечения $x = 390$ при разных числах Рейнольдса: 1 – ${\text{Re}} = 100$; 2 – ${\text{Re}} = 150$; 3 – ${\text{Re}} = 200$; 4 – двучленные асимптотики (2.1), (2.2) при $A = 0.0146$, $B = 0$.

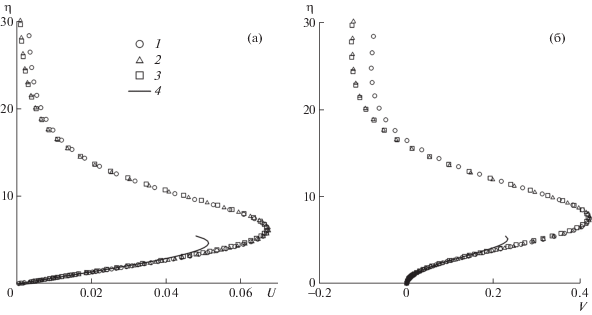
Наблюдается хорошее согласование автомодельных профилей скорости $U(\eta ,\varphi )$, $V(\eta ,\varphi )$, построенных по численному решению в разных поперечных сечениях $x = $ 200; 300; 400; 500; 600 при $\varphi = 0;\pi {\text{/}}4$. Для примера на рис. 4 представлены профили скорости, полученные для сечений $x = 200$; 500.

Рис. 4.

Труба прямоугольного сечения, ${\text{Re}} = 200$. Автомодельные профили продольной (а) и радиальной (б) скорости в разных поперечных сечениях: 1 – $x = 200$, $\varphi = 0$; 2 – $x = 200$, $\varphi = \pi {\text{/}}4$; 3 – $x = 500$, $\varphi = 0$; 4 – $x = 500$, $\varphi = \pi {\text{/}}4$; 5 – двучленные асимптотики (2.1), (2.2) с параметрами $A = 0.00173$, $B = 0$ при $\varphi = 0$; 6 – то же самое при $\varphi = \pi {\text{/}}4$.

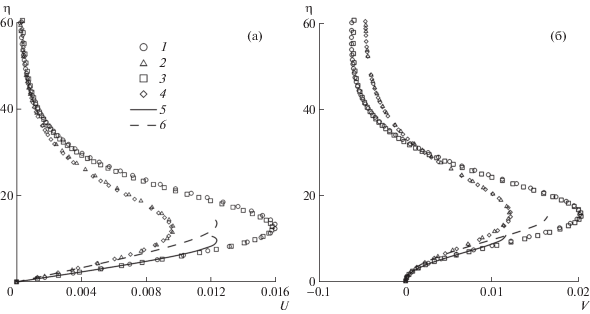
Автомодельные профили скорости на рис. 3 и 4 сравниваются с первыми двумя членами разложений (2.1), (2.2), в которых $A = 0.0146$ для трубы с круговым сечением и $A = 0.00173$ для трубы с прямоугольным сечением, B = 0 в обоих случаях. Константа B определена c помощью формулы (2.5) из численного решения. С ростом координаты $\eta $ радиальная скорость $V$ вначале растет, достигает максимума, затем убывает и становится отрицательной. Продольная скорость $U$ всюду положительна.

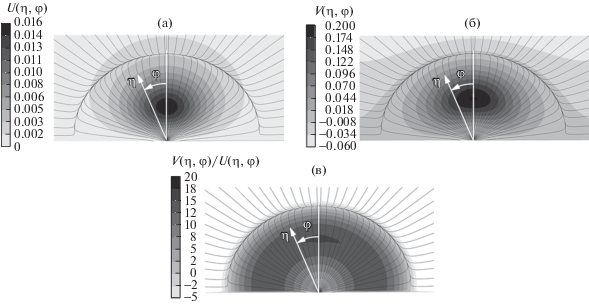
Численное решение позволяет установить некоторые приближенные свойства автомодельного решения. На рис. 5 показаны линии тока автомодельного течения в плоскости (η, φ). Можно видеть, что почти всюду линии тока направлены радиально, следовательно, азимутальная скорость существенно меньше радиальной. Радиальные линии тока всюду направлены к предельной линии тока, которая близка к полуокружности. Точка $\eta = 0$ является источником, пересечение плоскости симметрии с полуокружностью – стоком. Отклонение линий тока от радиального направления наблюдается только в непосредственной близости к полуокружности. На рис. 5в приведено поле отношения радиальной скорости к продольной $V(\eta ,\varphi ){\text{/}}U(\eta ,\varphi )$ на фоне линий тока автомодельного течения. Хорошо видно, что это поле практически не зависит от азимутального угла $\varphi $.

Рис. 5.

Труба прямоугольного сечения, ${\text{Re}} = 200$, $x = 600$. Автомодельные поля продольной скорости (а), радиальной скорости (б), отношения радиальной скорости к продольной (в). Показаны линии тока автомодельного течения.

5. СКРЫТЫЙ ЗАКОН СОХРАНЕНИЯ

Введем декартовы координаты $(x,y,z)$, ось y направлена по нормали к твердой стенке (рис. 1). Параболизованные уравнения Навье–Стокса (1.2)–(1.5) в случае плоского (не зависящего от z) течения переходят в уравнения пограничного слоя. В рамках этих уравнений получено [1, 2] точное автомодельное решение для пристенной струи, вытекающей из бесконечно тонкой щели:

(5.1)

$u = 1{\text{/}}{{x}^{{2k - 1}}}U(y{\text{/}}{{x}^{k}})$

Кроме того, для этой струи найден [1, 2] закон сохранения, который выполняется и в общем случае неавтомодельной пристенной струи:

(5.2)

$E = \int\limits_0^{ + \infty } {{{u}^{2}}} \psi dy = {\text{const}},\quad \psi (x,y) = \int\limits_0^y u (x,{{y}_{1}})d{{y}_{1}}$

Подставим в интеграл (5.2) решение (5.1). Получим, что интеграл E сохраняется на автомодельном решении при показателе автомодельности k = 3/4.

Теперь рассмотрим неавтомодельную струю, вытекающую из щели конечной ширины a со скоростью ${{u}_{0}}$. Из сохранения интеграла (5.2) следует $E \sim u_{0}^{3}{{a}^{2}} \sim {{u}^{3}}{{y}^{2}}$ (в используемых безразмерных переменных $a = 1$, ${{u}_{0}} = 1$). Здесь $u$, $y$ – характерные масштабы скорости и ширины струи. Из уравнения продольного импульса получаем ${{u}^{2}}{\text{/}}x \sim {\text{R}}{{{\text{e}}}^{{ - 1}}}u{\text{/}}{{y}^{2}}$. Приведенные оценки приводят к решению, которое учитывает зависимость от числа Рейнольдса и начального распределения скорости в щели (через инвариант E):

(5.3)

$u = {{E}^{{1/2}}}\mathop {\left( {\frac{x}{{{\text{Re}}}}} \right)}\nolimits^{ - 1/2} U\left( {{{E}^{{1/4}}}\mathop {\left( {\frac{x}{{{\text{Re}}}}} \right)}\nolimits^{ - 3/4} y} \right)$

Проблеме скрытых инвариантов для закрученных и незакрученных осесимметричных струй посвящены работы [15–22]. В случае осесимметричного течения из уравнений (1.2), (1.3) следует закон сохранения [21]:

(5.4)

$\int\limits_0^{ + \infty } {{{u}^{2}}} (\psi - {{\operatorname{Re} }^{{ - 1}}}x)rdr = {\text{const}},\quad \psi (x,r) = \int\limits_0^r u (x,{{r}_{1}}){{r}_{1}}d{{r}_{1}}$

Данная величина сохраняется в свободной затопленной струе и используется для построения второго координатного приближения в дальнем поле струи [22].

Размерности интегралов (5.2) и (5.4) равны размерности произведения потока импульса на расход. Хотелось бы иметь аналогичный закон сохранения и для трехмерного течения. Непосредственное обобщение интегралов (5.2) и (5.4) на трехмерный случай вряд ли возможно. Конечно, вместо одной функции тока в трехмерном течении можно определить две независимые компоненты векторного потенциала. Но при этом сложно представить себе интеграл, который в плоском случае переходит в (5.2), а в осесимметричном – в (5.4). С другой стороны, даже если бы существовал закон сохранения величины с размерностью ${{u}^{3}}{{\delta }^{4}}$, он не выполнялся бы для трехмерной пристенной струи, поскольку из него следует неправильный показатель автомодельности k = 3/2 вместо k = 4/3. В работе [3] при анализе данной задачи использовался закон сохранения момента импульса, который также приводит к неверному показателю автомодельности k = 2.

Предположим, что решение задачи зависит от единственного инварианта, который является величиной порядка $I \sim {{u}^{4}}{{\delta }^{5}}$, где $u$ – продольная скорость в струе, а $\delta $ – ширина струи. Выбранная размерность инварианта обеспечивает правильный показатель автомодельности k = 4/3. Тогда на основе данного инварианта, а также уравнений импульсов ${{u}^{2}}{\text{/}}x \sim \nu u{\text{/}}{{\delta }^{2}}$, $u{v}{\text{/}}x \sim p{\text{/}}\delta $ и неразрывности $u{\text{/}}x \sim {v}{\text{/}}\delta \sim w{\text{/}}\delta $ устанавливается вид решения:

(5.5)

$u(x,r,\varphi ) = {{I}^{{2/3}}}{{\xi }^{{ - 5/3}}}\tilde {U}({{I}^{{1/3}}}\eta ,\varphi )$

(5.6)

${v}(x,r,\varphi ) = {{I}^{{1/3}}}{{\operatorname{Re} }^{{ - 1}}}{{\xi }^{{ - 4/3}}}\tilde {V}({{I}^{{1/3}}}\eta ,\varphi )$

(5.7)

$w(x,r,\varphi ) = {{I}^{{1/3}}}{{\operatorname{Re} }^{{ - 1}}}{{\xi }^{{ - 4/3}}}\tilde {W}({{I}^{{1/3}}}\eta ,\varphi )$

(5.8)

$p(x,r,\varphi ) = {{I}^{{2/3}}}{{\operatorname{Re} }^{{ - 2}}}{{\xi }^{{ - 8/3}}}\tilde {P}({{I}^{{1/3}}}\eta ,\varphi )$

$\xi = x{\text{/Re}},\quad \eta = r{\text{/}}{{\xi }^{{4/3}}}$

где функции $\tilde {U}$, $\tilde {V}$, $\tilde {W}$, $\tilde {P}$ универсальны для любых (достаточно больших) чисел Рейнольдса и любых начальных условий (геометрия трубы, профиль скорости в трубе, расстояние от трубы до стенки).

Из соответствия формул (5.5)–(5.8) и асимптотических разложений (2.1)–(2.4) следует, что скрытый инвариант $I$ пропорционален константе A.

На рис. 6 приведено сравнение численных решений для труб кругового и прямоугольного поперечного сечений в универсальных переменных ${{A}^{{ - 2/3}}}{{\xi }^{{5/3}}}u$, ${{A}^{{ - 1/3}}}\operatorname{Re} {{\xi }^{{4/3}}}{v}$, ${{A}^{{1/3}}}\eta $ при φ = 0. При существенном различии начальных условий и констант A наблюдается совпадение автомодельных профилей скорости в указанном представлении.

Рис. 6.

Универсальные профили продольной (а) и радиальной (б) скорости в плоскости симметрии: 1 – труба кругового сечения, ${\text{Re}} = 150$, $x = 390$; 2 – труба прямоугольного сечения, ${\text{Re}} = 200$, $x = 400$; 3 – аппроксимации (6.1), (6.2).

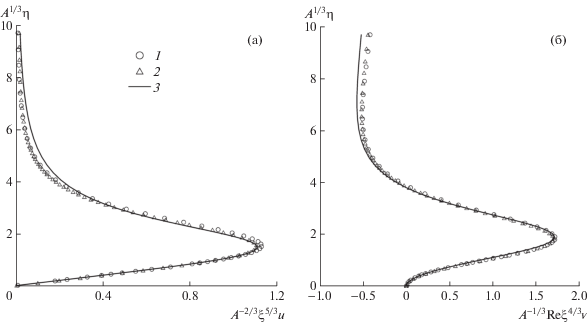
Из анализа полученного универсального профиля радиальной скорости оценена константа ${{F}_{0}}$ в разложении (3.1): ${{F}_{0}} \approx 4{\kern 1pt} - {\kern 1pt} 6$. Слабая точность связана с погрешностями численного решения при больших $r$. Из (5.6) следует, что эта константа на зависит от $I$ или $A$, т.е. одинакова для всех рассмотренных пристенных трехмерных струй.

Константа ${{P}_{0}}$ в разложении (1.9) определена из анализа универсального профиля давления при φ = 0, который получается при представлении численных данных в переменных ${{A}^{{ - 2/3}}}{\text{R}}{{{\text{e}}}^{2}}{{\xi }^{{8/3}}}p$, ${{A}^{{1/3}}}\eta $. Установлено ${{P}_{0}} = 0.2{{A}^{{2/3}}}$.

Определить константу $C$ в разложении (2.1) с помощью численного решения не удалось.

Рассмотрим границы применимости предложенной модели (5.5)–(5.8) дальнего поля трехмерной пристенной струи. Как известно, приближение пограничного слоя (1.2)–(1.5) имеет место только при больших числах Рейнольдса. Сравнение автомодельного решения (5.5)–(5.8) с численным решением уравнений Навье–Стокса позволяет заключить, что приближение пограничного слоя выполняется с достаточной точностью уже при числе Рейнольдса порядка сотни. При данном числе Рейнольдса струя неустойчива к малым возмущениям. Однако малые возмущения течения в трубе растут при Re ~ 100 очень медленно, что обеспечивает ламинарное поле течения на больших расстояниях от источника. При Re ~ 1000 можно ожидать, что течение станет турбулентным раньше, чем установится автомодельный режим (5.5)–(5.8). Из вида автомодельных переменных в (5.5)–(5.8) следует, что струя становится автомодельной на расстоянии от источника порядка числа Рейнольдса. При этом дальнейшее увеличение продольной координаты даже в предположении ламинарности потока приведет к нарушению условий приближения пограничного слоя вследствие достаточно быстрого расширения струи $\delta \sim {{(x{\text{/Re}})}^{{4/3}}}$. Согласно (5.5)–(5.8) продольная скорость порядка радиальной на расстоянии $x \sim {{\operatorname{Re} }^{4}}$, что является оценкой области применимости приближения пограничного слоя.

6. АППРОКСИМАЦИЯ ЧИСЛЕННОГО РЕШЕНИЯ

На основе решения (5.5)–(5.8), главных членов асимптотических разложений (2.1)–(2.3), (3.1) и установленных численно свойств дальнего автомодельного поля струи построена аппроксимация скоростей в струе:

(6.1)

$u = {{A}^{{2/3}}}\mathop {\left( {\frac{x}{{{\text{Re}}}}} \right)}\nolimits^{ - 5/3} \frac{{{{A}^{{1/3}}}\eta cos\varphi }}{{1 + 0.07 \cdot {{{({{A}^{{1/3}}}\eta )}}^{4}}}}$

(6.2)

${v} = {{\operatorname{Re} }^{{ - 1}}}{{A}^{{1/3}}}\mathop {\left( {\frac{x}{{{\text{Re}}}}} \right)}\nolimits^{ - 4/3} \frac{{{{{({{A}^{{1/3}}}\eta )}}^{2}}(1 - {{{({{A}^{{1/3}}}\eta {\text{/}}3.8)}}^{{1.6}}})cos\varphi }}{{1 + 0.02 \cdot {{{({{A}^{{1/3}}}\eta )}}^{{4.6}}}}}$

$w = 0$

$\eta = \mathop {\left( {\frac{x}{{{\text{Re}}}}} \right)}\nolimits^{ - 4/3} r$

Данная аппроксимация описывает продольную и радиальную скорости при φ = 0 с погрешностью относительно численного решения не более 10% (рис. 6) и обеспечивает качественное согласование при других значениях азимутального угла.

ЗАКЛЮЧЕНИЕ

В приближении пограничного слоя получено автомодельное решение (5.5)–(5.8) для дальнего поля трехмерной пристенной ламинарной струи. С помощью численного решения неавтомодельной задачи определены показатель автомодельности $k \approx 4{\text{/}}3$ и зависимость от числа Рейнольдса. Кроме того, установлена связь данного решения с условиями в источнике струи. Эта связь определяется константой A в главном члене асимптотического разложения дальнего поля струи (2.1) по малой радиальной координате. Проблема построения интегрального инварианта неавтомодельной струи, который позволяет связать данную константу с распределением скоростей в источнике, остается открытой. Получены координатные разложения автомодельного решения при малых и больших значениях радиальной координаты. В первом приближении разложения по малой координате азимутальная скорость отсутствует, а продольная и радиальная скорости зависят от азимутального угла одинаковым образом. Показано, что решение Гамеля для течения в конфузоре является главным членом разложения по большим значениям радиальной координаты. Численно показано, что геометрическое место точек нулевой радиальной скорости в поперечном сечении струи близко к полуокружности. Пределы применимости решения (5.5)–(5.8): Re ~ 100, ${\text{Re}} \leqslant x \ll {{\operatorname{Re} }^{4}}$.

Работа выполнена при финансовой поддержке Российского фонда фундаментальных исследований (№ проекта 19-01-00163).

Список литературы

Акатнов Н.И. Распространение плоской ламинарной струи вязкой жидкости вдоль твердой стенки // Труды Ленинградского политехнического института. 1953. № 5. С. 24–31.
Glauert M.B. The wall jet // Journal of Fluid Mechanics. 1956. V. 1. P. 625–643.
Krechetnikov R., Lipatov I. Hidden invariances in problems of two-dimensional and three-dimensional wall jets for Newtonian and non-Newtonian fluids // SIAM Journal on Applied Mathematics. 2002. V. 62. № 6. P. 1837–1855.
Баренблатт Г.И. Автомодельные явления – анализ размерностей и скейлинг. Долгопрудный: Издательский Дом: “Интеллект”, 2009. 216 с.
Schlichting H. Laminare Strahlausbreitung // Zeitschrift für Angewandte Mathematik und Mechanik. 1933. Bd. 13. H. 4. S. 260–263.
Ландау Л.Д. Об одном точном решении уравнений Навье–Стокса // Доклады АН СССР. 1944. Т. 43. № 7. С. 299–301.
Squire H.B. Some viscous fluid flow problems I: Jet emerging from a hole in a plane wall // The London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science. 1952. V. 43. № 344. P. 942–945.
Launder B.E., Rodi W. The turbulent wall jet // Progress in Aerospace Sciences. 1979. V. 19. P. 81–128.
Launder B.E., Rodi W. The turbulent wall jet measurements and modeling // Annual Review of Fluid Mecha-nics. 1983. V. 15. № 1. P. 429–459.
Craft T.J., Launder B.E. On the spreading mechanism of the three-dimensional turbulent wall jet // Journal of Fluid Mechanics. 2001. V. 435. P. 305–326.
Adane K.K., Tachie M.F. Numerical investigation of three-dimensional laminar wall jet of newtonian and non-newtonian fluids // AIAA Journal. 2008. V. 46. № 11. P. 2868–2880.
Adane K.F.K., Tachie M.F. Experimental and numerical study of laminar round jet flows along a wall // Journal of Fluids Engineering. 2010. V. 132. № 10. 101203.
Ландау Л.Д., Лифшиц Е.М. Теоретическая физика: Учебное пособие. В 10 т. Т. VI. Гидродинамика. М.: Наука, 1988. 736 с.
Гайфуллин А.М., Жвик В.В. Взаимодействие двух противоположно закрученных затопленных струй // Изв. РАН. МЖГ. 2019. № 3. С. 48–57.
Гольдштик М.А. О закрученных струях // Изв. АН СССР. МЖГ. 1979. № 1. С. 26–35.
Гольдштик М.А., Яворский Н.И. О затопленных струях // Прикладная математика и механика. 1986. Т. 50. № 4. С. 573–583.
Гольдштик М.А., Штерн В.Н., Яворский Н.И. Вязкие течения с парадоксальными свойствами. Новосибирск: Наука. Сибирское отделение, 1989. 336 с.
Goldshtik M.A. Viscous-flow paradoxes // Annual Review of Fluid Mechanics. 1990. V. 22. № 1. P. 441–472.
Яворский Н.И. О скрытом интеграле сохранения в теории затопленных струй // XII Всероссийский съезд по фундаментальным проблемам теоретической и прикладной механики. Аннотации докладов. 19–24 августа 2019 г. Уфа. 2019. С. 92.
Жвик В.В. Инварианты и асимптотики осесимметричных закрученных затопленных струй // Прикладная механика и техническая физика. 2020. Т. 61. № 2. С. 92–108.
Naz R. Conservation laws for laminar axisymmetric jet flows with weak swirl // Applicable Analysis: An International Journal. 2012. V. 91. № 5. P. 1045–1052.
Гайфуллин А.М., Жвик В.В. Связь дальней асимптотики струи с профилем скорости в отверстии // Доклады РАН. Физика, технические науки. 2020. Т. 495. С. 46–49.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Известия РАН. Механика жидкости и газа

Архивы выпусков Информация о журнале Отправить рукопись в журнал