Известия РАН. Механика жидкости и газа, 2021, № 6, стр. 66-73

ОБ УСТОЙЧИВОСТИ ФРОНТА ИНЖЕКЦИИ ВОДЫ В ВЫСОКОТЕМПЕРАТУРНЫЕ ПОРОДЫ

Г. Г. Цыпкин^a, *

^a Институт проблем механики им. А.Ю. Ишлинского РАН
Москва, Россия

Поступила в редакцию 20.06.2021
После доработки 22.06.2021
Принята к публикации 22.06.2021

DOI: 10.31857/S0568528121060165

Аннотация

Рассматривается задачи инжекции воды в высокотемпературный геотермальный резервуар, насыщенный перегретым паром. Методом нормальных мод исследуется устойчивость фронта фазового перехода, движущегося с постоянной скоростью. Проведено численное исследование полученного дисперсионного уравнения. При различных значениях основных параметров представлены дисперсионные кривые, характеризующие переход к неустойчивости. Показано, что переход от устойчивого режима распространения фронта к неустойчивому происходит при увеличении проницаемости и начальной температуры, а также при уменьшении начального давления.

Ключевые слова: геотермальный резервуар, инжекция, поверхность фазового перехода, устойчивость

Интерес к изучению течений с фазовыми переходами в геотермальных системах обусловлен как эксплуатацией геотермальных систем, так и природными процессами, происходящими в недрах Земли [1]. Формирование геотермальных систем связано, главным образом, с районами вулканической деятельности или с возникновением интенсивных конвективных течений, переносящих тепловую энергию к поверхности [2, 3]. Конвективные течения в геотермальных системах зачастую возникают в результате неустойчивости физической системы, которая сформировалась под действием температурного градиента, когда область, насыщенная водой, располагается над областью, насыщенной паром. При изменении внешних условий, например, температуры или давления, система теряет устойчивость [4, 5] и более легкий пар начинает двигаться к поверхности. В этом случае потеря устойчивости происходит под действием силы тяжести.

В [6] экспериментально исследовалась инжекция жидкости в пористую среду. Найдено, что в случае низкой температуры пористой среды поверхность фронта кипения остается регулярной, а при увеличении температуры неустойчивость приводит к образованию пальцев.

Технология эксплуатации геотермальных резервуаров, содержащих перегретый пар, заключается в закачке воды в высокотемпературные породы с последующим извлечением образующегося пара. При аналитических расчетах таких систем и получении оценок основных параметров течения, как правило, предполагается, что существует плоская поверхность, разделяющая области, насыщенные жидкой и газовой фазой [7, 8]. Устойчивость движущихся фронтов в геотермальных резервуарах или в пористых средах, где важную роль играет температурный фактор, в различных постановках исследовалась в [9–12].

В [13] рассматривалась упрощенная формулировка задачи об устойчивости движущейся поверхности раздела вода–пар при инжекции воды в высокотемпературный геотермальный резервуар. Предполагалось, что фронт находится вблизи закачивающей скважины и, из-за формирования области постоянной температуры за фронтом, пренебрегалось распространением возмущений температуры в этой области. Получено, что в рамках сформулированной задачи фронт всегда неустойчив. В [14] исследовалась устойчивость движущегося фронта кипения при падении давления в трещине низкопроницаемых высокотемпературных пород. Предполагалось, что поверхность кипения находится на значительном удалении от трещины и при распространении малых возмущений в области за фронтом эту область можно считать полубесконечной.

В настоящей работе подход, развитый в [14], применяется к задаче об инжекции воды в высокотемпературные породы, насыщенные перегретым паром. Методом нормальных мод исследована устойчивость фронта фазового перехода, движущегося с постоянной скоростью. Найдено, что неустойчивость возникает при увеличении проницаемости и температуры пород, а также при уменьшении начального давления.

1. ФОРМУЛИРОВКА ЗАДАЧИ

Пусть в начальном состоянии высокотемпературный геотермальный резервуар насыщен перегретым паром. При инжекции воды в окрестности закачивающей скважины образуется водонасыщенная область, отделенная от области пара движущимся фронтом фазового перехода. Для описания течений в обеих областях используются законы сохранения массы и энергии, закон Дарси, уравнения состояний и соотношения равновесной термодинамики. Система основных уравнений для областей, насыщенных водой и паром, имеет вид

(1.1)

$\phi \frac{{\partial {{\rho }_{j}}}}{{\partial t}} + {\text{div}}{{\rho }_{j}}{{{\mathbf{v}}}_{j}} = 0,\quad {{{\mathbf{v}}}_{j}} = - \frac{k}{{{{\mu }_{j}}}}{\text{grad}}{{P}_{j}}$

${{\lambda }_{{1,2}}} = \varphi {{\lambda }_{j}} + (1 - \varphi ){{\lambda }_{s}},\quad {{(\rho C)}_{{1,2}}} = \varphi {{\rho }_{j}}{{C}_{j}} + (1 - \varphi ){{\rho }_{s}}{{C}_{s}}$

${{\rho }_{w}} = {{\rho }_{{w0}}}[1 + {{\alpha }_{w}}({{P}_{w}} - {{P}_{0}})],\quad {{P}_{{v}}} = {{\rho }_{{v}}}RT,\quad j = {v},w$

Здесь ${\mathbf{v}}$ – вектор скорости фильтрации, $\phi $ – пористость, $k$ – проницаемость, $\mu $ – вязкость, ${{\alpha }_{w}}$ – сжимаемость воды, $R$ – газовая постоянная, $P$ – давление, $\rho $ – плотность, $C$ – теплоемкость, $T$ – температура, $\lambda $ – теплопроводность. Индексы $w$, ${v}$, $s$ соответствуют – вода, пар и матрице (скелету) пористой среды, 1 и 2 – области пара и воды.

На поверхности фазового перехода, которая является движущимся фронтом испарения или конденсации, справедливы условия баланса массы, энергии, импульса и уравнение Клаузиуса–Клапейрона термодинамического равновесия воды и пара

(1.2)

$\phi \left( {1 - \frac{{{{\rho }_{{v}}}}}{{{{\rho }_{w}}}}} \right){{V}_{n}} = \frac{{k{{\rho }_{{v}}}}}{{{{\mu }_{{v}}}{{\rho }_{w}}}}{{({\text{grad}}{{P}_{{v}}})}_{{n1}}} - \frac{k}{{{{\mu }_{w}}}}{{({\text{grad}}{{P}_{w}})}_{{n2}}}$

(1.3)

$\phi q{{\rho }_{{v}}}{{V}_{n}} + \frac{{kq{{\rho }_{{v}}}}}{{{{\mu }_{{v}}}}}{{({\text{grad}}{{P}_{{v}}})}_{{n1}}} = {{\lambda }_{2}}{{({\text{grad}}T)}_{{n2}}} - {{\lambda }_{1}}{{({\text{grad}}T)}_{{n1}}}$

(1.4)

${{T}_{ + }} = {{T}_{ - }} = {{T}_{ * }},\quad {{P}_{ + }} = {{P}_{ - }} = {{P}_{ * }}$

(1.5)

$\frac{{{{P}_{ * }}}}{{{{P}_{a}}}} = {\text{exp}}\left( {A + \frac{B}{{{{T}_{ * }}}}} \right) \equiv f({{T}_{ * }}),\quad A = 12.512,\quad B = - 4611.73$

Здесь V – скорость фронта, q – теплота фазового превращения, ${{P}_{a}} = {{10}^{5}}$ Па – атмосферное давление. Индексы соответствуют: $n$ – нормали, $ * $ – величинам на фронте.

В первом приближении можно пренебречь конвективным переносом тепла в области пара из-за его малой плотности. При инжекции воды в геотермальный резервуар было показано [15], что тепловой фронт движется медленнее фронта закачиваемой жидкости из-за высокой теплоемкости скелета пористой среды. В результате за движущимся фронтом фазового перехода образуется протяженная область постоянной температуры. Значение температуры в этой области определяется балансовыми соотношениями на фронте. Поэтому при исследовании устойчивости фронта конвективным переносом тепла в области жидкой фазы можно пренебречь. С учетом этих предположений система (1.1) упрощается и уравнения для областей пара и воды в первом приближении имеют вид

(1.6)

$\frac{{\partial P}}{{\partial t}} = {{a}_{{P1,2}}}\Delta P,\quad \frac{{\partial T}}{{\partial t}} = {{a}_{{T1,2}}}\Delta T$

${{a}_{{P1}}} = \frac{{k{{P}_{0}}}}{{\phi {{\mu }_{{v}}}}},\quad {{a}_{{P2}}} = \frac{k}{{\phi {{\mu }_{w}}{{\alpha }_{w}}}},\quad {{a}_{{T1,2}}} = \frac{{{{\lambda }_{{1,2}}}}}{{{{{(\rho C)}}_{{1,2}}}}}$

2. БАЗОВОЕ РЕШЕНИЕ

Для исследования устойчивости движущегося фронта фазового перехода рассмотрим течение, которое реализуется при повышении давления в закачивающей скважине таким образом, что градиент давления $\nabla {{P}_{ - }}$ в области пара остается постоянным. Тогда сформулированная задача допускает решение с фронтом кипения, движущимся с постоянной скоростью. При переходе в систему координат, движущейся со скоростью фронта, искомые функций характеризуются стационарными распределениями, которые могут быть исследованы на устойчивость классическими методами.

Оценки показывают, что при получении решения в виде бегущей волны с высокой степенью точности можно считать воду несжимаемой жидкостью и распределение давления в области жидкой фазы носит линейный характер. При высоких скоростях инжекции температура за фронтом постоянна, поэтому можно положить тепловой поток равным нулю в этой области для невозмущенного состояния и условие баланса тепла (1.3) принимает вид

(2.1)

$\phi q{{\rho }_{{v}}}{{V}_{n}} + \frac{{kq{{\rho }_{{v}}}}}{{{{\mu }_{{v}}}}}{{({\text{grad}}{{P}_{{v}}})}_{{n1}}} = - {{\lambda }_{1}}{{({\text{grad}}T)}_{{n1}}}$

Если начальное давление ${{P}_{0}}$ и температура ${{T}_{0}}$ постоянны, то при постоянном градиенте давления $\nabla {{P}_{ - }}$ за фронтом задача допускает решение в виде бегущей волны, которая распространяется с постоянной скоростью $V = {\text{const}}$. При заданном градиенте $\nabla {{P}_{ - }}$ распределение давления за фронтом имеет вид

(2.2)

${{P}_{{2st}}} = {{P}_{ * }} + \nabla {{P}_{ - }}\xi ,\quad \xi = x - Vt$

В области пара $\xi > 0$ решения для давления и температуры имеют вид

(2.3)

${{P}_{{1st}}} = ({{P}_{ * }} - {{P}_{0}})exp\left( { - \frac{V}{{{{a}_{{P1}}}}}} \right)\xi + {{P}_{0}}$

(2.4)

${{T}_{{1st}}} = ({{T}_{ * }} - {{T}_{0}})exp\left( { - \frac{V}{{{{a}_{{T1}}}}}} \right)\xi + {{T}_{0}}$

Подставляя решения (2.3) и (2.4) в уравнение баланса энергии (2.1) на поверхности раздела $\xi = 0$, получаем

(2.5)

$2 - \left( {\frac{{{{P}_{ * }}}}{{{{P}_{0}}}}} \right) - \frac{{{{\lambda }_{1}}{{T}_{0}}}}{{\phi q{{\rho }_{v}}{{a}_{{T1}}}}}\left( {\frac{{{{T}_{ * }}}}{{{{T}_{0}}}} - 1} \right) = 0$

Из уравнений (2.5) и (1.5) находятся значения искомых параметров ${{P}_{ * }}$ и ${{T}_{ * }}$ независимо от значения скорости $V$ фронта фазового перехода, которая вычисляется из условия баланса массы (1.2). Подставляя решения (2.2) и (2.3) в соотношения баланса массы (1.2), получаем соотношение на поверхности раздела, которое в безразмерной форме имеет вид

(2.6)

$1 + \frac{{{{\rho }_{{v}}}}}{{{{\rho }_{w}}}}\left( {\frac{{{{P}_{ * }}}}{{{{P}_{0}}}} - 2} \right) + \frac{{{{a}_{{P0}}}}}{{{{P}_{0}}}}\frac{{\nabla {{P}_{ - }}}}{V} = 0,\quad {{a}_{{P0}}} = \frac{{k{{P}_{0}}}}{{\phi {{\mu }_{w}}}}$

Из полученного выражения определяется отношение скорости фронта кипения V к градиенту давления $\nabla {{P}_{ - }}$.

Расчеты базового решения в виде бегущей волны, проведенные при характерных значениях параметров, показали наличие двух режимов инжекции, зависящих от начальной температуры и давления пара. При низком начальном давлении и высокой температуре распространяется фронт кипения, а при относительно низкой температуре и высоком начальном давлении – фронт конденсации.

3. ВЫВОД ДИСПЕРСИОННОГО УРАВНЕНИЯ

Представленное выше решение в виде бегущей волны справедливо на больших временах. Предполагая удаление фронта на достаточно большое расстояние от скважины, такое, что для описания развития возмущений за фронтом область 2 можно считать полубесконечной $ - \infty < \xi \leqslant 0$. Поскольку для возмущений не выполняется условие квазистационарности, то для получения решений в области 2 воспользуемся точными уравнениями (1.6).

Исследуем устойчивость решения в виде бегущей волны методом нормальных мод. Пусть ${{P}_{j}} \equiv {{P}_{j}}(\xi ,z,t) = {{P}_{{jst}}} + \delta {{P}_{j}}$, ${{T}_{j}} \equiv {{T}_{j}}(\xi ,z,t) = {{T}_{{jst}}} + \delta {{T}_{j}}$, $j = 1,\;2$, $\eta = \eta (z,t)$ – возмущение плоского фронта ξ = 0. Возмущения стационарного решения представим в виде:

$\delta {{P}_{{1,2}}} = P_{{1,2}}^{'}(\xi )exp({\text{i}}\kappa z + \sigma t),\quad \delta {{T}_{{1,2}}} = T_{{1,2}}^{'}(\xi )exp({\text{i}}\kappa z + \sigma t),$

$\eta = \eta {\text{'}}exp({\text{i}}\kappa z + \sigma t),\quad \eta {\text{'}} = {\text{const}}$

Из уравнений (1.6) следуют уравнения для амплитуд $P_{{1,2}}^{'}$ и $T_{{1,2}}^{'}$

(3.1)

${{a}_{{P1,2}}}\frac{{{{d}^{2}}P_{{1,2}}^{'}}}{{d{{\xi }^{2}}}} + V\frac{{dP_{{1,2}}^{'}}}{{d\xi }} - ({{a}_{{P1,2}}}{{\kappa }^{2}} + \sigma )P_{{1,2}}^{'} = 0$

(3.2)

${{a}_{{T1,2}}}\frac{{{{d}^{2}}T_{{1,2}}^{'}}}{{d{{\xi }^{2}}}} + V\frac{{dT_{{1,2}}^{'}}}{{d\xi }} - ({{a}_{{T1,2}}}{{\kappa }^{2}} + \sigma )T_{{1,2}}^{'} = 0$

Учитывая условия убывания возмущений на $ + \infty $ и $ - \infty $, решения уравнений (3.1) и (3.2) имеют вид

$P_{1}^{'} = {{d}_{1}}exp\left[ { - \frac{V}{{2{{a}_{{P1}}}}} - \sqrt {\frac{{{{V}^{2}}}}{{4a_{{P1}}^{2}}} + \frac{\sigma }{{{{a}_{{P1}}}}} + {{\kappa }^{2}}} } \right]\xi $

(3.3)

$T_{1}^{'} = {{e}_{1}}exp\left[ { - \frac{V}{{2{{a}_{{T1}}}}} - \sqrt {\frac{{{{V}^{2}}}}{{4a_{{T1}}^{2}}} + \frac{\sigma }{{{{a}_{{T1}}}}} + {{\kappa }^{2}}} } \right]\xi $

$P_{2}^{'} = {{d}_{2}}exp\left[ { - \frac{V}{{2{{a}_{{P2}}}}} + \sqrt {\frac{{{{V}^{2}}}}{{4a_{{P2}}^{2}}} + \frac{\sigma }{{{{a}_{{P2}}}}} + {{\kappa }^{2}}} } \right]\xi $

$T_{2}^{'} = {{e}_{2}}exp\left[ { - \frac{V}{{2{{a}_{{T2}}}}} + \sqrt {\frac{{{{V}^{2}}}}{{4a_{{T2}}^{2}}} + \frac{\sigma }{{{{a}_{{T2}}}}} + {{\kappa }^{2}}} } \right]\xi $

где ${{d}_{{1,2}}}$, e_{1, 2} – постоянные.

Подставляя решения (3.3) в граничные условия (1.2)–(1.5), на поверхности фазового перехода получаем систему уравнений относительно неизвестных d₁, d₂, e₁, e₂ и $\eta {\text{'}}$

${{d}_{1}} - {{d}_{2}} = \left[ {\nabla {{P}_{ - }} + \tfrac{V}{{{{a}_{{P1}}}}}({{P}_{ * }} - {{P}_{0}})} \right]\eta {\text{'}},$

${{e}_{1}} - {{e}_{2}} = \tfrac{V}{{{{a}_{{T1}}}}}({{T}_{ * }} - {{T}_{0}})\eta {\text{'}},$

${{d}_{1}} - \tfrac{{df}}{{dT}}{{e}_{2}} = \tfrac{V}{{{{a}_{{P1}}}}}({{P}_{ * }} - {{P}_{0}})\eta {\text{'}},$

$\left[ {\phi \left( {1 - \frac{{{{\rho }_{{v}}}}}{{{{\rho }_{w}}}}} \right)\sigma - \frac{k}{{{{\mu }_{{v}}}}}\frac{{{{\rho }_{{v}}}}}{{{{\rho }_{w}}}}\frac{{{{V}^{2}}}}{{a_{{P1}}^{2}}}\left( {{{P}_{ * }} - {{P}_{0}}} \right)} \right]\eta {\text{'}} + \frac{k}{{{{\mu }_{{v}}}}}\frac{{{{\rho }_{{v}}}}}{{{{\rho }_{w}}}}{{d}_{1}}\left( {\frac{V}{{2{{a}_{{P1}}}}} + \sqrt {\frac{{{{V}^{2}}}}{{4a_{{P1}}^{2}}} + \frac{\sigma }{{{{a}_{{P1}}}}} + {{\kappa }^{2}}} } \right) + $

(3.4)

$ + \;\frac{k}{{{{\mu }_{w}}}}{{d}_{2}}\left( { - \frac{V}{{2{{a}_{{P2}}}}} + \sqrt {\frac{{{{V}^{2}}}}{{4a_{{P2}}^{2}}} + \frac{\sigma }{{{{a}_{{P2}}}}} + {{\kappa }^{2}}} } \right) = 0,$

$\left[ {\phi q{{\rho }_{{v}}}\sigma + \frac{{kq{{\rho }_{{v}}}}}{{{{\mu }_{{v}}}}}\frac{{{{V}^{2}}}}{{a_{{P1}}^{2}}}\left( {{{P}_{ * }} - {{P}_{0}}} \right) + {{\lambda }_{1}}\frac{{{{V}^{2}}}}{{a_{{T1}}^{2}}}\left( {{{T}_{ * }} - {{T}_{0}}} \right)} \right]\eta {\text{'}} - {{d}_{1}}\frac{{kq{{\rho }_{{v}}}}}{{{{\mu }_{{v}}}}}\left( {\frac{V}{{2{{a}_{{P1}}}}} + \sqrt {\frac{{{{V}^{2}}}}{{4a_{{P1}}^{2}}} + \frac{\sigma }{{{{a}_{{P1}}}}} + {{\kappa }^{2}}} } \right) - $

$ - \,{{e}_{2}}{{\lambda }_{2}}\left( { - \frac{V}{{2{{a}_{{T2}}}}} + \sqrt {\frac{{{{V}^{2}}}}{{4a_{{T2}}^{2}}} + \frac{\sigma }{{{{a}_{{T2}}}}} + {{\kappa }^{2}}} } \right) - {{e}_{1}}{{\lambda }_{1}}\left( {\frac{V}{{2{{a}_{{T1}}}}} + \sqrt {\frac{{{{V}^{2}}}}{{4a_{{T1}}^{2}}} + \frac{\sigma }{{{{a}_{{T1}}}}} + {{\kappa }^{2}}} } \right) = 0$

Система уравнений (3.4) имеет нетривиальное решение, если детерминант системы равен нулю. Соответственно, дисперсионное уравнение безразмерной формы имеет вид ($\Sigma = {{a}_{{T1}}}\sigma {\text{/}}{{V}^{2}}$, $K = {{a}_{{T1}}}\kappa {\text{/}}V$)

(3.5)

$\begin{gathered} \left[ {{{\alpha }_{1}}\Sigma + {{\alpha }_{2}}({{\Gamma }_{1}} - 1) - {{\alpha }_{3}}{{\Gamma }_{2}}} \right]\left[ {{{\Gamma }_{3}} + {{\Gamma }_{4}} + {{\alpha }_{4}}{{\Gamma }_{1}}} \right] + \\ + \;\frac{{dF}}{{dT}}\left[ {{{\alpha }_{5}}\Sigma + {{\alpha }_{6}}(1 - {{\Gamma }_{1}}) + {{\alpha }_{7}}(1 - {{\Gamma }_{4}})} \right]\left[ {{{\alpha }_{8}}{{\Gamma }_{1}} + {{\alpha }_{9}}{{\Gamma }_{2}}} \right] = 0 \\ \end{gathered} $

Здесь

${{\alpha }_{1}} = 1 - \frac{{{{\rho }_{{v}}}}}{{{{\rho }_{w}}}},\quad {{\alpha }_{2}} = \frac{{{{\rho }_{{v}}}}}{{{{\rho }_{w}}}}\frac{{{{a}_{{T1}}}}}{{{{a}_{{P1}}}}}\left( {\frac{{{{P}_{ * }}}}{{{{P}_{0}}}} - 1} \right),\quad {{\alpha }_{3}} = \frac{{{{a}_{{T1}}}}}{{{{a}_{{P1}}}}}{{a}_{{P0}}}\frac{{\nabla {{P}_{ - }}}}{{{{P}_{0}}V}}$

${{\alpha }_{4}} = \frac{{\phi q{{\rho }_{{v}}}}}{{{{\lambda }_{1}}{{T}_{0}}}}{{a}_{{T1}}}\frac{{dF}}{{dT}},\quad {{\alpha }_{5}} = \frac{{\phi q{{\rho }_{{v}}}}}{{{{\lambda }_{1}}{{T}_{0}}}}{{a}_{{T1}}},\quad {{\alpha }_{6}} = \frac{{{{a}_{{T1}}}}}{{{{a}_{{P1}}}}}\frac{{\phi q{{\rho }_{{v}}}}}{{{{\lambda }_{1}}{{T}_{0}}}}{{a}_{{T1}}}\left( {\frac{{{{P}_{ * }}}}{{{{P}_{0}}}} - 1} \right)$

${{\alpha }_{7}} = \left( {\frac{{{{T}_{ * }}}}{{{{T}_{0}}}} - 1} \right),\quad {{\alpha }_{8}}\frac{{{{\rho }_{{v}}}}}{{{{\rho }_{w}}}},\quad {{\alpha }_{9}} = \frac{{{{a}_{{p0}}}}}{{{{a}_{{P1}}}}},\quad \frac{{dF}}{{dT}} = \frac{{df{\text{/}}{{P}_{0}}}}{{dT{\text{/}}{{T}_{0}}}}$

${{\Gamma }_{1}} = \frac{1}{2} + \sqrt {\frac{1}{4} + \frac{{{{a}_{{P1}}}}}{{{{a}_{{T1}}}}}\Sigma + \frac{{a_{{P1}}^{2}}}{{a_{{T1}}^{2}}}{{K}^{2}}} ,\quad {{\Gamma }_{2}} = - \frac{1}{2} + \sqrt {\frac{1}{4} + \frac{{{{a}_{{P2}}}}}{{{{a}_{{T1}}}}}\Sigma + \frac{{a_{{P2}}^{2}}}{{a_{{T1}}^{2}}}{{K}^{2}}} $

${{\Gamma }_{3}} = - \frac{1}{2} + \sqrt {\frac{1}{4} + \frac{{{{a}_{{T2}}}}}{{{{a}_{{T1}}}}}\Sigma + \frac{{a_{{T2}}^{2}}}{{a_{{T1}}^{2}}}{{K}^{2}}} ,\quad {{\Gamma }_{4}}\frac{1}{2} + \sqrt {\frac{1}{4} + \Sigma + {{K}^{2}}} $

4. ИСCЛЕДОВАНИЕ УСТОЙЧИВОСТИ

Непосредственно из уравнения (3.5), следует, что пара K = 0, $\Sigma = 0$ является корнем уравнения при любых значениях параметров. Поэтому все дисперсионные кривые проходят через начало координат на плоскости ($K,{\text{Re}}\Sigma $). Исследование дисперсионного уравнения (3.5) проводилось в широком диапазоне параметров. Численные эксперименты показали, что основными параметрами, влияющими на устойчивость, являются проницаемость, начальные температура и давление, а переход из устойчивого состояния в неустойчивое и наоборот происходит при конечном волновом числе.

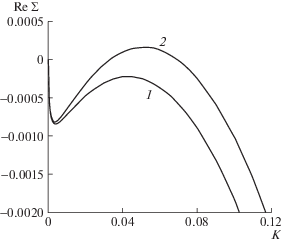
Рассмотрим переход к неустойчивости при умеренных значениях проницаемости $k = 5 \times {{10}^{{ - 15}}}$ м². На рис. 1 представлена деформация дисперсионных кривых в зависимости от значений начального давления, соответствующих режиму кипения воды. Дисперсионная кривая 1 расположена в нижней полуплоскости ${\text{Re}}\Sigma < 0$, что соответствует устойчивому режиму распространения фронта. При уменьшении начального давления дисперсионная кривая пересекает ось абсцисс и часть кривой располагается в верхней полуплоскости ${\text{Re}}\Sigma > 0$. Переход к неустойчивости происходит при конечных значениях волнового числа. Заметим, что коротковолновые возмущения, соответствующие большим значениям волновых чисел $K$, затухают при всех значениях начального давления. Естественно предположить, что к неустойчивости фронта приводит увеличение скорости движения жидкости вследствие падения давления в резервуаре. Неустойчивость фронта испарения с увеличением скорости инжекции в пористую среду наблюдалась экспериментально [6]. Было обнаружено, что процесс испарения не компенсировал быстрый рост возмущений поверхности фронта со временем.

Рис. 1.

Переход к неустойчивости фронта при уменьшении начального давления резервуара при умеренных значениях проницаемости при $\phi = 0.2$, $k = 5 \times {{10}^{{ - 15}}}$ м², ${{T}_{0}} = 580$ K: – 2 – ${{P}_{0}} = 1.33 \times {{10}^{6}},\;1.3 \times {{10}^{6}}$ Па.

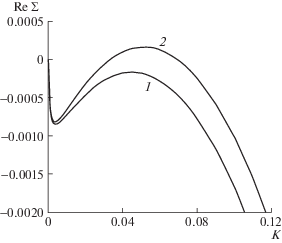
Аналогичные деформации дисперсионные кривые испытывают при изменении начальной температуры пласта (рис. 2). При ${{T}_{0}} = 580$ K фронт кипения неустойчив (кривая 2), а снижение температуры до ${{T}_{0}} = 579$ K приводит к его стабилизации (кривая 1). Также как и в предыдущем примере, переход от устойчивого состояния к неустойчивому осуществляется при конечных волновых числах. Стабилизация фронта кипения при снижении температуры пористой среды наблюдалась в экспериментах [6]. Можно предположить, что в основе механизма подавления возмущений лежит увеличение вязкости жидкости при снижении температуры. В результате снижается скорость движения жидкости и фронт становится устойчивым.

Рис. 2.

Переход к неустойчивости при увеличении начальной температуры геотермального резервуара при умеренных значениях проницаемости при $\phi = 0.2$, $k = 5 \times {{10}^{{ - 15}}}$ м², ${{P}_{0}} = 1.3 \times {{10}^{6}}$ Па: – 2 – ${{T}_{0}} = 579,\;580$ K.

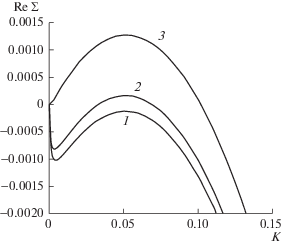
То, что увеличение скорости течения может приводить к неустойчивости, находит подтверждение также при анализе дисперсионных кривых, которые показаны на рис. 3, где представлены результаты расчетов при различных значениях проницаемости пласта. Движение фронта в высокопроницаемом резервуаре является неустойчивым (кривая 1). При снижении проницаемости декремент ReΣ наиболее неустойчивой моды снижается (кривая 2), а при уменьшении ниже порогового значения k дисперсионная кривая (линия 3) полностью переходит в нижнюю полуплоскость ReΣ.

Рис. 3.

Влияние проницаемости на возникновение неустойчивости фронта кипения при $\phi = 0.2$, ${{P}_{0}} = 1.3 \times {{10}^{6}}$ Па, $T = 580$ K: 1–3 – $k = 4 \times {{10}^{{ - 15}}},\;5 \times {{10}^{{ - 15}}},\;{{10}^{{ - 13}}}$ м².

На рис. 4 и 5 представлена эволюция дисперсионных кривых при изменении начальных давления и температуры в высокопроницаемом пласте. Также как и в случае умеренных проницаемостей, снижение давления и увеличение температуры приводит к возникновению неустойчивости фронта. Отличие состоит в том, что при увеличении проницаемости пласта критическое волновое число, соответствующее наиболее быстрорастущей моде, уменьшается.

Рис. 4.

Переход к режиму неустойчивости фронта при уменьшении начального давления в высокопроницаемом геотермальном резервуаре при $\phi = 0.2$, $k = {{10}^{{ - 13}}}$ м², ${{T}_{0}} = 580$ K: 1–3 – ${{P}_{0}} = 1.5,\;1.392,\;1.3$ МПа.

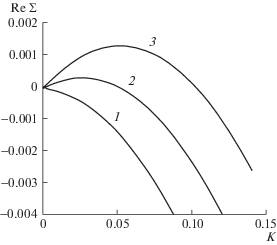
Рис. 5.

Переход к неустойчивости при увеличении начальной температуры высокопроницаемого геотермального резервуара при $\phi = 0.2$, $k = {{10}^{{ - 13}}}$ м², ${{P}_{0}} = 1.3 \times {{10}^{6}}$ Па: 1, 2 – ${{T}_{0}} = 570,\;580$ K.

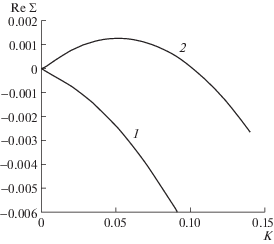
На рис. 3–5 проявляется одна качественная особенность поведения дисперсионных кривых, которую следует отметить. Как показывают численные эксперименты, все дисперсионные кривые, соответствующие неустойчивому состоянию фронта, имеют в окрестности нуля точки перегиба, расположенные в нижней полуплоскости ${\text{Re}}\Sigma $. Отсюда следует, что все переходы к неустойчивому состоянию реализуются при конечных критических волновых числах ${{K}_{{cr}}}$. При увеличении проницаемости величина ${{K}_{{cr}}}$ уменьшается, область перегиба прижимается к началу координат, а значения $\Sigma $ в этой области уменьшаются и становятся на несколько порядков меньше характерного значения. Соответственно эти особенности кривых неразличимы на рис. 3–5 .

Заметим, что все рассмотренные режимы перехода из устойчивого состояния в неустойчивое реализуются для фронта, движущегося в режиме испарения воды. Увеличение давления приводит к появлению режима конденсации, когда пар переходит в жидкость. Расчеты показали, что режимы конденсации всегда устойчивы. На этом основании можно сделать вывод, что динамика движения жидкости играет доминирующую роль в возникновении неустойчивости фронта инжекции воды в высокотемпературные породы.

ЗАКЛЮЧЕНИЕ

Методом нормальных мод проведено исследование устойчивости фронта фазового перехода, распространяющегося с постоянной скоростью при инжекции воды в высокотемпературный геотермальный резервуар, насыщенный перегретым паром. Получено дисперсионное соотношение, которое исследовано численно.

Как показали численные эксперименты, в режиме конденсации фронт фазового перехода всегда устойчив, а в режиме испарения может быть как устойчивым, так и неустойчивым. Переход к неустойчивости всегда реализуется при конечных волновых числах, значения которых существенно зависят от проницаемости пород. Коротковолновые возмущения как для устойчивых режимов, так и для неустойчивых быстро затухают при всех значениях физических параметров задачи.

Найдено, что переход от устойчивого режима к неустойчивому происходит при увеличении проницаемости и температуры геотермального резервуара, а также при уменьшении начального давления пара. Полученные результаты на качественном уровне хорошо согласуются с результатами экспериментов [6].

Работа выполнена при поддержке гранта РНФ № 21-11-00126.

Список литературы

Grant M., Bixley P.F. Geothermal reservoir engineering. London: Acad. Press, 2011. 378 p.
McGuinness M.J. Steady solution selection and existence in geothermal heat pipes-I. The convective case // Int. J. Heat Mass Transfer. 1996. V. 39. P. 259–274.
Pestov I. Stability of vapor–liquid counterflow in porous media // J. Fluid Mech. 1998. V. 364. P. 273–295.
Schubert G., Straus J.M. Gravitational stability of water over steam in vapor-dominated geothermal system // J. Geophys. Res. 1980. V. 85. № B11. P. 6505–6512.
Цыпкин Г.Г., Ильичев А.Т. Устойчивость стационарного фронта фазовых переходов вода-пар в гидротермальных системах // Докл. РАН. 2001. Т. 378. № 2. С. 197–200.
Il’ichev A.T., Tsypkin G.G. Catastrophic transition to instability of evaporation front in a porous medium // Eur. J. Mech. B/Fluids. 2008. V. 27. № 6. P. 665–677.
Pruess K., Calore C., Celati R., Wu Y.S. An analytical solution for heat transfer at a boiling front moving through a porous medium // Int. J. Heat Mass Transfer. 1987. V. 30. № 12. P. 2595–2602.
Fitzgerald S.D., Woods A.W. The instability of a vaporization front in hot porous rock // Nature. 1994. V. 367. P. 450–453.
Fitzgerald S.D., Woods A.W. Instabilities during liquid migration into superheated geothermal reservoir // Water Res. Research. 1998. V. 34. № 9. P. 2089–2101.
Pritchard D. The instability of thermal and fluid fronts during radial injection in a porous medium // J. Fluid Mech. 2004. V. 508. P. 133–163.
Hoffman B.T., Kovscek A.R. Displacement front stability of steam injection into high porosity diatomite rock // J. of Petroleum Sci. Eng. 2005. V. 46. P. 253–266.
Nouri-Borujerdi A., Noghrehabadi A.R., Rees D.A.S. The linear stability of a developing thermal front in a porous medium: The effect of local thermal non-equilibrium // Int. J. Heat and Mass Transfer. 2007. V. 50. P. 3090–3099.
Цыпкин Г.Г. Неустойчивость фронта фазового перехода при инжекции воды в высокотемпературные породы // Труды Математического института им. В.А. Стеклова. 2018. Т. 300. С. 197–204.
Tsypkin G.G., Il’ichev A.T. Superheating of water and morphological instability of the boiling front moving in the low-permeability rock // Int. J. Heat and Mass Transfer. 2021. V. 167. 120820.
Tsypkin G.G., Calore C. Influence of capillary forces on water injection into hot rock, saturated with superheated vapour // Int. J. Heat and Mass Transfer. 2007. V. 20. 3195–3202.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Известия РАН. Механика жидкости и газа

Архивы выпусков Информация о журнале Отправить рукопись в журнал