Известия РАН. Механика жидкости и газа, 2021, № 5, стр. 34-48

1. ПОСТАНОВКА ЗАДАЧИ УПРАВЛЕНИЯ

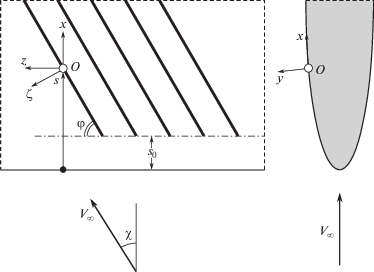
Рассмотрим задачу управления течением в ламинарном пограничном слое на крыле бесконечного размаха цилиндрической формы, обтекаемом равномерным потоком газа под углом скольжения χ с небольшой дозвуковой скоростью $V_{\infty }^{ \circ }$, плотностью ρ° и вязкостью μ° (кружками помечаем размерные величины). Введем криволинейную систему координат с началом в некоторой точке O обтекаемой поверхности на разгонном участке течения. Расстояние от передней кромки крыла до точки O, отсчитываемое вдоль стенки, обозначим s°. Ось x° направим вдоль поверхности перпендикулярно передней кромке в направлении разгона, ось y° – по нормали к стенке, а ось z° – вдоль образующей крыла в направлении скольжения (рис. 1). Соответствующие компоненты вектора скорости обозначим u°, ${v}^\circ $, w°, давление – p°. Значения параметров течения на внешней границе пограничного слоя будем помечать индексом e.

Будем предполагать, что система управления состоит из ряда исполнительных элементов, расставленных с постоянным шагом вдоль размаха крыла. Электроды актуаторов всюду составляют постоянный угол φ с образующей (рис. 1). Составляющие объемной силы вдоль обтекаемой поверхности и по нормали к ней обозначим, соответственно,  f ° и g°.

В дальнейшем будем использовать два масштаба длины – радиус кривизны профиля крыла на линии растекания r° и характерную толщину пограничного слоя

Введем безразмерные переменные с помощью равенств

В сделанных предположениях параметры течения удовлетворяют системе уравнений Навье– Стокса для несжимаемой жидкости

Здесь ${\text{R}} = \rho ^\circ V_{\infty }^{ \circ }\delta ^\circ {\text{/}}\mu ^\circ \gg 1$ – число Рейнольдса. В системе (1.1) опущены члены, связанные с кривизной поверхности крыла: в рассматриваемых задачах управления ими можно пренебречь [7].

Параметры течения удовлетворяют условиям прилипания на стенке и условиям сращивания с внешним течением

Процесс управления поперечным течением в пограничном слое будем иллюстрировать на примере скользящего крыла эллиптического сечения, обтекаемого под нулевым углом атаки. В этом случае скорость внешнего течения по нормали к образующей крыла u_e(s) задается параметрической зависимостью

где ε – отношение толщины профиля крыла к длине его хорды.

Опишем используемую здесь математическую модель силового воздействия. Как и в экспериментах [5, 8], исполнительные элементы имеют вытянутую конфигурацию, поэтому создаваемая ими объемная сила перпендикулярна электродам актуаторов, т.е. ее направление лежит в плоскости y, ς = z  sin φ − x cos φ (см. рис. 1).

Зададим компоненты объемной силы в виде

где erfc(η) – интеграл вероятностей [9]. За исключением небольшой окрестности переднего края системы актуаторов (s = s₀) равенства (1.3) описывают класс соленоидальных распределений объемных сил что является следствием закона сохранения заряда и хорошо согласуется с результатами экспериментов [10, 11]. Воздействие быстро затухает при y → ∞. Распределения (1.3) представляют собой единичные области силового воздействия гауссовой формы, размещенные с периодом Π/sin φ вдоль размаха крыла.

Для управления поперечным течением необходимо, чтобы приложенная объемная сила была локализована внутри пограничного слоя b = O(1). Область силового воздействия, создаваемого плазменным актуатором, имеет сравнимые продольный и поперечный размеры [10], т.е. a = O(1). Такое же ограничение накладывается и на среднюю интенсивность воздействия: c/Π = O(1). Множитель f_s(s) моделирует продольное распределение силового поля на передней границе области воздействия; в силу этого также l = O(1).

2. ТЕЧЕНИЕ В ОТСУТСТВИЕ СИЛОВОГО ВОЗДЕЙСТВИЯ

Для иллюстрации эффекта управления исследуем характеристики поперечного течения на скользящем крыле эллиптического сечения в отсутствие силового воздействия. Введем параметры классического пограничного слоя с помощью равенств

Функции Q = U, V/R, W, P удовлетворяют уравнениям Прандтля [1]. Введем обозначения для местной формы профиля скорости поперечного течения

а также для локального V_m и глобального V_max максимумов его интенсивности

Выберем конфигурацию управляемого течения для сравнения различных режимов воздействия. С этой целью изучим зависимость интенсивности поперечного течения от относительной толщины крыла и угла скольжения.

В пределе ε → 0 управляемое течение в выбранных масштабах соответствует симметричному обтеканию параболы. В этом случае V_max = 0.0727 при χ = 30°. При таком же угле скольжения для обтекания кругового цилиндра (ε = 1) имеем V_max = 0.104. На промежутке 0 < ε < 1 зависимость V_max(ε) близка к линейной; максимум интенсивности поперечного течения достигается в диапазоне 0.7 < s < 0.85, т.е. на расстоянии порядка одного радиуса кривизны носка от линии присоединения.

В предельных случаях χ = 0°, 90° на крыльях цилиндрической формы поперечное течение отсутствует. На промежутке 0° < χ < 90° график функции V_max(χ) имеет форму параболы с вершиной, немного смещенной влево. При ε = 0.2 эта функция с относительной точностью 0.2% аппроксимируется трехчленным степенным разложением

Максимальное значение интенсивности поперечного течения V_max = 0.0855 имеет место при χ = 41°.

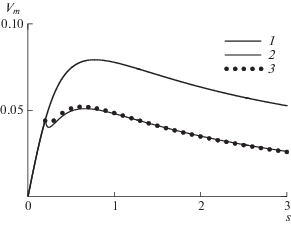
В данной работе все дальнейшие результаты приведены для случая ε = 0.2, χ = 30°. На рис. 2 показано соответствующее распределение V_m(s) (кривая 1). На передней кромке крыла поперечное течение отсутствует V_m(0) = 0, далее его интенсивность быстро растет по закону, близкому к линейному. Максимум достигается при s = 0.774, V_max = 0.0793, затем поперечное течение медленно затухает.

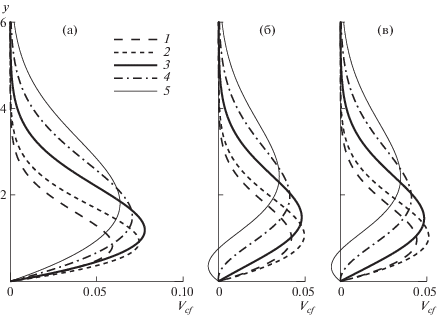
На рис. 3а показаны профили скорости поперечного течения в сечениях s = 0.3, 0.5, 1, 1.5, 2, расположенных вблизи места его наибольшей интенсивности. С ростом s наблюдается увеличение высоты положения максимума скорости. Это связано с возрастанием толщины пограничного слоя при удалении от передней кромки крыла.

3. ТЕЧЕНИЕ, УПРАВЛЯЕМОЕ ОСРЕДНЕННОЙ ПО РАЗМАХУ СИЛОЙ

Исследуем сначала течение в пограничном слое, формируемое полем осредненной по z силы (1.3)

Такое течение однородно по z, его параметры снова ищем в виде (2.1). Подставляя (2.1), (3.1) в задачу (1.1)–(1.2), получим

Задача (3.2) отличается от классической задачи Прандтля наличием источниковых членов в уравнениях импульса, ее решение рассчитывалось методом, аналогичным [1].

Зафиксируем параметры системы управления (1.3) a = 1, b = 1, c = 0.5, Π = 6, и изучим зависимость эффективности силового воздействия от угла наклона актуаторов. Выбор параметра s₀ = = 0.2, задающего положение переднего фронта системы управления, будет обоснован в разд. 4. Во всех расчетах параметр сглаживания l = 1.

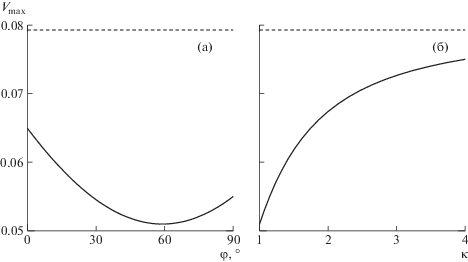
На рис. 4а показана зависимость абсолютного максимума скорости поперечного течения V_max от угла наклона исполнительных элементов φ. Штриховой линией отмечен уровень интенсивности поперечного течения в отсутствие управляющего воздействия. Наибольшая степень подавления поперечного течения достигается при φ = 59°.

Задача о полном устранении поперечного течения с помощью однородной вдоль размаха объемной силы рассматривалась в [4, 6]. Там было показано, что в оптимальном случае объемная сила должна быть всюду строго перпендикулярна местной внешней линии тока. В рассматриваемом здесь модельном случае “электроды” исполнительных элементов наклонены к образующей крыла под постоянным углом. Как показали проведенные расчеты, для обеспечения максимального подавления поперечного течения они должны быть наклонены под углом φ ≈ 58°−60°. В отсутствие управляющего воздействия внешняя линия тока составляет с образующей угол ψ = 51° в сечении с наиболее интенсивным поперечным течением. Таким образом, в рассматриваемой модели направление оптимального силового воздействия ориентировано почти перпендикулярно скорости внешнего течения над областью максимальных скоростей поперечного течения.

Продольное распределение интенсивности поперечного течения при φ = 60° приведено на рис. 2 (линия 2). Рассматриваемое силовое воздействие замедляет поперечное течение в 1.5−2 раза. Профили скорости управляемого поперечного течения в сечениях около места его наибольшей интенсивности показаны на рис. 3б.

Зафиксируем теперь параметры системы управления (a = 1, b = 1, c = 0.5, Π = 6, φ = 60°) и изучим изменение ее эффективности при увеличении скорости обтекания. Пусть новая скорость обтекания связана с прежним равенством

где κ > 1 – коэффициент увеличения скорости. В этом случае новая характерная толщина пограничного слоя имеет вид $\delta {{^\circ }^{'}} = \delta ^\circ {\text{/}}\sqrt \kappa $, а новые безразмерные параметры системы управления связаны со старыми соотношениями

Результаты расчета задачи (3.1)−(3.2) при новых безразмерных параметрах (3.3) приведены на рис. 4б. При возрастании скорости обтекания величина максимальной скорости поперечного течения, отнесенная к скорости набегающего потока, асимптотически стремится к ее значению в отсутствие силового воздействия. Этот эффект связан главным образом с заметным уменьшением безразмерной интенсивности силового воздействия. Отметим, что при этом наряду с относительной скоростью поперечного течения возрастает и число Рейнольдса ${\text{R'}} = \sqrt \kappa {\text{R}}$, что способствует дополнительной дестабилизации течения.

Отметим также, что при прочих равных условиях при изменении интенсивности воздействия в диапазоне 0 < c < 0.5 величина V_max меняется практически по линейному закону.

4. УСТОЙЧИВОСТЬ ОСРЕДНЕННОГО ТЕЧЕНИЯ

Сравним характеристики устойчивости течений, рассчитанных в разд. 2, 3. Для этого необходимо оценить величины характерных чисел R. Для условий, соответствующих эксперименту в низкоскоростной аэродинамической трубе, скорость набегающего потока $V_{\infty }^{ \circ }$ изменяется в пределах 10–80 м/с, кинематическая вязкость воздуха μ°/ρ° = 1.4 × 10^–5 м²/с. Радиус кривизны передней кромки модели примем равным r° = 0.1 м. При таких условиях число Рейнольдса лежит в диапазоне 270 < R < 760. В связи с этим все дальнейшие расчеты выполнены при R = 500.

Основной вид возмущений, приводящих к ламинарно-турбулентному переходу в пограничном слое на стреловидном крыле – стационарные вихри неустойчивости, генерируемые на неровностях обтекаемой поверхности [12, 13]. Для расчета характеристик неустойчивости поперечного течения представим параметры течения в виде

Подставим (4.1) в задачу (1.1)–(1.2) и произведем линеаризацию по параметру h $ \ll $ 1. Следуя [1], в полученной системе уравнений будем пренебрегать членами, содержащими V, ∂U/∂x, ∂W/∂x (плоскопараллельное приближение). Эта система может быть сведена к уравнению Орра–Зоммерфельда для функции ${v}{\text{*}}$. Налагая на его решение однородные граничные условия при y = 0, ∞, получим задачу на собственные значения для определения комплексного волнового числа α. Решение этой задачи строилось с помощью вычисления линейно независимых решений уравнения с использованием процедуры ортонормализации [14].

На рис. 5 представлены результаты расчета инкрементов нарастания

стационарных вихрей неустойчивости поперечного течения. Линиями 1 отмечены кривые нейтральной устойчивости (σ = 0), линии 2 – линии уровня инкрементов нарастания, нанесенные с интервалом 0.001.

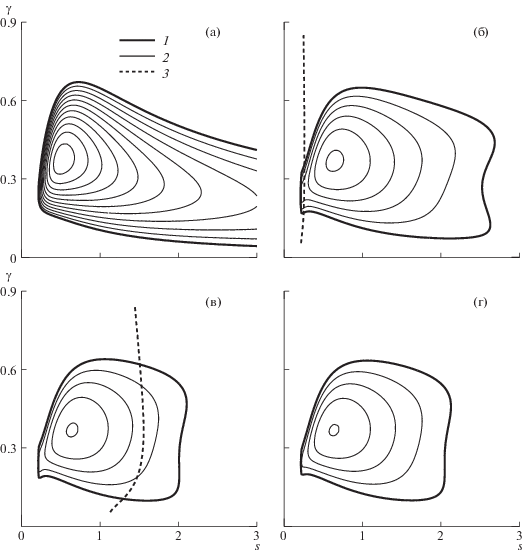
На рис. 5а проиллюстрирован случай отсутствия управляющего воздействия. Впервые течение теряет устойчивость в сечении s_c = 0.215 по отношению к возмущению с поперечным волновым числом γ_c = 0.244. Именно по этой причине передняя граница системы управления s₀ выбрана равной 0.2 (см. разд. 3). Максимальная скорость роста вихрей неустойчивости σ_max = 0.0106 наблюдается в сечении s = 0.51 при γ = 0.38.

Снова зафиксируем параметры системы управления (a = 1, b = 1, c = 0.5, Π = 6) и исследуем ее эффективность для различных углов наклона актуаторов. На рис. 5б показаны результаты расчета характеристик устойчивости управляемого течения при φ = 30°. Передняя граница области неустойчивости почти не сдвигается, а при s > 2.7 течение вновь становится устойчивым по отношению к возмущениям вида (4.1). Максимум инкремента нарастания имеет место при s = 0.63, γ = 0.37 и составляет σ_max = 5.1 × 10^–3, т.е. скорость роста уменьшается почти в 2 раза по сравнению со случаем отсутствия воздействия.

На рис. 3в приведены результаты расчета устойчивости для случая φ = 60°, когда управляющее воздействие близко к оптимальному (см. рис. 4а). Задняя граница области неустойчивости сдвигается к передней кромке крыла и расположена на расстоянии s ≈ 2.1. Максимум инкремента σ_max = 4.1 × 10^–3 достигается практически в той же точке (s = 0.64, γ = 0.37).

5. РЕАКЦИЯ ТЕЧЕНИЯ НА ПОПЕРЕЧНУЮ МОДУЛЯЦИЮ УПРАВЛЯЮЩЕГО ВОЗДЕЙСТВИЯ

Исследуем теперь восприимчивость течения к поперечной модуляции объемного силового воздействия. Применим здесь подход, использованный в [7] для случая, когда вектор объемной силы лежит в плоскости y, z (что соответствует φ = 90°). Осредненная по размаху сила порядка O(R^–1), действуя на расстояниях s = O(1), формирует течение, отличающееся от невозмущенного в главном приближении. В то же время колебательная компонента управляющей силы, имеющая тот же порядок, действует на расстояниях x = O(1), что приводит к уменьшению ее воздействия в R раз. Это позволило в [7] рассчитывать колебательную компоненту управляемого течения в линейном приближении по малому параметру R^–1.

Разложим функцию (1.3) F(ζ) в ряд Фурье

и разобьем колебательную составляющую поля объемной силы на два слагаемых

Представим решение задачи (1.1)–(1.3) в виде

где q' и q'' – результаты воздействий {f  ', g'} и {f  '', g''} соответственно. Следуя [7], будем рассчитывать функции q', q'' в линейном приближении и определим диапазон параметров системы управления, когда этот подход оправдан.

Функции q' описывают колебательную составляющую управляемого течения, для случая, когда однородное силовое воздействие применяется на всей поверхности крыла (s₀ = 0). Зададим их в форме ряда Фурье с локально медленно изменяющимися коэффициентами

Подобно классической теории устойчивости, коэффициенты разложения (5.3) будем рассчитывать в приближении квазипараллельного осредненного течения. В сделанных допущениях функции q_n удовлетворяют линейной системе

и однородным граничным условиям

Решения краевых задач (5.4)–(5.5) строились с помощью вычисления частного решения неоднородной системы (5.4) и трех линейно независимых решений соответствующей однородной системы, при расчете которых снова использовалась процедура ортонормализации Шмидта. Для определения самих возмущений (5.3) бесконечная сумма заменялась конечной 1 ≤ n ≤ N. Все расчеты производились с учетом N = 10 гармоник. В качестве характеристики интенсивности возмущений использовался максимум модуля возмущения скорости:

В частном случае при той же геометрии крыла для a = 1, b = 1, c = 0.5, Π = 6, R = 500, φ = 90°, s₀ = 0 задача управления рассматривалась в [7]. При этих условиях интенсивность (5.6) колебательной составляющей управляемого течения в промежутке 0 < s < 3 монотонно возрастала от 0.3 до 0.7, т.е. линеаризация задачи была оправданной.

Рассмотрим класс систем управления (1.3) с фиксированными параметрами a = 1, b = 1, s₀ = 0.2. Интенсивность осредненного воздействия оставим прежней, полагая с/Π = 1/12. В этих условиях исследуем возможность применения линейного приближения для расчета модуляций управляемого течения при различных углах наклона актуаторов φ и различных расстояниях Π между ними. Расчеты интенсивности модуляций течения проиллюстрированы на рис. 6.

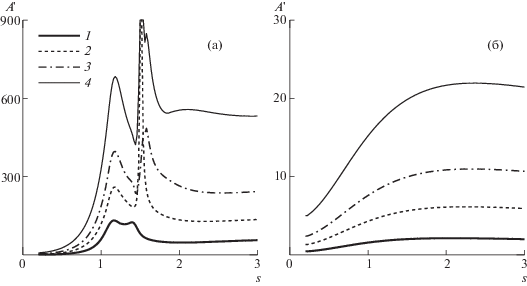
Рассмотрим сначала случай оптимального подавления поперечного течения в пограничном слое, управляемом осредненной по размаху силой (φ = 60°). На рис. 6а показаны результаты расчета соответствующих распределений (5.6) для Π = 6, 9, 12, 18. Проведенные вычисления показывают, что при параметре линеаризации R^–1 = 2 × 10^–3 рассматриваемый здесь подход применим лишь на узком начальном участке 0.2 < s < 0.5. Ниже по потоку вычисленная в линейном приближении колебательная компонента управляемого течения испытывает резкий рост, и линейный анализ перестает быть адекватным.

Объясним причину, по которой линейный подход, эффективный при φ = 90° [7], перестает работать при φ = 60°. Обозначим ψ – угол между осью z и местным направлением линии тока внешнего течения. Оси вихрей неустойчивости поперечного течения составляют с осью z угол θ, больший ψ на несколько градусов. Периодическая система исполнительных элементов генерирует ряд вторичных вихрей, оси которых направлены вдоль актуаторов. В месте, где угол наклона актуаторов φ совпадает с соответствующим углом θ виртуальной системы вихрей неустойчивости того же периода, наблюдается резонансное усиление модуляции управляемого течения. Поясним это в рамках рассматриваемой математической модели.

На разгонном участке течения функция ψ(s) монотонно возрастает; при ε = 0.2 она пробегает значения 0° ≤ ψ < 65°. Вместе с ней возрастают и углы θ_n для виртуальных систем стационарных вихрей неустойчивости с поперечными волновыми числами γ_n и соответствующими им комплексными волновыми числами α = α(γ_n). Выпишем условие, эквивалентное условию θ_n = φ параллельности оси вихрей “электродам” актуаторов:

Для не слишком больших φ равенство (5.7) имеет место в некотором сечении s. В окрестности области неустойчивости в силу |Re α| $ \gg $ |Im  α| в этом сечении выполнено α ≈ α_n , оператор в левой части системы (5.3) близок к вырожденному, и источниковые члены порождают отклик большой амплитуды.

Абстрагируясь от номера n гармоники в (5.3) и периода Π, которые могут принимать различные значения, перепишем равенство (5.7) в виде

На рис. 5б, в однопараметрические множества точек (s, γ), где выполнено условие (5.8), показаны линиями 3. С увеличением угла наклона актуаторов эта линия удаляется от передней кромки крыла.

Вернемся к рассмотрению случая φ = 60°. При Π = 6 поперечное волновое число первой гармоники γ₁ = 0.91 существенно больше волновых чисел γ, характерных для области неустойчивости (см. рис. 5в), величины Im α(γ₁) сравнительно велики, поэтому даже при выполнении равенства (5.7) амплитуда модуляции управляемого течения (5.6) принимает умеренное значение (рис. 6а, линия 1).

Увеличим теперь расстояние между актуаторами в полтора раза: Π = 9. В этом случае линия γ₁ = 0.60 проходит вблизи точки s_R = 1.51, γ_R = 0.62 – одной из двух точек точного резонанса, где наряду с условием (5.8) выполнено Im α(γ) = 0. Соответствующее распределение A'(s) имеет вблизи точки s = s_R резкий пик (рис. 6а, линия 2).

При Π = 12 линия γ₁ = 0.45 проходит через центральную часть области неустойчивости, где инкременты нарастания максимальны, поэтому распределение (5.6) (линия 3) не имеет точек резкого усиления, хотя его амплитуда существенно выше, чем в случае Π = 6. При Π = 18 распределение вновь имеет резкий максимум вблизи s = s_R, обусловленный резонансным усилением второй гармоники (γ₂ = 0.60) в разложении (5.3) (линия 4).

Заметим, что область корректного применения линейного подхода может быть увеличена путем уменьшения интенсивности управляющего воздействия, но при этом увеличится интенсивность поперечного течения и возрастет его неустойчивость. Тем не менее даже в случае c $ \ll $ 1 линейный анализ неприменим в окрестностях точек точного резонанса – точек пересечения нейтральной кривой с линией (5.8).

Все описанные особенности линейного подхода к расчету модуляций управляемого течения сохраняются и при φ < 60°, в частности – при φ = 30° (рис. 5б). Для корректного описания модуляций необходимо производить расчеты в нелинейной постановке, что выходит за рамки данного исследования. В любом случае, наличие описанного резонанса приведет к тому, что амплитуда модуляций течения, управляемого периодической последовательностью актуаторов, станет сравнимой с интенсивностью осредненного течения. Это может привести к появлению новых типов неустойчивости.

Проведенные в [7] расчеты подсказывают, что описанных выше нежелательных эффектов можно избежать, увеличив угол наклона актуаторов. При его возрастании в диапазоне φ > 60° кривая, определяемая равенством (5.8), быстро удаляется вниз по потоку от области неустойчивости, устраняя резонанс. Для иллюстрации рассмотрим случай φ = 75°. По сравнению с управлением системой оптимальной конфигурации это приводит к незначительному увеличению интенсивности поперечного течения (рис. 4а), причем усиление (на 2%) приходится на передний участок управления, где скорость поперечного течения максимальна. Ниже по течению эта скорость практически не меняется (рис. 2, рис. 3в). Характеристики устойчивости также меняются незначительно – область неустойчивости становится чуть длиннее, но ỳже (рис. 5г). При этом интенсивность колебательной составляющей управляемого течения меняется кардинально – она снижается на 2 порядка (рис. 6б). Как и в [7], в этом случае применение линейного подхода к расчету модуляций течения является оправданным.

Обратим внимание на то, что в окрестности задней границы области неустойчивости в результате продолжительного тормозящего воздействия вдоль хорды крыла у профиля V_cf сначала появляется вторая точка перегиба, а затем формируется обратное течение V_cf < 0 (рис. 3в). Чтобы это не привело к появлению неустойчивости нового типа, управляющее воздействие целесообразно завершить, как только течение стабилизируется (при s > s₁ ≈ 2).

В [4] было впервые экспериментально продемонстрировано затягивание ламинарно-турбулентного перехода, вызванного неустойчивостью поперечного течения, с помощью единичного плазменного актуатора, расположенного параллельно передней кромке скользящего крыла (что соответствует φ = 0°). Силовое воздействие, направленное к передней кромке крыла, уменьшало наполненность разгонного профиля скорости и увеличивало длину ламинарного участка течения на несколько процентов хорды. Установление ряда аналогичных актуаторов вниз по потоку могло бы привести, наряду с ослаблением поперечного течения, к усилению неустойчивости Толлмина–Шлихтинга и даже к отрыву потока.

В этой связи в [4] предполагалось в дальнейшем испытать периодическую вдоль размаха крыла систему искривленных актуаторов, направленных вдоль внешней линии тока. Анализ, проведенный в данной работе, показывает, что это может привести к резонансному усилению поперечной модуляции управляемого течения.

6. ВЛИЯНИЕ НАЧАЛЬНОГО УЧАСТКА СИСТЕМЫ УПРАВЛЕНИЯ

Если электроды исполнительных элементов перпендикулярны передней кромке крыла [3, 7], силовое воздействие может быть организовано от сàмой линии растекания (s₀ = 0). Цель рассматриваемого способа управления – снижение неустойчивости поперечного течения. В силу этого применять силовое воздействие имеет смысл только в области, где пограничный слой теряет устойчивость. Именно поэтому в данной работе все расчеты производились для s₀ = 0.2. В связи с этим необходимо изучить эволюцию возмущений, вносимых в течение передним фронтом системы управления. В рассматриваемой здесь линейной постановке эти возмущения представлены слагаемым q'' в (5.2).

Поместим начало системы координат в точку s = s₀. В этой системе функции f  '', g'' (5.1) как функции x имеют синусоидальную форму выше по течению и стремятся к 0 вниз по течению. В окрестности x = 0 объемные воздействия, описываемые этими функциями, создают продольную неоднородность, периодическую вдоль размах крыла. Подобно случаю неровности обтекаемой поверхности [12, 13], эта неоднородность приводит к генерации стационарной системы вихрей неустойчивости поперечного течения. Опишем процесс генерации, используя подход [13].

Представим компоненты f  '', g'' колебательной составляющей силового воздействия (5.1) в виде интегралов Фурье

где интегралы берутся по контурам, обходящим полюсы k = α_n сверху. Если сглаживающая функция f_s задана равенством (1.3), то

Расчет соответствующих параметров колебательной компоненты управляемого течения будем производить по следующей схеме. Анализ возмущений в ближнем поле |x| = O(1) выполним в предположении плоскопараллельного основного течения, параметры которого вычислены в точке s = s₀. Дальнейшее развитие системы возбуждаемых вихрей неустойчивости будем описывать в рамках закона эволюции возмущений в слабо неоднородных течениях [15].

В силу x/s₀ = O(R) $ \gg $ 1 в математической постановке задачи расчета ближнего поля будем считать – ∞ < x < +∞. В рамках рассматриваемой модели возмущения, порождаемые начальным участком системы управления, имеют вид

где коэффициенты Фурье ${{q}_{n}}$ удовлетворяют системе (5.4), в которой в левой части произведены замены действительного α_n на комплексное k (соответственно, $k_{n}^{2} = {{k}^{2}} + \gamma _{n}^{2}$), а правые части оставлены без изменений. Контуры интегрирования в (6.2) охватывают снизу все полюсы k = = α(γ_n), соответствующие моде неустойчивости поперечного течения, а полюсы k = α_n обходятся сверху.

Применяя теорему Коши о вычетах в области x < 0, получим, что при x → –∞ решение q'' стремится к решению q', взятому со знаком минус, т.е. суммарное возмущение стремится к 0. При x > 0 теорема о вычетах дает начальные амплитуды систем вихрей неустойчивости поперечного течения, генерируемых передней частью системы управления и распространяющихся вниз по потоку:

В формуле (6.3) суммирование ведется по номерам гармоник γ_n, для которых существует мода неустойчивости поперечного течения.

Опишем факторы, приводящие к увеличению амплитуды возмущений q'' в широкой области s ≥ s₀. Во-первых, уже начальная амплитуда q'' велика, если в точке s = s₀ для одной из гармоник выполнено α(γ_n) ≈ α_n. Это имеет место, например, при φ = 30°, Π = 10 (γ₁ = 0.31), когда линия (5.8) проходит вблизи сечения s = s₀ = 0.2 (рис. 5б). Как и в случае возмущений типа q', такая возможность может быть исключена выбором достаточно большого угла наклона актуаторов.

Во-вторых, возмущения q'' могут усиливаться благодаря нарастанию вихрей неустойчивости (6.3) вниз по потоку. Это происходит, когда одна или несколько гармоник находятся в диапазоне 0.1 < γ_n < 0.6. При наиболее благоприятной конфигурации системы управления линия γ = γ₁ = 2π sin  φ/Π расположена выше области неустойчивости, достижению чего способствуют увеличение угла наклона актуаторов и уменьшение расстояния между ними. Последнее трудно обеспечить на практике, поскольку толщина пограничного слоя мала.

Предположим теперь, что усилению подвержена лишь первая гармоника γ = γ₁, и преобразуем формулу (6.3) к виду, аналогичному (4.1)

Здесь собственная функция q* нормирована условием du*/dy = 1 при y = 0. Формула (6.4) позволяет вычислить начальную амплитуду возмущения q′′, определяемую аналогично (5.6)

Вниз по потоку от места возникновения амплитуду возмущения можно оценить с помощью приближенной формулы [15]

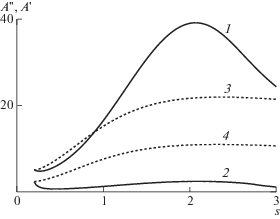
На рис. 7 приведен сравнительный анализ возмущений A'' и A', формируемых влиянием переднего края системы управления и местным воздействием поперечной модуляции силового поля. Расчеты произведены для конфигурации системы управления из разд. 5 с углами наклона актуаторов φ = 75°. При Π = 18 линия γ₁ = 0.34 проходит через среднюю часть области неустойчивости (см. рис. 5г). Вследствие этого амплитуда максимума кривой нарастания (линия 1) почти в 2 раза превышает амплитуду возмущения, порождаемого местной модуляцией поля силы (линия 3). При Π = 12 линия γ₁ = 0.51 пересекает лишь верхнюю часть области неустойчивости, и кривая нарастания A''(s) проходит ниже соответствующей кривой A'(s) (линии 2, 4). При Π = 9 амплитуда A'' в сравнении с A' становится исчезающе малой.

Проведем теперь более тщательный анализ течений, управляемых осредненной по размаху силой. В разд. 3 расчет таких течений производился в рамках системы уравнений пограничного слоя. Строго говоря, эта модель перестает работать в окрестности точки s = s₀, где силовое воздействие изменяется на масштабе Δx = O(1), что соответствует Δs $ \ll $ 1. Поскольку силовое воздействие на этом масштабе мало, корректный расчет осредненного течения в окрестности этой точки снова произведем в линейном приближении по параметру R^–1.

Представим искомое решение системы (1.1) в виде

где первое слагаемое соответствует параметрам пограничного слоя в отсутствие воздействия. Второе слагаемое вновь будем искать в форме интеграла Фурье где функция f  * определяется формулой (6.1) при n = 0. Подстановка (6.5) в систему (1.1), линеаризация ее по параметру R^–1 и использование плоскопараллельного приближения приводят к системе для фурье-образов, аналогичной (5.4), в которой произведены замены q_n → q_k , α_n → k , k_n → k, а величины γ_n и правые части системы вычислены с помощью формул (5.1) при n = 0.

На рис. 8 приведены результаты расчета продольного градиента давления, индуцируемого начальным участком осредненного силового воздействия. Согласно [16], на масштабе своего изменения объемная сила индуцирует градиент давления, значительно демпфирующий силовое воздействие. Проведенные расчеты показывают, что амплитуда индуцируемого градиента давления максимальна там, где силовое воздействие максимально (т.е. при y = 0), и быстро затухает при удалении от стенки.

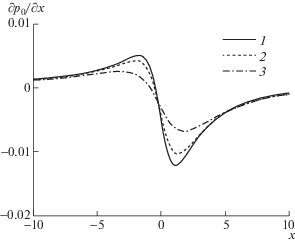
Если актуатор установлен в изначально покоящемся газе, то интегральное действие индуцированного градиента давления отсутствует [16]. В рассматриваемом случае система управления воздействует на уже имеющееся течение, тем не менее и здесь тормозящий эффект градиента на начальном участке воздействия при x < 0, где $\partial {{p}_{0}}{\text{/}}\partial x > 0$, компенсируется дополнительным разгоном течения при x > 0.

Заметим, что внешний градиент давления dp_e/ds и индуцируемый объемной силой градиент R^–1∂p₀/∂x в силу dx/ds = R имеют одинаковый порядок по числу R. Тем не менее величина первого из них в окрестности точки s₀ = 0.2 принимает значения, близкие −0.2, в то время как второго – на порядок меньшие (в диапазоне от −0.01 до 0.005). Поскольку наведенный градиент давления действует на очень коротком промежутке и является знакопеременным, то он не приводит к заметному искажению осредненного течения.

ЗАКЛЮЧЕНИЕ

На примере течения в пограничном слое на скользящем крыле эллиптического сечения теоретически исследован процесс подавления поперечного течения с помощью объемной силы, моделирующей воздействие периодической последовательности плазменных актуаторов. Изучена эффективность системы управления в зависимости от угла наклона актуаторов. Рассчитаны характеристики устойчивости течения, управляемого осредненной по размаху силой. Колебательная составляющая управляемого течения исследована в рамках линейного приближения по обратному числу Рейнольдса.

Показано, что направленность актуаторов вдоль местной внешней линии тока, являющаяся оптимальной в случае однородного воздействия, не является таковой в случае воздействия, периодического по размаху крыла. Это связано с наличием резонанса – высокой восприимчивостью течения к колебательной составляющей силового воздействия при условии близости направления актуаторов направлению внешней линии тока. Определены факторы, вызывающие повышенную восприимчивость течения к воздействию начального участка системы управления.

Предложен ряд мер, позволяющих избежать указанных негативных проявлений модуляции управляющего воздействия. Угол наклона актуаторов к передней кромке крыла должен быть больше угла наклона внешней линии тока на всем протяжении области силового воздействия. Актуаторы следует размещать с периодом, меньшим минимального периода моды неустойчивости поперечного течения. Протяженность области силового воздействия должна ограничиваться размером области неустойчивости управляемого течения.

Автор признателен А.П. Курячему за плодотворное обсуждение исследуемых явлений.