Известия РАН. Механика жидкости и газа, 2021, № 5, стр. 49-60
ЧИСЛЕННОЕ МОДЕЛИРОВАНИЕ ЭВОЛЮЦИИ ВОЗМУЩЕНИЙ В СВЕРХЗВУКОВОМ ПОГРАНИЧНОМ СЛОЕ НАД УГЛОМ РАЗРЕЖЕНИЯ
П. В. Чувахов a, b, *, И. В. Егоров a, b, **
a Центральный аэрогидродинамический институт им. проф. Н.Е. Жуковского
Жуковский, Россия
b Московский физико-технический институт (Национальный исследовательский университет)
Долгопрудный, Россия
* E-mail: pavel_chuvahov@mail.ru
** E-mail: i_v_egorov@mail.ru
Поступила в редакцию 23.10.2020
После доработки 20.04.2021
Принята к публикации 21.05.2021
Аннотация
В рамках уравнений Навье–Стокса расчетным путем исследованы линейная и нелинейная стадии развития возмущений в сверхзвуковом пограничном слое над углом разрежения 10°, число Маха 3. Анализируется влияние внезапного расширения потока на эволюцию возмущений. Обсуждается эффект стабилизации течения, наблюдаемый в аэродинамическом эксперименте.
УСЛОВНЫЕ ОБОЗНАЧЕНИЯ
| x, y, z | продольная, вертикальная и боковая Декартовы координаты, составляющие правую тройку |
| u, ${v}$, w | декартовы компоненты вектора скорости |
| p | давление |
| l | координата вдоль поверхности: l = x при x < 0 и l = x/cos(ε) при x ≥ 0 |
| dw | расстояние до стенки |
| $p_{w}^{'}$ | возмущение давления на стенке |
| M | число Маха |
| Re∞L | число Рейнольдса по характерному масштабу длины L |
| β | боковое волновое число |
| δ | толщина пограничного слоя по критерию u(δ) = 0.99ue |
| ω | круговая частота |
| ε | величина угла разрежения в градусах |
| Нижний индекс | |
| e | на внешней границе пограничного слоя |
| ∞ | в набегающем потоке |
| Сокращения | |
| FP | плоская пластина, ε = 0° |
| EC | угол разрежения, ε = 10° |
| WP | волновой пакет (линейный режим) |
| TS | турбулентное пятно (существенно нелинейный режим) |
Обтекание элементов сверхзвуковых летательных аппаратов сопряжено с образованием зон разгона и торможения потока. В них пограничный слой может взаимодействовать со скачками уплотнения, отрываться и формировать зоны повышенного теплообмена при последующем присоединении к поверхности. Турбулизация пограничного слоя значительно усиливает этот эффект. Зоны разгона потока с благоприятным (отрицательным) градиентом давления встречаются на практике не реже, чем зоны торможения. Несмотря на это фундаментальная проблема влияния благоприятного градиента давления, ускоряющего поток, на устойчивость ламинарного пограничного слоя и возврат турбулентного течения к ламинарному состоянию (реламинаризацию, см., напр., [1]) изучена значительно меньше.
Проблема реламинаризации исследовалась с середины прошлого века. Изучение дозвуковых турбулентных течений в присутствии большого отрицательного градиента давления указало на возможность полной реламинаризации пограничного слоя [2–5], которая связана с искривленным характером линий тока, а также благоприятными продольным и нормальным градиентами давления, которые приводят к быстрому сокращению масштаба турбулентных пульсаций на разгонном участке течения [6]. Величина продольного градиента статического давления и число Рейнольдса набегающего потока были отмечены как основные параметры течения, влияющие на возникновение и развитие процесса реламинаризации.
Реламинаризация на сверхзвуковом режиме течения ведет к значительному снижению сил вязкого трения и теплоотдачи от горячего газа к обтекаемой поверхности. Известно, что эффекты сжимаемости преобладают над другими эффектами во внешней части пограничного слоя (например, [7, 8]). К эффекту сжимаемости относятся слабое затухание и увеличение размера крупномасштабных вихревых структур в течении расширения при числе Маха 3 [7]. В [7] отмечено значительное подавление сдвиговых напряжений Рейнольдса, вследствие чего крупные вихри ослабевают вниз по потоку. Также указывается на значительное подавление мелкомасштабных структур сразу за веером волн разрежения. Эти выводы подтверждаются в экспериментах с числом Маха 4.9 [9, 10], где обнаружено, что область перемежаемости пограничного слоя в разгонном течении сокращается, смещаясь к его границе. Это затрудняет подмешивание газа из внешнего течения в пограничный слой.
В [11] при числе Маха 4 показана возможность частичной реламинаризации пограничного слоя (пристенная часть до 40% от его полной толщины). Отмечено, что рост числа Рейнольдса приводит главным образом к увеличению протяженности реламинаризованного участка течения, а больший разгон потока (больший отрицательный градиент давления) в области взаимодействия приводит к все большему уменьшению турбулентных пульсаций. Отмечено, что критерии реламинаризации, полученные при дозвуковых скоростях, можно применять при больших сверхзвуковых скоростях.
Эксперименты [12] в ударной аэродинамической трубе при числах Маха от 5 до 8 косвенно подтверждают стабилизирующее влияние благоприятного градиента давления на теле вращения “оживало-конус-конус-цилиндр”, а также указывают на реламинаризацию турбулентного клина за изолированной неровностью поверхности.
Экспериментальные работы, такие как [10], дают хорошую тестовую базу для разработки расчетных моделей данного типа течений, применимых совместно с уравнениями Рейнольдса и метода крупных вихрей. Однако из-за вычислительной сложности имеется очень мало публикаций по прямому численному моделированию устойчивости ламинарного течения и реламинаризации турбулентного течения при сверхзвуковых скоростях. Одними из немногих работ являются [13] при числе Маха M = 2.9 и [14] при числе Маха M = 2.7. В этих работах рассмотрено турбулентное обтекание угла разрежения. Обнаружена двухслойная структура разгонного течения вблизи угла, подтверждающая экспериментальные наблюдения. Течение в верхнем слое характеризуется сильным подавлением турбулентных пульсаций, которые медленно восстанавливаются вниз по потоку. В нижнем слое пульсации подавляются только в небольшой окрестности области поворота и быстро восстанавливаются вниз по потоку.
Механизмы нарастания возмущений и реламинаризации течения определяют процесс ламинарно-турбулентного перехода. Известно, что при малом уровне внешних возмущений, свойственном для полетных условий, переход в сверхзвуковом пограничном слое над гладкой поверхностью происходит через последовательное формирование, рост и слияние отдельных турбулентных пятен. Пятно формируется через нелинейную стадию развития волнового пакета, эволюция которого определяется параметрами невозмущенного течения, фоном возмущений, температурой обтекаемой поверхности. Согласно линейной теории устойчивости, над горячей (теплоизолированной) поверхностью доминируют наклонные волны первой моды; над охлаждаемой поверхностью при больших числах Маха — плоские волны второй моды. Хотя турбулентное пятно является существенно нелинейным объектом, на его развитие может влиять линейный механизм устойчивости. Расчеты [15] выявляют связь между характеристиками турбулентных пятен и линейных волновых пакетов. Имеется ряд экспериментальных и численных исследований (подробный обзор дан в [15]), которые подтверждают это утверждение.
Следует отметить, что расчетных данных по развитию волновых пакетов и турбулентных пятен в сверхзвуковых пограничных слоях над углами разрежения мало. В настоящей работе исследуется эволюция волнового пакета (линейный режим) и турбулентного пятна (нелинейный режим) в сверхзвуковом пограничном слое над углом разрежения при числе Маха 3. Ниже описаны используемые численные подходы (раздел 1) и представлен анализ численных результатов (раздел 2): среднее поле течения, развитие возмущений в физической плоскости, спектральные характеристики возмущений. Выводы даны в разделе 3.
1. МЕТОДОЛОГИЯ РАСЧЕТА
Численное моделирование полей течения выполнено с помощью авторского пакета расчетных программ HSFlow [16], в котором уравнения Навье–Стокса дискретизированы при помощи TVD-схемы конечного объема второго порядка точности. Реконструкция конвективных потоковых членов на грани ячейки выполняется с помощью схемы WENO-3. Для получения среднего стационарного поля течения используется метод установления решения по времени второго порядка точности с применением многоблочных структурированных расчетных сеток. Расчеты выполнены для совершенного газа – воздуха – с постоянными показателем адиабаты γ = 1.4 и числом Прандтля Pr = 0.72. Коэффициент вязкости вычисляется по формуле Сазерленда с характерной температурой T$_{\mu }^{*}$ = 110.4 K: μ = (1 + Tμ)/(T + Tμ)·T1.5. Скорость потока, его температура, плотность и давление обезразмериваются следующим образом: (u, ${v}$, w) = (u*, ${v}$*, w*)/u$_{\infty }^{*}$, T = = T*/T$_{\infty }^{*}$, ρ = ρ*/ρ$_{\infty }^{*}$, p = p*/(ρ$_{\infty }^{*}$u$_{\infty }^{{*2}}$); все размерные величины обозначены звездочкой в верхнем индексе. На стенке накладывается условие прилипания потока (u, ${v}$*, w) = (0, 0, 0); температура стенки постоянная и равна температуре восстановления потока, рассчитанной на основе заданной температуры торможения T$_{0}^{*}$ = 290 K для числа Маха набегающего потока M∞ = 3: T$_{w}^{*}$ = T$_{{ad}}^{*}$ = = T$_{e}^{*}$(1 + Pr0.50.5(γ – 1)M$_{\infty }^{2}$) ≈ 261.8 K; T$_{e}^{*}$ = T$_{0}^{*}$(1 + 0.5(γ – 1)M$_{\infty }^{2}$)–1 ≈ 103.57 K; Tw/Te ≈ 2.53. На давление ставится упрощенное граничное условие экстраполяции (∂p/∂n)w = 0. Для оценок размерных величин можно принять масштаб длины L* = 0.1 м и масштаб времени τ* = L*/u$_{\infty }^{*}$ ≈ 1.64 × × 10–4 с. Безразмерные частота и компоненты волнового вектора – ω = ω*L*/u$_{\infty }^{*}$ и (α, β) = (α, β)L* соответственно. В статье рассматриваются течение над плоской пластиной (ε = 0°, сокращенно FP) и над углом разрежения (ε = 10°, сокращенно EC). Над обеими геометриями в статье рассмотрено развитие волнового пакета (линейный режим, сокращенно WP) и турбулентного пятна (нелинейный режим, сокращенно TS) – всего четыре расчетных случая. Угол разрежения расположен при x = l = 0, где l – координата вдоль поверхности (x = l при x < 0; x = lcos(ε) при x ≥ 0).
Процедура расчета состоит из пяти шагов и гарантирует одинаковые начальные поля возмущений внутри групп WP и TS. Во-первых, методом установления по времени рассчитывается среднее течение на пластине при –7.5 ≤ x ≤ 0.2. На входной границе (левая и верхняя грани) накладываются условия набегающего потока; на выходной (задней) границе все переменные задачи линейно экстраполируются изнутри расчетной области.
Во-вторых, под головной ударной волной, порожденной вязко-невязким взаимодействием, выделяется подобласть, левая входная граница которой расположена при l = –7.2, 0 ≤ y ≤ ∼0.12. Течение фиксируется на новых входных границах на основе данных из шага 1. Далее среднее течение вновь уточняется методом установления до момента, когда рассчитываемые параметры потока меняются в пределах 10–11 за единицу расчетного времени.
В-третьих, среднее поле течения дублируется в третьем направлении по 0 ≤ z ≤ 0.7; в этом направлении применяются граничные условия симметрии. Возмущения вводятся в пограничный слой при помощи генератора типа “вдув–отсос” через квадратное отверстие на стенке: –6.9923 = = xs ≤ x ≤ xe = –6.6623, –0.036 = zs ≤ z ≤ ze = 0.036, который моделируется с помощью нестационарного граничного условия на расход газа в нормальном направлении к поверхности:
(1.1)
$\left( {{{\rho }}{v}} \right){\text{'}} = A \times {{\cos }^{3}}\left( {{{\pi }}\frac{{x - 0.5\left( {{{x}_{e}} + {{x}_{s}}} \right)}}{{{{x}_{e}} - {{x}_{s}}}}} \right){{\cos }^{3}}\left( {{{\pi }}\frac{{z - 0.5\left( {{{z}_{e}} + {{z}_{s}}} \right)}}{{{{z}_{e}} - {{z}_{s}}}}} \right)(\sin ({{{{\omega }}}_{0}}t) + \sin (2{{{{\omega }}}_{0}}t))$Здесь ω0 = 10.021 – базовая частота генератора, а A – его амплитуда. Для формирования линейного волнового пакета взято A = 5 × 10–7, а для порождения турбулентного пятна – A = 5 × 10–4. Генератор возбуждает возмущения вблизи нижней ветви нейтральной кривой для базовой гармоники ω0. Генератор работает в период времени 0 < t < π/ω0, что дает близкий к равномерному начальный спектр возмущений для ω < ω0, воспринимаемый пограничным слоем. Расчетная сетка в подобласти имеет избыточное разрешение Nx × Ny × Nz = 2023 × 262 × 330, которое соответствует примерно 90 точкам на продольную длину волны базовой гармоники ω0. Временнóе разрешение составляет около 125 точек на период базовой гармоники 2π/ω0. На данной сетке возмущения рассчитываются до момента времени t = 7.5, когда их передний фронт приближается к сечению l = 0.
В-четвертых, в соответствии с описанной выше процедурой рассчитывается среднее течение в расширенной области по x и z: 0 ≤ z ≤ 1.5; длина вдоль стенки l ≤ 6; левая граница подобласти начинается при l = –3.5, 0 ≤ y ≤ 0.55; размерности сетки составляют Nx × Ny × Nz = 1317 × 262 × 470. Расширенная сетка разрешает длину волны базового возмущения на 45 точках. Поперечное разрешение пограничного слоя по нормали к поверхности не изменилось по сравнению с исходной сеткой и составляет примерно 100–120 сеточных линий. При l > 6 расширенная расчетная область замыкается буферной зоной с сильно укрупненными ячейками по x и y для подавления возмущений, приходящих к выходной границе и способных вызвать неустойчивость численного метода в случае интенсивного турбулентного пятна.
В-пятых, путем вычитания среднего решения из возмущенного, определяется поле возмущений, полученное по результатам шагов 1–3. Оно добавляется к среднему течению над плоской пластиной или углом разрежения в расширенной расчетной области, полученному на шаге 4, с применением интерполяции 1-го порядка точности для переноса возмущений между несовпадающими расчетными сетками. Таким образом, начальные поля возмущений в расширенной расчетной области одинаковы для всех случаев, рассматриваемых в статье. Следует отметить, что процедура переноса возмущений с сетки на сетку не вносит каких-либо паразитных возмущений в решение. Расчеты продолжаются до тех пор, пока возмущения не покинут расчетную область, т.е. пока максимальная поправка к зависимым переменным задачи на шаге по времени не достигнет величины 10–7 (tmax = 20) для волновых пакетов и 10–4 (tmax = 26 угол разрежения, tmax = = 30.5 плоская пластина) для турбулентных пятен во всем поле течения. После этого анализируется поле возмущения давления p$_{w}^{'}$(t, l, z) на поверхности.
Расширенная расчетная область и установившееся невозмущенное поле течения в ней представлено на рис. 1 для случая угла разрежения в полной расчетной области (подробное обсуждение дано в разделе 2).
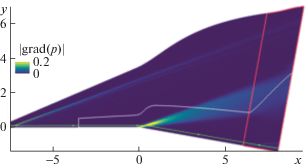
Рис. 1.
Установившееся поле модуля градиента давления; белой линией показана вырезанная подобласть (шаг 2) для моделирования эволюции возмущений; зеленой линией со стрелками отмечена линия тока, проходящая через сечение x = –1 на высоте 5δ от поверхности, δ(–1) ≈ 0.0221. Красной линией очерчена буферная зона. Цветовая палитра приведена в линейном масштабе.
По опыту предыдущих расчетов авторов статьи, сеточное разрешение в 90 (соответственно, 47) точек на длину волны приводит к снижению амплитуды возмущения на одной длине монохроматической акустической волны менее, чем 0.01% (соответственно, 0.27%) по отношению к естественному уровню ее вязкого затухания. Предварительный анализ в рамках линейной теории устойчивости показывает, что такое численное затухание мало по сравнению с физическим ростом или затуханием возмущений в пограничном слое. Суммарная погрешность расчета поля возмущений оценивается менее 10% к концу расчетной области для случая волнового пакета. В случае турбулентного пятна порождаются возмущения меньших масштабов, которые подвержены большему численному затуханию; предполагается, что это обстоятельство не может повлиять на выводы настоящей статьи.
2. РЕЗУЛЬТАТЫ
2.1. Среднее течение
Расчетное среднее поле течения над углом разрежения представлено на рис. 1. Невязкое приближение этого класса течений известно как течение Прандтля–Майера [17]. Параметры течения меняются быстро в малой окрестности угла l = 0; вязкость сглаживает распределения газодинамических величин в этой области. Давление на поверхности меняется на масштабе толщины пограничного слоя, посчитанной прямо перед изломом. Профили температуры и скорости перестраиваются на большем расстоянии. Толщина пограничного слоя быстро нарастает на нескольких масштабах величины δ перед углом.
На рис. 2 в нескольких сечениях до и за углом разрежения показаны рассчитанные профили модуля скорости, числа Маха M и статической температуры T; dw – расстояние до стенки. Профили перед углом хорошо соответствуют профилям для случая плоской пластины и начинают испытывать искажения лишь в непосредственной близости от угла, l > –0.1, – влияние угла разрежения вверх по потоку мало. Сразу за углом профили неоднородно искривляются. Далее вниз по потоку их прежнее поведение медленно восстанавливается – они вновь начинают походить на профили над плоской пластиной.
Рис. 2.
Профили среднего течения в различных сечениях l = const, приведенных в легенде: а) модуль скорости V = (u2 + ${{{v}}^{2}}$)0.5; б) число Маха M и статическая температура Tw (стрелки показывают движение профилей при удалении от угла разрежения).
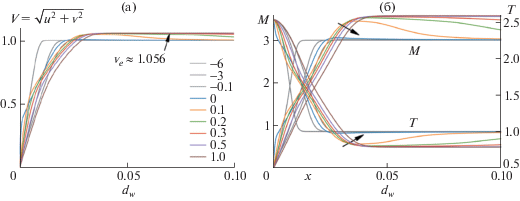
При переходе через угол скорость потока растет незначительно, новое значение модуля скорости на границе пограничного слоя Ve ≈ 1.056 на ∼6% выше соответствующего значения вверх по потоку от угла. Ускорение потока с точки зрения числа Маха осуществляется за счет охлаждения потока (рис. 2б). Из рис. 2 видно, что параметры течения на верхней границе пограничного слоя устанавливаются уже при l < 0.3, что составляет порядка 10δ. При этом веер волн разрежения расположен достаточно высоко над поверхностью, и пограничный слой формируется под ним. С увеличением числа Маха веер расположится более полого, из-за чего должна удлиниться область взаимодействия за углом.
Следует отметить, что параметры потока на границе пограничного слоя за углом хорошо соответствуют значениям, предсказываемым теорией Прандтля–Майера: Me ≈ 3.58, Te ≈ 0.79. Поэтому можно использовать эту теорию для быстрых оценок характеристик течения над углом разрежения. Оценим, например, отношение толщин пограничного слоя над углом и над пластиной в предположении постоянного расхода газа через пограничный слой:
(2.1)
$\frac{{{{{{\delta }}}_{2}}}}{{{{{{\delta }}}_{1}}}} = \frac{{{{{{\rho }}}_{1}}{{U}_{1}}}}{{{{{{\rho }}}_{2}}{{U}_{2}}}} = \frac{{{{{{\rho }}}_{1}}{{M}_{1}}}}{{{{{{\rho }}}_{2}}{{M}_{2}}}}\sqrt {\frac{{{{T}_{1}}}}{{{{T}_{2}}}}} = {{\left( {\frac{{2 + \left( {{{\gamma }} - 1} \right)M_{2}^{2}}}{{2 + \left( {{{\gamma }} - 1} \right)M_{1}^{2}}}} \right)}^{{\frac{{{{\gamma }} + 1}}{{2({{\gamma }} - 1)}}}}}\frac{{{{M}_{1}}}}{{{{M}_{2}}}}$Подставляя M1 = M∞ = 3, M2= Me2 ≈ 3.58, получим δ2/δ1 ≈ 1.7. Соответствующая величина из прямого расчета уравнений Навье–Стокса составляет 1.5.
Следует отметить, что быстрое утолщение пограничного слоя должно сопровождаться быстрым изменением характеристик его устойчивости. В частности, если допустить близость фазовых скоростей возмущений для FP и EC случаев, неустойчивый частотный диапазон должен масштабироваться вместе с толщиной пограничного слоя: f2/f1 ≈ λ1/λ2 ≈ δ1/δ2, где f – частота доминирующей гармоники возмущения. Поэтому следует ожидать, что растущие до угла возмущения превратятся в затухающие вниз по потоку от угла. Это предположение обсуждается ниже.
2.2. Эволюция возмущений в физической плоскости
Рассмотрим процесс развития возмущений на примере возмущения давления на стенке p$_{w}^{'}$ в несколько последовательных моментов времени (рис. 3).
Рис. 3.
Поле возмущения давления p$_{w}^{'}$(x, z) на поверхности пластины (верхняя половина) и угла разрежения (нижняя половина) в разные моменты времени t = 3.75 (а, д), 7.5 (б, е), 11.25 (в, ж), 15.00 (г, з); а–г – волновой пакет (WP); д–з – турбулентное пятно (TS). Цветовая палитра приведена в линейном масштабе.
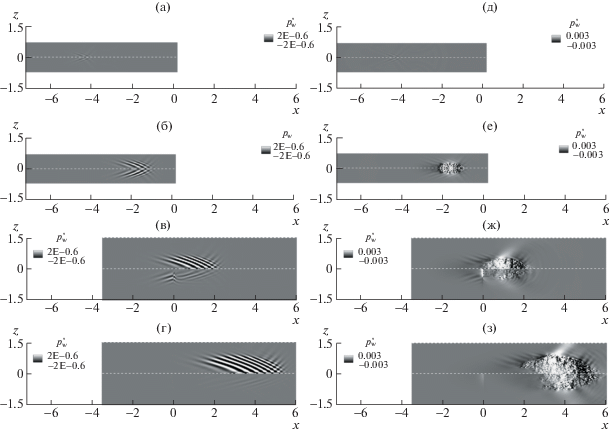
В соответствии с линейной теорией устойчивости для пограничного слоя на плоской пластине при рассматриваемых параметрах течения имеется одна неустойчивая мода – первая мода в терминологии Мэка [18, 19]. Возмущения первой моды являются наклонными волнами, которые распространяются с углом наклона фронтов около 60–70°, имеют продольную длину волны ∼10δ и фазовую скорость ∼0.5ue. Из рис. 3а–г видно, что волновой пакет FP монотонно усиливается вниз по потоку, увеличиваясь пропорционально в продольном и в боковом направлениях. Волновой пакет EC развивается идентично до излома поверхности при l = 0, а ниже по потоку затухает монотонно и быстро. Следует отметить, что при прохождении пакета EC над углом на поле величины p$_{w}^{'}$(x, z) не наблюдается появление новых возмущений в пограничном слое. Количественное сопоставление амплитуд волновых пакетов FP и EC дано на рис. 4а, где приведены распределения максимальной по z величины p$_{w}^{'}$(x, z) в каждом сеточном сечении x = = const. Амплитуда пакета FP растет практически экспоненциально вниз по потоку, в то время как пакет EC экспоненциально затухает при l > 0.
Рис. 4.
Распределение величины ${\text{max}}\;z{\text{|}}p_{w}^{'}(x,z){\text{|}}$ в моменты времени t = 8, 11, 14: а – волновой пакет (WP), б – турбулентное пятно (TS).
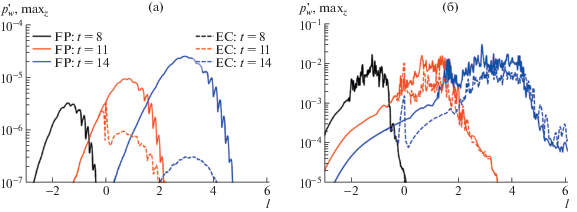
Турбулентное пятно на плоской пластине эволюционирует иначе (рис. 3д–з): оно монотонно растет вниз по потоку, но его амплитуда $\mathop {\max }\limits_z {\text{|}}p_{w}^{'}(x,z){\text{|}}$ остается примерно на одном уровне (рис. 4б). На периферии пятна (особенно в его передней части) имеется область пониженного давления, в теле пятна – область повышенного давления. В окрестности пятна, где нелинейное взаимодействие практически не наблюдается, формируются наклонные волновые фронты, геометрические параметры которых характерны для волнового пакета первой моды (рис. 3а–г). В отличие от случая волнового пакета, турбулентное пятно EC ослабевает при движении над углом разрежения, но это ослабление носит локальный характер, и пятно продолжает свой рост аналогично случаю FP при l > 1. Появление угла разрежения вносит задержку в развитие пятна. Это наблюдение подтверждается на рис. 4б: уровень максимальной амплитуды возмущений в пятне резко падает за углом и далее вниз по потоку медленно восстанавливается, приближаясь к соответствующему уровню возмущений над плоской пластиной.
2.3. Частотно-амплитудный анализ возмущений
Рассмотрим эволюцию возмущений в спектральной плоскости. Для этого рассмотрим поле двухмерного быстрого преобразования Фурье p$_{w}^{'}$(ω, β) для величины p$_{w}^{'}$(t, x, z) по переменным t, z; x – параметр. В случае волнового пакета спектры содержат два симметричных максимума, которые определяют угол наклона фронта волны (рис. 5а). Вниз по потоку частота и волновое число этих максимумов медленно убывают, что соответствует результатам линейной теории устойчивости и здесь подробно не обсуждается; величина максимумов растет вниз по потоку. До угла l < 0 спектры волновых пакетов для случаев FP и EC идентичны. За углом спектр возмущений в пакете EC монотонно и равномерно затухает во всем спектральном диапазоне, за исключением ближней окрестности нуля: β ∼ 2, ω ∼ 10. Здесь наблюдается слабый рост на уровне фонового шума. Предположительно, это новый волновой пакет, который зарождается из фоновых возмущений в перестроившемся пограничном слое. Из-за ограниченных размеров расчетной области более детальный анализ такого роста на базе проведенных расчетов представляется нецелесообразным.
Рис. 5.
Амплитуда двухмерного преобразования Фурье $\hat {p}_{w}^{'}$(ω, β) для волнового пакета (WP) в сечениях l = –0.5 (а), 0.5, (б), 2.5 (в): левая часть рисунков – плоская пластина (FP); правая часть рисунков – угол разрежения (EC). Цветовая палитра приведена в логарифмическом масштабе.
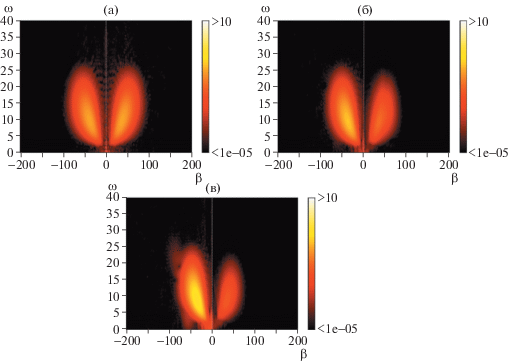
Соответствующие спектры для случая турбулентного пятна качественно отличаются. Из-за большой амплитуды генератора возмущений начальный спектр возмущений, порожденных в пограничном слое, не является простым, хотя вновь выделяются два максимума первой моды возмущений, соответствующие максимумам рис. 6. Нелинейное взаимодействие приводит к появлению гармоник с кратными частотами и волновыми числами; спектр быстро наполняется, дробится; появляется и усиливается гармоника (ω, β) = (0, 0), что свидетельствует о растущем изменении среднего течения внутри пятна. Вновь для l < 0 спектры оказываются идентичны, а различия появляются сразу при l ≥ 0. Основное отличие заключается в том, что спектр EC быстро теряет в амплитуде во всем частотно-волновом диапазоне и становится менее наполненным, однако вниз по потоку он медленно наполняется и восстанавливается по амплитуде. Тем не менее область наполненности не восстанавливается, оставаясь меньше по сравнению со случаем FP (рис. 6д, е).
Рис. 6.
Амплитуда двухмерного преобразования Фурье $\hat {p}_{w}^{'}$(ω, β) для турбулентного пятна (TS) в сечениях l = –3.4 (а), –3.0 (б), –2.0 (в), –0.5 (г), 0.5 (д), 2.5 (е): левая часть рисунков – плоская пластина (FP); правая часть рисунков – угол разрежения (EC). Цветовая палитра приведена в логарифмическом масштабе.
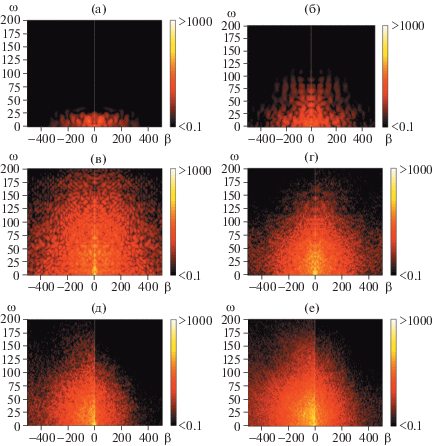
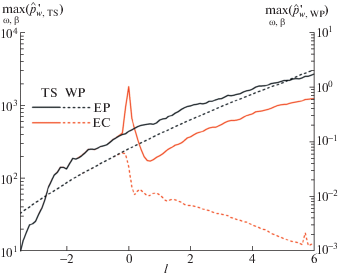
Описанное спектральное поведение волнового пакета и турбулентного пятна наглядно демонстрируют распределения максимальной амплитуды Фурье $\mathop {\max }\limits_{{{\omega }},{{\beta }}} {\text{|}}\hat {p}_{w}^{'}({{\omega }},{{\beta }}){\text{|}}$ на поверхности, представленные на рис. 7. Как видно, рост наиболее сильной гармоники пакета близок к экспоненциальному и совпадает для случаев FP и EC при l < 0; затухание этой гармоники за углом разрежения также близко к экспоненциальному. Рост наиболее сильной гармоники в турбулентном пятне, (ω, β) ≈ (0, 0), протекает наиболее активно на стадии формирования пятна, l < –2, и далее заметно замедляется. Сразу за углом разрежения эта гармоника скачкообразно ослабевает при 0 ≤ l ≤ 0.5, но возобновляет свой рост, причем темп роста (наклон кривой) близок к темпу роста для случая плоской пластины.
2.4. Задержка турбулентного пятна
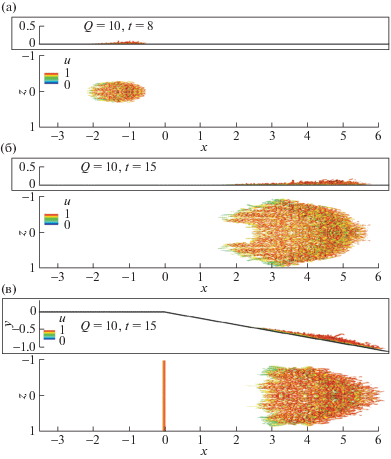
Как отмечено выше, присутствие угла разрежения задерживает развитие турбулентного пятна. Проиллюстрируем это утверждение. На рис. 8а турбулентное пятно визуализировано на пластине, когда оно полностью расположено при l < 0 (совпадает со случаем EC), а также после перехода через линию l < 0 для пластины и для угла разрежения. В обоих случаях (рис. 8б, в) форма пятен близка к треугольной. Однако в случае FP (рис. 8б) пятно оказывается больше, чем в случае EC (рис. 8в); структура пятна в профиль различается слабо. Следует ожидать, что вклад большего пятна в силу вязкого трения окажется больше.
Рис. 8.
Визуализация турбулентного пятна с помощью изоповерхностей Q-критерия, Q = 10, окрашенных в соответствии с величиной продольной составляющей u вектора скорости: а – FP, t = 8.0; б – FP, t = 15.0; в – EC, t = 15.0. Цветовая палитра приведена в линейном масштабе.
Вклад пятна можно рассчитать следующим образом:
где S – площадь обтекаемой поверхности, а Δcf, x – избыточный коэффициент трения по сравнению со случаем невозмущенного ламинарного течения. Коэффициент трения определяется стандартным образом:(2.3)
${{c}_{{f,x}}} = \frac{{2{{\tau }}_{{w,x}}^{*}}}{{{{\rho }}_{\infty }^{*}U_{\infty }^{{*2}}}} \equiv 2\frac{{{{{{\mu }}}_{w}}}}{{{{{\operatorname{Re} }}_{{\infty L}}}}}{{\left( {\frac{{\partial V}}{{\partial {\mathbf{n}}}}} \right)}_{{w,x}}},$(2.4)
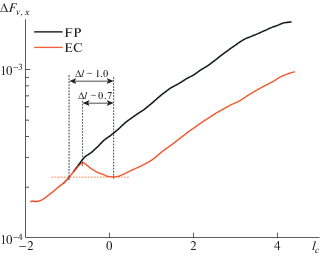
${{l}_{c}} = \iint\limits_S {{{ld{{F}_{{{v},x}}}} \mathord{\left/ {\vphantom {{ld{{F}_{{{v},x}}}} {\Delta {{F}_{{{v},x}}}}}} \right. \kern-0em} {\Delta {{F}_{{{v},x}}}}}}$На рис. 9 представлена эволюция вклада турбулентного пятна в силу вязкого сопротивления. При переходе через угол (случай EC) величина lc < 0. Это обусловлено тем, что часть турбулентного пятна, проникшая в область l > 0, быстро теряет интенсивность по сравнению с остальной частью пятна. Когда пятно EC полностью прошло в область l > 0, рост его вклада в силу вязкого трения возобновляется. При этом темпы роста для случаев FP и EC близки, что подтверждает предположение о задерживающем влиянии угла разрежения на эволюцию турбулентного пятна. Эффективная длина, на которой рост пятна задерживается углом разрежения, показана на рис. 9 и примерно равна единице.
3. ЗАКЛЮЧЕНИЕ
В рамках уравнений Навье–Стокса численно исследовано развитие волновых пакетов и турбулентных пятен в сверхзвуковом пограничном слое (число Маха 3) над углом разрежения 10°. Появление угла разрежения приводит к стабилизации течения. Показано, что волновые пакеты первой неустойчивой моды монотонно затухают за углом разрежения. Это обусловлено внезапной перестройкой течения, утолщением пограничного слоя и, как следствие, изменением характеристик устойчивости пограничного слоя. Неустойчивая область масштабируется по частоте вместе с толщиной пограничного слоя, изменение которой можно оценивать на основе теории Прандтля–Майера.
Также показано, что локализованные области турбулентного течения – турбулентные пятна – подавляются при переходе через угол разрежения лишь локально. Присутствие угла задерживает развитие пятна на масштабе порядка 40 толщин невозмущенного пограничного слоя перед углом; амплитуда возмущений уменьшается; частотно-волновой спектр становится менее наполненным. Ниже по потоку от этой области турбулентное пятно растет аналогично пятну в безградиентном течении над плоской пластиной. Поэтому эффект реламинаризации турбулентного течения, который наблюдается по картинам теплообмена в эксперименте, может в действительности говорить не о подавлении турбулентности, а лишь о ее локальном ослаблении.
Исследование случая второй неустойчивой моды пограничного слоя, которая возникает при больших числах Маха, а также поведения вязкого трения и теплообмена к поверхности угла разрежения в присутствии турбулентных пятен является предметом дальнейших исследований авторов.
Список литературы
Narasimha R., Viswanath P.R. Reverse Transition at an Expansion Corner in Supersonic Flow // AIAA Journal. 1975. P. 693–695.
Романенко Н.П., Леонтьев A.M., Соливин A.H. Исследование сопротивления и теплообмена при турбулентном течении воздуха в осесимметричных каналах с продольным градиентом давления // ПМТФ. 1961. Т. 2. № 5. С. 16–25.
Witte A.B., Harper E.Y. Experimental investigation of heat transfer rates in rocket thrust chambers // AIAA J. 1963. V. 1. № 2. P. 443–451.
Дейч М.Е., Лазарев Л.Я. Исследование перехода турбулентного пограничного слоя в ламинарный // Инженерно-физический журн. 1964. Т. VII. № 4. С. 18–24.
Гольдфельд М.А., Зиновьев В.Н., Лебига В.А. Структура и пульсационные характеристики сжимаемого турбулентного пограничного слоя за веером волн разрежения // Изв. РАН. МЖГ. 1987. № 1. С. 21–29.
Gillis J.C., Johnston J.P. Turbulent boundary-layer flow and structure on a convex wall and its redevelopment on a flat plate // J. Fluid Mech. 1983. V. 135. P. 123–153.
Arnette S.A., Samimy M., Elliot G.S. The effects of expansion on the turbulence structure of compressible boundary layers // J. Fluid Mech. 1998. V. 367. P. 67–105.
Kim J., Samimy M., Lee S. Effects of compression and expansion on turbulence intensity in supersonic boundary layers // AIAA J. 2001. V. 39. № 6. P. 1071–1077.
Humble R.A., Peltier S.J., Bowersox R.D.W. Visualization of the structural response of a hypersonic turbulent boundary layer to convex curvature // Phys. Fluids. 2012. V. 24. P. 106103-1–106103-24.
Tichenor N.R., Humble R.A., Bowersox R.D.W. Response of a hypersonic turbulent boundary layer to favorable pressure gradients // J. Fluid Mech. 2013. V. 722. P. 187–213.
Гольдфельд М.А., Нестуля Р.В., Шиплюк А.Н. Исследование реламинаризации турбулентного пограничного слоя при числе Маха M = 4 // ПМТФ. 2002. Т. 43. № 1. С. 91–99.
Ноев А.Ю. Влияние единичной неровности на ламинарно-турбулентный переход при гиперзвуковом обтекании тела вращения с изломами поверхности // XI Всероссийский съезд по фундаментальным проблемам теоретической и прикладной механики. Россия, Казань, 20–24 августа 2015. Сб. докл. Изд-во: Казанский (Приволжский) федеральный ун-т. С. 2802–2803.
Fang J., Yao Y., Zheltovodov A.A., Li Z., Lu L. Direct numerical simulation of supersonic turbulent flows around a tandem expansion-compression corner // Phys. Fluids. 2015. V. 27. P. 125104-1–125104-28.
Sun M., Hu Z., Sandham N.D. Recovery of a supersonic turbulent boundary layer after an expansion corner // Phys. Fluids. 2017. V. 29. P. 076103-1–076103-17.
Chuvakhov P.V., Fedorov A.V., Obraz A.O. Numerical simulation of turbulent spots generated by unstable wave packets in a hypersonic boundary layer // Computers & Fluids. 2018. V. 162. P. 26–38.
Егоров И.В., Новиков А.В. Прямое численное моделирование ламинарно-турбулентного обтекания плоской пластины при гиперзвуковых скоростях потока // Ж. вычисл. матем. и матем. физ. 2016. Т. 56. № 6. С. 1064–1081.
Anderson J.D., Jr. Fundamentals of aerodynamics. McGraw-Hill Science/Engineering/Math. 3rd edition. 2001. 892 p.
Mack L.M. Boundary layer stability theory // Document 900-277. Rev. A. 1969. JPL. Pasadena. California. 388 p.
Chuvakhov P.V., Fedorov A.V., Obraz A.O. Numerical modelling of supersonic boundary-layer receptivity to solid particulates // J. Fluid Mech. 2018. V. 859. P. 949–971.
Дополнительные материалы отсутствуют.
Инструменты
Известия РАН. Механика жидкости и газа