Известия РАН. Механика жидкости и газа, 2021, № 2, стр. 3-14
ИССЛЕДОВАНИЕ РАЗВИТИЯ ПОЛОСТИ В КЛЕТОЧНОМ СФЕРОИДЕ В ЗАВИСИМОСТИ ОТ МЕХАНИЗМОВ АКТИВНЫХ МЕЖКЛЕТОЧНЫХ ВЗАИМОДЕЙСТВИЙ
С. А. Логвенков a, b, *, Е. Н. Юдина b
a Национальный исследовательский университет “Высшая школа экономики”
Москва, Россия
b МГУ им. М.В. Ломоносова, Научно-исследовательский институт механики
Москва, Россия
* E-mail: logv@bk.ru
Поступила в редакцию 09.09.2020
После доработки 27.10.2020
Принята к публикации 27.10.2020
Аннотация
Решена задача об эволюции полости, сформировавшейся к начальному моменту времени в центральной части клеточного агрегата сферической формы. Разработанная ранее модель биологической среды, образованной проявляющими механическую активность клетками и внеклеточной жидкостью, была использована при исследовании влияния различных механизмов активных межклеточных взаимодействий (хаотического и направленного нелокального) на распространение фронта, отделяющего клеточную среду от жидкости. Численное решение показало, что в ряде случаев (характеризуемых давлением жидкости и плотностью начального распределения клеток) только хаотической активности клеток оказывается достаточно для увеличения радиуса внутренней полости. В других случаях развитие полости невозможно без участия нелокального механизма активных взаимодействий между клетками и взаимодействия клеток с внешней границей. Нелокальный механизм активных межклеточных взаимодействий при отсутствии взаимодействия клеток с внешней границей приводит к росту полости не при любых начальных размерах полости. Постановка и решение задачи дают более полное описание возможных сценариев формообразования на одной из ранних стадий эмбрионального развития.
Одним из фундаментальных механизмов, который наблюдается в самых разных биологических процессах, является развитие активных механических взаимодействий клеток между собой и с окружающими их внеклеточными компонентами биологической среды. Активные взаимодействия, характеризуемые активными напряжениями, создаются сократительными элементами клеточного скелета при участии поверхностных белков, обеспечивающих прочность скрепления мембран соседних клеток.
Результатом механической клеточной активности является перестройка биологических тканей, сопровождаемая, в частности, в эмбриональных тканях, миграцией клеток. Так, в процессе эмбрионального развития клетки эмбриональных тканей способны к движениям друг относительно друга. Взаимные перемещения клеток вследствие развития активных напряжений лежат в основе формирования структур, которые в дальнейшем трансформируются в ткани и органы.
Макроскопическое описание биологических сплошных сред, а также анализ предполагаемых механизмов, управляющих клеточными движениями, приводящими в результате к биологическому формообразованию, требуют привлечения математических моделей, которые адекватно учитывают участие механических факторов в фундаментальных процессах биологического формообразования на тканевом уровне с учетом активных механизмов, действующих на клеточном и субклеточном уровнях.
Общие принципы моделирования такого рода сред, представленные в [1, 2], были использованы в [3, 4] при построении модели сплошной среды, образованной проявляющими механическую активность рыхло связанными клетками и внеклеточной жидкостью. В модели учитывались различные механизмы активных взаимодействий между клетками – локальный, учитывающий хаотическую активность клеток, характеризуемую давлением, которое проявляется в отталкивании клеток, и нелокальный, учитывающий направленные активные взаимодействия между клетками, находящимися на некотором расстоянии (порядка характерного размера клетки) друг от друга. Активные напряжения являлись одним из управляющих параметров, контролирующих взаимные перемещения клеток друг относительно друга.
Более полный обзор работ, посвященных использованию методов механики при моделировании механо-зависимых реакций в биологических тканях, состоящих из механически активных клеток, можно найти в [1–4].
Полученная в [3, 4] модель использовалась при решении задачи об образовании полости в первоначально однородном клеточном сфероиде в результате потери устойчивости пространственно-однородного стационарного состояния. Такой механизм формообразования возможен на одной из ранних стадий эмбрионального развития. На этой стадии сплошное скопление слабо связанных клеток преобразуется в так называемую бластулу, внутренние клетки которой раздвигаются в радиальных направлениях, создавая заполненную жидкостью полость [5].
Постановка рассмотренной в [3, 4] задачи по сути описывает лишь начальную стадию процесса, в течение которой происходит значительное уменьшение плотности клеток в центральной части сфероида. Образование и дальнейшая эволюция заполненной жидкостью полости не рассматриваются. Начальное образование полости может быть вызвано и различными другими факторами, среди которых гибель клеток или изменение формы клеток в центральной части сфероида.
В предлагаемой работе решена задача об эволюции полости, которая к начальному моменту времени сформировалась в центральной части клеточного агрегата сферической формы. Изучен процесс распространения фронта, отделяющего клеточную среду от жидкости. Исследовано влияние различных механизмов активных межклеточных взаимодействий на распространение фронта и распределение объемной плотности клеток. Постановка и решение задачи являются продолжением исследования роли возможных механизмов межклеточных взаимодействий в формообразовании на одной из ранних стадий эмбрионального развития.
1. КОНТИНУАЛЬНАЯ МОДЕЛЬ КЛЕТОЧНОЙ СРЕДЫ
В работах [3, 4] разработана континуальная модель биологической среды, образованной механически активными клетками. Биологическая многоклеточная ткань рассматривается как трехфазная сплошная среда, состоящая из клеток, внеклеточной жидкости и дополнительной фазы, отвечающей за активное силовое взаимодействие между клетками. Эта дополнительная фаза может соответствовать, в частности, системе выростов различной формы и размеров, возникающих на поверхности клеток, и образующих контакты различной прочности и продолжительности с поверхностями соседних клеток или единой механически напряженной сети, составленной мембранами контактирующих клеток и выстилающими их поверхностными сократительными структурами. Активные межклеточные взаимодействия обеспечиваются посредством напряжений, развивающихся в дополнительной фазе в результате сократительной активности элементов клеточного скелета. В дальнейшем предполагается, что объемом дополнительной фазы можно пренебречь. Основные уравнения имеют следующий вид:
(1.3)
${{e}_{{ij}}} = \frac{1}{2}\left( {{{\nabla }_{i}}{{{v}}_{j}} + {{\nabla }_{j}}{{{v}}_{i}}} \right)$(1.4)
$e = \frac{1}{{2{{\mu }_{{adh}}}}}((1 - n)pI + \sigma _{{}}^{{(c)}}) - \frac{1}{{2{{\mu }_{{mot}}}}}\tau $(1.5)
$\tau (x) = - \Pi (n)I + m \cdot \frac{3}{{4\pi {{R}_{s}}^{4}}}\int\limits_S {n(x + r) \cdot r \otimes r} ds + f_{\Sigma }^{{}}$(1.7)
$\nabla \cdot (n \cdot {{\sigma }^{{(c)}}} + \tau ) + p\nabla n + {{k}_{0}}n(1 - n) \cdot ({\mathbf{w}} - {\mathbf{v}}) = 0$(1.8)
$ - \nabla ((1 - n) \cdot p) + p\nabla (1 - n) - {{k}_{0}}n(1 - n) \cdot ({\mathbf{w}} - {\mathbf{v}}) = 0$Здесь $n$ – объемная плотность клеток; ${\mathbf{v}}$ и ${\mathbf{w}}$ – скорости клеточной фазы и внеклеточной жидкости соответственно; ${{e}_{{ij}}}$ – компоненты тензора скоростей деформации клеточной фазы $e$; $p$ – давление во внеклеточной жидкости; I – единичный тензор;${{\sigma }^{{(с)}}}$ и $\tau $ – тензоры напряжений в клеточной фазе и дополнительной фазе соответственно; ${{\mu }_{{adh}}}$ и ${{\mu }_{{mot}}}$ – коэффициенты, характеризующие клеточную адгезию и подвижность соответственно [3, 4]; $\Pi (n)$ – давление, характеризующее хаотическое движение клеток [3, 4]; $S$ – часть поверхности сферы радиусом ${{R}_{s}}$ и центром в рассматриваемой точке, лежащая целиком внутри среды; ${{R}_{s}}$ называется радиусом чувствительности, он характеризует расстояние, на котором происходит силовое активное взаимодействие клеток и имеет порядок одного или нескольких клеточных размеров; $r$ – радиус-вектор точки на поверхности сферы; ${\text{f}}_{\Sigma }^{{}}$ – тензор, описывающий активные взаимодействия клеток с поверхностью, ограничивающей среду (считаем, что граничная поверхность образована клеточными и внеклеточными составляющими, обеспечивающими активные взаимодействия с клетками рассматриваемой среды); ${{k}_{0}}$ – коэффициент межфазного трения. Компоненты тензора ${\text{f}}_{\Sigma }^{{}}$ отличны от нуля лишь в пограничных точках – точках, удаленных от ограничивающей среду поверхности на расстояние меньше радиуса чувствительности ${{R}_{s}}$. Во внутренних точках среды взаимодействие с границей отсутствует. Конкретный вид тензора ${\text{f}}_{\Sigma }^{{}}$ будет указан в следующем разделе.
Ниже приведено краткое описание основных гипотез и физического смысла уравнений (1.1)–(1.8).
Уравнения неразрывности для фаз (1.1) и (1.2) написаны с учетом того, что в среде отсутствуют клеточные деления, гибель клеток и массообмен между клеточной фазой и внеклеточной жидкостью. Истинные плотности фаз считаются постоянными и равными между собой.
Деформация среды, отождествляемая с деформацией клеточной фазы, может происходить как в результате деформирования отдельных клеток, так и в результате относительных перемещений клеток друг относительно друга [1]. В данной работе примем допущение о малости слагаемого, описывающего скорость деформации среды за счет изменения клеточной деформации. Тогда тензор скоростей деформации клеточной фазы подчиняется стандартным кинематическим соотношениям (1.3) и описывает только переупаковку клеток.
Переупаковка клеток рассматривается как течение, управляемое напряжениями в клеточной фазе, давлением жидкости и активными напряжениями. Формулировка используемого закона (1.4) предполагает, что процесс взаимного перемещения клеток друг относительно друга может управляться физически различными механизмами, связанными с прочностью сцепления клеток (адгезией) и подвижностью клеток. Воздействие внешних по отношению к клеткам механических сил, приложенных в местах контакта между ними, приводит к разрыву одних и образованию других клеточных контактов с перемещением клеток одна относительно другой. Этот процесс, в некотором смысле аналогичный вязкому течению, контролируется прочностью межклеточных контактов, т.е. межклеточной адгезией – первое слагаемое уравнения (1.4). Физически коэффициент ${{\mu }_{{adh}}}$ можно рассматривать как коэффициент вязкости среды, определяемый в ряде экспериментов. Второе слагаемое (1.4) отвечает за перемещения клеток вследствие их механической активности, управляемой активными напряжениями. Этот механизм перемещения присущ клеткам эмбриональных тканей на определенной стадии развития. Он проявляется в их способности распластываться на субстрате в результате развития активных напряжений. В ткани эти клетки могут осуществлять перемещения и менять соседей в результате активных взаимодействий с поверхностями соседних клеток, используя их в качестве субстрата. Этот процесс можно рассматривать как проявление клеточной подвижности.
При выборе знаков коэффициентов предполагается, что активные напряжения в дополнительной фазе обеспечивают развитие стягивающих усилий между клетками и стимулируют их переупаковку, приводящую к уплотнению клеточной фазы, а давление в жидкости и растягивающие клеточные напряжения ей препятствуют. Зависимость (1.4) принята в линейном изотропном приближении.
Определяющее соотношение для активных напряжений (1.5), во-первых, учитывает хаотическую активность клеток. На макроскопическом уровне среднее значение потока импульса хаотического движения частиц через единицу поверхности среды характеризуется соответствующим давлением (1.6), проявляющимся в отталкивании частиц, что приводит к невозможности ее слишком большого сжатия.
Предполагается также, что клетки могут направленно реагировать на воздействие внешних факторов, таких как, например, неоднородная плотность адгезионных контактов. В этом случае клетки отвечают развитием активных напряжений в направлении внешнего стимула. При описании этого механизма развития активных напряжений между клетками использовано предположение о том, что анизотропия тензора активных напряжений определяется неоднородностью распределения плотности клеток (характеризующей неоднородность распределения адгезионных контактов) по некоторой сферической поверхности с радиусом (радиус чувствительности) порядка радиуса клетки (или несколько большим) и центром в рассматриваемой точке. Математическое описание второго механизма развития активных напряжений между клетками имеет вид зависимости тензора активных напряжений от интегрального функционала пространственного распределения объемной плотности клеток.
В работах [3, 4] в качестве определяющего уравнения для активных напряжений использовалось разложение подынтегральной функции в (1.5) в ряд по формуле Тейлора второго порядка точности. Получаемые таким образом определяющие соотношения в дифференциальной форме неявно учитывают взаимодействие клеток с ограничивающей среду поверхностью, поскольку при интегрировании членов ряда не учитываются различия пределов интегрирования для внутренних и пограничных точек. Решения задач с использованием таких соотношений не могут учитывать различные активные взаимодействий клеток с внешней границей.
В данной работе определяющие соотношения для активных напряжений изменены таким образом (по сравнению с [3, 4]), чтобы помимо параметров среды они содержали и расстояние до внешних границ – в (1.5) присутствуют слагаемые, описывающие развитие активных напряжений в пограничной области.
Уравнение импульсов для фаз (1.7) и (1.8), пренебрегая инерционными эффектами, приняты в традиционном для механики пористых сред виде [6, 7].
Система уравнений (1.1)–(1.8), дополненная соответствующими начальными и граничными условиями, является замкнутой и дает возможность нахождения неизвестных n, ${\mathbf{v}}$, ${\mathbf{w}}$, ${\mathbf{e}}$, ${{\sigma }^{{(с)}}}$, $\tau $, p.
2. ЗАДАЧА ОБ ЭВОЛЮЦИИ ПОЛОСТИ В КЛЕТОЧНОМ СФЕРОИДЕ
В рамках предшествующей постановки задачи [3, 4] рассматривалась эволюция плотности клеток в изначально однородном клеточном сфероиде. Результаты решения задачи показали возможность увеличения плотности клеток в направлении внешней границы сфероида, и формирование фронта, отделяющего клеточную среду от жидкости. Однако дальнейшее исследование распространения фронта в рамках такой постановки задачи невозможно, поскольку система уравнений теряет физический смысл при достижении нулевой объемной плотности клеток, и надо переходить к другой постановке задачи.
Рассмотрим клеточный агрегат, имеющий форму сферически симметричного слоя, ограниченного внешней поверхностью постоянного радиуса $r = {{R}_{{out}}}$ и внутренней поверхностью $r = {{R}_{{in}}}(t)$, радиус которой может меняться со временем и подлежит определению. Будем считать, что во внеклеточной жидкости на внешней поверхности $r = {{R}_{{out}}}$ поддерживаются нулевой поток жидкости и постоянное давление в жидкой фазе. Такое состояние может физически обеспечиваться осмотическими механизмами при участии активных ионных насосов, регулирующих поступление ионов из наружной среды [8]. В результате решения задачи будет изучена эволюция заполненной жидкостью полости, расположенной в центральной части клеточного агрегата.
Уравнения (1.1)–(1.8) для физических компонент векторов и тензоров в сферической системе координат, связанной с центром сфероида, в предположении сферической симметрии примут следующий вид:
(2.1)
${{\tau }_{{rr}}} = - E\frac{n}{{1 - n}} + m\frac{3}{{4\pi R_{s}^{4}}}\int\limits_S {n \cdot r_{r}^{2}} ds + {{f}_{{\Sigma rr}}}$Здесь ${{r}_{\theta }}$, ${{r}_{\varphi }}$ и ${{r}_{r}}$ – координаты радиус-вектора точек на поверхности сферы чувствительности S с центром в рассматриваемой точке и радиусом, равным радиусу чувствительности Rs, в локальном физическом базисе сферической системы координат.
Для тензора $f_{\Sigma }^{{}}(r)$, описывающего развитие активных напряжений в пограничной области, могут быть предложены разные зависимости от координаты. Будем предполагать, что сила взаимодействия клеток с внешней границей действует в направлении нормали к границе и создается сократительными структурами клеток в пограничной области. Предполагается, что величина силы должна взрастать по мере приближения к границе. В данном случае примем гипотезу, что радиальная сила взаимодействия клеток с внешней границей $r = {{R}_{{out}}}$ пропорциональна ${{S}_{\Sigma }}$ – площади поверхности контакта сферы чувствительности $S$ (с центром в рассматриваемой точке) с внешней границей, и единственную отличную от нуля компоненту тензора $f_{\Sigma }^{{}}(r)$ примем в следующем виде:${{f}_{{\Sigma rr}}}(r) = {{m}_{\Sigma }}n(r){{S}_{\Sigma }}{\text{/}}\pi R_{s}^{2}$ (вне пограничной области тензор $f_{{\Sigma \;}}^{{}}$ равен нулю).
Активные взаимодействия клеток с внеклеточными структурами на внешней границе характерны для раннего эмбрионального развития, по крайней мере, на стадии формирования внутренней полости [5]. Также стенки наружного слоя клеток могут отличаться по своей активности при развитии активных взаимодействий со своим окружением от других клеток (в частности у млекопитающих). В то же время будем считать, что активные взаимодействия клеток с внутренней границей отсутствуют, так как соответствующие внеклеточные структуры на внутренней поверхности начинают формироваться на более поздних стадиях.
В качестве граничных условий при $r = {{R}_{{out}}}$ примем: ${{{v}}_{r}} = {{w}_{r}} = 0$, p = p0. На внутренней поверхности сферического слоя будем учитывать непрерывность вектора напряжений в среде в целом и непрерывность гидростатического давления. Тогда на внутренней поверхности слоя получим условие: $ - (1 - n)p + n\sigma _{{rr}}^{{(c)}} + {{\tau }_{{rr}}} = - p$ при $r = {{R}_{{in}}}(t)$. Подставляя сюда выражение для напряжений в клеточной фазе $n\sigma _{{rr}}^{{(c)}}$ из (2.1) получим, что при $r = {{R}_{{in}}}(t)$:
(2.2)
${{n}^{2}}p + \left( {\frac{{{{\mu }_{{adh}}}}}{{{{\mu }_{{mot}}}}}n + 1} \right){{\tau }_{{rr}}} + 2{{\mu }_{{adh}}}n \cdot \frac{{\partial {{{v}}_{r}}}}{{\partial r}} = 0$Перемещение внутренней границы слоя определяется движением клеток, поэтому на этой границе считается выполненным условие
Граничное условие для $n$ не ставится, так как $r = {{R}_{{out}}}$ и $r = {{R}_{{in}}}(t)$ являются характеристиками для первого уравнения системы (2.1) и граничные условия в этих точках получаются из решения этого уравнения, записанного в точках $r = {{R}_{{out}}}$ и $r = {{R}_{{in}}}(t)$. Результат интегрирования суммы первого и второго уравнений системы (2.1) с учетом граничного условия ${{{v}}_{r}} = {{w}_{r}} = 0$ при $r = {{R}_{{out}}}$ приводит к соотношению
которым можно заменить второе уравнение (2.1).В качестве начальных условий примем, что $n(r,0) = {{n}_{0}}(r)$ и ${{R}_{{in}}}(0) = {{R}_{0}}$.
Введем безразмерные величины:
Здесь ${{\mu }_{0}}$ – некоторое характерное значение коэффициента, отвечающего за клеточную подвижность.
Оценим коэффициент межфазного трения $k_{0}^{*}$, характеризующий силу межфазного взаимодействия между клеточной и жидкой фазами, обусловленную вязким трением на межфазных поверхностях.
Характерные значения коэффициента вязкости клеточной среды для эмбриональных тканей согласно данным [9, 10] составляют ${{10}^{4}}{\kern 1pt} - {\kern 1pt} {{10}^{6}}$ Па с, а в [11] оценки этой величины доходят до ${{10}^{7}}$ Па с. В качестве оценок коэффициента межфазного трения ${{k}_{0}}$ приводятся значения ${{10}^{{12}}}{\kern 1pt} - {\kern 1pt} {{10}^{{14}}}$ Па с м–2 [12, 13]. В качестве значения ${{R}_{{out}}}$ примем оценку для радиуса бластулы морского ежа [14]: ${{R}_{{out}}} = 0.05$ мм. Если в качестве значений параметров принять ${{\mu }_{0}} = {{10}^{6}}$ Па с [10] и ${{k}_{0}} = 5 \times {{10}^{{12}}}$ Па с м–2 [13], согласующиеся с приведенными данными, тогда получаем оценку $k_{0}^{*} = 1.25 \times {{10}^{{ - 2}}}$.
Полученная оценка позволяет пренебречь в уравнениях импульсов для фаз силой межфазного взаимодействия за счет вязкого трения, а из последнего уравнения (2.1) в силу этой оценки следует, что гидростатическое давление в рассматриваемой области можно считать постоянным. Тогда уравнения для клеточной фазы можно решать отдельно от уравнений, описывающих движение жидкости. Скорость жидкости может быть найдена отдельно из уравнения (2.3).
В настоящее время отсутствуют экспериментальные данные, позволяющие получить оценки ряда других числовых параметров. Поэтому свойства системы будут исследованы в зависимости от значений безразмерных параметров, где в качестве базового набора, если не сказано иначе, в расчетах используются следующие значения:
Далее будем сохранять за безразмерными величинами прежние обозначения, опуская звездочку.
Преобразование координаты $\xi = (r - {{R}_{{in}}}(t)){\text{/}}(1 - {{R}_{{in}}}(t))$, позволяет перейти от решения задачи на отрезке $\left[ {{{R}_{{in}}}(t),1} \right]$ с подвижной нижней границей, к решению задачи на отрезке [0, 1]. После преобразований получим систему уравнений для $n$, ${v}$ и ${{R}_{{in}}}$:
(2.4)
$\frac{{\partial n}}{{\partial t}} + \frac{\partial }{{\partial \xi }}\left( {n\frac{{{v} - (1 - \xi )}}{{1 - {{R}_{{in}}}}}\frac{{d{{R}_{{in}}}}}{{dt}}} \right) + n\left( {\frac{{2{v}}}{r} - \frac{1}{{1 - {{R}_{{in}}}}}\frac{{d{{R}_{{in}}}}}{{dt}}} \right) = 0$(2.5)
$2\left( {\frac{1}{{{{{(1 - {{R}_{{in}}})}}^{2}}}} \cdot \frac{1}{{{{r}^{2}}}}\frac{\partial }{{\partial \xi }}\left( {{{r}^{2}}n{{\mu }_{{adh}}}\frac{{\partial {v}}}{{\partial \xi }}} \right) - \frac{{2n{{\mu }_{{adh}}}{v}}}{{{{r}^{2}}}}} \right) = - \left( {\frac{1}{{1 - {{R}_{{in}}}}}\frac{{\partial \Sigma }}{{\partial \xi }} + \Phi } \right)$Здесь $\Sigma = - n(1 - n){{p}_{0}} + \left( {\frac{{{{\mu }_{{adh}}}}}{{{{\mu }_{{mot}}}}}n + 1} \right){{\tau }_{{rr}}}$ и $\Phi = 2\left( {\frac{{{{\mu }_{{adh}}}}}{{{{\mu }_{{mot}}}}}n + 1} \right)\frac{{{{\tau }_{{rr}}} - {{\tau }_{{\varphi \varphi }}}}}{r} + {{p}_{0}}\frac{1}{{1 - {{R}_{{in}}}}}\frac{{\partial n}}{{\partial \xi }}$.
Система уравнений решается при следующих граничных и начальных условиях:
(2.7)
${{n}^{2}}p + \left( {\frac{{{{\mu }_{{adh}}}}}{{{{\mu }_{{mot}}}}}n + 1} \right){{\tau }_{{rr}}} + 2\frac{{{{\mu }_{{adh}}}}}{{1 - {{R}_{{in}}}}}n \cdot \frac{{\partial {v}}}{{\partial \xi }} = 0\quad {\text{при}}\quad \xi = 0$Решение системы уравнений на каждом временном шаге начинается с решения уравнения (2.5), значения объемной плотности клеток берутся с предыдущего шага по времени. Использование интегро-интерполяционного метода построения разностных схем [15] позволяет получить разностную схему, аппроксимирующую уравнение (2.5) с точностью $O(\Delta {{\xi }^{2}})$. При аппроксимации граничного условия при ξ = 0 ограничиваемся первым порядком аппроксимации $O(\Delta \xi )$.
Полученные значения ${v}$ далее используются при решении уравнений (2.4) и (2.6). Аппроксимация дивергентного слагаемого выполнена с использованием двухслойной разностной схемы [16] c весом 0.5, которая аппроксимирует уравнение (2.4) с точностью $O(\Delta {{\xi }^{2}} + \Delta {{t}^{2}})$. Для граничных узлов ограничиваемся первым порядком аппроксимации $O(\Delta \xi )$. Все полученные разностные уравнения решались методом прогонки [15]. Уравнение (2.6) решается методом Эйлера.
Интегралы, входящие в выражения для активных напряжений, вычисляются приближенно путем разложения подынтегральной функции в ряд по формуле Тейлора второго порядка точности. При вычислении активных напряжений в пограничных точках пределы интегрирования учитывают то, что интегрирование выполняется лишь по части поверхности сферы чувствительности, расположенной внутри сфероида.
В работах [3, 4] развитие активных напряжений описывалось дифференциальными соотношениями, полученными посредством разложения подынтегральной функции по формуле Тейлора до членов второго порядка. В рамках такой модели полная система уравнений имеет пространственно-однородное стационарное решение, которое удовлетворяет граничным условиям в задаче об образовании заполненной жидкостью полости в изначально однородном клеточном сфероиде при любых постоянных плотности клеток ${{n}_{0}}$ и гидростатическом давлении ${{p}_{0}}$. Формирование новой клеточной структуры происходит вследствие потери устойчивости однородного состояния.
3. РЕЗУЛЬТАТЫ РАСЧЕТОВ И ОБСУЖДЕНИЕ
1. В начале рассмотрим основные результаты решения задачи о развитии полости в однородном клеточном сфероиде, используя уравнения для активных напряжений в интегральном виде, предлагаемые в данной работе (постановка задачи и численная схема приведены в [4]). В этом случае система (2.1) имеет стационарное пространственно-однородное решение, удовлетворяющее граничным условиям при $m = {{m}_{\Sigma }} = 0$. При $m$ и ${{m}_{\Sigma }}$, отличных от нуля, стационарное решение существует лишь при специальном виде тензора ${{f}_{\Sigma }}$, и этот случай далее не рассматривается. Поэтому рассмотрим формирование новой клеточной структуры не в результате потери устойчивости стационарного решения, а лишь в результате эволюции некоторого начального распределения клеток $n(r,0) = {{n}_{0}}(r)$ при t = 0.
а) В случае только хаотической активности клеток без участия направленных (нелокальных) сократительных взаимодействий и активных взаимодействий с внешней границей ($m = {{m}_{\Sigma }} = 0$) происходит нарастание начальных неоднородностей, не приводящее к формированию новой структуры с характерным размером, сравнимым с характерным размером рассматриваемого объекта. График распределения объемной плотности клеток в момент времени t = 4.05 при начальном распределении $n(r,0) = {{n}_{0}} + 0.03\sin (10\pi r)$ приведен на рис. 1 (кривая 1). Расчеты, проведенные при случайных возмущениях пространственно-однородного начального распределения, приводили к формированию неупорядоченных структур.
Рис. 1.
Распределения объемной плотности клеток при участии различных механизмов активных взаимодействий: (1) $m = {{m}_{\Sigma }} = 0$, $n(r) = {{n}_{0}} + 0.03\sin (10\pi \times r)$, $t = 4.05$; (2) $m \ne 0$ и ${{m}_{\Sigma }} \ne 0$, $n(r) = {{n}_{0}}$, $t = 2.7$; (3) $m \ne 0$ и ${{m}_{\Sigma }}$ = 0, $n(r) = {{n}_{0}}$, $t = 1.76$.
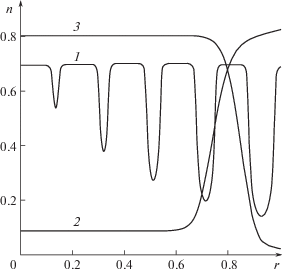
б) Участие нелокального механизма развития активных напряжений с учетом взаимодействия клеток с внешней границей ($m \ne 0$ и ${{m}_{\Sigma }} \ne 0$) приводит к формированию структуры, характеризуемой увеличением плотности клеток около внешней границы сфероида и формированием заполненной жидкостью полости в центральной части. График распределения объемной плотности клеток в момент времени $t = 2.7$ при однородном начальном распределении $n(r,0) = {{n}_{0}}$ приведен на рис. 1 (кривая 2). Распределение клеток, близкое к этому, получается при регулярных гармонических и случайных возмущениях однородного распределения вида n(r, 0) = n0 + + $0.001(2\;{\text{random(r)}}$ – 1). Функция ${\text{random(r)}}$ реализует значения равномерно распределенной на [0; 1] случайной величины.
в) Важную роль при формировании полости в центральной части клеточного сфероида играет взаимодействие клеток с внешней границей. Так, при $m \ne 0$ и ${{m}_{\Sigma }} = 0$ (участие нелокального механизма развития активных напряжений при отсутствии взаимодействия клеток с внешней границей), формирование новой структуры характеризуется скоплением клеток в центральной части сфероида – происходит “отрыв” клеток от внешней границы. График распределения плотности клеток в момент времени $t = 1.76$ при однородном начальном распределении $n(r,0) = {{n}_{0}}$ приведен на рис. 1 (кривая 3). Результат слабо зависит от того, используется ли гармоническое или случайное возмущение начального однородного распределения. Это имеет место и в последующих расчетах.
Увеличение плотности начального распределения приводит к тому, что, к примеру, при ${{n}_{0}} = 0.75$, стационарное решение становится устойчивым при хаотической активности клеток ($m = {{m}_{\Sigma }}$ = 0), а нелокальный механизм ($m \ne 0$ и ${{m}_{\Sigma }} \ne 0$) приводит лишь к незначительному возрастанию плотности клеток в направлении внешней границы, и заполненная жидкостью полость не формируется.
2. Далее рассмотрим результаты решения задачи об эволюции полости.
а) Исследуем влияние только хаотической активности клеток ($m = {{m}_{\Sigma }} = 0$) на эволюцию радиуса внутренней полости ${{R}_{{in}}}(t)$, сформировавшейся к начальному моменту времени. Графики зависимости ${{R}_{{in}}}(t)$ при различных начальных значениях радиуса полости ${{R}_{0}}$ и при начальной объемной плотности клеток $n(r,0) = {{n}_{0}}$ приведены на рис. 2а и рис. 2б, где ${{n}_{0}} = 0.5$ и ${{n}_{0}} = 0.75$ соответственно.
Рис. 2.
Графики зависимости ${{R}_{{in}}}(t)$ при $m = {{m}_{\Sigma }} = 0$, различных начальных значениях радиуса полости ${{R}_{0}}$ и при начальной объемной плотности клеток $n(r,0) = {{n}_{0}}$: (а) ${{n}_{0}} = 0.5$ и (б) ${{n}_{0}} = 0.75$ (пунктирная линия является горизонтальной асимптотой соответствующего графика). Распределения плотности клеток приближаются к одному и тому же пространственно-однородному распределению $n = {{n}_{\infty }}$.
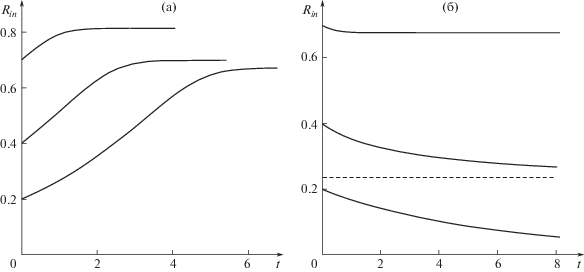
На графиках видно, что радиус внутренней полости стремится к некоторому постоянному значению. Вместе с тем распределения плотности клеток приближаются к одному и тому же пространственно-однородному распределению $n = {{n}_{\infty }}$. Стационарное значение ${{n}_{\infty }}$ может быть найдено из условия (2.7) при ${v} = 0$ и является наибольшим положительным корнем уравнения
(3.1)
$n\left( {\frac{{n(1 - n)}}{{\frac{{{{\mu }_{{adh}}}}}{{{{\mu }_{{mot}}}}}n + 1}} - \frac{1}{{{{p}_{0}}}}} \right) = 0$Первое слагаемое в скобках в (3.1) имеет колоколообразной вид при $n \in [0;\;1]$. Поэтому (3.1) имеет отличные от нуля корни не при любых значениях безразмерного параметра ${{p}_{0}}$. В случае “малых” давлений ${{p}_{0}}$, не превышающих критическое значение ${{p}_{{cr}}}$, при которых (3.1) имеет только одно решение n = 0, зависимости ${{R}_{{in}}}(t)$ являются убывающими функциями при любых ${{R}_{0}}$ и ${{n}_{0}}$. Таким образом, небольшое гидростатическое давление не может препятствовать радиальному перемещению клеток к центру. В этом случае давление $\Pi (n)$, создаваемое хаотической активностью клеток, приводит к схлопыванию полости. Уменьшение давления жидкости делает невозможным формирование неоднородной структуры и в изначально однородном клеточном агрегате в результате только хаотической клеточной активности.
Увеличение ${{p}_{0}}$ приводит к появлению двух положительных корней уравнения (3.1), где ${{n}_{\infty }}$ – больший корень уравнения. Таким образом, большие давления жидкости (${{p}_{0}} > {{p}_{{cr}}}$) приводят к увеличению радиуса полости при условии ${{n}_{0}} < {{n}_{\infty }}$ в результате только хаотической активности клеток, и уменьшению радиуса полости при ${{n}_{0}} > {{n}_{\infty }}$.
При базовом наборе параметров получим ${{n}_{\infty }} \approx 0.71$ и ${{p}_{{cr}}} \approx 5.83$. Тогда, при начальной плотности клеток ${{n}_{0}} = 0.5$ (${{p}_{0}} > {{p}_{{cr}}}$, ${{n}_{0}} < {{n}_{\infty }}$) радиус полости увеличивается под действием гидростатического давления в ней (рис. 2а), что приводит в результате к увеличению средней плотности клеток. В случае ${{n}_{0}} = 0.75$ (${{p}_{0}} > {{p}_{{cr}}}$, ${{n}_{0}} > {{n}_{\infty }}$) доминирующее влияние на изменение радиуса полости оказывает хаотическая подвижность клеток, характеризуемая давлением $\Pi (n) = n{\text{/}}(1 - n)$. С увеличением плотности клеток $\Pi (n)$ возрастает. Это приводит к тому, что давление жидкости в полости не может сдерживать движение фронта клеток к центру. Радиус полости уменьшается (рис. 2б), и, следовательно, уменьшается средняя плотность клеток.
Во всех случаях (и при участии нелокального механизма) увеличение p0 способствует увеличению скорости роста функции ${{R}_{{in}}}(t)$ и увеличению ее стационарного значения.
б) Исследуем влияние нелокального механизма активных взаимодействий между клетками и влияние взаимодействия клеток с внешней границей ($m \ne 0$ и ${{m}_{\Sigma }} \ne 0$) на эволюцию радиуса внутренней полости ${{R}_{{in}}}(t)$.
Вычисления, выполненные при базовом наборе параметров(${{p}_{0}} > {{p}_{{cr}}}$ и ${{n}_{0}} < {{n}_{\infty }}$), показали, что графики зависимости ${{R}_{{in}}}(t)$ при различных начальных значениях радиуса полости ${{R}_{0}}$ имеют вид, качественно сходный с графиками на рис. 2а. Однако значительно уменьшается характерное время развития полости (по сравнению с только хаотическими клеточными взаимодействиями): графики ${{R}_{{in}}}(t)$ быстрее приближаются к своим стационарным значениям. При этом стационарные значения радиуса полости увеличиваются незначительно (на 3–8%).
Одним из основных результатов участия нелокального активного механизма межклеточных взаимодействий является то, что он приводит к развитию полости и при таких значениях начальной плотности клеток n0 и давлениях жидкости p0, при которых хаотическая клеточная активность рост полости не обеспечивает. Участие нелокального активного механизма приводит к увеличению радиуса полости при любых ${{R}_{0}}$ в случае плотной начальной упаковки клеток и высокого давления жидкости (${{p}_{0}} > {{p}_{{cr}}}$, ${{n}_{0}} > {{n}_{\infty }}$). Так, при ${{n}_{0}} = 0.75$ графики зависимости ${{R}_{{in}}}(t)$ имеют вид, качественно сходный с графиками на рис. 2а, в отличие от графиков, полученных при том же наборе параметров при участии только хаотической клеточной активности (рис. 2б). Однако стационарные (финальные) значения размеров полости оказываются значительно меньшими, чем при рыхлой начальной упаковке клеток (${{n}_{0}} = 0.5$).
Уменьшение давления при плотной начальной упаковке клеток (${{p}_{0}} < {{p}_{{cr}}}$, ${{n}_{0}} > {{n}_{\infty }}$) приводит к остановке роста полости. При ${{p}_{0}} = 5$ и ${{n}_{0}} = 0.75$ ее радиус очень медленно уменьшается. Однако при рыхлой упаковке клеток (${{p}_{0}} < {{p}_{{cr}}}$, ${{n}_{0}} < {{n}_{\infty }}$) радиус полости будет расти при любых ${{R}_{0}}$, в отличие от графиков, полученных при таком же наборе параметров (${{p}_{0}} = 5$ и ${{n}_{0}} = 0.5$) в случае участия только хаотической клеточной активности.
Представленные выше результаты, относящиеся к росту или схлопыванию начальной полости в зависимости от давления жидкости и плотности начального распределения клеток, схематически представлены в табл. 1.
Таблица 1
| Хаотический механизм активных межклеточных взаимодействий $m = {{m}_{\Sigma }} = 0$ | Нелокальный механизм активных межклеточных взаимодействий $m \ne 0$, ${{m}_{\Sigma }} \ne 0$ | ||
|---|---|---|---|
| ${{p}_{0}} > {{p}_{{cr}}}$, ${{n}_{0}} < {{n}_{\infty }}$ | ${{p}_{0}} > {{p}_{{cr}}}$, ${{n}_{0}} > {{n}_{\infty }}$ | ${{p}_{0}} > {{p}_{{cr}}}$, ${{n}_{0}} < {{n}_{\infty }}$ | ${{p}_{0}} > {{p}_{{cr}}}$, ${{n}_{0}} > {{n}_{\infty }}$ |
| + | – | + | + |
| ${{p}_{0}} < {{p}_{{cr}}}$, ${{n}_{0}} < {{n}_{\infty }}$ | ${{p}_{0}} < {{p}_{{cr}}}$, ${{n}_{0}} > {{n}_{\infty }}$ | ${{p}_{0}} < {{p}_{{cr}}}$, ${{n}_{0}} < {{n}_{\infty }}$ | ${{p}_{0}} < {{p}_{{cr}}}$, ${{n}_{0}} > {{n}_{\infty }}$ |
| – | – | + | – |
| Примечание. Знаком (+) отмечено увеличение, а знаком (–) – схлопывание начальной полости в зависимости от давления жидкости ${{p}_{0}}$ и плотности начального распределения клеток ${{n}_{0}}$ | |||
в) Нелокальный механизм активных межклеточных взаимодействий при отсутствии взаимодействия клеток с внешней границей ($m \ne 0$ и ${{m}_{\Sigma }} = 0$) приводит к росту полости не при любых ее начальных размерах. Этот результат получен численно при всех используемых в расчетах (приведенных в табл. 1) значениях ${{p}_{0}}$ и ${{n}_{0}}$. Графики зависимости ${{R}_{i}}_{n}(t)$ при $m \ne 0$, ${{m}_{\Sigma }} = 0$ и различных начальных значениях радиуса полости ${{R}_{0}}$ при начальной объемной плотности клеток $n(r,0) = 0.5$ (${{p}_{0}} > {{p}_{{cr}}}$) приведены на рис. 3.
Рис. 3.
Графики зависимости ${{R}_{{in}}}(t)$ при $m \ne 0$, ${{m}_{\Sigma }} = 0$, различных начальных значениях радиуса полости ${{R}_{0}}$ и при начальной объемной плотности клеток $n(r,0) = 0.5$.
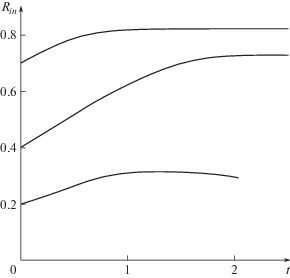
На графике видно, что полость с малым начальным радиусом (критическое значение ${{R}_{0}}$ зависит от ${{p}_{0}}$ и ${{n}_{0}}$) через некоторое время начинает схлопываться (рис. 3, нижняя кривая), хотя только хаотическая клеточная активность приводит к развитию полости при этих значениях ${{p}_{0}}$ и ${{n}_{0}}$. Эволюция полости малого начального радиуса, при отсутствии взаимодействия клеток с внешней границей, сопровождается уменьшением плотности клеток около внешней границы в результате нелокальных межклеточных взаимодействий. Это приводит к “отрыву” клеток от нее, и распределение клеток по толщине слоя принимает вид, аналогичный изображенному на рис. 1 (кривая 3). Отрыв клеток от внешней границы приводит к невозможности продолжения численных расчетов для нижней кривой на рис. 3 в рамках постановки задачи с неподвижной внешней границей. В полостях большего начального радиуса давление жидкости прижимает клетки к внешней границе, и развитие полости происходит лишь незначительно медленнее, чем при взаимодействии клеток с внешней границей ($m \ne 0$ и ${{m}_{\Sigma }} \ne 0$).
ЗАКЛЮЧЕНИЕ
Данная работа посвящена изучению свойств биологической клеточной среды как механической системы. Решена задача об эволюции радиуса внутренней полости, которая сформировалась в клеточном сфероиде к начальному моменту времени. Используется разработанная ранее математическая модель биологической ткани, описывающая один из фундаментальных биологических механизмов – развитие активных механических взаимодействий клеток между собой и с окружающими их внеклеточными компонентами биологической среды. Биологическая ткань рассматривается как трехфазная сплошная среда, состоящая из клеток, внеклеточной жидкости и дополнительной фазы, отвечающей за активное силовое взаимодействие между клетками. От разработанной нами ранее модели [3, 4] используемая в настоящей работе модель отличается видом уравнения для активных напряжений, развивающихся в результате активных межклеточных взаимодействий. В работе используется интегральная форма определяющих соотношений для активных напряжений, которая учитывает как нелокальные направленные взаимодействия клеток между собой, так и активные взаимодействия клеток с внешней границей. Это позволяет формулировать постановки задач с различными условиями для активных напряжений на внешней границе.
Решение задачи описывает движение фронта, отделяющего в начальный момент времени клеточную среду от жидкости. Исследовано влияние различных механизмов активных межклеточных взаимодействий на эволюцию радиуса полости и распределение объемной плотности клеток.
В результате решения получено, что в ряде случаев (характеризуемых давлением жидкости и плотностью начального распределения клеток) только хаотической активности клеток оказывается вполне достаточно для увеличения радиуса внутренней полости. В других случаях развитие полости оказывается невозможным без участия нелокального механизма активных взаимодействий между клетками и взаимодействия клеток с внешней границей. Нелокальный механизм активных межклеточных взаимодействий при отсутствии взаимодействия клеток с внешней границей приводит к росту полости не при любых начальных размерах полости. Эволюция полости достаточно малого начального радиуса сопровождается “отрывом” клеток от внешней границы в результате нелокальных межклеточных взаимодействий.
Постановка и решение задачи дают более полное понимание роли возможных механизмов межклеточных взаимодействий в формообразовании при раннем эмбриональном развитии.
Работа поддержана РФФИ (проект № 20-01-00329) и Госпрограммой АААА-А19-119012990119-3.
Список литературы
Белоусов Л.В., Логвенков С.А., Штейн А.А. Математическая модель активной биологической сплошной среды с учетом деформаций и переупаковки клеток // Изв. РАН. МЖГ. 2015. № 1. С. 3–14.
Stein A.A., Logvenkov S.A., Volodyaev I.V. Continuum modeling of mechano-dependent reactions in tissues composed of mechanically active cells // Biosystems. 2018. V. 173. P. 225–234.
Логвенков С.А., Штейн А.А.Математическая модель пространственной самоорганизации в механически активной клеточной среде // Биофизика. 2017. Т. 62. № 6. С. 1123–1133.
Логвенков С.А. Математическая модель биологической среды с учетом активных взаимодействий и взаимных перемещений составляющих ее клеток // Изв. РАН. МЖГ. 2018. № 5. С. 3–16.
Gilbert S.F. Developmental Biology, 6th edition // Sunderland, Mass.: Sinauer Associates, 2000, 749 p.
Нигматулин Р.И. Основы механики гетерогенных сред. М: Наука, 1978. 336 с.
Drew D.A., Segel L.A. Averaged equations for two-phase flows // Stud. Appl. Math. 1971. V. 50. № 3. P. 205–231.
Belousov L.V. Morphomechanics of Development // Cham: Springer International Publishing: Imprint: Springer, 2015. 195 p.
Forgacs G., Foty R.A., Shafrir Y., Steinberg M.S. Viscoelastic properties of living embryonic tissues: a quantitative study // Biophys. J. 1998. V. 74. P. 2227–2234.
Stirbat T.V., Mgharbel A., Bodennec S. et al. Fine tuning of tissues viscosity and surface tension through contractility suggests a new role for a-catenin // PLoS One. 2013. V. 8. № 2. e52554.
Gordon R., Goel N.S., Steinberg M.S., Wiseman L.L. Arheological mechanism sufficient to explain the kinetics of cell sorting // J. Theor. Biol. 1972. V. 37. P. 43–73.
Lubkin S.R., Jackson T. Multiphase Mechanics of Capsule Formation in Tumors // J. Biomech. Eng. 2002. V. 124. P. 237–243.
Boucher Y., Brekken C., Netti P.A., Baxter L.T., Jain R.K. Intratumoral infusion of fluid: estimation of hydraulic conductivity and implications for the delivery of therapeutic agents // British J. Cancer. 1998. V. 78. № 11. P. 1442–1448.
Burke R.D., Myers R.L., Sexton T.L., Jackson C. Cell Movements during the initial phase of gastrulation in the sea urchin embryo // Dev. Biol. 1991. V. 146. № 2. P. 542–557.
Самарский А.А. Теория разностных схем // М.: Наука, 1977. 656 с.
Самарский А.А., Вабищевич П.Н. Разностные схемы для уравнения переноса // Диф. уравн. 1998. Т. 34. № 12. С. 1675–1685.
Дополнительные материалы отсутствуют.
Инструменты
Известия РАН. Механика жидкости и газа


