Известия РАН. Механика жидкости и газа, 2019, № 4, стр. 33-41

ОСОБЕННОСТИ ТЕЧЕНИЯ В ГИПЕРЗВУКОВОМ ПОГРАНИЧНОМ СЛОЕ В ОКРЕСТНОСТИ ПЛОСКОСТИ СИММЕТРИИ ПЛОСКОГО КРЫЛА С ИЗЛОМОМ ПО ПЕРЕДНЕЙ КРОМКЕ

Г. Н. Дудин^a, b, А. В. Ледовский^a, b, *

^a Центральный аэрогидродинамический институт им. Н.Е. Жуковского
Московская обл., Жуковский, Россия

^b Московский физико-технический институт (государственный университет)
Московская обл., Долгопрудный, Россия

^* E-mail: avledovsky@gmail.com

Поступила в редакцию 04.10.2018
После доработки 19.10.2018
Принята к публикации 19.10.2018

DOI: 10.1134/S0568528119030034

Полный текст (PDF)

Аннотация

Исследовано течение в пространственном ламинарном пограничном слое в окрестности плоскости симметрии полубесконечного плоского крыла с изломом по передней кромке при сильном взаимодействии с внешним гиперзвуковым потоком. Выполнено асимптотическое разложение функций течения в степенные ряды по угловой координате в окрестности плоскости симметрии. Сформулирована и решена соответствующая краевая задача для первых членов разложения. Показана возможность существования нескольких решений в окрестности плоскости симметрии. Рассмотрено влияние угла стреловидности на особенности течения.

Ключевые слова: пограничный слой, треугольное крыло, сильное гиперзвуковое взаимодействие, асимптотические методы

Первые теоретические исследования течения в гиперзвуковом трехмерном пограничном слое на режиме сильного вязко-невязкого взаимодействия были выполнены в статьях [1, 2]. Пространственные течения в гиперзвуковом пограничном слое на плоском треугольном крыле впервые были исследованы в статье [3], в которой была показана возможность приведения задачи к автомодельной. Исследованию особенностей течения в окрестности плоскости симметрии на треугольном крыле была посвящена статья [4], в которой была показана возможность возникновения области невязкого течения и локальной неприменимости уравнений пограничного слоя. При этом для гиперзвукового пограничного слоя с сильным взаимодействием с внешним потоком решение оказывается неединственным [5]. В [6] выполнены исследования течения вблизи плоскости симметрии треугольного крыла с помощью асимптотических разложений и показана неединственность решения краевой задачи. В настоящей работе с использованием цилиндрической системы координат впервые построены решения в плоскости симметрии крыла с обратной стреловидностью передней кромки [7] и показана возможность существования неединственного решения.

1. ПОСТАНОВКА ЗАДАЧИ

Рассматривается симметричное течение в пограничном слое на полубесконечном плоском крыле с изломом передней кромки в плане на режиме сильного гиперзвукового вязко-невязкого взаимодействия. Набегающий поток имеет скорость ${{U}_{\infty }}$. Газ рассматривается совершенным с постоянным отношением удельных теплоемкостей γ = C_p/${{C}_{\text{v}}}$. Динамический коэффициент вязкости задается линейно зависящим от температуры: ${{{\mu }}^{0}}{\text{/}}{{{\mu }}_{\infty }} = {{C}_{\infty }}{{T}^{0}}{\text{/}}{{T}_{\infty }}$. Верхний индекс “0” означает размерные величины, а нижний индекс ∞ соответствует параметрам набегающего потока. Крыло находится под нулевым углом атаки и имеет постоянную температуру поверхности T_w. Задача рассматривается в цилиндрической системе координат (r⁰, θ⁰, y⁰), начало которой расположено в точке излома передней кромки, а ось y⁰ – по нормали к поверхности. Форма крыла определяется углом Θ (рис. 1), который может меняться в пределах 0° < Θ < 180°. Угол скольжения отсутствует (задача симметричная).

Рис. 1.

Схема крыла и система координат.

Рассматривается асимптотический гиперзвуковой предел: ${\text{M}} \to \infty $, ${{p}_{\infty }} \to 0$, ${{a}_{\infty }} \to 0$, ${{T}_{\infty }} \to 0$ [3]. В этом случае распределение давления на крыле можно определить с большой точностью по формуле касательного клина для режима сильного взаимодействия [7]

${{p}^{0}} = \frac{{\gamma + 1}}{2}{{{\rho }}_{\infty }}U_{\infty }^{2}{{\left[ {\cos ({{{\theta }}^{0}})\frac{{\partial {\delta }_{e}^{0}}}{{\partial {{r}^{0}}}} - \sin ({{{\theta }}^{0}})\frac{1}{{{{r}^{0}}}}\frac{{\partial {\delta }_{e}^{0}}}{{\partial {{{\theta }}^{0}}}}} \right]}^{2}}$

В соответствии с оценками для ламинарного пограничного слоя в гиперзвуковом потоке вводятся безразмерные переменные

${{r}^{0}} = Lr,\quad {{y}^{0}} = L\delta y,\quad {{{\theta }}^{0}} = \Theta {\theta }$

${{u}^{0}} = {{U}_{\infty }}u,\quad {{\text{v}}^{0}} = {{U}_{\infty }}\frac{\delta }{\Theta }V,\quad {{w}^{0}} = {{U}_{\infty }}w,\quad {{H}^{0}} = \frac{{U_{\infty }^{2}}}{2}H$

${{p}^{0}} = {{\rho }_{\infty }}U_{\infty }^{2}{{\delta }^{2}}p,\quad \delta _{e}^{0} = L\delta {{\delta }_{e}},\quad {{\rho }^{0}} = {{\rho }_{\infty }}{{\delta }^{2}}\rho ,\quad {{\mu }^{0}} = {{\mu }_{0}}\mu ,\quad \delta = \sqrt[4]{{\frac{\Theta }{{{{{\operatorname{Re} }}_{0}}}}}},\quad {{\operatorname{Re} }_{0}} = \frac{{{{\rho }_{\infty }}{{U}_{\infty }}L}}{{{{\mu }_{0}}}}$

Здесь L – характерный размер крыла, который при рассмотрении полубесконечного крыла не входит в конечные результаты, ${{\mu }_{0}}$ – динамический коэффициент вязкости при температуре торможения T₀, δ – характерная безразмерная толщина пограничного слоя, Re₀ – число Рейнольдса.

В уравнения пограничного слоя вводятся новые переменные с использованием преобразования Дородницына

(1.1)

$\lambda = \int\limits_0^y {\rho dy} ,\quad {{\text{v}}_{\delta }} = \rho V + \Theta u\frac{{\partial \lambda }}{{\partial r}} + \frac{w}{r}\frac{{\partial \lambda }}{{\partial \theta }}$

Выражение для толщины вытеснения пограничного слоя с учетом (1.1) принимает вид

${{\delta }_{e}} = \frac{{\gamma - 1}}{{2\gamma p}}\int\limits_0^\infty {(H - {{u}^{2}} - {{w}^{2}})} d\lambda $

При рассмотрении обтекания полубесконечных треугольных на режиме сильного вязко-невязкого взаимодействия краевая задача может быть сведена к автомодельной, если ввести соответствующие “автомодельные” переменные, которые позволяют учесть особенности поведения функций течения в окрестности точки излома (r = 0)

$\lambda * = {{r}^{{ - 1/4}}}\lambda ,\quad \text{v}* = {{\text{v}}_{\delta }}{{r}^{{3/4}}} + \Theta ru\frac{{\partial \lambda {\text{*}}}}{{\partial r}}$

$p = {{r}^{{ - 1/2}}}p{\text{*}}(r,\theta ),\quad \rho = {{r}^{{ - 1/2}}}\rho {\text{*}}(r,\theta ,\lambda *),\quad {{\delta }_{e}} = {{r}^{{3/4}}}\delta _{e}^{*}(r,\theta )$

Для упрощения записи выполнена замена

$N = {{(H - {{u}^{2}} - {{w}^{2}})}^{{\omega - 1}}} = {{\left( {\frac{{2\gamma }}{{\gamma - 1}}\frac{{p{\text{*}}}}{{\rho {\text{*}}}}} \right)}^{{\omega - 1}}} = \frac{\mu }{{H - {{u}^{2}} - {{w}^{2}}}} = \frac{{\mu \rho {\text{*}}}}{{p{\text{*}}}}\frac{{\gamma - 1}}{{2\gamma }},$

где ω – показатель степени в степенной зависимости коэффициента вязкости от температуры ${\mu }\sim {{T}^{{\omega }}}$. В случае линейной зависимости, то есть при ω = 1, получаем N = 1.

Для учета поведения функций течения вблизи передних кромок выполняются следующие преобразования:

${{\eta }_{*}} = \lambda {\text{*}}{{\left( {\frac{{2\gamma }}{{\gamma - 1}}\sqrt {1 - {{\theta }^{2}}} } \right)}^{{ - 1/2}}},\quad {{\text{v}}_{*}}({{\eta }_{*}},\theta ) = \text{v}{\text{*}}\frac{{{{{(1 - {{\theta }^{2}})}}^{{3/4}}}}}{{p{\text{*}}}}\sqrt {\frac{{\gamma - 1}}{{2\gamma }}} + (1 - {{\theta }^{2}})\frac{w}{{p{\text{*}}}}\frac{{\partial {{\eta }_{*}}}}{{\partial \theta }}$

${{p}_{*}} = {{(1 - {{\theta }^{2}})}^{{1/2}}}p{\text{*}}(r,\theta ),\quad \Delta = {{(1 - {{\theta }^{2}})}^{{ - 3/4}}}\delta _{e}^{*}(r,\theta )$

В результате этих преобразований система уравнений нестационарного пространственного пограничного слоя и граничные условия принимают вид

(1.3)

$\frac{{\partial {{\text{v}}_{*}}}}{{\partial {{\eta }_{*}}}} - \frac{{w\theta }}{{2{{p}_{*}}}} + \frac{{1 - {{\theta }^{2}}}}{{{{p}_{*}}}}\left( {\Theta r\frac{{\partial u}}{{\partial r}} + \frac{{\partial w}}{{\partial \theta }} + \frac{5}{4}\Theta u} \right) = 0$

(1.4)

$\frac{{1 - {{\theta }^{2}}}}{{{{p}_{*}}}}\left( {\Theta ru\frac{{\partial u}}{{\partial r}} + w\frac{{\partial u}}{{\partial \theta }} - \Theta {{w}^{2}}} \right) + {{\text{v}}_{*}}\frac{{\partial u}}{{\partial {{\eta }_{*}}}} = \Theta \frac{{1 - {{\theta }^{2}}}}{{{{p}_{*}}}}\frac{{\gamma - 1}}{{2\gamma }}(H - {{u}^{2}} - {{w}^{2}})\left( {\frac{1}{2} - \frac{r}{{{{p}_{*}}}}\frac{{\partial {{p}_{*}}}}{{\partial r}}} \right) + \frac{{{{\partial }^{2}}u}}{{\partial \eta _{*}^{2}}}$

(1.5)

$\frac{{1 - {{\theta }^{2}}}}{{{{p}_{*}}}}\left( {\Theta ru\frac{{\partial w}}{{\partial r}} + w\frac{{\partial w}}{{\partial \theta }} + \Theta uw} \right) + {{\text{v}}_{*}}\frac{{\partial w}}{{\partial {{\eta }_{*}}}} = - \frac{{\gamma - 1}}{{2\gamma }}(H - {{u}^{2}} - {{w}^{2}})\left( {\frac{\theta }{{{{p}_{*}}}} + \frac{{1 - {{\theta }^{2}}}}{{p_{*}^{2}}}\frac{{\partial {{p}_{*}}}}{{\partial \theta }}} \right) + \frac{{{{\partial }^{2}}w}}{{\partial \eta _{*}^{2}}}$

(1.6)

$\frac{{1 - {{\theta }^{2}}}}{{{{p}_{*}}}}\left( {\Theta ru\frac{{\partial H}}{{\partial r}} + w\frac{{\partial H}}{{\partial \theta }}} \right) + {{\text{v}}_{*}}\frac{{\partial H}}{{\partial {{\eta }_{*}}}} = \frac{1}{\sigma }\frac{{{{\partial }^{2}}H}}{{\partial \eta _{*}^{2}}} + \left( {1 - \frac{1}{\sigma }} \right)\frac{{{{\partial }^{2}}({{u}^{2}} + {{w}^{2}})}}{{\partial \eta _{*}^{2}}}$

(1.7)

$\Delta = \frac{1}{{{{p}_{*}}}}\sqrt {\frac{{\gamma - 1}}{{2\gamma }}} \int\limits_0^\infty {(H - {{u}^{2}} - {{w}^{2}})} d{{\eta }_{*}}$

(1.8)

${{p}_{*}} = \frac{{\gamma + 1}}{2}{{\left\{ {(1 - {{\theta }^{2}})\left( {\frac{3}{4}\Delta + r\frac{{\partial \Delta }}{{\partial r}}} \right)\cos (\Theta \theta ) + \frac{1}{\Theta }\sin (\Theta \theta )\left( {\frac{3}{2}\theta \Delta - (1 - {{\theta }^{2}})\frac{{\partial \Delta }}{{\partial \theta }}} \right)} \right\}}^{2}}$

${{\eta }_{*}} = 0$: $u = {{\text{v}}_{*}} = w = 0$, $H = {{H}_{w}}$

${{\eta }_{*}} \to \infty $: $u \to \cos (\Theta \theta )$, $w \to - \sin (\Theta \theta )$, $H \to 1$

Здесь σ – число Прандтля. Следует отметить также, что в систему уравнений (1.3)–(1.8) входят производные ${{{{\partial }^{2}}{{\Delta }_{e}}} \mathord{\left/ {\vphantom {{{{\partial }^{2}}{{\Delta }_{e}}} {\partial {{r}^{2}}}}} \right. \kern-0em} {\partial {{r}^{2}}}}$ и ${{{{\partial }^{2}}{{\Delta }_{e}}} \mathord{\left/ {\vphantom {{{{\partial }^{2}}{{\Delta }_{e}}} {\partial {{{\theta }}^{2}}}}} \right. \kern-0em} {\partial {{{\theta }}^{2}}}}$, и, следовательно, эта система уже не относится к параболическому типу и может допускать распространение возмущений против потока. В точке излома r = 0, и поэтому для полубесконечного крыла система вырождается в автомодельную с функциями течения, зависящими только от переменных ${{{\eta }}_{*}}$ и ${\theta }$.

Для исследования поведения функций течения в пространственном пограничном слое в окрестности плоскости симметрии оказывается удобным дополнительно ввести новые переменные

${\eta } = {{{\eta }}_{*}}p_{*}^{{ - 1/2}},{\text{ }}\text{v} = {{\text{v}}_{*}}p_{*}^{{1/2}} - \frac{1}{2}w(1 - {{\theta }^{2}})\frac{{\eta }}{{{{p}_{*}}}}\frac{{d{{p}_{*}}}}{{d\theta }}$

При таком преобразовании в уравнениях переноса и неразрывности в системе (1.3)–(1.8) давление в знаменателе останется только при производной от индуцированного давления.

В результате получается система уравнений

(1.9)

$\frac{{\partial \text{v}}}{{\partial \eta }} - \frac{{w\theta }}{2} + (1 - {{\theta }^{2}})\left( {\frac{{\partial w}}{{\partial \theta }} + \frac{w}{{2{{p}_{*}}}}\frac{{d{{p}_{*}}}}{{d\theta }} + \frac{5}{4}\Theta u} \right) = 0$

(1.10)

$q\frac{{\partial u}}{{\partial \theta }} + \text{v}\frac{{\partial u}}{{\partial \eta }} - q\Theta w = \Theta (1 - {{\theta }^{2}})\frac{{\gamma - 1}}{{4\gamma }}(H - {{u}^{2}} - {{w}^{2}}) + \frac{{{{\partial }^{2}}u}}{{\partial {{\eta }^{2}}}}$

(1.11)

$q\frac{{\partial w}}{{\partial \theta }} + \text{v}\frac{{\partial w}}{{\partial \eta }} + q\Theta u = - \frac{{\gamma - 1}}{{2\gamma }}(H - {{u}^{2}} - {{w}^{2}})\left( {\theta + \frac{{1 - {{\theta }^{2}}}}{{{{p}_{*}}}}\frac{{d{{p}_{*}}}}{{d\theta }}} \right) + \frac{{{{\partial }^{2}}w}}{{\partial {{\eta }^{2}}}}$

(1.12)

$q\frac{{\partial H}}{{\partial \theta }} + \text{v}\frac{{\partial H}}{{\partial \eta }} = \frac{1}{\sigma }\frac{{{{\partial }^{2}}H}}{{\partial {{\eta }^{2}}}} + \left( {1 - \frac{1}{\sigma }} \right)\frac{{{{\partial }^{2}}({{u}^{2}} + {{w}^{2}})}}{{\partial {{\eta }^{2}}}}$,

(1.13)

${{p}_{*}} = \frac{{\gamma + 1}}{2}{{\left\{ {\frac{3}{4}\Delta (1 - {{\theta }^{2}})\cos (\Theta \theta ) + \frac{1}{\Theta }\sin (\Theta \theta )\left( {\frac{3}{2}\theta \Delta - (1 - {{\theta }^{2}})\frac{{\partial \Delta }}{{\partial \theta }}} \right)} \right\}}^{2}}$

(1.14)

$\Delta = \frac{1}{{\sqrt {{{p}_{*}}} }}\sqrt {\frac{{\gamma - 1}}{{2\gamma }}} \int\limits_0^\infty {(H - {{u}^{2}} - {{w}^{2}})} d\eta .$

Граничные условия

(1.15)

$\eta = 0$: $u = \text{v} = w = 0$, $H = {{H}_{w}}$; $\eta \to \infty $: $u \to \cos (\Theta \theta )$, $w \to - \sin (\Theta \theta )$, $H \to 1$

2. РАЗЛОЖЕНИЕ ФУНКЦИЙ ТЕЧЕНИЯ В ОКРЕСТНОСТИ ПЛОСКОСТИ СИММЕТРИИ

Для исследования поведения функций течения в окрестности плоскости симметрии предполагается справедливость следующих разложений по угловой координате θ для функций течения

$u(\eta ,\theta ) = {{u}_{0}}(\eta ) + {{u}_{2}}(\eta ){{\theta }^{2}} + O({{\theta }^{4}})$

$\text{v}(\eta ,\theta ) = {{\text{v}}_{0}}(\eta ) + {{\text{v}}_{2}}(\eta ){{\theta }^{2}} + O({{\theta }^{4}})$

$w(\eta ,\theta ) = {{w}_{1}}(\eta )\theta + {{w}_{3}}(\eta ){{\theta }^{3}} + O({{\theta }^{5}})$

$H(\eta ,\theta ) = {{H}_{0}}(\eta ) + {{H}_{2}}(\eta ){{\theta }^{2}} + O({{\theta }^{4}})$

${{p}_{*}}(\theta ) = {{p}_{0}} + {{p}_{2}}{{\theta }^{2}} + {{p}_{4}}{{\theta }^{4}} + O({{\theta }^{6}})$

$\Delta (\theta ) = {{\Delta }_{0}} + {{\Delta }_{2}}{{\theta }^{2}} + O({{\theta }^{4}})$

При подставлении разложения в систему уравнений (1.9)–(1.14) с граничными условиями (1.15) получается следующая краевая задача (автомодельная) для членов нулевого порядка по $\theta $:

$\frac{{d{{\text{v}}_{0}}}}{{d\eta }} + {{w}_{1}} + \frac{5}{4}\Theta {{u}_{0}} = 0$

${{\text{v}}_{0}}\frac{{d{{u}_{0}}}}{{d\eta }} = \Theta \frac{{\gamma - 1}}{{4\gamma }}({{H}_{0}} - u_{0}^{2}) + \frac{{{{d}^{2}}{{u}_{0}}}}{{d{{\eta }^{2}}}}$

(2.1)

${{\text{v}}_{0}}\frac{{d{{w}_{1}}}}{{d\eta }} + {{w}_{1}}({{w}_{1}} + \Theta {{u}_{0}}) = - \frac{{\gamma - 1}}{{2\gamma }}({{H}_{0}} - u_{0}^{2})\left( {1 + \frac{{2{{p}_{2}}}}{{{{p}_{0}}}}} \right) + \frac{{{{d}^{2}}{{w}_{1}}}}{{d{{\eta }^{2}}}}$

${{\text{v}}_{0}}\frac{{d{{H}_{0}}}}{{d\eta }} = \frac{1}{\sigma }\frac{{{{d}^{2}}{{H}_{0}}}}{{d{{\eta }^{2}}}} + \left( {1 - \frac{1}{\sigma }} \right)\frac{{{{d}^{2}}u_{0}^{2}}}{{d{{\eta }^{2}}}}$,

${{p}_{0}} = \frac{3}{8}\sqrt {\frac{{(\gamma + 1)(\gamma - 1)}}{\gamma }} \int\limits_0^\infty {({{H}_{0}} - u_{0}^{2})} d\eta ,\quad {{\Delta }_{0}} = \frac{4}{3}\sqrt {\frac{{2{{p}_{0}}}}{{\gamma + 1}}} .$

Граничные условия

$\eta = 0$: ${{u}_{0}} = {{\text{v}}_{0}} = {{w}_{1}} = 0$, ${{H}_{0}} = {{H}_{w}}$; $\eta \to \infty $: ${{u}_{0}} \to 1$, ${{w}_{1}} \to - \Theta $, ${{H}_{0}} \to 1$

Для правильного задания граничных условий на внешней границе пограничного слоя необходимо исследовать асимптотическое поведение функций течений при $\eta \to \infty $. Из уравнения неразрывности в системе (2.1) можно получить оценки для функции v₀

$\frac{{d{{\text{v}}_{0}}}}{{d\eta }} = - {{w}_{1}} - \frac{5}{4}\Theta {{u}_{0}}\mathop \to \limits_{\eta \to \infty } \Theta - \frac{5}{4}\Theta = - 0.25\Theta $

${{\text{v}}_{0}}\mathop \to \limits_{\eta \to \infty } - 0.25\Theta \eta + {\text{const}}$

Рассматривается уравнение для продольного импульса

$u_{0}^{{''}} - {{\text{v}}_{0}}u_{0}^{'} + \Theta \frac{{\gamma - 1}}{{4\gamma }}({{H}_{0}} - u_{0}^{2}) = 0$

Здесь штрих означает производную по η. Далее выполняется замена $u = 1 - {{u}_{0}}$

$(1 - u){\text{''}} + {{\text{v}}_{0}}(1 - u){\text{'}} + \Theta \frac{{\gamma - 1}}{{4\gamma }}u(1 + {{u}_{0}}) = 0$

$u{\text{''}} - {{\text{v}}_{0}}u{\text{'}} - \lambda u(1 + {{u}_{0}}) = 0$, где $\lambda = \Theta (\gamma - 1){\text{/}}4\gamma $

Второй член в последнем уравнении можно исключить с помощью замены

$u = \xi \times \exp \left( {\int\limits_0^\eta {\frac{{{{\text{v}}_{0}}(s)}}{2}ds} } \right)$

Тогда уравнение принимает вид

$\xi {\text{''}} - q(\eta )\xi = 0,\quad q(\eta ) = \frac{{\text{v}_{0}^{2}}}{4} - \frac{{\text{v}_{0}^{'}}}{2} + \lambda (1 + {{u}_{0}})$

В соответствии с [8] это уравнение имеет асимптотику

$\xi \sim {{q}^{{ - 1/4}}}\exp \left( {\int\limits_0^\eta {{{q}^{{1/2}}}(s)ds} } \right)$

${{q}^{{ - 1/4}}}(\eta )\sim \text{v}_{0}^{{ - 1/2}}\sim {{\eta }^{{ - 1/2}}},\quad \eta \to \infty $

${{q}^{{1/2}}}(\eta ) = \frac{1}{2}{{\text{v}}_{0}} - \frac{{\text{v}_{0}^{'}}}{{2{{\text{v}}_{0}}}} + \frac{{2\lambda }}{{{{\text{v}}_{0}}}} + O\left( {\frac{1}{{{{\eta }^{3}}}}} \right)$

$\int\limits_0^\eta {\frac{{{{\text{v}}_{0}}(s)}}{2}ds} = \frac{1}{2}\int\limits_0^\eta {{{\text{v}}_{0}}d\eta } - \frac{1}{2}\ln {{\text{v}}_{0}} + \int\limits_0^\eta {\frac{{2\lambda }}{{{{\text{v}}_{0}}}}d\eta } + O\left( 1 \right)$

Тогда

(2.2)

${{u}_{0}} = 1 - \xi \exp \left( {\int\limits_0^\eta {\frac{{{{\text{v}}_{0}}}}{2}ds} } \right)\sim 1 - c{{\eta }^{{ - 1/2}}}\exp \left( {\frac{1}{2}\int\limits_0^\eta {{{\text{v}}_{0}}ds} - \frac{1}{2}} \right)\sim 1 - c{{\eta }^{{ - 1/2}}}\exp \left( { - \frac{1}{8}\Theta {{\eta }^{2}} - \frac{1}{2}} \right),\quad \eta \to \infty $

В (2.2) входит неизвестная константа c, которую можно определить итерационной процедурой при численном решении системы (2.1).

Аналогичным образом, рассмотрев уравнение для продольного импульса, можно получить асимптотическую оценку поведения функции w₁, которая является производной по θ от поперечной компоненты скорости

(2.3)

${{w}_{1}}\sim - \Theta + a{{\eta }^{3}}\exp \left( { - \frac{1}{8}\Theta {{\eta }^{2}} - b\eta } \right)$

Здесь a и b – константы, определяемые итерационно в процессе решения уравнений.

3. РЕЗУЛЬТАТЫ ЧИСЛЕННОГО РЕШЕНИЯ КРАЕВОЙ ЗАДАЧИ

Решения краевой автомодельной задачи (2.1) для членов нулевого порядка получены численно с помощью метода Рунге–Кутта четвертого порядка точности. Размер шага поперек пограничного слоя равнялся Δη = 0.01, а количество точек составляло 1000. Для нахождения всех решений краевая задача сводилась к задаче с начальными условиями на поверхности крыла. При этом производные на поверхности крыла подбирались итерационно для удовлетворения условиям на внешней границе пограничного слоя в соответствии с оценками (2.2), (2.3). Задача считалась сошедшейся при относительном изменении давления p₀ между итерациями меньше, чем 10^–5. Результаты расчетов приведены для параметров γ = 1.4, σ = 1, H_w = 1.

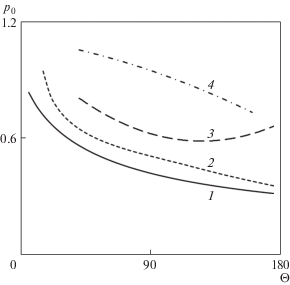
На рис. 2 для крыла с углом Θ = 45° показана зависимость давления p₀ от параметра p₂, который есть вторая производная давления по поперечной координате и может быть однозначно определен из решения краевой задачи для следующих членов асимптотического разложения. Найдено 4 различных решения для значений p₂ в диапазоне от –2 до 0, которые соответствующими цифрами обозначены на рисунке. Обрыв кривых на графиках связан с неустойчивостью решений при заданных параметрах. Полученные результаты хорошо согласуются с результатами исследования тонких треугольных крыльев в прямоугольной декартовой системе координат [6]. На рис. 2 кривая 5 (p₀ = –2p₂) соответствует изменению знака градиента давления в решаемой краевой задаче (2.1) в уравнении для w₁.

Рис. 2.

Зависимость давления p₀ от параметра p₂ для угла стреловидности передней кромки Θ = 45°: 1–4 – номера решений, 5 – линия p₂ = –2p₀.

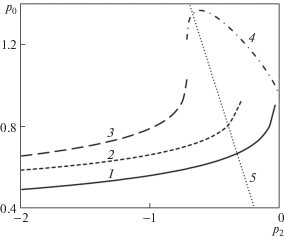
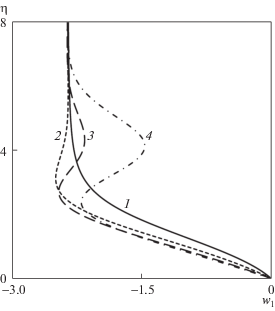
Для исследования крыла с передними кромками обратной стреловидности был выбран угол Θ = 135°. На рис. 3–5 для этого крыла показаны зависимости p₀, τ_u, τ_w при разных значениях p₂. Следует отметить немонотонное поведение давления, в особенности для решения 4, что говорит о перестроении решения в пограничном слое. Для значения параметра p₂ = –1 на рис. 6 показаны профили производной от поперечной скорости w₁ для всех найденных решений.

Рис. 3.

Зависимость давления p₀ от параметра p₂ для угла стреловидности передней кромки Θ = 135°, обозначения как рис. 2.

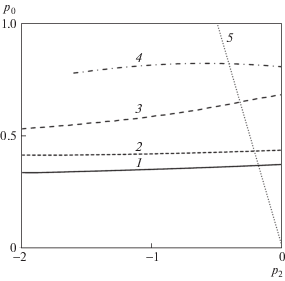
Рис. 4.

Зависимость напряжения трения τ_u в продольном направлении от параметра p₂ для угла стреловидности передней кромки Θ = 135°: 1–4 – номера решений, 5 – линия p₂ = –2p₀.

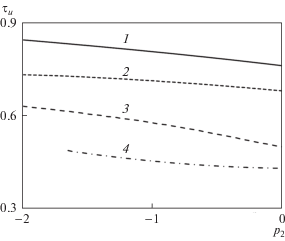
Рис. 5.

Зависимость напряжения трения τ_w в поперечном направлении от параметра p₂ для угла стреловидности передней кромки Θ = 135°, обозначения как на рис. 4.

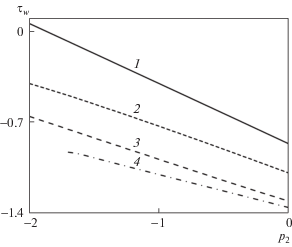
Рис. 6.

Профили w₁ для параметра p₂ = –1 и угла стреловидности передней кромки Θ = 135°, обозначения как на рис. 4.

Кроме того, также было исследовано влияние угла Θ на поведение функций течения. На рис. 7 представлено изменение давления p₀ для всех найденных решений при разных углах стреловидности передней кромки. Угол Θ рассматривался в диапазоне от 5° до 175°, но не для всех значений удалось подобрать начальные условия и константы. Наименее устойчивыми являются решения 3 и 4, так как они соответствуют наибольшей толщине пограничного слоя и имеют две точки перегиба в профиле скорости. Наблюдаемая нелинейность поведения давления связана с перестроением течения в плоскости симметрии – от стекания к плоскости симметрии до растекания.

Рис. 7.

Индуцированное давление p₀ в зависимости от параметра Θ, обозначения как на рис. 4.

ЗАКЛЮЧЕНИЕ

Построены координатные разложения для функций течения вблизи плоскости симметрии плоского крыла с изломом передней кромки с использованием цилиндрической системы координат. Сформулирована и численно решена соответствующая краевая задача для главных членов разложения. Показана неединственность решения уравнений пограничного слоя в окрестности плоскости симметрии. Для однозначного поиска решения необходимо выполнить асимптотическое сращивание с решениями в окрестности передних кромок. Исследование влияния угла стреловидности передней кромки на особенности течения показало сильную немонотонность поведения функций, связанную с перестроением течения в пограничном слое.

Список литературы

Lees L. On the Boundary-layer equations in hypersonic flow and their approximate solutions // J. Aeronautical Siences. 1953. P. 143–145.
Stewartson K. On the motion of a flat plate at high speed in a viscous compressible fluid. I. Impulsive motion // Mathematical Proceedings of the Cambridge Philosophical Society. 1955. V. 51. Iss. 1. P. 202–219.
Ладыженский М.Д. О пространственном гиперзвуковом течении около тонких крыльев // ПММ. 1964. Т. 28. Вып. 5. С. 835–844.
Нейланд В.Я. К теории взаимодействия гиперзвукового потока с пограничным слоем для отрывных двумерных и пространственных течений. Ч. 2. Двумерные течения и треугольное крыло // Уч. зап. ЦАГИ. 1974. Т. V. № 3. С. 28–39.
Brown S.N., Stewartson K. A non-uniqueness of the hypersonic boundary layer // Q. J. Mech. Appl. Math. 1975. V. XXVIII. Pt. 1. P. 75–90.
Дудин Г.Н., Нгуен Ф.Х. Обтекание треугольного крыла на режиме сильного вязко-невязкого взаимодействия // Изв. РАН. МЖГ. 2015. № 4. С. 68–82.
Дудин Г.Н., Нейланд В.Я. Теплообмен в окрестности точки излома передней кромки пластины при гиперзвуковом полете // Изв. АН СССР. МЖГ. 1980. № 3. С. 40–45.
Хартман Ф. Обыкновенные дифференциальные уравнения. М.: Мир, 1970. 720 с.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Известия РАН. Механика жидкости и газа

Архивы выпусков Информация о журнале Отправить рукопись в журнал