Известия РАН. Механика жидкости и газа, 2019, № 4, стр. 27-32
ТЕЧЕНИЕ ТОНКОГО СЛОЯ НАМАГНИЧИВАЮЩЕЙСЯ ЖИДКОСТИ В МАГНИТНОМ ПОЛЕ
А. Н. Тятюшкин *
МГУ им. М.В. Ломоносова, Научно-исследовательский институт механики
Москва, Россия
* E-mail: tan@imec.msu.ru
Поступила в редакцию 25.10.2018
После доработки 17.12.2018
Принята к публикации 18.12.2018
Аннотация
Аналитически решается задача о течении тонкого слоя несжимаемой жидкости, намагничивающейся по заданному закону, по твердой подложке в неоднородном магнитном поле в приближении теории смазки. Получено дифференциальное уравнение в частных производных, которое описывает изменение формы слоя со временем. Рассмотрена общая постановка задачи. Выписано решение задачи о тонком слое намагничивающейся жидкости в магнитном поле вертикального бесконечного цилиндрического проводника с заданным достаточно сильным током.
В [1] при помощи асимптотических методов исследовалось растекание тонкой пленки жидкости по вращающейся подложке. Влияние магнитного поля на этот процесс в случае намагничивающейся жидкости рассматривалось в [2, 3]. Цель настоящей работы – в приближении теории смазки получить общее уравнение, описывающее растекания тонкой пленки намагничивающейся жидкости по движущейся как твердое тело подложке и найти аналитическое решение выведенного уравнения для частного случая течения пленки намагничивающейся жидкости по горизонтальной подложке в поле вертикального проводника с током.
1. ПОСТАНОВКА ОБЩЕЙ ЗАДАЧИ
Рассмотрим слой несжимаемой намагничивающейся жидкости на абсолютно твердой плоской подложке, наклоненной под углом $\theta $ к горизонтали, в приложенном магнитном поле с заданной напряженностью ${{{\mathbf{H}}}_{{\text{a}}}}({\mathbf{r}},t)$, где ${\mathbf{r}}$ – трехмерный радиус-вектор, а $t$ – время. Подложка движется как твердое тело вдоль себя, вращаясь с угловой скоростью $\Omega = \Omega (t)$ вокруг некоторой мгновенной оси вращения, которая движется со скоростью ${\mathbf{V}} = {\mathbf{V}}(t)$. При этом $\Omega ||{\mathbf{k}}$, ${\mathbf{V}} \bot {\mathbf{k}}$, где k – вектор единичной нормали к плоскости подложки, направленный внутрь слоя. Жидкость в общем случае намагничивается по закону
где H и M – напряженность магнитного поля и намагниченность жидкости, $M(H)$ – заданная функция. Плотность, вязкость жидкости и поверхностное натяжение на границе с окружающей средой (воздухом) постоянны и равны соответственно $\rho $, $\eta $ и $\sigma $. Плотность и вязкость окружающей среды – пренебрежимо малы и давление в ней – постоянно.Магнитное поле считается настолько медленно меняющимся, что может описываться уравнениями Максвелла для квазистатического поля
Здесь ${{[A]}_{{\text{s}}}}$ обозначает скачок величины $A$ при переходе изнутри слоя наружу, ${\mathbf{n}}$ – вектор внешней единичной нормали к свободной поверхности слоя, $ \cdot $ и $ \times $ обозначают соответственно скалярное и векторное произведения, $\nabla $ обозначает трехмерный набла оператор.
Течение в слое рассматривается в системе отсчета, движущейся вместе с подложкой. Эволюция формы слоя описывается функцией $h({{u}^{1}},{{u}^{2}},t)$, где ${{u}^{1}}$, ${{u}^{2}}$ – координаты двумерной и, в общем случае, криволинейной системы координат для точки на поверхности подложки, $h$ – локальная толщина слоя. Пусть функция $h({{u}^{1}},{{u}^{2}},t)$ – такая, что
Здесь и далее ${{a}^{{\alpha \beta }}} = {{{\mathbf{e}}}^{\alpha }} \times {{{\mathbf{e}}}^{\beta }}$, ${{a}_{{\alpha \beta }}} = {{{\mathbf{e}}}_{\alpha }} \times {{{\mathbf{e}}}_{\beta }}$, ${{{\mathbf{e}}}_{\alpha }}$ и ${{{\mathbf{e}}}^{\alpha }}$ – векторы локального базиса, ${{\nabla }_{\alpha }}$ обозначают компоненты двумерного набла оператора ($\alpha = 1,2$; суммирование по повторяющимся индексам). Для того, чтобы удовлетворялось условие (1.1), необходимо, чтобы характеристическая длина неоднородности приложенного магнитного поля была много больше, чем толщина слоя всюду внутри него
(1.2)
$min\frac{{{{H}_{{\text{a}}}}({\mathbf{r}},t)}}{{\left| {\nabla {{H}_{{\text{a}}}}({\mathbf{r}},t)} \right|}} \gg maxh({{u}^{1}},{{u}^{2}},t)$Условия (1.1) и (1.2) позволяют считать напряженность магнитного поля и намагниченность жидкости постоянными вдоль толщины слоя.
Если выполняется условие
то можно пренебречь силой Кориолиса в уравнении, описывающем течение жидкости в системе отсчета, движущейся вместе с подложкой. Тогда условие (1.1) позволяет использовать приближение теории смазки, в котором эволюция слоя в системе отсчета, движущейся вместе с подложкой, определяется уравнением(1.3)
$\frac{{\partial h}}{{\partial t}} = {{\nabla }_{\alpha }}\left( {\frac{{{{h}^{3}}}}{{3\eta }}{{a}^{{\alpha \beta }}}{{f}_{\beta }}} \right)$(1.4)
$\begin{gathered} {{f}_{\alpha }} = \rho gcos\theta {{\nabla }_{\alpha }}h - \rho {\mathbf{g}} \cdot {{{\mathbf{e}}}_{\alpha }} - \sigma {{\nabla }_{\alpha }}({{a}^{{\beta \gamma }}}{{\nabla }_{\beta }}{{\nabla }_{\gamma }}h) - M{{\nabla }_{\alpha }}{{H}_{{\text{i}}}} - \\ - \;2\pi {{\nabla }_{\alpha }}\mathop {\left( {{\mathbf{M}} \cdot {\mathbf{n}}} \right)}\nolimits^2 - \rho {{\Omega }^{2}}{{a}_{{\alpha \beta }}}r_{{\text{s}}}^{\beta } + \rho \frac{{d\Omega }}{{dt}}{{\varepsilon }_{{\alpha \beta }}}r_{{\text{s}}}^{\beta } - \rho \frac{{d{{V}_{\alpha }}}}{{dt}} \\ \end{gathered} $Уравнение (1.3)–(1.4) является обобщением соответствующих уравнений, использующихся в работах [1–3], и выводится с помощью асимптотических методов, использующихся для вывода уравнения эволюции профиля тонкого слоя вязкой жидкости со свободной границей в приближении теории смазки (см., например, [1]).
2. РЕШЕНИЕ ДЛЯ ЧАСТНОГО СЛУЧАЯ
Рассмотрим слой намагничивающейся жидкости, текущий по неподвижной горизонтальной подложке в поле вертикального цилиндрического бесконечно длинного проводника с током $J$. Пусть магнитное поле – настолько сильное, что $M({{H}_{{\text{a}}}}){{H}_{{\text{a}}}} \gg max(\rho gh,\sigma {{a}^{{\beta \gamma }}}{{\nabla }_{\beta }}{{\nabla }_{\gamma }}h)$. Тогда уравнение (1.3)–(1.4) принимает вид дифференциального уравнения в частных производных первого порядка
(2.1)
$\frac{{\partial h}}{{\partial t}} = \frac{1}{{{{r}_{{\text{s}}}}}}\frac{\partial }{{\partial {{r}_{{\text{s}}}}}}\left[ {\frac{{2J}}{{3\eta c{{r}_{{\text{s}}}}}}M\left( {\frac{{2J}}{{c{{r}_{{\text{s}}}}}}} \right){{h}^{3}}} \right]$Уравнение (2.1) представляет собой квазилинейное дифференциальное уравнение в частных производных первого порядка. Система обыкновенных дифференциальных уравнений для его характеристик имеет вид
(2.2)
$\frac{{d{{r}_{{\text{s}}}}}}{{dt}} = - \frac{{2J{{h}^{2}}}}{{\eta c{{r}_{{\text{s}}}}}}M\left( {\frac{{2J}}{{cr_{{\text{s}}}^{2}}}} \right),\quad \frac{{dh}}{{dt}} = - \frac{{2J{{h}^{3}}}}{{3\eta cr_{{\text{s}}}^{3}}}\left[ {M\left( {\frac{{2J}}{{c{{r}_{{\text{s}}}}}}} \right) + \frac{{2J}}{{c{{r}_{{\text{s}}}}}}M{\text{'}}\left( {\frac{{2J}}{{c{{r}_{{\text{s}}}}}}} \right)} \right]$Решая систему уравнений (2.2) в квадратурах, получим решение уравнения (2.1) в параметрическом виде $h = h({{r}_{{{\text{s}}0}}},t)$, ${{r}_{{\text{s}}}} = {{r}_{{\text{s}}}}({{r}_{{{\text{s}}0}}},t)$ с начальным условием $h({{r}_{{\text{s}}}},0) = {{h}_{0}}({{r}_{{{\text{s}}0}}})$, ${{r}_{{\text{s}}}} = {{r}_{{{\text{s}}0}}}$ в виде следующих соотношений
(2.3)
$\int\limits_{{{r}_{{{\text{s}}0}}}}^{{{r}_{{\text{s}}}}({{r}_{{{\text{s}}0}}},t)} r_{{\text{s}}}^{{4/3}}\mathop {\left[ {\frac{{2J}}{c}M\left( {\frac{{2J}}{{c{{r}_{{\text{s}}}}}}} \right)} \right]}\nolimits^{ - 1/3} d{{r}_{{\text{s}}}} = - h_{0}^{2}\left( {{{r}_{{{\text{s}}0}}}} \right)\mathop {\left[ {\frac{{2J}}{{c{{r}_{{{\text{s}}0}}}}}M\left( {\frac{{2J}}{{c{{r}_{{{\text{s}}0}}}}}} \right)} \right]}\nolimits^{2/3} \frac{t}{\eta }$(2.4)
$h({{r}_{{{\text{s}}0}}},t) = {{h}_{0}}({{r}_{{{\text{s}}0}}})\mathop {\left[ {\frac{{{{r}_{{\text{s}}}}({{r}_{{{\text{s}}0}}},t)M\left( {\frac{{2J}}{{c{{r}_{{{\text{s}}0}}}}}} \right)}}{{{{r}_{{{\text{s}}0}}}M\left( {\frac{{2J}}{{c{{r}_{{\text{s}}}}(t,{{r}_{{{\text{s}}0}}})}}} \right)}}} \right]}\nolimits^{1/3} $Здесь параметр ${{r}_{{{\text{s}}0}}}$ параметризует конкретную точку свободной поверхности начального профиля и определяет характеристику, по которой можно проследить за изменением положения этой конкретной точки. Таким образом, эволюция профиля слоя, т.е. изменение со временем положения всех точек его свободной поверхности, полностью определяется начальной формой этой поверхности. Отметим, что точки свободной поверхности начального профиля могут быть параметризованы также и при помощи параметра ${{h}_{0}}$.
Для намагничивающейся жидкости с постоянной магнитной проницаемостью $\mu $
и решение уравнения (2.1) имеет вид(2.5)
$h = {{h}_{0}}({{r}_{{{\text{s}}0}}})\mathop {\left[ {1 - \frac{8}{3}\frac{{h_{0}^{2}({{r}_{{{\text{s}}0}}})}}{{r_{{{\text{s}}0}}^{4}}}\frac{{\left( {\mu - 1} \right){{J}^{2}}}}{{\pi {{c}^{2}}}}\frac{t}{\eta }} \right]}\nolimits^{1/4} $(2.6)
${{r}_{{\text{s}}}} = {{r}_{{{\text{s}}0}}}\mathop {\left[ {1 - \frac{8}{3}\frac{{h_{0}^{2}({{r}_{{{\text{s}}0}}})}}{{r_{{{\text{s}}0}}^{4}}}\frac{{\left( {\mu - 1} \right){{J}^{2}}}}{{\pi {{c}^{2}}}}\frac{t}{\eta }} \right]}\nolimits^{3/8} $Условие (1.2) удовлетворяется, если $min{{r}_{{\text{s}}}} \gg h\left( {min{{r}_{{\text{s}}}}} \right)$.
3. РЕШЕНИЯ С РАЗРЫВАМИ
Пусть функция, описывающая начальный профиль ${{h}_{0}}({{r}_{{{\text{s}}0}}})$ – непрерывная внутри интервала ${{r}_{1}} < {{r}_{{{\text{s}}0}}} < {{r}_{2}}$ (${{r}_{2}} > {{r}_{1}} > {{r}_{{\text{c}}}}$) и равна нулю на его концах и вне его. Тогда функция $h({{r}_{{\text{s}}}},t)$ имеет точки ветвления, в которых
Для случая постоянной магнитной проницаемости из (3.1) с учетом решения (2.5)–(2.6) следует условие
(3.2)
$t = \frac{{\pi {{c}^{2}}\eta }}{{2\left( {\mu - 1} \right){{J}^{2}}}}\frac{{3r_{{{\text{s}}0}}^{4}}}{{{{h}_{0}}({{r}_{{{\text{s}}0}}})\left[ {3{{r}_{{{\text{s}}0}}}{\text{'}}{{h}_{0}}({{r}_{{{\text{s}}0}}}) - 2{{h}_{0}}({{r}_{{{\text{s}}0}}})} \right]}}$Таким образом, в момент времени $t = {{t}_{{\text{d}}}}$, где ${{t}_{{\text{d}}}}$ – минимальное положительное значение выражения (3.2), появляется разрыв [1]. Разрыв распространяется со скоростью
4. УСТАНОВЛЕНИЕ ИЗНАЧАЛЬНО ОДНОРОДНОГО СЛОЯ К РАВНОВЕСНОМУ СОСТОЯНИЮ В ПОЛЕ БЕСКОНЕЧНОГО ПРОВОДНИКА С ТОКОМ
Как известно, будучи помещенной в поле бесконечного проводника с током, намагничивающаяся жидкость стремится принять некоторую осесимметричную форму, называемую магнитным мениском около проводника, определенную балансом магнитной и гравитационной сил (см. [4] и [5]). Уравнение (2.1) позволяет исследовать установление однородного тонкого горизонтального слоя, окружающего бесконечный вертикальный проводник к равновесной форме, принимаемой жидкостью, содержащейся в слое, при включении тока.
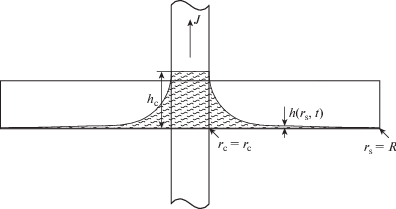
Рассмотрим тонкий слой намагничивающейся жидкости, содержащийся в осесимметричном сосуде с горизонтальным дном и вертикальными стенками (чашечке Петри) с бесконечно длинным вертикальным проводником, проходящим через ось симметрии сосуда, рис. 1. Радиус сечения проводника – ${{r}_{{\text{c}}}}$, а радиус сосуда – R. Изначально в проводнике нет тока, и толщина слоя – однородна и равна ${{h}_{{0{\text{m}}}}}$. В момент времени $t = 0$ включается ток силой J и поддерживается постоянным.
Решение (2.3)–(2.4) позволяет предположить, что процесс установления профиля слоя к равновесной форме происходит следующим образом. Сразу после того, как ток включается, образуются три области. В первой области ${{r}_{{\text{c}}}} < {{r}_{{\text{s}}}} < \mathop {{{r}_{{\text{s}}}}}\nolimits_1 (t)$, профиль слоя определяется уравнениями гидростатики (см. [4] и [5]), которые дают
(4.1)
$h({{r}_{{\text{s}}}},t) = {{h}_{1}}(t) + \frac{{2J}}{{\rho gc}}\int\limits_{{{r}_{{\text{s}}}}}^{\mathop {{{r}_{{\text{s}}}}}\nolimits_1 (t)} \frac{1}{{\mathop {{{r}_{{\text{s}}}}{\text{'}}}\nolimits^2 }}M\left( {\frac{{2J}}{{c{{r}_{{\text{s}}}}{\text{'}}}}} \right)d{{r}_{{\text{s}}}}{\text{'}}$Эволюция профиля во второй и третьей областях определяется уравнением (2.1) с начальным профилем, определенным следующими начальными условиями для второй и третьей области соответственно
(4.2)
$h({{r}_{{\text{s}}}},0) = {{h}_{{0{\text{m}}}}} = {\text{const}},\quad {{r}_{{\text{c}}}} \leqslant {{r}_{{\text{s}}}} < R$(4.3)
$h({{r}_{{\text{s}}}},0) = {{h}_{0}},\quad 0 \leqslant {{h}_{0}} < {{h}_{{0{\text{m}}}}},\quad {{r}_{{\text{s}}}} = R$Движущая граница между этими областями ${{r}_{{\text{s}}}} = \mathop {{{r}_{{\text{s}}}}}\nolimits_2 (t)$ определяется точкой поверхности начального профиля ${{r}_{{\text{s}}}} = R$, $h = {{h}_{{0{\text{m}}}}}$, т.е. $\mathop {{{r}_{{\text{s}}}}}\nolimits_2 (0) = R$, и функция $\mathop {{{r}_{{\text{s}}}}}\nolimits_2 (t)$ находится непосредственно из решения уравнения (2.1).
Отметим, что предположение о том, что эволюция профиля в третьей области определяется частью начального профиля, не являющегося свободной поверхностью жидкости, является довольно сильным. Тем не менее можно ожидать, что профиль слоя в третьей области достаточно близок к профилю, определенному уравнением (2.1) с начальным условием (4.3). Действительно, любой другой профиль должен быть результатом эволюции профиля либо с каверной, примыкающей к стенке сосуда, либо с частью жидкости, находящейся за стенками сосуда (либо с тем и другим).
В процессе установления профиля жидкость перетекает из второй области в первую и из третьей области во вторую. В момент времени t = t0, определяемый уравнением $\mathop {{{r}_{{\text{s}}}}}\nolimits_1 ({{t}_{0}}) = \mathop {{{r}_{{\text{s}}}}}\nolimits_2 ({{t}_{0}})$, вторая область схлопывается и жидкость начинает перетекать из третьей области непосредственно в первую. Эта последняя стадия установления профиля длится бесконечное время, при этом профиль слоя асимптотически стремится к равновесной форме.
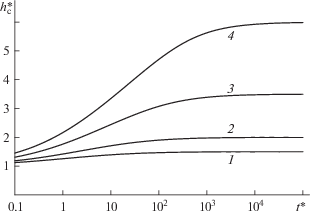
Таким образом, процесс установления всего профиля определяется решением уравнения (2.1) (2.3)–(2.4) с начальными условиями (4.2)–(4.3) и формулой (4.1). При этом необходимо найти функцию $\mathop {{{r}_{{\text{s}}}}}\nolimits_1 (t)$, которая определяется условием равенства объема жидкости в первой области убыли объема из второй и третьей областей. Это условие для случая постоянной магнитной проницаемости было получено аналитически в виде трансцендентного уравнения для неизвестного ${{h}_{1}}$, в которое время входит как параметр. Зная ${{h}_{1}}(t)$, можно найти $\mathop {{{r}_{{\text{s}}}}}\nolimits_1 (t)$, используя (2.5)–(2.6). Таким образом, задача об эволюции профиля была сведена к решению уравнения для ${{h}_{1}}$. Обезразмеренное уравнение для ${{h}_{1}}$ решалось численно для разных значений t, и по найденному решению определялась эволюция профиля слоя. В частности, определялось изменение со временем максимальной толщины слоя, которая достигается при ${{r}_{{\text{s}}}} = {{r}_{{\text{c}}}}$. На рис. 2 изображены зависимости безразмерной максимальной толщины слоя $h_{{\text{c}}}^{ * } = {{h}_{{\text{c}}}}{\text{/}}{{h}_{{0{\text{m}}}}}$ (${{h}_{{\text{c}}}} = h({{r}_{{\text{c}}}},t)$) от безразмерного времени
ЗАКЛЮЧЕНИЕ
Проведено теоретическое исследование течения тонкого слоя несжимаемой намагничивающейся жидкости с заданной зависимостью намагниченности от напряженности магнитного поля в неоднородном магнитном поле. Получено дифференциальное уравнение в частных производных, которое описывает эволюцию профиля слоя в приближении теории смазки. Выписаны условия, при которых законны приближения, использованные при выводе этого уравнения. В качестве применения этого уравнения решена задача о тонком слое намагничивающейся жидкости в магнитном поле вертикального бесконечного цилиндрического проводника с заданным достаточно сильным током.
Работа выполнена при частичной поддержке РФФИ (проекты № 19‑01‑00056‑а и № 17-01-00037-а).
Список литературы
Needham D.J., Merkin J.H. The development of nonlinear waves on the surface of a horizontally rotating thin liquid film // J. Fluid Mech. 1987. V. 184. P. 357–379.
Naletova V.A., Kim L.G., Turkov V.A. Hydrodynamics of a horizontally rotating thin magnetizable liquid film // J. Magn. Magn. Mater. 1995. V. 149. P. 162–164.
Naletova V.A., Turkov V.A. Film thickness discontinuity generation in a magnetic field // J. Magn. Magn. Mater. 1999. V. 201. P. 346–349.
Neuringer J.L., Rosensweig R.E. Ferrohydrodynamics // Phys. Fluids 1964. V. 7. P. 1927–1937.
Krueger D.A., Jones T.B. Hydrostatic profile of ferrofluid around a vertical current-carrying wire // Phys. Fluids 1974. V. 17. P. 1831–1833.
Дополнительные материалы отсутствуют.
Инструменты
Известия РАН. Механика жидкости и газа