Известия РАН. Механика твердого тела, 2023, № 6, стр. 136-154
АНИЗОТРОПИЯ ЭНЕРГИИ ОСТАТОЧНЫХ НАПРЯЖЕНИЙ В ДВУХКОМПОНЕНТНЫХ ПЛАСТИНЧАТЫХ КРИСТАЛЛИЧЕСКИХ СТРУКТУРАХ
Д. С. Лисовенко a, *, А. И. Епишин b, **
a Институт проблем механики им. А.Ю. Ишлинского РАН
Москва, Россия
b Институт структурной макрокинетики и проблем материаловедения им. А.Г. Мержанова РАН
Черноголовка, Россия
* E-mail: lisovenk@ipmnet.ru
** E-mail: a.epishin2021@gmail.com
Поступила в редакцию 26.06.2023
После доработки 03.07.2023
Принята к публикации 07.07.2023
- EDN: BNGLGT
- DOI: 10.31857/S0572329923600524
Аннотация
Получено аналитическое решение для остаточных напряжений и их энергии в упруго анизотропной двухкомпонентной пластинчатой структуре, где компоненты имеют идентичный тип упругой анизотропии, одинаковые или пропорциональные упругие константы и совпадающие главные оси упругой анизотропии. Полученное решение применено для анализа анизотропии упругой энергии таких кристаллических структур как рафт-структура γ/γ' монокристаллических никелевых жаропрочных сплавов, многослойных эрозионностойких нанопокрытий ZrN/CrN и однослойных покрытий различного типа. Показано, что фактор минимизации упругой энергии остаточных напряжений оказывает существенное влияние на кристаллографическую ориентацию интерфейса в многослойных структурах и направление оси ростовой текстуры покрытий.
1. Введение. Большинство конструкционных и функциональных материалов являются гетерофазными, то есть состоящими из двух или более компонентов, различающихся по химическому составу и разделенных между собой поверхностями раздела. При совмещении разнородных компонентов в них вследствие размерного несоответствия возникают остаточные напряжения, которые оказывают существенное влияние на физико-механические свойства образованного компаунда. Остаточные напряжения могут быть желательными или нежелательными. Например, растягивающие остаточные напряжения в более прочной фазе композиционного материала обеспечивают более низкий уровень напряжений в менее прочной фазе при нагружении материала внешней растягивающей нагрузкой. Классическим примером реализации такого принципа упрочнения является предварительно напряженный железобетон. Однако в большинстве случаев остаточные напряжения имеют отрицательный эффект и поэтому обычно компании-производители стремятся минимизировать уровень остаточных напряжений в выпускаемых материалах и изделиях. Обзор, посвященный остаточным напряжениям в конструкционных материалах, приведен в работе [1].
Широким классом гетерофазных материалов являются периодические пластинчатые структуры, например, многофазные сплавы, такие как мартенситные, бейнитные и перлитные стали [2], сплавы на основе γ-алюминида титана [3], направленно закристаллизованные композиты Nb/Nb5Si3 [4], многослойные защитные покрытия [5] и многие другие. Такие структуры могут формироваться в процессе кристаллизации материала (in-situ), путем последовательного нанесения его слоев, например, с использованием аддитивных технологий и при других технологических процессах. При этом возникающие остаточные напряжения могут не только непосредственно (механически) влиять на макроскопические свойства материала, но и косвенно видоизменяя его кристаллическую структуру и морфологию структурных составляющих, если процесс происходит при высоких температурах, когда структура материала формируется путем кристаллизации или диффузионно эволюционирует. Целью настоящей работы являлось развитие аналитической модели, которая позволяет оценивать уровень остаточных напряжений и их энергию в двухкомпонентных пластинчатых структурах. При этом рассматривается специальный случай пластинчатых структур, в которых компоненты имеют одинаковый тип упругой анизотропии, равные или пропорциональные упругие константы, а их главные оси упругой анизотропии совпадают. Полученные аналитические зависимости применены для исследования анизотропии упругой энергии пластинчатых кристаллических структур кубической сингонии, а именно: рафт-структуры γ/γ', формирующейся в монокристаллах никелевых жаропрочных сплавов в процессе высокотемпературной ползучести [6], многослойных эрозионностойких покрытиях, состоящих из множества нанослоев ZrN и CrN [5], и однослойных покрытий различного типа, нанесенных на жесткую подложку.
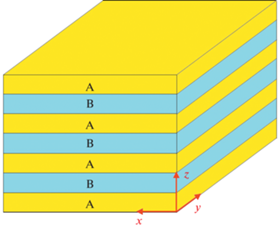
2. Постановка задачи. На рис. 1 представлена модель рассматриваемой пластинчатой структуры. Полагается, что структура состоит из множества периодически чередующихся в направлении z слоев компонентов A и B постоянной толщины. Длина пластин в направлениях x и y намного больше их толщины. Пластины жестко соединены в плоскости интерфейса, при этом размерное несоответствие пластин δ в плоскости xy компенсируются их упругими деформациями. Параметр δ определен следующим образом: $\delta = \left( {{{l}_{B}} - {{l}_{A}}} \right){\text{/}}{{l}_{A}}$, где lA и lB – линейный размер нестесненных пластин A и B, то есть в состоянии до их совмещения. Так как рассматривается структура многослойная и она состоит из длинных пластин, то считается, что изгибные деформации и концевые эффекты в этой структуре отсутствуют. Полагается, что компоненты A и B имеют одинаковый тип упругой анизотропии, главные оси их упругой анизотропии совпадают, а упругие податливости равны $S_{{ij}}^{A} = S_{{ij}}^{B} = {{S}_{{ij}}}$. Отсюда и далее будем обозначать компоненты матрицы упругих податливостей в главных осях упругой анизотропии большими символами Sij, а в лабораторной системе xyz малыми sij. Задача настоящего аналитического исследования состояла в получении решения для остаточных напряжений и упругой энергии в данной структуре в предположении, что интерфейс А/В имеет произвольную ориентацию по отношению к главным осям упругой анизотропии.
3. Основные уравнения и их решение. В отсутствие внешней нагрузки при произвольном сечении модели пластинчатой структуры (рис. 1) плоскостями, перпендикулярными осям x, y и z, разделенные части объекта должны оставаться в равновесии. Из сечения плоскостью, перпендикулярной z, следует, что все компоненты тензора напряжений с индексом z должны быть равны нулю: ${{{{\sigma }}}_{{zz}}} = {{{{\sigma }}}_{{zx}}} = {{{{\sigma }}}_{{xz}}} = {{{{\sigma }}}_{{zy}}} = {{{{\sigma }}}_{{yz}}} = 0$. То есть структура находится в плоском напряженном состоянии с ${{{{\sigma }}}_{{xx}}} \ne 0~$, ${{{{\sigma }}}_{{yy}}} \ne 0~$, ${{{{\sigma }}}_{{xy}}} = {{{{\sigma }}}_{{yx}}} \ne 0~$. Из сечений плоскостями, перпендикулярными осям x и y, следуют уравнения равновесия
где f B – объемная доля компонента B.При жестком соединении пластин A и B вдоль осей x и y должны выполняться уравнения совместности линейных деформаций
а также угловых деформаций в плоскости xyУчитывая только ненулевые компоненты тензора напряжений, по закону Гука получаем деформации
(3.7)
$\varepsilon _{{xx}}^{С} = {{s}_{{11}}}\sigma _{{xx}}^{С} + {{s}_{{12}}}\sigma _{{yy}}^{С} + {{s}_{{16}}}\sigma _{{xy}}^{С}$(3.8)
$\varepsilon _{{yy}}^{С} = ~{{s}_{{12}}}\sigma _{{xx}}^{С} + {{s}_{{22}}}\sigma _{{yy}}^{С} + {{s}_{{26}}}\sigma _{{xy}}^{С}$(3.9)
$\varepsilon _{{xy}}^{С} = \frac{1}{2}(~{{s}_{{16}}}\sigma _{{xx}}^{С} + {{s}_{{26}}}\sigma _{{yy}}^{С} + {{s}_{{66}}}\sigma _{{xy}}^{С})$(3.10)
$\varepsilon _{{zz}}^{C} = {{s}_{{13}}}\sigma _{{xx}}^{C} + {{s}_{{23}}}\sigma _{{yy}}^{C} + {{s}_{{36}}}\sigma _{{xy}}^{C}$Таким образом, имеется 12 линейных уравнений ((3.1)–(3.6) и (3.7)–(3.10)) × 2 относительно 12-ти неизвестных $\varepsilon _{{xx}}^{С}$, $\varepsilon _{{yy}}^{С}$, $\varepsilon _{{xy}}^{С}$, $\sigma _{{xx}}^{С}$, $\sigma _{{yy}}^{С}$, $\sigma _{{xy}}^{С}$ (C = A, B).
Решение данной системы уравнений имеет вид
где(3.18)
${{K}_{{xx}}} = \frac{{{{{{\beta }}}_{{22}}} - {{{{\beta }}}_{{12}}}}}{{{{{{\beta }}}_{{11}}}{{{{\beta }}}_{{22}}} - {{\beta }}_{{12}}^{2}}}$(3.19)
${{K}_{{yy}}} = \frac{{{{{{\beta }}}_{{11}}} - {{{{\beta }}}_{{12}}}}}{{{{{{\beta }}}_{{11}}}{{{{\beta }}}_{{22}}} - {{\beta }}_{{12}}^{2}}}$(3.20)
${{K}_{{xy}}} = \frac{{{{s}_{{16}}}\left( {{{{{\beta }}}_{{22}}} - {{{{\beta }}}_{{12}}}} \right) + {{s}_{{26}}}\left( {{{{{\beta }}}_{{11}}} - {{{{\beta }}}_{{12}}}} \right)}}{{{{s}_{{66}}}({{{{\beta }}}_{{11}}}{{{{\beta }}}_{{22}}} - {{\beta }}_{{12}}^{2})}}$Деформация $\varepsilon _{{zz}}^{C}$ и эффективный нормальный коэффициент Пуассона ν* могут быть получены, исходя из соотношений (3.10), (3.13)–(3.21),
(3.23)
$\nu {\text{*}} = - \frac{{{{{{\beta }}}_{{13}}}\left( {{{{{\beta }}}_{{22}}} - {{{{\beta }}}_{{12}}}} \right) + {{{{\beta }}}_{{23}}}\left( {{{{{\beta }}}_{{11}}} - {{{{\beta }}}_{{12}}}} \right)}}{{{{{{\beta }}}_{{11}}}{{{{\beta }}}_{{22}}} - {{\beta }}_{{12}}^{2}}}$Таким образом, тензоры деформаций и напряжений могут быть записаны в следующем виде
(3.24)
${{\hat {\varepsilon }}^{С}} = {{{{\alpha }}}^{C}}{{\delta }}\left( {\begin{array}{*{20}{c}} 1&0&0 \\ 0&1&0 \\ 0&0&{ - {{\nu }^{*}}} \end{array}} \right)$(3.25)
${{{{\hat {\sigma }}}}^{С}} = \left( {\begin{array}{*{20}{c}} {{{\sigma }}_{{xx}}^{С}}&{{{\sigma }}_{{xy}}^{С}}&0 \\ {{{\sigma }}_{{xy}}^{С}}&{{{\sigma }}_{{yy}}^{С}}&0 \\ 0&0&0 \end{array}} \right)$Следует отметить, что компоненты тензора деформаций, включая эффективный коэффициент Пуассона ν*, инвариантны относительно поворота осей x и y в плоскости пластин, в то время как компоненты тензора напряжений ориентационно зависимы.
Удельная упругая энергия компонентов структуры определяется соотношением
(3.26)
${{W}^{C}} = \frac{1}{2}({{\sigma }}_{{xx}}^{C}{{\varepsilon }}_{{xx}}^{C} + {{\sigma }}_{{yy}}^{C}{{\varepsilon }}_{{yy}}^{C}) + {{\sigma }}_{{xy}}^{C} \times ({{\varepsilon }}_{{xy}}^{C} = 0)$Подставляя в (3.26) напряжения и деформации из (3.11)–(3.21), получаем
где(3.28)
$K = {{K}_{{xx}}} + {{K}_{{yy}}} = \frac{{{{\beta }_{{11}}} + {{\beta }_{{22}}} - 2{{\beta }_{{12}}}}}{{{{\beta }_{{11}}}{{\beta }_{{22}}} - \beta _{{12}}^{2}}}$Удельная упругая энергия структуры в целом равна
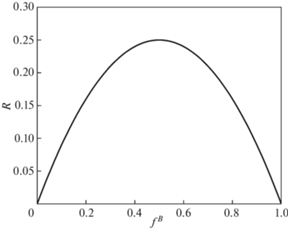
где $W = K{{\delta }^{2}}{\text{/}}2$ – упругая энергия отдельной пластины, двухосно деформированной с деформацией δ, а $R({{f}^{B}}) = {{f}^{B}}(1 - {{f}^{B}})$ – функция объемной доли компонента В, изменяющаяся от 0 до 0.25, см. рис. 2.Из рис. 2 видно, что рассматриваемая пластинчатая структура имеет максимальную удельную упругую энергию, равную W/4, при равных объемных долях компонентов ${{f}^{A}} = {{f}^{B}} = 0.5$. При стремлении объемной долей одного из компонентов к нулю напряжения в ней повышаются, и ее удельная упругая энергия стремится к максимальной предельной величине W. Однако, вклад этой компоненты в общую энергию структуры, определяемый ее объемной долей, также стремится к нулю. Удельная упругая энергия другого компонента стремится к нулю вследствие понижения в ней уровня остаточных напряжений и, следовательно, общая упругая энергия структуры стремится к нулю. Таким образом, структуры с близкими объемными долями компонентов имеют бóльшую упругую энергию, тогда как структуры с сильно различающимися объемными долями меньшую.
Все приведенные выше соотношения справедливы для двухкомпонентной пластинчатой структуры с любым типом упругой анизотропии при условии идентичности типов упругой анизотропии компонентов А и В, и равенства их упругих констант и совпадения главных осей упругой анизотропии.
Запись вышеприведенных формул упрощается, когда оси x и y совпадают с направлением главных напряжений в плоскости xy, то есть когда ${{K}_{{xy}}} = 0$ и, следовательно, $\sigma _{{xy}}^{C} = 0$, см. (3.15). Как следует из (3.20), (3.21) этот случай реализуется для ориентации, при которой выполняется условие:
(3.30)
${{s}_{{16}}}\left( {{{s}_{{22}}} - {{s}_{{12}}}} \right) + {{s}_{{26}}}\left( {{{s}_{{11}}} - {{s}_{{12}}}} \right) = 0$При этом все формулы могут быть упрощены путем замены ${{{{\beta }}}_{{ij}}} \to {{s}_{{ij}}}$.
Упругие податливости sij в произвольной системе координат xyz можно выразить через базовые упругие податливости Sij как ${{s}_{{ij}}} = f\left( {{{S}_{{ij}}},~{{\varphi }},\theta ,{{\psi }}} \right)$, где ${{\varphi }},\theta ,{{\psi }}$ – углы Эйлера, то есть соответственно углы прецессии, нутации и собственного вращения лабораторной системы координат по отношению к базовой кристаллографической. В рассматриваемом случае ψ – это угол вращения осей x и y в плоскости пластины, то есть вокруг оси z. Из физического смысла ясно, что энергия пластин (как и компоненты тензора деформаций, см. (3.24)) определяется только двумя углами φ и θ, однако жесткости пластины и компоненты тензора напряжений, имеющие индексы x и y, зависят от выбранной лабораторной системы координат xyz, то есть от угла ψ. При заданных φ и $\theta $ соотношение (3.30) определяет угол поворота ψ осей x и y вокруг z для ориентации их вдоль осей главных напряжений в пластинах.
Далее будем рассматривать только случай, когда пластины A и B являются кубическими кристаллами.
4. Пластинчатая структура с кубической кристаллической решеткой. Как отмечалось выше, энергия пластин W, определяемая ее двухосной жесткостью K, не зависит от ψ, поэтому для простоты ниже будем рассматривать только такие системы координат xyz для которых ψ = 0. Ориентационные преобразования компонент sij кубических кристаллов при ψ = 0 приведены в приложении.
Для кубических кристаллов целесообразно анализировать изменение энергии $W$ в двух характеристических случаях, в которых ψ = 0, а φ имеет постоянное значение, 0° или 45°, и поэтому величина W определяется только поворотом оси z (нормаль к поверхности пластин) на угол θ. При таком вращении z последовательно совпадет со всеми низкоиндексными осями кубического кристалла.
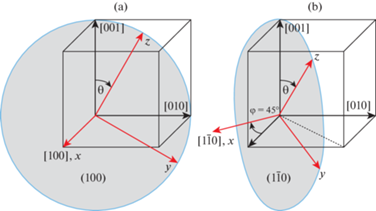
Первый случай – когда ось x лабораторной системы координат совпадает с [100] (φ = 0), а две другие y и z поворачиваются в плоскости (001) на угол θ (см. рис. 3,а), второй – когда ось x совпадает с $[1\bar {1}0]$ (φ = 45°), а y и z поворачиваются на угол θ в плоскости $\left( {1\bar {1}0} \right)$ (см. рис. 3,b). Покажем, что в обоих случаях оси x и y совпадают с осями главных напряжений, лежащими в плоскости xy. Ось z априори является осью главного напряжения ${{{{\sigma }}}_{{zz}}}$ поскольку все напряжения, в том числе касательные, с индексом z равны нулю.
Рис. 3.
Поворот лабораторной системы координат xyz относительно кристаллографической. (а) Ось поворота x совпадает с [100], ${{\varphi }} = 0$. (b) Ось поворота x совпадает с $\left[ {1\bar {1}0} \right]$, ${{\varphi }} = 45^\circ $.
Поскольку в рассматриваемых случаях ψ = 0, то для анализа можно использовать преобразования ${{s}_{{ij}}} = f\left( {{{S}_{{ij}}},{{\varphi }},\theta ,{{\psi }} = 0} \right)$, приведенные в приложении. Из формул (6A), (7A) видно, что компонента ${{s}_{{26}}} = - {{s}_{{16}}}{\text{co}}{{{\text{s}}}^{2}}\theta $ и, поэтому соотношение (3.30) может быть записано в виде
(4.1)
${{s}_{{16}}}[{{s}_{{22}}} - {{s}_{{12}}} - {\text{co}}{{{\text{s}}}^{2}}\theta \left( {{{s}_{{11}}} - {{s}_{{12}}}} \right)] = 0$То есть (3.30) выполняется, когда ${{s}_{{16}}} = 0$. Поскольку ${{s}_{{16}}} = - S{\text{/}}2{\text{sin}}4\varphi {\text{cos}}\theta $, то ${{s}_{{16}}} = 0$ при ${{\varphi }} = 45^\circ \times n$. Таким образом, условие (3.30) выполняется для обоих случаев, показанных на рис. 3, и соотношение (3.28) для жесткости пластины K может записано просто в упругих податливостях sij
(4.2)
$K = \frac{{{{s}_{{11}}} + {{s}_{{22}}} - 2{{s}_{{12}}}}}{{{{s}_{{11}}}{{s}_{{22}}} - s_{{12}}^{2}}}$Для первого случая, подставляя упругие податливости из (1A)–(3A) и учитывая, что ${{\varphi }} = 0^\circ $, получаем
(4.3)
$\frac{K}{E} = \frac{{2\left( {1 + \nu } \right) - \frac{A}{2}{\text{si}}{{{\text{n}}}^{2}}2\theta }}{{1 - {{\nu }^{2}} - \frac{A}{2}{\text{si}}{{{\text{n}}}^{2}}2\theta }}$Для второго случая, подставляя упругие податливости из (1A)–(3A) и учитывая, что ${{\varphi }} = 45^\circ $, получаем
(4.4)
$\frac{K}{E} = \frac{{2\left( {1 + \nu } \right) - \frac{A}{2}\left( {1 + 3{\text{co}}{{{\text{s}}}^{2}}\theta + \frac{3}{4}{\text{si}}{{{\text{n}}}^{2}}2\theta } \right)}}{{1 - {{\nu }^{2}} + \nu A{\text{co}}{{{\text{s}}}^{2}}\theta + \frac{{{{A}^{2}}}}{4}{\text{si}}{{{\text{n}}}^{2}}2\theta - \frac{A}{2}\left( {1 + {\text{co}}{{{\text{s}}}^{2}}\theta + \frac{3}{4}{\text{si}}{{{\text{n}}}^{2}}2\theta } \right)}}$Характеристическими направлениями в кубической кристаллической решетке являются низкоиндексные направления [001], [011] и [111]. Поэтому представляет интерес рассмотреть случаи, когда ось z совпадает с этими направлениями, а оси x и y совпадают с другими низкоиндексными направлениями. Такими ортогональными системами координат являются $\vec {x},\vec {y},\vec {z} = \left[ {100} \right],\left[ {010} \right],\left[ {001} \right]$; $\left[ {100} \right],\left[ {01\bar {1}} \right],\left[ {011} \right]$ и $\left[ {1\bar {1}0} \right],\left[ {11\bar {2}} \right]$, [111]. Первые две системы соответствуют случаю 1, описанному выше, то есть повороту системы координат xyz в плоскости (100), см. рис. 3,а, а третья система – случаю 2, то есть повороту xyz в плоскости (1$\bar {1}$0), см. рис. 3,b. Таким образом, во всех трех системах координат оси xyz совпадают с осями главных напряжений и полученные выше формулы (3.18), (3.19), (3.23), (3.28) могут быть упрощены путем подстановки ${{{{\beta }}}_{{ij}}} \to {{s}_{{ij}}}$, а упругая жесткость Kxy и касательное напряжение ${{\sigma }}_{{xy}}^{С}$ равны нулю. Проводя данную подстановку и используя ориентационные преобразования ${{s}_{{ij}}} = f\left( {{{S}_{{ij}}},{{\varphi }},\theta ,~{{\psi }} = 0} \right)$ из приложения были получены формулы для нормализованных упругих жесткостей ${{K}_{{xx}}}{\text{/}}E$, ${{K}_{{yy}}}{\text{/}}E$, K/E, и эффективного коэффициента Пуассона ν*, см. табл. 1. Следует отметить, что формулы для K/E и ν*, в отличие от формул для ${{K}_{{xx}}}{\text{/}}E$ и ${{K}_{{yy}}}{\text{/}}E$, зависят только от направления $\vec {z} = \left[ {hkl} \right]$, поэтому ниже будем использовать обозначение $K\left( {\vec {z}} \right) = {{K}_{{hkl}}}$.
Таблица 1.
Формулы для нормализованных упругих жесткостей ${{K}_{{xx}}}{\text{/}}E$, ${{K}_{{yy}}}{\text{/}}E$, K/E и эффективного коэффициента Пуассона ν* для низкоиндексных кристаллографических ориентаций
| $\vec {x},\vec {y},\vec {z}$ | $\left[ {100} \right],\left[ {010} \right],\left[ {001} \right]$ | $\left[ {100} \right],\left[ {01\bar {1}} \right],\left[ {011} \right]$ | $\left[ {1\bar {1}0} \right],\left[ {11\bar {2}} \right],\left[ {111} \right]$ |
|---|---|---|---|
| $\frac{{{{K}_{{xx}}}}}{E}$ | $\frac{1}{{1 - \nu }}$ | $\frac{{1 + \nu - A{\text{/}}2}}{{1 - {{\nu }^{2}} - A{\text{/}}2}}$ | $\frac{1}{{1 - \nu - A{\text{/}}3}}$ |
| $\frac{{{{K}_{{yy}}}}}{E}$ | $\frac{1}{{1 - \nu }}$ | $\frac{{1 + \nu }}{{1 - {{\nu }^{2}} - A{\text{/}}2}}$ | $\frac{1}{{1 - \nu - A{\text{/}}3}}$ |
| $\frac{K}{E}$ | $\frac{2}{{1 - \nu }}$ | $\frac{{2\left( {1 + \nu } \right) - A{\text{/}}2}}{{1 - {{\nu }^{2}} - A{\text{/}}2}}$ | $\frac{2}{{1 - \nu - A{\text{/}}3}}$ |
| ν* | $\frac{{2\nu }}{{1 - \nu }}$ | $\frac{{2\nu \left( {1 + \nu - A{\text{/}}2} \right) - A{\text{/}}2}}{{1 - {{\nu }^{2}} - A{\text{/}}2}}$ | $\frac{{2\left( {\nu - A{\text{/}}3} \right)}}{{1 - \nu - A{\text{/}}3}}$ |
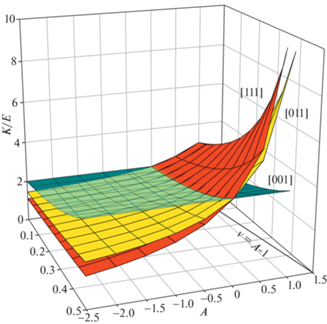
На рис. 4 представлена зависимость нормализованных упругих жесткостей ${{K}_{{001}}}{\text{/}}E$, ${{K}_{{011}}}{\text{/}}E$ и ${{K}_{{111}}}{\text{/}}E$ от коэффициента упругой анизотропии A и коэффициента Пуассона ν, аналогично диаграмме $\nu - A$, предложенной авторами ранее в работе [7]. Видно, что величины упругих жесткостей K001, K011 и K111 повышаются как с изменением A от отрицательных значений до предельного положительного значения $A = 1 + \nu $ (при данном ν), так и при увеличении $\nu $ от нуля до предельного значения 0.5. Причем при стремлении ν → 0.5 и A → 1.5, то есть к углу диаграммы $\nu - A$ величины упругих жесткостей K011 и K111 стремятся к бесконечности поскольку знаменатели формул для K011 и K111 стремятся к нулю. Соотношение величин ${{K}_{{001}}}$, ${{K}_{{011}}}$и ${{K}_{{111}}}$ определяется знаком A. При A < 0 выполняется неравенство ${{K}_{{001}}} > {{K}_{{011}}} > {{K}_{{111}}}$, при $A = 0$ все жесткости равны ${{K}_{{001}}} = {{K}_{{011}}} = {{K}_{{111}}}$, а при A > 0 неравенство меняет знак ${{K}_{{001}}} < {{K}_{{011}}} < {{K}_{{111}}}$. Независимо от знака A различие между величинами K001, K011 и K111 увеличивается с повышением $\nu $.
Рис. 4.
Зависимость нормализованных упругих жесткостей ${{K}_{{001}}}{\text{/}}E$, ${{K}_{{011}}}{\text{/}}E$ и ${{K}_{{111}}}{\text{/}}E$ от коэффициента упругой анизотропии A и коэффициента Пуассона ν.
5. Применение полученного решения для реальных структур. Полученное решение было применено для анализа анизотропии энергии остаточных напряжений в двухкомпонентных пластинчатых структурах следующих типов: в рафт-структуре γ/γ' монокристаллических никелевых жаропрочных сплавов и в многослойных эрозионностойких покрытиях, состоящих из множества чередующихся нанослоев ZrN и CrN.
Никелевые жаропрочные сплавы имеют двухфазную γ/γ'-микроструктуру, где матрицей является сложнолегированный γ-твердый раствор никеля (ГЦК, кубическая структура А1), а упрочнителем – дисперсные γ'-выделения (фаза на основе интерметаллида Ni3Al с упорядоченной кубической структурой L12). Кристаллические решетки γ- и γ'-фаз подобны, так как в обоих фазах атомы расположены в узлах ГЦК-решетки со структурой А1, при этом γ- и γ'-решетки имеют одинаковую кристаллографическую ориентацию, то есть для них выполняется следующее ориентационное соотношение ${{\left\{ {001} \right\}}_{\gamma }}\parallel {{\left\{ {001} \right\}}_{{\gamma '}}}$ и ${{\langle 100\rangle }_{\gamma }}\parallel {{\langle 100\rangle }_{{\gamma '}}}$. Рафт-структура γ/γ' формируется в никелевых жаропрочных сплавах в процессе высокотемпературной ползучести вследствие направленной коалесценции дисперсных выделений γ'-фазы. В результате этого процесса образуется периодическая структура, состоящая из протяженных γ- и γ'-пластин, разделенных (001) ориентированными интерфейсами. Образующиеся γ'-пластины термодинамически стабильны и эффективно тормозят движение деформационных дислокаций, таким образом многократно замедляя скорость ползучести сплава. Одним из факторов высокой термодинамической стабильности (001) ориентированной рафт-структуры является ее низкая удельная упругая энергия $\bar {W}$. В настоящей работе рассчитывали упругую энергию остаточных (мисфитных) напряжений в рафт-структуре [001] монокристаллов никелевого жаропрочного сплава CMSX-4 [8] после 150 часового испытания на ползучесть при температуре 1100°C и напряжении 120 МПа, проведенного в работе [9]. Для расчета $\bar {W}$ требуются следующие данные для сплава CMSX-4, соответствующие условиям испытаний: упругие податливости Sij γ- и γ'-фаз, объемная доля γ'-фазы ${{f}^{{\gamma '}}}$, и размерный мисфит γ- и γ'-пластин $\delta $. Согласно [10] Sij γ‑ и γ'-фаз очень близки и при 1100°C равны S11 = 14.27 ТПа–1, S12 = –6.01 ТПа–1, S44 = = 11.51 ТПа–1 и производные от них E = 70.1 ГПа, ν = 0.421 и A = +1.02; ${{f}^{{\gamma '}}}$(1100°C) = = 60.1% об. Размерный мисфит γ- и γ'-пластин ${{\delta }}$ в состоянии после ползучести является суммой мисфита кристаллических решеток изолированных γ- и γ'-фаз δ0, и деформационного мисфита ${{{{\delta }}}_{d}}$, обусловленного существенно большей пластической деформацией менее прочной γ-фазы, чем упрочняющей γ'-фазы. Согласно результатам измерений методом нейтронной дифракции δ0 сплава CMSX-4 при 1000°C равен –0.22% [11], а согласно рентгеноструктурным исследованиям ${{{{\delta }}}_{d}}$ сплава CMSX-4 после указанного выше испытания на ползучесть равен +0.31% [9]. Таким образом, результирующий размерный мисфит δ = –0.22% + 0.31% = +0.09%.
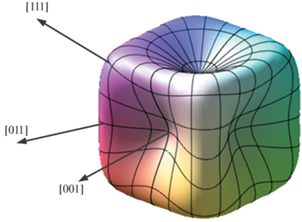
На рис. 5 показан 3D-график ориентационной зависимости $\bar {W} = f\left( {{{\varphi }},\theta } \right)$, рассчитанный с использованием вышеуказанных численных характеристик сплава CMSX-4. Видно, что при представлении в сферической системе координат поверхность $\bar {W} = f\left( {{{\varphi }},\theta } \right)$ имеет форму куба с вогнутыми внутрь гранями. Диагонали куба, вдоль которых $\bar {W}$ имеет максимальное значение, совпадают с кристаллографическими направлениями 〈111〉, а впадины на гранях куба, где $\bar {W}$ минимально, совпадают с направлениями 〈001〉. Кристаллографические направления 〈011〉 проходят через середину ребер куба, где $\bar {W}$ имеет промежуточное значение.
Рис. 5.
Представление ориентационной зависимости упругой энергии рафт-структуры γ/γ' $\bar {W} = f\left( {{{\varphi }},\theta } \right)$ сплава CMSX-4 в сферической системе координат.
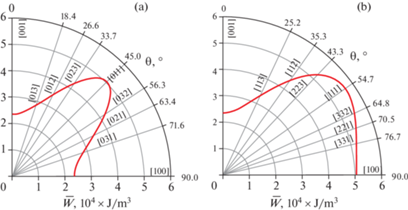
Более детально ориентационная зависимость упругой энергии может быть проанализирована в плоских сечениях поверхности $\bar {W} = f\left( {\varphi ,\theta } \right)$, как представлено на рис. 6. Зависимости $\bar {W} = f\left( {{{\varphi }} = 0,\theta } \right)$ и $\bar {W} = f\left( {{{\varphi }} = 45^\circ ,\theta } \right)$, соответствующие сечениям (100) и $\left( {1\bar {1}0} \right)$, построены в полярных координатах с использованием формул (3.27), (3.29), (4.3), (4.4). Из рис. 6 видно, что в этих сечениях лежит множество низкоиндексных направлений, которые обычно представляют наибольший интерес. Из рис. 6,а, зависимость $\bar {W} = f\left( {{{\varphi }} = 0,{{\theta }}} \right)$, и рис. 6,b, зависимость $\bar {W} = f\left( {{{\varphi }} = 45^\circ ,\theta } \right)$, видно, что энергия рафт-структуры сильно анизотропна. Минимально ее значение 2.35 ⋅ 104 Дж/м3 соответствует нормали [001] к плоскости интерфейса γ/γ', максимальное 5.68 ⋅ 104 Дж/м3 (в 2.4 раза выше, чем для [001]) соответствует нормали [111] и промежуточное значение 5.06 ⋅ 104 Дж/м3 (в 2.2 раза выше, чем для [001])) соответствует нормали [011]. Очевидно, что такая сильная анизотропия упругой энергии рафт-структуры стабилизирует ее в низкоэнергетической (001) ориентации, что оказывает положительный эффект на сопротивление ползучести [001] монокристаллов никелевых жаропрочных сплавов при высоких температурах.
Рис. 6.
Представление ориентационной зависимости упругой энергии рафт-структуры γ/γ' $\bar {W} = f\left( {{{\varphi }},\theta } \right)$ сплава CMSX-4 в полярной системе координат. (а) Вращение на угол θ вокруг оси [100], сечение (100), ${{\varphi }}$ = 0°. (b) Вращение на угол θ вокруг оси [1$\bar {1}$0], сечение $\left( {1\bar {1}0} \right)$, ${{\varphi }}$ = 45°.
Покрытия нитридов переходных металлов имеют высокую температуру плавления, высокую твердость, отличную физическую и химическую стабильность, что позволяет использовать эти покрытия для защиты деталей. Такие покрытия наносят методом ионно-плазменного напыления, в процессе которого образуются текстурированные покрытия с высокими остаточными напряжениями. Служебные свойства покрытий существенным образом зависят от кристаллографического направления их текстуры, которое определяется рядом факторов, таких как анизотропия скорости роста кристаллов, анизотропия энергии остаточных напряжений, кристаллографическая ориентация подложки и др. В настоящий работе будем рассматривать только фактор анизотропии энергии остаточных напряжений применительно к перспективным многослойным эрозионностойким покрытиям ZrN/CrN, состоящим из чередующихся нанослоев ZrN и CrN. Оба эти нитрида имеют кубическую кристаллическую решетку B1, структура типа NaCl. Для расчета энергии остаточных напряжений, как и вышеприведенном примере, требуются упругие податливости слоев Sij, объемная доля одного из слоев, например, CrN, и размерное несоответствие слоев δ. Согласно результатам работ [12, 13] упругие податливости ZrN и CrN близки и соответственно равны: $S_{{11}}^{{{\text{Zr}}}}$ = = 2.26 ТПа–1, $S_{{12}}^{{{\text{Zr}}}}$ = –0.355 ТПа–1, $S_{{44}}^{{{\text{Zr}}}}$ = 7.25 ТПа–1 для ZrN [12] и $S_{{11}}^{{{\text{Cr}}}}$ = 2.1 ТПа–1, $S_{{12}}^{{{\text{Cr}}}}$ = = –0.27 ТПа–1, $S_{{44}}^{{{\text{Cr}}}}$ = 10 ТПа–1 для CrN [13]. Далее в расчетах будем использовать величины упругих податливостей, усредненные как ${{\bar {S}}_{{ij}}} = (S_{{ij}}^{{{\text{ZrN}}}} + S_{{ij}}^{{{\text{CrN}}}}){\text{/}}2$: ${{\bar {S}}_{{11}}}$ = = 2.18 ТПа–1, ${{\bar {S}}_{{12}}}$ = –0.312 ТПа–1, ${{\bar {S}}_{{44}}}$= 8.62 ТПа–1 и производные от них E = 459 ГПа, ν = 0.143 и A = = –0.834. В работе [5] методом рентгеноструктурного анализа исследовали напыленное покрытие ZrN/CrN и получили следующие значения остаточных напряжений: ${{\sigma }}_{{xx}}^{{{\text{Zr}}}}$ = –550 МПа для слоя и ZrN и ${{\sigma }}_{{xx}}^{{{\text{Cr}}}}$ = +290 МПа для слоя CrN. Подставляя данное значение в уравнение равновесия (3.1), получаем объемную долю слоя CrN: f CrN = = ${{\sigma }}_{{xx}}^{{{\text{Zr}}}}{\text{/}}({{\sigma }}_{{xx}}^{{{\text{Zr}}}} - {{\sigma }}_{{xx}}^{{{\text{Cr}}}})$ = –550 МПа/(–550 МПа – 290 МПа) ≈ 65% об. Размерный мисфит δ в покрытии ZrN/CrN может быть оценен по формуле (3.13) как $\delta \, = \,{{\sigma }}_{{xx}}^{{{\text{Zr}}}}{\text{/}}{{f}^{{{\text{CrN}}}}}{{K}_{{xx}}}$. Согласно работе [14] преимущественным направлением текстуры покрытия ZrN/CrN является [111], поэтому используя соответствующую формулу для Kxx из табл. 1, выражение для δ может быть записано в виде ${{\delta }} = {{\sigma }}_{{xx}}^{{{\text{Zr}}}}{\text{/}}E \times \left( {1 - \nu - A{\text{/}}3} \right){\text{/}}{{f}^{{{\text{CrN}}}}}$. Подставляя сюда численные значения получаем δ ≈ –0.21%, то есть в нестественном состоянии слои ZrN длиннее чем слои CrN. Это согласуется с тем фактом, что размер элементарной ячейки ZrN больше чем CrN [5].
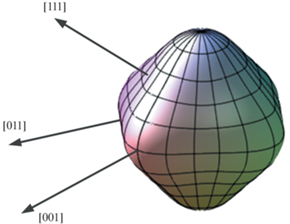
На рис. 7 показан 3D-график ориентационной зависимости $\bar {W} = f\left( {{{\varphi }},\theta } \right)$, рассчитанный с использованием вышеуказанных численных характеристик многослойного покрытия ZrN/CrN. Видно, что при представлении в сферической системе координат поверхность $\bar {W} = f\left( {{{\varphi }},\theta } \right)$ имеет форму близкую к октаэдру. Диагонали октаэдра, вдоль которых $\bar {W}$ имеет максимальное значение, совпадают с кристаллографическими направлениями 〈001〉, а нормали на граням октаэдра, где $\bar {W}$ минимально, совпадают с направлениями 〈111〉. Кристаллографические направления 〈011〉 проходят через середину ребер октаэдра, где $\bar {W}$ имеет промежуточное значение.
Рис. 7.
Представление ориентационной зависимости упругой энергии $\bar {W} = f\left( {{{\varphi }},\theta } \right)$ многослойного эрозионностойкого нанопокрытия ZrN/CrN в сферической системе координат.
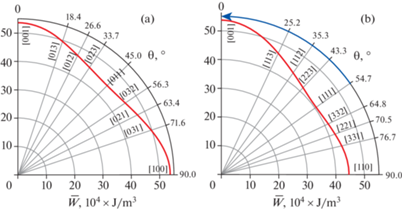
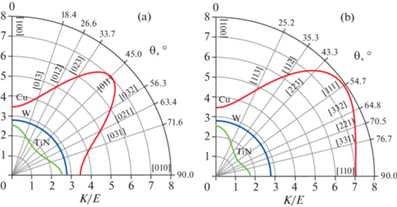
На рис. 8 ориентационная зависимость упругой энергии многослойного покрытия ZrN/CrN представлена в полярной системе координат, на рис. 8а – зависимость $\bar {W} = f\left( {{{\varphi }} = 0,\theta } \right)$, соответствующая сечению 3D-графика на рис. 7 плоскостью (100), и на рис. 8b – зависимость $\bar {W} = f\left( {{{\varphi }} = 45^\circ ,\theta } \right)$, соответствующая сечению 3D-графика плоскостью $\left( {1\bar {1}0} \right)$. Видно, что упругая энергия многослойного (111) ориентированного покрытия ZrN/CrN на порядок выше, чем упругая энергия (001) ориентированной рафт-структуры сплава CMSX-4, что объясняется как большим по абсолютной величине размерным мисфитом, ${\text{|}}{{\delta }^{{{\text{ZrN}}/{\text{CrN}}}}}{\text{|}}$ ≈ 0.21% против ${{\delta }^{{{\text{CMSX}} - 4}}}$ ≈ 0.09%, так и значительно большей жесткостью слоев нитридов, $K_{{111}}^{{{\text{ZrN}}/{\text{CrN}}}}$ ≈ 720 ГПа против $K_{{001}}^{{{\text{CMSX}} - 4}}$ ≈ ≈ 121 ГПа. В отличие от рафт-структуры сплава CMSX-4 с положительным коэффициентом анизотропии A = +1.02, для которого выполняется неравенство $\bar {W}_{{001}}^{{{\text{CMSX}} - 4}}$ < < $\bar {W}_{{011}}^{{{\text{CMSX}} - 4}}$ < $\bar {W}_{{111}}^{{{\text{CMSX}} - 4}}$, для многослойного покрытия ZrN/CrN с отрицательным коэффициентом анизотропии A = –0.834 выполнятся обратное неравенство $\bar {W}_{{001}}^{{{\text{ZrN}}/{\text{CrN}}}} > \bar {W}_{{011}}^{{{\text{ZrN}}/{\text{CrN}}}} > \bar {W}_{{111}}^{{{\text{ZrN}}/{\text{CrN}}}}$. Кроме того, степень анизотропии упругой энергии покрытия ZrN/CrN значительно меньше, чем для сплава CMSX-4, характеристическое отношение энергий для покрытия ZrN/CrN равно $\bar {W}_{{001}}^{{{\text{ZrN}}/{\text{CrN}}}}{\text{/}}\bar {W}_{{111}}^{{{\text{ZrN}}/{\text{CrN}}}}$ ≈ 1.3, тогда как для сплава CMSX-4 обратное характеристическое отношение равно $\bar {W}_{{111}}^{{{\text{CMSX}} - 4}}{\text{/}}\bar {W}_{{001}}^{{{\text{CMSX}} - 4}}$ ≈ ≈ 2.4. Такая низкая анизотропия упругой энергии покрытия ZrN/CrN возможно является причиной того, что при определенных условиях напыления покрытия может преобладать не фактор упругой энергии, а фактор ростовой анизотропии (более быстрый рост кубических кристаллов в направлении [001]), в результате чего в покрытиях ZrN/CrN, как и в ряде других нитридных покрытий, образуется не [111] ориентированная текстура, а текстуры с осями [113] или [001] [14–16], то есть происходит поворот оси текстуры в последовательности [111] → [113] → [001], как показано дуговой стрелкой на рис. 8,b.
Рис. 8.
Ориентационная зависимость упругой энергии $\bar {W} = f\left( {{{\varphi }},\theta } \right)$ многослойного покрытия ZrN/CrN в поляной системе координат. (а) Вращение на угол θ вокруг оси [100], сечение (100), ${{\varphi }}$ = 0°. (b) Вращение на угол θ вокруг оси [1$\bar {1}$0], сечение $\left( {1\bar {1}0} \right)$, ${{\varphi }}$ = 45°.
Упругое решение, полученное для двухкомпонентных структур, справедливо и для однослойных покрытий, если величину R(f B) в формуле (3.29) положить равной 1. Поэтому в настоящей работе с использованием полученного решения была также проанализирована анизотропия упругой энергии нескольких однослойных покрытий, нанесенных различными методами. Поскольку для большинства представленных в литературе покрытий размерный мисфит $\delta $ не известен, анализировалась только величина нормализованной жесткости K/E, которая напрямую связана с энергией W. На рис. 9 представлены ориентационные зависимости нормализованной жесткости K/E для трех типов покрытий: медного Cu, вольфрамового W и покрытия из нитрида титана TiN. Расчет зависимостей осуществляли по формулам (4.3), (4.4) с использованием литературных данных для упругих податливостей, для Cu и W из [17], и для TiN из [18]. Из рис. 9 видно, что для медного покрытия с положительным коэффициентом упругой анизотропии $A = + 0.98$ выполняется неравенство $K_{{001}}^{{{\text{Cu\;}}}}{\text{/}}{{E}^{{{\text{Cu}}}}} < K_{{011}}^{{C{\text{u}}~}}{\text{/}}{{E}^{{{\text{Cu}}}}} < K_{{111}}^{{C{\text{u}}~}}{\text{/}}{{E}^{{{\text{Cu}}}}}$, для покрытия TiN c $A = - 2.01$ справедливо обратное неравенство $K_{{001}}^{{{\text{TiN}}~}}{\text{/}}{{E}^{{{\text{TiN}}}}}$ > $K_{{011}}^{{{\text{TiN}}~}}{\text{/}}{{E}^{{{\text{TiN}}}}} > K_{{111}}^{{{\text{TiN}}~}}{\text{/}}{{E}^{{{\text{TiN}}}}}$, а для вольфрамового покрытия с $A \approx 0$ величина K/E практически изотропна, $K_{{001}}^{{{\text{W}}~}}{\text{/}}{{E}^{{\text{W}}}}\, \approx \,K_{{011}}^{{{\text{W}}~}}{\text{/}}{{E}^{{\text{W}}}}\, \approx \,K_{{111}}^{{{\text{W}}~}}{\text{/}}{{E}^{{\text{W}}}}$.
Рис. 9.
Ориентационные зависимости нормализованной жесткости $K{\text{/}}E = f\left( \theta \right)$ для трех типов покрытий – Cu (красные линии), W (синие линии) и TiN (зеленые линии). (а) – поворот осей x и y в плоскости (100). (b) – поворот осей x и y в плоскости $\left( {1\bar {1}0} \right)$.
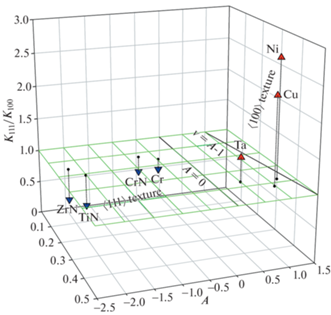
Как следует из графика на рис. 4 соотношение величин нормализованных упругих жесткостей покрытий ${{K}_{{001}}}{\text{/}}E$ и ${{K}_{{111}}}{\text{/}}E$, а, следовательно, и их упругих энергий W001 и W111, зависит от знака и величины коэффициента упругой анизотропии A, и величины коэффициента Пуассона ν. Поэтому следует ожидать корреляцию кристаллографического направления текстуры покрытий с величинами этих упругих характеристик. Для анализа этой корреляции для ряда покрытий был построен 3D-график, на котором горизонтальные оси показывают величины $A$ и $\nu $ материала покрытия, а вертикальная ось – соответствующее отношение ${{K}_{{111}}}{\text{/}}{{K}_{{001}}}$. Видно, что покрытия с положительным A (Ni, Cu, Ta), для которых отношение ${{K}_{{111}}}{\text{/}}{{K}_{{001}}} > 1$, показывают преимущественно текстуру 〈001〉, тогда как покрытия с отрицательным A (Cr, CrN, TiN, ZrN), для которых отношение ${{K}_{{111}}}{\text{/}}{{K}_{{001}}} < 1$, показывают преимущественно текстуру 〈111〉. Для построения данного графика использовались данные из следующих литературных источников: упругие константы для Ni, Cu, Ta и Cr из [17], TiN из [18], CrN из [13] и ZrN из [12]; данные о преимущественной ориентации текстуры для Ni из [19, 20], Cu из [20], Ta из [21], Cr из [20], CrN из [22], TiN из [15, 16] и ZrN из [16].
6. Упругая анизотропии с условием $S_{{ij}}^{A} = kS_{{ij}}^{B}$. Рассмотрим кратко в данном разделе пластинчатую структуру, аналогичную рассмотренной ранее в разделе 3, но не с равными упругими податливостями компонентов, а с пропорциональными, то есть для которых выполняется соотношение $S_{{ij}}^{A} = kS_{{ij}}^{B}$. Поскольку упругие податливости в лабораторной системе координат sij связаны с Sij линейной однородной связью, то для них справедливо аналогичное соотношение $s_{{ij}}^{A} = ks_{{ij}}^{B}$. Такое же соотношение следует из (3.21) для ${{{{\beta }}}_{{ij}}}$: ${{\beta }}_{{ij}}^{A} = k{{\beta }}_{{ij}}^{B}$. Используя соотношение $s_{{ij}}^{A} = ks_{{ij}}^{B}$ и (3.1)–(3.10), получаем формулы для компонент тензора деформаций и тензора напряжений, аналогичные (3.11)–(3.15), (3.22)
Однако величины сомножителей αC здесь другие
Упругие жесткости $K_{{xx}}^{C}$, $K_{{yy}}^{C}$ и $K_{{xy}}^{C}$ могут быть рассчитаны, используя формулы, аналогичные (3.18)–(3.21)
(6.9)
$K_{{xx}}^{C} = ~\frac{{\beta _{{22}}^{C} - \beta _{{12}}^{C}}}{{\beta _{{11}}^{C}\beta _{{22}}^{C} - {{{(\beta _{{12}}^{C})}}^{2}}}}$(6.10)
$K_{{yy}}^{C} = ~\frac{{\beta _{{11}}^{C} - \beta _{{12}}^{C}}}{{\beta _{{11}}^{C}\beta _{{22}}^{C} - {{{(\beta _{{12}}^{C})}}^{2}}}}$(6.11)
$K_{{xy}}^{C} = \frac{{s_{{16}}^{C}(\beta _{{22}}^{C} - \beta _{{12}}^{C}) + s_{{26}}^{C}(\beta _{{11}}^{C} - \beta _{{12}}^{C})}}{{s_{{66}}^{C}(\beta _{{11}}^{C}\beta _{{22}}^{C} - {{{(\beta _{{12}}^{C})}}^{2}})}}$При этом для упругих жесткостей выполняются соотношения пропорциональности
Формула для эффективного нормального коэффициента Пуассона ν* имеет вид, подобный (3.23)
(6.16)
$\nu {\text{*}} = - \frac{{\beta _{{13}}^{C}(\beta _{{22}}^{C} - \beta _{{12}}^{C}) + \beta _{{23}}^{C}(\beta _{{11}}^{C} - \beta _{{12}}^{C})}}{{\beta _{{11}}^{C}\beta _{{22}}^{C} - {{{(\beta _{{12}}^{C})}}^{2}}}}$Причем в силу пропорциональной связи ${{\beta }}_{{ij}}^{A} = k{{\beta }}_{{ij}}^{B}$ величина ν* не зависит от того какие ${{{{\beta }}}_{{ij}}}$ используются в расчете, ${{\beta }}_{{ij}}^{A}$ или ${{\beta }}_{{ij}}^{B}$.
Удельная упругая энергия компонентов структуры определяется соотношением (3.26) и записывается как
(6.18)
${{K}^{С}} = K_{{xx}}^{C} + K_{{yy}}^{C} = \frac{{\beta _{{11}}^{C} + \beta _{{22}}^{C} - 2\beta _{{12}}^{C}}}{{\beta _{{11}}^{C}\beta _{{22}}^{C} - {{{(\beta _{{12}}^{C})}}^{2}}}}$Здесь KC жесткость соответствующей пластины (A или B) при двухосной деформации, при этом как и для других жесткостей для KA и KB справедливо соотношение
Согласно (3.29), (6.7), (6.8) и (6.17) удельная упругая энергия структуры в целом равна
(6.20)
$\bar {W} = (1 - {{f}^{B}}){{W}^{A}} + {{f}^{B}}{{W}^{B}} = {{W}^{A}}\frac{{(k + 1 - {{f}^{B}})(1 - {{f}^{B}})}}{{k{{f}^{B}}}}$В случае k = 1 или $S_{{ij}}^{A} = S_{{ij}}^{B} = {{S}_{{ij}}}$ формулы, представленные в данном разделе, будут иметь вид формул, приведенных в разделе 3.
7. Выводы. Получено аналитическое решение для остаточных напряжений и их энергии в периодической двухкомпонентной пластинчатой структуре, где компоненты имеют идентичный тип упругой анизотропии, одинаковые или пропорциональные упругие константы и совпадающие главные оси упругой анизотропии. Полученное решение применено для анализа анизотропии упругой энергии таких кристаллических структур как рафт-структура γ/γ' монокристаллических никелевых жаропрочных сплавов, многослойных эрозионностойких нанопокрытий ZrN/CrN и однослойных покрытий различного типа. Показано, что сильная анизотропия упругой энергии стабилизирует низкоэнергетическую (001) ориентацию рафт-структуры [001] монокристаллов никелевых жаропрочных сплавов. Анизотропия упругой энергии многослойных нанопокрытий ZrN/CrN не столь сильно выражена, поэтому преимущественное направление текстуры покрытия [111], соответствующее наименьшей упругой энергии, может изменяться на [113] или [001] в зависимости от условий нанесения покрытий. В целом для покрытий наблюдается корреляция кристаллографического направления их текстуры и анизотропии упругой энергии, характер которой определяется величинами коэффициента упругой анизотропии $A$ и коэффициента Пуассона ν.
Работа выполнена при поддержке гранта Российского научного фонда (проект № 22-29-01200).
Приложение. Ниже приведены ориентационные зависимости упругих податливостей кубического кристалла
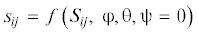 , где φ, θ и ψ – углы Эйлера. В настоящей работе рассматриваются только такие ориентации,
для которых ψ = 0. Приведенные формулы могут быть получены как с использованием общего
преобразования упругих податливостей, описанное в [23], так и специального упрощенного преобразования для кубических кристаллов, предложенного
в [24]. Матрица преобразования в углах Эйлера представлена в [25].
, где φ, θ и ψ – углы Эйлера. В настоящей работе рассматриваются только такие ориентации,
для которых ψ = 0. Приведенные формулы могут быть получены как с использованием общего
преобразования упругих податливостей, описанное в [23], так и специального упрощенного преобразования для кубических кристаллов, предложенного
в [24]. Матрица преобразования в углах Эйлера представлена в [25].
(2A)
${{s}_{{22}}} = {{S}_{{11}}} - \frac{S}{2}({\text{si}}{{{\text{n}}}^{2}}2{{\varphi co}}{{{\text{s}}}^{4}}\theta + {\text{si}}{{{\text{n}}}^{2}}2\theta )$(3A)
${{s}_{{12}}} = {{S}_{{12}}} + \frac{S}{2}{\text{si}}{{{\text{n}}}^{2}}2{{\varphi co}}{{{\text{s}}}^{2}}\theta $(4A)
${{s}_{{13}}} = {{S}_{{12}}} + \frac{S}{2}{\text{si}}{{{\text{n}}}^{2}}2{{\varphi si}}{{{\text{n}}}^{2}}\theta $(5A)
${{s}_{{23}}} = {{S}_{{12}}} + \frac{S}{2}\left( {1 - \frac{1}{4}{\text{si}}{{{\text{n}}}^{2}}2{{\varphi }}} \right){\text{si}}{{{\text{n}}}^{2}}2\theta $(9A)
${{s}_{{66}}} = {{S}_{{44}}} + 2S \times {\text{si}}{{{\text{n}}}^{2}}2{{\varphi co}}{{{\text{s}}}^{2}}\theta $Рис. 10.
Корреляция преимущественной ориентации текстуры покрытий кубических металлов и нитридов с их упругими характеристиками ν и A. Сравни с графиком на рис. 4.
Список литературы
Tabatabaeian A., Ghasemi A.R., Shokrieh M.M. et al. Residual stress in engineering materials: A review // Adv. Eng. Mater. 2022. V. 24. № 3. P. 2100786. https://doi.org/10.1002/adem.202100786
Wang X., Zurob H.S., Xu G. et al. Influence of microstructural length scale on the strength and annealing behavior of pearlite, bainite, and martensite // Metall. Mater. Trans. A. 2013. V. 44. P. 1454–1461. https://doi.org/10.1007/s11661-012-1501-1
Appel F., Clemens H., Fischer F. Modeling concepts for intermetallic titanium aluminides. Prog. Mater. Sci. 2016. V. 81. P. 55–124. https://doi.org/10.1016/j.pmatsci.2016.01.001
Svetlov I.L., Kuzmina N.A., Neiman A.V. et al. Effect of the rate of solidification on the microstructure, phase composition, and strength of Nb/Nb5Si3 in-situ composites // Bull. Russ. Acad. Sci. Phys. 2015. V. 79. P. 1146–1150. https://doi.org/10.3103/S1062873815090245
Muboyadzhyan S.A., Aleksandrov D.A., Gorlov D.S. Ion-plasma erosion-resistant nanocoatings based on metal carbides and nitrides // Russ. Metall. 2010. V. 2010. P. 790–799. https://doi.org/10.1134/S0036029510090077
Epishin A., Link T., Bruckner U., Portella P.D. Evolution of the γ/γ'-microstructure during high temperature creep of a nickel-base superalloy // Acta Mater. 2000. V. 48. P. 4169–4177. https://doi.org/10.1016/S1359-6454(00)00197-X
Епишин А.И., Лисовенко Д.С. Экстремальные значения коэффициента Пуассона кубических кристаллов // ЖТФ. 2016. Т. 86. № 10. С. 74–82.
Harris K., Erickson G.L., Sikkenga S.L. et al. Development of the rhenium containing superalloys CMSX-4 & CM 186 LC for single crystal blade and directionally solidified vane applications in advanced turbine engines // Superalloys. 1992. Warrendale, PA: TMS. P. 297–306. https://doi.org/10.7449/1992/Superalloys_1992_297_306
Epishin A., Link T., Brückner U. Microstructural stability of CMSX-4 and CMSX-10 under high temperature creep conditions. Materials for Advanced Power Engineering, FZ Jülich, 2006, P. 507–520.
Epishin A., Fedelich B., Finn M., Künecke G., Rehmer B., Nolze G., Leistner C., Petrushin N., Svetlov I. Investigation of elastic properties of the single-crystal nickel-base superalloy CMSX-4 in the temperature interval between room temperature and 1300°C // Crystals. 2021. V. 11. P. 152. https://doi.org/10.3390/cryst11020152
Glatzel U. Microstructure and internal strains of undeformed and creep deformed samples of a nickel-base superalloy. Berlin.: Verlag Dr. Köster, 1994. 80 p.
Chen X.-J., Struzhkin V.V., Wu Z. et al. Hard superconducting nitrides // PNAS USA. 2005. V. 102. № 9. P. 3198–3201. https://doi.org/10.1073/pnas.0500174102
Antonov V., Iordanova I. First principles study of crystallographic structure and elastic properties of chromium // AIP Conf. Proc. 2010. V. 1203. P. 1149–1154. https://doi.org/10.1063/1.3322328
Samim P.M., Fattah-alhosseini A., Elmkhah H., Imantalab O. Nanoscale architecture of ZrN/CrN coatings: microstructure, composition, mechanical properties and electrochemical behavior // J. Mater. Res. Technol. 2021. V. 15. P. 542–560. https://doi.org/10.1016/j.jmrt.2021.08.018
McKenzie D.R., Yin Y., McFall W.D., Hoang N.H. The orientation dependence of elastic strain energy in cubic crystals and its application to the preferred orientation in titanium nitride thin films // J. Phys.: Condens. Matter. 1996. V. 8. P. 5883–5890. https://doi.org/10.1088/0953-8984/8/32/008
Betsofen S.Y., Ashmarin A.A., Petrov L.M., Grushin I.A., Lebedev M.A. Effect of the ion-plasma process parameters on the texture and properties of TiN and ZrN coatings // Russ. Metall. 2021. V. 2021. P. 1238–1244. https://doi.org/10.1134/S0036029521100037
Second and higher order elastic constants // Ed. by D.F. Nelson. Springer, 1992. V. 29a of Landolt-Börnstein – Group III Condensed Matter. https://doi.org/10.1007/b44185
Kim J.O., Achenbach J.D., Mirkarimi P.B. et al. Elastic constants of single crystal transition metal nitride films measured by line focus acoustic microscopy // J. Appl. Phys. 1992. V. 72. P. 1805–1811. https://doi.org/10.1063/1.351651
Sampath S., Herman H. Rapid solidification and microstructure development during plasma spray deposition // J. Therm. Spray Technol. 1996. V. 5. P. 445–456. https://doi.org/10.1007/BF02645275
Ковенский И.М., Поветкин В.В. Металловедение покрытий, М.: СП Интермет Инжиниринг, 1999. 296 с.
Гончаров О.Ю., Ильин И.А., Титоров Д.Б., Титорова Д.В. Текстуры покрытий молибдена, тантала и борида гафния, полученных химическим газофазным осаждением // Перспективные материалы. 2008. № 4. С. 69–73.
Kirchlechner C., Martinschitz K.J., Daniel R. et al. Residual stresses and thermal fatigue in CrN hard coatings characterized by high-temperature synchrotron X-ray diffraction // Thin Solid Films. 2010. V. 518. № 8. P. 2090–2096. https://doi.org/10.1016/j.tsf.2009.08.011
Лехницкий С.Г. Теория упругости анизотропного тела. М.: Наука, 1977. 416 с.
Макклинток Ф., Аргон А. Деформация и разрушение материалов, М.: Мир, 1970. 443 с.
Голдстейн Г. Классическая механика. М.: Гостехиздат, 1957. 408 с.
Дополнительные материалы отсутствуют.
Инструменты
Известия РАН. Механика твердого тела