Известия РАН. Механика твердого тела, 2020, № 6, стр. 134-140

НАПРЯЖЕННОЕ СОСТОЯНИЕ НЕОГРАНИЧЕННОГО ПРОСТРАНСТВА ВБЛИЗИ ЦИЛИНДРИЧЕСКОЙ ПОЛОСТИ С НЕКРУГОВОЙ ФОРМОЙ ПОПЕРЕЧНОГО СЕЧЕНИЯ ДЛЯ СТАРЕЮЩИХ УПРУГОВЯЗКОПЛАСТИЧЕСКИХ МАТЕРИАЛОВ

Д. В. Гоцев^a, b, *, А. В. Ковалев^a, b, **, А. Ю. Яковлев^a, ***

^a Воронежский государственный университет
Воронеж, Россия

^b Военный учебно-научный центр Военно-воздушных сил “Военно-воздушная академия им. проф. Н.Е. Жуковского и Ю.А. Гагарина”
Воронеж, Россия

^* E-mail: rbgotsev@mail.ru
^** E-mail: kav-mail@mail.ru
^*** E-mail: yakovlev@amm.vsu.ru

Поступила в редакцию 18.05.2020
После доработки 11.06.2020
Принята к публикации 15.08.2020

DOI: 10.31857/S0572329920060082

Полный текст (PDF)

Аннотация

Настоящая работа посвящена определению напряженного состояния неограниченного пространства в окрестности цилиндрической полости (толстостенная плита с отверстием), имеющей в поперечном сечении форму близкую к правильной многоугольной (задача Галина–Ивлева). В качестве модели материала пространства использовалась модель среды, учитывающая стареющие упруговязкопластические свойства. Решение проводилось в рамках метода малого параметра, характеризующего отклонение формы отверстия от окружности, а также возмущение статических граничных условий. При этом невозмущенному состоянию соответствует осесимметричное упругопластическое напряженно-деформированное состояние толстой плиты с круговым отверстием из стареющего упруговязкопластического материала. В результате решения задачи получены аналитические выражения для компонент напряжений, а также уравнение для определения формы и размера границы раздела зон упругого и пластического деформирования плиты.

Ключевые слова: модель стареющего упруговязкопластического материала, двухосное растяжение, толстая плита с некруговым отверстием, метод возмущений, напряженное состояние

Модель наследственно стареющего вязкопластического материала была предложена Д.Д. Ивлевым и Н.Х. Арутюняном в работе [1]. В работах Ф.Б. Милявской построены поля напряжений в толстой плите из стареющего материала вблизи кругового [2] или эллиптического [3] отверстия при двухосном растяжении.

Подходы к постановке и исследованию неклассических задач наращивания вязкоупругих стареющих тел, основанные на приведении к задачам теории упругости, а также математические методы их решения активно и успешно разрабатываются в рамках научной школы, созданной А.В. Манжировым (см., например, [4–6]).

На основе общих идей теории возмущений в работах А.Н. Спорыхина и его учеников развита трехмерная линеаризированнная теория устойчивости сложных сред, в том числе сред, обладающих одновременно упругими, вязкими и пластическими свойствами при малых и конечных докритических деформациях [см., например, 7, 8]. С использованием схемы Ивлева–Ершова [9] получен ряд приближенных решений одного класса цилиндрических задач для упруговязкопластических материалов [см., например, 10], в том числе с учетом температурных эффектов [11].

Настоящим исследованием авторы продолжают цикл работ Д.Д. Ивлева и его учеников в направлении получения аналитических зависимостей, описывающих напряженные состояния в плоских упругопластических задачах о толстых плитах с некруговыми отверстиями методом малого параметра.

В данной статье решается задача о распределении поля напряжений в толстой плите, ослабленной цилиндрической полостью с формой поперечного сечения близкой к правильной m-угольной (m – количество сглаженных углов многоугольника). Материал плиты моделируется стареющей средой с упруговязкопластическими свойствами. На бесконечности плита растягивается взаимно перпендикулярными усилиями с интенсивностями P₁(t) и P₂(t). По внутренней поверхности полости приложена равномерно распределенная нагрузка интенсивностью P₀(t). Рассматривается такая схема нагружения, при которой в плите возникает зона пластического деформирования материала, полностью охватывающая внутреннюю поверхность цилиндрической полости. Необходимым условием реализации такого состояния является условие монотонного возрастания функциональных зависимостей P₁(t) и P₂(t). Задача решается методом малого параметра в рамках плоско-деформированного состояния в цилиндрической системе координат ($\rho ,\theta ,z$), при этом ось 0z направлена вдоль цилиндрической полости.

В зоне неупругих деформаций выполняется условие наследственной пластичности [1]

(1)

$\frac{1}{4}{{\left( {\frac{{{{\sigma }_{\rho }}(t) - {{\sigma }_{\theta }}(t)}}{{k(t)}} + ~\mathop \smallint \limits_0^t \left( {{{\sigma }_{\rho }}(\tau ) - {{\sigma }_{\theta }}(\tau )} \right)K{\kern 1pt} {\text{*}}(t,~\tau )d\tau } \right)}^{2}} + ~\,{{\left( {\frac{{{{\tau }_{{\rho \theta }}}}}{{k(t)}} + \,~\mathop \smallint \limits_0^t \,K{\kern 1pt} {\text{*}}(t,~\tau ){{\tau }_{{\rho \theta }}}(\tau )d\tau } \right)}^{2}} = 1$

где $K{\kern 1pt} {\text{*}}(t,~\tau )$ – ядро наследственного оператора [1–3], k(t) – переменный предел текучести, ${{\sigma }_{\rho }},\;{{\sigma }_{\theta }},\;{{\tau }_{{\rho \theta }}}$ – радиальная, тангенсальная и касательная компоненты тензора напряжений соответственно.

Решение будем проводить в рамках метода возмущений. В качестве малого параметра выберем величину δ, характеризующую отклонение формы рассматриваемого контура поперечного сечения полости от окружности, а также возмущение статических граничных условий. В этом случае все решения задачи представляются в виде рядов по степеням этого малого параметра [9, 10], при этом ограничимся только линейными по δ членами разложения

(2)

${{\sigma }_{\rho }} = \sigma _{\rho }^{{(0)}} + \delta \sigma _{\rho }^{{(1)}},\quad {{\sigma }_{\theta }} = \sigma _{\theta }^{{(0)}} + \delta \sigma _{\theta }^{{(1)}},\quad {{\tau }_{{\rho \theta }}} = \tau _{{\rho \theta }}^{{(0)}} + \delta \tau _{{\rho \theta }}^{{(1)}},\quad {{r}_{s}}\left( t \right) = r_{s}^{{\left( 0 \right)}}\left( t \right) + \delta r_{s}^{{\left( 1 \right)}}\left( t \right)$

где верхний индекс указывает на номер приближения, r_s(t) – радиус упругопластической границы в плите.

В плоскости плиты, перпендикулярной оси 0Z, согласно [10] запишем уравнение контура, ограничивающего отверстие в плите до деформации

(3)

$\rho = \alpha \left( {1 + \delta {{d}_{1}}\cos m\theta - \ldots } \right)$

где α – радиус кругового контура в невозмущенном состоянии.

Возмущение статических граничных условий примем в виде

(4)

$\frac{{{{P}_{1}}\left( t \right) - {{P}_{2}}\left( t \right)}}{2} = \delta \cdot {{d}_{2}}$

В соотношениях (3), (4) d₁, d₂ – константы, принимающие значения из отрезка [0, 1]. При этом вариант ${{d}_{1}} = 0$, ${{d}_{2}} \ne 0$ – соответствует двухосному растяжению толстой плиты с круговым отверстием, а в случае ${{d}_{2}} = 0$, ${{d}_{1}} \ne 0$ имеет место плита с отверстием близким по форме к правильному m-угольному под действием нормального давления.

Решение проведем в безразмерных параметрах и переменных, оставив им их прежние обозначения. При этом величины, имеющие размерность напряжений, отнесем к – ${{k}_{\infty }} = \mathop {\lim }\limits_{t \to \infty } k\left( t \right)$; величины, имеющие размерность длины отнесем к радиусу $r_{s}^{{(0)}}(0)$ упругопластической границы в плите для нулевого приближения в начальный момент времени; время t отнесем к некоторой константе t₀, имеющей размерность времени.

В качестве нулевого приближения выберем осесимметричное состояние неограниченного пространства, содержащего цилиндрическую полость, имеющую в поперечном сечении форму окружности радиуса α. На бесконечности данная конструкция растягивается взаимно перпендикулярными усилиями с интенсивностью P(t) = = ${{({{P}_{1}}\left( t \right) + {{P}_{2}}\left( t \right))} \mathord{\left/ {\vphantom {{({{P}_{1}}\left( t \right) + {{P}_{2}}\left( t \right))} {{{k}_{\infty }}}}} \right. \kern-0em} {{{k}_{\infty }}}}$.

В этом случае согласно [2, 3] поля напряжений в упругой области деформирования толстостенной плиты описываются формулами

(5)

$\sigma _{\rho }^{{\left( 0 \right)e}} = P\left( t \right) - \frac{{\varphi \left( t \right)k\left( t \right)}}{{{{\rho }^{2}}}},\quad \sigma _{\theta }^{{\left( 0 \right)e}} = P\left( t \right) + \frac{{\varphi \left( t \right)k\left( t \right)}}{{{{\rho }^{2}}}},\quad \tau _{{\rho \theta }}^{{\left( 0 \right)e}} = 0$

в пластической зоне соотношениями

(6)

$\sigma _{\rho }^{{\left( 0 \right)p}} = 2k\left( t \right)\varphi \left( t \right)\ln \left( {\frac{\rho }{\alpha }} \right) - {{P}_{0}}\left( t \right),\quad \sigma _{\theta }^{{\left( 0 \right)p}} = 2k\left( t \right)\varphi \left( t \right)\left( {\ln \left( {\frac{\rho }{\alpha }} \right) + 1} \right) - {{P}_{0}}\left( t \right),\quad \tau _{{\rho \theta }}^{{\left( 0 \right)p}} = 0$

Здесь и далее индекс “p” вверху величин указывает их принадлежность к пластической зоне, а индекс “e” – к упругой, φ(t) – функция от времени.

Радиус раздела зон упругого и пластического деформирования в толстой плите в нулевом приближении описывается следующим выражением

(7)

$r_{s}^{{\left( 0 \right)}}\left( t \right) = \alpha \cdot \sqrt {\exp \left( {\frac{{P\left( t \right) - {{P}_{0}}\left( t \right)}}{{k\left( t \right)\varphi \left( t \right)}} - 1} \right)} $

Знание аналитических зависимостей (5)–(7), описывающих нулевое приближение позволяет перейти к определению решения в первом приближении.

Граничные условия на бесконечности для первого приближения имеют вид [9]

(8)

$\sigma {{_{\rho }^{e}}^{\infty }} = P\left( t \right) - \delta {{d}_{2}}\cos ~2\theta ,\quad \sigma {{_{\theta }^{e}}^{\infty }} = P\left( t \right) + \delta {{d}_{2}}\cos ~2\theta ,\quad \tau {{_{{\rho \theta }}^{e}}^{\infty }} = \delta {{d}_{2}}\sin ~2\theta $

Общий вид линеаризованных условий сопряжения в напряжениях на упругопластической границе в плите для первого приближения описываются соотношениями

(9)

${{\left. {\left[ {\sigma _{{ij}}^{{(1)}} + \frac{{\partial \sigma _{{ij}}^{{(0)}}}}{{\partial \rho }}r_{s}^{{(1)}}} \right]} \right|}_{{\rho = 1}}} = 0$

В (9) и далее квадратные скобки обозначают разность стоящих в них величин в упругой и пластической областях.

Граничные условия на внутреннем контуре отверстия в толстой плите с учетом (3) и [1, 2, 12] представляются следующими выражениями

(10)

${{\left. {\sigma _{\rho }^{{\left( 1 \right)p}}} \right|}_{{\rho = \alpha }}} = - 2{{d}_{1}}k\left( t \right)\varphi \left( t \right)\cos m\theta ,\quad {{\left. {\tau _{{\rho \theta }}^{{\left( 1 \right)p}}} \right|}_{{\rho = \alpha }}} = - 2m{{d}_{1}}k\left( t \right)\varphi \left( t \right)\sin ~m\theta $

В пластической области плиты $\left( {\alpha < \rho < 1} \right)$, согласно [1, 9, 10] и с учетом условий (10) выражения для напряжений в первом приближении имеют вид

(11)

$\begin{array}{*{20}{c}} {\sigma _{\rho }^{{\left( 1 \right)p}} = \sigma _{\theta }^{{\left( 1 \right)p}} = \frac{2}{\rho }~\alpha {{d}_{1}}k\left( t \right)\varphi \left( t \right)(\sqrt {{{m}^{2}} - 1} \sin \gamma - \cos \gamma )\cos m\theta ,} \\ {\tau _{{\rho \theta }}^{{\left( 1 \right)p}} = \frac{2}{\rho }m\alpha {{d}_{1}}k\left( t \right)\varphi \left( t \right)\cos \gamma \sin m\theta } \end{array}$

где величина$\gamma = \sqrt {{{m}^{2}} - 1} \ln \left( {\rho {\text{/}}\alpha } \right)$.

В упругой области при ρ > 1 согласно [1, 3, 10, 13] и при учете граничных условий (8), напряженное состояние описывается формулами

$\begin{gathered} \sigma _{\rho }^{{\left( 1 \right)e}} = {{d}_{2}}\left( {\frac{4}{{{{\rho }^{4}}}} - \frac{3}{{{{\rho }^{2}}}} - 1} \right)\cos 2\theta + ~~\alpha {{d}_{1}}k\left( t \right)\varphi \left( t \right)\left( {\sqrt {{{m}^{2}} - 1} \sin \gamma {\kern 1pt} *\left( {\frac{{\left( {m + 2} \right)}}{{{{\rho }^{m}}}} - \frac{m}{{{{\rho }^{{ - m - 2}}}}}} \right)} \right. + \\ \left. {\, + \cos \gamma {\kern 1pt} *\left( {\frac{{\left( {m + 2} \right)\left( {m - 1} \right)}}{{{{\rho }^{m}}}} - \frac{{m\left( {m + 1} \right)}}{{{{\rho }^{{ - m - 2}}}}}} \right)} \right)\cos m\theta , \\ \end{gathered} $

(12)

$\begin{gathered} \sigma _{\theta }^{{\left( 1 \right)e}} = {{d}_{2}}\left( {\frac{3}{{{{\rho }^{4}}}} + 1} \right)\cos 2\theta + \alpha {{d}_{1}}k\left( t \right)\varphi \left( t \right)\left( {\sqrt {{{m}^{2}} - 1} \sin \gamma {\kern 1pt} *\left( {\frac{{\left( {m - 2} \right)}}{{{{\rho }^{m}}}} + \frac{m}{{{{\rho }^{{ - m - 2}}}}}} \right)} \right. + \\ \left. {\, + \cos \gamma {\kern 1pt} *\left( {\frac{{\left( {m - 2} \right)\left( {m - 1} \right)}}{{{{\rho }^{m}}}} + \frac{{m\left( {m + 1} \right)}}{{{{\rho }^{{ - m - 2}}}}}} \right)} \right)\cos m\theta , \\ \end{gathered} $

$\begin{gathered} \tau _{{\rho \theta }}^{{\left( 1 \right)e}} = {{d}_{2}}\left( {1 - \frac{3}{{{{\rho }^{4}}}} + \frac{2}{{{{\rho }^{2}}}}} \right)\cos 2\theta + m\alpha {{d}_{1}}k\left( t \right)\varphi \left( t \right)\left( {\sqrt {{{m}^{2}} - 1} \sin \gamma {\kern 1pt} *\left( {\frac{1}{{{{\rho }^{m}}}} - \frac{1}{{{{\rho }^{{ - m - 2}}}}}} \right)} \right. + \\ \left. {\, + \cos \gamma {\kern 1pt} *\left( {\frac{{\left( {m - 1} \right)}}{{{{\rho }^{m}}}} - \frac{{\left( {m + 1} \right)}}{{{{\rho }^{{ - m - 2}}}}}} \right)} \right) \\ \end{gathered} $

где $\gamma {\kern 1pt} * = {{\left. \gamma \right|}_{{\rho = 1}}}$.

Таким образом, полученные соотношения (11), (12) определяют напряженное состояние в толстой плите из стареющего упруговязкопластического материала для первого приближения.

Вид упругопластической границы в первом приближении $r_{s}^{{(1)}}$ определяется линеаризованным условием [2, 9]

(13)

$r_{s}^{{(1)}} = - {{\left. {[\sigma _{\theta }^{{(1)}}] \cdot {{{\left[ {\frac{{\partial \sigma _{\theta }^{{(0)}}}}{{\partial \rho }}} \right]}}^{{ - 1}}}} \right|}_{{\rho = 1}}}$

Из (13) с учетом (11), (12) получим соотношение для определения радиуса упругопластической границы в толстой плите для первого приближения в форме

(14)

$r_{s}^{{\left( 1 \right)}} = \frac{{{{d}_{2}}r_{s}^{{\left( 0 \right)}}\left( t \right)}}{{k\left( t \right)\varphi \left( t \right)}}\cos 2\theta + \alpha {{d}_{1}}(\sqrt {{{m}^{2}} - 1} \left( {m - 2} \right)\sin \gamma {\kern 1pt} * + m\left( {m - 1} \right)\cos \gamma {\kern 1pt} *)\cos m\theta $

Анализ выражений (11), (12), (14) показывает, что при постоянных нагрузках и $k(t) = k(0)$ решение совпадает с результатами упругопластической задачи [9, 10]; если в указанных соотношениях положить ${{d}_{1}} = 0$, то приходим к решению [2] задачи о двухосном растяжении толстой плиты с круговым отверстием; если в соотношениях (11), (12), (14) принять ${{d}_{2}} = 0$ и m = 2, то полученные решения совпадают с решениями [3] задачи о толстой плите с эллиптическим отверстием под действием нормального давления.

Для построения графических зависимостей, иллюстрирующих форму и размер упругопластической границы в плите в различные моменты времени, положим [3]

$k\left( t \right) = \frac{{1 - \beta \cdot {{e}^{{ - \alpha t}}}}}{{1 - \beta }},\quad K\left( \tau \right) = \frac{{\alpha \beta \left( {1 - \beta } \right) \cdot {{e}^{{ - \alpha t}}}}}{{{{{(1 - \beta \cdot {{e}^{{ - \alpha t}}})}}^{2}}}},\quad \varphi \left( t \right) = \frac{{{{{(1 - \beta \cdot {{e}^{{ - \alpha t}}})}}^{2}}}}{{{{{\left( {1 - \beta } \right)}}^{2}}}}$

В качестве оставшихся относительных исходных данных примем

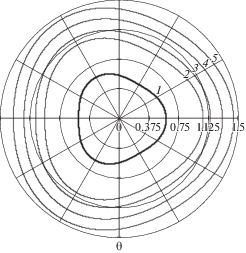
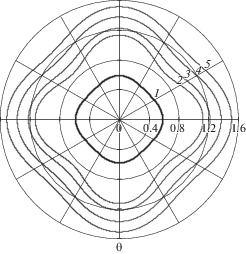
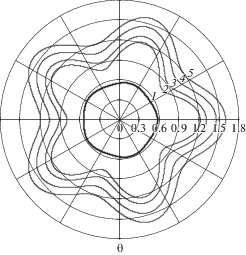
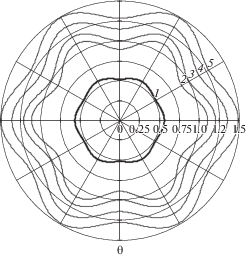
$\begin{gathered} {{P}_{0}}\left( t \right) = 0,\quad {{P}_{1}}\left( t \right) = 2 - 1.2 \cdot {{e}^{{ - 0.1t}}},\quad {{P}_{2}}\left( t \right) = 1.84 - 1.2 \cdot {{e}^{{ - 0.1t}}}, \\ \delta = 0.03,\quad {{d}_{1}} = {{d}_{2}} = 1,\quad \alpha = 0.5{\text{,}}\quad \beta \,\, = \,\,{\text{0}}{\text{.2}} \\ \end{gathered} $

На рисунках 1–4 представлены контур отверстия в плите (кривые 1), а также форма и размер границы раздела зон упругого и пластического деформирования материала в различные моменты времени (кривые 2, 3, 4, 5) для случаев контура отверстия близкой к правильной треугольной форме (m = 3 – рис. 1), квадратной (m = 4 – рис. 2), правильной пятиугольной (m = 5 – рис. 3) и правильной шестиугольной (m = 6 – рис. 4). При этом на каждом из рисунков 1–4 кривые 2 соответствуют начальному моменту времени t = 0, кривые 3, 4 – относительным моментам t = 12, 20, кривые 5 описывают положение и форму упругопластической границы при $t \to \infty $.

Рис. 1

Рис. 2

Рис. 3

Отметим, что используемый в настоящей работе подход применения метода малого параметра для получения аналитических зависимостей, описывающих поля напряжений и перемещениях в толстых плитах с некруговыми отверстиями допускает обобщение на случаи более сложных моделей сред, предложенных в [1]. В частности данный подход может быть использован для получения аналитических зависимостей для модели наследственно неоднородно-стареющего трансляционно-упрочняющегося упруговязкопластического тела.

Рис. 4

Список литературы

Арутюнян Н.Х., Ивлев Д.Д. К теории вязкопластичности неоднородно-стареющих тел // Изв. АН АрмССР. Механика. 1996. Т. 35. № 5. С. 22–26.
Милявская Ф.Б. Двуосное растяжение пластины с круговым отверстием из стареющего упругопластического материала // Краевые задачи и их приложения. Чебоксары: Чуваш. университет. 1986. С. 82–90.
Милявская Ф.Б. О двуосном растяжении толстой пластины с эллиптическим отверстием из стареющего материала // Краевые задачи и их приложения. – Чебоксары: Чуваш. университет. 1987. С. 169–174.
Арутюнян Н.Х., Манжиров А.В. Контактные задачи теории ползучести. Ереван: Институт механики НАН, 199. 320 с.
Manzhirov A.V. Fundamentals of mechanical design and analysis for am fabricated parts, Procedia Manufacturing. 2017. V. 7. P. 59–65. https://doi.org/10.1016/j.promfg.2016.12.017
Паршин Д.А. Аналитические решения задачи об аддитивном формировании неоднородного упругого шарового тела в произвольном нестационарном центральном поле сил // Изв. РАН. МТТ. 2017. № 5. С. 70–82.
Спорыхин А.Н., Шашкин А.И. Устойчивость равновесия пространственных тел и задачи механики горных пород. М.: ФИЗМАТЛИТ, 2004. 232 с.
Андреева И.Ю., Гоцев Д.В., Спорыхин А.Н. Устойчивость слоистой цилидрической оболочки с упруговязкопластическим заполнителем при нагружении // В сборнике: Современные проблемы механики и прикладной математики сб. трудов международной школы-семинара. Ответст. ред. А.Д. Чернышов. 2004. С. 20–23.
Горностаев К.К., Ковалев А.В. О симметричной деформации упрочняющейся упруговязкопластической трубы с учетом температуры // Вестник Чувашского государственного педагогического университета им. И.Я. Яковлева. Серия: Механика предельного состояния. 2015. № 3 (25). С. 176–184.
Ивлев Д.Д., Ершов Л.В. Метод возмущений в теории упругопластического тела. М.: Наука, 1978. 208 с.
Спорыхин А.Н., Ковалев А.В., Щеглова Ю.Д. Неодномерные задачи упруговязкопластичности с неизвестной границей. Воронеж: Изд-во ВГУ, 2004. 219 с.
Ковалев А.В., Яковлев Двухосное растяжение упругопластического пространства с призматическим включением // Современные методы в теории краевых задач. Воронежская весенняя математическая школа. 1999. С. 287.
Бицено К.Б., Граммель Р. Техническая динамика. Л.: Гостехиздат, 1950. Т. 1. 900 с.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Известия РАН. Механика твердого тела

Архивы выпусков Информация о журнале Отправить рукопись в журнал