Химическая физика, 2022, T. 41, № 9, стр. 33-44
Кинетическая модель газообразования в мелкодисперсной конденсированной системе
В. А. Дубовицкий 1, *, В. В. Барелко 1, З. С. Андрианова 1, Л. Н. Гак 1
1 Институт проблем химической физики Российской академии наук
Черноголовка, Россия
* E-mail: dubv@icp.ac.ru
Поступила в редакцию 24.05.2021
После доработки 08.02.2022
Принята к публикации 21.03.2022
- EDN: RSYFBS
- DOI: 10.31857/S0207401X22090035
Аннотация
Рассмотрена кинетическая модель изменения состава гомогенной смеси мелкодисперсного конденсированного вещества и газообразных компонент в замкнутой системе постоянного объема, принимающей поток тепла. Модель описывает быстрые переходные процессы при установлении детального равновесия и перестройках неустойчивых состояний. Расчеты показали, что предложенная модель качественно воспроизводит наблюдаемые взрывные процессы при движении разрушенного ледяного метеорита в атмосфере и прохождении импульса электрического тока в проводнике.
ВВЕДЕНИЕ
В природе и технике существуют явления, когда быстрые взрывоподобные изменения термодинамических параметров происходят в химически нейтральных системах, обменивающихся энергией с окружающей средой. Примерами такого рода являются взрывы автоклавов, метеоритов при движении в плотных слоях атмосферы, магматических очагов вулканов, электровзрыв проводника. Причины таких явлений давно дискутируются, но до сих пор не обрели устоявшейся теоретической схемы и поэтому эта тема сохраняет актуальность.
Предложенные в литературе подходы к объяснению взрывных явлений в химически инертных системах исходят из предположений о целостности исследуемого объекта. Так, при газодинамическом моделировании [1] процессов при движении болида рассматривается твердое тело, к которому применимы постулаты механики сплошных сред. В рамках такого подхода единственным каналом уменьшения массы болида является испарение либо абляция при поверхностном нагреве, которыми невозможно объяснить наблюдаемый во многих случаях практически мгновенный объемный взрыв и исчезновение метеоритов при входе в плотные слои атмосферы.
В рамках концепции “фазового взрыва” [2, 3] исходят из представлений о термодинамическом равновесии изолированной жидкофазной системы в изотермических условиях. Причиной взрывного газообразования здесь является наличие метастабильных особенностей термодинамического потенциала. Применимость этого подхода ограничивается отсутствием учета подвода энергии, а также изменением во времени компонент и температуры.
Один из возможных, но не изученных в литературе путей объяснения явлений такого рода – рассмотрение на элементарном уровне неизотермической кинетики процесса испарения и газообразования для мелкодисперсного вещества в конденсированном состоянии в условиях подвода внешнего потока энергии. Этот подход был высказан в работе [4] и существенно отличается от перечисленных выше концепций. Основной идеей здесь является предположение о четком разделении стадии разрушения изначально целостного объекта в конденсированном состоянии и следующей стадии, на которой в сформировавшейся мелкодисперсной системе по законам кинетики происходят реакции химических превращений, паро- и газообразования. И уже потом переведенное в газопаровое состояние сильно сжатое вещество взрывоподобно расширяется, приводя к объемному взрыву, который формирует ударную волну с катастрофическими последствиями.
В статье предложена общая кинетическая модель такого типа для многокомпонентной мелкодисперсной системы. Процесс разрушения и диспергирования не рассматривается и предполагается завершившимся к начальному моменту времени. Возможным механизмом разрушения в случае метеоритов могут служить механические напряжения и ударные волны в материале твердого болида, возникающие при торможении в атмосфере [5–7], потеря гидродинамической устойчивости [8–11]. Другим возможным механизмом диспергирования может служить также детонационное распространение волн фазовых превращений [12] в твердом теле, которое инициируется при торможении.
Очевидно, что более адекватная математическая модель должна быть значительно сложнее, согласованно включая описание процесса диспергирования и кинетику элементарных превращений компонент, газодинамику расширения системы, а также учитывать при описании испарения метеорита эффекты [13–16]. Эта проблематика выходит за рамками данной статьи.
МАТЕМАТИЧЕСКАЯ МОДЕЛЬ
Кинетические уравнения
Рассмотрим гомогенную систему постоянного объема, содержащую m компонент в мелкодисперсном конденсированном и газообразном состояниях. Будем предполагать следующее:
• вещества взаимодействуют по n обратимым реакциям, причем изменение объемных концентраций и температуры подчиняется обычным уравнениям химической кинетики;
• в систему поступает поток энергии, а обмен веществом с внешней средой пренебрежимо мал.
Постоянство объема системы неявно предполагает, что у этой системы либо есть внешнее ограничение (оболочка), либо длительность моделируемого процесса столь мала, что изменение объема пренебрежимо мало. В рассмотренных примерах это выполнено.
Запишем рассматриваемые обратимые элементарные реакции в форме
(1)
$\sum\limits_{i = 1}^m {{{\alpha }_{{ij}}}{{X}_{i}}} \leftrightarrow \sum\limits_{i = 1}^m {{{\beta }_{{ij}}}{{X}_{i}}} ,\,\,\,\,\,\,j = 1, \ldots ,n,$Обозначим через ${{x}_{1}},...,{{x}_{m}},$ и T концентрации компонент и температуру, введем в рассмотрение множества индексов компонент в газообразном и конденсированном состоянии: ${{I}_{g}},{{I}_{s}}.$ Будем полагать, что скорости химических превращений подчиняются закону действующих масс и имеют для прямых (w+) и обратных (w–) реакций вид
(2)
$\begin{gathered} w_{j}^{ + }(x,T) = \hat {k}_{j}^{ + }{{T}^{{{{d}_{j}}}}}\exp \left( {{{ - E_{j}^{ + }} \mathord{\left/ {\vphantom {{ - E_{j}^{ + }} {RT}}} \right. \kern-0em} {RT}}} \right)x_{1}^{{{{\alpha }_{{1j}}}}}...x_{m}^{{{{\alpha }_{{mj}}}}}, \\ w_{j}^{ - }(x,T) = \hat {k}_{j}^{ - }{{T}^{{{{d}_{j}}}}}\exp \left( {{{ - E_{j}^{ - }} \mathord{\left/ {\vphantom {{ - E_{j}^{ - }} {RT}}} \right. \kern-0em} {RT}}} \right)x_{1}^{{{{\beta }_{{1j}}}}}...x_{m}^{{{{\beta }_{{mj}}}}}, \\ \end{gathered} $(3)
$\begin{gathered} {{\hat {k}_{j}^{ + }} \mathord{\left/ {\vphantom {{\hat {k}_{j}^{ + }} {\hat {k}_{j}^{ - }}}} \right. \kern-0em} {\hat {k}_{j}^{ - }}} = \exp \left( {\sum\limits_{i = 1}^m {{{({{\beta }_{{ij}}} - {{\alpha }_{{ij}}}){{s}_{i}}} \mathord{\left/ {\vphantom {{({{\beta }_{{ij}}} - {{\alpha }_{{ij}}}){{s}_{i}}} R}} \right. \kern-0em} R}} } \right), \\ {{Q}_{j}} = \sum\limits_{i = 1}^m {({{\alpha }_{{ij}}} - {{\beta }_{{ij}}}){{h}_{i}}} ,\,\,\,\,E_{j}^{ - } - E_{j}^{ + } = {{Q}_{j}}, \\ \end{gathered} $В силу сделанных предположений из законов сохранения вещества и энергии получаем систему дифференциальных уравнений, описывающих изменение концентраций и температуры:
(4)
${{\dot {x}}_{i}} = \sum\limits_{j = 1}^n {({{\beta }_{{ij}}} - {{\alpha }_{{ij}}})\left[ {w_{j}^{ + }(x,T) - w_{j}^{ - }(x,T)} \right]} ,$(5)
$\begin{gathered} {{d\left( {\sum\limits_{i = 1}^m {{{c}_{i}}{{x}_{i}}T} } \right)} \mathord{\left/ {\vphantom {{d\left( {\sum\limits_{i = 1}^m {{{c}_{i}}{{x}_{i}}T} } \right)} {dt}}} \right. \kern-0em} {dt}} = \\ = \sum\limits_{j = 1}^n {{{Q}_{j}}\left[ {w_{j}^{ + }(x,T) - w_{j}^{ - }(x,T)} \right]} + J(t). \\ \end{gathered} $(6)
$\begin{gathered} \frac{d}{{dt}}H(x,T) = J(t), \\ H(x(t),\,\,\,\,T(t)) - H(x(0),\,\,\,\,T(0)) = \int\limits_0^t {J(\tau )d\tau } , \\ \end{gathered} $Примем, что давление газовых компонент в модели описывается уравнением состояния идеального газа:
Будем считать известными и неотрицательными начальные условия: ${{x}_{i}}(0) = x_{i}^{0},$ $T(0) = {{T}^{0}}.$ Свойства дифференциальных уравнений химической кинетики хорошо изучены [18]. В частности, при наличии для схемы реакций (1) положительного вектора материальных балансов и соотношений (3) решение (4), (5) определено на полуоси $t \geqslant 0,$ неотрицательно и ограничено. Решение (4), (5) в общем случае можно исследовать только численно, например путем численного интегрирования по программам, реализующим алгоритмы [19], основанные на неявной разностной схеме Эйлера.Отметим, что используемые нами понятия концентрации и скорости реакций описывают поведение мелкодисперсной системы в некотором промежуточном масштабе. Так, мольная концентрация дисперсного конденсированного вещества – это отношение количества молей этого вещества в некоторой области к ее объему при условии, что размер области мал, но больше характерного размера частиц. Скорости реакций (2) означают предел числа превращений в единичном объеме в единицу времени, который достигается при микроскопическом диспергировании и не зависит от распределения частиц по геометрической форме и размеру.
Асимптотика по быстрым реакциям и квазистационарное приближение
В случае быстрых обратимых реакций (1) решение кинетических уравнений (4), (5) обладает асимптотикой по большим константам скоростей реакций. Эта асимптотика полезна и позволяет просто описать поведение решения. Введем в рассмотрение малый параметр
Определим прямоугольную матрицу $B = \{ {{b}_{{li}}}\} ,$ $1 \leqslant l \leqslant L,$ $1 \leqslant i \leqslant m,$ состоящую из максимального набора линейно независимых балансов реакций (1), т.е. векторов решений $b = ({{b}_{1}},...,{{b}_{m}})$ однородной системы линейных уравнений:
Из соотношений (3) следует, что при любой температуре T набор концентраций ${{\tilde {x}}_{i}}(T) = $ $ = \exp ({{{{s}_{i}}} \mathord{\left/ {\vphantom {{{{s}_{i}}} R}} \right. \kern-0em} R} - {{{{h}_{i}}} \mathord{\left/ {\vphantom {{{{h}_{i}}} {RT}}} \right. \kern-0em} {RT}})$ является положительной точкой детального равновесия реакций (1), т.е. $w_{j}^{ + }(\tilde {x}(T),T) = w_{j}^{ - }(\tilde {x}(T),T).$ Согласно теории, изложенной в работе [18], для кинетических уравнений обратимых реакций в изотермических условиях решение (4) при $t \to \infty $ стремится к единственной положительной точке детального равновесия на балансной плоскости, проходящей через вектор начальных условий. Учитывая точное выполнение для системы (4), (5) законов сохранения, естественно ожидать, что предел при $\varepsilon \downarrow 0$ решения (4), (5) будет удовлетворять условиям детального равновесия, материального и энергетического баланса. Запишем формально эти уравнения:
(9)
$\sum\limits_{i = 1}^m {({{\beta }_{{ij}}} - {{\alpha }_{{ij}}})(RT\ln {{x}_{i}} - T{{s}_{i}} + {{h}_{i}})} = 0,\,\,\,\,1 \leqslant j \leqslant n,$(10)
$\sum\limits_{i = 1}^m {{{b}_{{li}}}\left( {{{x}_{i}} - x_{i}^{0}} \right)} = 0,\,\,\,\,1 \leqslant l \leqslant L,$– объемная плотность энергии, полученной системой к моменту времени t. Заметим, что уравнение (9) получается логарифмированием равенства $w_{j}^{ + }(x,T) = w_{j}^{ - }(x,T)$ для положительного вектора концентраций x. Кроме того, соотношения (9), (10) означают, что при фиксированной температуре T вектор концентраций x является решением экстремальной задачи:
где – функция объемной плотности свободной энергии Гиббса. То есть решение x минимизирует при заданной температуре T свободную энергию на неотрицательных векторах балансной плоскости, содержащей ${{x}^{0}}.$ В силу строгой выпуклости и гладкости функции $G(x,T)$ этот минимум существует и единственен. Обозначив его через ${{x}^{{eq}}}(T),$ получаем непрерывно дифференцируемую векторную функцию значений равновесных концентраций. С использованием значения ${{x}^{{eq}}}(T)$ определим равновесное значение полной энергии:Функция равновесной энергии имеет положительную нижнюю линейную оценку роста при $T \to \infty ,$ так как
В общем случае эта функция может иметь локальные экстремумы при $T \geqslant 0.$ Именно локальные максимумы ${{H}^{{eq}}}(T)$ определяют быстрые переходные процессы решения кинетической системы (4), (5).
Полезно в связи с этим ввести понятие критического значения энергии: значение энергии E называется критическим, если найдется такое число $T > 0,$ что ${{H}^{{eq}}}(T) = E,$ $\frac{d}{{dT}}{{H}^{{eq}}}(T) = 0.$ В противном случае E называется регулярным.
Множество всех критических значений E обозначим как E*. Как правило, оно пусто или состоит из конечного набора точек. Теперь мы можем точно охарактеризовать асимптотическое приближение точного решения (4), (5) к решению (9)–(11). Обозначим решение (4), (5) при начальных условиях $x(0) = {{x}^{0}},$ $T(0) = {{T}^{0}},$ соответствующее значению параметра $\varepsilon ,$ через ${{x}^{\varepsilon }}(t),{{T}^{\varepsilon }}(t).$
Предложение. Существует пара функций $\bar {x}(t),$ $\bar {T}(t),$ являющихся решением уравнений (9)–(11), таких что:
1) для времени t > 0 такого, что E(t) + $ + \,H({{x}^{0}},{{T}^{0}}) \notin E*,$ выполнены условия
2) для интервала времен  такого, что при
такого, что при 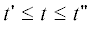 выполнено условие E(t) + $ + \,H({{x}^{0}},{{T}^{0}}) \notin E{\text{*}}$ (т.е. энергия системы не принимает на этом интервале критических значений), сходимость
равномерна по t.
выполнено условие E(t) + $ + \,H({{x}^{0}},{{T}^{0}}) \notin E{\text{*}}$ (т.е. энергия системы не принимает на этом интервале критических значений), сходимость
равномерна по t.
Доказательство Предложения сводится к обобщению рассуждений [18] о методе квазистационарных концентраций на случай неизотермической кинетики обратимых реакций и получается приложением теоремы Тихонова [20] для системы уравнений (4)–(6) с малым параметром при производной. Быстрыми переменными в этих уравнениях являются концентрации x, а медленными – материальные балансы и энергия H. Неравенство ${{d{{H}^{{eq}}}} \mathord{\left/ {\vphantom {{d{{H}^{{eq}}}} {dT}}} \right. \kern-0em} {dT}} \geqslant 0$ – это форма условия устойчивости корня для системы уравнений связи быстрых и медленных переменных в теореме Тихонова (так называемое присоединенное уравнение [16]).
Будем называть функции $\bar {x}(t),$ $\bar {T}(t)$ квазистационарным приближением решения (4), (5). Из сформулированного Предложения следует, что скачкообразное поведение решения $\bar {x}(t),\bar {T}(t)$ происходит при t = 0 и в моменты времени t, когда приобретенная системой в ходе накачки потоком энергия $E(t) + H({{x}^{0}},{{T}^{0}})$ принимает критические значения $E{\text{*}}{\text{.}}$ Первый скачок компонент происходит при t = 0 в ходе установления в системе равновесия, соответствующего начальным условиям. Далее с ростом E(t) происходит непрерывное изменение $\bar {x}(t),\bar {T}(t),$ которое прерывается при ${{d{{H}^{{eq}}}(\bar {T}(t))} \mathord{\left/ {\vphantom {{d{{H}^{{eq}}}(\bar {T}(t))} {dT}}} \right. \kern-0em} {dT}} = 0,$ т.е. при достижении энергией системы $E(t) + H({{x}^{0}},{{T}^{0}})$ критического значения. При этом скачок температуры минует участок с ${{d{{H}^{{eq}}}(T)} \mathord{\left/ {\vphantom {{d{{H}^{{eq}}}(T)} {dT}}} \right. \kern-0em} {dT}} < 0,$ соответствующий неустойчивым равновесным состояниям (4), (5). Температура после скачка принимает минимальное значение T, такое что
Вычисление асимптотических предельных функций $\bar {x}(t),\bar {T}(t)$ сводится к решению уравнений термодинамического равновесия (8)–(10) с заданной плоскостью материальных балансов и полной энергией. Оно эффективно реализуется алгоритмом, использующим итерации метода Ньютона, и не связано с численным интегрирование кинетических уравнений (4), (5).
Предположение о постоянстве удельных термодинамических величин ${{s}_{i}},{{h}_{i}},{{c}_{i}}$ не является существенным для теоретического анализа и сделано для краткости. Сформулированные результаты справедливы в более общем случае, когда удельные термодинамические функции зависят от T в рамках согласованного описания, приведенного в современных базах данных термохимии, например в [21].
ПРИМЕРЫ
Оценка кинетических параметров испарения и конденсации
Рассмотрим простейший вариант модели, в котором система состоит из одного мелкодисперсного конденсированного компонента X и его пара Y. Процессы испарения и конденсации описывает одна обратимая реакция: ${\text{X}} \leftrightarrow {\text{Y}}{\text{.}}$
Уравнения (4), (5) принимают вид
(14)
$\begin{gathered} \dot {x} = - {{k}^{ + }}(T)x + {{k}^{ - }}(T)y,\,\,\,\,\dot {y} = {{k}^{ + }}(T)x - {{k}^{ - }}(T)y, \\ \frac{d}{{dt}}[({{c}_{x}}x + {{c}_{y}}y)T] = Q\left[ {{{k}^{ + }}(T)x - {{k}^{ - }}(T)y} \right] + J(t), \\ x(0) = {{x}^{0}},\,\,\,\,y(0) = {{y}^{0}},\,\,\,\,T(0) = {{T}^{0}}, \\ \end{gathered} $(16)
${{k}^{ + }}(T) = {{\hat {k}}^{ + }}\exp \left( { - \frac{{{{E}^{ + }}}}{{RT}}} \right),\,\,\,\,{{k}^{ - }}(T) = {{\hat {k}}^{ - }}\exp \left( { - \frac{{{{E}^{ - }}}}{{RT}}} \right).$Интегральный закон сохранения энергии (6) применительно к системе уравнений (14) записывается как
(17)
$\begin{gathered} \text{[}({{c}_{x}}x + {{c}_{y}}y)T - ({{c}_{x}}{{x}^{0}} + {{c}_{y}}{{y}^{0}}){{T}^{0}}] + {{Q}_{{{\text{исп}}}}}(y - {{y}^{0}}) = \\ = \int\limits_0^t {J(\tau )d\tau } , \\ \end{gathered} $Нам неизвестны из литературы данные по кинетике испарения и конденсации, поэтому для оценки параметров будем исходить из естественных предположений:
• будем предполагать, что кинетика процесса конденсации описывается мономолекулярной реакцией первого порядка с типичными параметрами гомогенных газовых реакций теории абсолютных скоростей Эйринга [22]:
(18)
${{\hat {k}}^{ - }} = {{10}^{{13}}}\,\,{{{\text{с}}}^{{ - 1}}},\,\,\,\,{{E}^{ - }} = 160{\kern 1pt} 000\,\,{{{\text{Дж}}} \mathord{\left/ {\vphantom {{{\text{Дж}}} {{\text{моль}}}}} \right. \kern-0em} {{\text{моль}}}};$• для оценки параметров кинетики процесса испарения будем опираться на условие равенства скоростей испарения и конденсации при кипении для атмосферного давления, предполагая известными температуру кипения, начальную мольную плотность конденсированной фазы x0 и другие необходимые физические параметры вещества.
Условие равенства скорости испарения и конденсации при температуре кипения Tкип, уравнение состояния идеального газа, равенство разности энергий активации прямой и обратной реакций теплоте испарения приводят к следующим уравнениям:
Подставляя (16) в (19) и исключая y, найдем предэкспонент k± для реакции испарения:
(21)
${{\hat {k}}^{ + }} = {{\hat {k}}^{ - }}\frac{{{{P}_{{{\text{атм}}}}}}}{{R{{T}_{{{\text{кип}}}}}{{x}^{0}}}}\exp \left( {\frac{{{{Q}_{{{\text{исп}}}}}}}{{R{{T}_{{{\text{кип}}}}}}}} \right).$В случае однокомпонентной модели (14) легко выразить явно зависимость равновесного состава компонент и соответствующей полной энергии от температуры T. Решая уравнения (9)–(11), получим
(22)
$\begin{gathered} {{x}^{{eq}}}(T) = {{({{x}^{0}} + {{y}^{0}})} \mathord{\left/ {\vphantom {{({{x}^{0}} + {{y}^{0}})} {[1 + {{k}^{{eq}}}(T)]}}} \right. \kern-0em} {[1 + {{k}^{{eq}}}(T)]}}, \\ {{y}^{{eq}}}(T) = {{k}^{{eq}}}(T){{x}^{{eq}}}(T), \\ {{H}^{{eq}}}(T) = \frac{{({{c}_{x}}T + {{h}_{x}}) + {{k}^{{eq}}}(T)({{c}_{y}}T + {{h}_{y}})}}{{1 + {{k}^{{eq}}}(T)}}({{x}^{0}} + {{y}^{0}}), \\ \end{gathered} $Сведем числовые параметры системы (14) для рассматриваемых далее конкретных веществ в табл. 1. В последних двух колонках таблицы значения ${{\hat {k}}^{ + }},{{E}^{ + }}$ вычислены по формулам (20), (21), остальные значения – данные из [23, 24].
Таблица 1.
Характеристики конденсированных веществ
| Вещество | μ, моль/м3 | Сx, Дж/моль · К | Qисп, Дж/моль | Ткип, °C | x0, моль/м3 | ${{\hat {k}}^{ + }},$ с–1 | ${{E}^{ + }},$ Дж/моль |
|---|---|---|---|---|---|---|---|
| H2O | 18 | 75.35 | 48 898 | 100 | 55 555 | 4.116 ∙ 1016 | 208 898 |
| Al | 26 | 24.35 | 284 100 | 2518 | 98 460 | 9.165 ∙ 1013 | 444 100 |
| Cu | 64 | 24.44 | 304 600 | 2300 | 133 900 | 5.398 ∙ 1014 | 464 600 |
Для теплоемкости паров металлов возьмем значение ${{C}_{V}} = (3{\text{/}}2)R = 12.471\,\,{\text{Дж}} \cdot {\text{мол}}{{{\text{ь}}}^{{ - 1}}} \cdot {{{\text{K}}}^{{ - 1}}}$ (идеальный одноатомный газ), а для пара воды ${{C}_{V}} = (5{\text{/}}2)R = 20.786\,\,{\text{Дж}} \cdot {\text{мол}}{{{\text{ь}}}^{{ - 1}}} \cdot {{{\text{K}}}^{{ - 1}}}$ (многоатомный газ с линейными молекулами). Для удельных энтальпий примем значения, согласованные с теплотой испарения
Отметим, что энтальпии компонент в качестве параметров входят только в выражение для энергии H, которое при соблюдении материального баланса по x, y и сдвиге ${{h}_{x}},{{h}_{y}}$ на общую величину $c$ изменяется на $c(x + y) = {\text{const}}.$ Поэтому можно положить ${{h}_{y}} = 0,$ что сделано для упрощения формул.
В рассматриваемых ниже примерах постулируется наличие гомогенной мелкодисперсной системы постоянного объема с теплофизическими и кинетическим параметрами из табл. 1, примерно соответствующим конкретным веществам (вода, металлы). Разумеется, при использовании приведенных оценок кинетических параметров абстрагируются от многих деталей. В частности, отождествляются жидкая и твердая конденсированные фазы и их градации, занижаются скорости испарения и конденсации воды при температуре ниже 500 К. Но для описания качественной картины рассматриваемых быстрых взрывных процессов они пригодны. Гипотеза о постоянстве объема в примерах основана на малости рассматриваемого при моделировании интервала времени. Более точный расчет и проверка адекватности этой гипотезы нуждается в учете в модели баллистики компонент системы.
Моделирование электровзрыва проводника
Рассмотрим объект-проводник, через который идет электрический ток I большой интенсивности. Предполагаем следующее:
• частицы вещества находятся в мелкодисперсном конденсированном и парообразном состояниях, переход между которыми происходит по схеме обратимой реакции 1-го порядка;
• пренебрегаем изменением удельного электрического сопротивления и величины тока в рассматриваемом при моделировании диапазоне времен.
В рамках этих предпосылок, для концентраций и температуры получим систему дифференциальных уравнений (14) c объемной плотностью скорости тепловыделения J(t), равной джоулеву тепловыделению, генерируемому током:
где ρ и I – удельное электрическое сопротивление вещества проводника и плотность тока.Проведем численное интегрирование системы (14) для характеристик меди и алюминия из табл. 1. В качестве параметров, входящих в (23), возьмем характерное значение плотности тока при электровзрыве: I = 105 А/мм2 [25] и удельные электрические сопротивления меди и алюминия при 300 К [24]:
Типичная длительность импульса тока при электровзрыве, согласно [25], лежит в диапазоне от 10–6 до 10–5 с.
Формула (22) даст для плотности тепловыделения следующие значения:
(24)
$\begin{gathered} {{J}_{{{\text{Cu}}}}} = 1.75 \cdot {{10}^{{14}}}\,\,{\text{Дж}} \cdot {{{\text{м}}}^{{ - 3}}} \cdot {{{\text{с}}}^{{ - 1}}}, \\ {{J}_{{{\text{Al}}}}} = 2.71 \cdot {{10}^{{14}}}\,\,{\text{Дж}} \cdot {{{\text{м}}}^{{ - 3}}} \cdot {{{\text{с}}}^{{ - 1}}}. \\ \end{gathered} $Решаем численно систему (14) при начальных условиях $x(0) = {{x}^{0}},$ $y(0) = 0,$ $T(0) = 300\,\,{\text{K,}}$ используя алгоритм из работы [19] с переменным адаптирующимся шагом по времени, задав относительную точность аппроксимации компонент ~10–4.
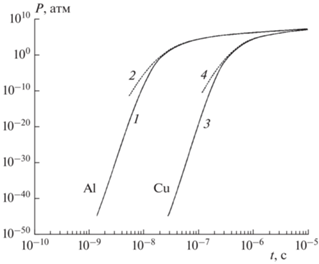
Изменение во времени концентрации металла в конденсированном состоянии, температуры и давления представлено на рис. 1 и 2. Из этих графиков видно, что для меди на временах порядка 10–6 с происходит разогрев системы до 104 К и рост давления до 103 атм. Концентрация меди к моменту времени 10–5 с устанавливается на малом положительном значении, соответствующем равновесию скорости испарения и конденсации; при этом температура и давление превышают соответственно 105 К и 105 атм. Из рис. 2 видно, что найденная методом численного интегрирования кинетическая кривая давления практически совпадает с кривой давления для квазистационарного приближения начиная с момента времени установления равновесия скоростей испарения и конденсации. Для алюминия наблюдаются те же эффекты, но приблизительно при тридцатикратно меньшем времени.
Рис. 1.
Изменение концентрации (моль/м3) металла и температуры при электровзрыве и T0 = 300 К: а – концентрация, б – температура.
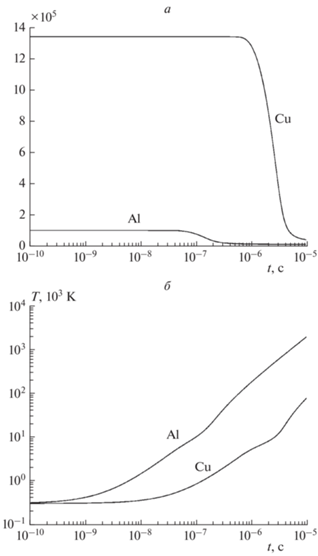
Рис. 2.
Сравнение давления паров металла при электровзрыве для численного решения кинетических уравнений и квазистационарного приближения при T0 = 300 К: 1, 2 – давление пара алюминия и квазистационар; 3, 4 – давление пара меди и квазистационар.
На рис. 3 для рассмотренных систем изображены графики изменения во времени прироста тепловой энергии, затрат энергии на парообразование, их суммы и джоулева тепловыделения. Видно, что закон сохранения энергии (17) выполнен с высокой точностью.
Рис. 3.
Баланс энергии (кДж/м3) при электровзрыве: а – медь, б – алюминий; 1 –приращение тепловой энергии; 2 – энергия, затраченная на испарение; 3 (маркеры) – сумма приращения тепловой энергии и энергии парообразования; 4 (линия) – джоулево тепловыделение тока.
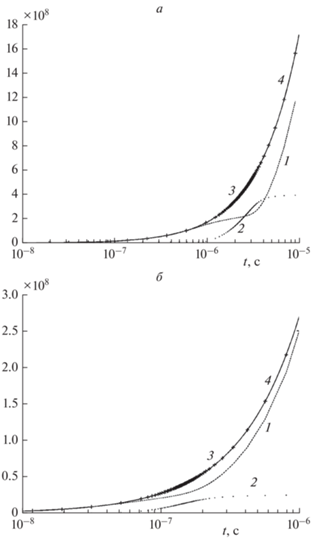
Отметим, что высказанная гипотеза о мелкодисперсном состоянии проводника согласуется с экспериментальными данными [25]: при прохождении импульса тока, приводящего к электровзрыву, происходит диспергирование проводника на частицы, диаметр которых распределен по логарифмически нормальному закону с максимумом плотности распределения от 10 до 500 нм. Пренебречь изменением объема системы из-за разлета частиц на временах порядка 10–6 с вполне допустимо.
Моделирование парового взрыва метеорита
Рассмотрим объект, который прямолинейно движется со скоростью V в атмосфере плотностью ${{\rho }_{{{\text{атм}}}}}.$ Предполагаем следующее:
• частицы вещества объекта находятся в мелкодисперсном конденсированном и парообразном состояниях, переход между которыми происходит по кинетическому механизму обратимой реакции 1-го порядка;
• в начальный момент времени t = 0 концентрации и температура во всех точках объекта одинаковы;
• объект проницаем для атмосферы при t > 0, часть проходящего потока воздуха задерживается при неупругих столкновениях с частицами объекта, отдавая импульс на торможение и кинетическую энергию на нагрев. Массовая интенсивность потока воздуха стационарна и зависит от расстояния l, пройденного в объекте, по формуле $I(l) = {{I}_{0}}\exp ( - \alpha l),$ где ${{I}_{0}}\,\,{\text{и}}\,\,\alpha > 0$ интенсивность потока при входе и коэффициент поглощения;
• пренебрегаем притоком вещества в объект, изменением скорости, влиянием на изменение концентраций и температуры в точке объекта их значений в соседних точках, а также изменением концентраций и температуры до момента достижения потоком воздуха точки объекта;
• объект имеет форму прямого цилиндра с осью, параллельной направлению движения, с основаниями (торцами) площадью S и расстоянием между ними L.
Предположение об экспоненциальном падении интенсивности потока от пройденного пути общепринято при описании поглощения разреженного потока любой природы, проходящего в однородной среде. Поскольку, по предположению, весь поток воздуха проходит через торец, массовая интенсивность его при входе есть ${{I}_{0}} = {{\rho }_{{{\text{атм}}}}}V.$
Рассмотрим одномерную декартову систему координат, движущуюся вместе с объектом со скоростью V с началом отсчета в плоскости переднего торца и положительным направлением, противоположным движению. Обозначим через l координату ортогональной проекции точки на координатную ось. В рамках сделанных предположений параметры состояния в объекте зависят только от l и t. Обозначая через $\tilde {x}(l,t),$ $\tilde {y}(l,t),$ $\tilde {T}(l,t),$ $\tilde {J}(l,t)$ концентраций, температуру и плотность скорости тепловыделения в точке объекта в момент времени t, получим, что при $t \leqslant l{\text{/}}V$
(26)
$\begin{gathered} \tilde {x}(l,t) = x(t - l{\text{/}}V),\,\,\,\,\tilde {y}(l,t) = y(t - l{\text{/}}V), \\ \tilde {T}(l,t) = T(t - l{\text{/}}V), \\ \end{gathered} $(27)
$J(t) = \alpha \exp ( - \alpha l){{\rho }_{{{\text{атм}}}}}{{{{V}^{3}}} \mathord{\left/ {\vphantom {{{{V}^{3}}} 2}} \right. \kern-0em} 2}.$Итак, в точке объекта на расстоянии l от переднего торца изменение компонент (концентрации, температура) описывается кинетической системой (14) с задержкой по времени $l{\text{/}}V,$ причем соответствующая плотность тепловыделения в силу (27) экспоненциально убывает с ростом l из-за поглощения. Определим также нужную для дальнейших рассмотрений долю $\theta (t)$ прошедшего через передний торец потока воздуха, поглощённого в объекте к моменту времени t. В силу сформулированных предположений о поглощении потока воздуха
Вычисление по этой формуле дает, что при $t \geqslant L{\text{/}}V$
(28)
$\begin{gathered} \theta (t) = 1 - \exp ( - \alpha L) + \\ + \,\,\frac{1}{{Vt}}\left[ {L\exp ( - \alpha L) - \frac{{1 - \exp ( - \alpha L)}}{\alpha }} \right]. \\ \end{gathered} $Проведем численное решение системы (14) для параметров воды из табл. 1, а в качестве значений ${{\rho }_{{{\text{атм}}}}},L,V$ возьмем примерные значения плотности Земной атмосферы на высоте 20 км, размеров и скорости Челябинского метеорита [4]:
Начальная температура T0 нам неизвестна, поэтому будем рассматривать при решении (14) три оценочных значения: T0 = 200, 300 и 400 К. Система (14) в данном примере содержит параметр поглощения потока воздуха, $\alpha .$ Его можно оценить по известным данным о торможении метеоритов в Земной атмосфере [26]. Рассмотрим мелкодисперсный ледяной метеорит малой толщины $\Delta L,$ тогда по закону сохранения импульса изменение импульса объекта P(t) равно импульсу поглощенной к моменту t доли потока воздуха, прошедшего через торец, т.е. $P(t) - P(0) = \theta (t){{\rho }_{{{\text{атм}}}}}S{{V}^{2}}t.$ Так как $P(0) = 0,$ по формуле (28) при $L = \Delta L$ и $t \geqslant \Delta L{\text{/}}V$ получим
Следовательно, ускорение торможения $a$ метеорита массой $\Delta LS{{\rho }_{{{{{\text{H}}}_{{\text{2}}}}{\text{O}}}}}$ по второму закону Ньютона выражается как
(29)
$\alpha = a\frac{{{{\rho }_{{{{{\text{H}}}_{{\text{2}}}}{\text{O}}}}}}}{{{{\rho }_{{{\text{атм}}}}}}}{{V}^{{ - 2}}}.$Согласно [26], для метеоритов, разрушающихся в верхних плотных слоях атмосферы, характерно большое ускорение торможения, масштабом которого при обработке наблюдений является км/с2. В числе данных на стр. 377 работы [26] есть ссылка на велограмму радиоизмерений падения метеорита в 1949 г., напоминающего по параметрам Челябинский болид. Для этой велограммы вычислено ускорение торможения a ≈ 0.5 км/с2, которое естественно взять в качестве опорного значения. Полагая ${{\rho }_{{{{{\text{H}}}_{{\text{2}}}}{\text{O}}}}} = 1000$ кг · м–3, a = 0.5 км/с2, из (29) получим оценку $\alpha = 0.0154$ м–1.
Формула (27) для плотности тепловыделения при l = 0 и 10 дает соответственно следующие значения:
В рассматриваемом примере $\alpha L = 0.154,$ поэтому плотность тепловыделения, определяемая выражением (27), и соответствующие решения кинетической системы (14) в моделируемом объекте при $0 \leqslant l \leqslant L$ изменяются несущественно. Приведем результаты интегрирования системы (14) только при $l = 0,$ т.е. для переднего торца. Изменение во времени концентрации воды, температуры и давления для трех начальных температур представлено на рис. 4, 5. Наблюдаются три характерные особенности решения:
Рис. 4.
Кинетические кривые концентрации (моль/м3) воды (а) и температуры (б) для трех значений начальных температур T0, К: 1 – 200, 2 – 300, 3 – 400.
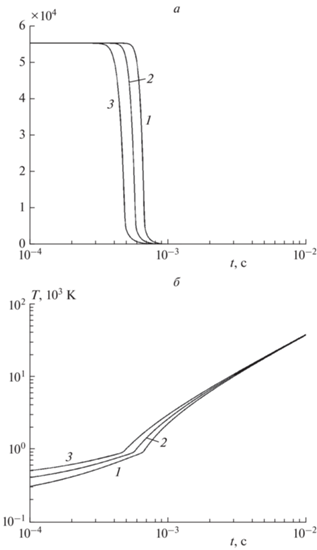
• начальный режим с плавным изменением компонент. Концентрация X медленно падает, постепенно с ускорением растут температура и давление, причем температура в конце достигает примерно 1000 К;
• промежуточный режим с экспоненциальным переходом конденсированного компонента Х в пар и экспоненциальным ростом температуры и давления. В конце конденсированное вещество полностью испаряется (точнее – устанавливается равновесие малого остатка компонента Х и пара Y).
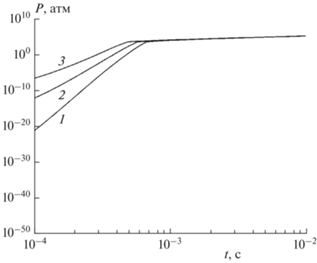
• финальный установившийся режим, при котором система состоит практически из одного пара, а температура и давление линейно растут, так как вся энергия поглощенной доли потока воздуха идет на нагрев пара. Этот режим представлен на рис. 5 в виде линейного участка, начало которого – излом на графике давления. Момент времени этого излома зависит от начальной температуры T 0 и примерно равен t* = 0.0007 с.
Итак, характер изменения температуры напоминает картину теплового взрыва: предвзрывной разогрев переходит в экспоненциальный рост. Затем следует установившийся режим неограниченного подъема температуры системы и давления пара, причем ко времени t* = 0.0007 с температура превышает 1100 К, а давление – 4000 атм. Такое поведение решения качественно напоминает явления [4, 6], наблюдавшиеся при падении Челябинского метеорита (взрыв, вспышка, полное превращение в облако пара). Заметим, что ко времени t* объект успеет пролететь 12.6 м. Доля задержанного к этому времени воздуха, согласно формуле (28), есть $\theta (t*) = 0.0875.$ Поэтому отношение массы задержанного воздуха к массе объекта, выраженное формулой $\theta (t*){{{{\rho }_{{{\text{атм}}}}}Vt{\text{*}}} \mathord{\left/ {\vphantom {{{{\rho }_{{{\text{атм}}}}}Vt{\text{*}}} {{{\rho }_{{{{{\text{H}}}_{{\text{2}}}}{\text{O}}}}}L}}} \right. \kern-0em} {{{\rho }_{{{{{\text{H}}}_{{\text{2}}}}{\text{O}}}}}L}},$ равно 1.103 ∙ 10–5, а уменьшение скорости при ускорении торможения a = 0.5 км · с–2 есть $\Delta V = 0.35$ м ∙ с–1. Эти оценки согласуются со сделанными предположениями – объект превратился в пар с высокой температурой и давлением при относительно небольшом перемещении с пренебрежимо малым изменением массы и скорости движения. Характерной особенностью кинетики испарения метеорита, описанного моделью, является наличие времени задержки процесса на время $l{\text{/}}V$ прохода потоком воздуха от переднего торца до точки объекта, что выражено формулой (25). Максимальное время задержки равно $L{\text{/}}V = 5.55 \cdot {{10}^{{ - 4}}}$ с – времени заполнения объекта потоком воздуха.
Методический интерес представляет сравнение найденного решения кинетических уравнений (14) и квазистационарного приближения. Для уравнений (14) имеем значение малого параметра $\varepsilon = \max ({1 \mathord{\left/ {\vphantom {1 {{{{\hat {k}}}^{ - }}}}} \right. \kern-0em} {{{{\hat {k}}}^{ - }}}},{1 \mathord{\left/ {\vphantom {1 {{{{\hat {k}}}^{ + }}}}} \right. \kern-0em} {{{{\hat {k}}}^{ + }}}}) = {{10}^{{ - 13}}}.$ При построении квазистационарного приближения методом Ньютона решается относительно неизвестной температуры T уравнение ${{H}^{{eq}}}(T) - H({{x}^{0}},{{y}^{0}},{{T}^{0}}) = tJ$ с использованием формул (21). Сравнение результатов численного интегрирования уравнений (14) и квазистационарной асимптотики показано на графике давления пара, представленном на рис. 6. Из этого рисунка видно, что в модели испарения метеорита численное решение и квазистационарное приближение хорошо совпадают только в финальном режиме, когда конденсированный компонент полностью исчез. На начальном участке квазистационарная асимптотика существенно завышает скорость испарения и рост давления. Причина расхождения кроется в недостаточной малости параметра ε. Например, используя значение ${{\hat {k}}^{ - }} = {{10}^{{23}}}$ с–1, получим, что численное решение уравнений (14) совпадет с квазистационарным при $t \geqslant 0.65 \cdot {{10}^{{ - 4}}}$ с, что также показано на рис. 6.
Рис. 6.
Сравнение давления пара для решения кинетических уравнений и квазистационарного приближения при ${{T}^{0}} = 400$ К: 1 – численное интегрирование, 2 – квазистационарное приближение, 3 – численное интегрирование для модели с ${{\hat {k}}^{ - }} = {{10}^{{23}}}\,\,{{{\text{с}}}^{{ - 1}}}.$
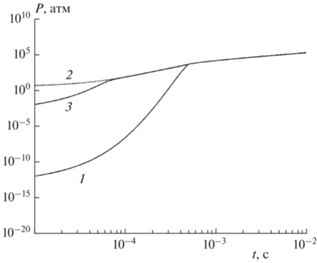
На рис. 7 для варианта расчета при T0 = 200 К изображены графики изменения во времени прироста тепловой энергии, затрат энергии на парообразование, их суммы и тепловыделения от потока воздуха. Видно, что закон сохранения энергии (17) выполнен с высокой точностью. Отметим особенность в этом примере графика изменения тепловой энергии – он имеет локальный максимум и минимум, что, вероятно, связано c соотношением молярных теплоемкостей воды и ее пара.
Рис. 7.
Баланс энергии (кДж/м3) воды и пара при T = = 200 K: 1 – приращение тепловой энергии; 2 – энергия, затраченная на испарение; 3 (маркеры) – сумма приращений тепловой энергии и энергии парообразования; 4 (линия) – тепловыделение от потока воздуха.

Высказанная в нашей постановке гипотеза о достижении метеоритом мелкодисперсного состояния при входе в плотные слои атмосферы довольно давно рассматривается в литературе [8–11]. В этих работах изучаются процессы, которые при определенных условиях приводят к быстрому взрывному дроблению вещества метеорита и напоминают цепные реакции. Момент достижения нулевого значения параметром верхней оценки размера частиц формально трактуется в этом направлении моделирования как взрыв с передачей кинетической энергии метеорита атмосфере. Предложенная в нашей статье модель испарения мелкодисперсного объекта естественно дополняет схемы фрагментирования описанием причины взрыва: на этапе достижения ансамблем фрагментов микронных размеров запускаются кинетические процессы, превращающие за время менее 1 мс в исходном объеме ледяного метеорита почти все конденсированное вещество в сильно сжатый высокотемпературный пар.
В заключение данного раздела уместно сделать замечание о асимптотическом приближении в приведенных примерах. На рис. 8 изображены графики зависимости от T энергии равновесного состава ${{H}^{{eq}}}(T)$ для рассмотренных модельных систем. Видно, что ${{H}^{{eq}}}(T)$ монотонно возрастает. Следовательно, в соответствии с изложенной теорией критических значений энергии для квазистационарного режима в этих примерах не существует и скачок давления из-за переходного процесса установления устойчивого равновесия может происходить только в начальный момент времени. Начальный скачок давления здесь пренебрежимо мал. Но если изменить в параметрах модели (14) числовые значения энтальпий образования компонент, то на кривой зависимости ${{H}^{{eq}}}(T)$ могут появиться экстремумы. На рис. 8 также изображена полная температурная зависимость энергии равновесного состава для системы вода–пар, где формально принято ${{h}_{x}} = Q = - 16{\kern 1pt} 000\,\,{{{\text{Дж}}} \mathord{\left/ {\vphantom {{{\text{Дж}}} {{\text{моль}}}}} \right. \kern-0em} {{\text{моль}}}},$ а остальные параметры сохранены. Для этих параметров график имеет S-образную форму с локальным максимумом и минимумом, т.е. существуют два критических значения энергии.
Рис. 8.
Зависимость равновесной энергии системы ${{H}^{{eq}}}(T)$ от температуры для рассмотренных систем: 1 – вода и пар, 2 – медь и пар, 3 – алюминий и пар, 4 – вода и пар с измененным значением энтальпии ${{h}_{x}} = Q = - 16000\,\,{{{\text{Дж}}} \mathord{\left/ {\vphantom {{{\text{Дж}}} {{\text{моль}}}}} \right. \kern-0em} {{\text{моль}}}}.$
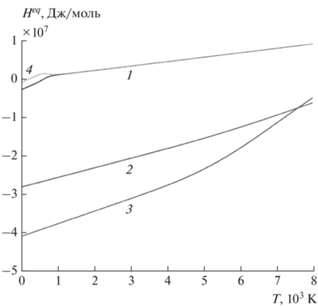
ЗАКЛЮЧЕНИЕ
В литературе периодически появляются публикации (см., например, [27, 28]), объясняющие отсутствие материальных следов некоторых наблюдавшихся метеоритов тем, что твердый монолитный метеорит и скорость его движения были столь большими (диаметр сотни метров, скорость 20–70 км/с), а траектория движения такова, что он прошел Земную атмосферу насквозь, вызвав свечение и ударную волну, сохранив при этом целостность и потеряв малую часть своей массы из-за поверхностной абляции. На наш взгляд, такая трактовка возможна, но только для объектов, удовлетворяющих соответствующим условиям. Предложенная же в статье модель объемного парового взрыва мелкодисперсной системы не накладывает при рассмотрении метеорита ограничений на его размер и траекторию движения, причем для возникновения взрывного эффекта достаточно существенно меньшей скорости входа в атмосферу.
В целом, предложенная модель позволяет качественно верно описать кинетику взрывного роста давления при испарении мелко раздробленного метеоритного тела и при прохождении интенсивного импульса тока в проводнике. Некоторый произвол в сделанной оценке кинетических параметров (параметры мономолекулярной реакции по Эйрингу, теплофизические параметры, начальная температура и т.п.) незначительно влияет на качественные эффекты в проведенных расчетах.
Работа выполнена по теме госзадания (регистрационные номера ЦИТИС AAAA-A19-119120690042-9, AAAA-A19-119022690098-3).
Список литературы
Стулов В.П., Мирский В.Н., Вислый А.И. Аэродинамика болидов. М.: Физматлит, 1995.
Мартынюк М.М. // Физика горения и взрыва. 1977. № 2. С. 213.
Debenedetti P.G. Metastable Liquids. Concepts and principles. Princeton, New Jersey: Princeton University press, 1996.
Барелко В.В., Дроздов М.С., Кузнецов М.И. // Наука в России. 2014. № 1. С. 36.
Григорян С.С. // Космич. исслед. 1979. Т. 17. № 6. С. 875.
Фортов В.Е., Султанов В.Г., Шутов А.А. // Геохимия. 2013. № 7. С. 609.
Султанов В.Г. Дис. … д-ра физ.-мат. наук. Черноголовка: ИПХФ РАН, 2018.
Hills J.G., Goba M.P. // Astronom. J. 1993. V. 105. P. 1114; https://doi.org/10.1086/116499
Crawford D.A. Models of fragment penetration and fireball evolution // International Astronomical Union Colloquium. V. 156: The Collision of Comet Shoemaker-Levy 9 and Jupiter, 1996. P. 133; https://doi.org/10.1017/S0252921100115490
Петров Д.В., Шубин О.Н., Елсуков В.П., Симоненко В.А. Взрывное торможение и фрагментация метеоритов в атмосфере. Доклад на междунар. конф. “XIII Забабахинские научные чтения”; http://vniitf.ru/ data/images/zst/2017/section_1/13_petrov_ru.pdf
Сызранова Н.Г., Андрушенко В.А., Головешкин В.А. // Механика композиц. матер. и конструкций. 2017. № 23. № 1. С. 104.
Pumir A., Barelko V.V // Eur. Phys. J. B. 1999. V. 10. P. 379.
Карпов И.В., Борчевкина О.П., Васильев П.А. // Хим. физика. 2020. Т. 39. № 4. С. 63.
Голубков Г.В., Шапочкин М.Б. // Хим. физика. 2019. Т. 38. № 7. С. 19.
Хомик С.В., Гук И.В., Иванцов А.Н., Медве-дев С.П. и др. // Хим. физика. 2021. Т. 40. № 8. С. 63.
Трофимов В.С., Веретенников В.А., Петров Е.В. // Хим. физика. 2021. Т. 40. № 4. С. 63.
Термодинамические свойства индивидуальных веществ. Справочное издание в 4-х томах / Под ред. Глушко В.П. М.: Наука, 1982.
Вольперт А.И., Худяев С.И. Анализ в классах разрывных функций и уравнения математической физики. М.: Наука, 1975.
Дубовицкий А.Я., Дубовицкий В.А. // Журн. вычисл. математики и мат. физики. 1983. Т. 23. № 5. С. 1960.
Тихонов А.Н. // Мат. сб. 1952. Т. 31. № 3. С. 575.
Burcat A., Rusic B. Third Millenium ideal gas and condensed phase thermodynamical database for combustion with updates from active thermochemical tables, ANL-05/20 and TAE 960 Technion-ITT. Aerospace Engineering, and Argonne National Laboratory, Chemistry Division, 2005; https://doi.org/10.2172/925269
Глесстон С., Лейдер К., Эйринг Г. Теория абсолютных скоростей реакций. М.: Гос. изд-во иностр. лит., 1948.
Варгафтик Н.Б. Справочник по теплофизическим свойствам газов и жидкостей. М.: Наука, 1976.
Зиновьев В.Е. Теплофизические свойства металлов при высоких температурах. М.: Металлургия, 1989.
Гусев А.И. Наноматериалы, наноструктуры, нанотехнологии. М.: Физматлит, 2007.
Астапович И.С. Метеорные явления в атмосфере Земли. М.: Физматлит, 1958.
Варламов С. // Квант. 2018. №9. С.4.
Khrennikov D.E., Titov A.K., Ershov A.E., Pariev A.E., Karpov S. // Monthly Notices Roy. Astronom. Soc. 2020. V. 493. P. 1344; https://doi.org/10.1093/mnras/staa329
Дополнительные материалы отсутствуют.
Инструменты
Химическая физика