Химическая физика, 2021, T. 40, № 9, стр. 80-90

ВВЕДЕНИЕ

Настоящая работа посвящена исследованию возникновения и развития турбулентности в задаче обтекания твердой сферы. Уравнения многомоментной гидродинамики привлечены для численного моделирования хаотического искажения регулярных режимов обтекания. В первой части настоящего исследования [1] представлен первый неустойчивый регулярный режим обтекания. Рассматриваются последствия распада ансамбля Гиббса, возникающего после потери устойчивости. В разд. 1 излагаются общие представления о неупорядоченных возмущениях (НВ). Рассматриваются особенности их поведения в неустойчивом режиме обтекания. В разд. 2 представлены результаты численного моделирования уравнения сохранения импульса, учитывающего эволюцию НВ.

1. МОДЕЛИРОВАНИЕ НЕУПОРЯДОЧЕННЫХ ВОЗМУЩЕНИЙ

Неупорядоченные возмущения могут появиться в среде вследствие внешнего воздействия. Они возникают в экспериментальных установках, на промышленных предприятиях, в окружающей среде. Само оборудование промышленных и экспериментальных установок может создавать неупорядоченные возмущения. Последние могут содержаться в резервуарах со средой, создающих течение в установке. Они также могут вноситься искусственно по воле экспериментатора.

Пусть коэффициент турбулентности ${{\bar {K}}_{d}}$ характеризует интенсивность НВ набегающего потока в задаче обтекания сферы радиуса а, т.е. интенсивность возмущений однородного течения перед сферой. Коэффициент турбулентности ${{\bar {K}}_{d}}$ является отношением характерной, средней во времени и пространстве, величины модуля неупорядоченного возмущения скорости набегающего потока $\Delta \bar {U}_{0}^{{(d)}}$ к самой характерной скорости течения перед сферой ${{U}_{0}}{\text{:}}$ ${{\bar {K}}_{d}} = {{\Delta \bar {U}_{0}^{{(d)}}} \mathord{\left/ {\vphantom {{\Delta \bar {U}_{0}^{{(d)}}} {{{U}_{0}}}}} \right. \kern-0em} {{{U}_{0}}}} \ll 1$ [2]. Наряду с ${{\bar {K}}_{d}}$ определим интенсивность модуля ${{K}_{d}}$ локального неупорядоченного возмущения: ${{K}_{d}} = {{\Delta U_{0}^{{(d)}}} \mathord{\left/ {\vphantom {{\Delta U_{0}^{{(d)}}} {{{U}_{0}}}}} \right. \kern-0em} {{{U}_{0}}}} \ll 1.$ Пусть ${{L}_{h}}$ есть характерный пространственный масштаб, на котором изменяется порядок величины скорости набегающего потока (в частности, ${{L}_{h}}$ может быть радиусом трубы, в которой проводится экспериментальное изучение обтекания сферы). Тогда ${{{{L}_{h}}} \mathord{\left/ {\vphantom {{{{L}_{h}}} {{{U}_{0}}}}} \right. \kern-0em} {{{U}_{0}}}}$ является характерным временны́м масштабом изменения скорости набегающего потока.

Положим тогда, что эволюция неупорядоченного возмущения $\Delta U_{0}^{{(d)}} = {{K}_{d}}U_{0}^{{}}$ протекает на масштабе времени возмущения ${{{{\tau }}}_{{d1}}} = {{{{K}_{d}}{{L}_{h}}} \mathord{\left/ {\vphantom {{{{K}_{d}}{{L}_{h}}} {{{U}_{0}}}}} \right. \kern-0em} {{{U}_{0}}}}.$ Отдельное неупорядоченное возмущение $\Delta U_{0}^{{(d)}}$ возникает и распадается на масштабе времени ${{{{\tau }}}_{{d1}}}.$ То есть отдельное НВ существует в течение времени ${{{{\tau }}}_{{d1}}}.$ По истечении этого времени в среде появляется следующее НВ. Жидкая частица, двигаясь вдоль материальной линии, несет в себе энергию возмущения, необходимую для возникновения очередного НВ. За время существования ${{{{\tau }}}_{{d1}}}$ жидкая частица, двигаясь вдоль материальной линии, переносит неупорядоченное возмущение $\Delta U_{0}^{{(d)}}$ на расстояние ${{l}_{d}} = {{K}_{d}}{{L}_{h}}.$

Внутреннее трение в среде способствует затуханию неупорядоченных возмущений. То есть среднее значение последовательно возникающих и распадающихся неупорядоченных возмущений $\Delta \bar {U}_{0}^{{(d)}}$ постепенно уменьшается (затухает). Потребуется некоторое количество ${{N}_{d}}$ циклов возникновения и последующего распада НВ (${{N}_{d}} \gg 1$), чтобы среднее неупорядоченное возмущение $\Delta \bar {U}_{0}^{{(d)}}$ затухло, т.е. перестало поддаваться измерению. Жидкая частица преодолеет некоторое расстояние ${{\bar {L}}_{d}} = {{N}_{d}}{{\bar {K}}_{d}}{{L}_{h}},$ прежде чем содержащееся в ней неупорядоченное возмущение $\Delta \bar {U}_{0}^{{(d)}}$ перестанет существовать. Соответственно, локальное неупорядоченное возмущение $\Delta U_{0}^{{(d)}}$ затухнет на расстоянии ${{L}_{d}} = {{N}_{d}}{{K}_{d}}{{L}_{h}}.$

Жидкая частица, двигаясь вдоль материальной линии, проникает в зону закручивания в следе за сферой из набегающего потока. Далее она совершает несколько оборотов вокруг фокуса зоны закручивания. После этого жидкая частица покидает зону закручивания, устремляясь вниз по потоку [3]. Геометрические размеры зоны закручивания позволяют приблизительно оценить расстояние ${{L}_{r}},$ которое преодолевает жидкая частица в зоне закручивания, двигаясь по материальной линии. Если ${{L}_{r}} \ll {{L}_{d}},$ то интенсивность неупорядоченного возмущения $\Delta U_{0}^{{(d)}}$ существенно не изменяется на расстоянии ${{L}_{r}}.$

Движущаяся жидкая частица доставляет возникающее перед сферой неупорядоченное возмущение $\Delta U_{0}^{{(d)}}$ в зону закручивания за сферой. В следе за сферой пропорциональный коэффициенту $\hat {C}_{{20}}^{{(0)}}$ член доминирует в распределении плотности потока числа частиц (уравнение (1.5) из [1]). Поэтому модуль НВ скорости течения $\Delta U_{0}^{{(d)}}$ следует интерпретировать в терминах модуля НВ коэффициента $\delta \hat {C}_{{20}}^{{d(0)}}.$ Используя уравнения (2.3) и (2.5) из [1], находим, что $\Delta U_{0}^{{(d)}}$ = ${{U}_{0}}\delta {{\hat {U}}^{{d(0)}}}$ = ${{U}_{0}}\operatorname{Re} \delta \hat {C}_{{20}}^{{d(0)}}.$ Тогда ${{K}_{d}} = \operatorname{Re} \delta \hat {C}_{{20}}^{{d(0)}},$ ${{\bar {K}}_{d}} = \operatorname{Re} \delta \hat {\bar {C}}_{{20}}^{{d(0)}}$ (число Рейнольдса $\operatorname{Re} $ определено в [1]).

В задаче обтекания сферы система уравнений многомоментной гидродинамики (1.4) из [1] диктует характерный гидродинамический масштаб времени ${{{{\tau }}}_{h}} = {{{{\operatorname{Re} a} \mathord{\left/ {\vphantom {{\operatorname{Re} a} {2U}}} \right. \kern-0em} {2U}}}_{0}}$ [4, 5]. Интервал времени ${{{{\tau }}}_{h}}$ является масштабом, на котором изменяется порядок величины решения $\hat {C}_{i}^{{(0)}} = \hat {\bar {C}}_{i}^{{(0)}} + \delta \hat {C}_{i}^{{r(0)}}(t),$ $i = 1,...,20,$ системы уравнений (1.4) из [1]. Зависящая от времени составляющая любой гидродинамической величины является линейной комбинацией членов, пропорциональных коэффициентам $\hat {C}_{i}^{{(0)}}$ (см. уравнения (4.4)–(4.10) из [6]). Поэтому порядок любой гидродинамической величины изменяется на масштабе времени ${{{{\tau }}}_{h}}.$ В соответствии с вышеизложенным эволюция неупорядоченного возмущения $\Delta U_{0}^{{(d)}}$ протекает на масштабе времени возмущения ${{{{\tau }}}_{{d1}}} = {{{{K}_{d}}{{L}_{h}}} \mathord{\left/ {\vphantom {{{{K}_{d}}{{L}_{h}}} {{{U}_{0}}}}} \right. \kern-0em} {{{U}_{0}}}}.$ Приведем характерное время возмущения ${{{{\tau }}}_{{d1}}}$ к безразмерному виду на масштабе характерного гидродинамического времени ${{{{\tau }}}_{h}}{\text{:}}$

В докритическом диапазоне $\operatorname{Re} < \operatorname{Re} _{0}^{*}$ стационарное решение $\hat {\bar {C}}_{i}^{{(0)}},$ $i = 1,...,20,$ системы уравнений (1.4) из [1] устойчиво. Малые отклонения от стационарного решения $\hat {\bar {C}}_{i}^{{(0)}}$ (регулярные и хаотические), которые возникают в некоторый начальный момент времени $t = 0,$ затухают. В результате малые отклонения дают пренебрежимо малый вклад в распределения гидродинамических величин, и необходимости в расчете отклонений не возникает.

Качественно иная картина имеет место в закритическом диапазоне $\operatorname{Re} > \operatorname{Re} _{0}^{*}.$ Достижение критического значения числа Рейнольдса $\operatorname{Re} _{0}^{*}$ сопровождается ростом малых отклонений. Растущая регулярная флуктуация $\delta \hat {C}_{i}^{{r(0)}}$ достигает порядка величины стационарного решения $\hat {\bar {C}}_{i}^{{(0)}}.$ Ансамбль Гиббса распадается. Потерявшее устойчивость решение $\hat {\bar {C}}_{i}^{{(0)}}$ не в состоянии удовлетворить законам сохранения числа частиц, импульса и энергии. В соответствии с представлениями из работы [7] каждая гидродинамическая величина в уравнениях сохранения дополняется хаотической флуктуационной компонентой. Дополнение уравнений многомоментной гидродинамики членами, ответственными за эволюцию неупорядоченных возмущений, позволяет выполнить уравнения сохранения. Таким образом, уравнения для НВ решаются совместно с уравнениями для регулярных коэффициентов $\hat {\bar {C}}_{i}^{{(0)}}$ и $\delta \hat {C}_{i}^{{r(0)}}(t).$ Для выполнения законов сохранения поведение во времени и в пространстве неупорядоченных возмущений должно подстроиться под поведение во времени и в пространстве гидродинамических величин. То есть уравнения сохранения “вынуждают” НВ вести себя во времени и пространстве вполне определенным образом в зоне закручивания.

Неупорядоченные возмущения скорости течения $\Delta U_{0}^{{(d)}}$ возникают в набегающем потоке вследствие внешнего воздействия. Движущаяся жидкая частица приносит возникающие перед сферой НВ в зону закручивания за сферой. Моделируя неупорядоченное возмущение коэффициента $\delta \hat {C}_{{20,i}}^{{d(0)}},$ $i = r,\theta $ (уравнение (2.1) из [1]), положим, что в некоторый начальный момент времени $t = 0$ возмущение $\delta \hat {C}_{{20,i}}^{{d(0)}}$ мгновенно появляется в каждой элементарной ячейке среды с линейным размером $\delta l$ в следе за сферой. Дальнейшая эволюция неупорядоченного возмущения $\delta \hat {C}_{{20,i}}^{{d(0)}}$ протекает в соответствии с законом сохранения импульса (2.16) из [1]. Решение уравнения (2.16) из [1] раскрывает поведение возникшего мгновенно неупорядоченного возмущения $\delta \hat {C}_{{20,i}}^{{d(0)}}{\text{:}}$ оно либо нарастает, либо уменьшается. В соответствии с уравнением (2.16) неупорядоченное возмущение $\delta \hat {C}_{{20,i}}^{{d(0)}}$ изменится в порядке своей величины на отрезке времени ${{{{\tau }}}_{{d2}}} = {{{{\tau }}}_{{d2}}}(t).$ Характерный интервал ${{{{\tau }}}_{{d2}}}$ определяется характерным временем изменения регулярной флуктуации:

В момент времени $t = {{{{\tau }}}_{{d1}}}$ жидкая частица приносит в ячейку следующее неупорядоченное возмущение $\delta \hat {C}_{{20,i}}^{{d(0)}},$ $i = r,\theta .$ В соответствии с моделью следующее НВ появляется в ячейке также мгновенно в момент времени $t = {{{{\tau }}}_{{d1}}}.$ Эволюция следующего НВ также протекает в соответствии с уравнением (2.16) из [1]. Уравнение (2.16) из [1] решается на каждом отрезке времени ${{{{\tau }}}_{{d1}}}$ независимо от результата решения этого уравнения в предшествующий отрезок времени.

Таким образом, при моделировании неупорядоченных возмущений необходимо принимать во внимание два масштаба времени, ${{{{\tau }}}_{{d1}}}$ и ${{{{\tau }}}_{{d2}}}.$ Масштаб ${{{{\tau }}}_{{d1}}}$ задает промежуток времени между поочередным появлением двух НВ в каждой ячейке зоны закручивания. Изменение НВ в зоне закручивания протекает в соответствии с уравнением (2.16) из [1], диктующим характерный временнóй масштаб ${{{{\tau }}}_{{d2}}}.$

В соответствии с представляемой моделью эволюция безразмерного неупорядоченного возмущения $\delta \hat {C}_{{20,i}}^{{d(0)}}$ протекает внутри элементарной ячейки с характерным линейным размером $\delta l{\text{:}}$

Возмущение $\delta \hat {\bar {C}}_{{20}}^{{d(0)}}(x) = {{{{{\bar {K}}}_{d}}(x)} \mathord{\left/ {\vphantom {{{{{\bar {K}}}_{d}}(x)} {\operatorname{Re} }}} \right. \kern-0em} {\operatorname{Re} }}$ может затухать в зоне закручивания из-за внутреннего трения на масштабе ${{\bar {L}}_{d}}.$ Поэтому $\delta \hat {\bar {C}}_{{20}}^{{d(0)}}(x)$ крайне слабо изменяется на масштабе размера ячейки $\delta l$ ($\delta l \ll {{\bar {L}}_{d}}$):

Положим, что в каждой точке n-ячейки с характерным линейным размером $\delta l$ неупорядоченное возмущение $\Delta \hat {C}_{{20,i(n)}}^{{d(0)}}$ имеет одно и то же значение. То есть возмущение $\Delta \hat {C}_{{20,i(n)}}^{{d(0)}}$ моделируется функцией, которая постоянна внутри каждой ячейки. Случайное число $\Delta \hat {C}_{{20,i(n)}}^{{d(0)}}$ мгновенно появляется в ячейке в некоторый начальный момент времени $t = 0.$ Номер ячейки $n$ определяет место ячейки в пространстве, $n = n(x).$ Таким образом, в соответствии с уравнением (1.4) пространственное распределение возмущения $\delta \hat {C}_{{20,i}}^{{d(0)}}(t,x)$ из уравнения (1.3) моделируется гистограммой в каждый момент времени t.

Представленная модель интерпретирует процессы возникновения и распада неупорядоченного возмущения $\delta \hat {C}_{{20,i}}^{{d(0)}}(t,x).$ Возможны другие варианты моделирования. При выборе оптимального варианта моделирования следует ориентироваться на критерий эволюции (уравнения (7.2) и (7.3) из [6]). В соответствием с этим критерием предпочтение отдается варианту, которой наиболее быстро уводит потерявшую устойчивость систему прочь от состояния статистического равновесия.

2. РЕЗУЛЬТАТЫ РАСЧЕТА

Следуя изложенному в разд. 1, будем интерпретировать неупорядоченные возмущения скорости набегающего потока $\Delta U_{{0,i}}^{{(d)}} = {{U}_{0}}\delta \hat {U}_{i}^{{d(0)}}$ в терминах неупорядоченного возмущения коэффициента $\delta C_{{20,i}}^{{d(0)}},$ $i = r,\theta $ (уравнения (2.5) и (2.17) из [1]). В соответствии с уравнением (1.1) характерный временнóй масштаб существования неупорядоченного возмущения $\delta C_{{20,i}}^{{d(0)}}$ в зоне закручивания составляет ${{{{\tau }}}_{{d1}}} = {{{{K}_{d}}{{L}_{h}}} \mathord{\left/ {\vphantom {{{{K}_{d}}{{L}_{h}}} {{{U}_{0}}}}} \right. \kern-0em} {{{U}_{0}}}},$ ${{K}_{d}} = \operatorname{Re} \delta \hat {C}_{{20}}^{{d(0)}}.$

Разделим пространство, занимаемое следом за сферой, на ячейки, обладающие линейным размером $\delta l.$ В соответствии с моделью (разд. 1) случайная величина $\delta \hat {C}_{{20,i}}^{{d(0,g)}}(t,x)$ мгновенно появляется в момент времени ${{t}_{{in}}}$ в каждой n-ячейке, $n = n(x).$ В момент времени ${{t}_{{in}}}$ неупорядоченные возмущения $\delta \hat {C}_{{20,i}}^{{d(0,g)}}({{t}_{{in}}},x),$ $i = r,\theta ,$ разыгрываются случайным образом около своего среднего значения $ \pm \delta \hat {\bar {C}}_{{20}}^{{d(0)}}$ с разбросом, равным $\delta \hat {\bar {C}}_{{20}}^{{d(0)}}.$ Учитывая уравнения (2.17) и (2.18) из [1], приведем (2.16) из [1] к безразмерному виду: интервал ${{\tau }_{h}}$ является характерным временны́м масштабом изменения первого члена левой части, интервал ${{\tau }_{{d1}}}$ – второго члена левой части. Пусть абсолютная величина любого из неупорядоченных возмущений $\delta \hat {C}_{i}^{{d(0)}},$ i = 5, 6, 7, 19, 23, …, 26, и $\delta \hat {C}_{{i,kl}}^{{d(0)}},$ i = 5, ..., 9, 18, 19, 27, ..., 33, значительно меньше абсолютной величины регулярной флуктуации $\delta \hat {C}_{i}^{{r(0)}},$ $i = 1,...,20.$ Оценив порядок величины членов в системе (1.4) из [1], находим, что третий член левой части уравнения (2.16) из [1] может быть опущен в этом случае. Тогда это уравнение дает

В уравнении (2.1) величина $\tau _{{d1}}^{{(1)}} = \tau _{{d1}}^{{(1)}}(x)$ определяется случайным образом в момент ${{t}_{{in}}}{\text{:}}$

Суммарный вклад регулярной флуктуации и неупорядоченного возмущения $\delta \hat {C}_{{20,i}}^{{rd(0)}},$ $i = r,\theta $ в момент ${{t}_{{in}}} + \tau _{{d1}}^{{(1)}}$ в каждой n-ячейке принимает вид

В соответствии с уравнением (2.1) положительно определенные неупорядоченные возмущения $\delta \hat {C}_{{20,i}}^{{d(0,g)}}({{t}_{{in}}},x) > 0$ нарастают, в то время как отрицательно определенные неупорядоченные возмущения $\delta \hat {C}_{{20,i}}^{{d(0,g)}}({{t}_{{in}}},x) < 0$ затухают.

На втором шаге неупорядоченное возмущение $\delta \hat {C}_{{20,i}}^{{d(0,g)}}\left( {{{t}_{{in}}} + \tau _{{d1}}^{{(1)}},x} \right),$ $i = r,\theta ,$ разыгрывается случайным образом около своего среднего значения $ \pm \delta \hat {\bar {C}}_{{20}}^{{d(0)}}$ в момент ${{t}_{{in}}} + \tau _{{d1}}^{{(1)}}$ и мгновенно появляется в момент ${{t}_{{in}}} + \tau _{{d1}}^{{(1)}}$ в каждой n-ячейке. В соответствии с моделью (разд. 1) эволюция неупорядоченного возмущения $\delta \hat {C}_{{20,i}}^{{d(0,g)}}\left( {{{t}_{{in}}} + \tau _{{d1}}^{{(1)}},x} \right)$ управляется уравнением (2.16) из [1] вплоть до момента ${{t}_{{in}}} + \tau _{{d1}}^{{(1)}} + \tau _{{d1}}^{{(2)}};$ здесь

Пошаговый процесс повторяется. На $(l + 1)$-шаге неупорядоченное возмущение $\delta \hat {C}_{{20,i}}^{{d(0,g)}}\left( {{{t}_{{in}}} + t_{{d1}}^{{(l)}},x} \right)$ разыгрывается случайным образом около своего среднего значения $ \pm \delta \hat {\bar {C}}_{{20}}^{{d(0)}}$ в момент ${{t}_{{in}}} + t_{{d1}}^{{(l)}}$ и появляется в момент ${{t}_{{in}}} + t_{{d1}}^{{(l)}}$ в каждой n-ячейке; здесь $t_{{d1}}^{{(l)}} = \tau _{{d1}}^{{(1)}}$ + $\tau _{{d1}}^{{(2)}} + ... + \tau _{{d1}}^{{(l)}}.$ Эволюция случайного возмущения $\delta \hat {C}_{{20,i}}^{{d(0,g)}}\left( {{{t}_{{in}}} + t_{{d1}}^{{(l)}},x} \right)$ управляется уравнением (2.16) из [1]. В соответствии с этим уравнением к моменту времени ${{t}_{{in}}} + t_{{d1}}^{{(l + 1)}}{\text{:}}$

В уравнении (2.3)

К моменту времени ${{t}_{{in}}} + t_{{d1}}^{{(l + 1)}}$ суммарный вклад регулярных флуктуаций и неупорядоченных возмущений $\delta \hat {C}_{{20,i}}^{{rd(0)}},$ $i = r,\theta $ (уравнение (2.2)) в каждой n-ячейке достигает величины

В соответствии с уравнением (2.3) положительно определенные неупорядоченные возмущения $\delta \hat {C}_{{20,i}}^{{d(0,g)}}\left( {{{t}_{{in}}} + t_{{d1}}^{{(l)}},x} \right) > 0$ нарастают, в то время как отрицательно определенные неупорядоченные возмущения $\delta \hat {C}_{{20,i}}^{{d(0,g)}}\left( {{{t}_{{in}}} + t_{{d1}}^{{(l)}},x} \right) < 0$ затухают. Пошаговый процесс завершается при обрыве решения $So{{l}_{0}}$ в момент $t = {{t}_{ * }}$ (см. разд. 1 в [1]).

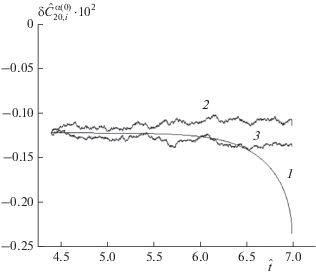
Рисунок 1 дает представление об эволюции регулярных флуктуаций и неупорядоченных возмущений. Расчет выполнен для $\operatorname{Re} = 400$, ${{L}_{h}} = 50a$ (а – радиус сферы), $\delta \hat {\bar {C}}_{{20}}^{{d(0)}} = 0.00001.$ Коэффициенту $\delta \hat {\bar {C}}_{{20}}^{{d(0)}} = 0.00001$ соответствует высокое значение коэффициента турбулентности ${{\bar {K}}_{d}} = 0.004 = 0.4\% ,$ зарегистрированное, например, в работе [8]. Кривая 1 на рис. 1 описывает поведение во времени коэффициента $\delta \hat {C}_{{20}}^{{r(0)}}(t),$ доминирующего в распределении скорости течения (см. уравнение (2.3) из [1]). Кривая 1, рассчитанная по решению $So{{l}_{0}}$, имеет характерную особенность. Начиная с момента времени ${{t}_{{in}}}$ и вплоть до момента времени ${{\hat {t}}_{a}} \approx 6.3$ коэффициент $\delta \hat {C}_{{20}}^{{r(0)}}(t)$ проявляет крайне слабую зависимость от времени. Начиная с момента времени ${{t}_{a}}$ и вплоть до обрыва решения $So{{l}_{0}}$ в момент $t = {{t}_{ * }}$ коэффициент $\delta \hat {C}_{{20}}^{{r(0)}}(t)$ демонстрирует резкий всплеск. В момент ${{\hat {t}}_{{in}}} = 5.5$ выполнено условие, позволившее опустить третий член левой части уравнения (2.16) из [1].

Рис. 1.

Поведение во времени коэффициентов, ответственных за регулярные флуктуации и неупорядоченные возмущения; $\operatorname{Re} = 400,$ ${{\bar {K}}_{d}} = 0.4\% ,$ $t = ({{\operatorname{Re} a} \mathord{\left/ {\vphantom {{\operatorname{Re} a} {2{{U}_{0}}}}} \right. \kern-0em} {2{{U}_{0}}}})\hat {t}.$ Кривая 1 определяет зависимость от времени коэффициента $\delta \hat {C}_{{20}}^{{r(0)}}.$ Кривые 2 и 3 определяют зависимость от времени коэффициента $\delta \hat {C}_{{20,\theta }}^{{rd(0)}}$ в двух произвольных точках зоны закручивания.

Неупорядоченные возмущения разыгрываются случайным образом около $ \pm \hat {\bar {C}}_{{20}}^{{d(0)}}$ с разбросом, равным $\delta \hat {\bar {C}}_{{20}}^{{d(0)}}.$ Допускаются как положительно определенные неупорядоченные возмущения $\delta \hat {C}_{{20,i}}^{{d(0)}} > 0,$ $i = r,\theta ,$ так и отрицательно определенные неупорядоченные возмущения $\delta \hat {C}_{{20,i}}^{{d(0)}} < 0.$ В соответствии с уравнением (2.16) из [1] производная по времени коэффициента $\delta \hat {C}_{{20}}^{{r(0)}}(t)$ должна быть сбалансирована производной во времени коэффициента $\delta \hat {C}_{{20,i}}^{{d(0)}}(t,x).$ Кривые 2 и 3 на рис. 1 описывают поведение во времени коэффициента $\delta \hat {C}_{{20,i}}^{{rd(0)}}(t,x)$ и соответствуют разным ячейкам следа за сферой, т.е. разным x. Случайный характер розыгрыша НВ предопределяет различие в поведении кривых 2 и 3. Численное интегрирование уравнения (2.16) из [1] показывает, что на отрезке времени ${{t}_{{in}}} < t < {{t}_{ * }}$ расхождение этих кривых достигнет основного порядка величины. Расхождение между коэффициентом $\delta \hat {C}_{{20}}^{{r(0)}}(t)$ (кривая 1) и коэффициентами $\delta \hat {C}_{{20,i}}^{{rd(0)}}(t,x)$ (кривые 2 и 3) также достигнет основного порядка величины.

Причина такого поведения коэффициентов заключается в следующем. Слабая зависимость коэффициента $\delta \hat {C}_{{20}}^{{r(0)}}(t)$ от времени на отрезке $0 < t < {{t}_{a}}$ предопределяет крайне слабое изменение коэффициента $\delta \hat {C}_{{20,i}}^{{d(0)}}(t,x)$ на любом интервале $\tau _{{d1}}^{{(l + 1)}},$ $l = 0,1,...$ (уравнеие (2.3)). На отрезке времени $0 < t < {{t}_{a}}$ характерное время изменения неупорядоченного возмущения $\tau _{{d2}}^{{(l + 1)}}{\text{:}}$ ${{\left( {\tau _{{d2}}^{{(l + 1)}}} \right)}^{{ - 1}}} = $ $ = {{\left( {\left| {\left( {{{\partial \delta C_{{20}}^{{r(0)}}} \mathord{\left/ {\vphantom {{\partial \delta C_{{20}}^{{r(0)}}} {\partial t}}} \right. \kern-0em} {\partial t}}} \right)\left( {{1 \mathord{\left/ {\vphantom {1 {\delta C_{{20,i}}^{{d(0)}}}}} \right. \kern-0em} {\delta C_{{20,i}}^{{d(0)}}}}} \right)} \right|} \right)}_{{t = {{t}_{{in}}} + t_{d}^{{(l)}}}}}$ (уравнение (1.2)), значительно превосходит характерное время существования неупорядоченного возмущения $\tau _{{d1}}^{{(l + 1)}},$ $\tau _{{d2}}^{{(l + 1)}} \gg \tau _{{d1}}^{{(l + 1)}},$ $l = 0,1,...$ Как положительно определенные, так и отрицательно определенные значения коэффициента $\delta \hat {C}_{{20,i}}^{{d(0)}}$ появляются в каждой n‑ячейке поочередно случайным образом. Однако на отрезке времени ${{t}_{{in}}} < t < {{t}_{a}}$ появление положительно определенных неупорядоченных возмущений $\delta \hat {C}_{{20,i}}^{{d(0)}} > 0$ значительно превалирует над появлением отрицательно определенных неупорядоченных возмущений $\delta \hat {C}_{{20,i}}^{{d(0)}} < 0$ при розыгрыше, соответствующем кривой 2 на рис. 1. Наоборот, на отрезке времени ${{t}_{{in}}} < t < {{t}_{a}}$ появление отрицательно определенных неупорядоченных возмущений $\delta \hat {C}_{{20,i}}^{{d(0)}} < 0$ значительно превалирует над появлением положительно определенных неупорядоченных возмущений $\delta \hat {C}_{{20,i}}^{{d(0)}} > 0$ при розыгрыше, соответствующем кривой 3 на рис. 1. В результате неравномерность в появлении знакопеременных коэффициентов $\delta \hat {C}_{{20,i}}^{{d(0)}}$ не позволяет им взаимно компенсировать друг друга на отрезке времени ${{t}_{{in}}} < t < {{t}_{a}}.$ Таким образом, расхождение кривых 2 и 3 на отрезке времени ${{t}_{{in}}} < t < {{t}_{a}}$ (рис. 1) является прямым следствием неравномерности возникновения больших неупорядоченных возмущений (${{\bar {K}}_{d}} = 0.4\% $). На отрезке времени ${{t}_{{in}}} < t < {{t}_{a}}$ поведение коэффициентов $\delta \hat {C}_{{20,i}}^{{rd(0)}}(t,x),$ соответствующих разным ячейкам следа за сферой (в частности, кривые 2 и 3), может быть проинтерпретировано как случайное блуждание в окрестности кривой 1.

На отрезке времени ${{t}_{a}} < t < {{t}_{ * }}$ характерное время изменения неупорядоченного возмущения $\tau _{{d2}}^{{(l + 1)}}$ примерно равно или меньше характерного времени существования неупорядоченного возмущения $\tau _{{d1}}^{{(l + 1)}},$ $\tau _{{d2}}^{{(l + 1)}} \leqslant \tau _{{d1}}^{{(l + 1)}},$ $l = 0,1,....$ На отрезке ${{t}_{a}} < t < {{t}_{ * }}$ коэффициент $\delta \hat {C}_{{20}}^{{r(0)}}(t)$ проявляет сильную зависимость от времени. Сильная временнáя зависимость коэффициента $\delta \hat {C}_{{20}}^{{r(0)}}(t)$ вынуждает отрицательно определенные неупорядоченные возмущения $\delta \hat {C}_{{20,i}}^{{d(0)}} < 0$ уменьшаться в порядке своей абсолютной величины на любом интервале $\tau _{{d1}}^{{(l + 1)}},$ $l = 0,1,....$ Начиная с любого момента времени ${{t}_{{in}}} + t_{{d1}}^{{(l)}}$ и вплоть до момента времени ${{t}_{{in}}} + t_{{d1}}^{{(l + 1)}}$ (уравнение (2.3)) сильная зависимость коэффициента $\delta \hat {C}_{{20}}^{{r(0)}}(t)$ обеспечивает рост положительно определенных неупорядоченных возмущений $\delta \hat {C}_{{20,i}}^{{d(0)}} > 0$ по порядку своей величины. В результате вклад нарастающих положительно определенных неупорядоченных возмущений $\delta \hat {C}_{{20,i}}^{{d(0)}} > 0$ компенсирует вклад перманентно падающей регулярной флуктуации $\delta \hat {C}_{{20}}^{{r(0)}}(t)$ (рис. 1, кривая 1). Поэтому на отрезке времени ${{t}_{*}}{\kern 1pt} - {\kern 1pt} {{t}_{a}}$ величина коэффициента $\delta \hat {C}_{{20,i}}^{{rd(0)}}(t,x)$ расположена в окрестности некоторого постоянного значения, расходящегося с кривой 1. Это значение составляет порядка –0.1 для кривой 2 и порядка –0.2 для кривой 3 на рис. 1. Неравномерность возникновения больших НВ разного знака вызывает случайные блуждания около этого постоянного значения. Таким образом, расхождение кривых 2 и 3 на полном отрезке времени ${{t}_{{in}}} < t < {{t}_{ * }}$ (рис. 1) является прямым следствием неравномерности возникновения больших НВ.

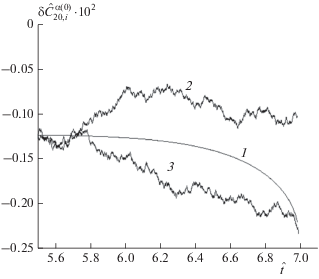
На рис. 2 представлена эволюция регулярных флуктуаций и неупорядоченных возмущений для $\operatorname{Re} = 400,$ ${{L}_{h}} = 50a,$ $\delta \hat {\bar {C}}_{{20}}^{{d(0)}} = 0.000001,$ ${{\hat {t}}_{{in}}} = 4.4.$ Коэффициенту $\delta \hat {\bar {C}}_{{20}}^{{d(0)}} = 0.000001$ соответствует коэффициент турбулентности ${{\bar {K}}_{d}} = 0.0004 = 0.04\% .$ Случайный характер розыгрыша НВ предопределяет различие в поведении кривых 2 и 3, описывающих поведение во времени коэффициента $\delta \hat {C}_{{20,i}}^{{rd(0)}}(t,x).$ Кривые 2 и 3 соответствуют разным ячейкам следа за сферой. Кривая 1 описывает поведение во времени коэффициента $\delta \hat {C}_{{20}}^{{r(0)}}(t).$ Численное интегрирование уравнения (2.16) из [1] показывает, что на отрезке времени $0 < t < {{t}_{a}}$ расхождение между коэффициентами $\delta \hat {C}_{{20}}^{{r(0)}}(t)$ и $\delta \hat {C}_{{20,i}}^{{rd(0)}}(t,x)$ крайне незначительно. Однако на отрезке времени ${{t}_{a}} < t < {{t}_{ * }}$ расхождение между коэффициентами $\delta \hat {C}_{{20}}^{{r(0)}}(t)$ и $\delta \hat {C}_{{20,i}}^{{rd(0)}}(t,x)$ достигнет основного порядка величины.

Рис. 2.

То же, что и на рис. 1, но при ${{\bar {K}}_{d}} = 0.04\% .$

Причина такого поведения коэффициентов заключается в следующем. Как положительно определенные, так и отрицательно определенные значения коэффициента $\delta \hat {C}_{{20,i}}^{{d(0)}}$ появляются в каждой n-ячейке поочередно случайным образом. Однако неизбежная неравномерность возникновения НВ разного знака не приводит к расхождению кривых 2 и 3 на отрезке времени ${{t}_{{in}}} < t < {{t}_{a}}$ (рис. 2). Слабая зависимость коэффициента $\delta \hat {C}_{{20}}^{{r(0)}}(t)$ от времени на отрезке $0 < t < {{t}_{a}}$ предопределяет крайне слабое изменение коэффициента $\delta \hat {C}_{{20,i}}^{{d(0)}}$ в любом интервале $\tau _{{d1}}^{{(l + 1)}},$ $l = 0,1,...$ ($\tau _{{d2}}^{{(l + 1)}} \gg \tau _{{d1}}^{{(l + 1)}}$ на отрезке времени ${{t}_{{in}}} < t < {{t}_{a}}$). Поэтому в силу невысоких значений коэффициента турбулентности (${{\bar {K}}_{d}} = 0.04\% $) неупорядоченные возмущения $\delta \hat {C}_{{20,i}}^{{d(0)}}$ не оказывают заметного влияния на поведение во времени коэффициента $\delta \hat {C}_{{20,i}}^{{rd(0)}}(t,x).$ Такое поведение последнего качественно отличается от поведения этого коэффициента при высоких значениях коэффициента турбулентности (${{\bar {K}}_{d}} = 0.4\% $). При ${{\bar {K}}_{d}} = 0.4\% $ превалирование неупорядоченных возмущений определенного знака разводит кривые на отрезке времени ${{t}_{{in}}} < t < {{t}_{a}}$ (кривые 2 и 3 на рис. 1).

Сильная зависимость коэффициента $\delta \hat {C}_{{20}}^{{r(0)}}(t)$ от времени на отрезке ${{t}_{a}} < t < {{t}_{ * }}$ приводит к тому, что отрицательно определенное возмущение $\delta C_{{20,i}}^{{d(0)}} < 0$ успевает полностью затухнуть на любом интервале $\tau _{{d1}}^{{(l + 1)}},$ $l = 0,1,...$ Положительно определенное возмущение $\delta \hat {C}_{{20,i}}^{{d(0)}} > 0$ растет начиная с любого момента времени ${{t}_{{in}}} + t_{{d1}}^{{(l)}}$ и вплоть до момента времени ${{t}_{{in}}} + t_{{d1}}^{{(l + 1)}}$ ($\tau _{{d2}}^{{(l + 1)}} \leqslant \tau _{{d1}}^{{(l + 1)}}$ на отрезке времени ${{t}_{a}} < t < {{t}_{ * }}$). Вклад нарастающего положительно определенного неупорядоченного возмущения $\delta \hat {C}_{{20,i}}^{{d(0)}} > 0$ компенсирует вклад перманентно падающей регулярной флуктуации $\delta \hat {C}_{{20}}^{{r(0)}}(t)$ (кривая 1). В результате коэффициент $\delta C_{{20,i}}^{{rd(0)}}(t,x)$ не претерпевает заметного изменения на отрезке времени ${{t}_{ * }}{\kern 1pt} - {\kern 1pt} {{t}_{a}}.$ Случайный характер розыгрыша крайне слабо влияет на поведение коэффициента $\delta C_{{20,i}}^{{rd(0)}}(t,x),$ т.е. кривые 2 и 3 на рис. 2 расходятся крайне слабо.

Кривые 2 и 3 на рис. 1 и 2 рассчитаны при условии, что внутренне трение не повлияло на интенсивность неупорядоченных возмущений в зоне закручивания, т.е. при ${{\bar {L}}_{d}} \gg {{L}_{r}}.$ Условие ${{\bar {L}}_{d}} \gg {{L}_{r}}$ обеспечивает сохранение величины коэффициента турбулентности ${{\bar {K}}_{d}}$ при круговом движении жидкой частицы около фокуса зоны закручивания. То есть интенсивность неупорядоченного возмущения $\Delta \bar {U}_{0}^{{(d)}} = {{\bar {K}}_{d}}{{U}_{0}}$ существенно не изменяется в течение времени, затраченного жидкой частицей на преодоление расстояния ${{L}_{r}}$ при оборотах вокруг фокуса зоны закручивания.

Рисунок 1 из [1] дает стационарную осесимметричную картину течения в зоне закручивания, представленную линиями тока. В стационарном случае линии тока совпадают с материальными линиями. Картина течения в зоне закручивания представлена гладкими непересекающимися материальными линиями. Материальные линии образуют овалы, имеющие правильную форму. Правильная форма овалов сопряжена как с осью абсцисс, так и с поверхностью сферы, которую огибает материальная линия.

На рис. 3 показана картина течения в зоне закручивания, представленная материальными линиями. Распределение скорости течения в зоне закручивания рассчитано по формуле (2.3) из [1], в которой пропорциональная коэффициенту $\hat {C}_{{14}}^{{(0)}}$ составляющая опущена. Вклад регулярных флуктуаций и неупорядоченных возмущений рассчитан по формулам (2.4) и (2.5) из [1]. Суммарный вклад регулярных флуктуаций и неупорядоченных возмущений, представленный коэффициентом $\delta \hat {C}_{{20,i}}^{{rd(0)}}(t,x),$ рассчитывается по формуле (2.4). Материальные линии на рис. 3 рассчитаны на отрезке времени $t = {{t}_{ * }}$ около точки обрыва решения. В окрестности $t = {{t}_{ * }}$ степень возбуждения зоны закручивания достигает максимального значения. Расчет выполнен для $\operatorname{Re} = 400,$ ${{\bar {K}}_{d}} = 0.4\% .$ Временнáя зависимость коэффициента $\delta \hat {C}_{{20,i}}^{{rd(0)}}(t,x)$ рассчитывается в каждой n-ячейке следа за сферой, $n = n(x),$ независимо от расчета в других ячейках следа. Результаты расчета $\delta \hat {C}_{{20,i}}^{{rd(0)}}(t,x)$ в двух произвольных ячейках следа представлены на рис. 1 кривыми 2 и 3.

Рис. 3.

Влияние неупорядоченных возмущений на картину течения, представленную материальными линиями: зона закручивания в следе за сферой. Материальные линии соответствуют времени обрыва $t = {{t}_{*}}$ решения $So{{l}_{0}}$ при $\operatorname{Re} = 400,$ ${{\bar {K}}_{d}} = 0.4\% .$

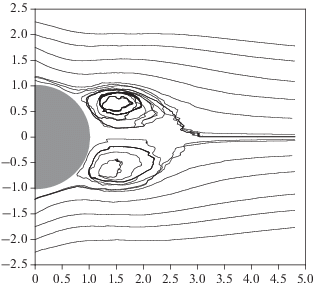
Картина течения в зоне закручивания, представленная на рис. 3, качественно отличается от картины течения в зоне закручивания, представленной на рис. 1 из [1], а именно, хаотические возмущения исказили гладкие материальные линии. Образованные материальными линиями овалы утратили правильную форму. На рис. 3 отчетливо просматриваются искажения правильной формы овала, имеющие порядок величины радиуса сферы а. Такие искажения вызваны расхождением коэффициентов $\delta \hat {C}_{{20,i}}^{{rd(0)}}(t,x)$ и $\delta \hat {C}_{{20}}^{{r(0)}}(t).$ Наряду с этими искажениями на рис. 3 просматриваются менее сильные искажения формы овала, обладающие порядком величины $0.1a.$ Менее сильные искажения вызваны неравномерностью возникновения неупорядоченных возмущений разного знака, проявляющихся на кривых 2 и 3 на рис. 3. Слабые искажения материальных линий, обладающие порядком величины $0.001a,$ не проявляются на масштабе рисунка. Слабые искажения вызваны неупорядоченными возмущениями $\delta \hat {C}_{{20,i}}^{{d(0)}}(t,x),$ доставляемыми жидкой частицей в зону закручивания из течения перед сферой.

Попадая в зону закручивания из набегающего потока, жидкая частица испытывает хаотические изменения направления движения, двигаясь по материальной линии. Покинув зону закручивания, она устремляется вниз по потоку, испытывая некоторое время столь же резкие хаотические изменения направления своего движения. Наряду с хаотическим изменением направления движения жидкая частица испытывает хаотические изменения модуля скорости движения, перемещаясь по материальной линии. В отличие от материальных линий, образующих правильные овальные траектории (рис. 1 из [1]), искаженные материальные линии на рис. 3 хаотически пересекаются в зоне закручивания. Хаотическое движение жидкой частицы по искаженным неупорядоченными возмущениями пересекающимся материальным линиям создает турбулентную картину течения в зоне закручивания.

Результаты расчета временнóй зависимости коэффициента $\delta \hat {C}_{{20,i}}^{{rd(0)}}(t,x)$ в двух произвольных ячейках следа, выполненные для $\operatorname{Re} = 400,$ ${{\bar {K}}_{d}} = 0.04\% ,$ представлены на рис. 2 кривыми 2 и 3. Последние крайне слабо расходятся между собой в течение полупериода ${{t}_{*}}$ пульсации зоны закручивания. Такое поведение коэффициента $\delta \hat {C}_{{20,i}}^{{rd(0)}}(t,x)$ характерно для любой ячейки следа за сферой. Использование коэффициента $\delta \hat {C}_{{20,i}}^{{rd(0)}}(t,x)$ для расчета материальных линий в зоне закручивания показывает, что картина течения крайне слабо отличается от картины течения, представленной на рис. 1 из [1]. Это означает, что слабая зависимость коэффициента $\delta \hat {C}_{{20,i}}^{{rd(0)}}(t,x)$ от номера ячейки в следе приводит к крайне слабому искажению правильной формы овалов. Таким образом, невысокий коэффициент турбулентности набегающего потока ${{\bar {K}}_{d}} = 0.04\% $ крайне слабо искажает регулярную картину течения в зоне закручивания. В экспериментальной установке увеличение коэффициента турбулентности ${{\bar {K}}_{d}}$ может быть достигнуто за счет повышения скорости набегающего потока, т.е. увеличения $\operatorname{Re} .$ Таким образом, различие в поведении кривых 2 и 3 на рис. 1 и 2 может быть проинтерпретировано в терминах изменения числа Рейнольдса. Такая интерпретация связывает возникновение турбулентной картины ближнего следа за сферой с увеличением $\operatorname{Re} .$

ЗАКЛЮЧЕНИЕ

Эксперимент регистрирует три устойчивых состояния среды при обтекании покоящейся твердой сферы. Устойчивое течение $U_{0}^{{exp}}(x)$ обладает осесимметричной зоной закручивания в ближнем следе (см. рис. 1 из [1]). Устойчивые течения $U_{1}^{{exp}}(x)$ и $U_{2}^{{exp}}(t,x)$ имеют несимметричные зоны закручивания. Каждое из трех устойчивых состояний: $U_{0}^{{exp}}(x),$ $U_{1}^{{exp}}(x)$ и $U_{2}^{{exp}}(t,x),$ обладает своим собственным отличным от других направлением развития турбулентности. Неустойчивый процесс начинает развиваться после достижения критического значения числа Рейнольдса: соответственно $\operatorname{Re} _{0}^{*},$ $\operatorname{Re} _{1}^{*}$ и $\operatorname{Re} _{2}^{*}.$ Развитие турбулентности неизбежно проходит через регулярный режим периодического вихревого испускания. Каждое из трех направлений развития неустойчивости обладает своими собственными, присущими только ему, характерными особенностями вихревого испускания [9].

Прямое численное интегрирование уравнений Навье–Стокса удовлетворительно воспроизводит устойчивые течения $U_{0}^{{exp}}(x),$ $U_{1}^{{exp}}(x)$ и $U_{2}^{{exp}}(t,x).$ Однако расчет не в состоянии поставить что-либо в соответствие ни одному из экспериментально наблюдаемых регулярных неустойчивых режимов [9]. Последовательность из трех устойчивых решений замещается в расчете многопериодическим, по существу хаотическим, решением.

Однако такой сценарий возникновения турбулентности противоречит эксперименту [10]. Во-первых, не существует экспериментов, в которых турбулентный режим непосредственно замещает какое-либо из устойчивых состояний среды $U_{0}^{{exp}}(x),$ $U_{1}^{{exp}}(x)$ или $U_{2}^{{exp}}(t,x).$ Развитие каждого из этих состояний неизбежно проходит через режим вихревого испускания. Во-вторых, коэффициент турбулентности ${{\bar {K}}_{d}}$ оказывает огромное влияние на развитие турбулентного процесса. При высоких значениях ${{\bar {K}}_{d}}$ первые элементы хаотичности начинают искажать регулярную структуру вихревого испускания при достаточно низких значениях $\operatorname{Re} ,$ достигающих нескольких сотен (в эксперименте, описанном в [8], $Re = 420$). Уменьшение ${{\bar {K}}_{d}}$ существенно увеличивает диапазон регулярности. В эксперименте из работы [11] строго регулярная картина течения наблюдалась во всем исследуемом диапазоне значений числа Рейнольдса, вплоть до Re = 30 000. Расчет не в состоянии воспроизвести эту характерную особенность возникновения турбулентности. Расчетом установлено, что значение числа Рейнольдса, отвечающее возникновению элементов хаотичности на регулярном решении ($\operatorname{Re} = 300$ в расчете [12]), очень слабо или вообще не зависит от интенсивности НВ в набегающем потоке. И наконец, постепенное нарастание возникших элементов хаотичности, завершающееся развитой турбулентностью, осуществляется в пределах широкого диапазона значений числа Рейнольдса ΔRe (в эксперименте из работы [8] $\Delta {\kern 1pt} \operatorname{Re} > 1000$). Напротив, результаты линейного анализа [13] и прямого численного интегрирования [12] показывают, что регулярная картина течения замещается хаотической крайне быстро, в пределах $\Delta {\kern 1pt} \operatorname{Re} \approx 50.$ Три существенных различия между расчетом и экспериментом позволяют сделать вывод о непригодности многопериодического детерминистического решения уравнений Навье–Стокса для интерпретации турбулентности, регистрируемой экспериментально [10]. В работах [9, 10, 14] ответственность за неудачу расчета возложена на сами уравнения Навье–Стокса.

В работах [15–17] указано направление усовершенствования уравнений классической гидродинамики, характеризующееся увеличением количества главных гидродинамических величин. В настоящей работе неустойчивые регулярные режимы обтекания и хаотическое искажение этих режимов исследуются посредством численного интегрирования уравнений многомоментной гидродинамики [18, Гл. 5]. При докритических значениях числа Рейнольдса $\operatorname{Re} < \operatorname{Re} _{0}^{*}$ решение $\hat {\bar {C}}_{i}^{{(0)}}$ системы (1.4) из [1] стационарно, устойчиво и соответствует всему ансамблю систем (ансамблю Гиббса). Устойчивое решение $\hat {\bar {C}}_{i}^{{(0)}}$ удовлетворительно воспроизводит основное устойчивое течение $U_{0}^{{exp}}(x).$ Неупорядоченные возмущения возникают в течении перед сферой. Жидкая частица, двигаясь по материальной линии, приносит возникающее перед сферой НВ в зону закручивания за сферой. Как положительно определенные неупорядоченные возмущения $\delta \hat {C}_{{20,i}}^{{d(0)}} > 0,$ так и отрицательно определенные возмущения $\delta \hat {C}_{{20,i}}^{{d(0)}} < 0$ затухают на масштабе времени ${{{{\tau }}}_{{d1}}}$ (уравнение (1.1)). Неравномерность возникновения НВ разного знака имеет место. Однако накопления неравномерно возникающих НВ не происходит, так как все возмущения затухают. В результате НВ дают пренебрежимо малый вклад в распределения гидродинамических величин.

Качественно иная картина имеет место после достижения первого критического значения числа Рейнольдса $\operatorname{Re} _{0}^{*}.$ При $\operatorname{Re} > \operatorname{Re} _{0}^{*}$ стационарное решение $\hat {\bar {C}}_{i}^{{(0)}}$ теряет свою устойчивость. Потеряв устойчивость, решение приобретает зависимость от времени. Ансамбль Гиббса распадается. Неустойчивое решение $\hat {C}_{i}^{{(0)}}(t) = \hat {\bar {C}}_{i}^{{(0)}} + \delta \hat {C}_{i}^{{r(0)}}(t)$ системы (1.4) из [1] удовлетворительно воспроизводит первый неустойчивый режим обтекания сферы: периодическую пульсацию зоны закручивания $V_{0}^{{exp}}(t,x)$ [11, 19]. Режим периодических пульсаций достаточно продолжителен по Re. Достижение второго критического значения $\operatorname{Re} _{0}^{{{\text{**}}}} > \operatorname{Re} _{0}^{*}$ сопровождается возникновением вихревого испускания [11]. Неустойчивое решение $\hat {C}_{i}^{{(0)}}(t)$ не смогло удовлетворить законам сохранения числа частиц, импульса и энергии.

Для выполнения законов сохранения потребовался учет НВ. В соответствии с представлениями [7] уравнения сохранения дополняются членами, ответственными за НВ. Таким образом, система уравнений для НВ решается совместно с системой уравнений для регулярных коэффициентов $\hat {\bar {C}}_{i}^{{(0)}}$ и $\delta \hat {C}_{i}^{{r(0)}}(t).$ То есть независимость в поведении НВ пропадает. В зоне закручивания уравнения сохранения “вынуждают” неупорядоченные возмущения вести себя во времени и в пространстве вполне определенным образом. Решение уравнения сохранения импульса (2.16) из [1] показывает, что отрицательно определенные неупорядоченные возмущения $\delta \hat {C}_{{20,i}}^{{d(0)}} < 0$ по-прежнему затухают, в то время как положительно определенные неупорядоченные возмущения $\delta \hat {C}_{{20,i}}^{{d(0)}} > 0$ нарастают. Это различие в поведении и неравномерность возникновения положительно и отрицательно определенных неупорядоченных возмущений $\delta \hat {C}_{{20,i}}^{{d(0)}}$ создает накопление возмущений, не исчезающих на масштабе времени ${{{{\tau }}}_{{d1}}}$ (уравнение (1.1)), отличном от масштаба изменения гидродинамических величин, ${{{{\tau }}}_{h}}.$ Накопление неисчезающих НВ приводит к различию суммарного вклада регулярной флуктуации и неупорядоченного возмущения $\delta \hat {C}_{{20,i}}^{{rd(0)}}(t,x)$ по порядку своей величины в каждой точке $x$ следа за сферой.

Изменение в поведении неупорядоченных возмущений привело к качественному изменению регулярной картины течения в зоне закручивания (см. рис. 1 из [1]). Перемещаясь по материальной линии, жидкая частица испытывает как хаотические изменения направления движения, так и хаотические изменения модуля скорости движения (рис. 3). В отличие от регулярных материальных линий, искаженные материальные линии хаотически пересекаются в зоне закручивания. Хаотическое движение жидкой частицы по искаженным неупорядоченными возмущениями пересекающимся материальным линиям создает турбулентную картину течения в зоне закручивания.

Таким образом, в результате численного интегрирования уравнений многомоментной гидродинамики установлено, что зона закручивания является регулярной составляющей турбулентности. Хаотической составляющей турбулентности являются непорядочные возмущения, возникающие в среде за счет внешнего воздействия. Интенсивность хаотичности, искажающей регулярную картину течения, напрямую определяется величиной коэффициента турбулентности набегающего потока ${{\bar {K}}_{d}}.$ Высокий коэффициент турбулентности (${{\bar {K}}_{d}} = 0.4\% $) создает ярко выраженную турбулентную картину течения в зоне закручивания (рис. 3). Невысокий коэффициент турбулентности (${{\bar {K}}_{d}} = 0.04\% $) крайне слабо искажает регулярную картину течения. Этот сценарий перехода к турбулентности качественно отличается от существующего бифуркационного сценария Ландау–Хопфа [20]. Как отмечено выше, сценарий Ландау–Хопфа, которому следуют решения уравнений Навье–Стокса, не пригоден для интерпретации турбулентности, регистрируемой экспериментально.

Турбулентность оказывает сильное влияние на окружающую действительность. Это предопределяет огромный интерес к изучению этого крайне сложного явления. Оказалось, что стохастические методы недостаточно эффективны для прогнозирования характеристик турбулентных процессов. Поэтому значительные усилия направлены на развитие детерминистического подхода к интерпретации турбулентности. Высокая вычислительная “стоимость” прямого численного интегрирования является причиной широкого использования менее затратных приближенных полуэмпирических методов расчета турбулентных течений – RANS и LES. В многомоментной гидродинамике вычислительные усилия ограничены решением системы нелинейных дифференциальных уравнений первого порядка (1.4) из [1], которые ответственны за ламинарное движение среды. Введение элементов стохастичности в эти уравнения не сопровождается существенными дополнительными вычислительными усилиями.

Анализ данных эксперимента привел исследователей к выводу, что возникновение турбулентности связано с появлением крупных вихрей (когерентных структур), зарождающихся вблизи ограничивающих течение поверхностей [1, 21]. В соответствии с существующими представлениями турбулентность интерпретируется в терминах эволюции когерентных структур.

Обтекание твердой сферы является простейшей задачей гидродинамики. Решение этой задачи при низких значениях $\operatorname{Re} $ (решение Стокса) найдено во времена создания уравнений Навье–Стокса. В диапазоне значений $\operatorname{Re} _{0}^{*} < \operatorname{Re} < \operatorname{Re} _{0}^{{{\text{**}}}}$ вихревое испускание отсутствует. В этом диапазоне в следе за сферой существует только одна когерентная структура – зона закручивания. Решения детерминистических уравнений многомоментной гидродинамики не в состоянии привнести элементы хаотичности в регулярную картину течения в зоне закручивания (см. рис. 1 из [1]). Эти элементы появляются в результате учета неупорядоченных возмущений, возникающих в среде из-за внешнего воздействия (см. рис. 3). Решения детерминистических уравнений Навье–Стокса успешно воспроизводят эволюцию когерентной структуры – устойчивой зоны закручивания. Однако решения уравнений Навье–Стокса теряют направление развития турбулентности после потери устойчивости [9].

В сложных задачах гидродинамики в поле течения возникает большое количество крупных вихрей. Существование большого числа когерентных структур создает иллюзию возможности интерпретации турбулентных течений в терминах решений детерминистических уравнений. Решение простейшей задачи гидродинамики развеивает эту иллюзию. Эволюция когерентных структур сама по себе не создает турбулентную картину течения, которая возникает за счет хаотического искажения когерентных структур. Поэтому возможность приведения детерминистических уравнений Навье–Стокса, а также уравнений RANS и LES к пригодному для интерпретации турбулентности виду следует искать на пути включения в эти уравнения стохастических составляющих.

Прямое численное интегрирование уравнений Навье–Стокса в задаче обтекания сферы предсказывает ранний и быстрый переход от устойчивого состояния сплошной среды к развитой турбулентности, что противоречит эксперименту. Возникновение развитой турбулентности сопровождается значительными качественными и количественными изменениями гидро- и аэродинамических характеристик обтекаемого тела. Учет этих изменений необходим при создании конструкций и аппаратов, перемещающихся в сплошной среде. Корректное воспроизведение турбулентных процессов, протекающих в окружающей среде, в промышленных и экспериментальных установках, столь же необходимо для созидательной деятельности. Это предопределяет актуальность решаемой в работе задачи.