Журнал высшей нервной деятельности им. И.П. Павлова, 2022, T. 72, № 3, стр. 370-386
Анализ локальной динамики распространения межприступных разрядов с помощью модели бегущих волн
А. А. Кузнецова 1, А. Е. Осадчий 2, *
1 Лаборатория социальной нейробиологии, Институт когнитивных нейронаук,
Высшая школа экономики
Москва, Россия
2 Центр биоэлектрических интерфейсов, Институт когнитивных нейронаук,
Высшая школа экономики
Москва, Россия
* E-mail: ossadtchi@gmail.com
Поступила в редакцию 29.08.2021
После доработки 29.08.2021
Принята к публикации 20.12.2021
- EDN: IFJMVM
- DOI: 10.31857/S0044467722030078
Аннотация
Эпилепсия − одно из наиболее распространенных неврологических заболеваний в мире, причем около 30% случаев не поддаются фармакологическому воздействию и могут требовать хирургического вмешательства. В процессе локализации эпилептогенной зоны − области, с которой связывают инициацию приступов у пациентов с фокальной эпилепсией, − различные области головного мозга исследуют на наличие межприступных разрядов. В данной работе мы предлагаем новую методологию неинвазивного исследования тонкой пространственно-временной структуры межприступных разрядов, наблюдаемых в магнитоэнцефалограмме (МЭГ). Для регуляризации обратной задачи МЭГ мы использовали модель бегущей волны. Алгоритм представляет нейронную активность, генерирующую межприступный разряд, как суперпозицию локальных волн, распространяющихся по радиальным путям и порождаемых одним точечным источником. С помощью метода LASSO с положительными коэффициентами мы определяем такое сочетание сгенерированных с разными параметрами волн, которое дает наилучшее совпадение с МЭГ-записью для каждого разряда. Для анализа свойств алгоритма мы использовали реалистичные симуляции МЭГ-данных. Затем мы применили наш метод для анализа МЭГ-данных трех пациентов с фармакорезистентной мультифокальной эпилепсией. Для части разрядов мы обнаружили волнообразные паттерны с четкой динамикой распространения, в то время как для другой части наблюдаемая активность не может быть объяснена моделью суперпозиции волн. Более того, разряды с четкой динамикой распространения демонстрировали выраженные пространственные кластеры и соотносились с эпилептогенными зонами, описанными в истории болезни для двух пациентов из трех.
Несмотря на то что феномен кортикальных бегущих волн был известен с 1930-х годов (Adrian, Matthews, 1934), (Adrian, Yamagiwa, 1935), в большинстве когнитивных исследований авторы придерживаются парадигмы Дондерса о пространственно-временной разделенности мозговой активности (Donders, 1969) и часто пользуются приемом усреднения эпох для выделения интересующей нейронной активности. Такое представление, однако, не подходит для описания кортикальной активности, распространяющейся в пространстве и обладающей высокой изменчивостью между эпохами. Вместе с тем все больше исследований показывают, что нейронная активность распространяется по коре головного мозга в виде бегущей волны: такой характер поведения нейрональной активации наблюдается для целого ряда биологических видов и областей мозга, включая зрительную кору черепахи (Prechtl et al., 1997); зрительную, слуховую и соматосенсорную кору кролика (Freeman, Barrie, 2000); сенсомоторную кору мышей в бодрствовании (Ferezou et al., 2007); а также первичную и вторичную зрительную кору у бодрствующих обезьян (Muller et al., 2014).
Бегущие кортикальные волны были обнаружены и в неокортексе человека (см. обзор (Muller et al., 2018)), например, известно, что распространяющаяся альфа-активность (Hindriks et al., 2014; Zhang et al., 2018) оказывает влияние на активацию в гамма-диапазоне (Bahramisharif et al., 2013). Кроме того, бегущие тета-волны встречаются у людей и в гиппокампе (Lubenov, Siapas, 2009). Компонента бегущей волны также присутствует в связанной с фиксацией лямбда-активности во время свободного созерцания (Giannini et al., 2018). Наконец, во время сна, как на больших масштабах (Massimini, 2004), так и локально (Hangya et al., 2011), наблюдается распространение медленных волн, и связанные со сном K-комплексы также имеют сложные волновые паттерны распространения (Mak-McCully et al., 2015).
Несмотря на то что существует множество свидетельств участия бегущих кортикальных волн в различных мозговых процессах, их механизмы и функции по-прежнему во многом не ясны (Ermentrout, Kleinfeld, 2001), (Wu et al., 2007), (Muller et al., 2018). Однако появляется все больше свидетельств, подтверждающих два тезиса: (1) бегущие волны играют функциональную роль в обработке информации мозгом в норме и (2) бегущие волны вносят вклад в распространение активности при патологии. Осцилляции, синхронизируя нейрональную активность на разных масштабах, играют важную роль в функциональной интеграции областей мозга. Согласно теории коммуникации через когерентность (Fries, 2005, 2015), на макроуровне функциональная интеграция нейрональных сетей осуществляется за счет установления когерентных осцилляций в вовлеченных в процесс областях коры. Дальнейшие исследования пространственно-временных характеристик распространения осцилляций, т.е. их исследование с точки зрения бегущих волн, позволят точнее понимать механизмы функционального взаимодействия в нейронных сетях головного мозга.
Функции бегущих волн в норме разнообразны. Например, они участвуют в механизмах рабочей памяти. Было показано, что испытуемые лучше справлялись с заданием на рабочую память, когда их кортикальные паттерны распространения активности были согласованы (Zhang et al., 2018). Кроме того, планирование движения и его характеристики в целом с точки зрения корковых бегущих волн коррелируют со временем реакции в моторной задаче, указывая на тот факт, что бегущие волны регулируют моторный контроль (Patten et al., 2012). Что касается патологии, бегущие волны были описаны в бикукулинной модели эпилепсии (Huang et al., 2004).
Локализация эпилептогенной зоны (ЭЗ) − области, с которой связывают инициацию приступов, − является одной из важнейших задач предоперационной диагностики. Для поиска ЭЗ различные области головного мозга исследуют на наличие межприступных разрядов. Согласно исследованию (Крылов и др., 2016), фармакорезистентность развивается приблизительно у 30% пациентов, имеющих фокальную эпилепсию, причем хирургическое удаление эпилептогенной зоны в 68% случаев позволяет добиться полного контроля над приступами.
В недавней работе (Komoltsev et al., 2020) авторы анализируют эпилептиформную активность, вызванную черепно-мозговой травмой, у человека и крысы. Авторы отмечают, что неинвазивные ЭЭГ-записи оказались нечувствительны к патологической активности, тогда как инвазивные записи показали ее наличие у 86% пациентов. В то же время пространственное разрешение МЭГ значительно выше, чем ЭЭГ, особенно при активации областей мозга, имеющих высокую кривизну (Nasiotis et al., 2017). В работе (Koptelova et al., 2018) было показано, что межприступные МЭГ-записи могут содержать значимую информацию, достаточную для правильной локализации ЭЗ и последующего хирургического вмешательства. В данной работе мы предлагаем методологию неинвазивного исследования тонкой пространственно-временной структуры межприступных разрядов, наблюдаемых в МЭГ-данных пациентов с фармакорезистентной формой эпилепсии.
МЕТОДИКА
Модель данных
В нашей модели мы рассматриваем межприступный разряд как эпизод распространения бегущей волны. Мы предполагаем, что волна исходит от порождающего источника и распространяется в $N_{d}^{*}$ разных направлениях вдоль поверхности коры. Имея в виду, что пройденное волной расстояние зависит от скорости её распространения, мы полагаем длины путей распространения всех волн равными между собой по количеству Ns узлов коры, в которых побывала волна. Таким образом, -е направление распространения можно представить как последовательность активных корковых источников ${{p}_{d}} = \,\,~\left[ {r_{d}^{1}, \ldots ,r_{d}^{{{{N}_{s}}}}} \right]$, где ${{r}_{i}} = \,\,~\left[ {{{x}_{i}},~{{y}_{i}},~{{z}_{i}}} \right]$ содержит координаты источника в трехмерном пространстве, $d~\,\, \in \,\,~\left[ {1, \ldots ,~N_{d}^{*}} \right]$, а первый источник одинаков для всех направлений (порождающий источник).
Временные ряды активации источников из набора pd образуют матрицу Sd размера ${{N}_{s}} \times \,\,~{{T}_{s}}$, где ${{T}_{s}}~\, = \,\,~T \cdot ~fs$ − количество временных отсчетов для рассматриваемого события, T − продолжительность события в секундах, fs − частота дискретизации в герцах. Чтобы представить распространение нейронной активности, порождающей разряд, в виде волны в пространстве и времени, временные ряды активации последующих источников сдвинуты во времени относительно предыдущих.
Располагая прямым оператором G с фиксированной ориентацией источников и размерностью ${{N}_{{ch}}}~\,\, \times \,\,~{{N}_{{src}}}$, где Nch − количество сенсоров и Nsrc − общее количество источников, многоканальный сигнал ЭЭГ или МЭГ $X$ можно представить как линейную комбинацию спроецированных в пространство сенсоров кортикальных бегущих волн ${{W}_{d}},~~d \in [1 \ldots N_{d}^{*}]$:
(1)
$X~\,\, = \,\,~\mathop \sum \limits_{d = 1}^{N_{d}^{*}} {{\alpha }_{d}}{{G}_{d}}{{S}^{d}} + ~\,\,E~\, = \,\,~\mathop \sum \limits_{d = 1}^{N_{d}^{*}} {{\alpha }_{d}}{{W}^{d}} + \,\,~E.$Матрица Gd размера ${{N}_{{ch}}} \times {{N}_{s}}$ формируется из столбцов матрицы прямого оператора G, соответствующих топографиям источников из пути pd. Матрица E моделирует не связанную с разрядом мозговую активность и аддитивный шум сенсоров. Коэффициенты ${{\alpha }_{d}},~~d~ \in \left[ {1 \ldots N_{d}^{*}} \right]$, соответствуют вкладу каждого направления распространения в наблюдаемую МЭГ-активность.
Базисные волны
Для представленной выше модели данных мы предполагаем, что распространение МЭГ-активности можно представить в виде линейной комбинации ${{W}_{d}},~~d~\,\, \in ~\,\,\left[ {1 \ldots {{N}_{d}}} \right]$ бегущих волн в пространстве сенсоров. Основная идея методики, предложенной в данной статье, состоит в том, чтобы генерировать шаблоны бегущих волн, которые мы называем базисными волнами, а затем находить их комбинацию с наименьшим количеством слагаемых, наилучшим образом объясняющую данные МЭГ. Ниже мы описываем алгоритм вычисления базисных волн.
Для простоты мы определяем количество активных кортикальных источников вдоль каждого пути распространения как равное количеству наблюдений, сделанных за время события: ${{N}_{s}}~\,\, = ~\,\,T~ \cdot ~fs$. В наших симуляциях мы рассматриваем случай, когда моделируемые временные ряды активации для каждого из Ns источников имеют синусоидальную форму волны и сдвинуты во времени относительно их последовательности от начальной точки. Для каждого направления распространения $d \in \left[ {1, \ldots ,{{N}_{d}}} \right]$ матрица временных рядов источников Sd формируется из строк:
(2)
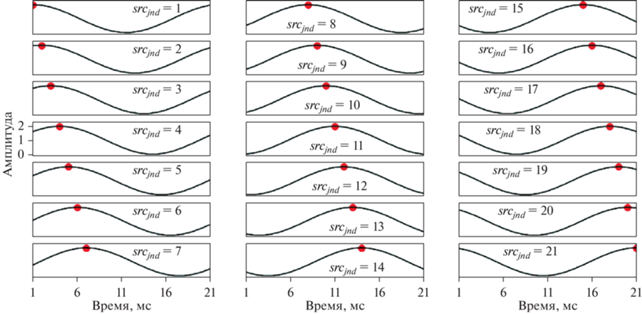
$\begin{gathered} S_{i}^{d} = 1 + \cos \left( {\frac{{2\pi \left( {t - {{k}_{i}}} \right)}}{{{{N}_{s}}}}} \right),~{\text{\;}} \\ {\text{для}}~~{{k}_{i}}~\,\, \in \,\,~\left[ {1, \ldots ,{{N}_{s}}\left] {,\,\,~t~ = ~} \right[1, \ldots ,{{N}_{s}}} \right]. \\ \end{gathered} $Пример временных рядов для ${{N}_{s}}~\, = 21$ кортикальных источников вдоль одного из направлений распространения изображен на рис. 1. Каждая панель соответствует одному источнику $sr{{c}_{{ind}}}~\, \in \,\,~\left[ {1, \ldots ,{{N}_{s}}} \right].$ Момент времени, соответствующий максимальной амплитуде активации, отмечен красной точкой. Выбор такой временной функции активации позволяет нам моделировать распространение активности одновременно и в пространстве, и во времени.
Рис. 1.
Временные профили активации для ${{N}_{s}} = \,\,~21$ источника. Красная точка демонстрирует распространение максимальной активации во времени и пространстве для каждого временного ряда.
Fig. 1. Activation timeseries for ${{N}_{s}} = \,\,~21$ cortical sources. Spatiotemporal propagation of peak maximum activation corresponds to red dot.
Положения источников ${{p}_{d}} = \left[ {r_{d}^{1}, \ldots ,r_{d}^{{{{N}_{s}}}}} \right]$ в каждом конкретном случае зависят от индивидуальной анатомии, положения исходного источника ${{v}_{s}} = \left[ {{{x}_{s}},{{y}_{s}},{{z}_{s}}} \right]$ и скорости распространения. Кортикальные пути для базисных волн генерируются с использованием поверхностей, рассчитанных программой Freesurfer (Fischl, 2012) и обработанных в программе Brainstorm (Tadel et al., 2011). Для каждой базисной волны нам нужно найти путь на графе с Nsrc вершинами, соединенными в соответствии с матрицей смежности $A$, определенной 3-D моделью коры. Для заданного начального положения на коре с Nd ближайшими соседями мы определяем Nd базисных волн, распространяющихся в направлениях этих ближайших соседей. Для удобства анализа в практических приложениях мы не добавляем новые вершины или ребра к графу, соответствующему модели коры. Ограничением этого подхода является тот факт, что количество направлений распространения зависит от плотности вершин в исследуемой области, а также, в случае адаптивных сеток, от локальной кривизны. Последнее имеет смысл, так как пространственное разрешение МЭГ коррелирует с локальной кривизной (Nasiotis et al., 2017).
Пути распространения для стартовой точки ${{v}_{s}}$ генерируются в соответствии со следующим алгоритмом:
1. Nd вершин ближайших соседей $\left[ {nn_{{{{v}_{s}}}}^{1}, \ldots ,nn_{{{{v}_{s}}}}^{d}} \right]$ для стартовой точки находятся из соответствующей строки матрицы смежности ${{A}_{{{{v}_{s}}}}}$;
2. Для аппроксимации нормали к участку поверхности коры, который образуется вершинами ближайших соседей $\left[ {nn_{{{{v}_{s}}}}^{1}, \ldots ,nn_{{{{v}_{s}}}}^{d}} \right]$, мы усредняем нормали в каждой из Nd точек: ${{n}_{{{\text{av}}}}} = \frac{1}{{{{N}_{d}}}}\sum\nolimits_{d = 1}^{{{N}_{d}}} {{{n}_{d}}} $. Нормируя к единице, получаем вектор $\widetilde {{{n}_{{{\text{av}}}}}}~\,\, = ~\,\,\frac{{{{n}_{{{\text{av}}}}}}}{{{{{\left\| {{{n}_{{{\text{av}}}}}} \right\|}}_{2}}}}$;
3. Вычисляем матрицу проекции на этот кортикальный путь как $P = I - \widetilde {{{n}_{{{\text{av}}}}}}{{\widetilde {{{n}_{{{\text{av}}}}}}}^{T}}$, где I − единичная матрица размером 3 × 3, а ${{\left( \cdot \right)}^{T}}$ − матричное транспонирование;
4. Добавляем $nn_{{{{v}_{s}}}}^{d}$ к пути pd;
5. Вычисляем вектор направления распространения ${{h}_{{sd}}} = \left( {{{v}_{s}} - {{v}_{d}}} \right) \cdot ~\,P$. Нормируем этот вектор: $\widetilde {{{h}_{{sd}}}}~\,\, = \,\,~\frac{{{{h}_{{sd}}}}}{{{{{\left\| {{{h}_{{sd}}}} \right\|}}_{2}}}}$;
6. Для каждого ближайшего соседа до тех пор, пока длина пути короче, чем $max\_step,$ повторяем:
a. Запоминаем вершину ближайшего соседа во вспомогательную переменную v и используем матрицу смежности, чтобы найти ближайших соседей этой вершины $\left[ {n{{n}_{1}}, \ldots ,n{{n}_{m}}} \right]$;
b. Среди всех найденных вершин выбираем ту, которая максимизирует выражение $nn{\text{*}}~\, = \,~\arg \max \left( {\frac{{(n{{n}_{i}}~\, - \,\,~v)~\, \cdot \,~P}}{{{{{\left\| {(n{{n}_{i}}~\,\, - \,\,~v)~\, \cdot \,~P} \right\|}}_{2}}~}} \cdot \widetilde {{{h}_{{sd}}}}} \right)$;
c. Добавляем вершину nn* к пути pd и повторяем шаг (6).
Полученные кортикальные пути td затем используются для определения конкретных местоположений источников (узлов) pd для различных скоростей распространения.
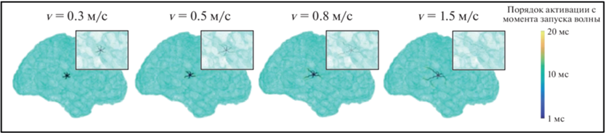
На рис. 2 показан пример сгенерированных наборов источников pd для разных скоростей распространения, от 0.3 до 1.5 м/с. По полученным путям распространения подмножества матрицы прямого оператора ${{G}_{d}},\,\,d = 1, \ldots ,{{N}_{d}}$ затем используются для вычисления базисных волн согласно уравнению (1).
Рис. 2.
Пример кортикальных источников для сгенерированных базисных волн в случае для различных скоростей распространения.
Fig. 2. Example of cortical source sets generated for basis waves with proragation directions for different velocities.
Помимо радиальных направленных волн мы также рассматривали сферическую волну, распространяющуюся одновременно во всех направлениях и состоящую из суммы радиальных волн ${{W}_{{sph}}} = \sum\nolimits_{d = 1}^{{{N}_{d}}} {{{W}_{d}}} $, однако наши тесты на симуляционных и реальных данных показали, что сферические волны не выбираются алгоритмом в качестве участников оптимальной комбинации. При изменении скорости распространения мы также вводим временную метку начала волны. Точное время инициирования волны неизвестно, но оптимальное значение можно найти с помощью метода скользящего окна. Мы автоматически сканируем временной интервал, содержащий межприступный разряд, подбираем к этому интервалу базисные волны и повторяем весь анализ для временного ряда, сдвинутого на один временной отсчет.
Оптимальная комбинация бегущих волн
После того как базисные волны сгенерированы, следующий этап анализа состоит в поиске их комбинации, которая наилучшим образом описывает наблюдаемые МЭГ-данные. Исходя из физиологических предположений, желаемая комбинация должна содержать только несколько базисных волн, соответствующих нескольким доминирующим направлениям распространения. Поэтому мы ищем наиболее разреженное решение, которое описывает данные и соответствует небольшому количеству четко определенных доминантных направлений распространения. Чтобы найти вклад каждой вычисленной заранее базисной волны в МЭГ-данные, мы использовали метод LASSO (Tibshirani, 1996), с дополнительным ограничением на то, что коэффициенты LASSO должны быть положительными. Задача оптимизации формализуется уравнением (3). Основным преимуществом этого метода является тот факт, что благодаря негладкому регуляризационному слагаемому со штрафом по норме L1 отбор признаков выполняется таким образом, чтобы коэффициенты неинформативных направлений распространения были равны нулю. Так как мы рассматриваем многоканальную задачу, мы векторизовали матрицу данных X и базисных волн на сенсорах $W_{d}^{s}$:
(3)
$\begin{gathered} \mathop {\min }\limits_{{{\alpha }_{0}} \ldots {{\alpha }_{{{{N}_{d}}}}}} {{\left\| {{\text{vec}}\left( X \right) - ~\mathop \sum \limits_{d = 0}^{{{N}^{d}}} {{\alpha }_{d}}{\text{vec}}\left( {{{W}_{d}}} \right)} \right\|}^{2}} + \lambda \mathop \sum \limits_{d = 0}^{{{N}_{d}}} \left| {{{\alpha }_{d}}} \right| \\ {\text{subject}}\,\,{\text{to}}\,\,{{\alpha }_{{d~}}} \geqslant 0,\,\,\,\,d = 0 \ldots {{N}_{d}}. \\ \end{gathered} $Затем данная процедура применяется ко всем наборам сгенерированных базисных волн с двумя параметрами: скоростью распространения и временем начала распространения волны. Лучшее решение выбирается в соответствии с метрикой R2 (т.е. процентом объясненной дисперсии). Важным вопросом при генерации базисных волн является обнаружение самого первого источника, инициирующего распространение волны. Мы определяем область интереса (ROI) в первом приближении с помощью алгоритма дипольной подгонки RAP-MUSIC (Mosher, Leahy, 1999). Чтобы повысить точность решения, мы сканируем ROI, используя попадающие туда узлы коры в качестве отправных точек, и сравниваем решения при помощи метрики ${{R}^{2}}.$
Схема алгоритма
Итоговый алгоритм для решения обратной задачи МЭГ с регуляризацией в виде предположения бегущей волны состоит из следующих этапов:
1. Определяем область интереса на коре, применяя алгоритм RAP-MUSIC (Mosher, Leahy, 1999) к МЭГ-данным и берем ее окрестность (например, радиусом 1 см). Затем для каждой вершины, принадлежащей к найденной области интереса, повторяем:
a. Используем выбранный кортикальный источник ${{v}_{s}}$ в качестве стартовой точки для генерации волн и вычисляем базисные волны для различных скоростей распространения;
b. Применяем метод LASSO (Tibshirani, 1996) с положительными коэффициентами, чтобы подогнать базисные волны к самому началу МЭГ-записи соответствующего события и определить значение метрики R2 вместе с числом ненулевых коэффициентов решения;
c. Сдвигаем МЭГ-сигнал назад во времени на p временных отсчетов и повторяем анализ. Находим оптимальный момент начала распространения волны и оптимальные скорости распространения в соответствии с величиной R2.
2. Сравниваем R2 в точке оптимума для всех вершин в ROI и выбираем лучшую точку как найденный источник распространения волны.
Симуляции Монте-Карло
Чтобы оценить качество работы алгоритма, мы выполнили ряд симуляций Монте-Карло. Синтетические данные МЭГ магнитометров были получены с помощью модели кортикальной поверхности высокого разрешения с 300 000 вершин, реконструированных из анатомических данных МРТ с использованием программного обеспечения FreeSurfer (Fischl, 2012). Матрица G прямой модели для дипольных источников с фиксированной ориентацией была рассчитана с использованием программного обеспечения Brainstorm (Tadel et al., 2011) с использованием модели перекрывающихся сфер.
Скорость распространения, учитываемая при анализе как модельных, так и реальных данных, выбиралась из следующего набора: S = [0.001, 0.005, 0.01, 0.05, 0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8] м/с. Мы проанализировали 300 эпох с равномерно распределенной скоростью распространения (25 эпох на каждое значение). Длительность волны была установлена равной T = 20 мс, а частота дискретизации имела значение 1000 Гц. При моделировании мы рассматривали два типа эпох. Первый тип − моделирование бегущей волны (300 эпох), а второй − симуляции статической колебательной активности (осциллирующий очаг активности, который не двигается в пространстве), также 300 эпох. Бегущие волны были сгенерированы с помощью алгоритма, описанного выше. Временной ряд активации осциллирующего очага вычислялся как $g\left( {x,~t} \right) = \frac{1}{2}\left( {1 + {\text{\;cos}}~\left( {\frac{\pi }{2}t} \right)~} \right)\frac{{B{{e}^{{ - {{c}^{2}}~ + ~{{x}^{2}}}}}}}{{2{{\sigma }^{2}}}}$.
Мы определили величину отношения сигнал-шум (SNR) для смоделированных данных в пространстве сенсоров как отношение нормы Фробениуса для 5 каналов с наивысшей мощностью в течение интервала наблюдения межприступного разряда к норме для данных с тех же каналов за период той же продолжительности, взятый до или после разряда. Мы проверяли данные, чтобы во втором периоде не было разрядов. Для каждого типа эпох случайно выбранная вершина играла роль генерирующего источника. Направление и скорость распространения были выбраны случайным образом из доступного набора параметров.
Мы моделировали мозговую активность, не относящуюся к разряду, при помощи $Q = 1000$ кортикальных источников, положения и временные ряды которых генерировались от эпохи к эпохе случайно. Временными рядами не относящихся к разряду источников служили узкополосные сигналы, полученные с помощью фильтрации с нулевой фазой реализаций гауссовского псевдослучайного процесса. Фильтрация проводилась полосовым БИХ-фильтром пятого порядка; полосы фильтра соответствовали тета- (4–7 Гц), альфа- (8–12 Гц), бета- (15–30 Гц) и гамма- (30–50 Гц, 50–70 Гц) активности. Мы скорректировали относительный вклад этих ритмических компонентов в соответствии с хорошо известной 1/f-характеристикой спектра шума МЭГ. Компоненты шума соответствовали характерному отношению сигнал–шум для записей МЭГ. Шумовые источники проецировались в пространство сенсоров с помощью соответствующих столбцов матрицы прямой модели. Мы смоделировали 300 эпох МЭГ-данных. Для каждой эпохи новый набор шумовых источников выбирался заново и создавались новые шумовые временные ряды со спектром профиля 1/f.
Кортикальная сетка высокого разрешения использовалась только для моделирования данных. Для реконструкции источников мы использовали более разреженную кортикальную сетку с 200 000 вершин. Кроме того, мы искусственно добавляли ошибку для обнаружения первого источника. Для этого мы сначала случайным образом выбрали точку генерации на коре из модели с высоким разрешением, а затем использовали эту точку в качестве порождающей для волны. Затем мы случайным образом определяли начальную точку для старта алгоритма, используя разреженную модель для 3-миллиметровой области вокруг истинного места генерации. Базисные волны были инициированы в этом новом месте.
Чтобы сравнить генерируемое и оцененное направления распространения, мы вычислили первое главное направление p* и приняли его в качестве истинного. Затем мы определили все направления, использованные в рассчитанном решении, и присвоили им веса $w_{p}^{i}$, которые были пропорциональны их вкладу в решение LASSO. Затем мы рассчитали первую взвешенную главную компоненту направления распространения для найденного решения $\tilde {p} = w_{p}^{i}{{p}_{i}}$. Ошибка оценки направления рассчитывалась как $e = 1 - \frac{{p{\text{*}}\hat {p}}}{{{{{\left\| {p{\text{*}}} \right\|}}_{2}}{{{\left\| {\hat {p}} \right\|}}_{2}}}}$. Чтобы свести к минимуму ошибки обнаружения волн из-за неточности локализации первой точки, мы сканировали область радиусом 5 мм вокруг этих точек и выбирали лучшую генерирующую точку как точку с самым высоким значением R2.
Регистрация МЭГ-данных
Мы применили предложенный алгоритм к МЭГ-записям от трех пациентов с мультифокальной эпилепсией. Данные были собраны в Московском МЭГ-центре с использованием системы Elekta-Neuromag Vectorview 306 (Elekta Oy, Финляндия), которая производит записи с 204 планарных градиометров и 102 магнитометров. Данные были собраны во время сна с частотой дискретизации 1000 Гц и предварительно обработаны с помощью программного обеспечения Elekta MaxFilter.
РЕЗУЛЬТАТЫ ИССЛЕДОВАНИЙ
Симуляции Монте-Карло
Симуляции методом Монте-Карло были посчитаны для трех уровней сигнал–шум (SNR): значений 1, 2 и 3. Полученные результаты представлены на верхней левой панели рис. 3: на графике изображены ROC-кривые, показывающие, насколько успешно предложенный алгоритм позволяет детектировать бегущие волны. Для построения этих кривых были использованы 300 испытаний Монте-Карло, в которых волновое распространение задавалось случайно равномерно выбранной из рассматриваемых вариантов скоростью распространения, и 300 испытаний, в которых симулировалась только статическая активность без распространения в пространстве. Соответствующие значения площади под кривой (ROC AUC) составляют 0.78, 0.95 и 0.97, что означает, что при разумно высоком отношении сигнал–шум предложенный метод успешно разделяет распространяющуюся и статическую активность.
Рис. 3.
Сравнение смоделированных (по оси x) и оцененных (по оси y) скоростей для трех уровней отношения сигнал–шум: 1, 2 и 3. Каждая точка соответствует одному испытанию методом Монте-Карло. К значениям добавляется небольшой случайный сдвиг для удобства визуализации. Для каждого значения реальной скорости определяется наиболее частое значение расчетной скорости, и соответствующие точки отображаются красным цветом.
Fig. 3. Comparison of modelled (x-axis) and estimated propagation velocities for three SNR levels: 1, 2, 3. Each dot corresponds to one Monte Carlo trial. Small random jitter was added for visualization purposes. Red dots demonstrate the most popular estimated velocity for each ground truth value.
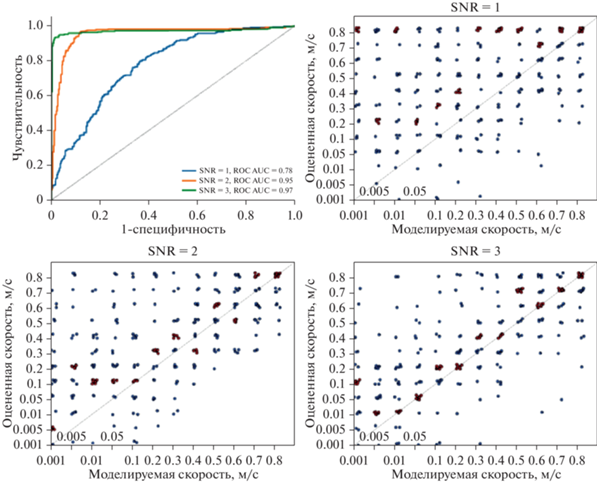
На трех других панелях рис. 3 показано соответствие симулируемых значений скорости распространения (по оси x) и значений, полученных в результате работы алгоритма (по оси y), для различных SNR. Каждая точка на графике соответствует одному испытанию Монте-Карло. Для более наглядной визуализации к значениям были добавлены небольшие случайные сдвиги. Для каждой из реальных скоростей было определено значение скорости, которое чаще всего находится с помощью алгоритма, и такие кластеры точек показаны красным цветом. Для SNR = 1 алгоритм имеет тенденцию значительно переоценивать скорость распространения по сравнению с истинным значением: красные кластеры не совпадают с настоящим значением, за исключением самой высокой скорости распространения. Для SNR = 2 наблюдается все еще много ошибок в определении скорости, но абсолютная разница между оцененными и фактическими значениями намного ниже, чем для предыдущего случая. Для SNR = 3 модальное оцененное значение совпадает с фактической скоростью или с ближайшим к ней значением для всех случаев, за исключением двух, когда оценка скорости оказывается завышенной.
Важно отметить, что ошибки в оценке скорости неизбежны даже для высоких значений SNR из-за ошибки, которую мы закладываем при локализации точки старта, и из-за использования более редкой модели кортекса. Учитывая то, что время распространения мы считаем фиксированным, в случае, если найденная алгоритмом начальная точка запуска волны смещена относительно фактической в сторону конечной точки пути распространения, естественным образом скорость окажется заниженной. И наоборот, если начальная точка смещена в противоположную сторону от конца пути, то скорость окажется завышенной. Чем выше SNR в данных, тем меньше эти ошибки.
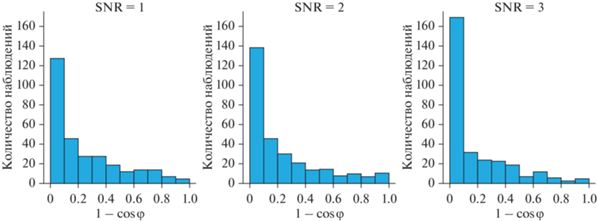
Затем мы оценили ошибки в найденном направлении распространения. На рис. 4 показано распределение этих ошибок для всех трех уровней отношения сигнал–шум. Ошибка рассчитывалась как $1 - \cos \varphi ~$, где φ − угол между фактическим и оцененным главными направлениями распространения. Значения такой метрики располагаются в диапазоне от нуля до единицы. Можно увидеть, что для всех уровней SNR большая часть ошибок меньше, чем 0.1, и все ошибки имеют тенденцию уменьшаться с увеличением отношения сигнал–шум.
Рис. 4.
Распределение ошибки детекции направления распространения 1 – cos φ, где φ − угол между главным направлением истинного распространения и главным направлением оцененного распространения. Результаты показаны для 300 испытаний методом Монте-Карло и для трех уровней отношения сигнал–шум: 1, 2, 3.
Fig. 4. Distribution of propagation direction detection error 1 – cos φ, where φ – angle between the first principal propagation direction of ground truth wave and first principal propagation direction of estimated wave. The obtained results are calculated for 300 Monte Carlo trials and three SNR levels: 1, 2, 3.
Данные пациентов
В качестве реальных данных мы использовали данные трех пациентов с эпилепсией: 10-минутные записи МЭГ во время сна. Для автоматической детекции межприступных разрядов мы использовали метод ASPIRE (Ossadtchi et al., 2004), в основе которого лежит метод независимых компонент (ICA). Мы выбрали те независимые компоненты, в которых наиболее четко наблюдается структура разрядов. Для ICA-разложения использовался метод Infomax. Детекция разрядов в выбранных компонентах производилась по установленному порогу для амплитуды компоненты. Затем для каждого из найденных событий мы подобрали соответствующие электрические диполи с помощью алгоритма RAP-MUSIC (Mosher, Leahy, 1999). Локализация источников, генерирующих найденные события на коре, позволяет оценить, насколько физиологически правдоподобными являются автоматически обнаруженные события. Мы использовали 0.97 как порог для метрики корреляции подпространств, и все события, для которых RAP-MUSIC обнаружил меньшую корреляцию, удалялись из последующего анализа.
Затем мы применили простой детерминированный алгоритм кластеризации на основе близости между полученными точками, чтобы объединить все источники в плотные кластеры радиусом не больше 1 см, каждый из которых содержит как минимум десять диполей. Параметры ASPIRE были найдены эмпирически и зафиксированы для всех пациентов. Несмотря на то, что описанная процедура автоматической детекции запускалась отдельно для градиометров и магнитометров, обнаруженные в итоге кластеры оказались примерно одинаковыми. Все показанные далее результаты посчитаны для предварительно предобработанных с помощью MaxFilter сигналов магнитометров.
Анализ отдельных разрядов
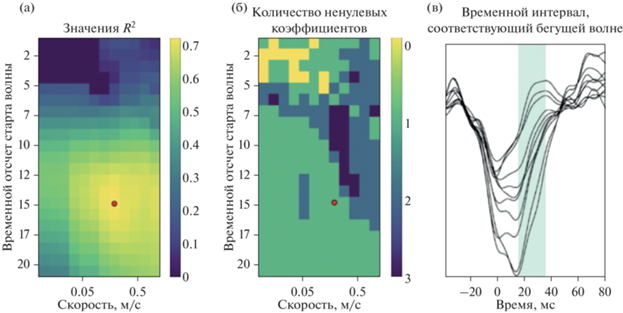
Предложенный алгоритм был применен к каждому найденному межприступному разряду отдельно. На рис. 5 показан подробный анализ для одного разряда. Точка начала разряда во времени определяется методом скользящего окна: длительность базисных волн составляет 20 мс, а длительность выбранной МЭГ-записи составляет 40 мс. На панели А показаны значения R2, полученные для различных скоростей распространения (ось x) и начальных моментов времени (ось y). На панели B показаны количества ненулевых коэффициентов в решении для каждой из соответствующих точек. Лучшее решение определяется по максимальному значению R2. Можно заметить, что у значений R2 есть четкий максимум (отмеченный красной точкой). Для данного разряда максимальное значение R2 составляет 0.72, и это решение соответствует физиологически объяснимой скорости распространения приблизительно в 0.3 м/с. Для объяснения этого разряда достаточно только одного направления распространения. Панель C показывает развитие сигнала разряда во времени, и интервал, который лучше всего объясняется с помощью бегущих волн, выделен цветом. Важно отметить, что волновая модель лучше всего объясняет растущую часть разряда.
Рис. 5.
Репрезентативный пример анализа одного межприступного разряда. (а) Значения R2, полученные для разного времени начала разряда и разных значений скорости распространения. Оптимальное решение отмечено красной точкой. (б) Соответствующие количества ненулевых коэффициентов. (в) Временные ряды МЭГ-сигналов для рассматриваемого разряда. Временной интервал, лучше всего объясненный волновой моделью, выделен цветом.
Fig. 5. A representative analysis of one interictal spike. (а) R2 values obtained for different spike starting time points and different propagation velocities. The optimal solution is marked with red dot. (б) Corresponding numbers of non-zero coefficients. (в) MEG timeseries for interictal spike under consideration. The time interval with the best model goodness of fit is highlighted.
Агрегированные результаты для трех пациентов
Описательные статистики для полученных кластеров межприступных разрядов для всех пациентов представлены в табл. 1. Переменная ${{N}_{{{\text{spikes}}}}}$ показывает количество найденных разрядов в каждом конкретном кластере, ${{T}_{{{\text{start}}}}}$ – это время первого события из кластера, в секундах от начала записи, а ${{T}_{{{\text{var}}}}}$ − стандартное отклонение временных отсчетов для разрядов в кластере, в секундах.
Таблица 1.
Описательные статистики для всех найденных кластеров для трех пациентов Table 1. Descriptive statistics for all detected epileptic regions for three patients
| Пациент 1 | Пациент 2 | Пациент 3 | |||||||
|---|---|---|---|---|---|---|---|---|---|
| № | Nspikes | Tstart | Tvar | Nspikes | Tstart | Tvar | Nspikes | Tstart | Tvar |
| 1 | 64 | 10.570 | 99.005 | 233 | 44.728 | 140.120 | 114 | 2.348 | 99.461 |
| 2 | 18 | 9.349 | 122.090 | 10 | 56.844 | 163.160 | 34 | 77.175 | 136.020 |
| 3 | 27 | 16.372 | 85.610 | 52 | 120.883 | 144.150 | 14 | 141.136 | 134.140 |
| 4 | 12 | 10.387 | 128.120 | 21 | 56.789 | 146.560 | |||
| 5 | 38 | 12.556 | 99.757 | 19 | 176.413 | 134.220 | |||
| 6 | 13 | 27.265 | 85.078 | 12 | 151.483 | 151.270 | |||
| 7 | 29 | 2.442 | 110.200 | 13 | 59.603 | 95.913 | |||
| 8 | 9 | 63.843 | 174.020 | ||||||
| 9 | 9 | 1.001 | 123.360 | ||||||
| 10 | 10 | 82.998 | 118.340 | ||||||
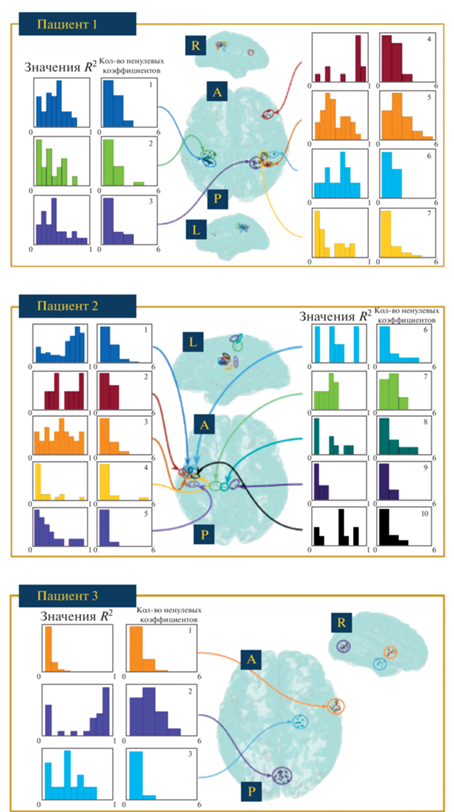
Мы применили предложенный метод к каждому обнаруженному межприступному разряду и агрегировали полученные значения R2 на основании их принадлежности к кластеру. Поскольку цель данного анализа − найти качественное, но при этом простое описание межприступного разряда, другой важный фактор — это количество направлений распространения в оптимальном решении. На верхней панели рис. 6 показано расположение семи предположительных зон эпилептогенеза (с помощью разных цветов) и распределения двух выбранных показателей для Пациента 1. Левая панель для каждого кластера показывает распределение значений R2 для разрядов, образующих этот кластер; это распределение показывает, насколько хорошо разряды соответствуют модели бегущих волн. На правой панели для каждого кластера показано распределение количества ненулевых коэффициентов в оптимальном решении, что позволяет оценить простоту модели. Средняя и нижняя панели рис. 6 демонстрируют результаты для Пациента 2 и Пациента 3 соответственно.
Рис. 6.
Локализация эпилептических очагов, автоматически обнаруженных методом ASPIRE для трех пациентов. Для каждого кластера показано распределение метрики R2 (качество подгонки модели) и количество направлений, используемых в оптимальном решении (простота модели).
Fig. 6. Localization of epileptic foci detected with ASPIRE technique for three patients. Histograms for each region demonstrate the distribution of R2 metrics (goodness of fit) and distribution of nonzero propagation direction numbers (model simplicity).
Анализ данных пациентов выявил вариабельность соответствия волновой модели в зависимости от конкретных разрядов. Волновая модель с выбором только нескольких доминирующих направлений подходит только для части из проанализированных разрядов. В табл. 2 показаны доли разрядов с качеством объяснения не меньше, чем 0.6 для всех пациентов.
Таблица 2.
Процент разрядов, хорошо объясненных моделью бегущих волн в каждом кластере для трех пациентов. Межприступный разряд считается хорошо объясненным, если значение R2 больше или равно 0.6 Table 2. Percentage ratio of successfully fitted with the traveling wave model spikes for each detected cluster in three patients. An interictal spike is considered as successfully fitted if the R2 value is not lower than 0.6
| № | Пациент 1, % | Пациент 2, % | Пациент 3, % |
|---|---|---|---|
| 1 | 3 | 70 | 0 |
| 2 | 5 | 57 | 69 |
| 3 | 14 | 34 | 7 |
| 4 | 67 | 4 | |
| 5 | 10 | 11 | |
| 6 | 15 | 25 | |
| 7 | 10 | 0 | |
| 8 | 11 | ||
| 9 | 0 | ||
| 10 | 30 |
Видно, что для Пациента 1 только разряды из кластера 4 хорошо соответствуют бегущей волне, так как 67% из всех содержащихся в нём разрядов хорошо объясняются с помощью волновой модели. Для двух других пациентов процент разрядов, объясняемых волновой моделью, значительно различается между кластерами. Для Пациента 2 кластер 1 содержит наибольшую долю волнообразных разрядов (70%), за ним следует кластер 2 (57%), пространственные характеристики которого близки к кластеру 1. У Пациента 3 большая часть разрядов с хорошим соответствием модели концентрируется в окципитальном кластере 2, в то время как остальные кластеры плохо соответствуют модели.
Во всех трех проанализированных наборах данных найденные кластеры различаются по процентному соотношению разрядов, хорошо объясненных моделью бегущих волн. Интересно, что области с наибольшим процентом хорошо объясненных разрядов для Пациента 1 и Пациента 2 совпадают с эпилептогенными очагами, которые были независимо определены нейрохирургами. В случае Пациента 1 эпилептогенность найденного очага также была подтверждена в результате двухлетнего наблюдения за пациентом после операции. Информация о расположении эпилептогенной области у Пациента 3 недоступна, так как операция не проводилась. Эти результаты согласуются с ранее полученными наблюдениями о том, что в эпилептогенной области межприступные разряды имеют устойчивое направление распространения (Tomlinson et al., 2016).
ОБСУЖДЕНИЕ РЕЗУЛЬТАТОВ
В настоящем исследовании мы предлагаем новый алгоритм поиска решения обратной задачи МЭГ, использующий физиологически обусловленное предположение о распространении активности в форме бегущей волны. Здесь мы исследуем свойства предложенного алгоритма в контексте применения к МЭГ-записям пациентов с мультифокальной эпилепсией, однако он также может быть полезен в любых экспериментах, предполагающих пространственно-временное распространение активности.
Локализация эпилептогенной зоны (ЭЗ) у пациентов с мультифокальной эпилепсией − основная цель предоперационной диагностики, в рамках которой мозговая активность записывается как во время межприступных периодов, так и в течение приступа. Обычно для решения этой проблемы используется макро-анализ: расположение ЭЗ определяется исходя из паттернов эпилептической активности всего мозга целиком (см. работу (Ossadtchi et al., 2005), формализующую этот подход). Несмотря на то, что такой подход к анализу полезен, динамика распространения как межприступной, так и приступной активности проявляется сразу на нескольких уровнях пространственного разрешения (Stead et al., 2010; Chamberlain et al., 2011). На макроуровне распространение межприступного разряда исследовали Томлинсон и коллеги, используя внутричерепные записи на основе субдуральных электродов (Tomlinson et al., 2016). Они предположили, что устойчивое согласованное направление распространения можно использовать в качестве биомаркера эпилептогенной области. В нескольких исследованиях также изучалось локальное распространение эпилептической активности. Мартине и коллеги (Martinet et al., 2017) изучали динамику приступов в миллиметровом пространственном масштабе. Используя массивы микроэлектродов размером 4 квадратных миллиметра, они показали, что небольшие группы нейронов, охватывающие кортикальные столбцы, генерируют быстро распространяющиеся волны, которые могут на макроуровне способствовать развитию приступа. Чижов и коллеги (Chizhov et al., 2018) разработали модель бегущей волны для приступной и межприступной активности, углубив тем самым понимание локальных механизмов распространения эпилептических разрядов.
В представленной статье мы предлагаем метод локализации бегущих волн и определения их параметров по записи неинвазивной магнитоэнцефалографии (МЭГ). Мы применяем предложенный подход для анализа динамики локального распространения межприступных разрядов у пациентов с фармакологически резистентной фокальной эпилепсией. МЭГ имеет временное разрешение порядка миллисекунды и пространственное разрешение порядка нескольких миллиметров (Nasiotis et al., 2017), что отвечает необходимым требованиям для анализа локальной динамики распространения эпилептической активности. Кроме того, в случае использования МЭГ-записи в паре с подходящими методами решения обратной задачи можно получить представление об анатомических путях бегущих волн.
Из-за того, что обратная задача МЭГ является плохо обусловленной, такая задача имеет фундаментальные ограничения и для поиска единственного решения необходимо использовать методы регуляризации (Hamalainen et al., 1993). Для того чтобы регуляризовать обратную задачу, мы моделируем межприступные разряды как суперпозицию бегущих волн, распространяющихся в радиальных направлениях во все стороны от источника. Эта модель достаточно хорошо работает как на симуляционных МЭГ-данных, так и на данных пациентов с эпилепсией, у которых волновые паттерны распространения активности очевидны для значительной части межприступных разрядов, возникающих в определенной области коры.
Разработанный алгоритм анализа в своей основе опирается на использование нового физиологически обусловленного приора для решения недоопределенной обратной задачи МЭГ. Полученное решение основано на получившей сейчас серьезное распространение в литературе гипотезе о бегущих кортикальных волнах. В доступном сейчас программном обеспечении FieldTrip (Oostenveld et al., 2011), MNE Python (Gramfort et al., 2013), Brainstorm (Tadel et al., 2011) реализован широкий спектр методик для решения обратной задачи. В литературе также предлагаются подходы, отказывающиеся от моделирования нейрональной активности с помощью набора токовых диполей, например, в (Petrov, 2012) в качестве решения рассматриваются сферические гармоники. Однако ни один из подходов не использует информацию о пространственно-временной связности изучаемой активности.
В данной работе мы рассматривали как в модельных, так и в реальных данных только случай фокальной эпилепсии, предполагая, что межприступный разряд генерируется хорошо локализованной областью коры и далее локально распространяется, задействуя механизм бегущей волны. Мы не рассматривали случай генерализованных межприступных разрядов, зачастую задействующих более глубокие структуры мозга, так как именно в сценарии фокальной эпилепсии применение разработанного алгоритма имеет практический смысл, позволяя получить дополнительную информацию для локализации ЭЗ.
Хотя предложенный метод успешно находит бегущие волны и реконструирует их анатомические пути, он по-прежнему подвержен ошибкам, связанным с (1) неопределенностями в оценке начальной точки волны и (2) неточностями параметризации кортикальной поверхности. Ошибки, происходящие по первой причине, могут быть сокращены в результате выбора высокоамплитудных разрядов для анализа. Вторую проблему можно решить, выполнив более точное сканирование мозга (7Т МРТ). Кроме того, представленный метод может быть использован не только для исследования кортикальной волновой динамики межприступных разрядов, но и для анализа вызванных и индуцированных ответов в парадигме с многократным предъявлением стимулов. В этом случае существенно облегчается задача поиска момента начала распространения локальной волны.
Несмотря на наличие источников ошибок, часть межприступных разрядов были успешно описаны с помощью волновой модели. Более того, эти разряды были сгенерированы одной кортикальной областью, и для пациентов, у которых были доступны данные об эпилептогенном очаге, эта область совпадает с очагом. На основании этих результатов, которые хорошо согласуются с инвазивными данными (Stead et al., 2010; Chamberlain et al., 2011), мы предполагаем, что анализ межприступных разрядов, записанных в МЭГ, может помочь в локализации эпилептогенного очага. Однако не все разряды могут быть одинаково хорошо объяснены волновой моделью с небольшим количеством преобладающих направлений распространения. Эти случаи требуют более детального дальнейшего изучения.
ВЫВОДЫ
В данной работе мы предлагаем методологию неинвазивного исследования тонкой пространственно-временной структуры межприступных разрядов, наблюдаемых в МЭГ, основанную на концепции бегущих кортикальных волн. Мы использовали метод LASSO с положительными коэффициентами для того, чтобы оценить оптимальную скорость и направления распространения волн. Мы протестировали работу алгоритма как на модельных данных, так и на реальных МЭГ-сигналах и продемонстрировали, что динамика распространения разрядов, записанных в МЭГ, может быть измерена в пространственно-временном масштабе миллиметр/миллисекунда.
Мы также заметили, что у всех трех пациентов, данные которых были проанализированы, волновое поведение характерно не для всех межприступных разрядов, причем “волновые” разряды объединяются в хорошо пространственно очерченные кластеры. В будущем анализ локальных моделей распространения межприступной активности может стать неотъемлемой частью предоперационной диагностики и поможет решать задачу дифференциации типов эпилепсии, локализации эпилептогенных зон и планирования максимально щадящей хирургической тактики резекции эпилептогенной ткани.
Предложенный алгоритм может быть легко расширен для анализа сегментов данных, относящихся к началу приступа, которые в ближайшем будущем станут более доступными, благодаря разработке новых мобильных МЭГ-установок с магнитометрами с оптической накачкой, которые пациент может носить на голове.
Важно подчеркнуть также, что разработанный алгоритм может быть применен не только для исследования эпилепсии, но также и в других нейрофизиологических исследованиях, изучающих активность головного мозга, которая имеет пространственно-временную структуру распространения.
Список литературы
Крылов В.В., Гехт А.Б., Трифонов И.С., Лебедева А.В., Каймовский И.Л., Синкин М.В., Григорьева Е.В., Гришкина М.Н., Шишкина Л.В., Кочеткова О.О. Исходы хирургического лечения пациентов с фармакорезистентными формами эпилепсии. Журнал неврологии и психиатрии им. С.С. Корсакова. 2016. 119(9–2): 13–18.
Adrian E.D., Matthews B.H.C. The interpretation of potential waves in the cortex. The Journal of Physiology. 1934. 81(4): 440–471.
Adrian E.D., Yamagiwa K. The origin of the Berger rhythm. Brain. 1935. 58(3): 323–351.
Bahramisharif A., van Gerven M.A.J., Aarnoutse E.J., Mercier M.R., Schwartz T.H., Foxe J.J., Ramsey N.F., Jensen O. Propagating neocortical gamma bursts are coordinated by traveling alpha waves. Journal of Neuroscience. 2013. 33(48): 18849–18854.
Chamberlain A., Viventi J., Blanco J., Kim D.H., Rogers J., Litt B. Millimeterscale epileptiform spike patterns and their relationship to seizures. Conference proceedings: Annual International Conference of the IEEE Engineering in Medicine and Biology Society. IEEE Engineering in Medicine and Biology Society. 2011. Conference, 2011: 761–764.
Chizhov A.V., Zefirov A.V., Amakhin D.V., Smirnova E.Yu., Zaitsev A.V. Minimal model of interictal and ictal discharges “Epileptor-2”. PLOS Computational Biology. 2018. 14(5): e1006186.
Donders F.C. On the speed of mental processes. Acta Psychologica. 1969. 30: 412–431.
Ermentrout G.B., Kleinfeld D. Traveling electrical waves in cortex. Neuron. 2001. 29(1): 33–44.
Ferezou I., Haiss F., Gentet L.J., Aronoff R., Weber B., Petersen C.C.H. Spatiotemporal dynamics of cortical sensorimotor integration in behaving mice. Neuron. 2007. 56(5): 907–923.
Fischl B. FreeSurfer. NeuroImage. 2012. 62(2): 774–781.
Freeman W.J., Barrie J.M. Analysis of spatial patterns of phase in neocortical gamma EEGs in rabbit. Journal of Neurophysiology. 2000. 84(3): 1266–1278.
Fries P. A mechanism for cognitive dynamics: neuronal communication through neuronal coherence. Trends in Cognitive Sciences. 2005. 9(10): 474–480.
Fries P. Rhythms for Cognition: Communication through Coherence. Neuron. 2015. 88(1): 220–235.
Giannini M., Alexander D.M., Nikolaev A.R., van Leeuwen C. Large-scale traveling waves in EEG activity following eye movement. Brain Topography. 2018. 31(4): 608–622.
Gramfort A., Luessi M., Larson E., Engemann D.A., Strohmeier D., Brodbeck C., Goj R., Jas M., Brooks T., Parkkonen L., Hämäläinen M.S. MEG and EEG data analysis with MNE-Python. Frontiers in Neuroscience. 2013. 7(267): 1–13.
Hamalainen M., Hari R., Ilmoniemi R.J., Knuutila J., Lounasmaa O.V. Magnetoencephalography – theory, instrumentation, and applications to noninvasive studies of the working human brain. Reviews on modern physics. 1993. 65(2).
Hangya B., Tihanyi B.T., Entz L., Fabo D., Eross L., Wittner L., Jakus R., Varga V., Freund T.F., Ulbert I. Complex propagation patterns characterize human cortical activity during slow-wave sleep. Journal of Neuroscience. 2011. 31(24): 8770–8779.
Hindriks R., van Putten M., Deco G. Intra-cortical propagation of EEG alpha oscillations. NeuroImage. 2014. 103: 444–453.
Huang X., Troy W. C., Yang Q., Ma H., Laing C.R., Schiff S.J., Wu J.-Y. Spiral waves in disinhibited mammalian neocortex. The Journal of neuroscience: the official journal of the Society for Neuroscience. 2004. 24(44): 9897—9902.
Komoltsev I.G., Sinkin M.V., Volkova A.A., Smirnova E.A., Novikova M.R., Kordonskaya O.O., Talypov A.E., Guekht A.B., Krylov V.V., Gulyaeva N.V. A Translational Study on Acute Traumatic Brain Injury: High Incidence of Epileptiform Activity on Human and Rat Electrocorticograms and Histological Correlates in Rats. Brain Sci. 2020. 10(9), 570.
Koptelova A., Bikmullina R., Medvedovsky M., Novikova S., Golovteev A., Grinenko O., Korsakova M., Kozlova A., Arkhipova N., Vorobyev A., Melikyan A., Paetau R., Stroganova T., Metsahonkala L. Ictal and interictal MEG in pediatric patients with tuberous sclerosis and drug resistant epilepsy. Epilepsy Res. 2018. 140: 162–165.
Lubenov E.V., Siapas A.G. Hippocampal theta oscillations are travelling waves. Nature. 2009. 373 459(7246): 534–539.
Mak-McCully R.A., Rosen B.Q., Rolland M., Régis J., Bartolomei F., Rey M., Chauvel P., Cash S.S., Halgren E. Distribution, amplitude, incidence, co-occurrence, and propagation of human k-complexes in focal transcortical recordings. Eneuro. 2015. 2(4): ENEURO.0028–15.2015.
Martinet L.-E., Fiddyment G., Madsen J.R., Eskandar E.N., Truccolo W., Eden U.T., Cash S.S., Kramer M.A. Human seizures couple across spatial scales through travelling wave dynamics. Nature Communications. 2017. 8(1).
Massimini M. The sleep slow oscillation as a traveling wave. Journal of Neuroscience. 2004. 24(31): 6862–6870.
Mosher J.C., Leahy R.M. Source localization using recursively applied and projected (RAP) MUSIC. IEEE Transactions on Signal Processing. 1999. 47(2): 332–340.
Muller L., Reynaud A., Chavane F., Destexhe A. The stimulus-evoked population response in visual cortex of awake monkey is a propagating wave. Nature Communications. 2014. 5(1).
Muller L., Chavane F., Reynolds J., Sejnowski T.J. Cortical travelling waves: mechanisms and computational principles. Nature Reviews Neuroscience. 2018. 19(5): 255–268.
Nasiotis K., Clavagnier S., Baillet S., Pack C.C. High-resolution retinotopic maps estimated with magnetoencephalography. NeuroImage. 2017. 145: 107–117.
Oostenveld R., Fries P., Maris E., Schoffelen J.M. FieldTrip: Open Source Software for Advanced Analysis of MEG, EEG, and Invasive Electrophysiological Data. Computational Intelligence and Neuroscience. 2011. Vol. 2011, Article ID 156869.
Ossadtchi A., Baillet S., Mosher J.C., Thyerlei D., Sutherling W., Leahy R.M. Automated interictal spike detection and source localization in magnetoencephalography using independent components analysis and spatiotemporal clustering. Clinical Neurophysiology. 2004. 115(3): 508–522.
Ossadtchi A., Mosher J.C., Sutherling W.W., Greenblatt R.E., Leahy R.M. Hidden markov modelling of spike propagation from interictal MEG data. Physics in Medicine and Biology. 2005. 50(14): 3447–3469.
Patten T.M., Rennie C.J., Robinson P.A., Gong P. Human cortical traveling waves: Dynamical properties and correlations with responses. PLoS ONE. 2012. 7(6): e38392.
Petrov Y. Harmony: EEG/MEG Linear Inverse Source Reconstruction in the Anatomical Basis of Spherical Harmonics. PLoS ONE. 2012. 7(10): e44439
Prechtl J.C., Cohen L.B., Pesaran B., Mitra P.P., Kleinfeld D. Visual stimuli induce waves of electrical activity in turtle cortex. Proceedings of the National Academy of Sciences. 1997. 94(14): 7621–7626.
Stead M., Bower M., Brinkmann B.H., Lee K., Marsh W.R., Meyer F.B., Litt B., Gompel J.V., Worrell G.A. Microseizures and the spatiotemporal scales of human partial epilepsy. Brain: a journal of neurology. 2010. 133(9): 2789–2797.
Tadel F., Baillet S., Mosher J., Pantazis D., Leahy R.M. Brainstorm: A user-friendly application for MEG/EEG analysis. Computational Intelligence and Neuroscience. 2011.
Tibshirani R. Regression shrinkage and selection via the lasso. Journal of the Royal Statistical Society. 1996. 58(1): 267–288.
Tomlinson S.B., Bermudez C., Conley C., Brown M.W., Porter B.E., Marsh E.D. Spatiotemporal mapping of interictal spike propagation: A novel methodology applied to pediatric intracranial EEG recordings. Frontiers in Neurology. 2016. 7.
Wu J.-Y., Huang X., Zhang C. Propagating waves of activity in the neocortex: What they are, what they do. The Neuroscientist. 2007. 14(5): 487–502.
Zhang H., Watrous A.J., Patel A., Jacobs J. Theta and alpha oscillations are traveling waves in the human neocortex. Neuron. 2018. 98(6): 1269–1281.e4.
Дополнительные материалы отсутствуют.
Инструменты
Журнал высшей нервной деятельности им. И.П. Павлова


