Геомагнетизм и аэрономия, 2021, T. 61, № 6, стр. 723-734
Особенности пространственного распределения пучка излучения свистового диапазона, падающего на ночную ионосферу сверху
В. Г. Мизонова 1, *, П. А. Беспалов 2, **
1 Нижегородский государственный технический университет
им. Р.Е. Алексеева (НГТУ)
г. Нижний Новгород, Россия
2 Институт прикладной физики РАН (ИПФ РАН)
г. Нижний Новгород, Россия
* E-mail: vermiz@mail.ru
** E-mail: peter@appl.sci-nnov.ru
Поступила в редакцию 01.03.2021
После доработки 16.04.2021
Принята к публикации 27.05.2021
Аннотация
Рассмотрена задача о численном расчете пространственной зависимости пучка излучения свистового диапазона, падающего на ночную ионосферу сверху. Для расчетов использованы совместно метод коллокаций решения граничной задачи, матричный алгоритм приближенного решения волновых уравнений в плавно неоднородной плоскослоистой плазме и метод быстрого преобразования Фурье по горизонтальным координатам. Проанализированы особенности пространственного распределения волнового поля при различных характеристиках падающего излучения. Вычислены доли энергии излучения, отраженной от верхней границы ионосферы и дошедшей до земной поверхности. Сопоставлено волновое электрическое поле на высоте 400 км, пространственное распределение поперечного магнитного поля и поляризации излучения вблизи поверхности Земли. Полученные результаты важны для сопоставления свойств КНЧ/ОНЧ-излучений, наблюдаемых на спутниках и на Земле.
1. ВВЕДЕНИЕ
Одним из не до конца понятных вопросов теории магнитосферного КНЧ/ОНЧ-излучения являются механизмы его распространения от верхней границы ионосферы до поверхности Земли. Тем не менее, понимание этих механизмов является связующим звеном между известными экспериментальными данными, полученными на спутниках и в наземных обсерваториях, и объяснением генерации этого излучения в магнитосфере. Кроме того, изучение закономерностей распространения КНЧ/ОНЧ-волн через ионосферу важно для понимания свойств ионосферной плазмы и происходящих в ней процессов, для сопоставления характеристик излучений, регистрируемых на спутниках и на Земле. Например, существует много данных об одновременной регистрации сигналов на спутниках и в наземных обсерваториях [Manninen et al., 2012; Nemec et al., 2013]. Однако в некоторых случаях излучение регистрируется на спутниках, но не обнаруживается на Земле [Manninen et al., 2013; Titova et al., 2015]. Различными и не всегда понятными оказываются наблюдаемые свойства этого излучения. В частности, в определенных условиях обнаруживается нетипичная для свистовых волн поляризация излучения вблизи земной поверхности [Титова и др., 2015].
Традиционным подходом при расчете волновых полей в неоднородной ионосферной плазме из многих однородных слоев является анализ закономерностей распространения плоской волны c заданным горизонтальным волновым вектором и затем сложение плоских волн для нахождения пространственной зависимости поля [Payne et al., 2007; Lehtinen and Inan, 2008]. Основной вычислительной трудностью при этом является численная расходимость, обусловленная большими декрементами нераспространяющихся мод в протяженной области ионосферы [Nygre’n, 1982; Budden, 1985; Kuzichev and Shklyar, 2010]. Еще одной проблемой является необходимость конкретизации распределения падающего на ионосферу сверху излучения.
В работах [Bespalov and Mizonova, 2017; Беспалов и Мизонова, 2018; Bespalov et al., 2018] для нахождения высотной зависимости поля, обусловленного плоской свистовой волной, падающей наклонно на границу ионосферы сверху, были использованы совместно метод коллокаций решения граничной задачи и матричный алгоритм приближенного решения волновых уравнений в плавно неоднородной плоскослоистой плазме. Такой подход позволил учесть реальные высотные зависимости ионосферных параметров сильно неоднородной ночной ионосферы и избежать проблемы расходимости численных решений на больших высотах. Разработанный в статье [Мизонова и Беспалов, 2021] алгоритм вычислений использован в настоящей работе для нахождения пространственной зависимости волнового поля излучения, падающего на ночную ионосферу сверху. Проводится анализ свойств излучений вблизи поверхности Земли, на спутниковых высотах, а также отраженного от верхней границы ионосферы, при разных параметрах задаваемого сверху пучка излучения. Полученные результаты важны для изучения взаимосвязи свойств КНЧ/ ОНЧ-волн, регистрируемых на спутниках и наземных станциях, а также для понимания природы естественного магнитосферного излучения.
2. ПОСТАНОВКА ЗАДАЧИ И АЛГОРИТМ ВЫЧИСЛЕНИЙ
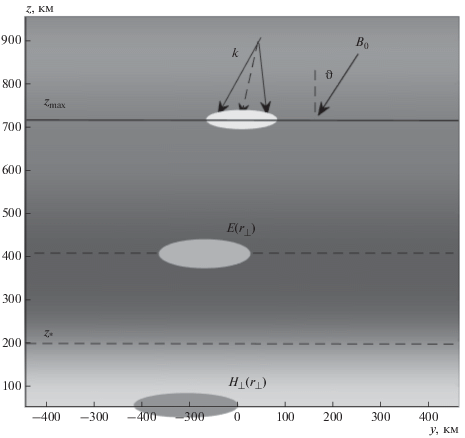
Предположим, что на верхнюю границу ионосферы падает сверху монохроматический пучок электромагнитного излучения свистового диапазона, и рассмотрим задачу о нахождении пространственной зависимости поля излучения в ионосфере и на земной поверхности. Для решения будем использовать модель плоскослоистой среды, параметры которой зависят от вертикальной координаты $z$, значения $z = 0$ и $z = {{z}_{{\max }}}$ соответствуют поверхности Земли и плоскости падения, плазма выше границы $z = {{z}_{{\max }}}$ считается однородной, магнитное поле лежит в плоскости $y{\kern 1pt} z$ и составляет с осью $z$ угол $\vartheta $. Схема, поясняющая постановку задачи, изображена на рис. 1.
Пространственное распределение напряженностей монохроматического электрического и магнитного полей ${\mathbf{E}}\left( {{{{\mathbf{r}}}_{ \bot }},z,t} \right) = {\mathbf{E}}\left( {{{{\mathbf{r}}}_{ \bot }},z} \right){{e}^{{ - i\omega t}}},$ ${\mathbf{H}}\left( {{{{\mathbf{r}}}_{ \bot }},z,t} \right) = {\mathbf{H}}\left( {{{{\mathbf{r}}}_{ \bot }},z} \right){{e}^{{ - i\omega t}}}$ с частотой $\omega $ удобно разложить в интеграл Фурье по поперечным координатам
(1)
$\begin{gathered} {\mathbf{E}}\left( {{{{\mathbf{r}}}_{ \bot }},z} \right) = \int {{\mathbf{E}}\left( {{{{\mathbf{n}}}_{ \bot }},z} \right)} {\text{ }}{{e}^{{i{{k}_{0}}{{{\mathbf{n}}}_{ \bot }}{{{\mathbf{r}}}_{ \bot }}}}}\frac{{d{{n}_{ \bot }}}}{{{{{\left( {2\pi } \right)}}^{2}}}}, \\ {\mathbf{H}}\left( {{{{\mathbf{r}}}_{ \bot }},z} \right) = \int {{\mathbf{H}}\left( {{{{\mathbf{n}}}_{ \bot }},z} \right)} {\text{ }}{{e}^{{i{{k}_{0}}{{{\mathbf{n}}}_{ \bot }}{{{\mathbf{r}}}_{ \bot }}}}}\frac{{d{{{\mathbf{n}}}_{ \bot }}}}{{{{{\left( {2\pi } \right)}}^{2}}}}, \\ \end{gathered} $Пусть распределение амплитуд по ${{{\mathbf{n}}}_{ \bot }}$ в падающем излучении задано. Высотное распределение напряженностей электромагнитного поля удовлетворяет уравнениям Максвелла
(2)
$\nabla \times {\mathbf{H}} = - i{{k}_{0}}\hat {\varepsilon }{\mathbf{E}}{\text{,}}\,\,\,\,\nabla \times {\mathbf{E}} = i{{k}_{0}}{\mathbf{H}},$(3)
${{d{\mathbf{F}}} \mathord{\left/ {\vphantom {{d{\mathbf{F}}} {dz}}} \right. \kern-0em} {dz}} = \hat {M}{\mathbf{F}}{\text{.}}$Здесь ${\mathbf{F}}$ – четырехкомпонентный вектор-столбец
(4)
${\mathbf{F}} = \left( {\begin{array}{*{20}{c}} {{{E}_{x}}} \\ {{{E}_{y}}} \\ {{{H}_{x}}} \\ {{{H}_{y}}} \end{array}} \right),$(5)
$\begin{gathered} \hat {\varepsilon } = \\ = \left( {\begin{array}{*{20}{c}} \varepsilon &{ - ig\cos \vartheta }&{ig\sin \vartheta } \\ {ig\cos \vartheta }&{\varepsilon co{{s}^{2}}\vartheta + \eta si{{n}^{2}}\vartheta }&{\left( {\eta - \varepsilon } \right)\sin \vartheta \cos \vartheta } \\ { - ig\sin \vartheta }&{\left( {\eta - \varepsilon } \right)\sin \vartheta \cos \vartheta }&{\varepsilon si{{n}^{2}}\vartheta + \eta co{{s}^{2}}\vartheta } \end{array}} \right) \\ \end{gathered} $(6)
$\begin{gathered} \varepsilon = 1 - \frac{{\omega _{{pe}}^{2}}}{{{{{(\omega + i{{\nu }_{e}})}}^{2}} - \omega _{{Be}}^{2}}}\frac{{\omega + i{{\nu }_{e}}}}{\omega } - \\ - \,\,\frac{{\omega _{{pi}}^{2}}}{{{{{(\omega + i{{\nu }_{i}})}}^{2}} - \omega _{{Bi}}^{2}}}\frac{{\omega + i{{\nu }_{i}}}}{\omega }, \\ \eta = 1 - \frac{{\omega _{{pe}}^{2}}}{{\omega \left( {\omega + i{{\nu }_{e}}} \right)}} - \frac{{\omega _{{pi}}^{2}}}{{\omega (\omega + i{{\nu }_{i}})}}, \\ {\text{ }}g = - \frac{{\omega _{{pe}}^{2}{{\omega }_{{Be}}}}}{{\omega \left( {{{{(\omega + i{{\nu }_{e}})}}^{2}} - \omega _{{Be}}^{2}} \right)}} + \frac{{\omega _{{pi}}^{2}{{\omega }_{{Bi}}}}}{{\omega \left( {{{{(\omega + i{{\nu }_{i}})}}^{2}} - \omega _{{Bi}}^{2}} \right)}}, \\ \end{gathered} $Представим вектор поля ${\mathbf{F}}$ (4) в виде суммы четырех волновых мод
(7)
$\begin{gathered} {\mathbf{F}}({{{\mathbf{n}}}_{ \bot }},z) = \\ = \sum\limits_{j{\kern 1pt} = {\kern 1pt} 1}^4 {{{a}_{j}}({{{\mathbf{n}}}_{ \bot }})\exp \left( { - \int\limits_z^{{{z}_{{\max }}}} {i{{\kappa }_{j}}} ({{{\mathbf{n}}}_{ \bot }},z{\kern 1pt} ')dz{\kern 1pt} '} \right){{{\mathbf{P}}}_{j}}({{{\mathbf{n}}}_{ \bot }},z),} {\text{ }} \\ \end{gathered} $Для нахождения поля в области $0 \leqslant z \leqslant {{z}_{{\max }}}$ дополним систему уравнений (3) четырьмя граничными условиями. Два из них определим на нижней границе $z = 0$, считая поверхность Земли идеально проводящей
(8)
${{E}_{x}}\left( {{{{\mathbf{n}}}_{ \bot }},z = 0} \right) = 0,\,\,\,\,{{E}_{y}}\left( {{{{\mathbf{n}}}_{ \bot }},z = 0} \right) = 0.$Учтем, что в свистовом диапазоне две волновые моды являются нераспространяющимися с большими декрементами затухания, что приводит к численной расходимости решения системы уравнений (3) в протяженном ионосферном слое [Lehtinen and Inan, 2008]. Для решения проблемы численной расходимости область решения $0 \leqslant z \leqslant {{z}_{{\max }}}$ разделим на две части, $0 \leqslant z \leqslant {{z}_{*}}$ и ${{z}_{*}} \leqslant z \leqslant {{z}_{{\max }}}$. Границу $z = {{z}_{*}}$ выберем таким образом, чтобы выше нее плазма была плавно неоднородной – характерный масштаб неоднородности существенно превышал длины волн распространяющихся мод и длины затухания нераспространяющихся мод.
Для нахождения поля в нижнем слое $0 \leqslant z \leqslant {{z}_{*}}$ используем метод коллокаций решения граничной задачи [Kierzenka and Shampine, 2001]. Для нахождения поля в верхнем плавно неоднородном слое ${{z}_{*}} \leqslant z \leqslant {{z}_{{\max }}}$ используем матричный алгоритм приближенного решения [Мизонова, 2019]. Решения, полученные двумя методами, должны сшиваться на границе $z = {{z}_{*}}$. Алгоритм вычисления волнового поля компоненты с заданным вектором ${{{\mathbf{n}}}_{ \bot }}$, комбинирующий два метода решений, подробно описан в работах [Bespalov et al., 2018; Мизонова и Беспалов, 2021]. Определив распределение амплитуды падающей волны ${{a}_{i}}({{{\mathbf{n}}}_{ \bot }})$ (7) на верхней границе $z = {{z}_{{\max }}}$ и вычислив далее интеграл Фурье (1), можно найти пространственное распределение волновых полей ${\mathbf{E}}\left( {{{{\mathbf{r}}}_{ \bot }},z} \right),{\mathbf{H}}\left( {{{{\mathbf{r}}}_{ \bot }},z} \right)$.
В частности, интересующее нас горизонтальное магнитное поле ${{H}_{ \bot }}(z = 0)$ и поляризация $\Pi $ на поверхности Земли равны соответственно
(11)
$\Pi = \left| \Pi \right|{{e}^{{i\phi }}} = {{{{E}_{{y{\kern 1pt} '}}}\left( {z = 0} \right)} \mathord{\left/ {\vphantom {{{{E}_{{y{\kern 1pt} '}}}\left( {z = 0} \right)} {{{E}_{{x{\kern 1pt} '}}}\left( {z = 0} \right)}}} \right. \kern-0em} {{{E}_{{x{\kern 1pt} '}}}\left( {z = 0} \right)}},$(12)
$E\left( {{{{\mathbf{r}}}_{ \bot }},z} \right) = \sqrt {{{{\left| {{{E}_{x}}\left( {{{{\mathbf{r}}}_{ \bot }},z} \right)} \right|}}^{2}} + {{{\left| {{{E}_{y}}\left( {{{{\mathbf{r}}}_{ \bot }},z} \right)} \right|}}^{2}} + {{{\left| {{{E}_{z}}\left( {{{{\mathbf{r}}}_{ \bot }},z} \right)} \right|}}^{2}}} .$(13)
${{S}_{{i,r}}} = {{(2{{Z}_{0}})}^{{ - 1}}}\operatorname{Re} \left[ {E_{{ \bot i,r}}^{*},{{H}_{{ \bot i,r}}}} \right].$(14)
${{R}_{\Sigma }} = \frac{{\int {{{S}_{{z(r)}}}\left( {{{{\mathbf{r}}}_{ \bot }},z = {{z}_{{\max }}}} \right)} d{{{\mathbf{r}}}_{ \bot }}}}{{\int {{{S}_{{z(i)}}}\left( {{{{\mathbf{r}}}_{ \bot }},z = {{z}_{{\max }}}} \right)} d{{{\mathbf{r}}}_{ \bot }}}}.$3. РЕЗУЛЬТАТЫ РАСЧЕТОВ
Для примера расчетов поля излучения используется нормальное распределение амплитуд (7) по горизонтальным компонентам волнового вектора в падающем сверху излучении
(15)
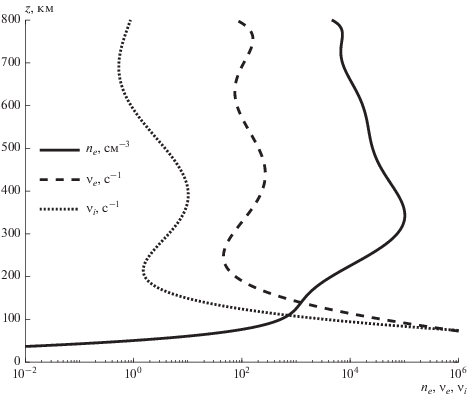
$\begin{gathered} {{A}_{1}}({{{\mathbf{n}}}_{ \bot }},{{z}_{{\max }}}) = {{E}_{0}}2\pi k_{0}^{2}{{L}_{x}}{{L}_{y}} \times \\ \times \,\,\exp \left( {{{ - k_{0}^{2}L_{x}^{2}n_{x}^{2}} \mathord{\left/ {\vphantom {{ - k_{0}^{2}L_{x}^{2}n_{x}^{2}} 2}} \right. \kern-0em} 2} - {{k_{0}^{2}L_{y}^{2}{{{({{n}_{y}} - {{n}_{{0y}}})}}^{2}}} \mathord{\left/ {\vphantom {{k_{0}^{2}L_{y}^{2}{{{({{n}_{y}} - {{n}_{{0y}}})}}^{2}}} 2}} \right. \kern-0em} 2}} \right), \\ \end{gathered} $Рис. 2.
Плазменная концентрация ${{n}_{e}}$ и частоты столкновений ${{\nu }_{e}},{{\nu }_{i}}$ электронов и ионов с нейтральными частицами.
На рисунках 3, 4 приведены результаты расчетов горизонтального магнитного поля (10) на земной поверхности, электрического поля (12) на высоте $z = 400{\text{ км}}$ и плотности потока энергии (13) отраженного излучения на высоте $z = 750{\text{ км}}$ при пространственных масштабах падающего излучения (15) ${{L}_{x}} = 30{\text{ км}},$ ${\text{ }}{{L}_{y}} = 60{\text{ км}}$ и различных значениях ${{n}_{{0y}}}$. Рисунок 3 соответствует излучению с частотой $f = 1.5{\text{ кГц}}$ и рис. 4 соответствует излучению с частотой $f = 3{\text{ кГц}}$. Соответствующие разным значениям ${{n}_{{0y}}}$ отношения (14) полных потоков энергии отраженного и падающего излучений на границе $z = 750{\text{ км}}$ равны RΣ = $ = 0.4360\left( {{{n}_{{0y}}} = 0} \right)$, ${{R}_{\Sigma }} = 0.1307\left( {{{n}_{{0y}}} = 1.6} \right)$ и RΣ = $ = 0.2547\left( {{{n}_{{0y}}} = 3.2} \right)$ в случае $f = 1.5{\text{ кГц}}$ и RΣ = $ = 0.429~\left( {{{n}_{{0y}}} = 0} \right)$, ${{R}_{\Sigma }} = 0.415~~\left( {{{n}_{{0y}}} = 0.2} \right)$ и RΣ = $ = 0.238\left( {{{n}_{{0y}}} = 0.8} \right)$ в случае $f = 3{\text{ кГц}}$. На рисунках 5–7 представлены примеры зависимостей от горизонтальных координат плотности потока энергии падающего излучения на высоте $z = 750{\text{ км}}$, электрического поля на высоте $z = 400{\text{ км}}$, горизонтального магнитного поля и параметра $\phi $, характеризующего поляризацию, на земной поверхности $(z = 0)$, при разных значениях частоты $f$, величины ${{n}_{{0 \bot }}}$ и пространственных масштабах ${{L}_{x}},{{L}_{y}}$ падающего излучения (15). Положительные значения величины $\phi $ соответствуют правой поляризации, типичной для свистовых волн, отрицательные значения $\phi $ – левой поляризации. Как видно из результатов, представленных на рисунках 5–7, в определенных условиях поляризация излучения вблизи земной поверхности оказывается левой, нетипичной для свистовых волн. Для пояснения эффекта изменения “характера поляризации” на рис. 8а, б приведены зависимости от величины ${{n}_{{0y}}}$ горизонтального магнитного поля $Н({{{\mathbf{n}}}_{ \bot }},z = 0)$ (10) и параметра $\phi $, характеризующего поляризацию $\Pi $ (11). Кроме магнитного поля, на тех же графиках изображены зависимости коэффициентов отражения по энергии $R = {{{{S}_{r}}} \mathord{\left/ {\vphantom {{{{S}_{r}}} {{{S}_{i}}}}} \right. \kern-0em} {{{S}_{i}}}}$ (13) от границы $z = 145{\text{ км}}$ и схематично пунктирной линией вертикальная компонента волнового числа ${{n}_{{0z}}} = \operatorname{Re} (\sqrt {1 - n_{ \bot }^{2}} )$. Звездочками отмечены точки, соответствующие левой поляризации. На рисунке 8в, г изображены высотные зависимости амплитуд волновых мод в случаях “правой” (в) и “левой” (г) поляризаций. Как видно из результатов, представленных на рис. 4, 5, в определенных условиях поляризация излучения вблизи земной поверхности оказывается левой, нетипичной для свистовых волн.
Рис. 3.
Нормированные горизонтальное волновое магнитное поле $(z = 0)$, электрическое поле $(z = 400{\text{ км}})$ и плотность потока энергии отраженного излучения $(z = 750{\text{ км}})$ для волны с частотой $f = 1.5{\text{ кГц}}$ и значениями ${{n}_{{0y}}} = 0$ (а), ${{n}_{{0y}}} = 1.6$ (б) и ${{n}_{{0y}}} = 3.2$ (в).
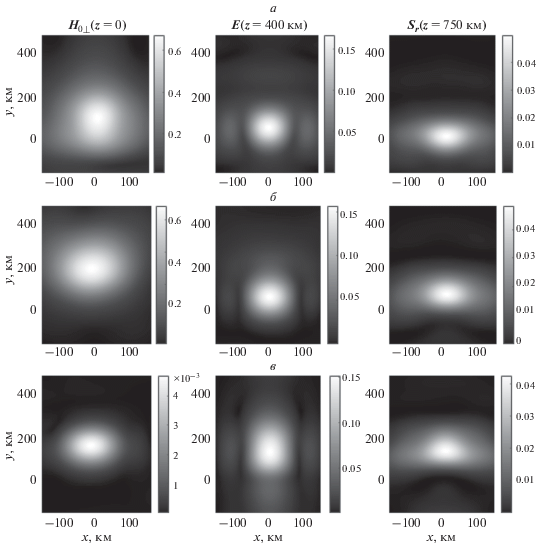
Рис. 4.
Нормированные горизонтальное волновое магнитное поле $(z = 0)$, электрическое поле $(z = 400{\text{ км}})$ и плотность потока энергии отраженного излучения $(z = 750{\text{ км}})$ для волны с частотой $f = 3{\text{ кГц}}$ и значениями ${{n}_{{0y}}} = 0$ (а), ${{n}_{{0y}}} = 0.3$ (б) и ${{n}_{{0y}}} = 0.8$ (в).
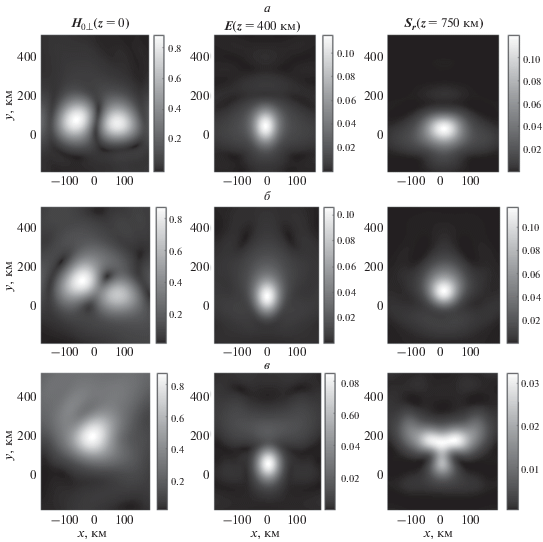
Рис. 5.
Нормированные плотность потока энергии падающего излучения $(z = 750{\text{ км}})$, электрическое поле $(z = 400{\text{ км}})$, горизонтальное волновое магнитное поле и параметр $\phi $, характеризующий поляризацию $(z = 0)$, при разных значениях ${{L}_{y}}$: $f = 1.5{\text{ кГц}}$, ${{n}_{{0y}}} = 0$.
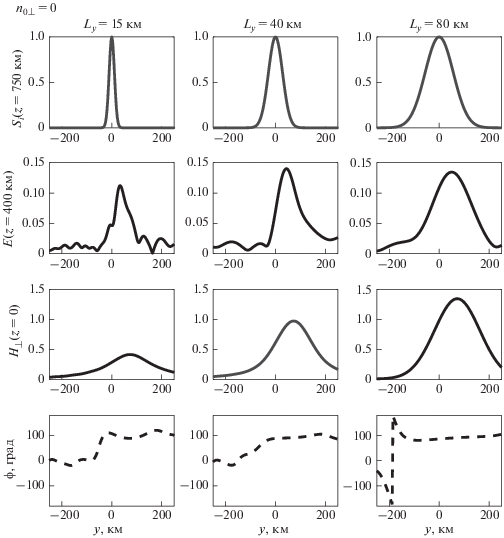
Рис. 6.
Нормированные плотность потока энергии падающего излучения $(z = 750{\text{ км}})$, электрическое поле $(z = 400{\text{ км}})$, горизонтальное волновое магнитное поле и параметр $\phi $, характеризующий поляризацию $(z = 0)$, при разных значениях ${{L}_{y}}$: $f = 1.5{\text{ кГц}}$, ${{n}_{{0y}}} = 2.5$.
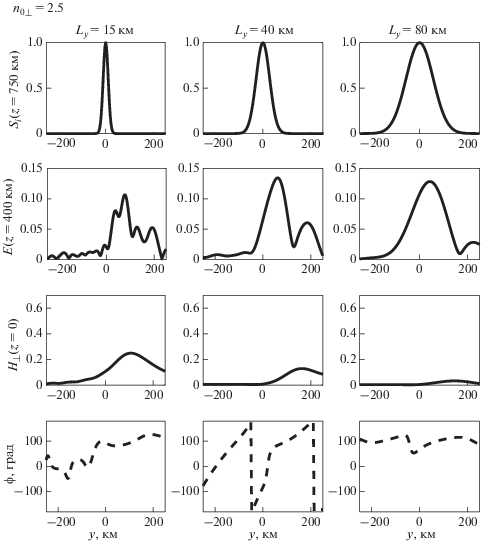
Рис. 7.
Нормированные плотность потока энергии падающего излучения $(z = 750{\text{ км}})$, электрическое поле $(z = 400{\text{ км}})$, горизонтальное волновое магнитное поле и параметр $\phi $, характеризующий поляризацию $(z = 0)$, при разных значениях ${{L}_{x}}$: $f = 3{\text{ кГц}}$, ${{n}_{{0x}}} = 0$.
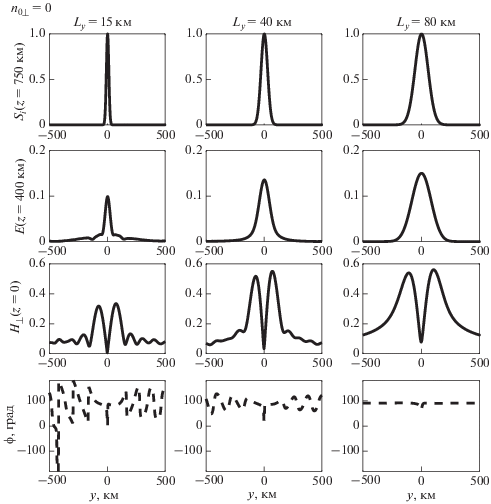
Рис. 8.
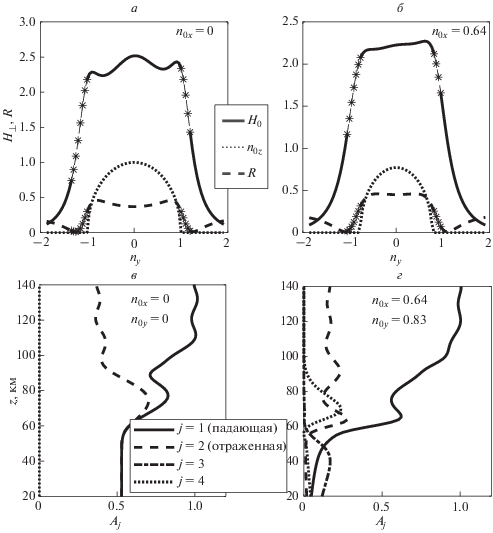
Нормированное горизонтальное магнитное волновое поле и параметр $\phi $, характеризующий поляризацию $(z = 0)$, при значениях ${{n}_{{0x}}} = 0$ (а) и ${{n}_{{0x}}} = 0.64$ (б) (зведочками отмечены значения, соответствующие “левой” поляризации); высотные зависимости амплитуд волновых мод в случаях “правой” (в) и “левой” (г) поляризаций.
4. ОБСУЖДЕНИЕ
Рассмотрена задача о нахождении пространственной зависимости поля излучения свистового диапазона с заданным распределением по ${{{\mathbf{n}}}_{ \bot }}$, падающего сверху на границу ночной ионосферы. Для исключения численной расходимости в вычислениях используется совместно два подхода – метод коллокаций решения граничной задачи на высотах ниже 145 км и матричный алгоритм приближенного решения в области от 145 до 750 км. Выбор верхней границы решения, во-первых, позволяет провести расчеты в приближении однородного магнитного поля, во-вторых, соответствует высотам спутниковых наблюдений. Выбор границы сшивки двух решений определялся двумя условиями. Во-первых, выше 145 км длины волн с частотами 1.5 кГц и выше не превышают 35 км, что меньше масштабов неоднородности ионосферной плазмы. Поэтому для нахождения поля в верхней области можно использовать приближенные методы решения. Во-вторых, в ограниченной области ионосферы ниже 145 км удается получить численно стабильное решение полной системы волновых уравнений.
Распределение по ${{{\mathbf{n}}}_{ \bot }}$ падающего излучения в общем случае несимметрично относительно вертикальной оси и соответствует пространственным горизонтальным масштабам в несколько десятков километров, что типично для данных спутниковых наблюдений [Титова и др., 2015]. Расчеты полей, выполненные для разных значений параметров распределения (15) падающего излучения, показывают, что характерные горизонтальные размеры пятна и величина электрического поля на спутниковых высотах (в расчетах 400 км) определяются в основном горизонтальными размерами $\left( {{{L}_{x}},{{L}_{y}}} \right)$ пятна падающего излучения и слабо зависят от его среднего направления ${{n}_{{0y}}}$ (см. рис. 3–7). Действительно, в плоскослоистой ионосфере горизонтальные компоненты волнового вектора, в соответствии с законом Снеллиуса, сохраняются, соответственно не изменяется существенно и распределение поля по горизонтальным координатам. При этом центр пучка смещается в направлении к северу примерно на 50–100 км.
Возможность выхода излучения на земную поверхность ограничена конусом ${{n}_{ \bot }} \leqslant 1.$ Поэтому излучение с отличными от нуля параметром ${{n}_{{0y}}}$ в распределении (15) может практически не достигать поверхности Земли (см. рис. 3в). Отметим, что из-за больших показателей преломления на высотах $z \sim 750{\text{ км}}$ угол падения волн с ${{n}_{ \bot }} = 1$ составляет всего несколько градусов. Поэтому даже незначительные отклонения пучка падающего излучения от вертикали сильно ограничивают возможность его выхода на Землю, практически не сказываясь при этом на распределении и величине волнового поля на значительных высотах. Например, значению ${{n}_{{0y}}} = 3.2$ соответствует угол падения ~15°. Магнитное поле на земной поверхности при этом (рис. 3в) уменьшается на два порядка по сравнению со случаем “нормального” падения (рис. 3а). Смещение в северном направлении пучка излучения на земной поверхности составляет от 100 до 200 км (рис. 3, 4). Кроме того, существует небольшая асимметрия пучка относительно плоскости $yz$ (плоскости магнитного меридиана).
В определенных условиях поляризация излучения вблизи земной поверхности оказывается левой, нетипичной для свистовых волн. Как видно из рис. 8а, б, левая поляризация соответствует значениям горизонтального волнового вектора ${{n}_{ \bot }}$, ненамного превышающим единицу. Величина магнитного поля при этих значениях резко уменьшается, а коэффициент отражения принимает минимальные значения. В некоторых случаях суммарный вклад таких “левополяризованных” компонент может оказаться преобладающим и изменить характер поляризации излучения вблизи Земли.
Изменение характера поляризации может быть связано с линейным взаимодействием мод в нижней ионосфере. Действительно, в плоскослоистых средах без пространственной дисперсии волновые уравнения имеют четыре линейно независимых решения. В свистовом диапазоне два из четырех решений соответствуют распространяющимся волновым модам с правой поляризацией, а два других решения – сильно затухающим нераспространяющимся модам с левой поляризацией. На высотах порядка 100 км и ниже становится существенным линейное взаимодействие мод, усиливается затухание волн, а также происходит их трансформация в вакуумные электромагнитные. В результате энергия может “перекачиваться” из “правополяризованных” мод в “левопорязированные”, определяя таким образом характер поляризации излучения вблизи поверхности Земли.
На рисунке 8в, г приведены примеры высотных зависимостей амплитуд ${{A}_{j}},{\text{ }}j = 1{\kern 1pt} - {\kern 1pt} 4$ четырех мод волнового уравнения разложения (7), (15) в слое $0 \leqslant z \leqslant {{z}_{*}}$. Амплитуды нормированы на амплитуду падающей на границу сшивки решений $z = 145{\text{ км}}$. Случай (в) соответствует нормальному падению волны $\left( {{{n}_{x}} = 0,{\text{ }}{{n}_{y}} = 0} \right)$, при этом амплитуды 3-й и 4-й мод остаются пренебрежимо малыми, а поляризация на земной поверхности правая круговая $\left( {\phi = 90^\circ } \right)$. Коэффициент отражения по энергии в этом случае равен $R = 0.3$. Случай (г) практически соответствует границе возможного выхода волны на поверхность Земли $\left( {{{n}_{x}} = 0.64,{\text{ }}{{n}_{y}} = 0.83,{\text{ }}{{n}_{ \bot }} = 1.05} \right)$. При этом амплитуды 3-й и 4-й мод в направлении к Земле растут и при $z = 0$ превышают амплитуды 1-й и 2-й мод, а поляризация левая $\left( {\phi = - 150^\circ } \right)$. Коэффициент отражения по энергии в этом случае в два с лишним раза меньше и равен $R = 0.13$.
Отношения полных потоков (14) энергии отраженного и падающего излучений на границе $z = 750{\text{ км}}$ в рассмотренных случаях составляют от 0.13 до 0.44, наибольшее его значение соответствуют симметричному относительно вертикали излучению (${{n}_{{0y}}} = 0$).
5. ВЫВОДЫ
Рассмотрена задача о падении пучка свистового излучения на ночную ионосферу сверху. Для модели плоскослоистой среды получено решение волновых уравнений и найдена пространственная зависимость поля излучения на высотах от 0 до 750 км. Проанализированы зависимости свойств излучения на высотах 400 км и вблизи поверхности Земли при различных распределениях пучка падающего излучения. Область, занимаемая полем на высотах 400 км, имеет приблизительно те же горизонтальные масштабы, что и падающее излучение, и смещается в направлении к северу на несколько десятков километров. Величина поля практически не зависит от угла наклона падающего пучка по отношению к вертикали. Величина магнитного поля вблизи земной поверхности из конуса выхода чувствительна к наклону падающего излучения. Поляризация излучения вблизи поверхности Земли преимущественно правая, типичная для свистовых волн. Однако в некоторых случаях может отмечаться левая поляризация. Изменения характера поляризации может быть связано с вкладом волн вблизи конуса выхода ${{n}_{ \bot }} \sim 1$ и объясняться эффектом линейного взаимодействия мод в нижней существенно неоднородной части ионосферы. В ночных условиях от верхней границы ионосферы отражается примерно от 15 до 45% энергии излучения.
Полученные результаты могут быть полезны для сопоставления свойств КНЧ/ОНЧ-излучений, распространяющихся от естественных магнитосферных источников и регистрируемых на спутниках и на Земле.
Список литературы
– Беспалов П.А., Мизонова В.Г. Особенности распространения падающих на ночную ионосферу сверху электромагнитных волн свистового диапазона // Космич. исслед. Т. 56. № 1. С. 33–39. 2018.
– Гуревич А.В., Шварцбург А.Б. Нелинейная теория распространения радиоволн в ионосфере. М.: Наука. 272 с. 1973.
– Мизонова В.Г. Матричный алгоритм приближенного решения волновых уравнений в неоднородной магнитоактивной плазме // Физика плазмы. Т. 45. № 8. С. 745–754. 2019.
– Мизонова В.Г., Беспалов П.А. Особенности отражения свистовых электромагнитных волн, падающих на ионосферу сверху, в дневных и ночных условиях // Космич. исслед. Т. 59. № 1. С. 19–27. 2021.
– Титова Е.Е., Демехов А.Г., Мочалов А.А. и др. КНЧ/ОНЧ возмущения над передатчиком HAARP, регистрируемые в верхней ионосфере на спутнике DEMETER // Изв. вузов. Радиофизика. Т. 58. № 3. С. 167–186. 2015.
– Bespalov P., Mizonova V. Propagation of a whistler wave incident from above on the lower nighttime ionosphere // Ann. Geophysicae. V. 35. P. 671–675. 2017.
– Bespalov P.A., Mizonova V.G., Savina O.N. Reflection from and transmission through the ionosphere of VLF electromagnetic waves incident from the mid-latitude magnetosphere // J. Atmos. Solar-Terr. Phys. V. 175. P. 40–48. 2018.
– Bilitza D., Reinisch B. International Reference Ionosphere 2007: Improvements and new parameters // Adv. Space Res. V. 42. P. 599–609. 2008.
– Budden K.G. The propagation of radio waves: The theory of radio waves of low power in the ionosphere and magnetosphere. Cambridge: Cambridge Univ. Press. 669 p. 1985.
– Cooley James W., Tukey John W. An algorithm for the machine calculation of complex Fourier series // Math. Comp. V. 19. P. 297–301. Cambridge 301. 1965.
– Kierzenka J., Shampine L.F. A BVP solver based on Residual Control and the MATLAB PSE // ACM TOMS. V. 27. № 3. P. 299–316. 2001.
– Kuzichev I.V., Shklyar D.R. On full-wave solution for VLF waves in the near-Earth space // J. Atmos. Solar-Terr. Phys. V. 72. P. 1044–1056. 2010.
– Lehtinen N.G., Inan U.S. Radiation of ELF/VLF waves by harmonically varying currents into a stratified ionosphere with application to radiation by a modulated electrojet // J. Geophys. Res. Space Phisics. V.113. A06301. 2008.
– Manninen J., Kleimenova N.G., Kozyreva O.V. et al. Experimental evidence of the simultaneous occurrence of VLF chorus on the ground in the global azimuthal scale – from pre-midnight to the late morning // Ann. Geophys. V. 30. P. 725–732. 2012.
– Manninen J., Kleimenova N.G., Kozyreva O.V. et al. Non-typical ground-basedquasi-periodic VLF emissions observed at L 5.3 under quiet geomagnetic conditions at night // J. Atmos. Solar-Terr. Phys. V. 99. P. 123–128. 2013.
– Nemec F., Santolık O., Parrot M. et al. Conjugate observations of quasi-periodic emissions by Cluster and DEMETER spacecraft // J. Geophys Res. Space. V. 118. P. 198–208. 2013.
– Nygre’n T. A method of full wave analysis with improved stability // Planet. Space Sci. V. 30. № 4. P. 427–430. 1982.
– Payne J.A., Inan U.S., Foust F.R. et al. HF modulated ionospheric currents // Geophys. Res. Lett. V. 34. L23101. 2007.
– Titova E.E., Kozelov B.V., Demekhov A.G. et al. Identification of the source of quasiperiodic VLF emissions using ground-based and Van Allen Probes satellite observations // Geophys. Res. Lett. V. 42. P. 6137–6145. 2015.
Дополнительные материалы отсутствуют.
Инструменты
Геомагнетизм и аэрономия