1. На главную
  2. Электронные версии
  3. Геомагнетизм и аэрономия
  4. T. 61, № 6, 2021

Геомагнетизм и аэрономия, 2021, T. 61, № 6, стр. 735-740

Связь среднего за месяц ионосферного индекса T с индексами солнечной и геомагнитной активности

М. Г. Деминов 1, *, Г. Ф. Деминова 1, В. Х. Депуев 1, А. Х. Депуева 1

1 Институт земного магнетизма, ионосферы и распространения радиоволн им. Н.В. Пушкова РАН (ИЗМИРАН)
г. Москва, г. Троицк, Россия

* E-mail: deminov@izmiran.ru

Поступила в редакцию 28.04.2021
После доработки 20.05.2021
Принята к публикации 27.05.2021

Полный текст (PDF)

Аннотация

Представлен анализ связи среднего за месяц ионосферного индекса T с индексами солнечной (F107) и геомагнитной (Ap) активности на основе массива данных этих индексов в интервале 1954–2020 гг., где F107 и Ap – средние за месяц поток радиоизлучения Солнца на длине волны 10.7 см и планетарный Ap-индекс геомагнитной активности. Получено, что эффективный индекс F = (F1070 + + F107–1)/2 обеспечивает высокую корреляцию между ионосферным и солнечным индексами, где F1070 и F107–1 – индексы F107 за данный и предыдущий месяцы. Зависимость T от F в виде полинома второй степени позволяет воспроизвести 95–98% вариаций T для анализируемого интервала времени. Поэтому дополнительный вклад Ap в T незначителен. Тем не менее, вклад Ap в T зависит от времени года: он не значим для января и значим для июля. Это выявленное свойство годовой аномалии в параметрах ионосферы сохраняется и для вклада аa-индекса геомагнитной активности в ионосферный индекс T. Во всех рассмотренных случаях увеличение Ap или aa приводит к уменьшению ионосферного индекса T, т.е. к среднему (глобальному) уменьшению медианы концентрации максимума F2-слоя, и, при прочих равных условиях, такое уменьшение более значительно для июля, чем для января.

1. ВВЕДЕНИЕ

В задачах долгосрочного прогноза критической частоты F2-слоя foF2 на основе эмпирических моделей, таких как IRI [Bilitza, 2018] или NeQuick [Nava et al., 2008], используются скользящие средние за 12 месяцев солнечные (Ri, F107) или ионосферные (T, IG) индексы солнечной активности, которые центрированы на данный месяц. Здесь Ri – международное число солнечных пятен (Версия 2), F107 – поток солнечного радиоизлучения на длине волны 10.7 см. Ионосферные индексы T и IG построены по экспериментальным данным медиан foF2 ряда ионосферных станций для замены солнечных индексов в эмпирических моделях с целью обеспечения минимальных ошибок вычисления foF2 по этим моделям [Caruana, 1990]. Поэтому обычно ионосферные индексы точнее солнечных индексов [Caruana, 1990], но в задачах долгосрочного прогноза ионосферы это преимущество ионосферных индексов может быть нивелировано неточностью прогноза ионосферных индексов [Zakharenkova et al., 2013]. Один из способов решения этой проблемы основан на определении связи ионосферных индексов с солнечными индексами на основе уравнений регрессии. На этом пути было получено, что индекс F107 точнее индекса Ri для решения данной задачи, т.е. долгосрочного прогноза ионосферного индекса солнечной активности, например, индекса T [Деминов и Деминова, 2019]. Это преимущество индекса T стало особенно заметным при переходе к солнечному циклу 24, когда связь между индексами T и F107 осталась практически неизменной, а связь между индексами T и F существенно изменилась.

Средний за месяц индекс T точнее среднего за 12 месяцев значения этого индекса для прогноза foF2 на 1–3 мес. вперед [Деминов и др., 2019]. Прогноз индекса T может быть выполнен на основе прогноза солнечного индекса F107, если известна связь индекса T c индексом F107. Определение такой устойчивой по времени связи для среднего за месяц индекса T было основной целью данной работы. Оценка возможного вклада геомагнитной активности в индекс T была еще одной целью данной работы. Ниже последовательно представлены результаты анализа связи индекса T c индексом F107 и возможной связи T c индексами геомагнитной активности.

2. СВЯЗЬ ИОНОСФЕРНОГО ИНДЕКСА T C ИНДЕКСОМ СОЛНЕЧНОЙ АКТИВНОСТИ

Для определения этой связи были использованы средние за месяц данные индексов F107 и T в интервале 1954–1996 гг., для которого связь ионосферных индексов с индексами солнечной активности была достаточно устойчивой по времени. По этим данным были получены коэффициенты уравнения регрессии:

(1)
$T = - 120 + 2F - 0.0033{{F}^{2}},$
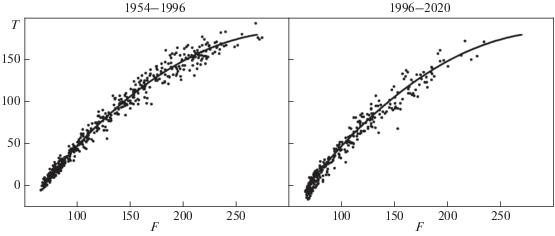
где F = (F1070 + F107–1)/2, F1070 и F107–1 – индексы F107 в данный и предыдущий месяцы. Это уравнение обладает достаточно высокой точностью: K = 0.992, σ = 7.1, где K – коэффициент корреляции между измеренными и вычисленными по уравнению (1) значениями T, σ – среднеквадратичное отклонение вычисленных значений T от измеренных. Индекс F использован, по-видимому, впервые для решения этой задачи. Он подбирался так, чтобы повысить точность уравнения регрессии при учете предыстории изменения F107, в то время как использование в уравнении регрессии индекса F1070 вместо F приводит к уменьшению точности такого уравнения: K = 0.985, σ = 9.4.

Обозначим через TF индекс T, который вычисляется по известному индексу F c помощью уравнения (1). Индекс TF получен по данным 1954–1996 гг. Анализ показал, что индекс TF применим для всего периода измерений индекса F, в том числе, для интервала 1996–2020 гг. Для этого интервала K = 0.983, σ = 8.5, где K – коэффициент корреляции индекса T c индексом TF. По данным на рис. 1 можно более наглядно судить о степени соответствия индекса TF экспериментальным данным для двух анализируемых интервалов времени. Отметим, что для всего интервала измерений индекса F107 (1948–2020 гг.) коэффициент корреляции K индекса T c индексом TF приблизительно равен 0.988. По данным коэффициентов K можно заключить, что уравнение (1) описывает приблизительно 95–98% вариаций индекса T для рассмотренных интервалов времени.

Рис. 1.

Зависимость ионосферного индекса T от индекса солнечной активности F для двух интервалов времени в годах (1954–1996 и 1996–2020) по экспериментальным данным (точки) и по уравнению регрессии (1) (сплошные линии).

3. СВЯЗЬ ИОНОСФЕРНОГО ИНДЕКСА T C ИНДЕКСАМИ ГЕОМАГНИТНОЙ АКТИВНОСТИ

Выше отмечалось, что связь ионосферного индекса T c индексом солнечной активности F является основной. Она описывается уравнением (1), и это уравнение воспроизводит 95–98% вариаций индекса T для всего интервала измерений индекса F. На остаток ΔT = T–TF приходится меньше 5% вариаций индекса T. Тем не менее, этот остаток может зависеть от геомагнитной активности через уравнение регрессии:

(2)
$\Delta T = a + b\left( {Ap - A{{p}_{{{\text{mid}}}}}} \right),$
где a и b – коэффициенты уравнения регрессии; Ap – средний за месяц Ap-индекс геомагнитной активности; Apmid – среднее для рассматриваемого интервала времени значение Ap. Например, Apmid = 15 для 1954–1996 гг. и Apmid = 10 для 1996–2020 гг. Анализ показал, что зависимость ΔT от Ap значима не во всех случаях и уровень этой значимости зависит от месяца года и диапазона изменений Ap-индекса. Анализ показал, что для выделения устойчивых зависимостей ΔT от Ap целесообразно использовать не месяц года, а три месяца года, центрированные на данный месяц. Например, параметры уравнения регрессии (2) для января получены по данным ионосферных индексов и индексов солнечной и геомагнитной активности за декабрь, январь и февраль; для июля они получены по данным за июнь, июль и август. Ниже январь, апрель, июль и октябрь являются такими центрированными месяцами, что соответствует четырем сезонам. Это обеспечивает увеличенное число данных в анализируемых массивах ионосферных индексов и индексов солнечной и геомагнитной активности для выбранного (центрированного) месяца. Зависимость ΔT от Ap практически отсутствует при очень низкой геомагнитной активности (Ap < 7). Поэтому в массиве данных для вычисления коэффициентов уравнения (2) оставлялись данные, которые удовлетворяли дополнительному условию

(3)
$Ap > 7.$

В таблице 1 приведены параметры уравнения регрессии (2) для перечисленных месяцев, полученные по данным об ионосферных индексах и индексах солнечной и геомагнитной активности за 1954–1996 и 1996–2020 гг. при дополнительном условии (3). Анализ показал, что для приведенных в табл. 1 данных зависимость (2) значима (при доверительном уровне 95% по критерию Фишера [Ramachandran and Tsokos, 2009]), если коэффициент корреляции K > 0.25–0.3. Из данных в табл. 1 следует, что для интервала 1954–1996 гг. зависимость (2) не значима для января и значима для остальных рассмотренных месяцев. Для интервала 1996−2020 гг. зависимость (2) не значима для января и апреля и значима для июля и октября. Во всех рассмотренных случаях коэффициент b < 0 в уравнении (2), т.е. увеличение Ap приводит к уменьшению ΔT. Между величинами K и b существует определенная связь: увеличенным значениям K соответствуют увеличенные значения модуля b, когда зависимость ΔT от Ap становится более отчетливой. Поэтому, например, для интервала 1954–1996 гг. зависимость ΔT от Ap наиболее отчетлива для июля. Объединяя эти результаты, можно утверждать, что в зависимости ΔT от Ap существуют годовой и полугодовой компоненты. Годовой компонент в зависимости ΔT от Ap с минимумом в январе и максимумом в июле, по-видимому, является устойчивой характеристикой ионосферного индекса T: коэффициент корреляции K и модуль коэффициента b в июле в 2–3 раза больше, чем в январе, для интервалов 1954–1996 и 1996–2020 гг. Полугодовой компонент в зависимости ΔT от Ap с максимумами в апреле и октябре менее стабилен. Например, для апреля эта зависимость значима в интервале 1954–1996 гг. и не значима в интервале 1996–2020 гг.

Таблица 1.  

Параметры уравнения регрессии (2): коэффициент корреляции K, стандартное отклонение σ, коэффициент b в этом уравнении и число измерений N для четырех месяцев и двух интервалов времени в годах (1954–1996 и 1996–2020)

Месяцы 1954−1996 1996−2020
K σ b N K σ b N
Январь 0.13 6.9 −0.21 121 0.19 7.7 −0.46 44
Апрель 0.36 6.7 −0.53 124 0.15 7.6 −0.33 58
Июль 0.43 6.2 −0.73 125 0.36 8.6 −0.92 45
Октябрь 0.33 6.8 −0.58 127 0.54 7.2 −1.15 55

Существование отчетливого годового компонента в зависимости ΔT от Ap явилось неожиданным свойством ионосферного индекса и индексов солнечной и геомагнитной активности, поскольку все рассмотренные индексы считаются планетарными индексами. Тем не менее, индекс Ap определен по данным 13 магнитных обсерваторий, из которых только две находятся в южном полушарии (в Австралии и Новой Зеландии). Было предположено, что данное свойство Ap-индекса может быть одной из причин существования годового компонента в зависимости ΔT от Ap, например, через увеличенную проводимость ионосферы северного полушария в июле. Для первой косвенной проверки этого предположения был использован средний за месяц aa-индекс геомагнитной активности, поскольку он определен по двум магнитным обсерваториям, расположенным в Англии и Австралии, т.е. достаточно симметрично относительно геомагнитного экватора. Для такой проверки использовано уравнение регрессии

(4)
$\Delta T = a + b\left( {aa - a{{a}_{{{\text{mid}}}}}} \right),$
которое отличается от уравнения (2) только заменой индекса Ap на aa и индекса Apmid на aamid. В таблице 2 приведены параметры уравнения регрессии (4) для перечисленных месяцев, полученные по данным об ионосферных индексах и индексах солнечной и геомагнитной активности за 1954–1996 и 1996–2020 гг. при дополнительном условии (3). Отметим, что дополнительное условие (3) выбрано одинаковым для уравнений регрессии (2) и (4), чтобы совпадали числа измерений индексов (N) для этих двух уравнений регрессии. Из данных в табл. 1 и 2 следует, что они во многом подобны: соответствующие коэффициенты корреляции K отличаются не больше, чем на 0.05, коэффициенты b < 0 для всех рассмотренных случаев. Зависимости ΔT от Ap и зависимости ΔT от aa не значимы для января и значимы для июля. Для всего анализируемого массива данных приближенно aa = 0.55Ap. Поэтому абсолютные значения коэффициентов b в табл. 2 меньше, чем в табл. 1, но коэффициент пропорциональности может отличаться от 0.55. Итак, характеры зависимости ΔT от Ap и зависимости ΔT от aa во многом совпадают. Поэтому приближенно можно считать, что отчетливый годовой компонент в зависимости ΔT от Ap не связан с особенностями вычисления индекса Ap по данным 13 магнитных обсерваторий.

Таблица 2.  

Параметры уравнения регрессии (4): коэффициент корреляции K, стандартное отклонение σ, коэффициент b в этом уравнении и число измерений N для четырех месяцев и двух интервалов времени в годах (1954–1996 и 1996–2020)

Месяцы 1954–1996 1996–2020
K σ b N K σ b N
Январь 0.16 6.8 −0.16 121 0.19 7.7 −0.27 44
Апрель 0.35 6.8 −0.32 124 0.12 7.6 −0.15 58
Июль 0.45 6.1 −0.45 125 0.38 8.5 −0.58 45
Октябрь 0.38 6.7 −0.36 127 0.59 6.9 −0.64 55

4. ОБСУЖДЕНИЕ

Уравнение (1) дает связь ионосферного индекса T c индексом солнечной активности F, в котором учтена предыстория изменения этой активности. Если обозначить через TF индекс T, который вычисляется по известному индексу F c помощью уравнения (1), то TF можно использовать как эффективный индекс солнечной активности для прогноза индекса T. Коэффициенты уравнения (1) можно считать постоянными величинами, что и позволяет использовать индекс TF для прогноза ионосферного индекса T на основе прогноза индекса солнечной активности F107 с учетом предыстории изменения F107. Для средних за месяц значений индекса T эта предыстория учтена, по-видимому, впервые. Уравнение (1) воспроизводит приблизительно 95–98% вариаций индекса T, поэтому оно является основным для прогноза этого индекса.

Приведенный здесь анализ основан на средних за месяц индексах T и F107. Ранее такой анализ был выполнен для средних за 12 месяцев значений этих индексов [Деминов и Деминова, 2020]. Сопоставление показало, что коэффициенты уравнения (1) для средних за месяц индексов T и F практически совпадают с коэффициентами аналогичного уравнения для средних за 12 месяцев индексов T и F107. Это позволяет использовать коэффициенты уравнения (1) для прогноза индекса T c разной заблаговременностью в зависимости от этой заблаговременности для индекса F107.

Остаток ΔT = T – TF может зависеть от Ap-индекса геомагнитной активности, где T –экспериментальное значение T, полученное на основе медиан критических частот F2-слоя foF2 ряда ионосферных станций, TF – значение T, вычисленное по уравнению (1) по известному индексу солнечной активности F. Возможность зависимости ΔT от Ap обусловлена тем, что медиана foF2 зависит не только от солнечной, но и от геомагнитной активности [Деминов и др., 2017]. Анализ зависимости ΔT от Ap позволил выявить достаточно устойчивый годовой компонент в этой зависимости: в январе эта зависимость не значима и обычно слабо выражена, в июле она значима и достаточно отчетлива. При этом во всех анализируемых случаях увеличение Ap приводит к уменьшению ΔT и, следовательно, к среднему (глобальному) уменьшению foF2. Данное свойство ионосферы сохраняется при замене Ap на индекс aa. Это может означать, что существование годового компонента в зависимости ΔT от Ap обусловлено свойствами ионосферы, а не особенностями вычислений индексов Ap или aa по данным магнитных обсерваторий. В свою очередь, остаются неизвестными свойства ионосферы, приводящие к возникновению годового компонента в зависимости ΔT от Ap. Ниже дано только предварительное качественное объяснение этого явления.

Годовой компонент в зависимости ΔT от Ap, по-видимому, является новым свойством годовой аномалии в параметрах ионосферы, когда средние (глобальные) параметры ионосферы в январе отличаются от этих параметров в июле при прочих равных условиях [Rishbeth and Müller-Wodarg, 2006]. Считают, что эта аномалия в конечном итоге обусловлена эллиптичностью орбиты Земли (расстояние Солнце–Земля минимально в начале января и максимально в начале июля), но конкретные проявления этой эллиптичности для параметров ионосферы в значительной степени остаются загадкой [Rishbeth and Müller-Wodarg, 2006; Brown et al., 2018].

На основе анализа ежедневных значений концентраций максимума F2-слоя NmF2 пары ионосферных станций Боулдер–Хобарт в полдень было получено, что суммарное значение NmF2 по этим станциям в январе больше, чем в июле, и эта разница при умеренной геомагнитной активности больше, чем при низкой активности [Деминов и Деминова, 2021]. Причинами зависимости амплитуды годовой аномалии в NmF2 на средних широтах от уровня геомагнитной активности, по-видимому, являются асимметрия зима/лето в частоте возникновения суббурь и годовая асимметрия в плотности термосферы [Деминов и Деминова, 2021]. Первый фактор определяет более высокую частоту суббурь местной зимой [Tanskanen et al., 2011; Newell et al., 2001, 2010], с которыми связана генерация крупномасштабных ВГВ в авроральной области [Hunsucker, 1982; Hocke and Schlegel, 1996]. Второй фактор обеспечивает увеличенные амплитуды ВГВ на средних широтах в январе через уменьшение затухания ВГВ, поскольку коэффициент молекулярной вязкости обратно пропорционален плотности термосферы [Брюнелли и Намгаладзе, 1988]. В свою очередь такие ВГВ являются наиболее частой причиной увеличенных значений NmF2 на средних широтах в полдень [Брюнелли и Намгаладзе, 1988].

Увеличение амплитуды годовой аномалии в NmF2 c ростом геомагнитной активности может происходить не только за счет увеличения NmF2 в январе, которое рассмотрено выше, но и за счет уменьшения NmF2 в июле из-за изменения температуры и состава термосферы. На средних широтах отрицательная фаза ионосферной бури, т.е. уменьшение NmF2 из-за изменения температуры и состава термосферы в периоды магнитных бурь, является основной и наиболее продолжительной по времени характеристикой этой бури [Buonsanto, 1999]. Уменьшение NmF2 из-за изменения температуры и состава термосферы может происходить не только в периоды магнитных бурь, но и в периоды продолжительной повышенной геомагнитной активности, что может соответствовать условиям, для которых получена медиана NmF2 (или медиана foF2) и, как следствие, ионосферный индекс T. Уменьшение ΔT при увеличении Ap, по-видимому, обусловлено этой причиной. При получении индекса T использованы значения медиан foF2 для всех часов суток [Caruana, 1990]. На средних широтах, при прочих равных условиях, относительные уменьшения foF2 из-за увеличения Ap, по-видимому, максимальны в ночные часы местным летом. Это обусловлено относительно низкими фоновыми значениями параметров термосферы и foF2 в эти часы для лета. На средних широтах местной зимой в ночные часы критическая частота foF2 в значительной степени контролируется диффузионным потоком ионосферной плазмы из плазмосферы, который относительно стабилен [Кринберг и Тащилин, 1984]. Эллиптичность орбиты Земли приводит к тому, что средние (глобальные) температуры и концентрации нейтральных компонентов термосферы минимальны в июле и максимальны в январе. В результате, годовая аномалия в зависимости ΔT от Ap с максимумом в июле может быть обусловлена наложением относительно сильного уменьшения foF2 местным летом из-за изменения состава термосферы с ростом геомагнитной активности и годовой асимметрии в параметрах термосферы из-за эллиптичности орбиты Земли, обеспечивая относительно более сильные изменения состава термосферы именно в июле. Данное предположение является предварительным даже на качественном уровне и требует специального анализа.

5. ВЫВОДЫ

Представлен анализ связи среднего за месяц ионосферного индекса T с индексами солнечной (F107) и геомагнитной (Ap) активности на основе массива данных этих индексов в интервале 1954–2020 гг., где F107 и Ap – средние за месяц поток радиоизлучения Солнца на длине волны 10.7 см и планетарный Ap-индекс геомагнитной активности. Получены следующие выводы.

1. Связь ионосферного индекса T c эффективным индексом F = (F1070 + F107–1)/2 является основной, где F1070 и F107–1 – индексы F107 в данный и предыдущий месяцы. Эта связь в виде полинома второй степени позволяет воспроизвести 95–98% вариаций T для анализируемого интервала времени. Коэффициенты этого полинома сохраняются практически постоянными для разных циклов солнечной активности, что позволяет использовать индекс F для прогноза индекса T.

2. Дополнительный вклад Ap в индекс T незначителен и зависит от сезона: для анализируемого интервала времени он не значим для января и значим для июля. Это выявленное свойство годовой аномалии в параметрах ионосферы сохраняется и для вклада аa-индекса геомагнитной активности в индекс T. Во всех рассмотренных случаях увеличение Ap или aa приводит к уменьшению ионосферного индекса T, т.е. к среднему (глобальному) уменьшению медианы концентрации максимума F2-слоя NmF2, и, при прочих равных условиях, такое уменьшение более значительно для июля, чем для января.

3. Годовая аномалия в зависимости ΔT от Ap с максимумом в июле может быть обусловлена наложением относительно сильного уменьшения NmF2 местным летом из-за изменения состава термосферы с ростом геомагнитной активности и годовой асимметрии в параметрах термосферы из-за эллиптичности орбиты Земли, обеспечивая относительно более сильные изменения состава термосферы именно в июле. Данное предположение является предварительным даже на качественном уровне и требует специального анализа.

Список литературы

  1. – Брюнелли Б.Е., Намгаладзе А.А. Физика ионосферы. М.: Наука, 528 с. 1988.

  2. – Деминов М.Г., Деминова Г.Ф. Индекс солнечной активности для долгосрочного прогноза критической частоты F2-слоя // Геомагнетизм и аэрономия. Т. 59. № 2. С. 191–198. 2019.

  3. – Деминов М.Г., Деминова Г.Ф. Эффективный индекс солнечной активности для медианы критической частоты F2-слоя // Геомагнетизм и аэрономия. Т. 60. № 5. С. 641–645. 2020.

  4. – Деминов М.Г., Деминова Г.Ф. Зависимость локального индекса годовой асимметрии для NmF2 от солнечной активности // Геомагнетизм и аэрономия. Т. 61. № 2. С. 224–231. 2021.

  5. – Деминов М.Г., Деминова Г.Ф., Депуев В.Х., Депуева А.Х. Зависимость медианы критической частоты F2-слоя на средних широтах от геомагнитной активности // Солнечно-земная физика. Т. 3. № 4. С. 74–81. 2017.

  6. – Деминов М.Г., Михайлов А.В., Михайлов В.В., Шубин В.Н., Цыбуля К.Г. Ионосферное моделирование и прогнозирование / Системный мониторинг ионосферы. Сб. науч. трудов. Ред. Н.Г. Котонаева. М.: ФИЗМАТЛИТ. С 286–343. 2019.

  7. – Кринберг И.А., Тащилин А.В. Ионосфера и плазмосфера. М.: Наука, 189 с. 1984.

  8. – Bilitza D. IRI the international standard for the ionosphere // Adv. Radio Sci. V. 16. P. 1–11. 2018.

  9. – Brown S., Bilitza D., Yigit E. Improvements to predictions of the ionospheric annual anomaly by the international reference ionosphere model // Ann. Geophysicae. Discuss., 2018.https://doi.org/10.5194/angeo-2018-97

  10. – Buonsanto M. Ionospheric storms – a review // Space Sci. Rev. V. 88. P. 563–601. 1999.

  11. – Caruana J. The IPS monthly T index // Solar-Terrestrial Prediction: Proc. Workshop at Leura, Australia (October 16–20, 1989). V. 2. P. 257–263. 1990.

  12. – Hocke K., Schlegel K. A review of atmospheric gravity waves and traveling ionospheric disturbances: 1982–1985 // Ann. Geophysicae. V. 14. № 9. P. 917–940. 1996.

  13. – Hunsucker K. Atmospheric gravity waves generated in the high-latitude ionosphere: a review // Rev. Geophys. Space Phys. V. 20. P. 293–315. 1982.

  14. – Nava B., Coisson P., Radicella S.M. A new version of the NeQuick ionosphere electron density model // J. Atmos. Solar-Terr. Phys. V. 70. P. 1856–1862. 2008.

  15. – Newell P.T., Greenwald R.A., Ruohoniemi J.M. The role of the ionosphere in aurora and space weather //Rev. Geophys. V. 39. № 2. P. 137–149. 2001.

  16. – Newell P.T., Sotirelis T., Wing S. Seasonal variations in diffuse, monoenergetic, and broadband aurora // J. Geophys. Res. V. 115. A03216. 2010. https://doi.org/10.1029/2009JA014805

  17. – Ramachandran K.M., Tsokos C.P. Mathematical statistics with applications. Oxford: Elsevier Academic Press, 824 p. 2009.

  18. – Rishbeth H., Müller-Wodarg I.C.F. Why is there more ionosphere in January than in July? The annual asymmetry in the F2-layer // Ann. Geophysicae. V. 24. № 12. P. 3293–3311. 2006.

  19. – Tanskanen E.I., Pulkkinen T.I., Viljanen A. et al. From space weather toward space climate time scales: Substorm analysis from 1993 to 2008 // J. Geophys. Res. V. 116. A00I34. 2011. https://doi.org/10.1029/2010JA015788

  20. – Zakharenkova I.E., Krankowski A., Bilitza D., et al. Comparative study of foF2 measurements with IRI-2007 model predictions during extended solar minimum // Adv. Space Res. V. 51. P. 620–629. 2013.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Геомагнетизм и аэрономия

Архивы выпусков Информация о журнале Отправить рукопись в журнал