Геомагнетизм и аэрономия, 2021, T. 61, № 6, стр. 763-768
Определение параметров перемещающихся ионосферных возмущений по ионограммам вертикального зондирования с дополнительными U-образными треками
О. А. Ларюнин *
Институт солнечно-земной физики СО РАН
г. Иркутск, Россия
* E-mail: laroleg@iszf.irk.ru
Поступила в редакцию 25.02.2021
После доработки 18.05.2021
Принята к публикации 27.05.2021
Аннотация
Рассмотрен случай, когда в результате перемещения дополнительного U-образного трека на ионограммах вертикального зондирования фиксируется повышенная критическая частота. Это соответствует появлению над точкой зондирования области с повышенной электронной концентрацией. Представлена методика исследования характеристик перемещающихся ионосферных возмущений по ионограммам в рамках двумерной модели возмущения. Исследованы изменения формы дополнительного трека ионограммы, к которым приводит варьирование параметров возмущения. Показаны возможности определения таких характеристик перемещающихся ионосферных возмущений, как интенсивность, масштаб локализации, горизонтальная скорость дрейфа.
1. ВВЕДЕНИЕ
На ионограммах вертикального и слабонаклонного зондирования можно часто наблюдать дополнительный U-образный трек, свидетельствующий о наличии перемещающегося ионосферного возмущения (ПИВ).
Еще в середине прошлого века было установлено [Munro and Heisler, 1956], что появление серпообразных особенностей на ионограммах связано с прохождением ПИВ, которые приводят к образованию горизонтальных градиентов электронной концентрации ионосферы и, соответственно, к невертикальным отражениям лучей при радиозондировании.
Дополнительные треки на ионограммах вертикального зондирования разнообразны как по форме, так и по динамическим проявлениям [Akchurin et al., 2011; Moskaleva and Zaalov, 2013; Lou et al., 2020; Zaalov and Moskaleva, 2020]. Помимо наиболее распространенных U-образных структур (серпов) можно встретить треки с более сложными формами, которые с трудом поддаются имитационному моделированию.
Моделирование серпов в условиях неслоистой среды было начато во второй половине XX века [Munro and Heisler, 1956; Lobb and Titheridge, 1977; Cooper and Cummack, 1986] и было продолжено в последующих работах [James and MacDougall, 1997; Cervera and Harris, 2014]. Тем не менее, корректное моделирование, например, переходного процесса слияния простого U-образного серпа с основным треком ионограммы до сих пор остается трудной задачей [Lou et al., 2020]. Тем более открытым остается вопрос об обратной задаче восстановления горизонтально-неоднородной структуры ионосферы по ионограммам с дополнительными треками.
В работах [Emmons et al., 2020; Ratovsky et al., 2008] представлены методики исследования динамики ПИВ по временны́м вариациям действующих высот на ионограммах. Истинные высоты там восстанавливаются из ионограмм методом Хуанга–Райниша в предположении плоско-слоистой среды. Указанные методики представляются эффективными в случаях, когда ПИВ не приводят к ярко выраженным боковым отражениям. Иная ситуация имеет место при ПИВ с бόльшими амплитудами, которые приводят к значительным горизонтальным градиентам электронной концентрации. В этом случае на ионограммах могут возникать характерные U-образные треки, для изучения которых уже становится необходимым траекторный синтез.
Таким образом, целью настоящей работы является модельное описание дополнительных U-образных треков на ионограммах вертикального зондирования, реконструкция ионосферных возмущений с помощью имитационного моделирования, а также исследование динамики перемещающихся ионосферных возмущений по последовательности ионограмм.
Представленные в работе ионограммы были получены в ежеминутном режиме в п. Торы (51°48′ N, 103°5′ E) в 100 км от Иркутска [Berngardt et al., 2017].
2. ИМИТАЦИОННОЕ МОДЕЛИРОВАНИЕ
Траекторный синтез ионограмм выполнялся на основе алгоритма двумерной пристрелки лучей в приближении геометрической оптики. Так, для каждой заданной рабочей частоты алгоритм позволяет рассчитывать набор траекторий, соответствующих углам излучения в выбранном интервале (от –1° до 45°) с определенным шагом (0.1°). Отметим, что отрицательные углы здесь не дают возвратных траекторий и не представляют интереса, однако важно, чтобы вертикальная траектория (0°) попала внутрь интервала. Полученный набор траекторий позволяет, использую сплайн-интерполяцию, построить дальностно-угловую характеристику D(φ). Далее численно решается уравнение D(φ) = 0: при вертикальном зондировании дальность трассы равна нулю. Наконец, для найденного угла излучения (или углов – в случае многолучевости) синтезируется траектория и фиксируется групповая задержка, которая впоследствии отображается в виде точки на ионограмме. Описанная процедура повторяется для других рабочих частот, при этом шаг по частоте составляет 0.025 МГц.
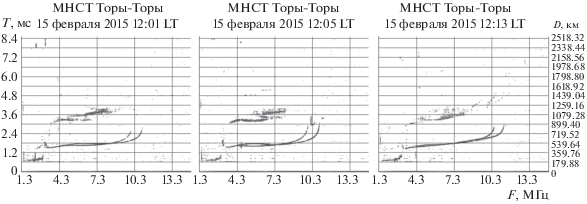
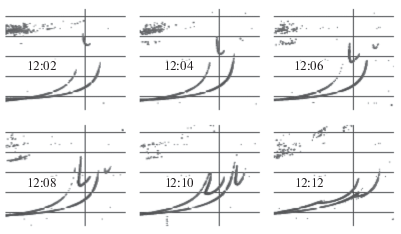
Рассмотрим часто наблюдаемый на ионограммах случай, когда в результате прохождения U-образной структуры устанавливается повышенная критическая частота. Такого рода событие проиллюстрировано на рисунках 1 и 2. Длительность события, т.е. временнóй интервал между спокойными ионограммами до и после появления серпа, составляет 12 мин, что подчеркивает недостаточность типичной для ионозондов скважности наблюдений в 15 мин для исследования динамических процессов в ионосфере. Так как на ионограммах устанавливается повышенная критическая частота, то будет обоснованным предположить появление области с повышенной электронной концентрацией над точкой зондирования. Траектории, образующие серп на ионограмме, формируются в переходный период за счет боковых (невертикальных) отражений на горизонтальных градиентах электронной концентрации.
Как показывает моделирование, плавность перехода от фоновой к повышенной электронной концентрации (т.е. величина горизонтального градиента) влияет на вид траектории луча и, следовательно, на групповой путь. Другими словами, форма возмущения задает форму серпа на ионограмме. Возникающая в этой связи обратная задача восстановления параметров возмущения будет решена путем многократного решения соответствующей прямой задачи с последующим фитированием.
Модель возмущения вида (1) представляется в данном контексте вполне адекватной, хотя данный выбор не носит принципиального характера.
(1)
$\left\{ \begin{gathered} {{f}_{p}}\left( {x,z} \right) = {{f}_{{po}}}\left( z \right)\left( {1 + \delta {\kern 1pt} \exp {\kern 1pt} \left( { - \frac{{{{{\left( {x - {{x}_{0}}} \right)}}^{4}}}}{{{{b}^{4}}}}} \right)} \right){\kern 1pt} ,~\,\,\,\,~x \leqslant {{x}_{0}} \hfill \\ {{f}_{p}}\left( z \right) = {{f}_{{po}}}\left( z \right)\left( {1 + \delta } \right),~\,\,\,~\,x > {{x}_{0}}. \hfill \\ \end{gathered} \right.$3. ПОДБОР ПАРАМЕТРОВ МОДЕЛИ
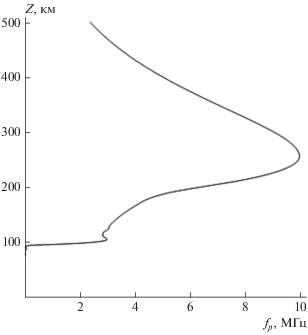
Интенсивность возмущения $\delta = \frac{{{{f}_{{c1}}} - {{f}_{{c0}}}}}{{{{f}_{{c0}}}}}$ определяется приращением критической частоты в результате прохождения серповидной структуры и составляет в данном случае 7%, ${{f}_{{c1}}} = 1.07{{f}_{{c0}}}$. При расчете за последнюю спокойную ионограмму перед событием взят момент времени 12:01 LT. По этой ионогорамме методом Хуанга–Райниша [Reinisch and Huang, 1983] определен фоновый профиль ${{f}_{{p0}}}\left( z \right)$ (рис. 3).
Первая спокойная ионограмма после события наблюдается в 12:13 LT. Параметр ${{x}_{0}}$ задает положение возмущения относительно приемника/передатчика так, что уменьшение ${{x}_{0}}$ приводит к сползанию серпа вниз и влево вдоль основного трека ионограммы. Действительно, приближение возмущения ведет к “укорачиванию” боковых траекторий и соответственно к уменьшению группового пути. Наконец, масштаб b в выражении (1) является фактором формы возмущения и варьирует горизонтальный градиент электронной концентрации (рис. 4), задавая плавность перехода от фоновых значений к возмущенному состоянию. Фактически, дальнейшая задача сводится к поиску значения b, наиболее точно отвечающему экспериментальной ионограмме. В качестве эталонной на данном этапе выбрана серповидная структура в 12:05 LT.
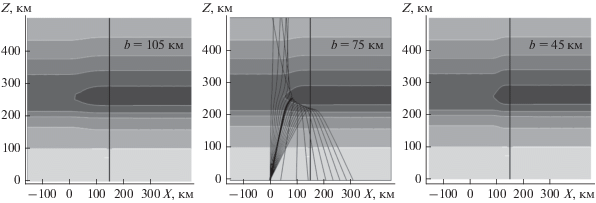
Рис. 4.
Горизонтально-неоднородная структура ионосферы и лучевые траектории при f = 10.3 МГц. b = 105 км (левая панель), b = 75 км (средняя панель) и b = 45 км (правая панель). Жирная кривая на средней панели соответствует возвратному лучу. Вертикальная линия соответствует центру возмущения, x0 = 150 км. При $x \geqslant {{x}_{0}}$ среда слоистая.
Если первым критерием соответствия модели и эксперимента служит совпадение правой асимптоты серпа – фактической критической частоты на возмущенной ионограмме, то за второй критерий целесообразно взять совпадение точек минимума серпа. Соответствующее фитирование представляет собой наиболее затратную часть с точки зрения компьютерного времени. Данная процедура сводится к перебору параметров b и ${{x}_{0}}$ с фиксацией ближайших к экспериментальному положений точек минимума и последующей интерполяцией.
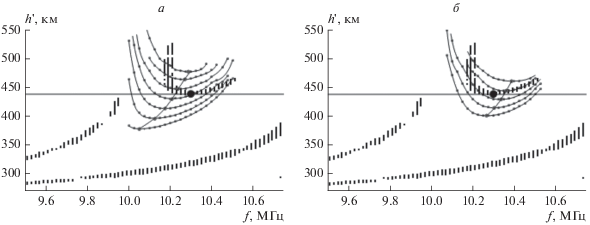
На рисунке 5 показан случай b = 75 км: синтезированный серп сползает вниз по мере уменьшения ${{x}_{0}}$. Точка (10.3 МГц, 439 км) соответствует эксперименту и является искомой при фитировании.
Рис. 5.
Серия синтезированных серпов, наложенных на экспериментальную ионограмму 12:05 LT, для b = = 75 км. Жирными точками показаны минимумы серпов.
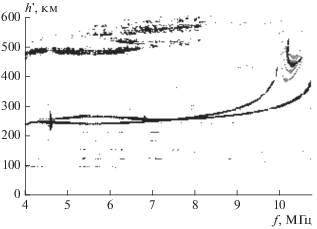
Рисунок 6 представляет собой аналог рис. 5в увеличенном масштабе для b = 90 км и b = 60 км соответственно.
Рис. 6.
Увеличенные фрагменты синтезированных ионограмм, наложенных на экспериментальную 12:05 LT. (а) b = = 90 км; (б) b = 60 км. Горизонтальная кривая задает уровень 439 км, соответствующий минимуму эталонного экспериментального серпа. В ходе фитирования мы добиваемся того, чтобы кривая, которую описывают минимумы синтезированного серпа, прошла через минимум экспериментального серпа.
Процедура фитирования проиллюстрирована на рисунках 5, 6, 7 и заключается в следующем. Для каждого значения b варьируется параметр ${{x}_{0}}$, т.е. заданное возмущение приближается к точке наблюдения. При этом соответствующий серп сползает вниз, и его минимум в какой-то момент проходит уровень h' = 439 км. Фиксируется частота, на которой произошло пересечение данного уровня. Последующее варьирование масштаба b позволяет найти пересечение уровня 439 км, максимально близкое к 10.3 МГц.
Рис. 7.
При значении b = 70 км (а) ‒ интерполяция прогнозирует прохождение синтезированного серпа через искомую точку (10.3 МГц, 439 км) на ионограмме, что подтверждает панель (б).
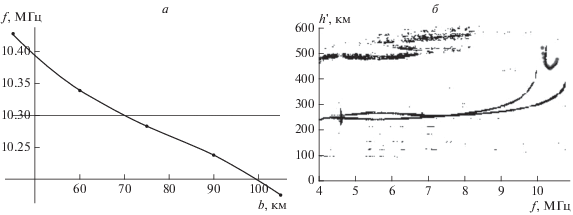
Можно видеть на рис. 6, что в первом случае (левая панель) пересечение уровня h ' = 439 км происходит слева, при f = 10.24 МГц, тогда как во втором случае (правая панель) – справа, при f = = 10.34 МГц. Далее аналогичным образом определяются точки пересечения для других значений b (рис. 7а). Можно видеть, что интерполяция прогнозирует наилучшее совпадение при b = 70 км, что и подтверждает рис. 7б.
Следует отметить визуальное расхождение данных модели и эксперимента в области левой асимптоты серпа. Очевидно, это связано с погрешностью модели (1). Вероятно, введение дополнительных параметров в модель (например, наклон возмущения или его локализация по высоте) приведет к лучшему соответствию. Однако соответствующее увеличение времени расчета в практических целях не представляется целесообразным.
4. ОЦЕНКА ГОРИЗОНТАЛЬНОЙ СКОРОСТИ ВОЗМУЩЕНИЯ
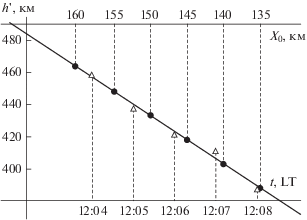
Представляет интерес исследование динамики ПИВ по последовательности экспериментальных ионограмм. Сползание серпа на ионограммах связано с движением ПИВ, и чем быстрее движется серп, тем быстрее перемещается соответствующее возмущение. Не составляет труда по набору ионограмм определить горизонтальную скорость возмущения. Для возмущения вида (1), где параметры $\delta $ = 7% и b = 70 км уже найдены в ходе фитирования, будем варьировать значение ${{x}_{0}}$. Возмущение при этом будет удаляться (с ростом ${{x}_{0}}$) или приближаться (по мере уменьшения ${{x}_{0}}$) к точке излучения, а синтезированный серп соответственно подниматься или опускаться подобно изображенному на рис. 4. Будем фиксировать действующую высоту h', соответствующую точке минимума каждого синтезированного серпа, получая таким образом зависимость $h_{{\min }}^{'}\left( {{{x}_{0}}} \right)$ (см. рис. 8, кружки). С другой стороны, временна́я зависимость $h_{{\min }}^{'}\left( t \right)$ устанавливается экспериментально: на рис. 8 она показана треугольниками.
Верхняя и нижняя горизонтальные оси на рис. 8 масштабированы так, чтобы результаты линейной регрессии для экспериментальной и модельной зависимостей отображались на одной кривой. Так, например, видно, что серп на экспериментальной ионограмме ${{t}_{1}} = 12{\text{:}}08$ соответствует локализации возмущения ${{x}_{{01}}} = 135.5$ км, а момент времени ${{t}_{2}} = 12{\text{:}}04$ отвечает значению ${{x}_{{02}}} = 158$ км. Тогда горизонтальная скорость перемещения возмущения по направлению к точке наблюдения ${{V}_{x}} = \frac{{{{x}_{{02}}} - {{x}_{{01}}}}}{{\left| {{{t}_{2}} - {{t}_{1}}} \right|}} \approx 94$ м/с.
5. ЗАКЛЮЧЕНИЕ
Описанная методика позволяет восстанавливать электронную концентрацию в горизонтально-неоднородной ионосфере (двумерный случай) по ряду экспериментальных ионограмм вертикального зондирования, содержащих дополнительные серповидные треки на основе траекторного синтеза с последующим фитированием.
Использованная гауссоподобная модель перехода от фоновой ионосферы к возмущенной показала свою состоятельность для воспроизведения наблюдаемых серпов при моделировании. В качестве примера, для выбранного набора ионограмм были определены такие характеристики возмущения, как интенсивность, пространственный масштаб, горизонтальная скорость перемещения.
При рассмотрении динамики возмущения оказалось, что экспериментальные ионограммы демонстрируют квазилинейное нисхождение серпа в рассматриваемом временнóм интервале. В то же время линейная зависимость положения серпа на ионограмме от горизонтальной координаты возмущения имеет место и при моделировании. В этой связи оказывается нетрудным определить горизонтальную скорость перемещения ионосферного возмущения, добиваясь совпадения экспериментальных и синтезированных серпов путем соответствующего масштабирования временнóй и координатной осей.
Список литературы
– Akchurin A.D., Bochkarev V.V., Ildiryakov V.R., Usupov K.M. TID selection and research of its characteristics on ionograms / Proc. 30th URSI General Assembly and Scientific Symposium. Istanbul, Turkey, 13–20 August 2011. GP1.23. 2011.
– Berngardt O.I., Perevalova N.P., Podlesnyi A.V., Kurkin V.I., Zherebtsov G.A. Vertical midscale ionospheric disturbances caused by surface seismic waves based on Irkutsk chirp ionosonde data in 2011–2016 // J. Geophys. Res. Space. V. 122. № 4. P. 4736–4754. 2017.
– Cervera M.A., Harris T.J. Modeling ionospheric disturbance features in quasi-vertically incident ionograms using 3-D magnetoionic ray tracing and atmospheric gravity waves // J. Geophys. Res. Space. V. 119. № 1. P. 431–440. 2014.
– Cooper J., Cummack C.H. The analysis of travelling ionospheric disturbance with nonlinear ionospheric response // J. Atmos. Solar Terr. Phys. V. 48. № 1. P. 61–64. 1986.
– Emmons D.J., Dao E.V., Knippling K.K., McNamara L.F., Nava O.A., Obenberger K.S., Colman J.J. Estimating horizontal phase speeds of a traveling ionospheric disturbance from digisonde single site vertical ionograms // Radio Sci. V. 55. № 8. e2020RS007089. 2020.
– James H.G., MacDougall J.W. Signatures of polar cap patches in ground ionosonde data // Radio Sci. V. 32. № 2. P. 497–513. 1997.
– Lobb R.J., Titheridge J.E. The effects of travelling ionospheric disturbances on ionograms // J. Atmos. Terr. Phys. V. 39. № 2. P. 129–134. 1977.
– Lou P., Wei N., Guo L., Feng J., Li X., Yang L. Numerical study of traveling ionosphere disturbances with vertical incidence data // Adv. Space Res. V. 65. № 4. P. 1306–1320. 2020.
– Moskaleva E.V., Zaalov N.Y. Signature of polar cap inhomogeneities in vertical sounding data // Radio Sci. V. 48. № 5. P. 547–563. 2013.
– Munro G.H., Heisler L.H. Cusp type anomalies in variable frequency ionospheric records // Aust. J. Phys. V. 9. P. 343–357. 1956.
– Ratovsky K.G., Medvedev A.V., Tolstikov M.V., Kushnarev D.S. Case studies of height structure of TID propagation characteristics using cross-correlation analysis of incoherent scatter radar and DPS-4 ionosonde data // Adv. Space Res. V. 41. № 9. P. 1454–1458. 2008.
– Reinisch B.W., Huang X. Automatic calculation of electron density profiles from digital ionograms. 3. Processing of bottomside ionograms // Radio Sci. V. 18. № 3. P. 477–492. 1983.
– Zaalov N.Y., Moskaleva E.V. Oblique and vertical incidence ionogram simulations with the presence of Es layer // Adv. Space Res. V. 66. № 7. P. 1713–1723. 2020.
Дополнительные материалы отсутствуют.
Инструменты
Геомагнетизм и аэрономия