Геомагнетизм и аэрономия, 2021, T. 61, № 6, стр. 751-762
Генерация электрического тока волной цунами в среднеширотной ионосфере
В. М. Сорокин 1, *, А. К. Ященко 1
1 Институт земного магнетизма, ионосферы и распространения радиоволн
им. Н.В. Пушкова РАН (ИЗМИРАН)
г. Москва, г. Троицк, Россия
* E-mail: sova@izmiran.ru
Поступила в редакцию 26.02.2021
После доработки 26.03.2021
Принята к публикации 27.05.2021
Аннотация
Распространение волны цунами сопровождается возмущением геомагнитного поля, генерацией акустико-гравитационной волны и ее распространением в ионосферу. Рассматривается механизм формирования электрического тока волной цунами в океане и в ионосфере в низких и средних широтах. Источником тока в морской среде является ее движение в геомагнитном поле. Источником тока в ионосфере является ее движение под действием акустико-гравитационной волны в геомагнитном поле. Величина электрического тока в морской среде и в ионосфере сравнимы в результате экспоненциального роста акустико-гравитационной волны при ее распространении вверх. Выведены уравнения возмущения геомагнитного поля в модели океан–атмосфера–ионосфера в наклонном магнитном поле. Проведены расчеты пространственного распределения возмущения магнитного поля в атмосфере и ионосфере. Проанализировано влияние электрического тока в ионосфере и наклонного геомагнитного поля на характеристики его возмущения магнитного поля. Показана возможность спутникового мониторинга цунами на средних широтах по регистрации электромагнитных полей.
1. ВВЕДЕНИЕ
Многочисленные наблюдения показывают, что распространение волны цунами сопровождается возмущениями ионосферы и магнитного поля. В работе [Sugioka et al., 2014] приведены данные подводной сети магнитометров во время прохождения волны цунами, возникшей в результате землетрясения в Чили 27.02.2010 г. Данные сравнивались с записями придонного давления на глубине 4800 м. Возмущения магнитного поля и изменения придонного давления, связанные с цунами, составляли 0.5 нТл и 1200 Ра соответственно. Сравнение показывает значительное отличие регистрируемой формы сигналов. Manoj and Maus [2011] наблюдали возмущения геомагнитного поля, сопровождающее цунами от сильного землетрясения в Чили 27.02.2010 г. Измерения, проведенные на расстоянии 3500 км на запад от эпицентра, обнаружили периодический сигнал амплитудой 1 нТл, совпадающий по времени c приходом волны цунами. Данные регистрации магнитного поля в нескольких точках до и после возникновения волны цунами, связанной с землетрясением в Тохоку 11.03.2011 г., приведены в работе [Tatehata et al., 2015]. Результаты регистрации свидетельствуют о генерации возмущений магнитного поля волной цунами и отличием формы сигнала от формы смещения морской среды в волне. Toh et al. [2011] были зарегистрированы вариации геомагнитного поля, связанных с прохождением волны цунами от двух землетрясений в районе Курильских островов 15.11.2006 г. и 13.01.2007 г. Эти данные дали возможность определить направление распространения волны цунами. Амплитуда горизонтальной компоненты геомагнитного возмущения изменяла знак на противоположенный для стадий роста и спада волны.
Kopytenko et al. [2014] зарегистрировали возмущение магнитного поля амплитудой 6–12 нТл на поверхности земли на расстоянии порядка 30 км от берега и 130 км от эпицентра землетрясения 11.03.2011 г. Возмущение магнитного поля начиналось через 5–7 мин после землетрясения. Zhang et al. [2014] привели данные наблюдения возмущения магнитного поля примерно на таком же расстоянии от берега во время землетрясения 11.03.2011 г. В этой работе было выполнено численное моделирование возмущения магнитного поля с использованием модели источника, которым является электрический ток, протекающий в движущейся проводящей морской среде. Проведено сопоставление результатов расчета поля по закону Био–Савара и по 3D-модели с результатами регистрации на суше. Из сопоставления следует значительное различие. Именно, амплитуда наблюдаемого поля в разы превышает амплитуду моделируемого сигнала и находится с ним в противофазе. Аналогичные отличия поведения наблюдаемых аномалий магнитного поля индуцированных цунами и модельных расчетов отмечены в работе [Wang and Liu, 2013].
Вертикальные смещения поверхности морской среды в волне цунами сопровождаются генерацией акустико-гравитационной волны (АГВ). Ее распространение вверх приводит к появлению ионосферных возмущений. Возможность регистрации цунами с использованием методов мониторинга ионосферных возмущений впервые обсуждалась в работе [Peltier and Hines, 1976]. Исследования возмущения ионосферы с помощью метода GPS зондирования вызванного волной цунами от землетрясения в Перу 23 июня 2001 г. проведены в работе [Artru et al., 2005]. Обнаружены возмущения полного электронного содержания ионосферы, коррелируемые с волной цунами после 2006 г. на Курильских о-вах, 2009 г. на о-ве Самоа и 2010 г. в Чили [Rolland et al., 2010]. Galvan et al. [2012] провели наблюдения возмущения полного электронного содержания ионосферы волной цунами после землетрясения Тохоку 11 марта 2011 г. Обнаружены движущиеся ионосферные возмущения в направлении от эпицентра со скоростями 3400, 1000 с и 200–300 м/с. Coïsson et al. (2015) анализировали данные наблюдений возмущения полного электронного содержания ионосферы над Тихим океаном после землетрясения Тохоку 11 марта 2011 г. Анализ данных показал, что характерная вертикальная длина волны составляла 50 км, а область возмущения охватывала интервал высот порядка 200 км.
Считается, что источником возмущения геомагнитного поля является электрический ток, возникающий в результате движения проводящей морской среды под действием волны цунами в этом поле. Однако, анализ результатов сопоставления свидетельствует о значительном отличии наблюдаемых возмущений магнитного поля и их модельных расчетов, основанных на этом механизме. Сорокин и др. [2019] показали, что волна цунами генерирует возмущение геомагнитного поля, которое формируется не только электрическим током в морской среде, но и током в ионосфере. Электрический ток в проводящей ионосфере возникает в результате ее движения в геомагнитном поле под действием АГВ. Показано, что величина плотности тока в ионосфере может быть сравнимой или больше величины плотности тока в морской среде. Рассмотрен механизм генерации возмущений магнитного поля в модели вертикального геомагнитного поля для уединенной волны цунами. Особенности влияния различных механизмов возникновения цунами на характеристики возмущения магнитного поля проанализированы в работе [Sorokin et al., 2019]. Ниже развита модель генерации электрических токов и полей в системе морская среда – ионосфера в наклонном геомагнитном поле, выведены уравнения и проведены расчеты пространственно-временны́х характеристик поля в атмосфере и ионосфере.
2. УРАВНЕНИЯ ЭЛЕКТРОМАГНИТНОГО ПОЛЯ
Рассмотрим распространение волны цунами в северном полушарии. Введем декартову систему координат $x,y,z$ с осью $z$, направленной вертикально вверх и началом координат, расположенным на поверхности моря. Ось $x$ направлена к экватору, а ось $y$ направлена на восток. Ось $\xi $ системы координат $\xi ,\zeta ,z$ направлена под углом $\alpha $ к оси $x$, как показано на рис. 1. Одномерная волна цунами распространяется вдоль оси $\xi $. Вектор ${\mathbf{r}} = \left( {x,y} \right)$ расположен в горизонтальной плоскости. Координаты $\xi ,\varsigma $ связаны с координатами $x,y$ формулами:
(1)
$\begin{gathered} \xi = x\cos \alpha + y\sin \alpha , \\ \varsigma = - x\sin \alpha + y\cos \alpha . \\ \end{gathered} $Рис. 1.
Локальная система координат в северном полушарии. $\sigma $ – проводимость нижней ионосферы.
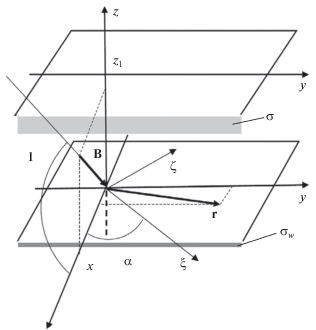
Однородное геомагнитное поле B = –B × × $\left( {\cos I,0,\sin I} \right)$ c геомагнитным наклонением $I$ расположено в плоскости меридиана $(x,z)$. В интервале высот $ - h < z < 0$ расположена морская среда, в интервале высот $0 < z < {{z}_{1}}$ расположена атмосфера, на высотах $z > {{z}_{1}}$ расположена ионосфера.
Движение проводящей морской среды в геомагнитном поле генерирует в ней электрический ток. Вертикальное смещение поверхности морской среды волной цунами сопровождается генерацией акустико-гравитационной волны, которая распространяясь вверх приводит в движение проводящую ионосферу в присутствии геомагнитного поля ${\mathbf{B}}$ и возникновению электрического тока [Сорокин и др., 2019]. Рассмотрим возмущение электромагнитного поля $\left( {{\mathbf{E}}{\text{,}}{\mathbf{b}}} \right)$ формируемого этим током в морской среде. Воспользуемся системой уравнений Максвелла в квазистационарном приближении, пренебрегая током смещения [Bladel, 2007]:
(2)
$\nabla \times {\mathbf{b}} = {{\mu }_{0}}{\mathbf{j}}{\kern 1pt} ,\,\,\,\,\nabla \times {\mathbf{E}} = - \frac{{\partial {\mathbf{b}}}}{{\partial t}},\,\,\,\,\nabla \cdot {\mathbf{b}} = 0.$(3)
${\mathbf{j}} = {{\sigma }_{w}}\left( {{\mathbf{E}} + {\mathbf{V}} \times {\mathbf{B}}} \right).$Проводимость ${{\sigma }_{w}}$ морской среды считаем однородной по ее глубине. Электропроводности атмосферы и грунта много меньше, чем у морской воды. Источником тока является движение морской среды со скоростью ${\mathbf{V}}\left( {{\mathbf{r}},t} \right)$ в крупномасштабной волне цунами. Как показано в работе [Сорокин и др., 2019], взаимная индукция токов в морской среде и в ионосфере является пренебрежимо малой. Поэтому, возможно пренебречь влиянием проводящей ионосферы на генерацию электромагнитного поля в морской среде. Используя уравнения (2), закон Ома (3) и условие не сжимаемости жидкости $\nabla \cdot {\mathbf{V}} = 0$, получим:
(4)
$\Delta {\mathbf{b}} - {{\mu }_{0}}{{\sigma }_{w}}\frac{{\partial {\mathbf{b}}}}{{\partial t}} = - {{\mu }_{0}}{{\sigma }_{w}}\left( {{\mathbf{B}} \cdot \nabla } \right){\mathbf{V}}.$Проводимостью грунта и атмосферы пренебрегаем по сравнению с проводимостью морской воды. Согласно уравнению (4) возмущение магнитного поля в этих средах определяется уравнением Лапласа:
Рассмотрим генерацию возмущения электромагнитного поля в плоскослоистой ионосфере при распространении в ней АГВ. Возмущение электромагнитного поля в ионосфере определяется системой уравнений (2). Закон Ома для ионосферной плазмы имеет вид:
Проводимость ионосферы в системе координат $\left( {x,y,z} \right)$ в северном полушарии представляет собой тензор $\hat {\sigma }$, компоненты которого зависят от высоты [Ratcliffe, 1960]:
(7)
$\hat {\sigma } = \left( {\begin{array}{*{20}{c}} {{{\sigma }_{\parallel }}{{{\cos }}^{2}}I + {{\sigma }_{{\text{P}}}}{{{\sin }}^{2}}I}&{{{\sigma }_{{\text{H}}}}\sin I}&{\left( {{{\sigma }_{\parallel }} - {{\sigma }_{{\text{P}}}}} \right)\sin I\cos I} \\ { - {{\sigma }_{{\text{H}}}}\sin I}&{{{\sigma }_{{\text{P}}}}}&{{{\sigma }_{{\text{H}}}}\cos I} \\ {\left( {{{\sigma }_{\parallel }} - {{\sigma }_{{\text{P}}}}} \right)\sin I\cos I}&{ - {{\sigma }_{{\text{H}}}}\cos I}&{{{\sigma }_{\parallel }}{{{\sin }}^{2}}I + {{\sigma }_{{\text{P}}}}{{{\cos }}^{2}}I} \end{array}} \right),$Полагая проводимость ионосферы ${{\sigma }_{{{\text{P,H}}}}} \leqslant $ $ \leqslant {{10}^{{ - 3}}}\,\,{1 \mathord{\left/ {\vphantom {1 {{\text{Ом}}\,\,{\text{м}}}}} \right. \kern-0em} {{\text{Ом}}\,\,{\text{м}}}}$ получим ${{\mu }_{0}}{{\sigma }_{{{\text{P,H}}}}}aL \leqslant 0.01$. Следовательно, в системе уравнений (2) пренебрегаем индукционными эффектами. Определим потенциал электрического поля $\varphi $ по формуле ${\mathbf{E}} = - \nabla \varphi $. Условие непрерывности тока $\nabla \cdot {\mathbf{j}} = 0$ и закон Ома (6) позволяют получить систему уравнений для потенциала в квазистатическом приближении в ионосфере:
(8)
$\nabla \cdot \left[ {\hat {\sigma }\left( {\nabla \varphi - {\mathbf{v}} \times {\mathbf{B}}} \right)} \right] = 0.$В ионосфере выполняется неравенство ${{\sigma }_{\parallel }} \gg {{\sigma }_{{{\text{P,H}}}}}$. Компоненты тензора ${{\sigma }_{{{\text{P,H}}}}}$ отличны от нуля в тонком слое толщиной $l$ с максимумом на высоте $z = {{z}_{1}}$. Величина скин-слоя в ионосфере $\sqrt {{\tau \mathord{\left/ {\vphantom {\tau {2\pi {{\mu }_{0}}{{\sigma }_{{{\text{P,H}}}}}}}} \right. \kern-0em} {2\pi {{\mu }_{0}}{{\sigma }_{{{\text{P,H}}}}}}}} \approx {{10}^{3}}$ км значительно превышает толщину проводящего слоя ионосферы. Для оценки использовано значение периода волны $\tau \sim 10$ мин и выбрано значение проводимости ионосферы ${{10}^{{ - 4}}}\,\,{{{\text{См}}} \mathord{\left/ {\vphantom {{{\text{См}}} {\text{м}}}} \right. \kern-0em} {\text{м}}}$. Электромагнитное поле и скорость газа ${\mathbf{v}}$ в АГВ мало меняются поперек проводящего слоя ионосферы. На нижней границе проводящего слоя ионосферы вертикальная компонента электрического тока равна нулю. На верхней границе проводящего слоя ионосферы вертикальная компонента электрического тока ${{j}_{z}}$ определяется продольным током ${{j}_{\parallel }}$ по формуле ${{j}_{z}} = {{j}_{\parallel }}\sin I$. Продольный ток из северного полушария замыкается на сопряженную область ионосферы южного полушария. Интегрируя уравнение непрерывности тока в ионосфере (8) по высоте тонкого проводящего слоя $l$ ионосферы, получим:
(9)
$\begin{gathered} {{\nabla }_{h}} \cdot \left( {\hat {\Sigma }{{{\mathbf{E}}}_{h}} + {\mathbf{J}}} \right) + {{j}_{\parallel }}\sin I = 0, \\ {\mathbf{J}} = \hat {\Sigma }\left( {{{{\mathbf{v}}}_{1}} \times {\mathbf{B}}} \right), \\ \end{gathered} $(10)
$\hat {\Sigma } = \left( {\begin{array}{*{20}{c}} {\frac{{{{\Sigma }_{{\text{P}}}}}}{{{{{\sin }}^{2}}I}}}&{\frac{{{{\Sigma }_{{\text{H}}}}}}{{\sin I}}} \\ { - \frac{{{{\Sigma }_{{\text{H}}}}}}{{\sin I}}}&{{{\Sigma }_{{\text{P}}}}} \end{array}} \right),\,\,\,\,{{\Sigma }_{{{\text{P}},{\text{H}}}}} = \int\limits_{{{z}_{1}} - {l \mathord{\left/ {\vphantom {l 2}} \right. \kern-0em} 2}}^{{{z}_{1}} + {l \mathord{\left/ {\vphantom {l 2}} \right. \kern-0em} 2}} {{{\sigma }_{{{\text{P,H}}}}}\left( z \right)dz} .$(11)
$ - {{\nabla }_{h}} \cdot \left( {\hat {\Sigma }{{\nabla }_{h}}{{\varphi }_{1}}} \right) + {{\nabla }_{h}} \cdot {\mathbf{J}} + {{j}_{\parallel }}\sin I = 0.$(12)
$ - {{\nabla }_{h}}\left( {\hat {\Sigma }{{\nabla }_{h}}{{\varphi }_{1}}} \right) - {{j}_{\parallel }}\sin I = 0.$(13)
${{{\mathbf{j}}}_{\parallel }} = \frac{{{{{\mathbf{e}}}_{\parallel }}}}{{2\sin I}}{{\nabla }_{h}} \cdot {\mathbf{J}},\,\,\,\,{{{\mathbf{e}}}_{\parallel }} = \frac{{\mathbf{B}}}{{{{B}_{0}}}}.$(14)
${{\nabla }_{h}} \cdot \hat {\Sigma }{{\nabla }_{h}}{{\varphi }_{1}} = \frac{1}{2}{{\nabla }_{h}} \cdot {\mathbf{J}}.$(15)
$\begin{gathered} {\mathbf{j}}\left( {{\mathbf{r}},z} \right) = \left( {\hat {\Sigma }{\mathbf{E}} + {\mathbf{J}}} \right)\delta \left( {z - {{z}_{1}}} \right) + \\ + \,\,\frac{{{{{\mathbf{e}}}_{\parallel }}}}{{2\sin I}}{{\nabla }_{h}} \cdot {\mathbf{J}}\theta \left( {z - {{z}_{1}}} \right), \\ \end{gathered} $3. ИСТОЧНИКИ ЭЛЕКТРИЧЕСКОГО ТОКА В МОРСКОЙ СРЕДЕ И ИОНОСФЕРЕ, ФОРМИРУЕМЫЕ ВОЛНОЙ ЦУНАМИ
Волна цунами является поверхностной гравитационной волной в несжимаемой морской среде с длиной волны $\lambda \gg h$. Распространение волны цунами в линейном приближении, без учета ее дисперсии и силы Кориолиса описывается уравнениями [Pelinovsky, 2006]:
(17)
$\frac{{\partial \eta }}{{\partial t}} + {{\nabla }_{h}} \cdot \left( {h{{{\mathbf{V}}}_{h}}} \right) = 0,\,\,\,\,\frac{{\partial {{{\mathbf{V}}}_{h}}}}{{\partial t}} + g{{\nabla }_{h}}\eta = 0,$(18)
${{V}_{z}}\left( {{\mathbf{r}},z,t} \right) = \left( {1 + \frac{z}{h}} \right)\frac{{\partial \eta ({\mathbf{r}},t)}}{{\partial t}}.$(19)
${{\Delta }_{h}}\eta - \frac{1}{{{{a}^{2}}}}\frac{{{{\partial }^{2}}\eta }}{{\partial {{t}^{2}}}} = 0,\,\,\,\,a = \sqrt {gh} .$Это уравнение описывает распространение волны вдоль поверхности океана без дисперсии с постоянной скоростью $a$.
Рассмотрим распространение волны цунами, смещение поверхности в которой зависит только от расстояния вдоль направления ее распространения. Гребни волны ориентированы перпендикулярно направлению распространения волны. Пусть волна цунами распространяется вдоль оси $\xi $ под углом $\alpha $ к оси $x$, как показано на рис. 1. Все величины в волне зависят от координаты $\xi $ вдоль направления распространения волны. Величины в волне не зависят от $\varsigma $. В направлении поперек распространения ${\partial \mathord{\left/ {\vphantom {\partial {\partial \zeta }}} \right. \kern-0em} {\partial \zeta }} = 0$. Решение уравнения (19) имеет вид двух волн, распространяющихся вдоль оси $\xi $ без изменения формы в положительном и отрицательном направлениях со скоростями $ \pm \,a$. Рассмотрим уединенную волну цунами, движущуюся в положительном направлении оси $\xi $. Зависимость вертикального смещения поверхности океана в волне, выберем в виде:
(20)
$\eta \left( {\xi - at} \right) = \frac{{{{\eta }_{m}}}}{{{{{\operatorname{ch} }}^{2}}\left[ {{{\left( {\xi - at} \right)} \mathord{\left/ {\vphantom {{\left( {\xi - at} \right)} L}} \right. \kern-0em} L}} \right]}}.$(21)
$\begin{gathered} f\left( {\xi ,t} \right) = \\ = \frac{1}{{{{{\left( {2\pi } \right)}}^{2}}}}\int\limits_{ - \infty }^\infty {\exp \left( { - i\omega t} \right)d\omega \int\limits_{ - \infty }^\infty {\bar {f}\left( {k,\omega } \right)\exp \left( {ik\xi } \right)dk} } , \\ \bar {f}\left( {k,\omega } \right) = \int\limits_{ - \infty }^\infty {\exp \left( {i\omega t} \right)dt\int\limits_{ - \infty }^\infty {f\left( {\xi ,t} \right)\exp \left( { - ik\xi } \right)d\xi } } . \\ \end{gathered} $(22)
$\begin{gathered} \bar {\eta }\left( {k,\omega } \right) = 2\pi \bar {G}\left( k \right)\delta \left( {\omega - ka} \right), \\ \bar {G}\left( k \right) = \frac{{\pi {{\eta }_{m}}{{L}^{2}}k}}{{\operatorname{sh} \left( {{{\pi Lk} \mathord{\left/ {\vphantom {{\pi Lk} 2}} \right. \kern-0em} 2}} \right)}}. \\ \end{gathered} $Вертикальное смещение поверхности океана в крупномасштабной волне цунами генерирует АГВ в атмосфере. Уравнение, определяющее скорость газа ${\mathbf{v}}\left( {{\mathbf{r}},t} \right)$ в АГВ, распространяющейся в слоисто-неоднородной изотермической атмосфере, в линейном приближении и в отсутствие ветра, имеет вид [Nappo, 2002; Гершман, 1974]:
(23)
$\frac{{{{\partial }^{2}}{\mathbf{v}}}}{{\partial {{t}^{2}}}} = \nabla \left( {{{c}^{2}}\nabla \cdot {\mathbf{v}} + {\mathbf{g}} \cdot {\mathbf{v}}} \right) + \left( {\gamma - 1} \right){\mathbf{g}}\left( {\nabla \cdot {\mathbf{v}}} \right),$(24)
${{{v}}_{z}}\left( {{\mathbf{r}},0,t} \right) = {{V}_{z}}\left( {{\mathbf{r}},0,t} \right) = \frac{\partial }{{\partial t}}\eta \left( {{\mathbf{r}},t} \right).$(25)
$\begin{gathered} \frac{{{{d}^{2}}{{{\bar {v}}}_{z}}}}{{d{{z}^{2}}}} - \frac{1}{H}\frac{{d{{{\bar {v}}}_{z}}}}{{dz}} + \left[ {\frac{{{{\omega }^{2}}}}{{{{c}^{2}}}} + {{k}^{2}}\left( {\frac{{\omega _{g}^{2}}}{{{{\omega }^{2}}}} - 1} \right)} \right]{{{\bar {v}}}_{z}} = 0, \\ {{{\bar {v}}}_{\xi }} = \frac{{ik}}{{{{k}^{2}} - {{{{\omega }^{2}}} \mathord{\left/ {\vphantom {{{{\omega }^{2}}} {{{c}^{2}}}}} \right. \kern-0em} {{{c}^{2}}}}}}\left( {\frac{{d{{{\bar {v}}}_{z}}}}{{dz}} - \frac{{{{{\bar {v}}}_{z}}}}{{\gamma H}}} \right), \\ \end{gathered} $(26)
$\begin{gathered} {{{\bar {v}}}_{z}}\left( {k,z,\omega } \right) = {{{\bar {v}}}_{z}}\left( {k,0,\omega } \right)\exp \left( {iKz + \frac{z}{{2H}}} \right), \\ K = - {\text{sign}}\left( \omega \right)q(k,\omega ), \\ q = \sqrt {\frac{{{{\omega }^{2}}}}{{{{c}^{2}}}} + {{k}^{2}}\left( {\frac{{\omega _{g}^{2}}}{{{{\omega }^{2}}}} - 1} \right) - \frac{1}{{4{{H}^{2}}}}} . \\ \end{gathered} $(27)
${{\bar {v}}_{z}}\left( {{\mathbf{k}},0,\omega } \right) = - i\omega \bar {\eta }({\mathbf{k}},\omega ).$(28)
$\begin{gathered} {{v}_{z}}\left( {\xi ,z} \right) = \\ = \frac{a}{\pi }\operatorname{Im} \int\limits_0^\infty {\bar {G}\left( k \right)\exp \left[ {\frac{z}{{2H}} + ik\xi - i{{K}_{0}}\left( k \right)z} \right]} {\kern 1pt} kdk, \\ {{K}_{0}}\left( k \right) = \sqrt {\frac{{\omega _{g}^{2}}}{{{{a}^{2}}}} - \frac{1}{{4{{H}^{2}}}} - {{k}^{2}}\left( {1 - \frac{{{{a}^{2}}}}{{{{c}^{2}}}}} \right){\kern 1pt} } . \\ \end{gathered} $(29)
$\begin{gathered} {{v}_{\xi }}\left( {\xi ,z} \right) = - \frac{{a{{c}^{2}}}}{{\pi ({{c}^{2}} - {{a}^{2}})}} \times \\ \times \,\,\operatorname{Re} \int\limits_0^\infty {\bar {G}\left( k \right)\left[ {\Gamma + i{{K}_{0}}\left( k \right)} \right] \times } {\kern 1pt} \\ \times \,\,\exp \left[ {\frac{z}{{2H}} + ik\xi - i{{K}_{0}}\left( k \right)z} \right]dk, \\ \Gamma = {{\left( {2 - \gamma } \right)} \mathord{\left/ {\vphantom {{\left( {2 - \gamma } \right)} {2\gamma H.}}} \right. \kern-0em} {2\gamma H.}} \\ \end{gathered} $4. МАГНИТНОЕ ПОЛЕ ТОКА В МОРСКОЙ СРЕДЕ И В ИОНОСФЕРЕ
Рассмотрим характеристики магнитного поля тока, протекающего в морской среде. Величина скин-слоя в морской среде $\sqrt {{\tau \mathord{\left/ {\vphantom {\tau {2\pi {{\mu }_{0}}{{\sigma }_{w}}}}} \right. \kern-0em} {2\pi {{\mu }_{0}}{{\sigma }_{w}}}}} \approx 10$ км значительно превышает ее глубину. Для оценки использовано значение периода изменения поля $\tau \sim $ мин, совпадающее с периодом волны цунами, и выбрано значение проводимости ${{\sigma }_{w}} = 3\,\,{{{\text{См}}} \mathord{\left/ {\vphantom {{{\text{См}}} {\text{м}}}} \right. \kern-0em} {\text{м}}}$ морской среды. Следовательно, возмущение магнитного поля в морской среде мало меняется в зависимости от ее глубины. Рассмотрим компоненту ${{b}_{z}}$ геомагнитного возмущения. Из формулы (18) и неравенства $L \gg h$ получаем правую часть уравнения (4) в виде:
(30)
$\left( {{\mathbf{B}} \cdot \nabla } \right){{V}_{z}} \approx \frac{{{{B}_{{0z}}}}}{h}\frac{{\partial \eta }}{{\partial t}}.$(31)
$\Delta {{b}_{z}} - {{\mu }_{0}}{{\sigma }_{w}}\frac{{\partial {{b}_{z}}}}{{\partial t}} = - {{\mu }_{0}}{{\sigma }_{w}}\frac{{{{B}_{{0z}}}}}{h}\frac{{\partial \eta }}{{\partial t}}.$(32)
$\begin{gathered} {{\left\{ {{{b}_{z}}} \right\}}_{{z = 0}}} = 0, \\ {{\left\{ {\frac{{\partial {{b}_{z}}}}{{\partial z}}} \right\}}_{{z = 0}}} = {{\mu }_{0}}{{\Sigma }_{w}}\frac{{\partial {{b}_{z}}(z = 0)}}{{\partial t}} - {{\mu }_{0}}{{\Sigma }_{w}}\frac{{{{B}_{{0z}}}}}{h}\frac{{\partial \eta }}{{\partial t}}. \\ \end{gathered} $(33)
${{\bar {b}}_{z}} = - i{{B}_{z}}\omega \frac{{\bar {\eta }}}{h}\frac{{\exp \left( { - kz} \right)}}{{k{{c}_{w}} - i\omega }},\,\,\,\,{{c}_{w}} = \frac{2}{{{{\mu }_{0}}{{\Sigma }_{w}}}}.$(34)
$\begin{gathered} {{b}_{z}}\left( {\xi ,z} \right) = \frac{{2{{\eta }_{m}}B\sin I}}{{{{\pi }^{2}}h}} \times \\ \times \,\,\operatorname{Re} \left[ {\frac{{ia{{c}_{w}} - {{a}^{2}}}}{{c_{w}^{2} + {{a}^{2}}}}{{\psi }^{{\left( 1 \right)}}}\left( {\frac{1}{2} + \frac{{z - i\xi }}{{\pi L}}} \right)} \right], \\ \end{gathered} $Рассмотрим генерацию электрического тока и магнитного поля в ионосфере в результате распространения уединенной волны цунами вдоль оси $\xi $ под углом к магнитному меридиану, воспользовавшись выражением для тока (15) и уравнением для возмущения магнитного поля (16) в системе координат $\left( {\xi ,\zeta ,z} \right)$. Уравнение для вертикальной компоненты магнитного поля ${{b}_{z}}$ (16) в системе координат $\xi ,\zeta ,z$ имеет вид:
(35)
$\frac{{{{\partial }^{2}}{{b}_{z}}}}{{\partial {{\xi }^{2}}}} + \frac{{{{\partial }^{2}}{{b}_{z}}}}{{\partial {{z}^{2}}}} = - {{\mu }_{0}}\frac{{\partial {{j}_{\varsigma }}}}{{\partial \xi }}.$(36)
$\begin{gathered} {{J}_{\xi }} = {{v}_{{1\xi }}}B\left( {{{\Sigma }_{H}} - {{\Sigma }_{P}}\frac{{\sin \alpha \cos \alpha \cos I}}{{{\text{tg}}I}}} \right) + \\ + \,\,{{v}_{{1z}}}B\left( {{{\Sigma }_{H}}\frac{{\cos \alpha }}{{{\text{tg}}I}} - {{\Sigma }_{P}}\sin \alpha \cos I} \right), \\ {{J}_{\varsigma }} = {{v}_{{1\xi }}}B\left( {{{\Sigma }_{P}}\frac{{{{{\sin }}^{2}}\alpha + {{{\cos }}^{2}}\alpha {{{\sin }}^{2}}I}}{{\sin I}} + {{\Sigma }_{H}}\sin 2\alpha } \right) - \\ - \,\,{{v}_{{1z}}}B\left( {{{\Sigma }_{P}}\cos \alpha \cos I + {{\Sigma }_{H}}\frac{{{\text{sin}}\alpha }}{{{\text{tg}}I}}} \right). \\ \end{gathered} $Так как поверхностный ток протекает в тонком проводящем слое и поле мало меняется поперек этого слоя, то уравнение (35) можно проинтегрировать по высоте. В результате получаем граничные условия $z = {{z}_{1}}$. Граничное условие на тонкой по сравнению глубиной скин-слоя проводящей морской среде получаем из равенства (32) полагая $\eta = 0$. Так как волна движется вдоль оси $\xi $ с постоянной скоростью $a$, то заменим в (32) производную по времени ${\partial \mathord{\left/ {\vphantom {\partial {\partial t}}} \right. \kern-0em} {\partial t}} = - a{\partial \mathord{\left/ {\vphantom {\partial {\partial \xi }}} \right. \kern-0em} {\partial \xi }}$. Применяя преобразования Фурье по координате $\xi $ и времени $t$ к уравнению (35) в верхней ионосфере $z > {{z}_{1}}$, в атмосфере $0 < z < {{z}_{1}}$ и ниже проводящей морской среды $z < 0$, а также к граничным условиям при $z = {{z}_{1}}$ и $z = 0$, получим решение для Фурье-компоненты магнитного поля. Применяя к полученному решению обратное Фурье-преобразование (21), получим пространственное распределение возмущение магнитного поля в атмосфере и ионосфере. Вертикальная компонента возмущения магнитного поля в атмосфере $0 < z < {{z}_{1}}$ определяется интегралом:
(37)
$\begin{gathered} {{b}_{z}}\left( {\xi ,z} \right) = \frac{{{{\mu }_{0}}}}{{2\pi }}\operatorname{Re} \int\limits_0^\infty {D\left( {k,z} \right)\exp \left( {ik\xi - k{{z}_{1}}} \right)dk,} \\ D\left( {k,z} \right) = u\left( {k,z} \right)\left[ {{{{\bar {J}}}_{\varsigma }}\left( k \right) + S\left( {\alpha ,I} \right){{{\bar {J}}}_{\xi }}\left( k \right)} \right]. \\ \end{gathered} $(38)
$\begin{gathered} {{b}_{z}}\left( {\xi ,z} \right) = - \frac{{{{\mu }_{0}}}}{2}\frac{{\sin \alpha {\text{tg}}I}}{{{{{\cos }}^{2}}\alpha + {\text{t}}{{{\text{g}}}^{2}}I}} \times \\ \times \,\,\left\{ {{{J}_{\xi }}\left[ {\xi - \frac{{\left( {z - {{z}_{1}}} \right)\cos \alpha }}{{{\text{tg}}I}}} \right] - {{J}_{\xi }}\left( \xi \right)} \right\} + \\ + \,\,\frac{{{{\mu }_{0}}}}{{2\pi }}\operatorname{Re} \int\limits_0^\infty {D\left( {k,{{z}_{1}}} \right)\exp \left( {ik\xi - kz} \right)dk} . \\ \end{gathered} $Компонента ${{b}_{\varsigma }}$ определяется непосредственно из уравнения Максвелла ${{\left( {\nabla \times {\mathbf{b}}} \right)}_{z}} = {{\mu }_{0}}{{j}_{z}}$:
(39)
$b_{\varsigma }^{{}}\left( {\xi ,z} \right) = - \frac{{{{\mu }_{0}}}}{2}{{J}_{\xi }}\left[ {\xi - \frac{{\left( {z - {{z}_{1}}} \right)\cos \alpha }}{{{\text{tg}}I}}} \right]\theta \left( {z - {{z}_{1}}} \right).$Полученные формулы пространственного распределения магнитного поля совпадают с формулами, полученными в работе [Сорокин и др., 2019] для частного случая вертикального геомагнитного поля ($I = 90^\circ $) при распространении волны вдоль оси $x$ ($\alpha = 0$).
5. РЕЗУЛЬТАТЫ РАСЧЕТА ПРОСТРАНСТВЕННОГО РАСПРЕДЕЛЕНИЯ МАГНИТНОГО ПОЛЯ
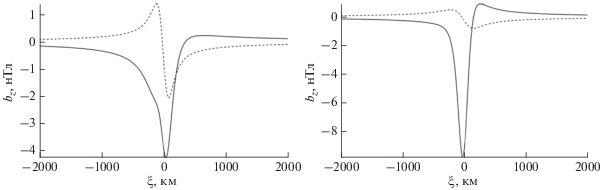
Расчет характеристик возмущения магнитного поля тока в морской среде проведен по формулам (34), а возмущения магнитного поля тока в ионосфере проведен по формулам (37) и (38), (39). Расчеты проведены с использованием пакета программ “Wolfram Mathematica”. Для расчетов выбраны следующие параметры: ${{\Sigma }_{{{\text{P}},{\text{H}}}}} = 10\,\,{{{\text{См}}} \mathord{\left/ {\vphantom {{{\text{См}}} {\text{м}}}} \right. \kern-0em} {\text{м}}}$, ${{z}_{1}} = 120\,\,{\text{км}}$, ${{B}_{0}} = 5 \times {{10}^{{ - 5}}}\,\,{\text{нТл}}$, $H = 8\,\,{\text{км}}$, $h = 1\,\,{\text{км}}$, $L = 100\,\,{\text{км}}$, ${{\eta }_{m}} = 0.5\,\,{\text{м}}$. Влияние электрического тока в ионосфере на формирование возмущения магнитного поля иллюстрирует рис. 3. На этом рисунке приведены результаты расчета амплитуды магнитного поля тока в морской среде (пунктирная линия) и амплитуды магнитного поля суммы токов, протекающих как в морской среде, так и в ионосфере (сплошная линия). На левой панели рис. 3 приведены результаты расчета амплитуд на поверхности морской среды, а на правой панели – в ионосфере. Из графиков следует, что на поверхности морской среды ток в ионосфере в дополнение к току в морской среде, значительно меняет форму сигнала и увеличивает его амплитуду в два раза по сравнению с полем тока в морской среде. В ионосфере амплитуда поля тока в морской среде убывает в два раза, в то время как амплитуда поля тока в ионосфере возрастает на порядок.
Рис. 3.
Зависимость амплитуды вертикальной компоненты магнитного поля ${{b}_{z}}$ от координаты $\xi $ для углов $I = 30^\circ ,\,\,\alpha = 45^\circ $. Левая панель – поверхность морской среды, правая панель – высота $800\;{\text{км}}$. Сплошная линия – магнитное поле суммы токов в морской среде и в ионосфере, пунктирная линия – магнитное поле тока в морской среде.
Проведен анализ зависимости амплитуды компонент магнитного поля токов от координаты $\xi $ на поверхности морской среды и в ионосфере для различных широт и направления распространения волны. Пример расчета приведен на рис. 4. Анализ показал, что пространственная форма возмущения магнитного поля на поверхности морской среды мало меняется в зависимости от угла наклонения геомагнитного поля и направления распространения волны относительно геомагнитного меридиана. Горизонтальная компонента магнитного поля меняет полярность в зависимости от координаты, в то время как вертикальная компонента остается однополярной. Амплитуда возмущения достигает 3–6 нТл. Амплитуда горизонтальной компоненты магнитного возмущения возрастает с ростом широты при распространении вдоль геомагнитного меридиана. Амплитуда и горизонтальный размер возмущения возрастает в зависимости от увеличения угла $\alpha $ для фиксированного угла наклонения геомагнитного поля. В ионосфере возмущение магнитного поля имеет три компоненты в отличие от двух компонент в морской среде. Из расчетов следует, что пространственные зависимости компонент магнитного поля являются знакопеременные импульсы с амплитудой 5–15 нТл и горизонтальным пространственным масштабом 200–500 км. С ростом угла наклонения геомагнитного поля амплитуда возмущения магнитного поля, как правило, возрастает как на поверхности морской среды, так и в магнитосфере. Амплитуда поля в ионосфере может существенно превосходить амплитуду на поверхности морской среды, а пространственная форма поля в ионосфере значительно отличается от соответствующей формы на поверхности морской среды. Это факт свидетельствует о принципиальной роли электрического тока в ионосфере в формировании магнитного поля волной цунами. На рисунке 5 приведена зависимость максимального модуля магнитного поля от угла наклона $I$ для различных углов распространения волны относительно магнитного меридиана. Расчеты показали, что при распространении вдоль магнитного меридиана модуль поля возрастает с увеличением угла наклона, а при распространении в широтном направлении с увеличением угла наклона модуль поля убывает. При распространении волны под углом 45° модуль поля имеет минимум для угла наклона 30°.
Рис. 4.
Результат расчета амплитуды компонент магнитного поля токов от координаты $\xi $. Левая панель – поверхность морской среды $\left( {z = 0} \right)$. Обозначено: сплошная линия – компонента ${{b}_{\xi }}$ вдоль направления распространения волны; пунктирная линия – вертикальная компонента ${{b}_{z}}$. Правая панель – ионосфера $\left( {z \geqslant {{z}_{1}}} \right)$. Обозначено: сплошная линия – компонента ${{b}_{\xi }}$ вдоль направления распространения волны; штриховая линия – компонента ${{b}_{\varsigma }}$ перпендикулярно направлению распространения волны в горизонтальной плоскости, пунктирная линия – вертикальная компонента ${{b}_{z}}$. Выбраны значения $I = 45^\circ $, $\alpha = 45^\circ $.
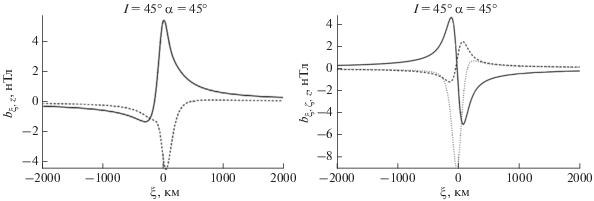
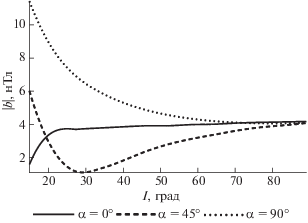
Рис. 5.
Зависимость максимума амплитуды магнитного поля токов в ионосфере от угла наклона $I$ геомагнитного поля для различных углов $\alpha $. Сплошная линия – $\alpha = 0$, штриховая линия – $\alpha = 45^\circ $, пунктирная линия – $\alpha = 90^\circ $.
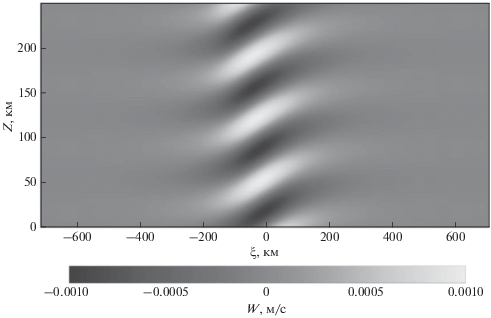
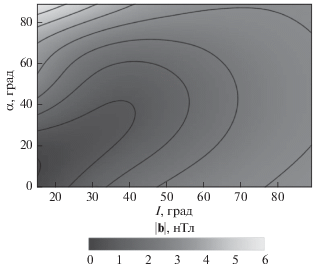
Для анализа характеристик магнитного поля в ионосфере проведен расчет пространственного распределения максимального модуля магнитного поля в вертикальной плоскости $\left( {\xi ,z} \right)$. Результаты расчета приведены на рис. 6. Из расчетов следует, что возмущение магнитного поля локализуется в ионосфере в окрестности продольного тока. Такой характер пространственного распределения магнитного поля определяется убыванием с высотой поля поверхностного тока, протекающего в проводящем слое ионосферы, в то время как влияние продольного тока на формирование магнитного поля с высотой возрастает. Эту особенность иллюстрирует рис. 7, на котором приведены результаты расчета высотной зависимости максимума модуля магнитного поля в ионосфере $z > {{z}_{1}}$. Из расчетов следует, что величина магнитного поля тока, текущего в морской среде, стремится к нулю с высотой. Величина магнитного поля суммы токов, протекающих в морской среде и в ионосфере, стремится к постоянному значению с ростом высоты. Такой характер высотной зависимости магнитного поля в ионосфере обусловлен наличием продольного тока, текущего в сопряженную область ионосферы. Распределение максимального модуля магнитного поля в ионосфере, рассчитанное в плоскости $\left( {I,\alpha } \right)$, приведено на рис. 8. Расчеты показали, что магнитное поле с наибольшей амплитудой формируется в интервале углов (0–50)°. Можно ожидать, что наибольшие амплитуды поля будут наблюдаться в низких и средних широтах для волн, распространяющихся преимущественно в меридиональном направлении.
Рис. 6.
Пространственное распределение максимума модуля магнитного поля в вертикальной плоскости $\left( {\xi ,z} \right)$ в ионосфере. Выбраны следующие значения: $I = 45^\circ ,\,\,\alpha = 0$.
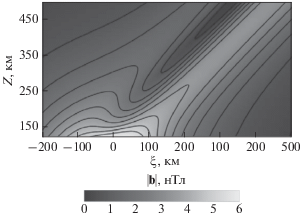
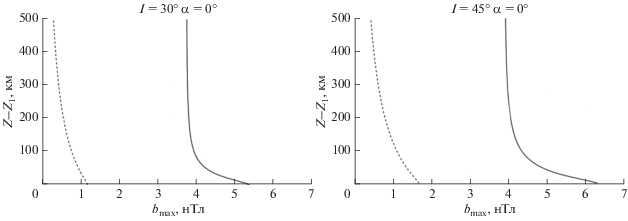
Рис. 7.
Зависимость максимальной амплитуды магнитного поля от высоты $z - {{z}_{1}}$ в ионосфере при распространении волны вдоль магнитного меридиана. Левая панель – $I = 30^\circ $, правая панель – $I = 45^\circ $. Обозначено: сплошная линия – магнитное поле суммы токов в морской среде и в ионосфере; пунктирная линия – магнитное поле тока в морской среде.
6. ЗАКЛЮЧЕНИЕ
Волна цунами приводит к движению проводящую морскую среду и ионосферу в результате генерации акустико-гравитационной волны (АГВ). Их движение в геомагнитном поле сопровождается генерацией электрического тока и, следовательно, магнитного поля. Электрический ток в ионосфере замыкается на сопряженную ионосферу с помощью продольного тока. Наблюдаемое магнитное поле представляет собой сумму полей электрических токов в морской среде и в ионосфере. В результате экспоненциального роста амплитуды АГВ с высотой величина электрического тока в ионосфере может быть сопоставимой или больше величины тока в морской среде несмотря на то, что проводимость ионосферы значительно меньше проводимости морской среды.
Расчеты характеристик возмущения магнитного поля проведены для уединенной волны цунами, распространяющейся под углом к магнитному меридиану в низких и средних широтах. Наличие электрического тока в ионосфере значительно меняет характеристики возмущения геомагнитного поля, генерируемого волной цунами. Меняется высотная зависимость амплитуды возмущения в слое Земля–ионосфера. При этом в ионосфере возникают поперечные компоненты магнитного и электрического полей. Пространственная форма возмущения магнитного поля на поверхности морской среды мало меняется в зависимости от угла наклонения геомагнитного поля и направления распространения волны относительно геомагнитного меридиана. Амплитуда возмущения достигает 3–6 нТл. Возмущение магнитного поля в ионосфере имеет три компоненты в отличие от двух компонент в морской среде. Пространственные зависимости компонент магнитного поля являются знакопеременными с амплитудой 5–15 нТл и горизонтальным пространственным масштабом 200–500 км. С ростом угла наклонения геомагнитного поля амплитуда возмущения, как правило, возрастает как на поверхности морской среды, так и в ионосфере. Амплитуда возмущений в ионосфере может существенно превосходить амплитуду на поверхности морской среды, а пространственная форма возмущений в ионосфере значительно отличается от соответствующей формы на поверхности морской среды. Это факт свидетельствует о принципиальной роли электрического тока в ионосфере в генерации возмущения магнитного поля волной цунами.
Величина магнитного поля в ионосфере тока, текущего в морской среде, стремится к нулю с высотой. Величина магнитного поля суммы токов, протекающих в морской среде и в ионосфере, стремится к постоянному значению с ростом высоты. Такой характер высотной зависимости магнитного поля в ионосфере обусловлен наличием продольного тока, текущего в сопряженную область ионосферы. Возмущение магнитного поля в ионосфере локализуется в окрестности продольного тока. Амплитуда магнитного поля и продольного тока могут достигать значений порядка 10 нТл и ${{10}^{{ - 8}}}\,\,{{\text{А}} \mathord{\left/ {\vphantom {{\text{А}} {{{{\text{м}}}^{{\text{2}}}}}}} \right. \kern-0em} {{{{\text{м}}}^{{\text{2}}}}}}$, а амплитуда электрического поля достигает величины 10 мВ/м. Регистрация электромагнитных возмущений в ионосфере может быть использована для мониторинга волны цунами спутниковыми методами в низких и средних широтах.
Список литературы
– Альвен Г., Фельтхаммар К.Г. Космическая электродинамика. М.: Мир. 260 с. 1967.
– Гершман Б.Н. Динамика ионосферной плазмы. М.: Наука. 256 с. 1974.
– Градштейн И.С., Рыжик И.М. Таблицы интегралов, сумм, рядов и произведений. М: Гос. Изд. Физ.-мат. Лит. 1108 с. 1963.
– Сорокин В.М., Ященко А.К., Сурков В.В. Генерация геомагнитных возмущений в ионосфере волной цунами // Геомагнетизм и аэрономия. Т. 59. № 2. С. 236–248. 2019.
– Artru J., Ducic V., Kanamori H., Lognonné P., Murakami M. Ionospheric detection of gravity waves induced by tsunamis // Geophys. J. Int. V. 160. P. 840–848. 2005.
– Bladel J. van. Electromagnetic fields. 2nd ed. / IEEE Press series on electromagnetic wave theory. Chichester: Hoboken N.J., Wiley-Interscience. 1155 p. https://doi.org/10.1002/047012458X. 2007.
– Coïsson P., Lognonné P., Walwer D., Rolland L.M. First tsunami gravity wave detection in ionospheric radio occultation data: Tsunami detection using radio occultation// Earth and Space Science. V. 2. P. 125–133. 2015.
– Galvan D.A., Komjathy A., Hickey M.P., Stephens P., Snively J., Tony Song Y., Butala M.D., Mannucci A.J. Ionospheric signatures of Tohoku-Oki tsunami of March 11, 2011: Model comparisons near the epicenter: Tsunami ionospheric signatures near epicenter // Radio Sci. V. 47. № 4. 2012.
– Kopytenko Yu.A., Ismaguilov V.S., Hayakawa M. Investigation of ULF magnetic field variations induced by tsunami in a coastal zone // Proc. 10th Intl. Conf. “Problems of Geocosmos”, St.-Petersburg. P. 104–108. 2014.
– Lyons L.R., Williams D.J. Quantitative aspects of magnetospheric physics. D. Reidel Pub. Co.; Sold and distributed in the U.S.A. and Canada by Kluwer Academic Publishers, Dordrecht; Boston Hingham, MA, U.S.A. 1984.
– Manoj C., Maus S. Observation of magnetic fields generated by tsunamis // EOS. V. 92. № 2. P. 13–14. 2011.
– Nappo C.J. An introduction to atmospheric gravity waves. San Diego: Academic Press, 276 p. 2002.
– Pelinovsky E. Hydrodynamics of tsunami waves / Waves in Geophysical Fluids. Eds. Grue J., Trulsen K. Vienna: Springer Vienna. P. 1–48. 2006.
– Peltier W.R., Hines C.O. On the possible detection of tsunamis by a monitoring of the ionosphere // J. Geophys. Res. V. 81. P. 1995–2000. 1976.
– Ratcliffe J.A. Physics of the upper atmosphere. New York: Academic Press, 586 p.1960.
– Rolland L.M., Occhipinti G., Lognonné, P., Loevenbruck A. Ionospheric gravity waves detected offshore Hawaii after tsunamis: Tsunamis detection from the ionosphere // Geophys. Res. Lett. V. 37. № 17. 2010.
– Sorokin V.M., Yaschenko A.K., Surkov V.V. Geomagnetic field perturbations resulted from tsunami wave impact on the ionosphere // Progress in electromagnetics research B. V. 85. P. 49–63. 2019.
– Sugioka H., Hamano Y., Baba K., Kasaya T., Tada N., Suetsugu D. Tsunami: Ocean dynamo generator // Sci. Rep. (4:3596) 2014.https://doi.org/10.1038/srep03596
–Tatehata H., Ichihara H., Hamano Y. Tsunami-induced magnetic fields detected at Chichijima Island before the arrival of the 2011 Tohoku earthquake tsunami // Earth Planets Space. 67:185. 2015.https://doi.org/10.1186/s40623-015-0347-3
– Toh H., Satake K., Hamano Y., Fujii Y., Goto T. Tsunami signals from the 2006 and 2007 Kuril earthquakes detected at a seafloor geomagnetic observatory // J. Geophys. Res. V. 116. № B2. 2011.
– Wang B., Liu H. Space-time behaviour of magnetic anomalies induced by tsunami waves in open ocean // Proc. Roy. Soc. A. V. 469. № 257. 2013.
– Zhang L., Utada H., Shimizu H., Baba K., Maeda T. Three-dimensional simulation of the electromagnetic fields induced by the 2011 Tohoku tsunami: Simulation of the EM fields of tsunami // J. Geophys. Res. Sol. Ea. V. 119. № 1. P. 150–168. 2014.
Дополнительные материалы отсутствуют.
Инструменты
Геомагнетизм и аэрономия