Геомагнетизм и аэрономия, 2021, T. 61, № 4, стр. 499-505
Оценка величины проникшего в ионосферу тропосферного электрического поля, связанного с Африканской зоной грозовой активности
В. В. Хегай 1, *, Л. П. Корсунова 1, **, А. Д. Легенька 1, ***
1 Институт земного магнетизма, ионосферы и распространения радиоволн
им. Н.В. Пушкова РАН (ИЗМИРАН)
г. Москва, г. Троицк, Россия
* E-mail: hegai@izmiran.ru
** E-mail: lpkors@rambler.ru
*** E-mail: leg@izmiran.ru
Поступила в редакцию 17.11.2020
После доработки 14.01.2021
Принята к публикации 28.01.2021
Аннотация
На основе расчетов исследовано проникновение в ночную ионосферу электрических полей в Африканской зоне грозовой активности. Эти поля обусловлены как кулоновскими зарядами грозовых облаков, так и электрическим током, генерируемым ими как элементами глобальной электрической цепи в рассматриваемой зоне. В первом случае электрическое поле создается суммой кулоновских полей от каждого из 600 грозовых облаков зоны, а во втором случае – направленным вверх усредненным суммарным током, величиной в 600 А (по 1 А от каждого грозового облака, когда оно рассматривается как элементарный квазистационарный точечный биполярный источник тока в рамках модели глобальной электрической цепи в Африканской зоне грозовой активности). Получено, что тропосферные кулоновские заряды создают в ионосфере незначительные электрические поля, которые по своей величине не превосходят 1 мкВ/м. Однако электрическое поле в ионосфере за счет суммарного тока от грозовых облаков в Африканской зоне грозовой активности может достигать на ионосферных высотах ~0.2 мВ/м в ночных условиях зимой в период низкой солнечной активности.
1. ВВЕДЕНИЕ
Грозовое облако (ГО) является мощным источником кулоновского электрического поля и молниевых разрядов в приземной атмосфере, которые обеспечивают поддержание отрицательного электрического заряда Земли и глобального атмосферного электрического поля (см. работу [Имянитов и Шифрин, 1962]). Простейшая электрическая модель грозового облака представляет его в виде двух объемных разноименных кулоновских зарядов, расположенных по вертикали друг под другом, как это принято в исследованиях [Chalmers, 1967; Френкель, 2007]. Обычно вверху находится положительный заряд, а внизу – отрицательный. В типичном грозовом облаке центр отрицательного заряда расположен на высотах 2–4 км, а центр положительного заряда – на высотах 8–12 км согласно работам [Uman, 1969; Weisberg, 1976], но в так называемом “гигантском” грозовом облаке (ГГО) центр положительного заряда может находиться на высоте ~18 км. Абсолютная величина электрических зарядов ГО оценивается для обычного ГО от 5 до 25 Кл, а в ГГО она может превышать 50 Кл, что следует из работ [Malan, 1963; Kazemir, 1965].
На основе модельных вычислений в работе [Park and Dejnakarintra, 1973] было показано, что электрическое поле кулоновских зарядов ГГО при определенных условиях в заметной мере проникает в ночную ионосферу высоких и средних широт и максимальная величина проникшего поля может составлять ~0.65 мВ/м. Однако, в работе [Park and Dejnakarintra, 1973] пренебрегалось ионосферной проводимостью Педерсена выше 150 км. При ее учете величина поля от ГГО на ионосферных уровнях получается более чем в 2 раза меньше, как это показано в работе [Kim and Hegai, 2015].
Одна из самых активных зон грозовой активности Земли расположена в тропической области Африки. В период зимы в северном полушарии она расположена в географическом широтно-долготном секторе приблизительно от 10° до 30° S и от 10° до 50° E и лежит достаточно далеко к югу от магнитного экватора (магнитное наклонение поля I = 0), см., в частности, работы [Brooks, 1925; Crichlow et al., 1971] и рис. 8 работы [Kartalev et al., 2006]. В этой зоне одномоментно может находиться около 600 грозовых облаков. Представляет интерес исследовать вопрос о проникновении электрического поля такого массива грозовых облаков в ионосферу. Этот вопрос ранее был рассмотрен в рамках общей модели глобальной электрической цепи (ГЭЦ) в работе [Hays and Roble, 1979]. Авторы получили, что суммарный ток, текущий вверх от всех грозовых облаков в Африканской зоне грозовой активности (АЗГА, далее всюду – суммарный ток АЗГА), вызывает появление в ионосфере поперечного относительно геомагнитного поля электростатического электрического поля и его максимальная напряженность может достигать ~0.3 мВ/м. Исходным (и ключевым) моментом этой модели является представление тока грозовых облаков совокупностью усредненных единичных квазистационарных источников вертикального электрического тока, определенным образом распределенных в атмосфере вокруг Земли. При этом модель вычисляет не сумму электрических полей на ионосферных высотах от всех отдельных токовых источников, а сглаженную усредненную картину суммарного тока АЗГА. Аналогичный подход используется, в частности, и в более поздней работе [Making and Ogawa, 1984], см. также статью [Davydenko et al., 2004].
В настоящей работе выполнен расчет распределения электрического поля на ионосферных высотах, обусловленного: а) системой кулоновских зарядов всех 600 грозовых облаков, расположенных в АЗГА (в виде суммы вкладов в поле от каждого ГО), а также б) суммарным током АЗГА – усредненным модельным представлением текущего вверх суммарного тока величиной в 600 А (по 1 А от одного грозового облака, когда каждое грозовое облако рассматриваетcя как элементарный квазистационарный точечный биполярный источник тока в рамках модели ГЭЦ в области АЗГА) для 600 грозовых облаков, одновременно находящихся в области АЗГА. При этом никакие нестационарные процессы в работе не рассматриваются, а исследование проводится в рамках электро- и токостатики (см., в частности, работу [Мареев, 2010]).
2. ПОСТАНОВКА ЗАДАЧИ
Для определения электрического поля, создаваемого в ионосфере кулоновской системой электрических зарядов массива из 600 грозовых облаков, расположенных в Африканской зоне грозовой активности, мы сначала определим электрическое поле за счет одного ГО, а затем искомое поле найдем как векторную сумму этих полей от всех облаков. При этом будем считать, что все грозовые облака имеют одинаковую диполярную электрическую структуру и равномерно распределены в области их расположения, которую будем аппроксимировать прямоугольником с размерами 2000 км и 3000 км соответственно в меридиональном и зональном направлениях с центром в географической точке (20° S, 25° E), что соответствует зимнему сезону.
В качестве системы координат для вычисления электрического поля над отдельным ГО естественно принять цилиндрическую систему координат (r, φ, z), начало которой поместим на поверхности Земли в точку пересечения ее с вертикальной электрической осью ГО, вдоль которой расположены центры положительного и отрицательного зарядов грозового облака. Ось z направим вертикально вверх. В стационарных условиях распределение электростатического поля над ГО до высоты 90 км может быть определено из уравнения непрерывности для электрического тока
при этом где J – вектор плотности электрического тока; σ – электрическая проводимость атмосферы; E – вектор напряженности электрического поля; φ – электростатический потенциал.Выше 90 км, в силу значительно более высокой величины проводимости ионосферы вдоль геомагнитных линий по сравнению с величиной проводимости поперек геомагнитных линий, геомагнитные силовые линии для электрических полей с характерными поперечными относительно геомагнитного поля размерами более нескольких км можно считать эквипотенциальными (см., например, статью [Farley, 1960]). Таким образом, электростатический потенциал выше уровня 90 км по высоте полностью определяется распределением потенциала на высоте 90 км. Далее мы принимаем, что геомагнитное поле B является вертикальным. Учет наклона магнитного поля со срединной точкой зоны АЗГА с географическими координатами (20° S, 25° E) в соответствии с работами [Denisenko et al., 2018; Хегай, 2020], может быть выполнен умножением полученной величины поля на фактор |sin I|, где I – величина магнитного наклонения в точке (20° S, 25° E), равная примерно – 60°, и |sin I| ≅ 0.866. Более того, даже в самой северной точке границы зоны АЗГА (наиболее близкой к магнитному экватору), географические координаты которой в принятой нами модели определяются как 8.76° S и 25° E, величина I ≅ –44°, тогда |sin I| ≅ 0.7. Из рисунка 8 работы [Kartalev et al., 2006], на котором зеленой линией показан магнитный экватор, где I = 0 и зона АЗГА для рассматриваемых нами зимних условий, хорошо видно, что вся зона АЗГА лежит достаточно далеко от магнитного экватора. Таким образом, применение модели расчета в приближении вертикального геомагнитного поля с указанной последующей коррекцией в данном случае можно считать вполне правомерным (более подробно см. работу [Хегай, 2020]).
Полагая, что проводимость атмосферы σ изотропна и зависит только от z, можно получить из уравнения (1) с учетом азимутальной симметрии задачи следующее уравнение для потенциала φ:
(3)
${{{{\partial }^{2}}\varphi } \mathord{\left/ {\vphantom {{{{\partial }^{2}}\varphi } {\partial {{r}^{2}}}}} \right. \kern-0em} {\partial {{r}^{2}}}} + ({1 \mathord{\left/ {\vphantom {1 r}} \right. \kern-0em} r}){{\partial \varphi } \mathord{\left/ {\vphantom {{\partial \varphi } {\partial r}}} \right. \kern-0em} {\partial r}} + ({1 \mathord{\left/ {\vphantom {1 \sigma }} \right. \kern-0em} \sigma }){\partial \mathord{\left/ {\vphantom {\partial {\partial z}}} \right. \kern-0em} {\partial z}}({{\sigma {\kern 1pt} \partial \varphi } \mathord{\left/ {\vphantom {{\sigma {\kern 1pt} \partial \varphi } {\partial z}}} \right. \kern-0em} {\partial z}}) = 0.$(4)
${{\sigma }_{i}} = {{s}_{i}}{\text{exp}}\left\{ {{{\left( {z - {{z}_{{i{\kern 1pt} - {\kern 1pt} 1}}}} \right)} \mathord{\left/ {\vphantom {{\left( {z - {{z}_{{i{\kern 1pt} - {\kern 1pt} 1}}}} \right)} {{{h}_{i}}}}} \right. \kern-0em} {{{h}_{i}}}}} \right\},$(5)
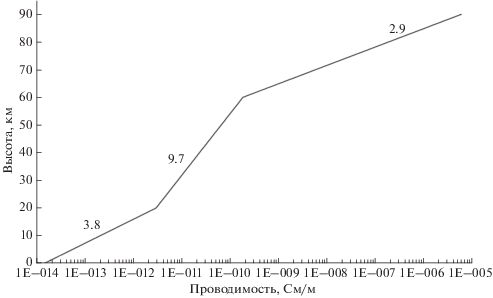
$\begin{gathered} {{\varphi }_{i}}({{z}_{{i{\kern 1pt} - {\kern 1pt} {\text{1}}}}} \leqslant z \leqslant {{z}_{i}}) = \int\limits_0^\infty {{{J}_{{\text{0}}}}(kr)} \text{[}{{A}_{i}}(k){\text{exp}}\{ {{a}_{i}}(z - {{z}_{{i{\kern 1pt} - {\kern 1pt} {\text{1}}}}})\} + \\ + \,\,{{B}_{i}}(k){\kern 1pt} {\text{exp}}\{ {{b}_{i}}(z - {{z}_{{i{\kern 1pt} - {\kern 1pt} {\text{1}}}}})\} ]{\kern 1pt} dk, \\ \end{gathered} $Рис. 1.
Принятый высотный профиль атмосферной проводимости. Цифры у профиля дают значения характерного масштаба экспоненциально изменяющейся проводимости для каждой секции в км.
Эквипотенциальность геомагнитных силовых линий выше 90 км позволяет рассматривать ионосферу как тонкий проводящий слой с интегральной вдоль геомагнитной силовой линии проводимостью Педерсена Σp. При этом уравнение непрерывности для тока на высоте z = 90 км можно записать в следующем виде (см. также работы [Denisenko et al., 2008; Hegai et al., 2015; Хегай, 2020]):
(6)
${{\sigma \partial \varphi } \mathord{\left/ {\vphantom {{\sigma \partial \varphi } {\partial z}}} \right. \kern-0em} {\partial z}} = {{\Sigma }_{p}}[{{{{\partial }^{2}}\varphi } \mathord{\left/ {\vphantom {{{{\partial }^{2}}\varphi } {\partial {{r}^{2}}}}} \right. \kern-0em} {\partial {{r}^{2}}}} + ({1 \mathord{\left/ {\vphantom {1 r}} \right. \kern-0em} r})({{\partial \varphi } \mathord{\left/ {\vphantom {{\partial \varphi } {\partial r)}}} \right. \kern-0em} {\partial r)}}].$Для вычисления векторной суммы электрических полей, создаваемых на ионосферных высотах z ≥ 90 км кулоновскими зарядами всех 600 грозовых облаков, используем декартову систему координат (х, у, z'), начало которой поместим на поверхности Земли в центр прямоугольника (20° S, 25° E), а оси х, у, z' направим соответственно на восток, на север и вертикально вверх.
Чтобы найти распределение электрического поля в ионосфере (z ≥ 90 км), которое обусловлено грозовыми облаками в зоне АЗГА как генераторами квазистационарного тока в качестве составляющих элементов глобальной электрической цепи (ГЭЦ), мы примем, что средний эффективный электрический ток вверх, приходящийся на одно ГО составляет 1 А, как это указано в работах [Muhleisen, 1976; Мареев, 2010]. Тогда 600 грозовых облаков в области АЗГА обеспечивают направленный вверх ток величиной 600 А суммарно. Выберем полярную систему координат (r', φ', z"), начало которой расположено на поверхности Земли в точке (20° S, 25° E), а ось z" направлена вертикально вверх. Далее мы будем полагать, что плотность направленного вверх суммарного вертикального тока на некоторой высоте над системой грозовых облаков АЗГА имеет в зависимости от r ' гауссоподобное распределение следующего вида:
(7)
$I(r{\kern 1pt} ') = {{I}_{0}}{\kern 1pt} {\text{exp}}{\kern 1pt} {\kern 1pt} [ - {\text{ln}}10{{({{r{\kern 1pt} '} \mathord{\left/ {\vphantom {{r{\kern 1pt} '} {{{R}_{0}}}}} \right. \kern-0em} {{{R}_{0}}}})}^{2}}],$Для определения электростатического потенциала над одним ГО из уравнения (5) наложим следующие граничные условия (см. также работу [Kim and Hegai, 2015]):
1. φ = (Q/4πε0)[(r 2 + (zb – hp)2)–1/2 – (r 2 + (zb – – hn)2)–1/2] при z = zb,
2. φ – равномерно непрерывен при z = 20 и 60 км,
3. σ∂φ/∂z = Σp[∂2φ/∂r2 + (1/r)(∂φ/∂r)] при z = = 90 км,
где Q – абсолютная величина кулоновских зарядов ГО; ε0 – диэлектрическая проницаемость вакуума; zb – высота горизонтальной плоскости, расположенной непосредственно над ГО; hp и hn – высоты центров положительного и отрицательного объемных зарядов ГО соответственно. Первое граничное условие вытекает из принятой электрической модели грозового облака. Мы полагаем также, что ГО не влияет на проводимость атмосферы на высотах z ≥ zb.
4. РЕЗУЛЬТАТЫ И ОБСУЖДЕНИЕ
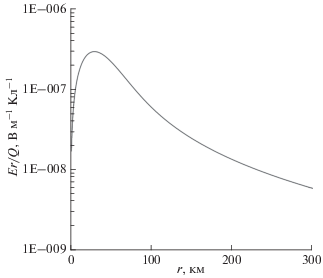
Рисунок 2 показывает горизонтальную компоненту электрического поля Er = –∂φ/∂r, нормированную на Q, в зависимости от расстояния r в ночной ионосфере на высотах z ≥ 90 км для типичного ГО (hn = 3 км, hp = 8 км). Мы приняли, что zb = 10 км, а Σp = 0.4 См (ночь, условия низкой солнечной активности). Как следует из рисунка, максимальное значение Er при Q = 10 Кл в ночной ионосфере составляет ~0.3 мкВ/м примерно в 30 км от электрической оси ГО.
Рис. 2.
Зависимость от r нормированной на Q горизонтальной компоненты электрического поля Er, создаваемого в ночной ионосфере на высотах z ≥ 90 км кулоновскими зарядами типичного ГО.
Так как Σp является одним из ключевых параметров при расчетах величины электрического поля в ионосфере и ее увеличение уменьшает эффективность проникновения электростатического поля от поверхности земли или уровня тропосферы в ионосферу при прочих равных условиях (см. работы [Denisenko et al., 2008, 2018; Хегай, 2020]), остановимся на этом вопросе подробнее. В нашей постановке эта величина получается как сумма проводимостей, вычисленных для центральной точки зоны АЗГА и магнитосопряженной с ней точки, т.е. Σp = ΣP + $\Sigma _{P}^{*},$ где ΣP – интегральная проводимость Педерсена для географических координат точки (20° S, 25° E), а $\Sigma _{P}^{*}$ – интегральная проводимость Педерсена для магнитосопряженной точки. Расчет Σp в соответствии моделями ионосферы IRI-2016 (https://ccmc.gsfc.nasa.gov/ modelweb/models/iri2016_vitmo.php) и нейтральной атмосферы NRLMSIS-00 (https://modelweb. gsfc.nasa.gov/atmos/nrlmsise00.html) показывает, что для условий низкой солнечной активности 2008 г. величина Σp(22.12.2008 г., 00 UT) ≅ 0.27 См (декабрь), а Σp(22.07.2008 г., 00 UT) ≅ 0.56 См (июль), тогда его средняя величина Σp ≅ 0.4 См. Отметим здесь, что проникновение квазистатического поля в ионосферу наиболее эффективно ночью в периоды низкой солнечной активности (см. работы [Hegai et al., 2015; Denisenko et al., 2018]).
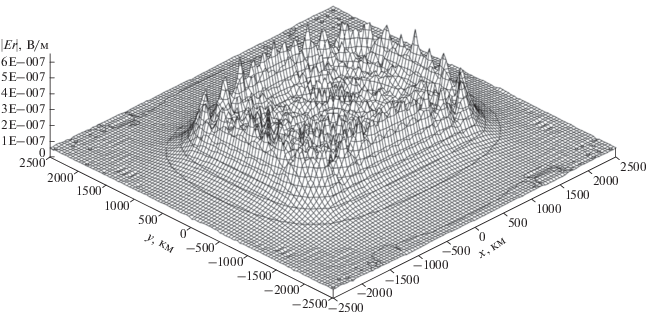
Распределение напряженности горизонтального электрического поля, создаваемого в ночной ионосфере всеми 600 грозовыми облаками при Q = 10 Кл, иллюстрирует рис. 3. Видно, что величина поля над внутренней частью зоны достигает всего 0.2 мкВ/м, что объясняется взаимной компенсацией полей от разных облаков. Поле максимально над границей зоны, где электрические поля от отдельных грозовых облаков складываются, образуя своеобразную корону, но по своей величине суммарное поле не превосходит 0.65 мкВ/м. Таким образом, кулоновские заряды всех 600 грозовых облаков АЗГА создают в ночной ионосфере незначительное электростатическое поле, величина которого менее 1 мкВ/м в любой точке над зоной (даже для вертикальных геомагнитных линий).
Рис. 3.
Распределение модуля напряженности горизонтального электрического поля (|Er| = [Ex2 + Ey2]1/2) , создаваемого в ночной ионосфере кулоновскими зарядами всех 600 грозовых облаков АЗГА при Q = 10 Кл. Ось х направлена на восток, а ось у – на север.
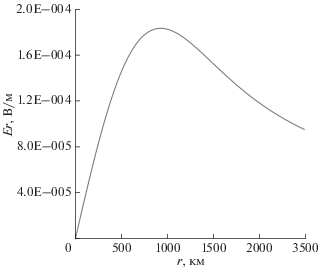
Для расчета распределения электрического поля Er в ночной ионосфере, которое обусловлено суммарным током АЗГА, соотношение (7) представляет собой нижнее граничное условие задачи при z = zb, а остальные граничные условия остаются такими же, как в задаче для одного грозового облака. На рис. 4 показаны результаты расчета Er при Σp = 0.4 См. Максимальное значение поля достигается на расстоянии ~950 км от центра зоны и составляет ≈0.18 мВ/м.
Рис. 4.
Распределение электрического поля Er в ночной ионосфере над АЗГА, которое обусловлено суммарным электрическим током АЗГА.
Расчетная величина Er здесь получилась в предположении вертикальных силовых линий магнитного поля и значении Σp = 0.4 См, однако учет наклона магнитного поля в точке (20° S, 25° E) в соответствии с работами [Denisenko et al., 2018; Хегай, 2020], требует умножения полученной величины поля на фактор |sin I|, где I – величина угла магнитного наклонения в точке (20° S, 25° E), равная примерно – 60°, и |sin I| ≅ 0.866. Таким образом, получаем Er max ≅ 0.18 мВ/м × 0.866 ≈ ≈ 0.16 мВ/м. Это достаточно близко к полученным в работе [Hays and Roble, 1979] результатам, согласно которой максимальная величина горизонтальной компоненты поля над АЗГА может составить 0.3 мВ/м.
С другой стороны, в работе [Denisenko et al., 2019], посвященной математическому моделированию электрического поля в ионосфере в рамках ГЭЦ, получено, что для условий высокой солнечной активности в июле горизонтальное поле в ионосфере нигде не превосходит 10 мкВ/м для 19 UT. Полагая положение зоны АЗГА неизменным, получим (в соответствии с моделью IRI-2016) для 1989 г. высокой солнечной активности Σp(22.07.1989 г., 19 UT) ≅ 6.55 См (июль). Тогда, по нашим расчетам, в зоне АЗГА для этого момента времени UT с учетом наклона геомагнитных линий Er max ≅ 0.011 мВ/м × 0.866 ≈ ≈ 0.0095 мВ/м = 9.5 мкВ/м, что согласуется с представленным в работе [Denisenko et al., 2019] результатом. Величина поля в зоне АЗГА, по-видимому, в этом случае будет еще меньше, так как для летнего сезона зона АЗГА лежит значительно ближе к магнитному экватору (см. рис. 10 работы [Kartalev et al., 2006]).
Для ночных условий зимнего сезона 2008 г. низкой солнечной активности, как указано выше, Σp(22.12.2008 г., 00 UT) ≅ 0.27 См (декабрь), и для верткальных геомагнитных силовых линий Er max|I= 90° ≅ 0.27 мВ/м. Тогда в зоне АЗГА (за счет суммарного тока АЗГА) получим Er max ≅ 0.27 мВ/м × × 0.866 ≅ 0.23 мВ/м ≈ 0.2 мВ/м.
5. ВЫВОДЫ
Проведен расчет электрических полей, создаваемых в ночной ионосфере над Африканской зоной грозовой активности (АЗГА) за счет кулоновских зарядов 600 грозовых облаков, одномоментно расположенных в зоне, и суммарного тока АЗГА – усредненного модельного представления текущего вверх суммарного тока величиной в 600 А (по 1 А от каждого грозового облака, когда каждое грозовое облако рассматривается как элементарный квазистационарный точечный биполярный источник тока в рамках модели ГЭЦ в области АЗГА). Получено, что величина суммарного электрического поля, обусловленного кулоновскими зарядами грозовых облаков, очень мала и не превосходит 1 мкВ/м. В то же время электрическое поле, связанное с интегральным током АЗГА, может в максимуме достигать ~0.2 мВ/м для ночных зимних условий в период низкой активности Солнца.
Список литературы
– Имянитов И.М., Шифрин К.С. Современное состояние исследований атмосферного электричества // УФН. Т. 76. № 4. С. 593–642. 1962. https://doi.org/10.3367/UFNr.0076.196204a.0593
– Мареев Е.А. Достижения и перспективы исследований глобальной электрической цепи // УФН. Т. 180. № 5. С. 527–534. 2010. https://doi.org/10.3367/UFNr.0180.201005h.0527
– Френкель Я.И. Теория явлений атмосферного электричества. М.: КомКнига. 160 с. 2007.
– Хегай В.В. Аналитическая модель сейсмогенного электрического поля по данным измерений в приземном слое атмосферы средних широт и расчет его величины на уровне ионосферы // Геомагнетизм и аэрономия. Т. 60. № 4. С. 528–541. 2020. https://doi.org/10.31857/S0016794020030086
– Brooks C.E.P. The distribution of thunderstorms over the globe // Geophys. Mem. London. V. 3. Iss. 24. P. 147–164. 1925.
– Chalmers J.A. Atmospheric electricity. London: Pergamon Press. 515 p. 1967.
– Crichlow W.Q., Davis R.C., Disney R.T., Clark M.W. Hourly probability of world-wide thunderstorm occurrence / Telecommunications Research Report OT/ITS RR 12, U.S. Department of Commerce, Boulder, Colo., April 1971.
– Davydenko S.S., Mareev E.A., Marshall T.C., Stolzenburg M. On the calculation of electric fields and currents of mesoscale convective systems // J. Geophys. Res. V. 109. D11103. 2004. https://doi.org/10.1029/2003JD003832
– Denisenko V.V., Boudjada M.Y., Horn M., Pomozov E.V., Biernat H.K., Schwingenschuh K., Lammer H., Prattes G., Cristea E. Ionospheric conductivity effects on electrostatic field penetration into the ionosphere // Nat. Hazards Earth Syst. Sci. V. 8. Iss. 5. P. 1009–1017. 2008. https://doi.org/10.5194/nhess-8-1009-2008
– Denisenko V.V., Nesterov S. A., Boudjada M.Y., Lammere H. A mathematical model of quasistationary electric field penetration from ground to the ionosphere with inclined magnetic field // J. Atmos. Solar-Terr. Phys. V. 179. P. 527–537. 2018. https://doi.org/10.1016/j.jastp.2018.09.002
– Denisenko V., Rycroft M., Harrison G. Mathematical simulation of the ionospheric electric field as a part of the Global Electric Circuit // Surv. Geophys. V. 40. Iss. 1. P. 1–35. 2019. https://doi.org/10.1007/s10712-018-9499-6
– Farley Jr., D.T. A theory of electrostatic fields in the ionosphere at nonpolar geomagnetic latitudes // J. Geophys. Res. V. 65. № 3. P. 869–877. 1960. https://doi.org/10.1029/JZ065i003p00869
– Hays P.B., Roble R.G. A quasi-static model of global atmospheric electricity. 1. The lower atmosphere // J. Geophys. Res. V. 84. № A7. P. 3291–3305. 1979. https://doi.org/10.1029/JA084iA07p03291
– Hegai V.V., Kim V.P., Liu J.Y. On a possible seismo-magnetic effect in the topside ionosphere // Adv. Space Res. V. 56. Iss. 8. P. 1707–1713. 2015. https://doi.org/10.1016/j.asr.2015.07.034
– https://ccmc.gsfc.nasa.gov/modelweb/models/iri2016_ vitmo.php
– https://modelweb.gsfc.nasa.gov/atmos/nrlmsise00.html
– Kartalev M.D., Rycroft M.J., Fuellekrug M., Papitashvili V.O., Keremidarska V.I. A possible explanation for the dominant effect of South American thunderstorms on the Carnegie curve // J. Atmos. Solar-Terr. Phys.V. 68. Iss. 3–5. P. 457–468. 2006. https://doi.org/10.1016/j.jastp.2005.05.012
– Kasemir H.W. The thundercloud / Problems of Atmospheric and Space Electricity. Ed. Coroniti S. C. N.Y.: Elsevier. P. 215–235. 1965.
– Kim V.P., Hegai V.V. On the electric fields produced by dipolar coulomb charges of an individual thundercloud in the ionosphere // J. Astron. Space Sci. V. 32. № 2. P. 141–144. 2015. https://doi.org/10.5140/JASS.2015.32.2.141
– Making M., Ogawa T. Responses of atmospheric electric field and air-earth current to variations of conductivity profiles // J. Atmos. Terr. Phys. V. 46. Iss. 5. P. 431–445. 1984. https://doi.org/10.1016/0021-9169(84)90087-4
– Malan D.J. Physics of Lightning. London: The English University Press Ltd., 176 p. 1963.
– Muhleisen R. The global circuit and its parameters / Electrical Processes in Atmospheres. Eds. Dolezalek H., Reiter R., Landsberg H. E. Darmstadt: Dr. Dietrich Steinkopff Verlag GmbH & Co. KG., 1976. P. 467–476. https://doi.org/10.1007/978-3-642-85294-7_73
– Park C.G., Dejnakarintra M. Penetration of thundercloud electric fields into the ionosphere and magnetosphere: 1. Middle and subauroral latitudes // J. Geophys. Res. V. 78. № 28. P. 6623–6633. 1973. https://doi.org/10.1029/JA078i028p06623
– Rycroft M.J., Odzimek A., Arnold N.F., Fullekrug M., Kulak A., Neubert T. New model simulations of the global atmospheric electric circuit driven by thunderstorms and electrified shower clouds: The roles of lightning and sprites // J. Atmos. Solar-Terr. Phys. V. 69. Iss. 17–18. P. 2485–2509. 2007. https://doi.org/10.1016/j.jastp.2007.09.004
– Uman M.A. Lightning. N.Y.: McGraw-Hill, 162 p. 1969.
– Weisberg J.S. Meteorology: The Earth and its weather. Boston: Houghton Mifflin. Company, 241 p. 1976.
Дополнительные материалы отсутствуют.
Инструменты
Геомагнетизм и аэрономия


