Геомагнетизм и аэрономия, 2021, T. 61, № 4, стр. 506-519
Отличия прогнозов условий КВ-радиосвязи между передатчиком на средних широтах и приемником в арктическом регионе при использовании различных эмпирических моделей ионосферы
И. В. Мингалев 1, 2, *, З. В. Суворова 1, В. Н. Шубин 3, А. М. Мерзлый 4, В. В. Тихонов 5, А. Б. Талалаев 6, В. С. Мингалев 1
1 Полярный геофизический институт (ПГИ)
г. Мурманск, г. Апатиты (Мурманская обл.), Россия
2 Мурманский Арктический государственный университет (МАГУ)
г. Апатиты (Мурманская обл.), Россия
3 Институт земного магнетизма, ионосферы и распространения радиоволн
им. Н.В. Пушкова РАН (ИЗМИРАН)
г. Москва, г. Троицк, Россия
4 Институт космических исследований РАН (ИКИ РАН)
г. Москва, Россия
5 АО “Радиотехнические и информационные системы воздушно-космической обороны”
г. Тверь (Тверская обл.), Россия
6 АО “РТИ”
г. Москва, Россия
* E-mail: mingalev_i@pgia.ru
Поступила в редакцию 03.09.2020
После доработки 29.12.2020
Принята к публикации 28.01.2021
Аннотация
Сопоставлены результаты прогнозов условий радиосвязи в КВ-диапазоне между передатчиком, расположенным на средних широтах, и приемниками, расположенными в районах Норвежского и Баренцева морей. В качестве основы расчета прогнозов были использованы модели ионосферы IRI-2016 и Global Dynamic Model of Ionosphere (GDMI), разработанная в ИЗМИРАН. Прогноз условий радиосвязи основан на расчетах трехмерных лучевых траекторий радиоволн в приближении геометрической оптики с учетом анизотропии ионосферной плазмы и ее пространственной неоднородности. Показано, что прогноз условий радиосвязи, рассчитанный при помощи модели GDMI, может существенно отличаться от прогноза, рассчитанного при помощи модели IRI-2016. Также показано, что в середине декабря рассчитанные с помощью моделей GDMI и IRI-2016 значения МПЧ для радиотрассы Санкт-Петербург–Longyearbyen (Лонгйирбюен) (Шпицберген) для односкачковых траекторий днем превышают экспериментальные значения МПЧ на 5–20%, а ночью ниже экспериментальных на 30–40%. При этом для второй половины дня точность прогноза МПЧ, полученного с использованием модели GDMI, лучше, чем точность прогноза МПЧ, полученного с использованием модели IRI-2016. Для остального времени суток наоборот, использование модели IRI-2016 обеспечивает лучшую точность прогноза МПЧ.
1. ВВЕДЕНИЕ
Обеспечение надежной КВ-радиосвязи с морскими и воздушными судами, а также сухопутными объектами в высоких широтах имеет большое прикладное значение. Распространение КВ-радиоволн определяется пространственным распределением концентрации электронов в ионосфере, которое на средних и высоких широтах имеет сложную неоднородную структуру как в горизонтальном, так и в вертикальном направлениях. Основные крупномасштабные неоднородности – это овал полярных сияний (ОПС) и главный ионосферный провал (ГИП). Их положение существенно меняется в зависимости от времени суток и от геофизических условий.
Для прогноза условий радиосвязи, а также для оценки состояния ионосферы по работе различных радиотрасс давно применяется численное моделирование распространения радиоволн КВ-диапазона с расчетом лучевых траекторий в приближении геометрической оптики [Кравцов и Орлов, 1980; Budden, 1985; Крашенинников и Егоров, 2005; Андреев и др., 2007а, б; Крашенинников и др., 2017, 2018; Крашенинников и Шубин, 2020].
Для расчета лучевых траекторий распространения радиоволн КВ-диапазона необходимо рассчитывать плазменную частоту и частоту столкновений электронов в ионосфере во всей области прохождения лучевых траекторий. Для задания распределения этих параметров в ионосфере разработаны эмпирические модели, построенные на основе анализа данных наблюдений о состоянии ионосферы, самые известные из которых – это Международная Справочная модель Ионосферы(IRI) [Bilitza et al., 2017] и модель NeQuick [Nava et al., 2008].В модели GDMI, разработанной в ИЗМИРАН, основные параметры F2-слоя ионосферы для спокойных геомагнитных условий рассчитываются по моделям hmF2 [Shubin et al., 2013; Shubin, 2015] и foF2 [Шубин, 2017], которые построены на основе данных наземного зондирования ионосферы и профилей электронной концентрации, полученных радиозатменным методом с помощью спутников. Модели IRI, NeQuick и GDMI существенно различаются между собой и могут быть использованы для расчета лучевых траекторий радиоволн КВ-диапазона в приближении геометрической оптики.
Общая схема вычислений в этих моделях следующая. Над заданной точкой на поверхности Земли по аналитическим формулам рассчитываются высоты максимумов критической частоты и значения этой частоты на высоте для D, E, F1 и F 2-слоев ионосферы. Аналитические формулы подбирают для выбранной базы данных. Затем с помощью перечисленных параметров также по аналитическим формулам рассчитываются вертикальные профили в узлах сетки по высоте электронной концентрации и плазменной частоты, а также профили температуры электронов и частоты их столкновений [Banks, 1966; Schunk and Nagy, 1978; Часовитин и др., 1988].
Указанные выше модели отличаются между собой используемыми аналитическими формулами для расчета основных параметров слоев ионосферы, а также базами данных, с помощью которых эти формулы построены.
Цель данной работы – сравнить прогнозы условий КВ-связи между передатчиком, расположенным на средних широтах, и приемниками, расположенными в районах Норвежского и Баренцева морей, рассчитанные при использовании моделей ионосферы IRI-2016 и GDMI.
Область на поверхности Земли, в которую попадают выходящие из одного передатчика односкачковые лучевые траектории радиоволн КВ-диапазона, существенно меняется в течение суток. В дальнейшем будем называть эту область зоной засветки передатчика.
В данной работе с помощью численного моделирования исследуются изменения этой зоны для передатчика, расположенного в Санкт-Петербурге, в течение суток 21 июня 2019 г. для разных частот КВ-диапазона, близких к максимальной применимой частоте (МПЧ) для данных условий. Проводится анализ моделирования и делается вывод о возможности односкачковой КВ-радиосвязи между Санкт-Петербургом и районами, расположенными к северу от него в секторе азимутальных углов от –30° до 30° от направления на север.
Также проводится сравнение экспериментальных ионограмм наклонного зондирования (НЗ) для радиотрассы Санкт-Петербург–Longyearbyen (Лонгйирбюен) (Шпицберген), полученных техническими средствами ААНИИ в течение одних суток (14–15 декабря 2001 г.) для пяти моментов времени, и численно синтезированных с использованием эмпирических моделей ионосферы ионограмм для этой же радиотрассы для тех же моментов времени.
Кроме того, приведено описание используемой в работе численной модели распространения радиоволн КВ-диапазона. Эта модель является дальнейшим развитием модели, использовавшейся в работах [Андреев и др., 2007а, б].
2. МЕТОД РАСЧЕТА ЛУЧЕВЫХ ТРАЕКТОРИЙ КВ-РАДИОВОЛН
Для численного моделирования распространения КВ-радиоволн используется приближение геометрической оптики [Кравцов и Орлов, 1980] с учетом анизотропии ионосферной плазмы, обусловленной геомагнитным полем. Лучевые траектории находятся путем численного решения системы уравнений эйконала:
(1)
$\frac{{d{\mathbf{r}}}}{{d\tau }} = {\mathbf{p}} - \frac{1}{2}{{\vec {\nabla }}_{{\mathbf{p}}}}\left( {n_{{\text{в}}}^{2}} \right),\,\,\,\,\frac{{d{\mathbf{p}}}}{{d\tau }} = \frac{1}{2}{{\nabla }_{{\mathbf{r}}}}\left( {n_{{\text{в}}}^{2}} \right),$Дисперсионное уравнение (2) определяет два решения для двух волновых мод – обыкновенной и необыкновенной волн, которые распространяются с различными показателями преломления, фазовыми и групповыми скоростями, причем обыкновенная волна имеет левую поляризацию, а необыкновенная волна – правую. Решение дисперсионного уравнения можно представить в виде $n = {{\left[ {\frac{{ - B \pm D}}{{2A}}} \right]}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}},$ где D = (B 2 – 4AC)1/2.
Для численного интегрирования системы уравнений эйконала используется схема Рунге–Кутты 4-го порядка точности с коррекцией гамильтониана на каждом шаге траектории. Особенностью используемой нами схемы является расчет компонент градиента в декартовых координатах, при этом параметры среды задаются на сетке в сферической системе координат. Такой подход позволяет избежать накопления дополнительной погрешности, которая непременно возникала бы при расчете траектории в сферической системе координат вследствие большего количества вычислительных операций (вычисление коэффициентов Ламе, более громоздкие уравнения с большим количеством слагаемых и пр.).
3. ЗАДАНИЕ ПАРАМЕТРОВ ИОНОСФЕРЫ
Для задания этих параметров использовались две эмпирические модели ионосферы – модель IRI-2016 и разработанная в ИЗМИРАН модель ионосферы GDMI. Для проведения расчетов были выбраны две даты – 21 июня 2019 г. и 21 декабря 2018 г. – и заданы спокойные геофизические условия (индекс Ap = 3, F10.7 = 70, F10.7A = 70).
На рисунках 1 и 2 представлены вертикальные профили критической частоты плазмы, рассчитанные по указанным выше моделям, в точках, расположенных на долготе 30° E и на широтах 60°, 65°, 70° N в разные моменты времени. На рисунке 1 представлены вертикальные профили критической частоты плазмы для даты 21.12.2018 г. в моменты, когда в Санкт-Петербурге полночь (а) и полдень (б). На рисунке 1а видно, что в полночь для всех трех точек максимальные критические частоты в F-слое, рассчитанные по модели GDMI, больше, чем рассчитанные по модели IRI-2016. Высоты максимумов F-слоя для точек с широтами 60° и 65°, рассчитанные по модели GDMI, ниже, чем рассчитанные по модели IRI-2016, примерно на 40 и 25 км соответственно. Градиент электронной концентрации на высотах 170–190 км, рассчитанный по модели GDMI, существенно больше, чем рассчитанный по модели IRI-2016, что сильно влияет на распространение КВ-радиоволн. Различия между моделями на высотах ниже 170 км незначительны.
Рис. 1.
Вертикальные профили критической частоты плазмы, рассчитанные по моделям GDMI и IRI-2016 для даты 21.12.2018 г. для спокойных геофизических условий (индекс Ap = 3, F10.7 = 70, F10.7A = 70), для моментов времени UT = 22:00 (а) и UT = 10:00 (б).
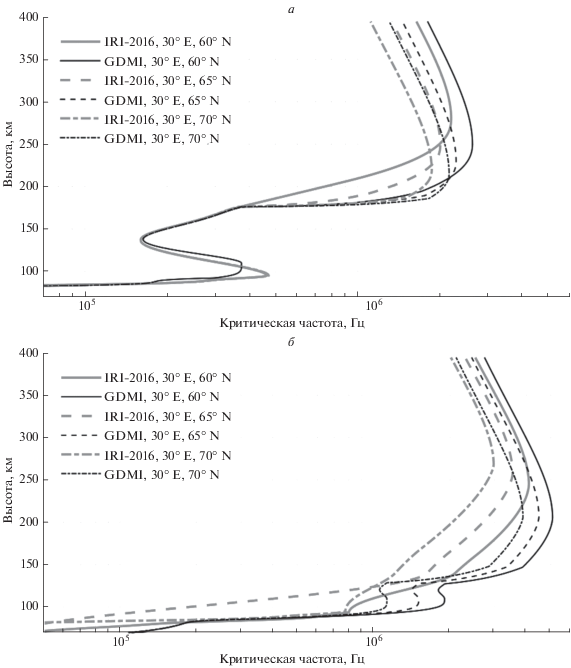
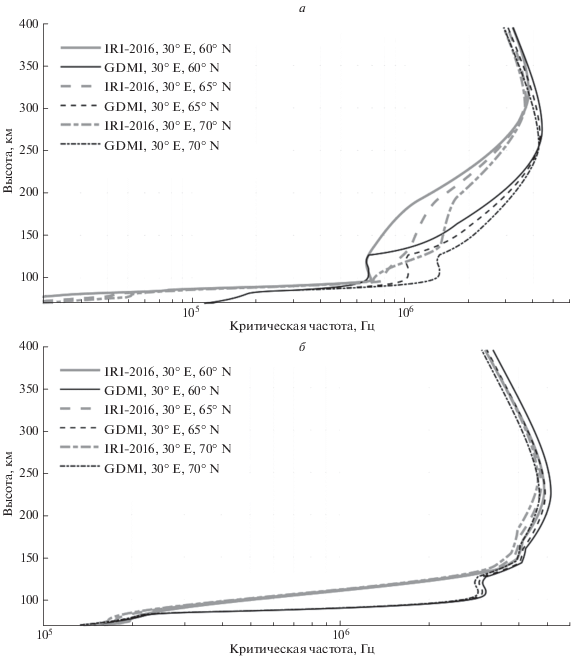
Рис. 2.
Вертикальные профили критической частоты плазмы, рассчитанные по моделям GDMI и IRI-2016 для даты 21.06.2019 г. для спокойных геофизических условий (индекс Ap = 3, F10.7 = 70, F10.7A = 70), для моментов времени UT = 22:00 (а) и UT = 10:00 (б).
На рисунке 1б видно, что в полдень для всех трех точек максимальные критические частоты в F-слое, рассчитанные по модели GDMI, больше, чем рассчитанные по модели IRI-2016. Высоты максимумов F-слоя для всех точек, рассчитанные по модели GDMI, ниже, чем рассчитанные по модели IRI-2016, примерно на 40–50 км. Градиент электронной концентрации на высотах 130–150 км, рассчитанный по модели GDMI, существенно больше, чем рассчитанный по модели IRI-2016, что сильно влияет на распространение КВ-радиоволн. Различия между моделями на уровне E-слоя ионосферы также весьма существенны. Это связано с тем, что в модели GDMI в области ОПС дополнительно учитывается источник ионизации атмосферы, вызванный высыпающимися из магнитосферы заряженными частицами [Бадин и др., 2013]. Поэтому модель GDMI дает выраженный максимум E-слоя на высоте 110 км, а в модели IRI-2016 такого максимума нет.
На рисунке 2 представлены вертикальные профили критической частоты плазмы для даты 21.06.2019 г. в моменты, когда в Санкт-Петербурге полночь (а) и полдень (б). На рисунке 2а видно, что в полночь для всех трех точек имеются существенные различия между профилями, рассчитанными по модели GDMI и по модели IRI-2016, на высотах 90–120 км и 130–300 км. Для всех трех профилей модель GDMI дает высоту максимума F-слоя ~260 км, а модель IRI-2016 – ~320 км. При этом максимальные критические частоты F-слоя, рассчитанные по этим двум моделям, различаются незначительно (модель IRI-2016 дает значения foF2 примерно на 0.5 МГц меньше). Градиент электронной концентрации на высотах 130–150 км, рассчитанный по модели GDMI, существенно больше, чем рассчитанный по модели IRI-2016, что сильно влияет на распространение КВ-радиоволн.
На рисунке 2б видно, что в полдень для всех трех точек профили, рассчитанные по модели GDMI и по модели IRI-2016, на высотах выше 130 км близки между собой. Различия между моделями на высотах 90–120 км весьма существенны. Модель GDMI дает выраженный максимум E-слоя на высоте 110 км, а модель IRI-2016 такого максимума не дает. Градиент электронной концентрации на высотах 90–120 км, рассчитанный по модели GDMI, существенно больше, чем рассчитанный по модели IRI-2016, что сильно влияет на распространение КВ-радиоволн. Критические частоты на высоте 100 км, рассчитанные по модели GDMI, больше, чем рассчитанные по модели IRI-2016, примерно в 6 раз.
4. РЕЗУЛЬТАТЫ МОДЕЛИРОВАНИЯ ЗОНЫ ДОСЯГАЕМОСТИ ОДНОСКАЧКОВЫХ ТРАЕКТОРИЙ
Моделирование проводилось следующим образом. Передатчик располагался в точке с координатами 30.5° E, 60.0° N. Для выбранной частоты и выбранного времени суток рассчитывался следующий набор выходящих из передатчика лучевых траекторий для обыкновенной моды (необыкновенная мода затухает сильнее). Углы возвышения выбирались следующим образом: в диапазоне от 6° до 10° – с шагом 0.5 градуса, от 11° до 18° – с шагом 1 градус, от 20° до 32° – с шагом 2 градуса. Для каждого угла возвышения рассчитывались лучевые траектории, выходящие из передатчика в секторе азимутальных углов от –30° до 30° от направления на север с шагом 2 градуса. Точки падения на поверхность Земли траекторий, вышедших из передатчика с одним углом возвышения и разными азимутами, соединялись одной линией. Полученная область на поверхности Земли, ограниченная крайними кривыми, соответствовала зоне засветки передатчика на данной частоте при данных геофизических условиях.
Возможны случаи, когда в одну точку попадают две и более лучевых траекторий, выходящих из передатчика при разных углах возвышения и разных азимутальных углах. Такие ситуации соответствуют многолучевому распространению, когда лучевая траектория, вышедшая из передатчика с меньшим углом возвышения, отражается от Е-слоя ионосферы, а вышедшая из передатчика с большим углом возвышения отражается от F-слоя ионосферы. В случае, когда все траектории отражаются от одного и того же слоя ионосферы, ближайшие к передатчику кривые соответствуют большим углам возвышения, дальние кривые – меньшим углам.
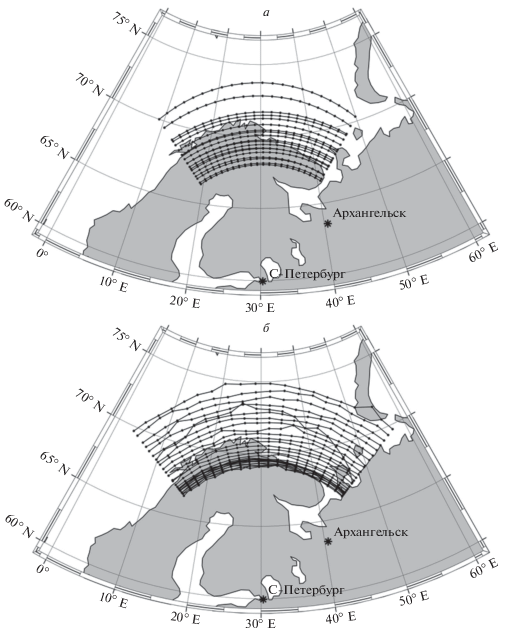
На рисунке 3 изображены зоны засветки передатчика на частоте 4 МГц, рассчитанные для даты 21 декабря 2018 г., UT = 22:00 (полночь в СПб) и спокойных геофизических условий (индексы Ap = 3, F10.7 = 70, F10.7A = 70), для случаев, когда параметры ионосферы заданы по модели GDMI (а) и по модели IRI-2016 (б). Видно, что на рис. 3а зона засветки по дальности лежит в пределах примерно от 800 до 1900 км от передатчика, а на рис. 3б эта зона располагается на расстоянии от 1200 км до 1800 км от передатчика. Это обусловлено тем, что в случае, когда ионосфера задана по модели IRI-2016, траектории с углами возвышения от 21 до 32 градусов проходят сквозь ионосферу и не попадают на поверхность Земли, а в случае задания ионосферы по модели GDMI эти траектории отражаются от ионосферы и попадают на поверхность Земли. Такое различие связано с тем, что концентрация электронов на высотах 180–250 км, рассчитанная по модели GDMI, существенно выше, чем концентрация, рассчитанная по модели IRI-2016, как видно из рис. 1а.
Рис. 3.
Зоны засветки расположенного в СПб передатчика на частоте 4 МГц, рассчитанные для момента времени 21 декабря 2018 г. UT = 22:00 и для ионосферы, заданной по модели GDMI (а) и по модели IRI-2016 (б).
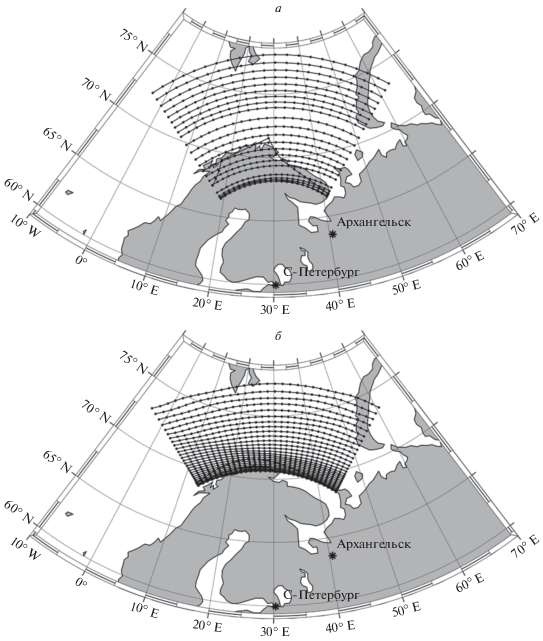
На рисунке 4 изображены зоны засветки передатчика на частоте 5 МГц, рассчитанные для даты 21 декабря 2018 г. UT = 10:00 (полдень в СПб) и спокойных геофизических условий (индексы Ap = 3, F10.7 = 70, F10.7A = 70), для случаев, когда параметры ионосферы заданы по модели GDMI (а) и по модели IRI-2016 (б). Видно, что на рис. 4а зона засветки по дальности лежит в пределах примерно от 500 до 1300 км от передатчика, а на рис. 4б эта зона располагается на расстоянии от 1400 км до 2000 км от передатчика. Столь существенная разница обусловлена тем, что в случае, когда ионосфера задана по модели GDMI, траектории с углами возвышения от 6 до 32 градусов отражаются от нижней части F-слоя ионосферы на высотах от 130 до 150 км, а в случае задания ионосферы по модели IRI-2016 эти же траектории отражаются от ионосферы на высотах ~200–250 км. Такое различие связано с тем, что концентрация электронов на высотах 100–250 км, рассчитанная по модели GDMI, существенно выше, чем концентрация, рассчитанная по модели IRI-2016, как видно из нижней части рис. 1.
Рис. 4.
Зоны засветки расположенного в СПб передатчика на частоте 5 МГц, рассчитанные для момента времени 21 декабря 2018 г. UT = 10:00 для ионосферы, заданной по модели GDMI (а) и по модели IRI-2016 (б).
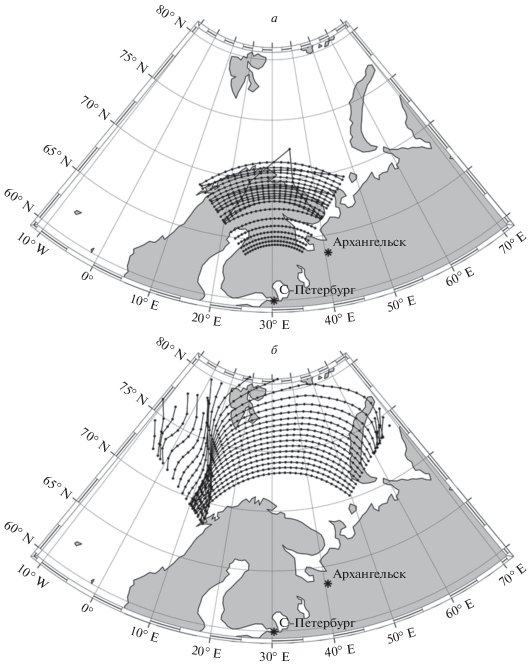
На рисунке 5 представлены зоны засветки передатчика на частоте 6 МГц, рассчитанные для даты 21 июня 2019 г. UT = 22:00 (полночь в СПб) и спокойных геофизических условий (индексы Ap = 3, F10.7 = 70, F10.7A = 70), для случаев, когда параметры ионосферы заданы по модели GDMI (а) и по модели IRI-2016 (б). Видно, что на рис. 5а зона засветки по дальности лежит в пределах примерно от 800 до 1800 км от передатчика, а на рис. 5б эта зона располагается на расстоянии от 1400 км до 2000 км от передатчика. Имеющаяся разница между зонами засветки обусловлена тем, что в случае, когда ионосфера задана по модели GDMI, концентрация электронов на высотах 140–250 км существенно выше концентрации, рассчитанной по модели IRI-2016. Это приводит к тому, что лучевые траектории в первом случае отражаются на меньших высотах, чем во втором случае, что, в свою очередь, приводит к уменьшению расстояния между передатчиком и точками падения траекторий в первом случае.
Рис. 5.
Зоны засветки расположенного в СПб передатчика на частоте 6 МГц, рассчитанные для момента времени 21 июня 2019 г. UT = 22:00 для ионосферы, заданной по модели GDMI (а) и по модели IRI-2016 (б).
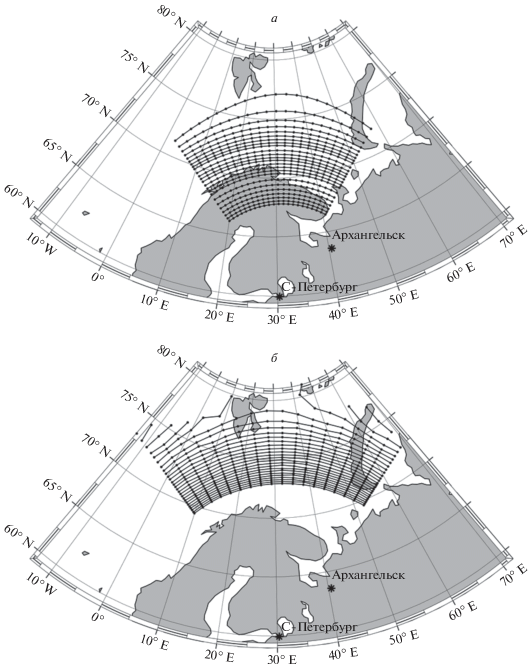
На рисунке 6 представлены зоны засветки передатчика на частоте 10 МГц, рассчитанные для даты 21 июня 2019 г., времени UT = 10:00 (полдень в СПб) и спокойных геофизических условий (индексы Ap = 3, F10.7 = 70, F10.7A = 70), для случаев, когда параметры ионосферы заданы по модели GDMI (а) и по модели IRI-2016 (б). Видно, что на рис. 6а зона засветки по дальности лежит в пределах примерно от 800 до 1400 км от передатчика, а на рис. 6б эта зона располагается на расстоянии от 900 км до 1600 км от передатчика. Разница в зонах засветки не столь существенна, как на рис. 3 и 4. Имеющиеся различия обусловлены тем, что концентрация электронов на высотах 80–130 км, рассчитанная по модели GDMI, существенно выше, чем концентрация, рассчитанная по модели IRI-2016, как видно из нижней части рис. 1б, а на высотах более 130 км концентрации, рассчитанные по обеим моделям, близки между собой.
5. СРАВНЕНИЕ ЭКСПЕРИМЕНТАЛЬНЫХ И СИНТЕЗИРОВАННЫХ ИОНОГРАММ
Для сравнения экспериментальных и численно синтезированных ионограмм НЗ были выбраны ионограммы для радиотрассы Санкт-Петербург–Лонгйирбюен (Шпицберген), полученные техническими средствами ААНИИ в течение одних суток (14–15 декабря 2001 г.) для пяти моментов времени. Эти ионограммы приведены в работе [Андреев и др., 2007a].
Для этой радиотрассы и для этих же моментов времени нами были рассчитаны ионограммы НЗ в двух случаях. В первом случае трехмерное распределение электронной концентрации было рассчитано при помощи модели IRI-2016, а во втором случае – при помощи модели GDMI. Для данных расчетов нами была создана программа, использующая метод “пристрелки” и метод расчета лучевых траекторий, описанный выше в разделе 2. В этой программе расчеты полностью трехмерные, учитывается анизотропия ионосферной плазмы, а также отклоняющее поглощение.
На рисунках 7–11 приведены экспериментальные и синтезированные ионограммы НЗ для пяти моментов времени: 14 декабря 2001 г. UT = 12:48, UT = 14:48, UT = 20:48, UT = 23:48 и 15 декабря 2001 г. UT = 8:48.
Рис. 7.
Ионограммы наклонного зондирования для радиотрассы Санкт-Петербург–Лонгйирбюен (Шпицберген) для момента времени 12:48 UT 14 декабря 2001 г., полученные экспериментально (а), численно синтезированные с использованием модели IRI-2016 (б) и численно синтезированные с использованием модели GDMI (в).
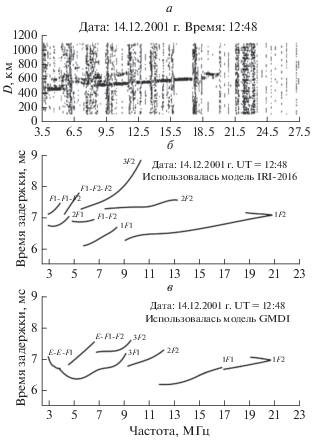
Рис. 8.
Ионограммы наклонного зондирования для радиотрассы Санкт-Петербург–Лонгйирбюен (Шпицберген) для момента времени 14:48 UT 14 декабря 2001 г., полученные экспериментально (а), численно синтезированные с использованием модели IRI-2016 (б) и численно синтезированные с использованием модели GDMI (в).
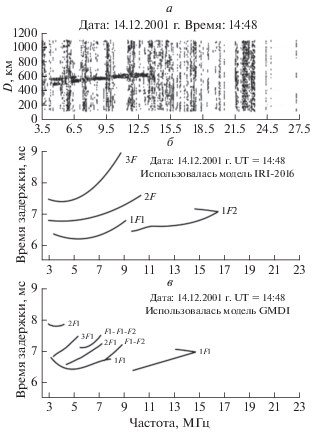
Рис. 9.
Ионограммы наклонного зондирования для радиотрассы Санкт-Петербург–Лонгйирбюен (Шпицберген) для момента времени 20:48 UT 14 декабря 2001 г., полученные экспериментально (а), численно синтезированные с использованием модели IRI-2016 (б) и численно синтезированные с использованием модели GDMI (в).
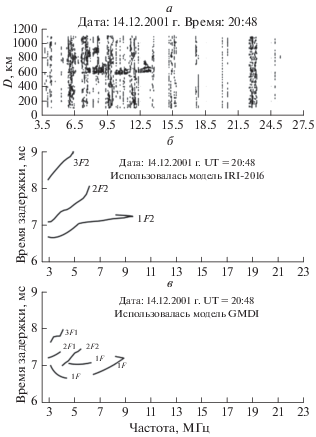
Рис. 10.
Ионограммы наклонного зондирования для радиотрассы Санкт-Петербург–Лонгйирбюен (Шпицберген) для момента времени 23:48 UT 14 декабря 2001 г., полученные экспериментально (а), численно синтезированные с использованием модели IRI-2016 (б) и численно синтезированные с использованием модели GDMI (в).
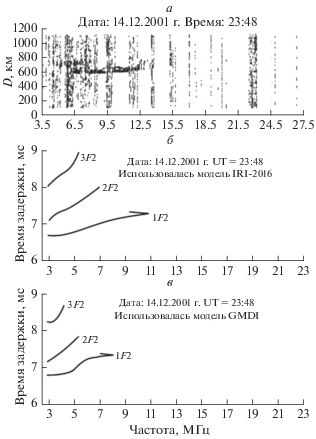
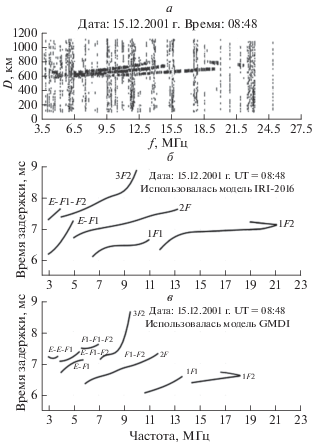
Рис. 11.
Ионограммы наклонного зондирования для радиотрассы Санкт-Петербург–Лонгйирбьен (Шпицберген) для момента времени 8:48 UT 15 декабря 2001 г., полученные экспериментально (а), численно синтезированные с использованием модели IRI-2016 (б) и численно синтезированные с использованием модели GDMI (в).
В момент времени 14 декабря 2001 г. UT = 12:48 значение геомагнитного 3-часового индекса ap = 7, а среднее значение этого индекса за предыдущие сутки Ap = 2.75. Значение индекса F10.7 = 217. На верхней части рисунка видно, что экспериментальная МПЧ для односкачковых траекторий, отражающихся от F2-слоя, составила ~20 МГц. Из средней и нижней частей рисунка видно, что МПЧ для этих же траекторий, рассчитанных с помощью моделей IRI-2016 и GDMI, составила ~21 МГц. Таким образом, для данного момента времени МПЧ для односкачковых траекторий на синтезированных ионограммах превышает экспериментальную МПЧ примерно на 1 МГц, что говорит о том, что эмпирические модели дали более высокую концентрацию электронов в F2-слое в центральной части радиотрассы, чем в реальности. Аналогично при сравнении МПЧ двухскачковых траекторий, отражающихся от F2-слоя, видно, что экспериментальная МПЧ совпадает с МПЧ, рассчитанной с помощью модели GDMI, и составляет ~12 МГц, а МПЧ, рассчитанная с помощью модели IRI-2016, составляет 13 МГц. Таким образом, отличие экспериментальной МПЧ от рассчитанных с помощью эмпирических моделей не превышает 1 МГц.
Аналогичные сравнения МПЧ для 1- и 2-скачковых траекторий проведены для других моментов времени. Результаты сравнения, а также значения индексов ap, Ap, F10.7 приведены в табл. 1. Как видно из таблицы, для момента времени 14.12.2001 г. UT = 14:48 для односкачковых траекторий, отражающихся от F2-слоя, экспериментальная МПЧ составляет ~14 МГц, МПЧ, рассчитанная с помощью модели GDMI, превышает экспериментальную на 0.7 МГц, а МПЧ, рассчитанная с помощью модели IRI-2016, превышает экспериментальную на 2.5 МГц. Экспериментальная МПЧ для двухскачковых траекторий, отражающихся от F2-слоя, составляет ~6.7 МГц, МПЧ, рассчитанная с помощью модели GDMI, превышает экспериментальную на 2.3 МГц, а МПЧ, рассчитанная с помощью модели IRI-2016, превышает экспериментальную на 3.6 МГц. Таким образом, для данного момента времени модель IRI-2016 дает большую погрешность в МПЧ, чем модель GDMI, как для односкачковой связи, так и для двухскачковой, при этом погрешность при определении МПЧ для двухскачковой связи превышает таковую для односкачковой. Указанный факт означает, что обе модели завышают электронную концентрацию в данный момент времени, причем IRI-2016 завышает больше, чем модель GDMI.
Таблица 1.
Результаты сравнения экспериментальных и синтезированных ионограмм НЗ
| Дата/время | ap | Ap | F10.7 | МПЧ для 1-скачковых траекторий, МГц | МПЧ для 2-скачковых траекторий, МГц | ||||
|---|---|---|---|---|---|---|---|---|---|
| эксперимент | GDMI | IRI-2016 | эксперимент | GDMI | IRI-2016 | ||||
| 14.12.2001 UT = 12:48 | 7 | 2.75 | 217 | 20 | 21 | 21 | 12 | 12 | 13 |
| 14.12.2001 UT = 14:48 | 7 | 2.75 | 217 | 14 | 14.7 | 16.5 | 6.7 | 9 | 10.3 |
| 14.12.2001 UT = 20:48 | 7 | 3.375 | 217 | 13.5 | 8.9 | 9.7 | 9.5 | 5.5 | 6.2 |
| 14.12.2001 UT = 23:48 | 7 | 3.375 | 217 | 13 | 8 | 11 | 8 | 5.5 | 7 |
| 15.12.2001 UT = 08:48 | 7 | 7.75 | 218 | 22 | 18 | 21 | 14.7 | 11.7 | 13.2 |
Для момента времени 14.12.2001 г. UT = 20:48 для односкачковых траекторий, отражающихся от F2-слоя, экспериментальная МПЧ составляет ~13.5 МГц, МПЧ, рассчитанная с помощью модели GDMI, меньше экспериментальной на 5.2 МГц, а МПЧ, рассчитанная с помощью модели IRI-2016, меньше экспериментальной на 3.8 МГц. Экспериментальная МПЧ для двухскачковых траекторий, отражающихся от F2-слоя, составляет ~9.5 МГц, МПЧ, рассчитанная с помощью модели GDMI, меньше экспериментальной на 4 МГц, а МПЧ, рассчитанная с помощью модели IRI-2016, меньше экспериментальной на 3.2 МГц. Таким образом, для данного момента времени модель IRI-2016 дает меньшую погрешность в МПЧ, чем модель GDMI, как для односкачковой связи, так и для двухскачковой. Указанный факт означает, что обе модели занижают электронную концентрацию в данный момент времени, причем IRI-2016 занижает меньше, чем модель GDMI.
Для момента времени 14.12.2001 г. UT = 23:48 экспериментальная МПЧ для односкачковых траекторий, отражающихся от F2-слоя, составляет ~13 МГц, МПЧ для этих же траекторий, рассчитанная с помощью модели GDMI, меньше экспериментальной на 5 МГц, а МПЧ, рассчитанная с помощью модели IRI-2016, меньше экспериментальной на 2 МГц. Экспериментальная МПЧ для двухскачковых траекторий, отражающихся от F2-слоя, составляет ~8 МГц, МПЧ для этих же траекторий, рассчитанная с помощью модели GDMI, меньше экспериментальной на 2.5 МГц, а МПЧ, рассчитанная с помощью модели IRI-2016, меньше экспериментальной на 1 МГц. Таким образом, для данного момента времени модель IRI-2016 дает меньшую погрешность в МПЧ, чем модель GDMI, как для односкачковой связи, так и для двухскачковой. Указанный факт означает, что обе модели занижают электронную концентрацию в данный момент времени, причем IRI-2016 занижает меньше, чем модель GDMI.
Для момента времени 15.12.2001 г. UT = 08:48 для односкачковых траекторий, отражающихся от F2-слоя, экспериментальная МПЧ составляет ~22 МГц, МПЧ, рассчитанная с помощью модели GDMI, меньше экспериментальной на 4 МГц, а МПЧ, рассчитанная с помощью модели IRI-2016, меньше экспериментальной на 1 МГц. Экспериментальная МПЧ для двухскачковых траекторий, отражающихся от F2-слоя, составляет ~14.7 МГц, МПЧ, рассчитанная с помощью модели GDMI, меньше экспериментальной на 3 МГц, а МПЧ, рассчитанная с помощью модели IRI-2016, меньше экспериментальной на 1.5 МГц. Таким образом, для данного момента времени модель IRI-2016 дает меньшую погрешность в МПЧ, чем модель GDMI, как для односкачковой связи, так и для двухскачковой. Указанный факт означает, что обе модели занижают электронную концентрацию в данный момент времени, причем IRI-2016 занижает меньше, чем модель GDMI.
Проведенное выше сравнение экспериментальных ионограмм НЗ и численно синтезированных показало, что наилучшую точность (~5%) прогноза МПЧ для односкачковых траекторий, отражающихся от F2-слоя, численно синтезированные с использованием эмпирических моделей ионограммы НЗ обеспечивают во второй половине дня, когда местное время LT в пределах от 14:30 до 19:00 (UT от 12:30 до 17:00). Несколько хуже точность прогноза МПЧ в первой половине дня, когда местное время LT в пределах от 10:30 до 11:00 (UT от 8:30 до 9:00). В ночное время, когда местное время LT в пределах от 22:30 до 2:00 (UT от 20:30 до 24:00), имеют место наибольшие отклонения МПЧ для отражающихся от F2-слоя односкачковых траекторий, рассчитанных с помощью эмпирических моделей, от экспериментальной МПЧ. При этом использование модели GDMI во второй половине дня обеспечивает лучшую точность прогноза МПЧ, чем использование модели IRI-2016, а ночью и в первой половине дня наоборот, использование модели IRI-2016 обеспечивает лучшую точность прогноза МПЧ.
6. ВЫВОДЫ
Проведенный в разделе 5 сравнительный анализ полученных техническими средствами ААНИИ в течение одних суток 14–15 декабря 2001 г. экспериментальных ионограмм НЗ для радиотрассы Санкт-Петербург–Лонгйирбюен (Шпицберген) и ионограмм НЗ, численно синтезированных с использованием эмпирических моделей ионосферы для этой же радиотрассы, позволяет сделать вывод о том, что рассчитанные с помощью моделей GDMI и IRI-2016 значения МПЧ для односкачковых траекторий днем превышают экспериментальные значения МПЧ на 5–20%, а ночью ниже экспериментальных на 30–40%. При этом для второй половины дня точность прогноза МПЧ, полученного с использованием модели GDMI, лучше, чем точность прогноза МПЧ, полученного с использованием модели IRI-2016. В остальное время суток наоборот, использование модели IRI-2016 обеспечивает лучшую точность прогноза МПЧ.
Представленные в разделах 4 и 5 данной работы результаты численного моделирования распространения радиоволн КВ-диапазона показали, что прогноз условий радиосвязи, рассчитанный при помощи модели GDMI, может существенно отличаться от прогноза, рассчитанного при помощи модели IRI-2016. Зоны засветки поверхности Земли односкачковыми лучевыми траекториями радиоволн КВ-диапазона на одной и той же частоте, полученные для расположенного в Санкт-Петербурге передатчика при использовании этих двух моделей, имеют следующие отличия. И ближняя, и дальняя границы зоны засветки, рассчитанной с использованием модели GDMI, расположены, как правило, ближе к передатчику, чем границы зоны, рассчитанной при использовании модели IRI-2016, причем в некоторых случаях на 500–600 км. Это связано с тем, что модель GDMI по сравнению с моделью IRI-2016 в большинстве случаев дает более высокую концентрацию электронов в E-слое и нижней части F-слоя ионосферы.
Также стоит отметить, что средние характерные параметры ионосферы заметно изменились за последние десятилетия. По этой причине крайне важны дальнейшее развитие и расширение отечественной системы мониторинга ионосферы, создание отечественной базы данных ионосферных параметров за длительный период времени, а также уточнение с помощью этой базы данных существующих эмпирических моделей ионосферы.
Список литературы
– Андреев М.Ю., Благовещенский Д.В., Выставной В.М., Мингалев В.С., Мингалева Г.И. Интерпретация экспериментальных данных распространения коротких радиоволн на трассе Санкт-Петербург–арх. Шпицберген // Геомагнетизм и аэрономия. Т. 47. № 4. С. 534–542. 2007a.
– Андреев М.Ю., Мингалева Г.И., Мингалев В.С. Численное моделирование структуры высокоширотного ионосферного слоя F и прохождения через него коротких радиоволн в меридиональном направлении // Геомагнетизм и аэрономия. Т. 47. № 4. С. 518–527. 2007б.
– Бадин В.И., Деминов М.Г., Деминов Р.Г., Шубин В.Н. Модель медианы критической частоты Е-слоя для авроральной области // Солнечно-земная физика. Вып. 8. С. 145–146. 2013.
– Кравцов Ю.А., Орлов Ю.И. Геометрическая оптика неоднородных сред. М.: Наука, 304 с. 1980.
– Крашенинников И.В., Шубин В.Н. Частотная зависимость энергетических параметров волнового поля на предельной дальности односкачкового распространения радиоволн в условиях низкой солнечной активности // Геомагнетизм и аэрономия. Т. 60. № 2. С. 220–228. 2020.
– Крашенинников И.В., Егоров И.Б. Формирование комбинированных модов в ионосферном прохождении радиоволн // Геомагнетизм и аэрономия. Т. 45. № 2. С. 241–244. 2005.
– Крашенинников И.В., Павлова Н.М., Ситнов Ю.С. Модель IRI в задаче прогнозирования ионосферного прохождения радиоволн в условиях высокой солнечной активности // Геомагнетизм и аэрономия Т. 57. № 6. С. 774–782. 2017.
– Крашенинников И.В., Гивишвили Г.В., Стаханова И.Г. Оценка критической частоты в задаче радиопросвечивания ионосферы с высокоорбитальных космических аппаратов в арктическом регионе // Геомагнетизм и аэрономия. Т. 58. № 5. С. 669–675. 2018.
– Часовитин Ю.К., Широчков А.В., Беспрозванная А.С. и др. Глобальная эмпирическая модель распределения электронной концентрации, температуры и эффективной частоты соударений электронов в ионосфере // Ионосферные исслед. № 44. С. 6–13. 1988.
– Шубин В.Н. Глобальная эмпирическая модель критической частоты F2-слоя ионосферы для спокойных геомагнитных условий // Геомагнетизм и аэрономия. Т. 57. № 4. С. 450–462. 2017.
– Banks P. Collision frequencies and energy transfer // Planet. Space Sci. V. 14. P. 1085–1103. 1966.
– Bilitza D., Altadil D., Truhlik V., Shubin V., Galkin I., Reinisch B., Huang X. International Reference Ionosphere 2016: from ionospheric climate to real-time weather predictions // Space Weather. V. 15. P. 418–429. 2017. https://doi.org/10.1002/2016SW001593
– Budden K.G. The propagation of radio waves. Cambridge: Cambridge University Press. 669 p. 1985.
– Nava B., Coпsson P., Radicella S.M.A new version of the NeQuick ionosphere electron density model // J. Atmos. Solar-Terr. Phys. V. 70. № 15. P. 1856–1862. 2008. https://doi.org/10.1016/j.jastp.2008.01.015
– Schunk R.W., Nagy A.F. Electron temperatures in the F region of the ionosphere: Theory and observations // Rev. Geophys. Space Ge. V. 16. № 3. P. 355–399. 1978. https://doi.org/10.1029/rg016i003p00355
– Shubin V.N. Global median model of the F2-layer peak height based on ionospheric radio-occultation and ground-based Digisonde observations // Adv. Space Res. V. 56. P. 916–928. 2015.
– Shubin V.N., Karpachev A.T., Tsybulya K.G. Global model of the F2 layer peak height for low solar activity based on GPS radio-occultation data // J. Atmos. Solar-Terr. Phys. V. 104. P. 106–115. 2013.
Дополнительные материалы отсутствуют.
Инструменты
Геомагнетизм и аэрономия