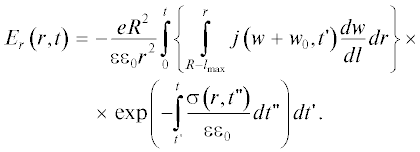Геомагнетизм и аэрономия, 2021, T. 61, № 4, стр. 490-498

1. ВВЕДЕНИЕ

Одним из важных факторов воздействия окружающей среды на космические аппараты (КА) являются потоки электронов и ионов высоких энергий, которые способны глубоко проникать в толщу материалов и внутренние части КА [Кузнецов, 2007; Lai, 2011].В результате такого воздействия КА приобретает электрические заряды, которые распределяются по поверхностям проводящих конструкций и в толще диэлектрических материалов. Процесс приобретения материалами электрических зарядов существенно зависит от их проводимости и вторично-эмиссионных процессов, которые, в свою очередь, подвержены изменениям под действием космических лучей и других факторов космического пространства. Однако характер этих изменений еще мало изучен. Анализ электризации реального КА представляет собой сложную задачу, поскольку конструкция современных КА содержит большое количество проводящих и диэлектрических материалов, между которыми возникают разности потенциалов, достигающие в отдельных случаях десятков киловольт [Новиков и др., 2007; Lai and Cahoy, 2017; Безродных и др., 2016; Lai et al., 2018]. При облучении диэлектриков релятивистскими электронами с энергиями $1{\kern 1pt} - {\kern 1pt} 10$ МэВ, характерными для радиационных поясов Земли (РПЗ), глубина их проникновения в диэлектрик превышает несколько миллиметров, создавая опасность электрического пробоя и разрушения материалов [Акишин и Новиков, 1985]. Электрические разряды в диэлектрических образцах, которые наблюдались при проведении научных экспериментов на борту КА CRESS, предположительно обусловлены потоками электронов РПЗ [Weber, 1964]. В результате образования разрядных каналов могут резко ухудшаться оптические и механические свойства диэлектрических материалов. Кроме того, электрические разряды, возникающие на поверхности и внутри корпуса КА, являются одной из важных причин появления сбоев и отказов в работе бортовой аппаратуры КА [DeForest, 1972; Новиков и др., 2007; Lai, 2011; Безродных и др., 2016; Lai and Cahoy, 2017; Lai et al., 2018].

Для математического моделирования электризации конструкций современных КА обычно применяются численные методы [Lai, 2011; Novikov et al., 2017]. Аналитические результаты могут быть получены для некоторых КА, имеющих относительно простую шаровую конфигурацию. К их числу относятся пассивные лазерные спутники Ларец, BLITS, GFZ–1, WESTPAC, предназначенные для калибровки наземных измерительных средств с использованием высокоточных лазерных измерений [Сурков и Мозгов, 2019]. В частности, наноспутник BLITS (Ball Lens In The Space), запущенный в сентябре 2009 г. на круговую солнечно-синхронную орбиту с наклонением 98.77° и высотой 832 км, был сделан в форме стеклянного шара, выполненного по принципу оптической линзы Люнеберга [Kucharski et al., 2011; Васильев, 2018]. Конструктивно он состоял из двух стеклянных полусфер, наклеенных на стеклянную шаровую линзу. На наружную поверхность одной из полусфер было нанесено отражающее зеркальное покрытие.

В работе [Сурков и Мозгов, 2019] исследовался эффект электризации пассивных диэлектрических спутников типа BLITS под влиянием потока электронов РПЗ и рассчитывалось распределение электрического поля внутри спутника. Целью настоящей работы является обобщение результатов данной работы и развитие более совершенной модели явлений, учитывающей образование экранирующего плазменного слоя на поверхности спутника и возникновение радиационной проводимости в его объеме.

2. ПОСТАНОВКА И ОБЩЕЕ РЕШЕНИЕ ЗАДАЧИ

Рассмотрим модель наноспутника в виде вращающегося диэлектрического шара, движущегося в бесконечной разреженной двухкомпонентной плазме, состоящей из электронов и положительных ионов (рис. 1). Радиус шара $R$ считаем малым по сравнению с длиной пробега частиц плазмы. Шар поглощает потоки релятивистских электронов РПЗ, приобретая отрицательный электрический заряд q. В результате возмущения плазмы электрическим полем этого заряда вокруг шара образуется слой экранирующего плазменного заряда. В системе отсчета, связанной со спутником, электрический потенциал этого поля $\varphi $ и плотность электрического заряда ${{\rho }_{e}}$ удовлетворяют уравнению Лапласа ${{\nabla }^{2}}\varphi = - {{{{\rho }_{e}}} \mathord{\left/ {\vphantom {{{{\rho }_{e}}} {{{\varepsilon }_{0}},}}} \right. \kern-0em} {{{\varepsilon }_{0}},}}$ а функции распределения электронов и ионов определяются кинетическими уравнениями Больцмана [Альперт и др., 1964].

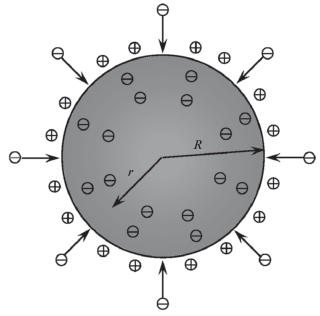
Учитывая, что период вращения шара порядка 0.2 с, т.е. намного меньше характерного времени релаксации зарядов в диэлектрике [Сурков и Мозгов, 2019], упростим задачу, полагая, что средний за период вращения шара вектор плотности потока электронов РПЗ направлен всюду радиально в центр шара и одинаков по модулю во всех точках поверхности шара. Пусть $j$ обозначает модуль средней плотности потока электронов в интервале энергий $\left( {w,w + dw} \right).$ Число электронов с такими энергиями, падающих за время $dt$ на поверхность шара, равно: ${{d}^{2}}N = 4\pi {{R}^{2}}jdtdw.$ Полагаем, что в среднем электроны РПЗ внедряются в шар равномерно, т.е. объемный заряд шара и его электрическое поле сферически симметричные. Если пренебречь асимметрией потока космической плазмы, обтекающей спутник, то потенциал электрического поля в плазме, окружающей шар, также зависит только от расстояния $r$ до центра шара. Поэтому задача в целом становится сферически-симметричной.

Средняя длина пробега l заряженных частиц в веществе зависит от их энергии w. Пусть функция $l = l\left( w \right)$ определяет данную зависимость. Предположим, что за время $dt$ частицы с энергиями в заданном интервале значений $\left( {w,w + dw} \right)$ внедряются в шар и занимают шаровой слой с радиусом $r = R - l\left( w \right)$ и толщиной $dr = dl\left( w \right).$ Дальнейшее изменение объемной плотности электрического заряда определяется малой, но конечной по величине электропроводностью диэлектрика.

Учитывая симметрию задачи, используем сферическую систему координат, начало которой расположено в центре шара. Если пренебречь временем торможения падающих электронов, предполагая, что они внедряются в вещество практически мгновенно, то уравнение непрерывности, определяющее закон сохранения электрического заряда внутри шара, имеет вид:

где ${{J}_{r}}$ – радиальная проекция плотности электрического тока; ${{\rho }_{e}}$ – плотность электрического заряда; $e$ – элементарный заряд. Подставляя сюда выражение для ${{d}^{2}}N,$ используя уравнение Максвелла ${{{{\rho }_{e}}} \mathord{\left/ {\vphantom {{{{\rho }_{e}}} {\left( {\varepsilon {{\varepsilon }_{0}}} \right)}}} \right. \kern-0em} {\left( {\varepsilon {{\varepsilon }_{0}}} \right)}} = \nabla \cdot {\mathbf{E}}$ и закон Ома ${\mathbf{J}} = \sigma {\mathbf{E}},$ где ${\mathbf{E}}$ – напряженность электрического поля; $\varepsilon $ и $\sigma $ – диэлектрическая проницаемость и проводимость вещества, а ${{\varepsilon }_{0}}$ – электрическая постоянная, перепишем уравнение (1) в виде: где ${{E}_{r}}$ – радиальная составляющая вектора напряженности электрического поля.

При прохождении заряженных частиц через диэлектрик их кинетическая энергия расходуется, в основном, на возбуждение молекул и ионизацию вещества, которая сопровождается образованием электрон-дырочных пар и других заряженных дефектов структуры, и, как следствие, возникновением радиационной проводимости диэлектрика. Например, согласно лабораторным экспериментам и расчетам работы [Rodgers et al., 2000], при облучении тефлонового и эпоксидного образцов электронами с энергетическим спектром, соответствующим условиям на геостационарной орбите, радиационная проводимость первого образца превосходила его собственную проводимость в 3 раза, а второго – на 2 порядка. В дальнейшем предполагаем, что проводимость $\sigma $ в уравнении (2) включает в себя и собственную, и радиационную, которая зависит от расстояния до поверхности шара.

Предположим, что шар окружен двухкомпонентной плазмой, состоящей из электронов и положительных однозарядных ионов одного типа. Электрическое поле заряженного шара приводит к нарушению квазинейтральности плазмы на расстояниях порядка радиуса Дебая r_D = $ = {{\left\{ {{{{{\varepsilon }_{0}}{{k}_{{\text{B}}}}{{T}_{e}}{{T}_{i}}} \mathord{\left/ {\vphantom {{{{\varepsilon }_{0}}{{k}_{{\text{B}}}}{{T}_{e}}{{T}_{i}}} {\left[ {{{n}_{e}}{{e}^{2}}\left( {{{T}_{e}} + {{T}_{i}}} \right)} \right]}}} \right. \kern-0em} {\left[ {{{n}_{e}}{{e}^{2}}\left( {{{T}_{e}} + {{T}_{i}}} \right)} \right]}}} \right\}}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}},$ где ${{n}_{e}}$ – концентрация космической плазмы; ${{k}_{{\text{B}}}}$ – постоянная Больцмана; ${{T}_{e}}$ и ${{T}_{i}}$ – температуры электронов и ионов соответственно [Альперт и др., 1964]. Используя следующие усредненные значения параметров ионосферы для высоты 1500 км [Новиков и др., 2007]: ${{n}_{e}} \approx 1.6 \times {{10}^{{10}}}$ м^–3, ${{T}_{e}} \approx 3300$ К, ${{T}_{i}} \approx 2050$ К, получаем, что ${{r}_{{\text{D}}}} \approx 2.1$ см. Рассматривая в качестве примера наноспутник BLITS-M, имеющий форму шара с радиусом $R = 11$ см, можно полагать, что вокруг спутника образуется узкий заряженной плазменный слой с характерным размером $\sim {\kern 1pt} {{r}_{{\text{D}}}} \ll R \ll {{\lambda }_{{e,i,n}}},$ где ${{\lambda }_{{e,i,n}}}$ обозначает длины свободного пробега электронов, ионов и нейтральных частиц. Снаружи этого слоя потенциал принимает значение ${{\varphi }_{1}} \approx - 0.690{{{{k}_{{\text{B}}}}{{T}_{{e,i}}}} \mathord{\left/ {\vphantom {{{{k}_{{\text{B}}}}{{T}_{{e,i}}}} {e,}}} \right. \kern-0em} {e,}}$ а затем его значение стремится к нулю при $r \to \infty $ по асимптотическому закону $\varphi \approx - {{0.237{{k}_{{\text{B}}}}{{T}_{{e,i}}}{{R}^{2}}} \mathord{\left/ {\vphantom {{0.237{{k}_{{\text{B}}}}{{T}_{{e,i}}}{{R}^{2}}} {(e{{r}^{2}})}}} \right. \kern-0em} {(e{{r}^{2}})}}$ [Альперт и др., 1964]. При указанных выше численных значениях параметров получаем, что ${{\varphi }_{1}} \approx - 0.2$ В. Из дальнейшего анализа будет видно, что для потенциала, ${{\varphi }_{0}}$, поверхности спутника выполняется соотношение $e\left| {{{\varphi }_{0}}} \right| \gg {{k}_{{\text{B}}}}{{T}_{{e,i}}},$ т.е. $\left| {{{\varphi }_{0}}} \right| \gg \left| {{{\varphi }_{1}}} \right|.$ Таким образом, заряженный плазменный слой, окружающий спутник, практически полностью экранирует его электрическое поле на расстояниях, превышающих ${{r}_{{\text{D}}}}.$

Учитывая узость этого слоя, можно грубо оценить потери энергии электронов в дебаевском слое следующим образом: ${{w}_{0}}\sim e\left| {{{\varphi }_{0}}} \right|\sim e{{E}_{0}}{{r}_{{\text{D}}}},$ где ${{E}_{0}}$ – электрическое поле на поверхности спутника. Предположим, что кинетическая энергия налетающих электронов РПЗ меняется в пределах от ${{w}_{{\min }}}$ до ${{w}_{{\max }}}.$ Учитывая потери энергии электронов в дебаевском слое и полагая вначале, что ${{w}_{{\min }}} > {{w}_{0}},$ заключаем, что энергии электронов, достигающих поверхности шара, варьируются в пределах ${{w}_{{\min }}} - {{w}_{0}} < w < {{w}_{{\max }}} - {{w}_{0}}.$ Плотность потока этих электронов на поверхности шара определяется функцией $j = j\left( {w + {{w}_{0}},t} \right).$

Пусть ${{l}_{{\max }}}$ обозначает максимальный средний пробег в диэлектрике налетающих частиц с максимальной энергией ${{w}_{{\max }}} - {{w}_{0}}.$ В силу сферической симметрии задачи напряженность электрического поля внутри шара в области $r < R - {{l}_{{\max }}}$ равна нулю. Учитывая это обстоятельство, проинтегрируем уравнение (2) по радиусу от $R - {{l}_{{\max }}}$ до r. В результате получим:

Решение уравнения (3) с нулевым начальным условием имеет вид:

В этом соотношении функция $j\left( {w + {{w}_{0}},t} \right)$ равна плотности потока падающих электронов, длина пробега которых в веществе шара равна расстоянию $r = l\left( w \right).$ Если функция $l\left( w \right)$ известна, то с ее помощью можно найти неявную зависимость $j$ от радиуса r. Заметим, что функция $j$ может зависеть от времени, если изменяются внешние условия, связанные с активностью Солнца, магнитными бурями и другими причинами.

3. СТАЦИОНАРНОЕ РАСПРЕДЕЛЕНИЕ ПОЛЕЙ И ОБЪЕМНЫХ ЗАРЯДОВ

Исследуем полученное решение для случая, когда плотность потока падающих электронов $j$ не зависит от времени. Характерное время релаксации электрических зарядов $\tau = {{\varepsilon {{\varepsilon }_{0}}} \mathord{\left/ {\vphantom {{\varepsilon {{\varepsilon }_{0}}} \sigma }} \right. \kern-0em} \sigma }$ в формуле (4) составляет от нескольких часов до нескольких дней в зависимости от типа диэлектрика и характера его проводимости [Сурков и Мозгов, 2019]. Если $t \gg \tau $ то решение (4) упрощается. Его можно легко получить из уравнения (3), если пренебречь производной по времени от ${{E}_{r}}$ и считать, что $\sigma $ не зависит от t. Подставляя затем в интеграл $dr = - dl$ и переходя к переменной интегрирования $w$ получаем, что стационарное распределение электрического поля в шаре имеет вид:

Здесь $w\left( r \right)$ обозначает кинетическую энергию электронов с пробегом $R - r,$ а $\sigma \left( r \right)$ задает радиальное распределение электропроводности при $t \gg \tau .$

Формула (5) описывает стационарный режим, при котором распределение зарядов и электрического поля внутри шара остается постоянным. В этом режиме поток электронов РПЗ, падающих на поверхность, и поток электронов, выходящих из объема на поверхность вследствие электропроводности шара, равны друг другу. Заряд, образующийся на поверхности шара, не влияет на поле внутри шара из-за сферической симметрии задачи. Кроме того, этот поверхностный заряд достаточно быстро эмитирует в окружающее пространство вследствие фотоэффекта и вторичной электронно-ионной эмиссии [Сурков и Мозгов, 2019]. Поэтому поле снаружи шара, в основном, определяется объемным зарядом.

Плотность потока электронов РПЗ может меняться в широких пределах в зависимости от энергии электронов, солнечной активности и т.п. На дневной стороне ионосферы при умеренной солнечной активности зависимость $\log j$ от $\log w$ приблизительно линейная в диапазоне энергий электронов от 0.1 до $2{\kern 1pt} - {\kern 1pt} 3$ МэВ [Кузнецов, 2007]. Поэтому связь величин $j$ и $w$ можно аппроксимировать приближенной степенной зависимостью вида: $j\left( w \right) = {{b}_{1}}{{w}^{{ - {{b}_{2}}}}}.$ Для высот в $500{\kern 1pt} - {\kern 1pt} 600$ км плотность потока электронов $j$ в интересующем нас диапазоне энергий уменьшается от ${{10}^{6}}$ до ${{10}^{2}}$ см^–2 с^–1 МэВ^–1. При этом параметры данной зависимости имеют следующие значения: b₁ = $ = 2 \times {{10}^{3}}$ см^–2 с^–1 ${\text{Мэ}}{{{\text{В}}}^{{{{b}_{2}} - 1}}},$ ${{b}_{2}} = 2.7$ [Сурков и Мозгов, 2019]. Подставляя это соотношение в интеграл (5) и производя интегрирование, получим:

Аналогичным образом можно описать электрическое поле, обусловленное потоком протонов или других заряженных частиц, падающих на поверхность спутника. Однако, учитывая, что на низких орбитах плотность потока электронов приблизительно на три порядка большее плотности потока протонов [Кузнецов, 2007], будем в дальнейшем пренебрегать вкладом потока протонов.

Длина пробега в веществе электронов с энергиями порядка $0.1{\kern 1pt} - {\kern 1pt} 10$ МэВ определяется следующей эмпирической формулой [Weber, 1964]:

где ${{a}_{1}} = 0.55$ г см^–2 МэВ^–1, ${{a}_{2}} = 0.9841$ и ${{a}_{3}} = $ = 3 МэВ^–1 – эмпирические параметры; ${{\rho }_{m}}$ – плотность вещества, выраженная в г/см³, а энергия электронов $w$ измеряется в МэВ. Заменяя в соотношении (7) $l\left( w \right)$ на $r$ и выражая из него w, получаем следующую зависимость:

Если ${{w}_{{\min }}} > {{w}_{0}},$ то соотношения (7) и (8) применимы в диапазоне $R - {{l}_{{\max }}} < r < R - {{l}_{{\min }}}.$

Радиационная электропроводность, возникающая под действием потока электронов РПЗ, падающих на шар, имеет максимальное значение ${{\sigma }_{r}}$ на его поверхности. В направлении вглубь шара она убывает с характерным масштабом $\bar {l},$ равным средней длине пробега электронов в веществе шара. Для радиусов r, удовлетворяющих условию $R - r \gg \bar {l},$ радиационная электропроводность становится меньше собственной электропроводности ${{\sigma }_{0}}.$ Учитывая, что $R \gg \bar {l}$ и ${{\sigma }_{r}} \gg {{\sigma }_{0}},$ используем следующую аппроксимацию:

где $\bar {l}$ средний по потоку пробег электронов:

Соотношение (10) применимо при условии, что ${{w}_{{\min }}} > {{w}_{0}}.$ Если выполняется противоположное неравенство, то часть налетающих электронов не сможет достигнуть поверхности шара из-за электростатического отталкивания в дебаевском слое, окружающем шар. Поверхности шара достигнут только те электроны, чья энергия превосходит ${{w}_{0}}.$ Поэтому в этом случае необходимо заменить в соотношении (10) ${{w}_{{\min }}}$ на ${{w}_{0}}.$

Среднюю длину пробега найдем, подставляя соотношения для $j\left( w \right)$ и $l\left( w \right)$ в формулу (10). После некоторых преобразований получим:

Подставляя функции $w\left( r \right)$ и $\sigma \left( r \right)$ в формулу (6), получим распределение электрического поля в шаре по радиусу. Если ${{w}_{{\min }}} > {{w}_{0}},$ то это распределение применимо в диапазоне $R - {{l}_{{\max }}} < r < R - {{l}_{{\min }}},$ где ${{l}_{{\max }}}$ и ${{l}_{{\min }}}$ − длины пробега электронов с энергиями ${{w}_{{\max }}} - {{w}_{0}}$ и ${{w}_{{\min }}} - {{w}_{0}},$ соответственно. Если ${{w}_{{\min }}} < {{w}_{0}},$ то формально ${{l}_{{\min }}} = 0.$ В узком слое, ограниченном радиусами $R - {{l}_{{\min }}} < r < R,$ электроны отсутствуют, поскольку в модели не рассматриваются электроны с начальными энергиями, меньшими ${{w}_{{\min }}}.$ Тогда модуль электрического поля на поверхности спутника ${{E}_{0}} \approx \varepsilon \left| {{{E}_{r}}} \right|,$ где ${{E}_{r}}$ в формуле (6) берется в точке $r = R - {{l}_{{\min }}}.$ Энергию ${{w}_{0}}\sim e{{r}_{{\text{D}}}}{{E}_{0}},$ теряемую падающими электронами в дебаевском слое, оценим так:

Следует отметить, что если ${{w}_{{\min }}} < {{w}_{0}},$ то в формулах (10)−(12) необходимо заменить ${{w}_{{\min }}}$ на ${{w}_{0}}.$ В этом случае формула (12) определяет неявную зависимость ${{w}_{0}}$ от параметров задачи.

Проведем численные оценки полученных величин. Лабораторные эксперименты и расчеты показывают, что при облучении диэлектрических образцов электронами с энергиями, соответствующими условиям на геостационарной орбите, их проводимость может увеличиваться от нескольких раз до двух-трех порядков величины [Tyutnev et al., 2015].В качестве примера используем параметры кварцевого стекла: $\varepsilon = 3.7$, ${{\sigma }_{0}} = {{10}^{{ - 16}}}$ См/м и ${{\rho }_{m}} = 2.3$ г/см³ [Бабичев и др., 1991]. Используя эти значения и указанные выше параметры, а также ${{\sigma }_{r}} = {{10}^{{ - 14}}}$ См/м, ${{w}_{{\min }}} = 0.1$ МэВ и ${{w}_{{\max }}} = 3{\kern 1pt} - {\kern 1pt} 10$ МэВ, получаем следующие оценки: ${{w}_{0}} = 0.73$ кэВ, ${{E}_{0}} = 0.56$ кВ/см, ${{l}_{{\min }}} = 0.06$ мм и ${{l}_{{\max }}} = 0.65{\kern 1pt} - {\kern 1pt} 2.3$ см. В этом случае потерями энергии налетающих электронов в плазменном слое можно пренебречь по сравнению с начальной энергией электронов.

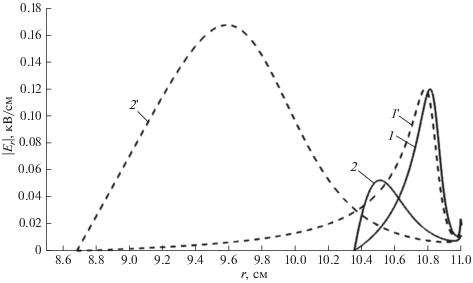
Зависимость ${{E}_{r}}\left( r \right),$ рассчитанная при указанных выше параметрах, проиллюстрирована на рис. 2 линиями 1 и 1 ' для случаев, когда ${{w}_{{\max }}} = 3$ МэВ и ${{w}_{{\max }}} = 10$ МэВ, соответственно. Поскольку ${{E}_{r}} < 0,$ то для удобства изображены графики функции $\left| {{{E}_{r}}} \right|.$ Как видно из этих графиков, один из максимумов находится вблизи поверхности на расстоянии ${{l}_{{\min }}}$ от нее. Второй максимум, имеющий большую величину, располагается в глубине. Для графика, изображенного линией 1, максимальное значение поля, равное 0.175 кВ/см, достигается при $r = 10.86$ см. Для линии 1 ' данные значения равны 0.166 кВ/см и 10.83 см, соответственно. Эти величины очень близки, т.е. для указанных выше параметров величина и положение максимума электрического поля мало зависят от величины ${{w}_{{\max }}}.$

Для орбит высотой ~1500 км плотность потока электронов РПЗ с интересующими нас энергиями варьируется в пределах порядка ${{10}^{4}}{\kern 1pt} - {\kern 1pt} $ 10⁷ см^–2 с^–1 МэВ^–1. Для этого диапазона энергий параметры, определяющие зависимость $j\left( w \right),$ имеют следующие значения: b₁ = 3.2 × × 10⁵ см^–2 с^–1 ${\text{Мэ}}{{{\text{В}}}^{{{{b}_{2}} - 1}}},$ ${{b}_{2}} = 1.5$ [Сурков и Мозгов, 2019]. В этом случае получаем, что ${{w}_{0}} = 21{\kern 1pt} - {\kern 1pt} 23$ кэВ, ${{E}_{0}} = 11$ кВ/см, т.е. поправка ${{w}_{0}}$ становится существенной. Зависимость $\left| {{{E}_{r}}} \right|$ от $r$ для этого случая показана на рис. 2 линиями 2 и 2 ', которым отвечают значения ${{w}_{{\max }}} = 3$ и 10 МэВ, соответственно. Для удобства изображения, значения $\left| {{{E}_{r}}} \right|$ уменьшены в 50 раз. Эти графики также имеют немонотонный характер. Для кривой 2 максимальное значение, равное 7.19 кВ/см, достигается при $r = 10.60$ см. Для кривой 2 ' эти значения равны 12.8 кВ/см и $r = 9.89$ см, соответственно. Таким образом, при указанной выше плотности потока электронов величина и положение максимума графиков, а также глубина проникновения поля (0.65 см и 2.3 см для линий 2 и 2 ', соответственно) существенно зависят от величины ${{w}_{{\max }}}.$

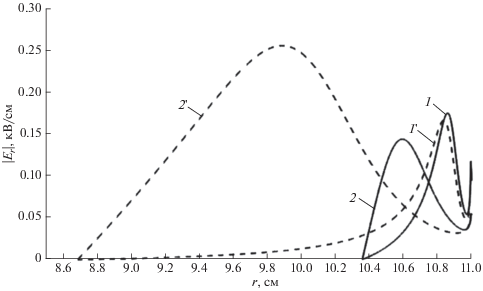
Теперь проанализируем, каким образом влияет на электрическое поле параметр ${{\sigma }_{r}},$ определяющий максимальное значение радиационной проводимости диэлектрика. На рисунке 3 приведены зависимости модуля радиальной составляющей электрического поля от радиуса при тех же параметрах, которые использовались для рис. 2, но для значения ${{\sigma }_{r}} = 5 \times {{10}^{{ - 14}}}$ См/м. Прежде всего отметим, что графики, по-прежнему, имеют немонотонный характер. Сравнение с рис. 2 показывает, что увеличение радиационной проводимости ${{\sigma }_{r}}$ приводит к уменьшению максимумов электрического поля и смещению их положений по направлению к центру шара. Например, для кривых 1 и 2 максимумы уменьшаются до значений 0.12 и 2.61 кВ/см, соответственно. Координаты соответствующих максимумов, $r = 10.81$ и 10.51 см, располагаются немного ближе к центру шара по сравнению с рис. 2.

4. ОБСУЖДЕНИЕ

Отметим, что результаты работы носят оценочный характер, поскольку используется простейшая модель сферического спутника, в которой не учитывается зависимость свойств материала от температуры, не рассматриваются суточные и сезонные вариации потока электронов РПЗ, падающих на спутник, и ряд других факторов. Тем не менее, полученные в работе аналитические результаты позволяют проанализировать процесс электризации спутников в зависимости от различных параметров, включая радиационную электропроводность диэлектриков.

Результаты расчета показывают, что электрическое поле и заряды распределяются вблизи поверхности спутника в слое толщиной от $0.65$ до $2.3$ см в зависимости от максимальной энергии электронов РПЗ. Немонотонный характер зависимостей ${{E}_{r}}\left( r \right),$ представленных на рис. 2 и 3, отличается от результатов работы [Сурков и Мозгов, 2019], где модуль ${{E}_{r}}$ монотонно увеличивался в направлении к поверхности шара. Одним из важных факторов, влияющих на немонотонный характер функции ${{E}_{r}}\left( r \right),$ является зависимость радиационной проводимости диэлектрика от радиуса, которая не учитывалась в работе [Сурков и Мозгов, 2019].

Для лучшего понимания полученных выше закономерностей сделаем ряд упрощений в формулах (6)−(8). Полагая, что ${{{{a}_{2}}} \mathord{\left/ {\vphantom {{{{a}_{2}}} {\left( {1 + {{a}_{3}}w} \right)}}} \right. \kern-0em} {\left( {1 + {{a}_{3}}w} \right)}} \ll 1,$ опустим соответствующее слагаемое в формуле (7). Тогда из соотношения (8) следует, что $w \approx {{x{{\rho }_{m}}} \mathord{\left/ {\vphantom {{x{{\rho }_{m}}} {{{a}_{1}},}}} \right. \kern-0em} {{{a}_{1}},}}$ где $x = R - r$ − расстояние до поверхности шара. Анализ числовых значений параметров показывает, что вблизи точки максимума $\left| {{{E}_{r}}} \right|,$ во-первых, можно пренебречь вторым слагаемым в квадратных скобках в формуле (6) и, во-вторых, положить, что множитель ${{{{R}^{2}}} \mathord{\left/ {\vphantom {{{{R}^{2}}} {{{r}^{2}}}}} \right. \kern-0em} {{{r}^{2}}}} \approx 1.$ Тогда соотношение (6) упрощается к виду:

Функция в числителе соотношения (13) определяет зависимость электрического поля от длины пробега электронов РПЗ в корпусе спутника. Эта функция убывает с расстоянием x, поскольку ${{b}_{2}} > 1.$ Если бы проводимость $\sigma $ была бы постоянной величиной, то электрическое поле также убывало бы расстоянием в соответствии с результатами работы [Сурков и Мозгов, 2019]. Но, поскольку электропроводность в знаменателе (13) также убывает, то функция ${{E}_{r}}\left( x \right)$ может быть немонотонной. Для нахождения экстремальных точек найдем производную выражения (13) по x. Приравняв ее к нулю, получаем неявное уравнение, определяющее экстремальные точки:

В этом соотношении $\bar {l}$ зависит от ${{w}_{{\max }}},$ ${{b}_{2}}$ и других параметров задачи в соответствии с соотношением (11). При указанных выше значениях параметров уравнение (14) имеет два корня, один из которых определяет минимум, а другой – максимум функции ${{E}_{r}}\left( x \right).$ Например, для параметров, отвечающих кривым 1 ' и 2 ' на рис. 2, решение уравнения (14) дает следующие приблизительные координаты точек максимумов: ${{r}_{{\max 1}}} = R - {{x}_{{\max 1}}}$ ≈ ≈ 10.85 см для первой кривой и ${{r}_{{\max 2}}} \approx 9.61$ см для второй, которые близки к координатам соответствующих максимумов кривых 1 ' и 2 '.

Анализ распределения объемных зарядов ${{\rho }_{e}}$ показывает, что ${{\rho }_{e}} < 0$ во внутренней области $R - {{l}_{{\max }}} < r < {{r}_{0}},$ где ${{r}_{0}}$ приблизительно совпадает с координатой максимума ${{E}_{r}}.$ Однако, в области $r > {{r}_{0}},$ где меняет знак производная ${{E}_{r}},$ появляется положительно заряженный слой. Физически это связано с тем, что функция ${{\rho }_{e}}$ зависит не только от распределения внедренных в диэлектрик электронов, но и от $\nabla \sigma .$

Таким образом, особенности пространственных распределений электрического поля и зарядов вызваны тем, что концентрация внедренных электронов и радиационная проводимость диэлектрика увеличиваются с радиусом. “Конкуренция” этих двух тенденций, одна из которых увеличивает поле, а другая его уменьшает, приводит к тому, что у функции ${{E}_{r}}$ возникает максимум вблизи поверхности спутника. Координата расположения этого максимума и его величина существенно зависят как от параметров потока электронов РПЗ, так и от радиационной проводимости материала спутника.

Расчеты показывают, что увеличение плотности потока и энергии электронов РПЗ ведет к росту электрического поля в диэлектрике, при этом величина максимума поля приблизительно на два порядка меньше напряженности пробоя диэлектрика в лабораторных условиях. Однако, эксперименты на КА CRESS [Frederickson et al., 1992; Акишин и др., 2007] показали, что в космических условиях пробой на объемных электрических зарядах в диэлектрике возникает при флюенсе электронов на $2{\kern 1pt} - {\kern 1pt} 3$ порядка меньше пороговой величины, при которой пробой наблюдается в лабораторных условиях. Поэтому можно предположить, что электрические микропробои могут возникать в поверхностном слое диэлектрика, особенно вблизи неоднородностей, микротрещин и неровностей поверхности, где локальное электрическое поле больше среднего значения. Инициаторами пробоя могут, например, послужить галактические или солнечные космические протоны с большими энергиями, длина пробега которых сравнима с диаметром спутника или превышает его.

Локальный разогрев вещества при микропробоях может сопровождаться термическими деформациями и микроразрушениями вещества, которые будут накапливаться со временем. С этой точки зрения продолжительное облучение диэлектрического спутника электронами РПЗ аналогично действию длительных механических нагрузок, которые приводят к усталостному разрушению материалов.

5. ЗАКЛЮЧЕНИЕ

Результаты модельных расчетов показывают, что облучение диэлектрического спутника электронами РПЗ с энергиями $0.1{\kern 1pt} - {\kern 1pt} 10$ МэВ приводит к возникновению электрического поля и зарядов в поверхностном слое диэлектрика толщиной $\sim {\kern 1pt} 0.65{\kern 1pt} - {\kern 1pt} 2.3$ см. Налетающие электроны теряют частично свою энергию в дебаевском экранирующем слое, образующемся на внешней поверхности спутника вследствие поляризации космической плазмы в электрическом поле спутника. Потери энергии электронов, согласно оценкам, составляют $1{\kern 1pt} - {\kern 1pt} 23$ кэВ в зависимости от высоты орбиты спутника. В результате этого эффекта снижается длина пробега электронов в диэлектрике.

Еще одним важным эффектом является увеличение электропроводности поверхностных слоев спутника вследствие ионизации вещества, производимой потоком налетающих электронов. Расчеты, учитывающие эффект радиационной проводимости диэлектрика, показывают, что зависимость электрического поля от радиуса имеет немонотонный характер. Из анализа полученного решения следует, что такой вид зависимости ${{E}_{r}}\left( r \right)$ обусловлен неоднородностью радиационной проводимости диэлектрика.

При увеличении плотности потока и энергии электронов РПЗ максимум электрического поля увеличивается, а его положение смещается от поверхности вглубь спутника. Для выбранных значений параметров и орбит высотой ~1500 км максимальное значение поля оценивается как $2.5{\kern 1pt} - {\kern 1pt} 7$ кВ/см при максимальной энергии электронов 3 МэВ и $8{\kern 1pt} - {\kern 1pt} 13$ кВ/см, если ${{w}_{{\max }}} = 10$ МэВ. Несмотря на то, что эти величины приблизительно на два порядка меньше порога электрического пробоя диэлектрика, можно ожидать локальных электрических разрядов вблизи неоднородных включений и неровностей на поверхности диэлектрика. Вероятность микропробоев диэлектрика возрастает в периоды максимума солнечной активности.

Несмотря на оценочный характер проведенного исследования, результаты этой работы могут быть применены к низкоорбитальным наноспутникам сферической формы типа BLITS и BLITS-M.