Журнал физической химии, 2020, T. 94, № 8, стр. 1285-1290

Современные теоретические работы, направленные на расчет термодинамических свойств флюидов используют либо численное моделирование на основе методов Монте-Карло или молекулярной динамики, либо методы, опирающиеся на теорию интегральных уравнений, с различными приближениями для их замыкания (в частности, упрощенный вариант – теория функционала плотности). Каждый из этих подходов имеет свои достоинства и недостатки, обусловленные точностью описания, сложностью моделирования и величиной компьютерных ресурсов, необходимых для проведения расчетов.

В данной работе используется модификация модели решеточного газа (МРГ) [1–3], требующая гораздо меньших компьютерных ресурсов, чем в численном эксперименте, менее трудоемкая, чем интегральные уравнения, и обеспечивающая лучшую точность в околокритической области, чем теория функционала плотности, а также более гибкая, чем все перечисленные теории, для микронеоднородных систем, в частности для расчета свойств границ раздела фаз (адсорбции и поверхностного натяжения).

Подходы с МРГ, как правило, используют простейшие аппроксимации, позволяющие замкнуть уравнения на распределения компонентов смеси: приближение молекулярного поля (ПМП) или квазихимическое приближение (КХП). Однако ПМП (аналогично теория функционала плотности) обладает серьезным дефектом, связанным с пренебрежением эффектов корреляций в пространственном распределении компонентов, что не позволяет его использовать для задач химической кинетики – получающиеся уравнения для равновесного распределения из кинетического рассмотрения не согласуются с прямым построением уравнений для равновесного распределения [2, 3]. КХП свободно от этого недостатка и дает возможность самосогласованного описания равновесия и кинетики в конденсированных фазах при любых степенях отклонения от равновесия и любых плотностях.

В работах [3–6] МРГ была расширена за счет движения частиц внутри ячейки и построены уравнения, описывающие смещения частиц из центра ячейки. Движение центра масс частицы внутри ячейки приводит к тому, что плотность вероятности для нахождения молекулы внутри ячейки есть непрерывная функция ее координаты.

В традиционной дискретной форме записи состояния занятости узлов 1 ≤ f ≤ N задаются с помощью величин $\gamma _{f}^{i}:\gamma _{f}^{i}$ = 1, если в узле находится молекула сорта i, иначе $\gamma _{f}^{i}$ = 0; 1 ≤ i ≤ s, где s – число разных состояний занятости любого узла, включая вакансию. Решеточная система рассматривается как система, находящаяся в равновесии с внешним термостатом, определяющим химический потенциал молекул, поэтому при статистическом описании удобно использовать большой канонический ансамбль. Полная энергия смеси в большом каноническом ансамбле записывается следующим образом [2]:

где $\nu _{f}^{i}$ = $--{{\beta }^{{ - 1}}}\ln (А_{f}^{i}{{P}_{i}})$ – одночастичный вклад в энергию системы, обусловленный взаимодействием молекулы сорта i с узлом решетки  f (1 ≤ f ≤ N), и отношением статсумм молекул, находящихся в решеточной системе и в термостате; β = = (k_BT)^–1, k_B – константа Больцмана; Р_i – парциальное давление молекул i в термостате, для вакансии $a_{f}^{{v}}{{P}_{{v}}}$ = 1; $А_{f}^{i}$ = ($F_{f}^{i}$)βexp(β$Q_{f}^{i}$)/F_i – локальная константа удерживания для частицы i на узле f (для адсорбции и абсорбции это константа Генри); $F_{f}^{i}$ – статсумма молекул i в узле f, F_i – статсумма молекулы i в газовой фазе термостата, $Q_{f}^{i}$ – энергия связи молекулы i с узлом f (это взаимодействие с поверхностью при адсорбции или с твердым телом в междоузельном пространстве при абсорбции). В рассматриваемой ниже объемной фазе $Q_{f}^{i}$ = 0. Вклад латерального взаимодействия описывается через $\varepsilon _{{fg}}^{{ij}}$ – энергию парного взаимодействия ближайших частиц i и j, находящихся на узлах f и g; $\varepsilon _{{fg}}^{{iV}}$ = 0 (энергия взаимодействия любой частицы i с вакансией равна нулю). Индекс g пробегает по всем узлам z(χ) координационной сферы χ. Для простоты ограничимся учетом взаимодействия ближайших соседей.

В континуальном описании движения молекул внутри ячеек введем случайную величину $\gamma _{f}^{i}$(r), которая определяет событие того, что центр массы частицы i находится в точке r внутри ячейки  f, r ∈ ${v}$(f), где ${v}$(f) – объем ячейки  f [4–6]. Тогда полная энергия смеси формально запишется как H = H₁ + H₂, где

где, как и выше, величина $\nu _{f}^{i}$(r_i) = $--{{\beta }^{{ - 1}}}\ln [a_{f}^{i}({{{\mathbf{r}}}_{i}}){{р}_{i}}]$, где $a_{f}^{i}({{{\mathbf{r}}}_{i}})$ = $F_{f}^{i}({{{\mathbf{r}}}_{i}})\beta {\text{/}}{{F}_{i}}$ – локальная константа удерживания частицы i в ячейке f, она отражает поступательное движение частицы i в ячейке f и усредненным образом ее колебания, которые не учитывают сорт соседних молекул; ε_ij – энергия взаимодействия частиц ij, имеющих координаты $r_{f}^{i}$ и $r_{g}^{j}$ в ячейках  f и g.

В континуальном квазихимическом приближении (КХП) [6] все высшие функции распределений аппроксимируются через унарную $\theta _{f}^{i}$(r_i) и парные $\theta _{{fg}}^{{ij}}$(r_ir_j) функции распределения (ФР). В нем учитываются прямые корреляции между взаимодействующими частицами. В этом случае уравнения на равновесное распределение частиц записываются в виде: выражение для унарной функций распределений

и уравнение для парных ФР имеет подобный вид с учетом фиксации частицы ℓ на фрагменте {ζ} относительно частицы i (здесь g ≠ ζ, что обозначено как {g} ∈ z) Для континуальных унарных и бинарных ФР имеют место нормировочные соотношения где функции $\theta _{f}^{i}$ и $\theta _{{fg}}^{{ij}}$ являются обычными функциями дискретной решеточной задачи, 1 ≤ i, j ≤ s [2–4]. В континуальном КХП решение ищется относительно функции распределений $\theta _{f}^{i}(r_{f}^{i})$ и $\theta _{{fg}}^{{ij}}({{r}_{i}}{{r}_{j}})$. Найденное решение системы уравнений позволяет рассчитать давление расширения и все другие термодинамические функции системы.

Общую запись этих интегральных уравнений будем конкретизировать для частицы сорта А и вакансий (в дискретной модели это число состояний занятости узла равно двум). Для практической реализации описания распределения частицы А внутри ячейки сделаем следующее построение: разобьем каждую ячейку с номером f на микроячейки. Центр микроячейки характеризуется своей координатой r_f, и будем считать, что частица сорта i, находящаяся в микроячейке с координатой r_f , описывает вероятность $\theta _{f}^{i}(r_{f}^{i})$ нахождения указанной частицы в данной ячейке. Само состояние частицы в положении $r_{f}^{i}$ будем считать квазисортом частицы i. Таким образом, разделим узел-ячейку на микроячейки и будем считать что ситуация, когда центр масс частицы находится в микроячейке с координатой r_i , соответствует сорту i частиц:

Тогда интегрирование по объему ячейки представляет собой суммирование по всем микроячейкам что эквивалентно суммированию по всем сортам частиц i = 1, …, s – 1. Как и раньше, сорт s относится к вакансиям, положение частицы в ячейке не фиксируется своей координатой.

Такая дискретизация положений частицы по микроячейкам и представление микроячеек как эффективных сортов частиц позволяет формально выразить континуальная КХП-модель в виде дискретной многокомпонентной модели решеточного газа [7–12], которая может быть решена теми же средствами, что и обычное КХП в дискретной модели. В итоге, размерность редуцированной системы уравнений совпадает с числом микроячеек в каждой ячейке.

Ниже приводятся результаты сопоставления использования континуальной и дискретной версии КХП, чтобы продемонстрировать те отличия, к которым приводит учет континуальности решеточной модели. Расчеты проведены с учетом взаимодействия только между ближайшими соседями и ограничены областью однофазности состояний атомов аргона. Для континуального описания это означает, что учитываются все взаимодействиям между различными положениями двух соседних частиц А, находящихся внутри этих двух макроячеек. Естественно, что при этом расстояния между частицами АА могут быть больше, чем параметр дискретной модели, равный 2^1/2 σ, где σ – параметр потенциала Леннард–Джонса, отвечающий твердой сфере частицы. Ограничения на сближение двух части АА определяются величиной σ.

На рис. 1 показаны распределения центра масс частицы А внутри центральной ячейки для двух решеток для переменной плотности флюида (поле слева), а также распределение функции t_VA(r) (поле справа) при тех же условиях (здесь z – число ближайших соседей, D – размерность системы, βε – безразмерный энергетический параметр, n – число дроблений стороны ячейки). Функция t_VA(r) отражает вероятность нахождения соседней частицы А относительно вакансии в центральной ячейке.

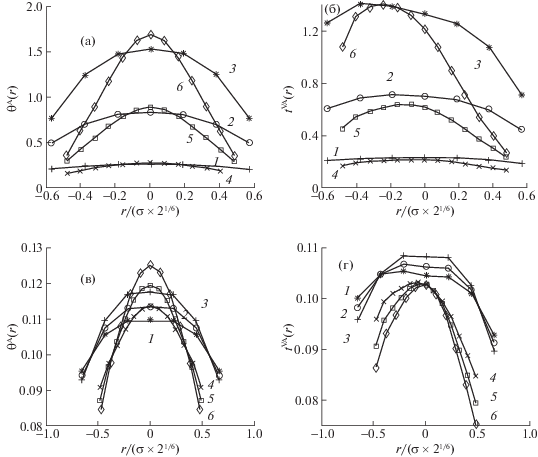
На рис. 1а продемонстрирован распределенный характер положения центра масс частицы А. Вероятность ее нахождения в центре больше, чем около границы ячейки. По мере увеличения плотности локализация частицы в центре становится более выраженной. Для газовых плотностей центр масс распределен практически постоянно вдоль сечения ячейки. Характер распределений для разных решеток одинаковый, диапазон изменения смещений от центра определяется разными размерами ячеек.

Из рис. 1б (поле справа) следует, что соседняя частица А отражает отсутствие рядом другой частицы А, и центр ее распределения смещен в стороны вакансии. Положение максимума зависит от типа решетки, плотности системы и от температуры. Для малых плотностей распределение частиц рядом с вакансией практически равномерное.

Влияние температуры системы при фиксированной плотности показано на рис. 1 для тех же сечений ячейки для распределения центральной частицы А (рис. 1в) и для частицы А рядом с вакансией (рис. 1г). Характер кривых на рис. 1а и 1б аналогичен рассмотренному выше. Здесь следует отметить, что для любой фиксированной плотности кривые распределения центра масс при разных температурах должны давать постоянную величину среднего значения плотности. Отличия связаны с тем, что демонстрируется только одно сечение ячейки, а внутри нее распределение не является сферически симметричным. В целом, при интегрировании по объему ячейки условие нормировки, естественно, сохраняется (все изложенное относится и к кривым на поле рис. 1а). Помимо анизотропии распределения частиц внутри ячейки отличия между кривыми на рис. 1г связаны с тем, что эти функции напрямую зависят от температуры.

Относительные распределения двух частиц АА позволяют рассчитать радиальную функцию распределения g(r) [13, 14]. Она представлена на вставке рис. 2 для плоской гексагональной решетки. Кривая не сдержит отдельных вкладов от множества отдельных координационных сфер, которые наблюдаются в твердом теле [15]. Тем не менее, на ней можно выявить характерные для жидкого состояния размытые пики для групп молекул, находящихся на разных расстояниях.

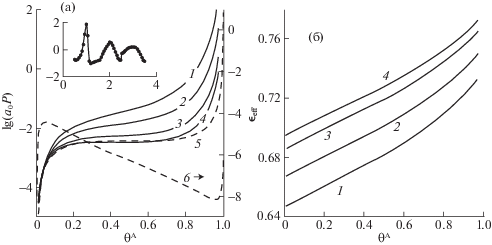
Основное поле рис. 2а демонстрирует изотермы, рассчитанные в ККХП для разных температур с увеличением температур от критической (кривая 1) до надкритических (кривые 2–4) во всем диапазоне плотностей. На поле рис. 2б показаны соответствующие данным изотермам значения эффективных параметров латерального взаимодействия, которые зависят от плотности для каждой из изотерм слева.

Решение системы интегральных уравнений позволяет найти искомые функции распределений, показанные на рис. 1 и 2, и с их помощью рассчитать энергетические параметры

где сумма по f и g берется по всем парам ближайших ячеек [4–6]. Физический смысл этого выражения легко понять на примере малых плотностей, когда КХП-формулы приводят к аналитическим связям между парными функциями и локальными заполнениями на любой решетке (с характерным размером макро- и микроячеек): Тогда эффективный параметр ${{\hat {\varepsilon }}_{{AA}}}$ равен отношению средних величин на разных шкалах (макро и микро) ${{\hat {\varepsilon }}_{{AA}}} = {{\left\langle {{{\varepsilon }_{{AA}}}{{\theta }_{{AA}}}} \right\rangle }_{{{\text{micro}}}}}{\text{/}}{{\theta }_{{AA}}}$, где ${{\theta }_{{AA}}} = {{\theta }^{2}} \times $ $ \times \;\exp [\beta {{\varepsilon }_{{AA}}}({{r}_{0}})]$, r₀ – среднее расстояние между частицами в дискретной модели, и ${{\left\langle {{{{\varepsilon }}_{{AA}}}{{{\theta }}_{{AA}}}} \right\rangle }_{{{\text{micro}}}}}$ = $ = \sum\limits_{f,g} {\int\limits_{\Delta (f)} {\int\limits_{\Delta (g)} {\varepsilon _{{fg}}^{{AA}}(r_{f}^{A},r_{g}^{A})\theta _{f}^{A}(r_{f}^{A})\theta _{g}^{A}(r_{g}^{A}) \times } } } $$ \times \;\exp [\beta \varepsilon _{{fg}}^{{AA}}(r_{f}^{A},r_{g}^{A})]{\kern 1pt} dr_{f}^{A}dr_{g}^{A}$. Отсюда следует, что эффективный параметр ${{\hat {\varepsilon }}_{{AA}}}$ всегда меньше величины параметра латерального взаимодействия, используемого в обычной модели МРГ. На рис. 2б этот параметр при указанных температурах меняется от 0.64 до 0.76.

Аналогичный параметр для решетки z = 12 меняется около 0.5. Это значение объясняет давно замеченный факт при моделировании: решетка z = 6 дает лучшее описание экспериментальных данных по инертным газам [11, 16–19], чем z = 12. Хотя структурные данные [15, 20, 21] для инертных газов соответствуют окружению любого атома 12 соседями, а не шестью. Этот факт так и оставался без объяснения. Данная модель позволяет дать ему корректную интерпретацию. Общая энергия взаимодействия равна $z{{\varepsilon }_{{AA}}}$. В силу уменьшения средней энергии реального взаимодействия ${{\hat {\varepsilon }}_{{AA}}}$ в 2 раза по сравнению с величиной ε_AA получаем, что общей энергии взаимодействия соответствует величина z = 6 (т.е. 12ε_AA/2 = 6ε_AA).

Данные рис. 1 и 2 показывают, что модель полностью снимает исходное локализованное состояние молекул и является аналогом интегральных континуальных уравнений. Отметим также, что предложенная версия континуального представления смещений не является единственной, возможна другая версия ее реализации, в которой задача сводится известной проблеме размещения на решеточной структуре больших частиц, блокирующих множество соседних узлов [7–12]. Преимущества каждого из подходов еще предстоит выяснить.

На рис. 3 показано сравнение между собой наиболее распространенных термодинамических функций, рассчитанных в дискретной и континуальной моделях в надкритической области при одинаковых приведенных температурах τ = = Т/Т_крит. Несмотря на использование одних и тех же параметров межчастичного взаимодействия отличия между кривыми значительно превосходят точность экспериментальных измерений, что необходимо учитывать при использовании континуального описания для интерпретации экспериментов.

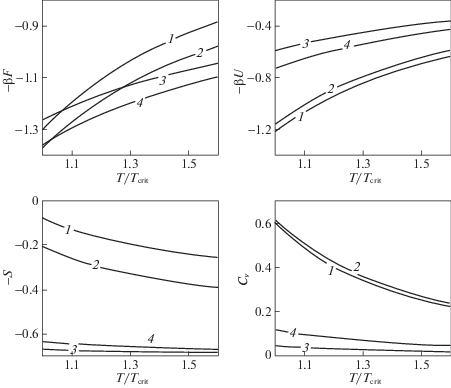
Таким образом, предложенная версия описания континуального распределения молекул внутри ячеек МРГ позволяет в явном виде снять ограничение на фиксацию молекул в центре ячеек для дискретного варианта МРГ. Это значительно меняет концентрационные и температурные зависимости термодинамических функций. Данный подход позволяет дать молекулярную интерпретацию известных подходов с использованием эффективных параметров молекулярных моделей.

Следует отметить, что континуальная версия КХП теории расширяет возможность описания распределения молекул в парном приближении с учетом эффектов корреляции. Это позволяет построить коррелированную теорию типа функционала плотности, что качественно меняет ее смысл и позволяет выйти на самосогласованные расчеты кинетических характеристик, включая скорости элементарных стадий и диссипативные коэффициенты.

Работа выполнена при поддержке Российского фонда фундаментальных исследований (код проекта 18-03-00030а).