Журнал физической химии, 2020, T. 94, № 8, стр. 1279-1284
Частотная дисперсия коэффициента сдвиговой вязкости и магнитовязкий эффект в магнитных жидкостях
К. Комилов a, А. К. Зарипов a, *, Убайди Абдул Маджид b
a Таджикский национальный университет
Душанбе, Таджикистан
b Бадахшанский университет
Бадахшан, Файзабад, Афганистан
* E-mail: afzal.z@mail.ru
Поступила в редакцию 28.10.2019
После доработки 28.10.2019
Принята к публикации 10.12.2019
Аннотация
На основе статистической теории и модели двухкомпонентной системы получено динамическое выражение для коэффициента объемной и сдвиговой вязкости. На основе выбора потенциальных энергий для межмолекулярных и диполь-дипольных взаимодействий, радиальных функций распределения, а также учета влияния внешнего магнитного поля, проведены расчеты зависимости коэффициентов сдвиговой вязкости магнитных жидкостей, приготовленных на основе воды, керосина и ундекана от частоты и величины внешнего магнитного поля. Продемонстрированы области частотных дисперсий для коэффициентов сдвиговой вязкости исследуемых жидкостей и рассмотрен магнитовязкий эффект, существующий в магнитных жидкостях.
Когда первые синтезированные магнитные жидкости показали широкую возможность управлять их физическими свойствами внешним магнитным полем, они сразу нашли свое применение в науке, технике и самых различных областях человеческой деятельности. Вместе с тем были развиты различные теории по физико-химическим свойствам магнитных жидкостей, начиная от простых моделей идеальной магнитной жидкости до сложных теорий, учитывающих в них неравновесную намагниченность и другие внутренние явления.
Работы, посвященные макроскопической и микроскопической теории, основанной на модели идеальной магнитной жидкости [1–3], давали хорошее согласие с экспериментами. Однако, эти теории не могли описать такие явления, как сильное уменьшение вязкости с ростом скорости сдвига, сильный магнитовязкий эффект и другие реологические эффекты. Другие теоретические модели, учитывающие эти эффекты, такие как кластерная модель, вейс-модель, цепочечная модель и т.д., подробно проанализированы в обзорах [4, 5], где описаны преимущества и недостатки этих моделей.
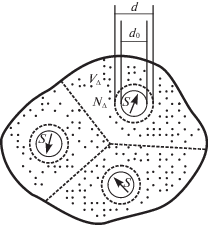
Одна из теоретических моделей, использующихся для описания свойств жидкостей, – ячеечная модель (рис. 1), особенность которой заключается в ее связанности со свойствами межмолекулярного взаимодействия и удачном выборе потенциалов взаимодействия между структурными единицами системы. В работе [6] на основе ячеечной модели построена статистическая теория, позволяющая рассматривать магнитную жидкость как совокупность двух независимых подсистем: магнитная подсистема, состоящая из феррочастиц, и молекулярная подсистема, состоящая из молекул жидкости-носителя. Такой подход показывает, что свободные энергии подсистемы дают аддитивный вклад в полную свободную энергию системы, и соответственно термодинамика системы аддитивна по отношению к термодинамикам подсистемы. Независимость подсистем позволяет проводить независимые вычисления их корреляционных функций.
В монографии [7] также на основе представлений ячеечной модели исследованы физические свойства магнитных жидкостей. Рассмотрены магнитная подсистема при слабых и произвольных полях, поведение магнитной восприимчивости в зависимости от параметров системы, а также свободная энергия и магнитостатика системы. Согласно этой модели, некоторый объем $V$ магнитной жидкости содержащий $N$ молекул жидкости-носителя и $n$ феррочастиц, покрытых слоем поверхностно-активного вещества, разбивается на $n$ ячеек так, чтобы в каждой ячейке содержалась одна феррочастица и молекулы жидкости-носителя. Объемная концентрация феррочастиц с диаметром $d \approx 5{\kern 1pt} - {\kern 1pt} 10$ нм считается малой: $\varphi \approx 0.1{\kern 1pt} - {\kern 1pt} 0.001$. В каждой ячейке в среднем будет содержаться ${{N}_{\Delta }} = N{\text{/}}n = {{10}^{5}}{\kern 1pt} - {\kern 1pt} {{10}^{7}}$ молекул.
При таком разбиении станет возможным: 1) пренебрегать энергией взаимодействия молекул из разных ячеек по сравнению с энергией взаимодействия молекул внутри ячейки; 2) для каждой феррочастицы, кроме феррит-ферритного взаимодействия, учитывается ее взаимодействие с молекулами только из ее ячейки (из-за того, что размер феррочастицы много больше размера молекулы, а убывание потенциала имеет степенной характер, погрешность расчета энергии $\sim {\kern 1pt} N_{\Delta }^{{ - 1/3}}$). Таким образом, сделанные допущения позволяют считать ячейки независимыми, и, в силу аддитивного свойства потенциальной энергии, магнитную жидкость можно рассматривать как совокупность двух независимых подсистем: магнитной подсистемы (состоящей из феррочастиц, находящихся во внешнем магнитном поле и взаимодействующих между собой посредством диполь-дипольного потенциала и короткодействующим отталкивательном потенциалом поверхностно-активного слоя) и молекулярной подсистемы (состоящей из молекул жидкости-носителя, взаимодействующих между собой посредством потенциала, имеющего сферически симметричную асимптотику, и диполь-дипольного взаимодействия).
Нами ранее на основе метода кинетической теории были исследованы вязкоупругие, термоупругие и акустические свойства магнитных жидкостей [8–11]. На основе кинетических уравнений для одно- и двухчастичных функций распределения были выведены уравнения обобщенной гидродинамики, получены выражения для коэффициентов переноса, модулей упругости, скорости и коэффициента поглощения акустических волн, учитывающих внутренние релаксационные процессы. Результаты расчетов по физическим характеристикам магнитной жидкости дали удовлетворительные результаты, качественно согласующиеся с литературными данными. Однако было сделано несколько допущений, которые могли привести к некоторым неточностям.
Как отмечается в [5], во многих теориях при исследовании магнитных жидкостей внимание концентрируется на коллоидной части этой системы. Аналогично, при исследовании электролитов как трехкомпонентных систем, состоящих из ион-ионных и молекулярных подсистем, из-за невероятной сложности задачи прибегают к теории Дебая, где растворитель рассматривают как некоторую сплошную среду с диэлектрической проницаемостью $\varepsilon $, а ионную подсистему описывают уравнениями статистической механики [10].
В наших работах на основании этих представлений кинетические уравнения были построены таким образом, что описывали эволюцию феррочастиц в однородной среде жидкости-носителя. Вклад жидкости-носителя в изменение свойств магнитной жидкости в этом случае учитывался только посредством диэлектрической проницаемости. Проведенные расчеты по вязкостным свойствам для умеренных концентраций удовлетворительно согласуются с экспериментальными данными в отличие от результатов расчетов для концентрированных магнитных жидкостей. Также эти выражения не могут описать сильные магнитовязкие эффекты, проявляющиеся при нахождении магнитной жидкости во внешнем магнитном поле.
В связи с этим в данной работе на основании ячеечной модели магнитную жидкость рассматриваем как бинарную систему, состоящую из компонентов ферритной $f$ и молекулярной $s$ части. Тогда кинетические уравнения для одночастичной ${{f}_{1}}({{{\mathbf{q}}}_{1}},{{{\mathbf{p}}}_{1}},t)$ и двухчастичной ${{f}_{2}}({{{\mathbf{q}}}_{1}},{{{\mathbf{q}}}_{2}},{{{\mathbf{p}}}_{1}},{{{\mathbf{p}}}_{2}},t)$ функций распределения необходимо записать для обоих сортов частиц. Обычно для двухкомпонентных систем с компонентами $a$ и $b$ для учета корреляции распределения частиц обоих сортов двухчастичную функцию распределения выбирают как функцию координат и импульсов частиц сортов $a$ и $b$, т.е. ${{f}_{2}}({\mathbf{q}}_{1}^{{(a)}},{\mathbf{q}}_{2}^{{(b)}},{\mathbf{p}}_{1}^{{(a)}},{\mathbf{p}}_{2}^{{(b)}},t)$. Поскольку в данной модели подсистемы считаются независимыми, двухчастичная функция распределения, описывающая определенную подсистему, является функцией координат и импульсов только данной подсистемы, т.е. ${{f}_{2}}({\mathbf{q}}_{1}^{{(f)}},{\mathbf{q}}_{2}^{{(f)}},{\mathbf{p}}_{1}^{{(f)}},{\mathbf{p}}_{2}^{{(f)}},t)$ и ${{f}_{2}}({\mathbf{q}}_{1}^{{(s)}},{\mathbf{q}}_{2}^{{(s)}},{\mathbf{p}}_{1}^{{(s)}},{\mathbf{p}}_{2}^{{(s)}},t)$.
Таким образом, обозначая массу и концентрацию частицы сорта $i = f,s$ системы через ${{m}_{i}}$ и ${{n}_{i}}$, кинетические уравнения, соответствующие компоненту $i$, запишем в следующем виде:
(1)
$\begin{gathered} \frac{{\partial {{f}_{{1i}}}}}{{\partial t}} + \frac{{p_{1}^{\alpha }}}{{{{m}_{i}}}}\frac{{\partial {{f}_{{1i}}}}}{{\partial q_{1}^{\alpha }}} + {{F}^{\alpha }}({{{\mathbf{q}}}_{1}},t)\frac{{\partial {{f}_{{1i}}}}}{{\partial p_{1}^{\alpha }}} - \\ - \;\int {\frac{{\partial {{\Phi }_{i}}(\left| {{{{\mathbf{q}}}_{1}} - {{{\mathbf{q}}}_{2}}} \right|)}}{{\partial q_{1}^{\alpha }}}\frac{{\partial {{f}_{{2i}}}}}{{\partial p_{1}^{\alpha }}}d{{{\mathbf{q}}}_{2}}d{{{\mathbf{p}}}_{2}}} = \\ = \;{{\beta }_{i}}\frac{\partial }{{\partial p_{1}^{\alpha }}}\left[ {\frac{{\tilde {p}_{1}^{\alpha }}}{{{{m}_{i}}}}{{f}_{{1i}}} + kT({{{\mathbf{q}}}_{1}},t)\frac{{\partial {{f}_{{1i}}}}}{{\partial p_{1}^{\alpha }}}} \right], \\ \end{gathered} $(2)
$\begin{gathered} \frac{{\partial {{f}_{{2i}}}}}{{\partial t}} + \sum\limits_{n = 1}^2 {\left[ {\frac{{p_{n}^{\alpha }}}{{{{m}_{i}}}}\frac{{\partial {{f}_{{2i}}}}}{{\partial q_{n}^{\alpha }}} + {{F}^{\alpha }}({{{\mathbf{q}}}_{n}},t)\frac{{\partial {{f}_{{2i}}}}}{{\partial p_{n}^{\alpha }}}} \right. - } \\ - \;\frac{{\partial {{\Phi }_{i}}(\left| {{{{\mathbf{q}}}_{1}} - {{{\mathbf{q}}}_{2}}} \right|)}}{{\partial q_{n}^{\alpha }}}\frac{{\partial {{f}_{{2i}}}}}{{\partial p_{n}^{\alpha }}} - \\ \left. { - \;\int {\frac{{\partial {{\Phi }_{i}}(\left| {{{{\mathbf{q}}}_{n}} - {{{\mathbf{q}}}_{3}}} \right|)}}{{\partial q_{n}^{\alpha }}}\frac{{\partial {{f}_{{3i}}}}}{{\partial p_{n}^{\alpha }}}d{{{\mathbf{q}}}_{3}}d{{{\mathbf{p}}}_{3}}} } \right] = \\ = \;\sum\limits_{n = 1}^2 {{{\beta }_{i}}} \frac{\partial }{{\partial p_{n}^{\alpha }}}\left[ {\frac{{{{{\tilde {p}}}_{n}}^{\alpha }}}{{{{m}_{i}}}} + kT({{{\mathbf{q}}}_{n}},t)\frac{\partial }{{\partial p_{n}^{\alpha }}}} \right]{{f}_{{2i}}}, \\ \end{gathered} $На основании системы уравнений (1) и (2) после проведения стандартных расчетов [8] получена система уравнений обобщенной гидродинамики, в которых входящие в нее тензор напряжения
(3)
$\begin{gathered} \sigma _{i}^{{\alpha \beta }}({{{\mathbf{q}}}_{1}},t) = - {{P}_{i}}{{\delta }^{{\alpha \beta }}} - K_{i}^{{\alpha \beta }}({{{\mathbf{q}}}_{1}},t) + \\ + \;\frac{1}{2}\int {\frac{{\partial {{\Phi }_{i}}(r)}}{{\partial r}}\frac{{{{r}^{\alpha }}{{r}^{\beta }}}}{r}{{n}_{{2i}}}({{{\mathbf{q}}}_{1}},{\mathbf{r}},t)d{\mathbf{r}}} \\ \end{gathered} $Для исследования вязкостных свойств магнитных жидкостей необходимо получить явные молекулярные выражения для тензоров напряжения магнитной жидкости. Согласно (3), тензор напряжения $\sigma _{i}^{{\alpha \beta }}\left( {{{{\mathbf{q}}}_{1}},t} \right)$ определяется функцией бинарной плотности частиц ${{n}_{{2i}}}({{{\mathbf{q}}}_{1}},{\mathbf{r}},t)$, для которой необходимо иметь уравнение. Ранее в [8] нами было получено уравнение для ${{n}_{2}}({{{\mathbf{q}}}_{1}},{\mathbf{r}},t)$, которое для i-й подсистемы запишется в следующем виде:
(4)
$\frac{{\partial n_{{2i}}^{'}}}{{\partial t}} + {{\omega }_{{0i}}}{{\hat {L}}_{i}}n_{{2i}}^{'}({{{\mathbf{q}}}_{1}},{\mathbf{r}},t) = {{R}_{i}}({{{\mathbf{q}}}_{1}},{\mathbf{r}},t),$Следуя [12], общее решение уравнение (4) представим в виде
(5)
$n_{{2i}}^{'}({{{\mathbf{q}}}_{1}},{\mathbf{r}},t) = \int\limits_0^t {d{{t}_{1}}\int\limits_{ - \infty }^\infty {{{G}_{i}}(r,{{r}_{1}},t - {{t}_{1}})R({{{\mathbf{q}}}_{1}},{{{\mathbf{r}}}_{1}},{{t}_{1}})d{{{\mathbf{r}}}_{1}}} } ,$(6)
$\begin{gathered} {{\eta }_{s}}(\omega ) = \sum\limits_{i = f,s} {\frac{{{{n}_{i}}kT{{\tau }_{{1i}}}}}{{1 + {{{({{\omega }_{i}}{{\tau }_{{1i}}})}}^{2}}}}} + \\ + \;\sum\limits_{i = f,s} {\frac{{n_{i}^{2}\sigma _{i}^{3}}}{{120\pi }}\int\limits_0^\infty {\frac{{\partial {{\Phi }_{i}}}}{{\partial r}}\int\limits_0^\infty {{{G}_{i}}(r,{{r}_{1}},\omega )\frac{{\partial {{g}_{i}}}}{{\partial {{r}_{1}}}}d{{{\mathbf{r}}}_{1}}d{\mathbf{r}}} } } + \\ + \;\frac{{n_{f}^{2}\sigma _{f}^{3}}}{{360\pi }}\int\limits_0^\infty {\frac{{\partial {{\Phi }_{f}}}}{{\partial r}}\int\limits_0^\infty {{{G}_{f}}(r,{{r}_{1}},\omega )\frac{{{{\mu }_{0}}}}{{{{\beta }_{f}}}}\left( {{\mathbf{m}}\nabla } \right)\frac{{\partial H}}{{\partial {v}}}\frac{{\partial {{g}_{f}}}}{{\partial {{r}_{1}}}}d{{{\mathbf{r}}}_{1}}d{\mathbf{r}}} } , \\ \end{gathered} $Для проведения численных расчетов, следуя [4] и [7], потенциальные энергии взаимодействия между частицами подсистем выбираем в следующем виде:
(7)
$\begin{gathered} {{\Phi }_{f}}(r,\theta ,H) = \Phi _{f}^{{L - J}}(r) + {{\Phi }^{{mm}}}(r,\theta ,H) + {{\Phi }^{H}}(\theta ,H), \\ {{\Phi }_{s}}(r,\theta ) = \Phi _{s}^{{L - J}}(r) + {{\Phi }^{{pp}}}(r,\theta ), \\ \end{gathered} $(8)
$\begin{gathered} {{g}_{f}}(r,T) = \exp [ - {{\Phi }_{f}}(r,\theta ,H){\text{/}}kT], \\ {{g}_{s}}(r,n,T) = {{y}_{s}}(\rho *)\exp [ - {{\Phi }_{s}}(r,\theta ){\text{/}}kT]. \\ \end{gathered} $Учитывая (7) и (8), приведем выражения (6) к удобному виду для проведения численных расчетов:
(9)
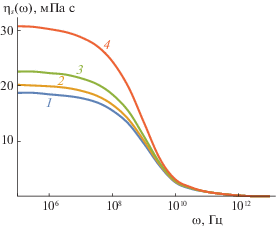
${{\eta }_{s}}(\omega ) = \sum\limits_{i = f,s} {\frac{{{{n}_{i}}kT{{\tau }_{{1i}}}}}{{1 + {{{({{\omega }_{i}}{{\tau }_{{1i}}})}}^{2}}}} + \sum\limits_{i = f,s} {\frac{{4{{\varepsilon }_{i}}n_{i}^{2}\sigma _{i}^{3}}}{{kT}}{{J}_{{si}}}} } ,$На основе (9) проведен расчет динамических коэффициентов сдвиговой вязкости магнитных жидкостей на основе воды, керосина и ундекана с частицами Fe3O4.
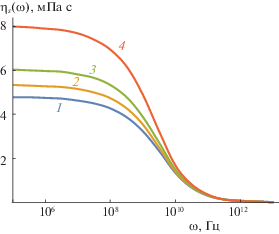
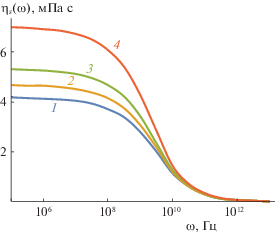
На рис. 2–4 представлены зависимости коэффициента сдвиговой вязкости магнитных жидкостей от частоты внешнего воздействия. На этих рисунках $H = 0$ (1), 50 (2), 100 (3) и $H = 200$ кА (4). Согласно рис. 2–4, область частотной дисперсии ${{\eta }_{s}}(\omega )$ является широкой ($\sim {\kern 1pt} {{10}^{3}}{\kern 1pt} - {\kern 1pt} {{10}^{4}}$ Гц), когда экспериментальные данные по дисперсии вязкости жидкостей дают узкую область ($\sim {\kern 1pt} {{10}^{2}}$ Гц).
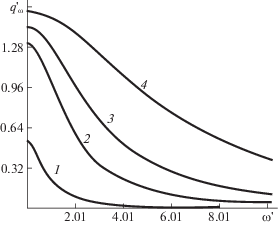
На рис. 5 приведены результаты [14] – зависимости величины $q_{\omega }^{'} = \frac{1}{{(3{\text{/}}2){{\eta }_{o}}\rho }}\operatorname{Re} \eta _{\omega }^{A}$ от безразмерной частоты $\omega {\text{'}}$ для различных значений внешнего магнитного поля. Как видно, результаты наших расчетов качественно согласуются с данными [14].
Рис. 5.
Зависимости безразмерной величины $q{{_{\omega }^{'}}_{{}}}$ от безразмерной частоты $\omega {\text{'}}$ [14].
Результаты расчетов зависимости отношений коэффициентов вязкости $\Delta {{\eta }_{s}}(\omega ) = \frac{{{{\eta }_{s}}(\omega ,H)}}{{{{\eta }_{s}}(\omega ,0)}}$ от величины внешнего магнитного поля приведены на рис. 6 и 7. Кривые 1, 2 на рис. 7 соответствуют объемной концентрации $\varphi = 0.1$, кривые 3, 4 – $\varphi = 0.15$. Как видно, отношение коэффициентов вязкости в магнитных жидкостях для всех концентраций имеют одинаковый нелинейный характер.
Рис. 6.
Зависимости $\Delta {{\eta }_{s}}(\omega )$ от величины $H$ для магнитной жидкости на основе воды; 1 – $\varphi = 0.05$, 2 – $\varphi = 0.12$.
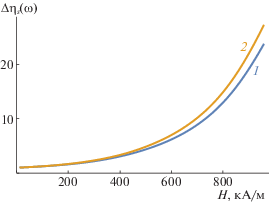
Рис. 7.
Зависимости $\Delta {{\eta }_{s}}(\omega )$ от величины $H$ для магнитной жидкости на основе керосина (2, 4) и ундекана (1, 3).
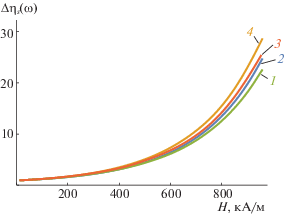
Согласно рис. 6 и 7, проведенные расчеты показывают существование сильного магнитовязкого эффекта для исследуемых магнитных жидкостей, что находится в удовлетворительном согласии с данными [15, 16], и подтверждают правильный учет дипольного взаимодействия.
Как отмечается в [17, 18], при воздействии внешних электромагнитных полей в области высоких частот значения коэффициентов вязкости сильно уменьшается. Как следует из результатов наших расчетов и авторов [14], внешнее возмущение в области высоких частот также приводит к сильному уменьшению вязкости магнитных жидкостей, что требует его необходимого учета во время технического применения в условии агрессивного внешнего воздействия.
Анализ результатов проведенных расчетов показывает, что в присутствии внешнего возмущения гидродинамические факторы сильнее влияют на вязкостные свойства магнитных жидкостей, чем дипольное взаимодействие.
Список литературы
Shliomis M.I. // Sov. Phys. JETP. 1972. V. 34. № 6. P. 1291.
Levi A.C., Hobson R.F., McCourt F.R. // Canad. J. Phys. 1973. V. 51. № 2. P. 180.
Martsenyuk M.A., Raikher Yu.L., Shliomis M.I. // Sov. Phys. JETP. 1974. V. 38. № 2. P. 413.
Huke B., Lucke M. // Rep. Prog. Phys. 2004. V. 67. P. 1731−1768.
Ilg P., Odenbach S. // Lect. Notes Phys. 2009. V. 763. P. 249. https://doi.org/10.1007/978-3-540-85387-9_4.
Берковский Б.М., Каликманов В.И., Филинов В.С. // ТВТ. 1987. Т. 25. № 6. С. 1126.
Kalikmanov V.I. Statistical Physics of Fluids. Basic Concepts and Applications. Springer-Verlag Berlin Heidelberg, 2001. 260 p.https://doi.org/10.1007/978-3-662-04536-7
Одинаев С., Комилов К., Зарифов А. // Журн. физ. химии. 2006. Т. 80. № 5. С. 864.
Одинаев С., Комилов К., Зарипов А. // Там же. 2010. Т. 84. № 7. С. 1368.
Комилов К., Зарипов А.К. // Вестн. ТНУ. Серия естеств. наук. 2017. № 1/4. С. 99.
Мартынов Г.А. Классическая статистическая механика. Теория жидкостей. Долгопрудный: Издательский Дом “Интеллект”, 2011. 328 с.
Одинаев С., Адхамов А.А. Молекулярная теория структурной релаксации и явлений переноса в жидкостях. Душанбе: Дониш, 1998. 230 с.
Ландау Л.Д., Лифшиц Е.М. Теория упругости. М.: Наука, 1965. 202 с.
Зубарев А.Ю., Юшков А.В. // ЖЭТФ. 1998. Т. 114. Вып. 3(9). С. 892.
Zubarev A.Yu., Iskakova L.Yu. // J. Phys.: Condens. Matter. 2006. V. 18. № 38. P. S2771. https://doi.org/10.1088/0953-8984/18/38/S16
Pop L.M., Odenbach S. // J. Phys.: Condens. Matter. 2006. V. 18. № 38. P. S2785–S2802. https://doi.org/10.1088/0953-8984/18/38/S16
Shliomis. M.I., Morozov K.I. // J. Phys. Fluids. 1994. V. 6. № 8. P. 2855.
Галимбеков А.Д. // Вестн. Башкирск. ун-та. 2004. № 3. С. 65.
Дополнительные материалы отсутствуют.
Инструменты
Журнал физической химии