Журнал физической химии, 2020, T. 94, № 8, стр. 1206-1214
Моделирование ик-спектров возбужденных квадрупольных молекул с нарушенной симметрией в полярных растворителях
А. Е. Назаров a, А. И. Иванов a, *
a Волгоградский государственный университет
Волгоград, Россия
* E-mail: Anatoly.Ivanov@volsu.ru
Поступила в редакцию 15.10.2019
После доработки 27.12.2019
Принята к публикации 21.01.2020
Аннотация
Разработан подход, позволяющий по временно-разрешенным ИК-спектрам определять параметры возбужденной квадрупольной молекулы, ответственные за изменения колебательных частот в состояниях с нарушенной переносом заряда симметрией. Подход апробирован на молекуле вида A-π-D-π-A, где A – электронно-акцепторная и D – электронно-донорная группы, объединенные π-сопряженными связями, состоящей из ядра пирролопиррола D и двух акцепторов цианофенила. Показано, что полученное выражение для ИК-спектра молекулы с нарушенной симметрией хорошо описывает экспериментальные данные. Найдены численные значения параметра асимметрии в серии растворителей различной полярности, а также параметры самой молекулы, не зависящие от растворителя.
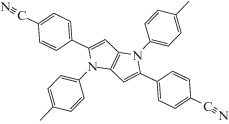
Квадрупольные молекулы вида A-π-D-π-A и D-π-A-π-D, где A – электронно-акцепторная и D – электронно-донорная группы, объединенные π-сопряженными связями, привлекают внимание исследователей своим большим квадрупольным моментом, который ведет к большому сечению двухфотонного поглощения [1]. Исследование таких молекул показало, что они в возбужденном состоянии могут приобретать значительный дипольный момент, т.е. исчезает центр инверсии, и таким образом, симметрия понижается (нарушение симметрии) [2–17]. Идея нарушения симметрии подтверждена методами инфракрасной спектроскопии с высоким временным разрешением [18–21]. В этих экспериментах наблюдается ИК-поглощение двух идентичных (–C≡N или –C≡C–) групп с тройными связями, симметрично расположенных на разных ветвях квадрупольной молекулы. Нарушение симметрии сопровождается расщеплением характеристической полосы колебаний –C≡N или –C≡C–, и величина расщепления коррелирует с масштабом нарушения симметрии. Эксперименты с временным разрешением показали, что начальное расщепление равно нулю, т.е. состояние Франка–Кондона молекулы, как и его основное состояние, не является асимметричным. Временная эволюция величины расщепления свидетельствует о том, что релаксация поляризации растворителя контролирует динамику нарушения симметрии [19].
Наблюдаемое в квадрупольных молекулах нарушение симметрии было объяснено несимметричным переносом заряда с центральной группы на концевые группы в возбужденном состоянии. Модель “существенных” электронных состояний, предложенная в работе [22], позволила описать нарушение симметрии, а также одно- и двухфотонные электронные спектры. Эта модель, требующая сложных расчетов, была упрощена уменьшением числа электронных состояний до двух (два возбужденных вырожденных цвиттер-ионных состояния) [23], что позволило получить аналитическое решение и существенно облегчить анализ экспериментальных результатов. Недавно было показано [24], что двухуровневая модель предсказывает результаты, очень близкие к модели “существенных” электронных состояний, если разность энергий между вторым и первым возбужденными состояниями существенно меньше, чем между первым возбужденным и основным, что выполняется для подавляющего большинства молекул. Двухуровневая модель объяснила пороговую зависимость степени нарушения симметрии с ростом полярности растворителя, наблюдаемую в молекуле, состоящей из ядра пирролопиррола D и двух акцепторов цианофенила (ADA) [23, 25].
Отметим, что изучение процессов нарушения симметрии важно и актуально не только для описанных выше групп молекул, но и в целом для органической химии, где селективный и эффективный синтез асимметричных молекул остается сложной проблемой [26]. Проблемы асимметричного металлического катализа, являющегося одной из интенсивно развивающихся областей химии, также связаны с процессом нарушения симметрии [27].
Развитые ранее теории устанавливают связь параметра асимметрии, определяемого как разность зарядов в единицах заряда электрона на левой и правой ветвях молекулы, с параметрами молекулы и растворителя. Эти параметры могут быть рассчитаны методами квантовой химии, но с невысокой точностью. В то же время эти параметры необходимы для количественного описания нарушения асимметрии и сопровождающих его изменений ИК-спектров. Кроме этого, количественное описание явления существенно повышает уровень достоверности модели. В данной работе развит подход, позволяющий по ИК-спектрам определять эти параметры. Возможности подхода продемонстрированы на примере молекулы ADA.
МОДЕЛЬ НАРУШЕНИЯ СИММЕТРИИ ПЕРЕНОСОМ ЭЛЕКТРОНА В ВОЗБУЖДЕННЫХ КВАДРУПОЛЬНЫХ МОЛЕКУЛАХ
Теоретическое описание нарушения симметрии квадрупольной молекулы подробно представлено в [23], а ее расширение, учитывающее взаимодействие между электронной и ядерной подсистемами, изложено в работе [25]. Здесь представим только краткое описание этого подхода.
Математическая модель использует всего два базисных состояния, а сама квадрупольная молекула описывается следующей волновой функцией:
(1)
$\Psi = {{a}_{{\text{L}}}}{{\varphi }_{{\text{L}}}} + {{a}_{{\text{R}}}}{{\varphi }_{{\text{R}}}},$(2)
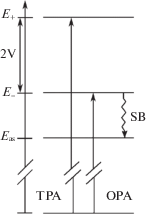
$H = {{H}_{{\text{M}}}} + {{H}_{{\text{S}}}} + {{H}_{{\text{C}}}} + {{H}_{{{\text{V}}0}}} + {{U}_{{{\text{int}}}}},$Рис. 1.
Схема энергетических уровней электронных состояний квадрупольной молекулы A-π-D-π-A, где SB обозначает переход из антисимметричного состояния с энергией E– в асимметричное состояние c энергией Eas, E+ – энергия симметричного состояния, OPA и TPA обозначают одно- и двухфотонное поглощение соответственно.
Второе слагаемое, ${{H}_{{\text{S}}}}$, описывающее дипольное взаимодействие квадрупольной молекулы с полярной средой, имеет вид
где $D$ – параметр асимметрии, пропорциональный величине дипольного момента молекулы, и определяется равенством: $D = a_{{\text{L}}}^{2} - a_{{\text{R}}}^{2}$, подчеркивающим, что параметр асимметрии служит мерой нарушения симметрии распределения зарядов в квадрупольной молекуле. Оператор асимметрии имеет вид $\hat {D} = {{\hat {P}}_{{\text{L}}}} - {{\hat {P}}_{{\text{R}}}}$, где ${{\hat {P}}_{{{\text{L}},{\text{R}}}}}$ – проекционные операторы, ${{\hat {P}}_{{{\text{L}}\left( {\text{R}} \right)}}}({{a}_{{\text{L}}}}{{\varphi }_{{\text{L}}}} + {{a}_{{\text{R}}}}{{\varphi }_{{\text{R}}}}) = {{a}_{{{\text{L(R)}}}}}{{\varphi }_{{{\text{L}}\left( {\text{R}} \right)}}}$. Среднее значение оператора асимметрии равно величине дипольного параметра, т.е. $\left\langle {\Psi \left| {\hat {D}} \right|\Psi } \right\rangle = D$. В уравнении (4) как параметр, так и оператор асимметрии безразмерные, поэтому размерность энергии имеет только величина $\lambda $, которая может быть оценена с использованием формулы Онзагера [28]: где ${{\mu }_{0}}$ – величина дипольного момента молекулы в состоянии с локализацией зарядов на одном акцепторе ($D = 1$), в состоянии с произвольным параметром асимметрии среднее значение дипольного момента молекулы равно ${{\mu }_{0}}D$, ${{r}_{{\text{d}}}}$ – эффективный радиус молекулы, ${\Delta }f = f({{\varepsilon }_{{\text{s}}}}) - f({{n}^{2}})$ характеризует полярность растворителя, $f(x) = 2(x - 1){\text{/}}(2x + 1)$, ${{\varepsilon }_{{\text{s}}}}$ и $n~~~$ – статическая диэлектрическая проницаемость и показатель преломления соответственно.Третье слагаемое ${{H}_{{\text{C}}}}$ – гамильтониан кулоновского взаимодействия
(6)
${{H}_{{\text{C}}}} = - {{\gamma }_{{\text{С}}}}D\hat {D},\quad {{\gamma }_{{\text{С}}}} = \frac{{{{e}^{2}}}}{{4{{\varepsilon }_{{{\text{im}}}}}{{R}_{{{\text{LR}}}}}}},$Последние два слагаемых в (2) ${{H}_{{{\text{V}}0}}}$ и ${{U}_{{{\text{int}}}}}$ описывают внутримолекулярные колебания и электронно-колебательное взаимодействие соответственно. Нарушение симметрии приводит к перераспределению внутримолекулярной электронной плотности, что изменяет колебательную подсистему через электронно-колебательное взаимодействие. В рамках гармонического приближения, колебательный гамильтониан квадрупольной молекулы, обладающий инверсионной симметрией, имеет вид
(7)
${{H}_{{{\text{V}}0}}} = \frac{1}{2}\mathop \sum \limits_i \,[p_{{{\text{s}}i}}^{2} + \omega _{{{\text{s}}i}}^{2}x_{{{\text{s}}i}}^{2}] + \frac{1}{2}\mathop \sum \limits_j \,[p_{{{\text{a}}j}}^{2} + \omega _{{{\text{a}}i}}^{2}x_{{{\text{a}}j}}^{2}],$(9)
$U_{{{\text{int}}}}^{{(1)}} = \hat {D}\mathop \sum \limits_j \,{{\zeta }_{j}}{{x}_{{{\text{a}}j}}},$(10)
$\begin{gathered} U_{{{\text{int}}}}^{{(2)}} = \hat {D}{\kern 1pt} \mathop \sum \limits_{ij} \,{{\delta }_{{ij}}}{{x}_{{{\text{a}}j}}}{{x}_{{{\text{s}}j}}} + \\ + \;\frac{{D~\hat {D}}}{2}\mathop \sum \limits_{ik} \,[{{\alpha }_{{ik}}}{{x}_{{{\text{a}}i}}}{{x}_{{{\text{a}}k}}} + {{\beta }_{{ik}}}{{x}_{{{\text{s}}i}}}{{x}_{{{\text{s}}k}}}]. \\ \end{gathered} $Для определения стационарных состояний молекулы и соответствующих им энергий необходимо решить стационарное уравнение Шредингера:
где $H = {{H}_{{\text{M}}}} + {{H}_{{\text{S}}}} + {{H}_{{\text{C}}}} + {{H}_{{{\text{V}}0}}} + U_{{{\text{int}}}}^{{(1)}}$ – гамильтониан квадрупольной молекулы, взаимодействующей с полярной средой. Отметим, что в приближении, когда внутримолекулярные колебания адиабатически следуют за флуктуациями среды, линейное электронно-колебательное взаимодействие описывается выражением: $U_{{{\text{int}}}}^{{(1)}} = - \bar {\zeta }D\hat {D}$, где $\bar {\zeta } = \sum\nolimits_j {\frac{{\zeta _{j}^{2}}}{{\omega _{{{\text{a}}j}}^{2}}}} $ [25]. Влиянием квадратичного электронно-колебательного взаимодействия $U_{{{\text{int}}}}^{{(2)}}$ на электронную подсистему пренебрегаем, поскольку оно мало по сравнению с линейным слагаемым $U_{{{\text{int}}}}^{{(1)}}$. Отметим, что уравнение (11) является системой нелинейных уравнений относительно коэффициентов разложения и имеет четыре решения: два решения описывают антисимметричное (${{a}_{{\text{L}}}} = - {{a}_{{\text{R}}}}$) и симметричное (${{a}_{{\text{L}}}} = {{a}_{{\text{R}}}}$) состояния с энергиями ${{E}_{ - }} = - V$ и ${{E}_{ + }} = V$ соответственно. Оставшиеся два решения описывают вырожденные асимметричные состояния с электронной плотностью, сосредоточенной преимущественно на одной из веток молекулы $\left| {{{a}_{{{\text{L}}|}}}} \right| \ne \left| {{{a}_{{\text{R}}}}} \right|$. Энергия этих вырожденных состояний определяется простыми выражениями [23, 25]:(14)
$\bar {\zeta } = \mathop \sum \limits_j \frac{{\zeta _{j}^{2}}}{{\omega _{{{\text{a}}j}}^{2}}}.$СПЕКТР ПОГЛОЩЕНИЯ КВАДРУПОЛЬНОЙ МОЛЕКУЛЫ В СОСТОЯНИИ С НАРУШЕННОЙ СИММЕТРИЕЙ
В общем случае нарушение симметрии ведет к перестройке всей колебательной подсистемы. Изменение частот делокализованных нормальных колебаний ожидается незначительным. В связи с этим представляют интерес характеристические локализованные колебания. Для этого в молекулу включают группы –C≡N или –C≡C–, симметрично расположенные в левой и правой ветвях [18]. В симметричном и антисимметричном состояниях частоты этих колебаний должны совпадать. В асимметричном состоянии ожидается расщепление данных частот. Эти эквивалентные валентные колебания, локализованные на каждой из ветвей квадрупольной молекулы, описываются координатами ${{x}_{{\text{L}}}}$ и ${{x}_{{\text{R}}}}$. В силу симметрии молекулы нормальными координатами являются их антисимметричная и симметричная комбинация: ${{x}_{{{\text{s}}/{\text{a}}}}} = \frac{1}{{\sqrt 2 }}({{x}_{{\text{L}}}} \pm {{x}_{{\text{R}}}})$. Взаимодействие между этими локальными модами приводит к появлению одной антисимметричной и одной симметричной нормальных мод с координатами ${{x}_{{\text{a}}}}$, ${{x}_{{\text{s}}}}$ и частотами ${{\omega }_{{\text{a}}}}$, ${{\omega }_{{\text{s}}}}$ соответственно. Ангармонизм и линейное электронно-колебательное взаимодействие могут приводить к различию частот ${{\omega }_{{\text{a}}}}$ и ${{\omega }_{{\text{s}}}}$ [25].
Для вычисления ИК-спектра возбужденной квадрупольной молекулы в состоянии с нарушенной симметрией используется классическая теория поглощения света. Классические уравнения молекулярных колебаний, взаимодействующих с электромагнитной волной на частоте $\omega $, можно записать в следующем виде:
(16)
$\begin{gathered} {{{\ddot {x}}}_{{\text{a}}}} = - \frac{{\partial {{H}_{{\text{V}}}}}}{{\partial {{x}_{{\text{a}}}}}} - {{\eta }_{{\text{a}}}}{{{\dot {x}}}_{{\text{a}}}} + {{F}_{{\text{a}}}}\cos (\omega t), \\ {{F}_{{\text{a}}}} = {{F}_{0}}(1 - {{\xi }_{{\text{a}}}}{{D}^{2}}), \\ \end{gathered} $(17)
$\begin{gathered} {{{\ddot {x}}}_{{\text{s}}}} = - \frac{{\partial {{H}_{{\text{V}}}}}}{{\partial {{x}_{{\text{s}}}}}} - {{\eta }_{{\text{s}}}}{{{\dot {x}}}_{{\text{s}}}} + {{F}_{{\text{s}}}}\cos (\omega t), \\ {{F}_{{\text{s}}}} = {{F}_{0}}{{\xi }_{{\text{s}}}}D, \\ \end{gathered} $Частное решение системы линейных неоднородных дифференциальных уравнений (16)–(17) можно найти в виде суммы комплексно сопряженных решений ${{x}_{{{\text{a}},{\text{s}}}}}(t) + x_{{{\text{a}},{\text{s}}}}^{*}(t)$, где ${{x}_{{{\text{a}},{\text{s}}}}}(t) = {{\bar {x}}_{{{\text{a}},{\text{s}}}}}{{e}^{{i\omega t}}}$. Комплексные амплитуды ${{\bar {x}}_{{\text{a}}}}$ и ${{\bar {x}}_{{\text{s}}}}$ определяются системой линейных алгебраических уравнений:
(18)
$(\omega _{{\text{a}}}^{2} + {{D}^{2}}\alpha - {{\omega }^{2}} + i{{\eta }_{{\text{a}}}}){{\bar {x}}_{{\text{a}}}} + D\delta {{\bar {x}}_{{\text{s}}}} = {{F}_{{\text{a}}}},$(19)
$(\omega _{{\text{s}}}^{2} + {{D}^{2}}\beta - {{\omega }^{2}} + i{{\eta }_{{\text{s}}}}){{\bar {x}}_{{\text{s}}}} + D\delta {{\bar {x}}_{{\text{a}}}} = {{F}_{{\text{s}}}}.$(20)
${{\bar {x}}_{{\text{a}}}} = \frac{{{{F}_{{\text{a}}}}{{\Delta }_{{\text{s}}}} - {{F}_{{\text{s}}}}D\delta }}{{{{\Delta }_{{\text{a}}}}{{\Delta }_{{\text{s}}}} - {{D}^{2}}{{\delta }^{2}}}},\quad {{\bar {x}}_{{\text{s}}}} = \frac{{{{F}_{{\text{s}}}}{{\Delta }_{{\text{a}}}} - {{F}_{{\text{a}}}}D\delta }}{{{{\Delta }_{{\text{a}}}}{{\Delta }_{{\text{s}}}} - {{D}^{2}}{{\delta }^{2}}}},$(21)
${{\Delta }_{{\text{a}}}} = \bar {\omega }_{{\text{a}}}^{2} - {{\omega }^{2}} + i{{\eta }_{{\text{a}}}}\omega ,\quad {{\Delta }_{{\text{s}}}} = \bar {\omega }_{{\text{s}}}^{2} - {{\omega }^{2}} + i{{\eta }_{{\text{s}}}}\omega ,$(22)
$\bar {\omega }_{{\text{a}}}^{2} = \omega _{0}^{2} - {{\varkappa }^{2}} + {{D}^{2}}\alpha ,\quad \bar {\omega }_{{\text{s}}}^{2} = \omega _{0}^{2} + {{D}^{2}}\beta .$Согласно классической теории поглощения, количество поглощенной энергии в единицу времени равняется работе внешних сил в течение того же интервала времени. Отсюда получаем
(23)
$\begin{gathered} I(\omega ) = \frac{1}{T}\mathop \smallint \limits_0^T \left[ {{{F}_{{\text{a}}}}\frac{d}{{dt}}({{x}_{{\text{a}}}}(t) + x_{{\text{a}}}^{*}(t))} \right. + \\ + \;\left. {{{F}_{{\text{s}}}}\frac{d}{{dt}}({{x}_{{\text{s}}}}(t) + x_{{\text{s}}}^{*}(t))} \right]\cos (\omega t)dt, \\ \end{gathered} $(24)
$I(\omega ) = - 2\omega {\kern 1pt} [{{F}_{{\text{a}}}}\operatorname{Im} {{\bar {x}}_{{\text{a}}}} + {{F}_{{\text{s}}}}\operatorname{Im} {{\bar {x}}_{{\text{s}}}}],$СРАВНЕНИЕ РЕЗУЛЬТАТОВ ТЕОРИИ С ЭКСПЕРИМЕНТАЛЬНЫМИ ДАННЫМИ
Полученное выражение (24) предсказывает появление второй полосы поглощения в состоянии с нарушенной симметрией. Отношение интенсивностей полос определяется параметром асимметрии. Формы этих полос близки к профилю функции Лоренца, поскольку в модели учитывается только однородное уширение. Получаемые в экспериментах полосы ИК-поглощения могут быть описаны функцией Фойгта, так как включают как однородное, так и неоднородное уширение. Таким образом, первичные экспериментальные данные следует аппроксимировать суммой двух функций Фойгта, $f(\omega )$, с независимыми лоренцевыми и гауссовыми ширинами:
(25)
$\begin{gathered} f(\omega ) = {{Z}^{{ - 1}}}\omega {\kern 1pt} \text{[}V(\omega - {{\omega }_{1}},{{\gamma }_{1}},{{\sigma }_{1}}) + \\ + \;\epsilon V(\omega - {{\omega }_{2}},{{\gamma }_{2}},{{\sigma }_{2}})]~, \\ \end{gathered} $(26)
$V(\omega ,\sigma ,\gamma ) = \mathop \smallint \limits_{ - \infty }^\infty G(\omega {\text{'}},\sigma )L(\omega - \omega {\text{'}},\gamma )d\omega {\text{'}},$(27)
$\begin{gathered} G(\omega ,\sigma ) = \frac{1}{{\sigma \sqrt {2\pi } }}{{e}^{{ - {{\omega }^{2}}/(2{{\sigma }^{2}})}}}, \\ L(\omega ,\gamma ) = \frac{\gamma }{{\pi ({{\omega }^{2}} + {{\gamma }^{2}})}}~, \\ \end{gathered} $(28)
${{f}_{{\text{D}}}}(\omega ) = {{\tilde {Z}}^{{ - 1}}}\omega {\kern 1pt} [L(\omega - {{\omega }_{1}},{{\gamma }_{1}}) + \epsilon L(\omega - {{\omega }_{2}},{{\gamma }_{2}})],$Моделируемый спектр (24) подгоняется к профилю ${{f}_{{\text{D}}}}(\omega )$, чтобы определить как параметры квадрупольной молекулы (${{\omega }_{0}}$, $~\varkappa $, $~\alpha $, $~\beta $, $~{{\xi }_{{\text{a}}}}$, ${{\xi }_{{\text{s}}}}$), так и отклик среды, который косвенно отражен в параметре асимметрии $D$ для получаемого ИК-спектра в данном растворителе. Оставшиеся параметры, коэффициенты трения, связаны с однородным уширением через простые соотношения: ${{\eta }_{{\text{a}}}} = 2{{\gamma }_{1}}$, ${{\eta }_{{\text{s}}}} = 2{{\gamma }_{2}}$. Рассматриваемый фитинг содержит большое количество подгоночных параметров. Для улучшения сходимости оптимизационная процедура разделяется на три вложенных друг в друга уровня.
На первом уровне, самом глубоком, множество параметров асимметрии $\{ {{D}_{i}}\} $ в разных растворителях рассматриваются как независимые подгоночные параметры, тогда как параметры молекулы считаются фиксированными. Значения $\{ {{D}_{i}}\} $ находятся с помощью метода золотого сечения в диапазоне от 0 до 1. 2.
На втором уровне, параметры $\alpha $, $\beta $, $\varkappa $, ${{\xi }_{{\text{a}}}}$ и ${{\xi }_{{\text{s}}}}$ подбираются с применением метода роя частиц. На этом этапе величина ${{\omega }_{0}}$ подразумевается фиксированной, поскольку она сильно влияет на профиль моделируемого спектра. Для уменьшения времени вычислений метод роя частиц может использоваться как начальное приближение для алгоритма оптимизации Нелдера–Мида.
На третьем, самом верхнем уровне, значение ${{\omega }_{0}}$ определятся методом золотого сечения на интервале, границы которого определяются шириной полосы слабой интенсивности. Таким образом, формируется трехкратно вложенная оптимизационная задача. Для улучшения точности определения параметров молекулы необходимо использовать по меньшей мере два разных растворителя.
Хорошо известно, что решение обратной задачи, к которой относится восстановление параметров модели, не гарантирует нахождения их истинных значений. Предложенный в данной работе метод оптимизации в своей основе содержит метод роя частиц, который носит стохастический характер и нацелен на поиск глобального минимума нелинейного функционала. Выполненный нами многократный перезапуск роя частиц на заданной области с равномерным начальным распределением всегда приводил к одному и тому же набору значений параметров модели, что свидетельствует об истинности значений искомых параметров. Эти параметры имеют прозрачный физический смысл, и полученные значения соответствуют представлениям о процессах, протекающих в ADA.
Далее теоретические спектры сравниваются с ИК-спектрами поглощения квадрупольной молекулы ADA, включающей две группы –C≡N (схема 1), полученными для серии растворителей: циклогексан (CHX), ди-н-бутиловый эфир (DBE), диэтиловый эфир (DEE), хлороформ (CHCl3), тетрагидрофуран (THF), бензонитрил (BZN), диметилсульфоксид (DMSO), н-метилформамид (NMF) [19, 21]. В фитинге использованы ИК-спектры, полученные с временной задержкой 20 пс, когда параметр асимметрии достигает максимального значения. Естественно ожидать, что значения параметра $D$ будут разными в растворителях разной полярности. По данным 2D-ИК-спектроскопии, однородное уширение полосы большей интенсивности составляет ∼$10$ см–1 для рассматриваемых растворителей [29]. Поскольку обе полосы связаны с одними и теми же валентными колебаниями групп –C≡N, то их времена релаксации, ответственные за однородное уширение, должны быть близки, поэтому определение параметров моделируемого спектра выполнятся в приближении одинаковой ширины полос: ${{\eta }_{{\text{a}}}} = {{\eta }_{{\text{s}}}} = 10$ см–1.
Результаты первичной аппроксимации экспериментальных данных кривыми Фойгта (25), а также дековолюцированные спектры (28) представлены на рис. 2, значения полученных параметров даны в табл. 1. Из рис. 2 видно, что качество аппроксимации функцией $f(\omega )$ во всех растворителях высокое; слабая полоса имеет небольшую относительную интенсивность, $\epsilon $, а также большое перекрывание с основной полосой (пунктирные и сплошные линии) для всей серии растворителей. Оба этих факта приводят к заметной неточности определения положения максимума, ${{\omega }_{2}}$, слабой полосы в деконволюцированном спектре. С использованием профиля ${{f}_{D}}(\omega )$ в качестве данных для фитинга восстанавливаются параметры моделируемого спектра поглощения (24). Результаты этого фитинга с параметрами, представленными в табл. 2, показаны на рис. 3. В основном они хорошо согласуется с деконволюцированными спектрами. Наблюдаются заметные отклонения только для NMF и THF. Причиной этих отклонений может быть недостаточно точное определение положения максимума слабой полосы во время первичной аппроксимации экспериментальных данных, а также ограниченность модели, включающей только взаимодействие дипольного момента молекулы с поляризацией растворителя и не учитывающей специфические взаимодействия. Несмотря на эти отклонения, точность определения параметров квадрупольной молекулы ожидается приемлемой, так как рассматривается серия растворителей широкой степени полярности.
Рис. 2.
Результаты первичной обработки экспериментальных данных спектра поглощения валентных колебаний –C≡N-групп молекулы ADA в серии растворителей, где точки – экспериментальные данные; пунктирные линии – $f\left( \omega \right)$, аппроксимация двумя функциями Фойгта; сплошные линии – ${{f}_{D}}(\omega )$, деконволюцированный спектр, включающий только однородное уширение.
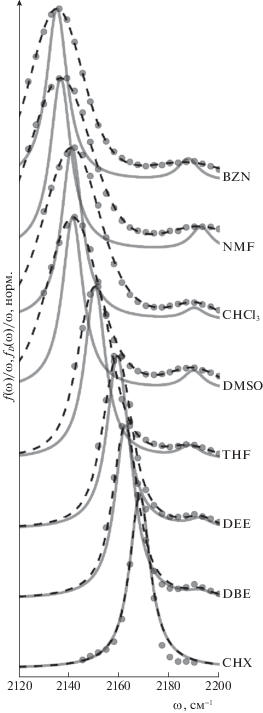
Таблица 1.
Параметры, полученные из фитинга кривых Фойгта (25) к экспериментальным ИК-спектрам при фиксированных значениях ${{\gamma }_{1}} = {{\gamma }_{2}} = 5$ см–1 для серии растворителей
| Раство-ритель | $\epsilon $ | ${{\omega }_{1}}$, см–1 | ${{\sigma }_{1}}$, см–1 | ${{\omega }_{2}}$, см–1 | ${{\sigma }_{2}}$, см–1 |
|---|---|---|---|---|---|
| CHX | 0.000 | 2168.3 | 0.00 | – | – |
| DBE | 0.031 | 2162.5 | 2.14 | 2192.2 | 0.00 |
| DEE | 0.049 | 2159.4 | 3.03 | 2192.1 | 2.35 |
| THF | 0.072 | 2150.6 | 4.36 | 2188.2 | 6.02 |
| DMSO | 0.107 | 2141.7 | 7.82 | 2189.6 | 7.31 |
| CHCl3 | 0.068 | 2141.3 | 8.73 | 2189.9 | 5.83 |
| NMF | 0.137 | 2136.9 | 9.82 | 2192.5 | 10.79 |
| BZN | 0.129 | 2135.4 | 8.14 | 2187.5 | 12.8 |
Таблица 2.
Параметры ADA в серии растворителей, полученные из фитинга моделируемого ИК-спектра поглощения (24) к деконволюцированному спектру (28) с параметрами, приведенные в табл. 1. Значения D даны для временной задержки 20 пс
| ADA | Растворитель | D | |
|---|---|---|---|
| ${{\omega }_{0}}$, см–1 | 2193.0 | CHX | 0.0 |
| $\varkappa $, см–1 | 328.0 | DBE | 0.20 |
| ${\Delta }{{\omega }_{0}}$, см–1 | 24.5 | DEE | 0.25 |
| $\delta {\text{/}}{{\omega }_{0}}$ | 0.010 | THF | 0.35 |
| $\alpha {\text{/}}\omega _{0}^{2}$ | –0.128 | DMSO | 0.43 |
| $\beta {\text{/}}\omega _{0}^{2}$ | –0.020 | CHCl3 | 0.43 |
| ${{\xi }_{{\text{a}}}}$ | 0.000 | NMF | 0.46 |
| ${{\xi }_{{\text{s}}}}$ | 0.511 | BZN | 0.47 |
Рис. 3.
Результаты фитинга моделируемого спектра (пунктирные линии) к экспериментальным спектрам поглощения валентных колебаний –C≡N-групп молекулы ADA в серии растворителей после удаления неоднородного уширения (сплошные линии).
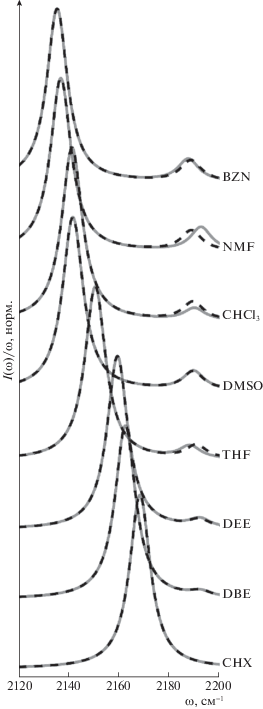
Фитинг ИК-спектров валентных колебаний –C≡N-групп показывает, что в антисимметричном состоянии уже существует расщепление полос симметричных и антисимметричных колебаний ${\Delta }{{\omega }_{0}} = 24.5$ см–1, хотя симметричное колебание в ИК-спектрах не проявляется. Для экспериментального определения этой величины необходимо использовать методы спектроскопии комбинационного рассеяния, однако до сих пор такие эксперименты не были выполнены. С ростом параметра D эволюция спектров определяется величинами $\alpha $, $\beta $ и $\delta $. Отрицательные значения $\alpha $ и $\beta $ приводят к уменьшению частот обеих полос, тогда как параметр $\delta $ определяет величину их взаимного отталкивания. Совместное действие механизмов, связанных с этими тремя параметрами, приводит к почти неизменному положению слабой полосы и значительному сдвигу в низкочастотную область сильной полосы. Отметим, что малая интенсивность второй полосы – следствие значительного расщепления ${\Delta }{{\omega }_{0}} = 24.5$ см–1 в антисимметричном состоянии. В молекулах с ${\Delta }{{\omega }_{0}} = 0$ теория предсказывает одинаковую интенсивность этих полос при малых значениях D. Анализ выражения (24) показывает, что ненулевое значение ${{\xi }_{{\text{s}}}}$ отражает существенное различие дипольных моментов –C≡N-групп, расположенных в разных ветвях молекулы, в состоянии с нарушенной симметрией.
Чтобы понять механизм влияния растворителя на степень асимметрии молекулы, на рис. 4 представлена зависимость параметра D от полярности растворителя $\Delta f$. Полученные данные показывают рост параметра D с увеличением полярности растворителя, который согласуется с предсказаниями теории. В то же время разброс значений D, полученных из фитинга ИК-спектров, свидетельствует о том, что полярность растворителя – не единственный фактор, влияющий на нарушение симметрии. Экспериментальные исследования зависимости величины расщепления ИК-полос валентных колебаний –C≡N-групп также показывают существенное влияние на нее недипольных и специфических взаимодействий [21].
Рис. 4.
Зависимость параметра асимметрии $D$ от полярности среды и ее аппроксимация уравнением (15). Символами представлены значения$~D$ из табл. 2, поделенные на $g = 0.55$. Сплошная кривая получена с параметрами: ${{\lambda }_{1}} = 3900$ см–1, $\gamma = 1020$ см–1, пунктирная – ${{\lambda }_{1}} = 3700$ см–1, $\gamma = 1140$ см–1, штрихпунктирная – ${{\lambda }_{1}} = 4100$ см–1, $\gamma = 900$ см–1.
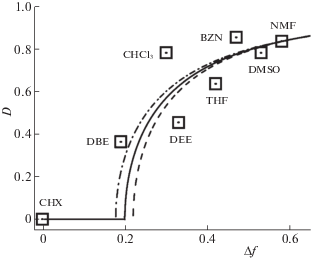
Фитинг выражения (15) к полученной зависимости $D\left( {{\Delta }f} \right)$ дает возможность определить значения параметров модели $g$, $\gamma $ и ${{\lambda }_{1}}$. Для рассматриваемой молекулы ADA величина расщепления полос одно- и двухфотонного поглощения дает $V~ = 1800$ см–1 [23]. Кроме того, известно, что спектр флуоресценции ADA в ацетонитриле сдвинут в красную область относительно спектра в циклогексане на 1600 см–1 [19]. Учитывая, что в циклогексане нет нарушения симметрии и возбужденное состояние имеет энергию $--V$, а в ацетонитриле (${\Delta }f = 0.61$) энергия асимметричного состояния, как следует из уравнения (12), равна $ - (0.61{{\lambda }_{1}} + \gamma )$, получим $ - V + (0.61{{\lambda }_{1}} + \gamma ) = 1600$ см–1. Таким образом, между ${{\lambda }_{1}}$ и $\gamma $ имеется связь: $0.61{{\lambda }_{1}} + \gamma = 3400$ см–1, означающая, что в фитинге $D({\Delta }f)$ имеются только два независимых параметра $g$ и ${{\lambda }_{1}}$. Фитинг, результаты которого представлены на рис. 4, дает значения $g = 0.55$ и ${{\lambda }_{1}} = 3900$ см–1. Полученные значения $\gamma $ и ${{\lambda }_{1}}$ согласуются с оценками, предсказываемыми выражениями (5) и (6). Для демонстрации масштаба влияния отклонений от выбранных значений параметров на качество фитинга на рис. 4 приведены еще две кривые для значений ${{\lambda }_{1}} = 4100$ и $3700$ см–1, при этом величина $~\gamma $ тоже варьировалась, чтобы выполнялось условие: $0.61{{\lambda }_{1}} + \gamma = 3400$ см–1. Как видно из рис. 4, эти вариации слабо влияют на максимальное значение параметра $D$, что указывает на хорошую точность определения параметра $g$ = 0.55. Чтобы получить истинные значения параметров, перечисленных в табл. 2, необходимо $~~D$ поделить на 0.55, $\delta $, ${{\xi }_{a}}$ и ${{\xi }_{{\text{s}}}}$ умножить на 0.55, значения $\alpha $ и $\beta $ умножить на 0.552. Таким образом, совместное использование данных оптических и ИК-спектров квадрупольной молекулы в серии растворителей различной полярности позволяет найти абсолютные значения всех параметров, включая параметр асимметрии$~D$.
Таким образом, нарушение симметрии переносом заряда, сопровождающее оптическое возбуждение квадрупольной молекулы A-π-D-π-A, ведет к изменениям спектров –C≡N-колебаний, наблюдаемых в экспериментах [19]. Построенная математическая модель нарушения симметрии хорошо описывает наблюдаемое изменение ИК-спектров в растворителях различной полярности. Разработанная методика позволила определить параметр асимметрии и параметры возбужденной квадрупольной молекулы, ответственные за изменения колебательных частот в состояниях с нарушенной симметрией, по стационарным оптическим и временно-разрешенным ИК-спектрам.
Авторы благодарны профессору Женевского университета Э. Вотэ (Eric Vauthey) за предоставленные экспериментальные данные, показанные на рис. 2 и 3. Исследование выполнено при финансовой поддержке РФФИ и Администрации Волгоградской области в рамках научного проекта № 19-43-340003р_а.
Список литературы
Le Droumaguet C., Mongin O., Werts M.H.V., Blanchard-Desce M. // Chem. Commun. 2005. P. 2802. https://doi.org/10.1039/B502585K
Mataga N., Yao H., Okado T., Retting W. // J. Phys. Chem. 1989. V. 93. P. 3383. https://doi.org/10.1021/j100346a004
Piet J.J., Schuddeboom W., Wegewijs B.R. et al. // J. Am. Chem. Soc. 2001. V. 123. P. 5337. https://doi.org/10.1021/ja004341o
Beljonne W., Wenseleers E., Zojer Z. et al. // Adv. Funct. Mater. 2002. V. 12. P. 631–641. https://doi.org/10.1002/1616-3028(20020916)12:9<631::AID-ADFM631>3.0.CO;2-W
Kovalenko A., Lustres J.L.P., Ernsting N.P., Rettig W. // J. Phys. Chem. A. 2003. V. 107. P. 10228. https://doi.org/10.1021/jp026802t
Lewis D., Daublain P., Zhang L. et al. // J. Phys. Chem. B 2008. V. 112. P. 3838. https://doi.org/10.1021/jp710718p
Bhosale S., Sisson A.L., Talukdar P. et al. // Sci. 2006. V. 313. P. 84. https://doi.org/10.1126/science.1126524
Banerji N., Fürstenberg A., Bhosale S. et al. // J. Phys. Chem. B. 2008. V. 112. P. 8912. https://doi.org/10.1021/jp801276p
Banerji N., Duvanel G., Perez-Velasco A. et al. // J. Phys. Chem. A. 2009. V. 113. P. 8202. https://doi.org/10.1021/jp903572r
Giaimo J.M., Gusev A.V., Wasielewski M.R. // J. Amer. Chem. Soc. 2002. V. 124. P. 8530. https://doi.org/10.1021/ja026422l
Holman M.W., Yan P., Adams D.M. et al. // J. Phys. Chem. A. 2005. V. 109. P. 8548. https://doi.org/10.1021/jp0502050
Hu H., Przhonska O.V., Terenziani F. et al. // Phys. Chem. Chem. Phys. 2013. V. 15. P. 7666. https://doi.org/10.1039/C3CP50811K
Sissa C., Delchiaro F., Maiolo F.D. et al. // J. Chem. Phys. 2014. V. 141. P. 164317. https://doi.org/10.1063/1.4898710
Rebane A., Drobizhev M., Makarov N.S. et al. // J. Phys. Chem. A. 2014. V. 118 P. 3749. https://doi.org/10.1021/jp5009658
Trinh C., Kirlikovali K., Das S. et al. // J. Phys. Chem. C. 2014. V. 118. P. 21834. https://doi.org/10.1021/jp506855t
Carlotti B., Benassi E., Spalletti A. et al. // Phys. Chem. Chem. Phys. 2014. V. 16. P. 13984. https://doi.org/10.1039/C4CP00631C
Carlotti B., Benassi E., Fortuna C.G. et al. // Chem. Phys. Chem. 2016. V. 17. P. 136. https://doi.org/10.1002/cphc.201500784
Dereka B., Rosspeintner A., Li Z. et al. // J. Am. Chem. Soc. 2016. V. 138. P. 4643. https://doi.org/10.1021/jacs.6b01362
Dereka B., Rosspeintner A., Krzeszewski M. et al. // Angew. Chem. Int. Ed. 2016. V. 55. P. 15624. https://doi.org/10.1002/anie.201608567
Dereka B., Rosspeintner A., Stezycki R. et al. // J. Phys. Chem. Lett. 2017. V. 8. P. 6029–6034. https://doi.org/10.1021/acs.jpclett.7b02944
Dereka B., Vauthey E. // J. Phys. Chem. Lett. 2017. V. 8. P. 3927. https://doi.org/10.1021/acs.jpclett.7b01821
Terenziani F., Painelli A., Katan C. et al. // J. Am. Chem. Soc. 2006. V. 128. P. 15742. https://doi.org/10.1021/ja064521j
Ivanov A.I., Dereka B., Vauthey E. // J. Chem. Phys. 2017. V. 146. P. 164306. https://doi.org/10.1063/1.4982067
Ivanov A.I., Tkachev V.G. // J. Chem. Phys. 2019. V. 151. P. 124309. https://doi.org/10.1063/1.5116015
Ivanov A.I. // J. Phys. Chem. C. 2018. V. 122. P. 29165. https://doi.org/10.1021/acs.jpcc.8b10985
Colobert F., Wencel-Delord J. (Eds). C-H Activation for Asymmetric Synthesis. Wiley, 2019. 296 p.
Pellissier H. Asymmetric Metal Catalysis in Enantioselective Domino Reactions. Wiley, 2019. 408 p.
Onsager L. // J. Am. Chem. Soc. 1936. V. 58. P. 1486. https://doi.org/10.1021/ja01299a050
Dereka B., Helbing J., Vauthey E. // Angew. Chem. Int. Ed. 2018. V. 57. P. 17014. https://doi.org/10.1002/anie.201808324
Дополнительные материалы отсутствуют.
Инструменты
Журнал физической химии