1. На главную
  2. Электронные версии
  3. Доклады Российской академии наук. Математика, информатика, процессы управления
  4. T. 499, № 1, 2021

Доклады Российской академии наук. Математика, информатика, процессы управления, 2021, T. 499, № 1, стр. 44-48

О ПОКРЫТИИ ПЛОСКИХ МНОЖЕСТВ

А. Д. Толмачев 1, *, Д. С. Протасов 1, **

1 Московский физико-технический институт (национальный исследовательский университет)
Долгопрудный, Московская обл., Россия

* E-mail: tolmachev.ad@phystech.edu
** E-mail: dmitry.protasov@gmail.com

Поступила в редакцию 22.04.2021
После доработки 22.04.2021
Принята к публикации 02.05.2021

Полный текст (PDF)

Аннотация

В статье предлагаются методы улучшения верхних и нижних оценок для различных покрытий множеств на плоскости. Приведены новые оценки для различного количества частей разбиения, а также предложения по обобщению представленных методов.

Ключевые слова: проблема Борсука, диаметр множества, покрытия плоских множеств, универсальные покрывающие системы, хроматическое число

1. ВВЕДЕНИЕ И ОСНОВНЫЕ ОПРЕДЕЛЕНИЯ

Пусть F – произвольное ограниченное множество на плоскости, $n \in \mathbb{N}$. Определим следующую величину:

$\begin{gathered} {{d}_{n}}(F) = \inf \{ x \in {{\mathbb{R}}^{ + }}{\kern 1pt} :\;\exists {{F}_{1}}, \ldots ,{{F}_{n}}:F \subseteq {{F}_{1}} \cup \ldots \cup {{F}_{n}}, \\ \forall \,i\,\,\,{\text{diam}}({{F}_{i}}) \leqslant x\} . \\ \end{gathered} $

Другими словами, среди всех покрытий множества F некоторыми $n$ множествами ${{F}_{1}}, \ldots ,{{F}_{n}}$ мы хотим выбрать покрытия, состоящие из множеств как можно меньшего диаметра.

Заметим, что величина ${{d}_{n}}(F)$ не изменится, если потребовать, чтобы все множества покрытия были выпуклыми и замкнутыми. Это следует из того, что диаметр замыкания выпуклой оболочки произвольного множества F совпадает с диаметром F.

Заметим, что для произвольного F последовательность ${{d}_{n}}(F)$ является невозрастающей, поскольку в классе всех покрытий n + 1 множествами существует подкласс, для которого ${{F}_{{n + 1}}} = \emptyset $, совпадающий с классом всех покрытий $n$ множествами.

Определим величину ${{d}_{n}} = sup{{d}_{n}}(F)$, где супремум берется по всем множествам F единичного диаметра на плоскости. Из сделанного выше замечания ясно, что последовательность dn не возрастает.

Исследование величин dn глубоко мотивировано классической проблемой Борсука о разбиении множеств на части меньшего диаметра (см. [1–4]). В разные годы Х. Ленц (см. [5]), М. Дембиньски и М. Лассак (см. [6]), В. Филимонов (см. [7]), Д. Белов и Н. Александров (см. [8]), В. Коваль (см. [9]) оценивали величину dn для различных значений $n$. Нам удалось существенно усилить многие из предшествующих результатов. Новые результаты мы приведем в разделе 2, а ниже дадим еще несколько определений, важных для формулировок и их доказательств.

Определение 1. Множество $\Omega \subset {{\mathbb{R}}^{2}}$ называется  универсальной покрышкой, если любое плоское множество $F$ единичного диаметра может быть полностью накрыто $\Omega $ (т.е. на плоскости существует множество ${{\Omega }_{0}}$, конгруэнтное $\Omega $, такое что $F \subset {{\Omega }_{0}}$).

В 1920 г. Й. Пал доказал [10], что правильный шестиугольник со стороной $\tfrac{1}{{\sqrt 3 }}$ является универсальной покрышкой. Введем для него обозначение ${{\Omega }_{6}}$. Приведем еще одно определение.

Определение 2. Система множеств S = = ${{\{ {{\Omega }_{\alpha }}\} }_{{\alpha \in I}}}$ называется  универсальной покрывающей системой, если любое плоское множество F единичного диаметра может быть полностью накрыто одним из множеств ${{\Omega }_{\alpha }}$. Здесь $I$ – некоторый (возможно, бесконечный) набор индексов.

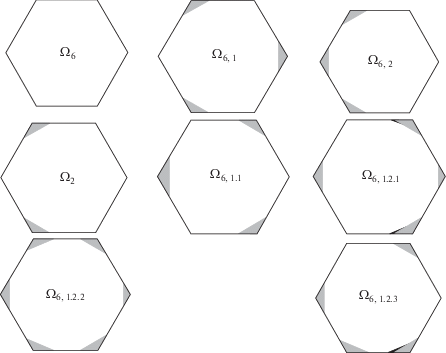
Рассмотрим произвольное множество F единичного диаметра. Накроем его множеством ${{\Omega }_{6}}$ и проведем все шесть прямых, которые перпендикулярны отрезкам, соединяющим центр шестиугольника со всеми его вершинами, и отстоят от центра на расстояние $\frac{1}{2}$. Эти прямые отсекают от ${{\Omega }_{6}}$ шесть треугольников. Очевидно, для каждой пары треугольников, содержащих противоположные вершины, хотя бы один из них не содержит внутренних точек F (поскольку расстояние между этими треугольниками равно единице). Назовем такой треугольник отсеченным. Далее покрышку с тремя подряд такими отсеченными уголками обозначим ${{\Omega }_{{6,2}}}$, а покрышку с тремя отсеченными через один уголками обозначим ${{\Omega }_{{6,1}}}$. Несложно видеть, что $\{ {{\Omega }_{{6,1}}},{{\Omega }_{{6,2}}}\} $ – универсальная покрывающая система.

Заметим, что правильный шестиугольник со стороной $\tfrac{1}{{\sqrt 3 }}$ (т.е. покрышка ${{\Omega }_{6}}$) с двумя отсеченными указанным выше способом уголками при вершинах, идущих через одну, тоже является универсальной покрышкой, потому что им можно накрыть и ${{\Omega }_{{6,1}}}$, и ${{\Omega }_{{6,2}}}$. Обозначим такую универсальную покрышку ${{\Omega }_{2}}$.

Кроме того, будем рассматривать величину

$\begin{gathered} d_{n}^{'}(F) = \inf \{ x \in {{\mathbb{R}}^{ + }}{\kern 1pt} :\;\exists {{F}_{1}}, \ldots ,{{F}_{n}}:F \subseteq {{F}_{1}} \cup \ldots \cup {{F}_{n}}, \\ \forall i\,\forall X,Y \in {{F}_{i}}:{\text{|}}XY{\text{|}} \ne x\} , \\ \end{gathered} $
где $F$ – произвольное ограниченное множество на плоскости, $n \in \mathbb{N}$. Другими словами, $d_{n}^{'}(F)$ – инфимум по всем таким x, что $F$ можно правильно покрасить в $n$ цветов, если $x$ считать за величину запрещенного расстояния. Таким образом, величина $d_{n}^{'}(F)$ мотивирована классической проблемой Нелсона–Хадвигера о раскраске плоскости (см. [11–17]).

Далее определим величину $d_{n}^{'} = supd_{n}^{'}(F)$, где супремум берется по всем множествам F единичного диаметра на плоскости. Ясно, что последовательность $d_{n}^{'}$ невозрастающая. Более того, $d_{n}^{'} = 0$ при всех натуральных $n \geqslant 7$ как следствие известной оценки $\chi ({{\mathbb{R}}^{2}}) \leqslant 7$ для хроматического числа плоскости (см. [11]).

В следующем разделе мы приведем формулировки новых результатов и их сопоставление с ранее известными, а также вкратце обсудим идеи доказательств.

2. УЛУЧШЕННЫЕ РЕЗУЛЬТАТЫ

2.1. Формулировки

Приведем таблицу улучшенных результатов для элементов последовательности ${{d}_{n}}$ при $1 \leqslant n \leqslant 30$ (табл. 1). В столбце “комментарий” указано, на сколько процентов уменьшился “зазор” между верхней и нижней оценкой в результате предложенных в данной работе улучшений. В последнем столбце указан список фигур, рассматриваемых в качестве универсальной покрывающей системы для доказательства оценки сверху.

Таблица 1.

Полученные результаты

n Новая оценка снизу Старая оценка снизу Старая оценка сверху Новая оценка сверху Коммен-тарий Используемая УПС
1 – 1.0000 1.0000 – точная –
2 – 1.0000 1.0000 – точная –
3 – 0.8660 0.8660 – точная –
4 – 0.7071 0.7071 – точная –
5 – 0.5877 0.6020 0.5953 47% ${{\Omega }_{{6,2}}},{{\Omega }_{{6,1.1}}},{{\Omega }_{{6,1.2.1}}},$${{\Omega }_{{6,1.2.2}}},{{\Omega }_{{6,1.2.3}}}$
6 – 0.5051 0.5344 – – –
7 – 0.5000 0.5000 – точная –
8 – 0.4338 0.4456 – – –
9 – 0.3826 0.4047 – – –
10 0.3667 0.3420 0.4012 – 41% –
11 0.34201) 0.3333 0.3970 0.3942 19% ${{\Omega }_{2}}$
12 – 0.3333 0.3660 – – –
13 – 0.3333 0.3660 0.3550 33% ${{\Omega }_{2}}$
14 – 0.3090 0.3324 – – –
15 – 0.2928 0.3324 0.3226 24% ${{\Omega }_{2}}$
16 – 0.2817 0.3324 0.3191 26% ${{\Omega }_{6}}$
17 – 0.2701 0.3324 0.3010 48% ${{\Omega }_{2}}$
18 – 0.2588 0.3324 0.29892) 46% ${{\Omega }_{6}}$
19 – 0.2500 0.2857 – – –
20 – 0.2500 0.2857 – – –
21 – 0.2393 0.2857 0.2723 29% ${{\Omega }_{2}}$
22 – 0.2323 0.2857 0.2650 39% ${{\Omega }_{2}}$
23 – 0.2225 0.2857 0.2650 33% ${{\Omega }_{2}}$
24 – 0.2167 0.2849 0.2610 35% ${{\Omega }_{{6,1}}},{{\Omega }_{{6,2}}}$
25 – 0.2079 0.2776 0.2610 24% ${{\Omega }_{{6,1}}},{{\Omega }_{{6,2}}}$
26 – 0.2030 0.2709 0.2610 15% ${{\Omega }_{{6,1}}},{{\Omega }_{{6,2}}}$
27 – 0.2000 0.2646 0.2610 5% ${{\Omega }_{{6,1}}},{{\Omega }_{{6,2}}}$
28 – 0.2000 0.2587 0.2500 15% ${{\Omega }_{2}}$
29 – 0.1950 0.2531 0.2500 5% ${{\Omega }_{2}}$
30 – 0.1939 0.2479 – – –
1) Точное значение полученной нижней оценки для d11 равно sin(π/9). 2) Точное значение полученной верхней оценки для d18 равно $\sqrt {\frac{{2 - \sqrt 3 }}{3}} $.

На рис. 1 изображены все покрывающие множества, используемые для получения верхних оценок. Разбиения для доказательства верхних оценок приведены в [18]. В доказательствах нижних оценок величин ${{d}_{{10}}}$, ${{d}_{{11}}}$ и ${{d}_{{54}}}$ в качестве множества диаметра 1 был рассмотрен круг единичного диаметра.

Все константы приведены с четырьмя верными знаками после запятой. Кроме улучшений, показанных в таблице, доказаны оценки $\tfrac{1}{{\sqrt {52} }} \leqslant {{d}_{{54}}}$ и $d_{6}^{'} \leqslant 0.5.$

2.2. Идеи доказательств

Для доказательства того, что ${{d}_{n}} \leqslant \rho $, где $\rho $ – некоторое фиксированное число, рассмотрим некоторую универсальную покрывающую систему $S$ и разобьем каждое из множеств, входящих в нее, на n частей, диаметр каждой из которых не превосходит $\rho $. В табл. 1 в столбце “используемая УПС” приведена универсальная покрывающая система, используемая в доказательстве указанной верхней оценки величины dn для соответствующего значения $n$.

Разбиения элементов универсальной покрывающей системы на n частей диаметра ρ для всех улучшенных оценок мы не будем подробно описывать в данной работе, однако рассмотрим одно из наиболее красивых разбиений, которое значительно улучшает верхнюю оценку величины ${{d}_{{18}}}$.

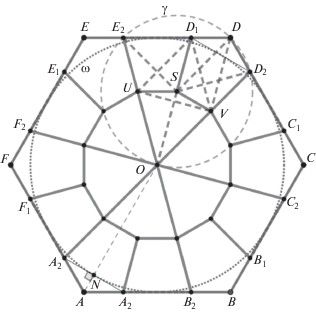
Положим $\rho = \sqrt {\tfrac{{2 - \sqrt 3 }}{3}} \approx 0.2989$ и будем доказывать, что ${{d}_{{18}}} \leqslant \rho $. Рассмотрим универсальную покрывающую систему S, состоящую из одного множества – универсальной покрышки ${{\Omega }_{6}}$.

На рис. 2 правильный шестиугольник $ABCDEF$ со стороной $\tfrac{1}{{\sqrt 3 }}$ соответствует покрышке ${{\Omega }_{6}}$. Окружность $\omega $ вписана в этот шестиугольник. Отрезок AO пересекает окружность $\omega $ в точке N, а перпендикуляр к прямой AO, проходящий через точку N, пересекает отрезки AB и AF в точках ${{A}_{1}}$ и ${{A}_{2}}$ соответственно. Аналогично получим точки ${{B}_{1}},{{B}_{2}}$, ..., F1, F2. Можно показать, что двенадцатиугольник ${{F}_{1}}{{F}_{2}}...{{B}_{1}}{{B}_{2}}{{A}_{1}}{{A}_{2}}$ является правильным. Тогда разобьем исходный шестиугольник на 6 равных четырехугольников $O{{A}_{2}}A{{B}_{2}}$, $O{{B}_{2}}B{{C}_{2}}$, …, $O{{F}_{2}}F{{A}_{2}}$. Рассмотрим один из этих четырехугольников и покажем, как его разбить на три части диаметра в точности, $\rho $, откуда будет следовать, что исходный шестиугольник можно разбить на 18 частей диаметра $\rho $. Без ограничения общности будем рассматривать четырехугольник $O{{D}_{2}}D{{E}_{2}}$, который является вписанным, так как $\angle {{E}_{2}}O{{D}_{2}} = 60^\circ $ и $\angle {{E}_{2}}D{{D}_{2}} = 120^\circ $. Пусть $\gamma $ – описанная около $O{{D}_{2}}D{{E}_{2}}$ окружность, а $S$ – центр $\gamma $. Можно показать, что радиус окружности $\gamma $ равен в точности $\rho \, = \,\sqrt {\tfrac{{2 - \sqrt 3 }}{3}} $. Окружность радиуса $\rho $ с центром в точке ${{D}_{1}}$ пересекает отрезки $O{{E}_{2}}$ и $O{{D}_{2}}$ вточках U и V соответственно. Тогда четырехугольник $O{{D}_{2}}D{{E}_{2}}$ разбивается на два четырехугольника $OUSV$, $US{{D}_{1}}{{E}_{2}}$ и один пятиугольник $D{{D}_{1}}SV{{D}_{2}}$, диаметр каждого из которых равен $\rho $. На рис. 2 длины отрезков, выделенных жирным пунктиром, равны $\rho $. Тем самым показано, что шестиугольник $ABCDEF$ можно разбить на 18 частей, диаметр каждой из которых равен $\rho $. На рис. 2 выделены части данного разбиения.

Рис. 1.

Фигуры, используемые в УПС.

Рис. 2.

Разбиение ${{\Omega }_{6}}$ на 18 частей.

Выше мы показали, как получается верхняя оценка на примере оценки величины d18. Также важно отметить, что эта оценка – единственная, которую удалось точно выразить в радикалах среди всех полученных в данном исследовании оценок.

Список литературы

  1. Borsuk K. Drei Sätze über die n-dimensionale euklidische Sphäre // Fundamenta Math. 1933. V. 20. P. 177–190.

  2. Raigorodskii A.M. Coloring Distance Graphs and Graphs of Diameters // Thirty Essays on Geometric Graph Theory. J. Pach ed. Springer. 2013. P. 429–460.

  3. Райгородский А.М. О разбиении множеств на части меньшего диаметра // Доклады РАН. Математика, информатика, процессы управления. 2020. Т. 495. С. 74–77.

  4. Berdnikov A.V., Raigorodskii A.M. Bounds for Borsuk’s numbers using special distance graphs // submitted to Information Transmission Problems.

  5. Lenz H. Zerlegung ebener Bereiche in konvexe Zellen von möglichst kleinem Durchmesser // Jber. Deutsch. Math. Verein. 1956. V. 58. P. 87–97.

  6. Dembiński M., Lassak M. Covering plane sets with sets of three times less diameter // Demonstratio Math. 1985. V. 18. № 2. P. 517–526.

  7. Филимонов В.П. О покрытии плоских множеств // Матем. сборник. 2010. Т. 201. № 8. С. 127–160.

  8. Белов Д., Александров Н. О разбиении плоских множеств на шесть частей малого диаметра // Труды МФТИ. 2012. Т. 4. № 1. С. 11–13.

  9. Коваль В.О. О разбиении плоских множеств на 6 частей малого диаметра // Зап. научн. сем. ПОМИ. 2020. Т. 497. С. 100–123.

  10. Pal J. Uber ein elementares Variationsproblem // Danske Videnskab. Selskab. Math.-Fys. Meddel. 1920. V. 3. № 2.

  11. Райгородский А.М. Проблема Борсука и хроматические числа метрических пространств // Успехи матем. наук. 2001. Т. 56. № 1. С. 107–146.

  12. Просанов Р.И. Контрпримеры к гипотезе Борсука, имеющие большой обхват // Матем. заметки. 2019. Т. 105. № 6. С. 890–898.

  13. Боголюбский Л.И., Райгородский А.М. Замечание о нижних оценках хроматических чисел пространств малой размерности с метриками ${{l}_{1}}$ и ${{l}_{2}}$ // Матем. заметки. 2019. Т. 105. № 2. С. 187–213.

  14. Raigorodskii A.M., Koshelev M.M. New bounds on clique-chromatic numbers of Johnson graphs // Discrete and Applied Math. 2020. V. 283. P. 724–729.

  15. Райгородский А.М., Кошелев М.М. Новые оценки клико-хроматических чисел графов Джонсона // Доклады РАН. Математика, информатика, процессы управления. 2020. Т. 490. С. 78–80.

  16. Prosanov R. A new proof of the Larman–Rogers upper bound for the chromatic number of the Euclidean space // Discrete Applied Mathematics. 2020. №. 276. P. 115–120.

  17. Купавский А.Б., Сагдеев А.А. Теория Рамсея в пространстве с чебышевской метрикой // Успехи матем. наук. 2020. Т. 75. № 5. С. 191–192.

  18. Разбиения для верхних оценок. https://github.com/Vosatorp/Partitions

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Доклады Российской академии наук. Математика, информатика, процессы управления

Архивы выпусков Информация о журнале Отправить рукопись в журнал