Доклады Российской академии наук. Математика, информатика, процессы управления, 2021, T. 499, № 1, стр. 54-57
ОПЕРАТОРНЫЕ ОЦЕНКИ ДЛЯ ЗАДАЧИ СТЕКЛОВА В НЕОГРАНИЧЕННОЙ ОБЛАСТИ С БЫСТРО МЕНЯЮЩИМИСЯ УСЛОВИЯМИ НА ГРАНИЦЕ
1 Московский государственный университет
имени М.В. Ломоносова
Москва, Россия
* E-mail: chechkina@gmail.com
Поступила в редакцию 10.02.2021
После доработки 21.05.2021
Принята к публикации 31.05.2021
Аннотация
Рассмотрена спектральная задачи типа Стеклова для лапласиана в неограниченной области с гладкой границей. Условие Стеклова быстро чередуется с однородным условием Дирихле на части границы. Получены операторные оценки, с помощью которых изучено асимптотическое поведение собственных элементов исходной задачи при стремлении малого параметра к нулю. Малый параметр характеризует размер участков границы с условием Дирихле, расстояние между которыми имеет порядок логарифма малого параметра в отрицательной степени.
Большой интерес последнее время вызывает задача Стеклова, зависящая от малого параметра (см., например, [1–5]). Предполагается, что микронеоднородность сосредоточена на границе, аналогичные задачи см. [6–9]. В этой работе рассматривается задача в неограниченной области, у которой условие Стеклова быстро чередуется с условием Дирихле на границе. Мы получаем операторные оценки для этой задачи, а также и для аналогичной задачи в ограниченной области. Некоторые интегральные оценки для подобных задач см. в [10, 11].
Отметим, что техника операторных оценок, впервые появившаяся в работах М.С. Бирмана, Т.А. Суслиной, В.В. Жикова, С.Е. Пастуховой и G. Griso (см. работы [12, 13], а также ссылки в них), позволяет получать значительно более строгие результаты (сходимость резольвент в соответствующих нормах) по сравнению с результатами, получаемыми в теории сингулярных возмущений и теории усреднения. Слабая и сильная сходимость решений (из теории возмущений и теории усреднения) влечет только частичные результаты о сходимости спектра.
В настоящей работе рассмотрена задача в неограниченной области, что приводит к существенному усложнению структуры спектра задачи, при этом получены точные по порядку оценки скорости сходимости, которые позволяют с помощью стандартных результатов спектральной теории самосопряженных операторов в гильбертовых пространствах доказать результат о сходимости спектра и соответствующих спектральных проекторов.
1. ПОСТАНОВКА ЗАДАЧИ И ВСПОМОГАТЕЛЬНЫЕ УТВЕРЖДЕНИЯ
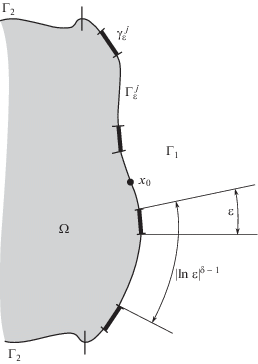
Пусть связная область $\Omega $ с непустой границей лежит в пространстве ${{\mathbb{R}}^{2}}$ с локальными координатами $x = ({{x}_{1}},{{x}_{2}})$. Предполагается, что граница области $\Omega $ имеет гладкость ${{C}^{2}}$ и равномерно ограниченную кривизну. Отметим еще раз, что ограниченность области $\Omega $ не предполагается.
Выберем на границе $\partial \Omega $ точку ${{x}_{0}}$ и назовем ${{\Gamma }_{1}}$ множество точек $x(s) \in \partial \Omega $ таких, что $\left| s \right| < 1$, где s – длина дуги от ${{x}_{0}}$ до данной точки. Пусть sk = = $k \cdot {{\left| {ln\varepsilon } \right|}^{{\delta - 1}}},$ ${{x}_{k}} = x({{s}_{k}})$, где δ ∈ (0, 1), $k \in \mathbb{Z}$, а $\varepsilon $ – положительный малый параметр. Обозначим ${{\Upsilon }_{\varepsilon }} = \{ k:{\text{|}}k \cdot {{\left| {ln\varepsilon } \right|}^{{\delta - 1}}}{\text{|}} < 1\} $.
Таким образом, ${{\Gamma }_{1}}$ – часть границы $\partial \Omega $ длины 2. Обозначим оставшуюся часть границы за ${{\Gamma }_{2}}$, т.е. ${{\Gamma }_{2}}: = \partial \Omega {{\backslash }}{{\bar {\Gamma }}_{1}}$. Мы предполагаем, что $\partial \Omega $ имеет в окрестности ${{\Gamma }_{1}}$ гладкость C3. При этом ${{\Gamma }_{1}}$ состоит из двух быстро чередующихся частей (см. рис. 1): ${{\Gamma }_{1}}\, = \,{{\gamma }_{\varepsilon }}\, \cup \,{{\Gamma }_{\varepsilon }},$ где ${{\gamma }_{\varepsilon }}\, = \,\bigcup\limits_{k \in {{\Upsilon }_{\varepsilon }}} {\gamma _{\varepsilon }^{k}} $, ${{\Gamma }_{\varepsilon }}\, = \,\bigcup\limits_{k \in {{\Upsilon }_{\varepsilon }}} {\Gamma _{\varepsilon }^{k}} $. Длина ${\text{|}}\gamma _{\varepsilon }^{k}{\text{|}}$ = ε, $\bar {\gamma }_{s}^{j} \cup \bar {\Gamma }_{s}^{k} = \left[ {x({{s}_{k}}),x({{s}_{{k + 1}}})} \right]$, $k \in {{\Upsilon }_{\varepsilon }}$.
Рассмотрим следующую сингулярно возмущенную спектральную задачу с краевым условием Стеклова:
(1)
$\begin{gathered} \hat {\mathcal{H}}{{u}_{\varepsilon }} = 0\quad {\text{в}}\quad \Omega , \\ \frac{{\partial {{u}_{\varepsilon }}}}{{\partial n}} = \lambda {{u}_{\varepsilon }}\quad {\text{на}}\quad {{\Gamma }_{2}} \cup {{\Gamma }_{\varepsilon }}, \\ {{u}_{\varepsilon }} = 0\quad {\text{на}}\quad {{\gamma }_{\varepsilon }}, \\ \end{gathered} $Здесь ${{A}_{{ij}}} = {{A}_{{ij}}}(x)$, ${{A}_{j}} = {{A}_{j}}(x)$, ${{A}_{0}} = {{A}_{0}}(x)$ – действительнозначные функции, определенные в $\bar {\Omega }$, а i – мнимая единица. Предполагаем, что Aij и ${{A}_{j}} \in {{C}^{1}}(\bar {\Omega })$, ${{A}_{0}} \in C(\bar {\Omega })$, ${{A}_{{ij}}} = {{A}_{{ji}}}$ и все эти функции равномерно ограничены на $\bar {\Omega }$,
Основное требование к области $\Omega $ следующее. В пространстве $W_{2}^{1}(\Omega )$ введем полуторалинейную форму:
Предполагается, что существуют такие константы ${{c}_{1}} > 0$ и ${{\lambda }_{0}} > 0$, что для всех $u \in W_{2}^{1}(\Omega )$ верна оценка
(2)
$\mathfrak{h}(u,u) + {{\lambda }_{0}}\left\| u \right\|_{{{{L}_{2}}(\partial \Omega )}}^{2} \geqslant {{c}_{1}}\left\| u \right\|_{{{{L}_{2}}(\Omega )}}^{2}.$Имеет место
Лемма 1. Полуторалинейная форма
${{\mathfrak{h}}_{0}}(u,{v})$ := $h(u,{v}) + {{\lambda }_{0}}{{(u,{v})}_{{{{L}_{2}}(\partial \Omega )}}}$
определяет эквивалентное скалярное произведение в $W_{2}^{1}(\Omega )$.
Обозначим через $W_{2}^{{\frac{1}{2}}}(\partial \Omega )$ пространство следов функций из $W_{2}^{1}(\Omega )$ на $\partial \Omega $. Определим норму в $W_{2}^{{\frac{1}{2}}}(\partial \Omega )$ как
Эта норма естественно возникает, если рассматривать пространство $W_{2}^{{\frac{1}{2}}}(\partial \Omega )$ как факторпространство $W_{2}^{1}(\Omega ){\text{/}}{{\mathop H\limits^ \circ }^{1}}(\Omega )$, где ${{\mathop H\limits^ \circ }^{1}}(\Omega )$ – подпространство $W_{2}^{1}(\Omega )$, состоящее из функций с нулевым следом на границе $\Omega $.
Для функций $u \in {{\mathop H\limits^ \circ }^{1}}(\Omega )$ неравенство (2) принимает форму
и, следовательно, краевая задача(3)
$\begin{gathered} \hat {\mathcal{H}}U = 0\quad {\text{в}}\quad \Omega , \\ U = g\quad {\text{на}}\quad \partial \Omega \\ \end{gathered} $Обозначим через $\mathcal{A}$: $W_{2}^{{\frac{1}{2}}}(\partial \Omega ) \to W_{2}^{1}(\Omega )$ оператор, отображающий функцию $g \in W_{2}^{{\frac{1}{2}}}(\partial \Omega )$ в решение U задачи (3). Можно заметить, что
Это дает возможность определить скалярное произведение в пространстве $W_{2}^{{\frac{1}{2}}}(\partial \Omega )$.
Рассмотрим краевую задачу
(4)
$\begin{gathered} \hat {\mathcal{H}}{{U}_{\varepsilon }} = 0\quad {\text{в}}\quad \Omega , \\ \frac{{\partial {{U}_{\varepsilon }}}}{{\partial n}} + {{\lambda }_{0}}{{U}_{\varepsilon }} = g\quad {\text{на}}\quad {{\Gamma }_{2}} \cup {{\Gamma }_{\varepsilon }}, \\ {{U}_{\varepsilon }} = 0\quad {\text{на}}\quad {{\gamma }_{\varepsilon }}, \\ \end{gathered} $(5)
${{\mathfrak{h}}_{0}}({{U}_{\varepsilon }},{v}) = {{(g,{v})}_{{{{L}_{2}}({{\Gamma }_{2}} \cup {{\Gamma }_{\varepsilon }})}}}$Обозначим оператор в $W_{2}^{{\frac{1}{2}}}(\partial \Omega )$, отображающий каждую функцию $g \in W_{2}^{{\frac{1}{2}}}(\partial \Omega )$ в след решения задачи (4) на границе $\Omega $, через ${{\mathcal{H}}_{\varepsilon }}$. Ясно, что эти следы равны нулю на ${{\gamma }_{\varepsilon }}$. Тогда задача нахождения собственных значений задачи (1) может быть записана в виде
Пусть ${{\mathcal{H}}_{0}}$ – тот же оператор, что и ${{\mathcal{H}}_{\varepsilon }}$, но в случае ${{\gamma }_{\varepsilon }} = \not {0}$, ${{\Gamma }_{2}} \cup {{\Gamma }_{\varepsilon }} = \partial \Omega $. Ясно, что оба этих оператора, ${{\mathcal{H}}_{\varepsilon }}$ и ${{\mathcal{H}}_{0}}$ ограничены.
2. ОСНОВНЫЕ РЕЗУЛЬТАТЫ
Первая теорема – об операторной сходимости.
Теорема 1. Операторы ${{\mathcal{H}}_{\varepsilon }}$ и ${{\mathcal{H}}_{0}}$ являются самоcопряженными в пространстве $W_{2}^{{\frac{1}{2}}}(\partial \Omega )$. Имеет место оценка
Следующий результат — о сходимости спектра оператора ${{\mathcal{H}}_{\varepsilon }}$.
Теорема 2. Спектр оператора ${{\mathcal{H}}_{\varepsilon }}$ сходится к спектру ${{\mathcal{H}}_{0}}$. Спектральные проекторы оператора ${{\mathcal{H}}_{\varepsilon }}$ сходятся к спектральным проекторам оператора ${{\mathcal{H}}_{0}}$. А именно, если ${{\lambda }_{0}}$ – дискретное собственное значение оператора ${{\mathcal{H}}_{0}}$ кратности $n$ при $\varepsilon \to 0$, то существует ровно $n$ собственных значений оператора ${{H}_{\varepsilon }}$ с учетом кратности, сходящихся к ${{\lambda }_{0}}$ при $\varepsilon \to 0$. И полный проектор этих собственных значений сходится в норме ограниченных операторов в $W_{2}^{{\frac{1}{2}}}(\partial \Omega )$ к проектору на собственное подпространство, порожденное ${{\lambda }_{0}}$.
Список литературы
Mel’nyk T.A. Asymptotic behavior of eigenvalues and eigenfunctions of the Steklov problem in a thick periodic junction // Nonlinear Oscillations. 2001. V. 4. № 1. P. 91–105.
Pérez E. On periodic Steklov type eigenvalue problems on half-bands and the spectral homogenization problem // Discrete Contin. Dyn. Syst. Ser. B. 2007. V. 7. № 4. P. 859–883.
Назаров С.А. Асимптотика решения спектральной задачи Стеклова в области с затупленным пиком // Мат. заметки. 2009. Т. 86. № 4. С. 571–587.
Чечкина А.Г. Усреднение спектральных задач с сингулярным возмущением условия Стеклова // Известия РАН. 2017. Т. 81. № 1. С. 203–240.
Chechkina A.G., D’Apice C., De Maio U. Rate of Convergence of Eigenvalues to Singularly Perturbed Steklov–Type Problem for Elasticity System // Applicable Analysis. 2019. V. 98. № 1-2. P. 32–44.
Гадыльшин Р.Р., Чечкин Г.А. Краевая задача для Лапласиана с быстро меняющимся типом граничных условий в многомерной области // Сиб. мат. журнал. 1999. Т. 40. № 2. С. 271–287.
Перес М.Е., Чечкин Г.А., Яблокова (Доронина) Е.И. О собственных колебаниях тела с “легкими” концентрированными массами на поверхности // Успехи мат. наук. 2002. Т. 57. Вып. 6. С. 195–196.
Chechkin G.A. On Vibration of Partially Fastened Membrane with Many “Light” Concentrated Masses on the Boundary // C. R. Mécanique. 2004. V. 332. № 12. P. 949–954.
Amirat Y., Chechkin G.A., Gadyl’shin R.R. Asymptotics of the Solution of a Dirichlet Spectral Problem in a Junction with Highly Oscillating Boundary // C. R. Mécanique. 2008. V. 336. № 9. P. 693–698.
Chechkin G.A., Koroleva Yu.O., Persson L.-E. On the Precise Asymptotics of the Constant in the Friedrich‘s Inequality for Functions, Vanishing on the Part of the Boundary with Microinhomogeneous Structure // Journal of Inequalities and Applications. 2007. V. 2007. article ID 34138. 13 pages. https://doi.org/10.1155/2007/34138
Chechkin G.A., Koroleva Yu.O., Meidell A., Persson L.-E. On the Friedrichs inequality in a domain perforated aperiodically along the boundary. Homogenization procedure. Asymptotics for parabolic problems. // Russ. J. Math. Phys. 2009. V. 16, P. 1–16.
Суслина Т.А. Усреднение задачи Дирихле для эллиптических уравнений высокого порядка с периодическими коэффициентами // Алгебра и анализ. 2017. Т. 29. № 2. С. 139–192.
Griso G. Interior error estimate for periodic homogenization. // Anal. Appl. 2006. V. 4. P. 61–79.
Дополнительные материалы отсутствуют.
Инструменты
Доклады Российской академии наук. Математика, информатика, процессы управления