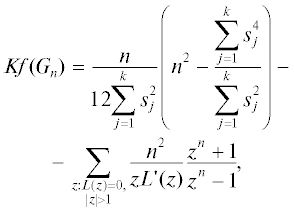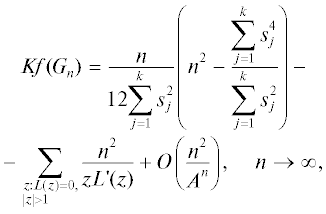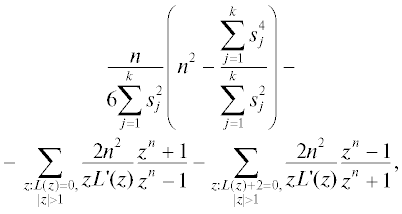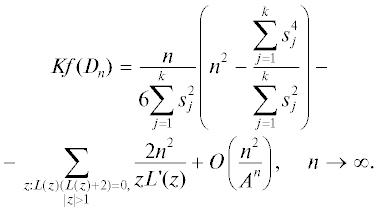1. На главную
  2. Электронные версии
  3. Доклады Российской академии наук. Математика, информатика, процессы управления
  4. T. 494, № 1, 2020

Доклады Российской академии наук. Математика, информатика, процессы управления, 2020, T. 494, № 1, стр. 43-47

ИНДЕКС КИРХГОФА ДЛЯ ЦИРКУЛЯНТНЫХ ГРАФОВ И ЕГО АСИМПТОТИКА

А. Д. Медных 1, 2, *, И. А. Медных 1, 2, **

1 Институт математики им С.Л. Соболева Сибирского отделения Российской академии наук
Новосибирск, Россия

2 Новосибирский государственный университет
Новосибирск, Россия

* E-mail: smedn@mail.ru
** E-mail: ilyamednykh@mail.ru

Поступила в редакцию 06.12.2019
После доработки 29.08.2020
Принята к публикации 31.08.2020

Полный текст (PDF)

Аннотация

Целью сообщения является нахождение явной аналитической формулы для индекса Кирхгофа циркулянтных графов ${{C}_{n}}({{s}_{1}},{{s}_{2}},\; \ldots ,\;{{s}_{k}})$ и ${{C}_{{2n}}}({{s}_{1}},{{s}_{2}},\; \ldots ,\;{{s}_{k}},n)$ с четной и нечетной валентностью вершин соответственно. Изучено асимптотическое поведение индекса Кирхгофа при n, стремящемся к бесконечности. Доказано, что индекс Кирхгофа представляется в виде суммы кубического многочлена от n и экспоненциально малого остаточного члена.

Ключевые слова: циркулянтный граф, матрица Лапласа, собственное число, индекс Винера, индекс Кирхгофа

Пусть G – связный конечный граф на $n$ вершинах. Обозначим через $D(G)$ диагональную матрицу, составленную из валентностей вершин G, а через $A(G)$ – матрицу смежности графа G. Матрица $L(G) = D(G) - A(G)$ называется матрицей Лапласа графа G. Известно [1], что eсли граф связен, то все собственные значения $L(G)$, за исключением одного, равного 0, строго положительны. То есть спектр матрицы Лапласа графа G имеет вид $0 = {{\lambda }_{1}} < {{\lambda }_{2}} \leqslant \ldots \; \leqslant {{\lambda }_{n}}$.

Изначально индекс Кирхгофа графа G был определен Клейном и Рандичем [2] как среднее резистивное расстояние между его вершинами. Точнее, пусть вершины графа G обозначаются $1,2, \ldots ,n$. Тогда резистивное расстояние между вершинами i и j, обозначаемое ${{r}_{{ij}}} = {{r}_{{ij}}}(G)$, определяется как эффективное сопротивление между ними, если мы наделим каждое ребро G единичным сопротивлением. Следуя [2], определим индекс Кирхгофа графа G как величину

$Kf(G) = \frac{1}{2}\sum\limits_{i = 1}^n {\sum\limits_{j = 1}^n {{{r}_{{ij}}}} } .$

Такое определение было мотивировано известным индексом Винера W(G), подсчитывающим сумму расстояний между парами вершин графа $G$ [3]. То есть

$W(G) = \frac{1}{2}\sum\limits_{i = 1}^n {\sum\limits_{j = 1}^n {{{d}_{{ij}}}} } ,$
где через dij обозначается расстояние вершинами между i и j. Клейн и Рандич [2] показали, что $Kf(G) \leqslant W(G)$, где равенство достигается тогда и только тогда, когда граф G – это дерево. Интересная зависимость между индексом Кирхгофа и спектром матрицы Лапласа была независимо найдена в работах [4, 5]:

(1)
$Kf(G) = n\sum\limits_{j = 2}^n {\frac{1}{{{{\lambda }_{j}}}}} .$

Индексы Кирхгофа для различных семейств графов были изучены в работах [6–13].

Цель настоящей работы – найти явные аналитические формулы для индекса Кирхгофа циркулянтных графов ${{C}_{n}}({{s}_{1}},{{s}_{2}},\; \ldots ,\;{{s}_{k}})$ и ${{C}_{{2n}}}({{s}_{1}},{{s}_{2}},\; \ldots ,\;{{s}_{k}},n)$, а также изучить их асимптотическое поведение при $n$, стремящемся к бесконечности. Указанные формулы будут представлены в виде конечного не зависящего от n числа слагаемых, каждое из которых представляет собой рациональную функцию, вычисленных в корнях некоторого фиксированного многочлена.

1. ОСНОВНЫЕ ОПРЕДЕЛЕНИЯ

Рассмотрим конечный связный граф G, допускающий кратные ребра, но не имеющий петель. Обозначим через $V(G)$ и $E(G)$, соответственно, множество вершин и ребер графа G. Матрица $A = A(G) = {{{\text{\{ }}{{a}_{{u{v}}}}{\text{\} }}}_{{u,{v} \in V(G)}}}$, где ${{a}_{{u{v}}}}$ – число ребер между u и ${v}$, называется матрицей смежности графа G. Обозначим через $d({v})$ валентность вершины ${v} \in V(G)$ и рассмотрим диагональную матрицу $D = D(G)$ с элементами ${{d}_{{{vv}}}} = d({v})$. Матрица L = L(G) = $D(G) - A(G)$ называется матрицей Лапласа, или лапласианом графа G.

Пусть ${{s}_{1}},\;{{s}_{2}},\; \ldots ,\;{{s}_{k}}$ – целые числа, такие что $1 \leqslant {{s}_{1}} < {{s}_{2}} < \; \ldots \; < {{s}_{k}} \leqslant \tfrac{n}{2}$. Циркулянтным графом ${{C}_{n}}({{s}_{1}},{{s}_{2}},\; \ldots ,\;{{s}_{k}})$ на n вершинах $0,1,2, \ldots ,n - 1$ называется простой граф, у которого вершина i, $0 \leqslant i$ ≤ ≤ n – 1, смежна вершинам $i \pm {{s}_{1}},i \pm {{s}_{2}}, \ldots ,i \pm {{s}_{k}}$ (mod n). Если ${{s}_{k}} < n{\text{/}}2$, то все вершины графа имеют четную валентность 2k. В случае когда n – четно и ${{s}_{k}} = n{\text{/}}2$, все вершины графа имеют нечетную валентность 2k – 1. Циркулянтный граф ${{C}_{n}}({{s}_{1}},{{s}_{2}},\; \ldots ,\;{{s}_{k}})$ связен, если $gcd({{s}_{1}},{{s}_{2}},\; \ldots ,\;{{s}_{n}}) = 1$. Это условие в рамках сообщения всегда предполагаем выполненным.

2. ИНДЕКС КИРХГОФА ДЛЯ ЦИРКУЛЯНТНЫХ ГРАФОВ С ЧЕТНОЙ ВАЛЕНТНОСТЬЮ

В текущем разделе будут приведены явные формулы для индекса Кирхгофа $Kf({{G}_{n}})$ циркулянтных графов

${{G}_{n}} = {{C}_{n}}({{s}_{1}},{{s}_{2}}, \ldots ,{{s}_{k}}),\quad 1 \leqslant {{s}_{1}} < {{s}_{2}} < \; \ldots \; < {{s}_{k}} < n{\text{/}}2.$

Данные формулы представляются в виде сумм ${{s}_{k}}$ членов, каждый из которых выражается через полиномы Чебышева порядка n, вычисленные в корнях заданного полинома степени sk.

Tеорема 1. Индекс Кирхгофа циркулянтного графа ${{G}_{n}} = {{C}_{n}}({{s}_{1}},{{s}_{2}}, \ldots ,{{s}_{k}})$ вычисляется по формуле

$\begin{gathered} Kf({{G}_{n}}) = \frac{n}{{12\sum\limits_{j = 1}^k {s_{j}^{2}} }}\left( {{{n}^{2}} - \frac{{\sum\limits_{j = 1}^k {s_{j}^{4}} }}{{\sum\limits_{j = 1}^k {s_{j}^{2}} }}} \right) + \\ + \;\sum\limits_{p = 2}^{{{s}_{k}}} {} \frac{{{{n}^{2}}{{U}_{{n - 1}}}({{w}_{p}})}}{{(1 - {{T}_{n}}({{w}_{p}}))Q{\text{'}}({{w}_{p}})}}, \\ \end{gathered} $
где wp – отличные от 1 корни полинома Q(w) = = $\sum\limits_{j = 1}^k {(2 - 2{{T}_{{{{s}_{j}}}}}(w))} $, а ${{T}_{n}}(w)$ и ${{U}_{{n - 1}}}(w)$ – полиномы Чебышева первого и второго рода соответственно.

Доказательство основано на следующих рассуждениях. Заметим, что собственные значения оператора Лапласа графа Gn имеют вид

$\begin{gathered} {{\lambda }_{j}} = 2k - 2\sum\limits_{i = 1}^k {cos} \left( {\tfrac{{2\pi j{{s}_{i}}}}{n}} \right) = \\ = \;2k - 2\sum\limits_{i = 1}^k {{{T}_{{{{s}_{i}}}}}} \left( {cos\left( {\tfrac{{2\pi j}}{n}} \right)} \right) = \\ = \;Q\left( {cos\left( {\tfrac{{2\pi j}}{n}} \right)} \right),\quad j = 1,\; \ldots ,\;n, \\ \end{gathered} $
а числа $cos\left( {\tfrac{{2\pi j}}{n}} \right)$ являются корнями полинома $P(z) = {{T}_{n}}(z) - 1$. В силу связности, граф Gn имеет ровно одно нулевое собственное значение. Отсюда, z = 1 – единственный общий корень полиномов P(z) и Q(z). Воспользуемся следующим вспомогательным предложением.

Предложение 1. Пусть P(z) и Q(z) – полиномы степеней $n$ и m, соответственно, имеющие простые корни. Обозначим корни полинома P(z) через ${{\alpha }_{1}},{{\alpha }_{2}}, \ldots ,{{\alpha }_{n}}$, а корни полинома Q(z) через ${{\beta }_{1}},{{\beta }_{2}}, \ldots ,{{\beta }_{m}}$. Предположим, что P(z) и Q(z) имеют единственный общий корень ${{\alpha }_{1}} = {{\beta }_{1}} = 1$. Тогда имеет место равенство

$\sum\limits_{j = 2}^n {\frac{1}{{Q({{\alpha }_{j}})}}} = - \mathop {{\text{Res}}}\limits_{z = 1} \frac{1}{{Q(z)}}\frac{{P{\text{'}}(z)}}{{P(z)}} - \sum\limits_{j = 2}^m {} \frac{1}{{Q{\text{'}}({{\beta }_{j}})}}\frac{{P{\text{'}}({{\beta }_{j}})}}{{P({{\beta }_{j}})}}.$

Для доказательства предложения заметим, что

$\mathop {{\text{Res}}}\limits_{z = {{\alpha }_{j}}} \tfrac{1}{{Q(z)}}\tfrac{{P\,{\text{'}}(z)}}{{P(z)}} = \tfrac{1}{{Q({{\alpha }_{j}})}},$

$\mathop {{\text{Res}}}\limits_{z = {{\beta }_{j}}} \tfrac{1}{{Q(z)}}\tfrac{{P\,{\text{'}}(z)}}{{P(z)}} = \tfrac{1}{{Q\,{\text{'}}({{\beta }_{j}})}}\tfrac{{P\,{\text{'}}({{\beta }_{j}})}}{{P({{\beta }_{j}})}}.$

Тогда, по классической теореме о вычетах, имеем

$\begin{gathered} 0 = \frac{1}{{2\pi {\text{i}}}}\int\limits_{|z| = R} {\frac{1}{{Q(z)}}} \frac{{P\,{\text{'}}(z)}}{{P(z)}}dz = \mathop {{\text{Res}}}\limits_{z = 1} \frac{1}{{Q(z)}}\frac{{P\,{\text{'}}(z)}}{{P(z)}} + \\ + \;\int\limits_{j = 2}^n {\frac{1}{{Q({{\alpha }_{j}})}}} + \sum\limits_{j = 2}^m {\frac{1}{{Q{\text{'}}({{\beta }_{j}})}}} \frac{{P\,{\text{'}}({{\beta }_{j}})}}{{P({{\beta }_{j}})}}, \\ \end{gathered} $
где $R > \mathop {max}\limits_{j,k} \left\{ {\left| {{{\alpha }_{j}}} \right|,\left| {{{\beta }_{k}}} \right|} \right\}$. Полученное равенство доказывает предложение.

Вычет в точке z = 1 находится с помощью следующей леммы, которая доказывается непосредственным разложением P(z) и Q(z) в степенные ряды.

Лемма 1. Пусть полиномы P(z) и Q(z) имеют общий корень z = 1 кратности 1. Тогда

$\mathop {{\text{Res}}}\limits_{z = 1} \tfrac{1}{{Q(z)}}\tfrac{{P\,{\text{'}}(z)}}{{P(z)}} = \tfrac{1}{{2Q{\text{'}}(1)}}\left( {\tfrac{{P\,{\text{''}}(1)}}{{P\,{\text{'}}(1)}} - \tfrac{{Q\,{\text{''}}(1)}}{{Q\,{\text{'}}(1)}}} \right).$

Для доказательства теоремы 1 положим P(w) = = ${{T}_{n}}(w) - 1$ и $Q(w) = \sum\limits_{i = 1}^k {(2 - 2{{T}_{{{{s}_{i}}}}}(w))} $. Поскольку индекс Кирхгофа

$Kf({{G}_{n}}) = n\sum\limits_{j = 2}^n {1{\text{/}}{{\lambda }_{j}}} = n\sum\limits_{j = 2}^n {{1 \mathord{\left/ {\vphantom {1 {Q\left( {cos\left( {\tfrac{{2\pi j}}{n}} \right)} \right)}}} \right. \kern-0em} {Q\left( {cos\left( {\tfrac{{2\pi j}}{n}} \right)} \right)}}} ,$
для его вычисления используем предложение 1 и лемму 1. Непосредственными вычислениями по лемме 1 получим

$\mathop {{\text{Res}}}\limits_{z = 1} \tfrac{1}{{Q(z)}}\tfrac{{P{\text{'}}(z)}}{{P(z)}} = - \tfrac{1}{{12\sum\limits_{j = 1}^k {s_{j}^{2}} }}\left( {{{n}^{2}} - \tfrac{{\sum\limits_{j = 1}^k {s_{j}^{4}} }}{{\sum\limits_{j = 1}^k {s_{j}^{2}} }}} \right).$

Учитывая, что $T_{n}^{'}(w) = n{{U}_{{n - 1}}}(w)$, по предложению 1, завершим доказательство теоремы.

Для исследования асимптотического поведения индекса Кирхгофа при n → $\infty $ удобно переписать теорему 1 в следующем виде.

Tеорема 2. Индекс Кирхгофа циркулянтного графа ${{G}_{n}} = {{C}_{n}}({{s}_{1}},{{s}_{2}}, \ldots ,\;{{s}_{k}})$ вычисляется по формуле

где $L(z) = 2k - \sum\limits_{j = 1}^k {({{z}^{{{{s}_{j}}}}} + {{z}^{{ - {{s}_{j}}}}})} $, а суммирование ведется по всем корням L(z), модуль которых больше 1.

Теорема 2 получается из теоремы 1 с помощью замены переменных $w = (z + {{z}^{{ - 1}}}){\text{/}}2$ и равенств ${{T}_{n}}((z + {{z}^{{ - 1}}}){\text{/}}2) = ({{z}^{n}} + {{z}^{{ - n}}}){\text{/}}2$ и Un – 1((z + z–1)/2) = = $({{z}^{n}} - {{z}^{{ - n}}}){\text{/}}(z - {{z}^{{ - 1}}})$.

Как следствие, мы получим следующую асимптотическую формулу поведения индекса Кирхгофа для циркулянтных графов ${{G}_{n}} = {{C}_{n}}({{s}_{1}},{{s}_{2}}, \ldots ,{{s}_{k}})$ при n, стремящемся к бесконечности.

Следствие 1. Имеет место асимптотическая формула

где $L(z) = 2k - \sum\limits_{j = 1}^k {({{z}^{{{{s}_{j}}}}} + {{z}^{{ - {{s}_{j}}}}})} $, а $A = min\{ {\text{|}}z{\text{|}}$ : L(z) = 0, |z| > 1} – константа, зависящая только от ${{s}_{1}},{{s}_{2}}, \ldots ,{{s}_{k}}$.

Заметим, что главный член асимптотики представляет собой кубический полином от n со свободным членом, равным нулю.

3. ИНДЕКС КИРХГОФА ДЛЯ ЦИРКУЛЯНТНЫХ ГРАФОВ С НЕЧЕТНОЙ ВАЛЕНТНОСТЬЮ

Текущий раздел содержит явные аналитические формулы для индекса Кирхгофа $Kf({{D}_{n}})$ циркулянтных графов с нечетной валентностью вершин

$\begin{gathered} {{D}_{n}} = {{C}_{{2n}}}({{s}_{1}},{{s}_{2}},\; \ldots ,\;{{s}_{k}},n), \\ 1 \leqslant {{s}_{1}} < {{s}_{2}} < \; \ldots \; < {{s}_{k}} < n. \\ \end{gathered} $

Эти формулы содержат суммы, слагаемые которых представляют собой простые аналитические выражения, вычисленные в корнях заданного полинома степени $2{{s}_{k}}$. Справедлива следующая

Tеорема 3. Индекс Кирхгофа $Kf({{D}_{n}})$ циркулянтного графа с нечетной валентностью вершин

${{D}_{n}} = {{C}_{{2n}}}({{s}_{1}},{{s}_{2}},\; \ldots ,\;{{s}_{k}},n),\quad 1 \leqslant {{s}_{1}} < {{s}_{2}} < \; \ldots \; < {{s}_{k}} < n$
задается формулой
где $L(z) = 2k - \sum\limits_{j = 1}^k {({{z}^{{{{s}_{j}}}}} + {{z}^{{ - {{s}_{j}}}}})} $.

Доказательство теоремы 3 проводится по той же схеме, что и доказательство аналогичного утверждения для циркулянтных графов с четной валентностью. Теорема 3, как и теорема 2, может быть сформулирована в терминах полиномов Чебышева.

Следующее утверждение позволяет вычислить асимптотику индекса Кирхгофа для циркулянтных графов с нечетной валентностью.

Следствие 2. Справедлива следующая асимп-тотическая формула для индекса Кирхгофа

Здесь $L(z) = 2k - \sum\limits_{j = 1}^k {({{z}^{{{{s}_{j}}}}} + {{z}^{{ - {{s}_{j}}}}})} $, а A = min{|z|: $L(z)(L(z) + 2) = 0,{\text{|}}z{\text{|}} > 1\} $ – константа, зависящая только от ${{s}_{1}},{{s}_{2}},\; \ldots ,\;{{s}_{k}}$.

4. ПРИМЕРЫ

1. Циклический граф Cn. Индекс Кирхгофа циклического графа равен

$Kf({{C}_{n}}) = \frac{{{{n}^{3}} - n}}{{12}}.$

2. Граф ${{C}_{n}}(1,2)$. Для данного семейства графов индекс Кирхгофа может быть вычислен по формуле

$Kf({{C}_{n}}(1,2)) = \frac{n}{{300}}(5{{n}^{2}} - 17) + \frac{{{{n}^{2}}{{F}_{{2n}}}}}{{25F_{n}^{2}}},$
где Fn – $n$-е число Фиббоначи. Заметим, что $\frac{{{{F}_{{2n}}}}}{{F_{n}^{2}}}$ = 1 + O$\left( {\frac{1}{{{{\phi }^{{2n}}}}}} \right)$, где $\phi = \frac{{1 + \sqrt 5 }}{2}$ – золотое сечение.

3. Граф ${{C}_{n}}(1,3).$ Индекс Кирхгофа циркулянтных графов ${{C}_{n}}(1,3)$ имеет следующее асимптотическое поведение:

$\begin{gathered} Kf({{C}_{n}}(1,3)) = \\ = \frac{n}{{600}}(5{{n}^{2}} + 6\sqrt {110 + 50\sqrt 5 } n - 41) + O\left( {\frac{{{{n}^{2}}}}{{{{A}^{n}}}}} \right),\,\,n \to \infty , \\ \end{gathered} $
где $A = \sqrt {\frac{1}{2}(1 + \sqrt 5 + \sqrt {2(1 + \sqrt 5 )} )} \simeq 1.700015\; \ldots $

4. Граф Лестница Мёбиуса ${{C}_{{2n}}}(1,n).$ Индекс Кирхгофа лестницы Мёбиуса ${{C}_{{2n}}}(1,n)$ имеет следующее асимптотическое поведение:

$\begin{gathered} Kf({{C}_{{2n}}}(1,n)) = \\ = \;\frac{n}{6}({{n}^{2}} + 2\sqrt 3 n - 1) + O\left( {\frac{{{{n}^{2}}}}{{{{A}^{n}}}}} \right),\quad n \to \infty , \\ \end{gathered} $
где $A = 2 + \sqrt 3 \simeq 3.73205$. (Ср. с результатом [13].)

5. Граф ${{C}_{{2n}}}(1,2,n).$ Для графа ${{C}_{{2n}}}(1,2,n)$ индекс Кирхгофа допускает следующее асимптотическое поведение:

$\begin{gathered} Kf({{C}_{{2n}}}(1,2,n)) = \\ = \frac{n}{{1650}}(55{{n}^{2}} + Kn - 187) + O\left( {\frac{{{{n}^{2}}}}{{{{A}^{n}}}}} \right),\quad n \to \infty , \\ \end{gathered} $
где K = $2(66\sqrt 5 + 25\sqrt {99 + 44\sqrt 3 } )$ и A = = $\frac{1}{4}( - 1 + \sqrt {33} + \sqrt {2(9 - \sqrt {33} )} )$ $ \simeq $ 1.824051.

Список литературы

  1. Mohar B. In: Y. Alavi, G. Chartrand, O.R. Oellermann, A.J. Schwenk (eds.). Graph theory, combinatorics, and applications, Wiley, New York, 2 (1991), 871–898.

  2. Klein D.J., Randić M. // J. Math. Chem. 1993. V. 12. P. 81–95.

  3. Wiener H. // J. Amer. Chem. Soc. 1947. V. 1. № 69. P. 17–20.

  4. Gutman I., Mohar B. // J. Chem. Inf. Comput. Sci. 1996. V. 36. P. 982–985.

  5. Zhu H.Y., Klein D.J., Lukovits I. // J. Chemical Information and Computer Sciences 1996. V. 36. № 3. P. 420-428.

  6. Lukovits I., Nikolić S., Trinajstić N. // Int. J. Quantum Chem. 1999. V. 71. P. 217–225.

  7. Palacios J.L. // Int. J. Quantum Chem. 2001. V. 81. P. 135–140.

  8. Zhang H., Yang Y. // Int. J. Quantum Chem. 2007. V. 107. P. 330–339.

  9. Xiao W., Gutman I. // Theor. Chem. Acc. 2009. V. 110. P. 284–289.

  10. Luzhen Ye // Linear and Multilinear Algebra. 2011. V. 59. № 6. P. 645–650.

  11. Cinkir Z. // J. Math. Chem. 2016. V. 54. № 4. P. 955–966.

  12. Kagan M., Mata B. // Math. Comput. Sci. 2019. V. 13. P. 105–115.

  13. Baigonagova G.A., Mednykh A.D. // Sib. Electron. Math. Rep. 2019. V. 16, P. 1654–1661.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Доклады Российской академии наук. Математика, информатика, процессы управления

Архивы выпусков Информация о журнале Отправить рукопись в журнал