Доклады Российской академии наук. Математика, информатика, процессы управления, 2020, T. 494, № 1, стр. 38-42
О ЧИСЛЕННОМ РЕШЕНИИ СКАЛЯРНЫХ ЗАДАЧ ДИФРАКЦИИ В ИНТЕГРАЛЬНЫХ ПОСТАНОВКАХ НА СПЕКТРАХ ИНТЕГРАЛЬНЫХ ОПЕРАТОРОВ
А. А. Каширин 1, *, член-корреспондент РАН С. И. Смагин 1, **
1 Вычислительный центр Дальневосточного отделения Российской академии наук, Хабаровский Федеральный исследовательский центр Дальневосточного отделения Российской академии наук
Хабаровск, Россия
* E-mail: elomer@mail.ru
** E-mail: smagin@ccfebras.ru
Поступила в редакцию 10.03.2020
После доработки 10.03.2020
Принята к публикации 31.07.2020
Аннотация
Рассмотрены граничные интегральные уравнения Фредгольма первого рода с одной неизвестной функцией, каждое из которых условно эквивалентно скалярной задаче дифракции (трансмиссии) на трехмерном однородном включении и решается численно. Предложена и апробирована модификация метода численного решения задачи дифракции на спектре интегрального оператора, где нарушаются условия корректной разрешимости интегрального уравнения и его эквивалентности исходной задаче.
Рассматривается задача дифракции (трансмиссии) акустических волн на трехмерном однородном включении. Для нее получены и исследованы два слабо сингулярных граничных интегральных уравнения Фредгольма первого рода с одной неизвестной функцией, каждое из которых условно эквивалентно исходной задаче. Методика и результаты численного решения этих уравнений при выполнении условий эквивалентности представлены в [1]. Вычислительные эксперименты показали, что предлагаемый подход позволяет находить приближенные решения задачи дифракции с высокой точностью в широком диапазоне волновых чисел.
Упомянутые граничные интегральные уравнения обладают следующим свойством: у входящих в их состав интегральных операторов имеется спектр – счетное множество положительных волновых чисел, на котором нарушаются условия эквивалентности этих уравнений соответствующей задаче дифракции. В этом случае интегральные уравнения либо не имеют решений, либо разрешимы неединственным образом, в отличие от исходной задачи, которая всегда корректно разрешима. Для областей общего вида спектры операторов заранее неизвестны, а их поиск является весьма трудоемкой задачей. Отметим, что аналогичными свойствами обладают и некоторые другие интегральные формулировки задач дифракции [2].
Одним из путей расширения возможностей применяемой методики для решения задач дифракции на спектре интегральных операторов является модификация используемых интегральных представлений [3]. Получаемые при этом интегральные уравнения полностью эквивалентны исходной задаче, но имеют более сложную структуру и менее удобны для численного решения. Другие способы, связанные с модификацией метода численного решения рассматриваемых задач на спектре, обсуждаются, например, в статьях [4, 5].
Применяемый в данной работе подход основан на использовании исходных интегральных формулировок задач дифракции с близкими к точкам спектра волновыми числами, когда соответствующие интегральные уравнения заведомо корректно разрешимы. Ранее он применялся при численном решении трехмерных краевых задач для уравнения Гельмгольца в интегральных постановках [6].
1. ИСХОДНАЯ ЗАДАЧА ДИФРАКЦИИ И ЭКВИВАЛЕНТНЫЕ ЕЙ ИНТЕГРАЛЬНЫЕ УРАВНЕНИЯ
Рассмотрим трехмерное евклидово пространство R3 с ортогональной системой координат ox1x2x3, разделенное произвольной замкнутой поверхностью Γ ∈ C r + β, r + β > 1, на внутреннюю и внешнюю области Ωi и Ωe (${{\Omega }_{e}} = {{R}^{3}}{\backslash }{{\bar {\Omega }}_{i}}$), заполненные однородными изотропными средами с плотностями ρi(e), скоростями звука сi(e) и коэффициентами поглощения γi(e).
Если в области Ωe имеются гармонические источники звука, то возбуждаемые ими звуковые волны распространяются в ней и, достигая включения, заполняющего область Ωi, рассеиваются на нем. В результате в области Ωe возникают отраженные волны, а в области Ωi появляются проходящие волны. Поэтому комплексную амплитуду полного волнового поля давлений u можно представить в виде
Исходная задача. В областях Ωi и Ωe найти комплекснозначные функции ui и ue, удовлетворяющие уравнениям
условиям сопряжения на границе Γ раздела сред из Ωi и Ωe(2)
$\begin{gathered} u_{i}^{ - } - u_{e}^{ + } = {{u}_{0}}, \\ {{p}_{i}}{{\left( {\frac{{\partial {{u}_{i}}}}{{\partial n}}} \right)}^{ - }} - {{p}_{e}}{{\left( {\frac{{\partial {{u}_{e}}}}{{\partial n}}} \right)}^{ + }} = {{p}_{e}}\frac{{\partial {{u}_{0}}}}{{\partial n}},\quad x \in \Gamma , \\ \end{gathered} $(3)
$\frac{{\partial {{u}_{e}}}}{{\partial \left| x \right|}} - i{{k}_{e}}{{u}_{e}} = o({{\left| x \right|}^{{ - 1}}}),\quad \left| x \right| \to \infty .$Здесь и далее знаками “–” и “+” отмечаются предельные значения соответствующих выражений на Γ, когда x → Γ из Ωi и из Ωe, n(x) – вектор единичной внешней нормали к поверхности Γ в точке x, ki(e) – волновые числа,
Исходная задача (обобщенная постановка). Найти функции ui(e) ∈ H1(Ωi(e), Δ), удовлетворяющие интегральным тождествам
(4)
$\begin{gathered} \int\limits_{{{\Omega }_{{i(e)}}}} {\nabla {{u}_{{i(e)}}}\nabla {v}_{{i(e)}}^{*}dx} - k_{{i(e)}}^{2}\int\limits_{{{\Omega }_{{i(e)}}}} {{{u}_{{i(e)}}}{v}_{{i(e)}}^{*}dx} = 0 \\ \forall {{{v}}_{{i(e)}}} \in H_{0}^{1}\left( {{{\Omega }_{{i(e)}}}} \right), \\ \end{gathered} $(5)
$\begin{gathered} {{\left\langle {u_{i}^{ - } - u_{e}^{ + },\mu } \right\rangle }_{\Gamma }} = {{\left\langle {{{f}_{0}},\mu } \right\rangle }_{\Gamma }}\quad \forall \mu \in {{H}^{{{{ - 1} \mathord{\left/ {\vphantom {{ - 1} 2}} \right. \kern-0em} 2}}}}(\Gamma ), \\ {{\left\langle {\eta ,{{p}_{i}}{{N}^{ - }}{{u}_{i}} - {{p}_{e}}{{N}^{ + }}{{u}_{e}}} \right\rangle }_{\Gamma }} = {{\left\langle {\eta ,{{p}_{e}}{{f}_{1}}} \right\rangle }_{\Gamma }}\quad \forall \eta \in {{H}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}(\Gamma ), \\ \end{gathered} $Здесь ${v}{\text{*}}$ – комплексно-сопряженная к ${v}$ функция, $\left\langle { \cdot , \cdot } \right\rangle $Γ – отношение двойственности на H1/2(Γ) × × H–1/2(Γ), обобщающее скалярное произведение в Н0(Г), ${{u}^{ \pm }} \equiv {{\gamma }^{ \pm }}u$, γ–: H1(Ωi) → H1/2(Γ), γ+: H1(Ωe) → → H1/2(Γ) – операторы следов, N–: H1(Ωi, Δ) → H–1/2(Γ), N+: H1(Ωe, Δ) → H–1/2(Γ) – операторы нормальных производных [7], ${{f}_{{\text{0}}}} = u_{0}^{ + }$, ${{f}_{1}} = {{N}^{ + }}{{u}_{0}}$.
Замечание. Если Im(ke) = 0, то ${{u}_{e}}\, \in \,H_{{{\text{loc}}}}^{1}({{\Omega }_{e}},\Delta )$.
Введем следующие обозначения:
(6)
$\begin{gathered} \left( {{{A}_{{i(e)}}}q} \right)(x) \equiv {{\left\langle {{{G}_{{i(e)}}}(x, \cdot ),q} \right\rangle }_{\Gamma }}, \\ \left( {{{B}_{{i(e)}}}q} \right)(x) \equiv {{\left\langle {{{N}_{x}}{{G}_{{i(e)}}}(x, \cdot ),q} \right\rangle }_{\Gamma }}, \\ \end{gathered} $Решение задачи (3)–(5) будем искать в виде потенциалов
(7)
$\begin{gathered} {{u}_{e}}(x) = ({{A}_{e}}q)(x),\quad x \in {{\Omega }_{e}}, \\ {{u}_{i}}(x)\, = \,({{p}_{{ei}}}{{A}_{i}}({{f}_{1}}\, + \,{{N}^{ + }}{{u}_{e}})\, - \,B_{i}^{ * }({{f}_{{\text{0}}}}\, + \,u_{e}^{ + }))(x),\quad x\, \in \,{{\Omega }_{i}}, \\ \end{gathered} $В этом случае данная задача условно эквивалентна слабо сингулярному граничному интегральному уравнению Фредгольма I рода [1]:
(8)
${{\left\langle {Cq,\mu } \right\rangle }_{\Gamma }} = {{\left\langle {{{f}_{2}},\mu } \right\rangle }_{\Gamma }}\quad \forall \mu \in {{H}^{{{{ - 1} \mathord{\left/ {\vphantom {{ - 1} 2}} \right. \kern-0em} 2}}}}\left( \Gamma \right),$Исходная задача допускает еще одну условно эквивалентную формулировку в виде граничного интегрального уравнения Фредгольма I рода со слабой особенностью в ядре. Ее решение можно представить в виде
(10)
${{\left\langle {Dq,\mu } \right\rangle }_{\Gamma }} = {{\left\langle {{{f}_{0}},\mu } \right\rangle }_{\Gamma }}\quad \forall \mu \in {{H}^{{{{ - 1} \mathord{\left/ {\vphantom {{ - 1} 2}} \right. \kern-0em} 2}}}}\left( \Gamma \right),$Теорема 1 [1]. Пусть f0 ∈ H1/2(Γ), f1 ∈ H−1/2(Γ), γe > 0 или ω не является собственной частотой задачи
Тогда уравнения (8) и (10) корректно разрешимы в классе плотностей q ∈ H−1/2(Γ) и формулы (7) и (9) дают решение исходной задачи.
Лемма. Пусть γe = 0 и ω – собственная частота задачи (11). Тогда однородные уравнения (8) и (10) имеют нетривиальные решения $q_{n}^{'}$, связанные с собственными функциями un задачи (11) равенствами
Теорема 2. Пусть выполнены условия леммы, f0 ∈ H1/2(Γ), f1 ∈ H−1/2(Γ). Тогда решение уравнения (10) существует и имеет вид $q = {{q}_{i}} + q{\text{'}}$, где qi – его частное решение,
an – произвольные комплексные числа, m – кратность собственной частоты ω. Подстановка частного решения qi в формулы (9) дает решение исходной задачи.Решение уравнения (8) существует, если ${{\left\langle {{{f}_{2}},q{\text{'}}} \right\rangle }_{\Gamma }}$ = 0. Его можно представить в виде $q = {{q}_{e}} + q{\text{'}}$, где qe – частное решение этого уравнения. Решение qe, подставленное в формулы (7), дает решение исходной задачи.
2. О ЧИСЛЕННОМ РЕШЕНИИ ЗАДАЧИ ДИФРАКЦИИ НА СПЕКТРЕ ИНТЕГРАЛЬНОГО ОПЕРАТОРА
Основной целью данной работы является рассмотрение наиболее трудных с вычислительной точки зрения случаев, когда решение задачи дифракции ищется на собственных частотах задачи (11). Для численного решения интегральных уравнений используется согласованный с шагом сетки метод осреднения интегральных операторов со слабыми особенностями в ядрах, который не требует предварительной триангуляции поверхности включения. Он позволяет строить дискретные аналоги исходных задач по весьма простым аналитическим формулам. Его подробное изложение имеется, например, в публикациях [1, 6].
Опишем модификацию метода для численного решения интегральных уравнений на спектре. Обозначим через ke > 0 некоторое собственное волновое число задачи (11), а через q(ke) – зависящее от него частное решение неоднородного уравнения (8) или (10). Выберем некоторое число δ > 0. Тогда для искомого частного решения интегрального уравнения имеет место интерполяционная формула для плотности
(12)
$\begin{gathered} q\left( {{{k}_{e}}} \right) = 4q\left( {{{k}_{e}} + i\delta } \right) - q\left( {{{k}_{e}} - \delta + i\delta } \right) - \\ - \;q\left( {{{k}_{e}} + \delta + i\delta } \right) - q\left( {{{k}_{e}} + 2i\delta } \right) + O({{\delta }^{4}}), \\ \end{gathered} $Формула (12) подразумевает, что искомое частное решение интегрального уравнения существует. В тех случаях, когда оно не существует, искомое приближенное решение задачи дифракции может быть найдено по аналогичной формуле для ui(e):
(13)
$\begin{gathered} {{u}_{{i(e)}}}\left( {{{k}_{e}}} \right) = 4{{u}_{{i(e)}}}\left( {{{k}_{e}} + i\delta } \right) - {{u}_{{i(e)}}}\left( {{{k}_{e}} - \delta + i\delta } \right) - \\ - \;{{u}_{{i(e)}}}\left( {{{k}_{e}} + \delta + i\delta } \right) - {{u}_{{i(e)}}}\left( {{{k}_{e}} + 2i\delta } \right) + O({{\delta }^{4}}), \\ \end{gathered} $3. РЕЗУЛЬТАТЫ ЧИСЛЕННЫХ ЭКСПЕРИМЕНТОВ
Для выполнения расчетов были использованы вычислительные ресурсы ЦКП “Центр данных ДВО РАН”. Правильность и точность предлагаемого подхода проверялись для задач дифракции, имеющих известные точные решения.
Пример. Рассматривается задача дифракции плоской акустической волны на единичном шаре с центром в начале координат и тремя различными наборами параметров вмещающей среды и включения, где в качестве ke выбраны собственные числа задачи (11). Комплексная амплитуда исходного волнового поля давлений имеет вид
I) ki = 12.5, ρi = 4, ke = 7.725251836937, ρe = 3;
II) ki = 7, ρi = 2, ke = 16.9236212852138, ρe = 5;
III) ki = 21, ρi = 7, ke = 13.6980231532492, ρe = 4.5.
Исследование уравнения (8) показало, что в этом случае оно не имеет решения. Поэтому применение формулы (12) в данном случае не дает правильного результата и необходимо использовать формулу (13). Существование частного решения уравнения (10) следует из теоремы 2. Оно может быть приближенно найдено при помощи формулы (12).
Задачи из примера решались дважды – с интерполяцией решения (формула (12), δ = 0.01) и без нее. Количество точек дискретизации M варьировалось от 500 до 128 000. Полученные в результате дискретизации системы линейных алгебраических уравнений (СЛАУ) решались численно обобщенным методом минимальной невязки (GMRES) [8] с точностью 10–8. Для нахождения приближенного решения второй и последующих вспомогательных задач в качестве первого приближения в GMRES использовалось приближенное решение первой вспомогательной задачи. Это позволяло получать их решения с точностью порядка δ уже на первой итерации.
На рис. 1 и 2 приведены погрешности решений задач дифракции, полученных путем решения уравнения (8). Погрешности вычислены в норме пространств сеточных функций $H_{h}^{0}({{\Omega }_{{i(e)}}})$. Здесь и далее сплошной линией обозначены погрешности функций ui, пунктиром – погрешности функций ue. Результаты расчетов, относящиеся к первому, второму и третьему набору параметров, отмечены на графиках треугольниками, кругами и квадратами соответственно. Видно, что уравнение (8) не может быть использовано без интерполяции решения для нахождения приближенных решений задач дифракции, так как погрешности при увеличении размерностей СЛАУ не уменьшаются. При этом интерполяция по формуле (13) позволяет находить эти решения с погрешностями, которые при достаточно больших значениях M имеют порядок не хуже h2 ∼ M–1, где параметр h характеризует шаг сетки на границе включения.
Рис. 1.
Погрешности решений задачи дифракции из примера, найденных с использованием уравнения (8) без интерполяции решений.
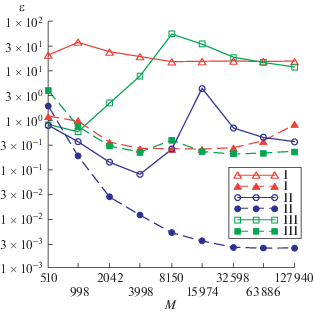
Рис. 2.
Погрешности решений задачи дифракции из примера, найденных с использованием уравнения (8) с интерполяцией решений по формулам (13).
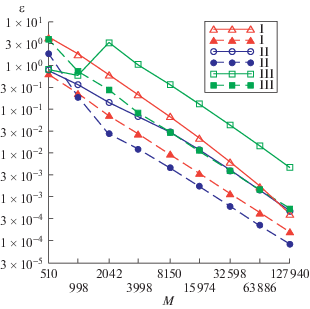
Рис. 3.
Погрешности решений задачи дифракции из примера, найденных с использованием уравнения (10) без интерполяции решений.
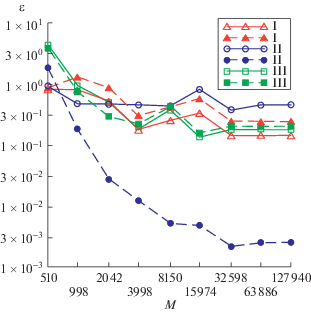
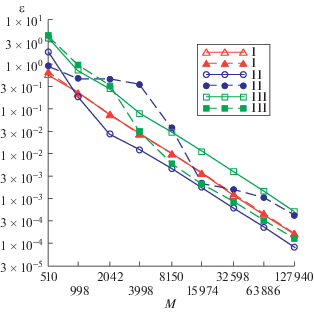
Для приближенных решений задач дифракции, полученных с использованием уравнения (10) с интерполяцией решения по формуле (12), погрешности также имеют порядок O(h2) (рис. 4). Расчеты без интерполяции решения, представленные на рис. 3, в этом случае дают неудовлетворительные результаты, что согласуется с теоремой 2. Сравнение представленных результатов численных экспериментов показывает достаточно высокую эффективность применяемого подхода с интерполяцией решения.
Рис. 4.
Погрешности решений задачи дифракции из примера, найденных с использованием уравнения (10) с интерполяцией решений по формулам (12).
Список литературы
Каширин А.А., Смагин С.И. // Вычислительные технологии. 2018. Т. 23. № 2. С. 20–36.
Martin P.A. // Wave Motion. 1991. V. 13. № 2. P. 185–192.
Kleinman R.E., Martin P.A. // SIAM J. Appl. Math. 1988. V. 48. № 2. P. 307–325.
Mohsen A., Hesham M. // Communications in Numerical Methods in Engineering. 2006. V. 22. № 11. P. 1067–1076.
Laliena A.R., Rapun M.-L., Sayas F.-J. // Appl. Numer. Math. 2009. V. 59. № 11. P. 2814–2823.
Каширин А.А., Смагин С.И. // ЖВМиМФ. 2012. Т. 52. № 8. С. 1492–1505.
McLean W. Strongly elliptic systems and boundary integral equations. Cambridge: Cambridge University Press, 2000. 372 p.
Saad Y., Schultz M. // SIAM J. Sci. Statist. Comput. 1986. V. 7. № 3. P. 856–869.
Дополнительные материалы отсутствуют.
Инструменты
Доклады Российской академии наук. Математика, информатика, процессы управления


