Акустический журнал, 2022, T. 68, № 5, стр. 520-529

ВВЕДЕНИЕ

Направленные свойства акустического поля обычно характеризуются угловым спектром. Угловой спектр является одной из важнейших характеристик поля и широко применяется при прогнозировании работоспособности различных гидроакустических устройств. Возможности устройства по угловому разрешению нескольких источников или выделению сосредоточенного источника на фоне помех тесно связаны с решением таких важных технических задач, как обнаружение и пеленгование. Для моделирования углового спектра используются как теоретические модели [1, 2], так и аппроксимации экспериментальных данных [3]. Для накопления экспериментальных данных, их обобщения и последующего уточнения представлений о процессах, формирующих шумовые поля, необходимо проводить исследования направленности морских (океанских) шумов в различных диапазонах частот. Экспериментально в условиях открытого моря оценка углового спектра обычно выполняется с помощью протяженных многоэлементных узконаправленных антенн [4–8], имеющих размер несколько десятков длин волн. Большие габариты этих устройств существенно усложняют проведение экспериментов. Кроме того, для многоэлементных антенн характерно значительное расширение характеристики направленности с уменьшением частоты [5], что затрудняет анализ направленных свойств поля в этом диапазоне.

Комбинированный векторно-скалярный приемник (ВСП) [9] в отличие от протяженной антенны имеет размер существенно меньше длины волны и поэтому может входить в состав компактных средств исследования океана. ВСП включает в себя ненаправленный приемник давления (скалярная часть) и два или три приемных канала, имеющих взаимно перпендикулярные дипольные характеристики направленности (векторная часть). ВСП обладает следующей важной особенностью: характеристики направленности канала давления и каналов его векторной части близки к теоретическим и практически неизменны в широком диапазоне частот, доходящем до двух–трех декад. Это свойство позволяет анализировать широкополосные сигналы, принятые приемником, полагая характеристики направленности всех его каналов равными теоретическим и не зависящими от частоты. Будем также считать, что фазовые центры всех приемных каналов совпадают, а выходные сигналы каналов векторной части пропорциональны компонентам колебательной скорости.

ВСП применяется для решения различных гидроакустических задач [10]. Используемые при этом методы часто именуются векторно-фазовыми. Теоретическое изучение статистических свойств поля [11] и пеленгования [12] с помощью комбинированных приемников, выполненное для гауссовых (нормальных) полей, показало, что ВСП обладает весьма ограниченными возможностями по исследованию направленных свойств поля и разрешению локальных источников. Однако, известны экспериментальные данные ([10], с. 221), показывающие, что с помощью ВСП возможно разрешение, по крайней мере, двух источников. Это указывает на необходимость углубления понимания возможностей ВСП, что требует не только расширения представлений о статистических свойствах гауссова поля, но и применения модели морского шума, обладающей более широкими возможностями по варьированию свойств моделируемого поля.

МОДЕЛЬ ШУМОВОГО ПОЛЯ

В традиционных моделях [1, 2, 13] шумовое поле рассматривается как результат сложения гармонических волн, излучаемых многочисленными точечными монопольными, дипольными или иными источниками с равными среднеквадратическими интенсивностями, но со случайными фазами. Источники равномерно располагаются в объеме, на сфере, в конусе, на плоскости или прямой. Такие модели хорошо подходят для анализа свойств гауссовых полей и находящихся в них устройств в узкой полосе частот. Для исследования полей, формируемых широкополосными сигналами, требуется иной подход. Пример такого подхода изложен в [12]. Он основан на представлении, что события, приводящие к излучению шумов, происходят независимо друг от друга в различных точках водной толщи или на ее поверхностях. Считается, что некоторые из этих событий порождаются сходными процессами и при этом излучаются близкие по форме импульсы. Такими процессами могут быть: падение капель, разрушение гребней волн, растрескивание и торошение льда, звуки, издаваемые животными одного вида, схлопывание кавитационных пузырьков, некоторые виды технических шумов и т.п. Общей особенностью перечисленных процессов является то, что они создают короткие звуковые импульсы. В рамках модели рассматриваются статистические свойства акустического поля, создаваемого в безграничном однородном и изотропном пространстве источниками, находящимися на окружности достаточно большого радиуса r, лежащей в плоскости xОy. Такое приближение допустимо, поскольку в [1] отмечалось, что корреляционные характеристики поля при определенных условиях будут одинаковыми как в случае объемной изотропной модели, так и при расположении точечных источников на поверхности сферы большого радиуса. Плоская двумерная модель выбрана для сокращения объема формул и может быть при необходимости преобразована в трехмерную.

Пусть поле формируется в результате последовательности событий, заключающихся в том, что в случайные моменты времени ${{t}_{i}}$ в точках, лежащих на окружности радиуса r под углом ${{\varphi }_{i}}$, $ - {{\pi }} \leqslant {{\varphi }_{i}} < {{\pi }}$, происходит кратковременный импульс, создающий в центре окружности изменение давления

Здесь r₀ – единичный радиус, a и φ – независимые случайные величины, $g(\varphi )$ – неслучайная функция, $s(t)$ – ограниченный во времени импульс, $s(t) = 0$, если $t < {{ - {{\tau }}} \mathord{\left/ {\vphantom {{ - {{\tau }}} 2}} \right. \kern-0em} 2}$ и $t > {{{\tau }} \mathord{\left/ {\vphantom {{{\tau }} 2}} \right. \kern-0em} 2}$, τ – длительность импульса, с – скорость звука в среде. Соответствующее такому случайному процессу давление в центре окружности равно:

а компоненты колебательной скорости где ρ – плотность среды. Происходит сдвиг фазы на π, так как импульс распространяется в сторону, противоположную источнику (см. рис. 1а). В качестве допустимого упрощения принято, что при достаточно большом r связь между скоростью и давлением во всем рассматриваемом частотном диапазоне соответствует плоской волне. Далее исследуется случайный процесс, имеющий нормированные составляющие:

Согласно [12], если процесс (1) является пуассоновским, то его характеристическая функция имеет вид:

Здесь w_a и w_φ – плотности вероятности случайных величин a_i и φ_i, а q – средняя частота появления импульсов, ${{g}_{1}}(\varphi ) = g(\varphi )$, ${{g}_{2}}(\varphi ) = - g(\varphi )\cos \varphi $ и ${{g}_{3}}(\varphi ) = - g(\varphi )\sin \varphi $. Соответствующие кумулянты равны:

Величина $n + k + l$ – порядок кумулянта. Кумулянты первого порядка – средние значения, второго – центральные моменты второго порядка, т.е. дисперсии и функции взаимной корреляции процессов P, X, Y. Следовательно, дисперсия пульсаций давления равна:

Здесь $\sigma _{a}^{2} = \int_{ - \infty }^\infty {{{a}^{2}}{{w}_{a}}(a)da} $, $\sigma _{s}^{2} = \int_{ - \infty }^\infty {{{s}^{2}}(t)dt} $. Аналогично вычисляются дисперсии компонент колебательной скорости:

Взаимная корреляционная функция компонент колебательной скорости дается формулой:

а взаимные корреляционные функции давления и компонент колебательной скорости равны:

Из полученных формул видно, что дисперсии и взаимные корреляционные функции давления и колебательной скорости зависят только от функции $G(\varphi ) = q\sigma _{a}^{2}\sigma _{s}^{2}{{g}^{2}}(\varphi ){{w}_{\varphi }}(\varphi )$, которую назовем угловой плотностью поля. На зависимость функции G(φ) от угла влияет как относительная частота попадания импульсов в различные секторы углов (угловая плотность вероятности w_φ(φ)), так и квадрат локальной амплитуды импульсов (функция g²(φ)). По влиянию на дисперсии и корреляционные функции эти факторы эквивалентны.

ВЕКТОР УМОВА

Анализируя движение энергии в волновых полях в упругой среде, Н.А. Умов пришел к выводу [13–15], что в каждый момент времени направление движения энергии задается вектором, который для жидкости в принятых здесь обозначениях имеет вид: ${\mathbf{J}}(t) = {{p}_{s}}(t){\mathbf{v}}(t)$, где ${\mathbf{v}}(t)$ – вектор колебательной скорости, в двумерном пространстве равный ${\mathbf{v}}(t) = {{v}_{x}}(t) + i{{v}_{y}}(t)$. Эта величина под названием вектор Умова (Умова–Пойнтинга) [10], а для аналитического сигнала в форме, указанной в [17], широко применяется в акустике, в том числе для статистического анализа полей [10–12].

Рассмотрим случайный процесс

отличающийся от вектора Умова только постоянным множителем. Далее вектором Умова для краткости будем называть процесс I(t). Его характеристическая функция равна:

Соответствующий ей кумулянт первого порядка – математическое ожидание процесса I равно:

Иногда эту функцию называют потоком акустической мощности и возлагают на нее особые надежды в решении ряда задач [10, 18]. Однако, приведенное выражение показывает, что математические ожидания компонент вектора Умова M[I_x] и M[I_y] совпадают с взаимными корреляционными функциями давления и компонент колебательной скорости R_PX и R_PY. Как вытекает из формулы (3), эти функции полностью определяются первой гармоникой разложения угловой плотности в ряд Фурье по углу φ [12], и ожидание того, что с их помощью удастся получить полное описание направленных свойств поля, представляется необоснованным.

Более перспективно изучение свойств распределений, которые могут быть получены на основании мгновенных значений вектора Умова, описываемых его модулем I(t) = |I(t)| и аргументом (фазой) θ(t):

$0 \leqslant {{\theta }}(t) < 2\pi $, причем если I_x(t) = 0, то значение θ(t) не определено.

Следует заметить, что все приведенные соотношения выполняются независимо от величины произведения (интенсивности процесса) qτ, определяющего характер поля. При высокой интенсивности qτ $ \gg $ 1 в результате взаимного наложения большого числа импульсов процесс (1), как известно, приближается к нормальному [19]. В противоположном случае qτ $ \ll $ 1 будут наблюдаться отдельные импульсы почти без наложения. Различия в формировании вектора Умова в том и другом случае иллюстрирует рис. 1. Рассмотрим эти два предельных случая подробнее.

УГЛОВАЯ ПЛОТНОСТЬ МОДУЛЯ И ПЛОТНОСТЬ ВЕРОЯТНОСТИ АРГУМЕНТА ВЕКТОРА УМОВА В СЛУЧАЕ РЕДКИХ ИМПУЛЬСОВ

Когда средняя частота появления импульсов низкая, а сами импульсы короткие: qτ $ \ll $ 1, вероятность наложения следующих друг за другом импульсов мала. Для упрощения анализа совсем исключим такие события из рассмотрения. При этом условии в течение времени прохождения через точку начала координат i-го импульса процесса (1) значение аргумента вектора Умова будет равно: θ_i = φ_i + π.

Выделим малую дугу (θ', θ' + Δθ) такую, чтобы выполнялось условие |1 – θ'/(θ' + Δθ)| $ \ll $ 1, что делает возможным только малое изменение значений функции exp(θ), когда θ' ≤ θ < θ' + Δθ. Из исходного процесса (1) выберем подпоследовательность, для которой θ' ≤ θ_i < θ' + Δθ. Так как в рассматриваемом случае углы θ и φ связаны однозначно: φ_i = θ_i – π, вероятность попадания i-го импульса в указанный интервал и его включения в новую подпоследовательность равна:

причем вероятность F не зависит от номера импульса i. При выполнении этого условия новая подпоследовательность также будет пуассоновским процессом со средней частотой появления импульсов qF ([19], с. 410–411). Переобозначим новую последовательность в порядке возрастания t_k. Запишем новый процесс в виде:

Найдем математическое ожидание вектора Умова ${{{\mathbf{I}}}_{{\Delta {{\theta }}}}}(t) = {{P}_{{\Delta {{\theta }}}}}(t){{{\mathbf{V}}}_{{\Delta {{\theta }}}}}(t)$, порождаемого источниками, находящимися на выделенной дуге. Характеристическая функция процесса ${{{\mathbf{I}}}_{{\Delta {{\theta }}}}}(t)$ отличается от (4) только пределами интегрирования по φ и равна:

Соответствующее ей математическое ожидание равно:

Если произведение ${{g}^{2}}(\varphi )\exp (i\varphi )$ мало изменяется при θ' – π ≤ φ ≤ θ' + Δθ – π, то

Если произведение ${{g}^{2}}(\varphi )w(\varphi )$ является непрерывной функцией угла $\varphi $, то существует предел отношения M[I_Δθ]/Δθ при уменьшении длины дуги Δθ, равный:

Заметим, что модуль полученного выражения:

равен угловой плотности поля G(θ–π) = G(φ). Для сравнения процессов удобнее использовать нормированную угловую плотность:

Заметим также, что при условии непрерывности функции w_φ(φ) из (7) вытекает, что пределом отношения F/Δθ при уменьшении дуги Δθ является угловая плотность вероятности w_φ(θ – π):

Таким образом, в случае редкого процесса вычисление угловых распределений модуля и аргумента вектора Умова позволяет получить достоверные оценки угловой плотности и угловой плотности вероятности поля.

УГЛОВАЯ ПЛОТНОСТЬ МОДУЛЯ И ПЛОТНОСТЬ ВЕРОЯТНОСТИ АРГУМЕНТА ВЕКТОРА УМОВА В ГАУССОВОМ ПОЛЕ

В [12] найдены выражения для совместной плотности вероятности модуля и аргумента вектора Умова и плотности вероятности его аргумента (фазы) для случайного процесса вида (1). Совместная плотность вероятности модуля и аргумента вектора Умова после замены функции Макдональда порядка ½ ее выражением через элементарные функции ([20], ф-ла 8.469.3) принимает вид:

Эта формула справедлива, если случайный процесс (1) является стационарным, нормальным и центрированным. Коэффициенты c_i представляют собой измеренные или рассчитанные статистические моменты второго порядка пульсаций давления и компонент колебательной скорости: ${{c}_{0}} = \sigma _{P}^{2}$, ${{c}_{1}} = \sigma _{X}^{2}$, ${{c}_{2}} = \sigma _{Y}^{2}$, ${{c}_{3}} = {{R}_{{PX}}}$, ${{c}_{4}} = {{R}_{{PY}}}$, ${{c}_{5}} = {{R}_{{XY}}}$, а коэффициенты α, β и C выражаются через них:

Интегрирование (10) по I от 0 до ∞ приводит к следующему выражению

связывающему плотность вероятности аргумента вектора Умова θ и вторые центральные статистические моменты процесса (1). Плотность вероятности модуля I при условии, что аргумент равен θ, найдем из (10) как условную плотность вероятности [21]:

Следовательно, математическое ожидание модуля вектора Умова при условии, что его аргумент равен θ, рассчитывается по формуле:

По аналогии с (8) угловая плотность модуля вектора Умова в гауссовом поле U_g равна произведению условного математического ожидания на плотность вероятности аргумента:

Функцию G_g(φ) = U_g(θ – π) формально можно рассматривать как оценку угловой плотности, полученную в гауссовом поле, так же как функцию w_g(θ – π) как оценку угловой плотности вероятности w_φ(φ). Оценка нормированной угловой плотности в гауссовом поле равна:

В гауссовом поле угловые плотности аргумента (11) и модуля (12) вектора Умова вычисляются через дисперсии и функции взаимной корреляции компонент поля, которые зависят только от нулевой, первой и второй гармоник разложения G(φ) по углу φ. Это позволяет предположить, что оценки угловой плотности G_g(φ) и угловой плотности вероятности w_g(φ) могут существенно отличаться от функций G(φ) и w_φ(φ).

ЭВОЛЮЦИЯ УГЛОВОЙ ПЛОТНОСТИ МОДУЛЯ И ПЛОТНОСТИ ВЕРОЯТНОСТИ АРГУМЕНТА ВЕКТОРА УМОВА ПРИ ИЗМЕНЕНИИ ИНТЕНСИВНОСТИ ПРОЦЕССА

Полученные в предыдущих разделах формулы позволяют проанализировать асимптотическое поведение статистических характеристик поля при qτ → 0 и qτ → ∞. Однако, можно ожидать, что в практически важных случаях процесс (1) будет иметь некоторое промежуточное значение интенсивности qτ. Анализ изменения статистических характеристик поля при изменении интенсивности процесса (1) проведем численно.

В качестве примера рассмотрим шумовое поле, имеющее угловую плотность в виде суммы изотропного и трех локальных составляющих шума. В качестве модели такого шумового поля был сконструирован трехкомпонентный дискретный по времени процесс (P₀, X₀, Y₀). Частота дискретизации  f_d принята равной 1. Длина выборки составляла N отсчетов. Изотропная составляющая шума моделировалась пуассоновским процессом, образованным импульсами, следующими со средней частотой q₀ = 1/16, плотность вероятности распределения импульсов по длине выборки равномерная. Амплитуда импульсов a₀ распределена нормально со средним значением, равным 0, и дисперсией 1. Распределение по углу φ в области –π ≤ φ < π равномерное. Локальные шумовые составляющие представляли собой независимые пуассоновские последовательности со средними частотами следования импульсов: q₁ = 1/64, q₂ = = 1/32, q₃ = 1/128. Распределение по углу φ локальных составляющих шума – нормальное со средними значениями φ₀₁ = –90°, φ₀₂ = 0°, φ₀₃ =  90° и равными среднеквадратическими отклонениями σ_φ = 5°. Длина импульсов всех составляющих равна 1. Отношение дисперсий амплитуд локальных и изотропной составляющих шума составляло: $g_{1}^{2} = {{{{\sigma }}_{{a1}}^{2}} \mathord{\left/ {\vphantom {{{{\sigma }}_{{a1}}^{2}} {{{\sigma }}_{{a0}}^{2}}}} \right. \kern-0em} {{{\sigma }}_{{a0}}^{2}}} = 1$, $g_{2}^{2} = {{{{\sigma }}_{{a2}}^{2}} \mathord{\left/ {\vphantom {{{{\sigma }}_{{a2}}^{2}} {{{\sigma }}_{{a0}}^{2}}}} \right. \kern-0em} {{{\sigma }}_{{a0}}^{2}}} = {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}$, $g_{3}^{2} = {{{{\sigma }}_{{a3}}^{2}} \mathord{\left/ {\vphantom {{{{\sigma }}_{{a3}}^{2}} {{{\sigma }}_{{a0}}^{2}}}} \right. \kern-0em} {{{\sigma }}_{{a0}}^{2}}} = 2$. Фрагмент полученного процесса приведен на рис. 2. Описанному процессу соответствует угловая плотность вероятности

и угловая плотность

Для изменения формы и длительности импульсов использовалась операция фильтрования. В качестве фильтров применялись цифровые фильтры Баттерворта первого порядка с частотами среза f_j = 0.256 × 2^–j, j = 1…9, индекс 0 соответствует исходному процессу. Зависимости от времени нормированных откликов фильтров h_j(t) на импульс единичной амплитуды при различных частотах среза приведены на рис. 3.

Для исходного (P₀, X₀, Y₀) и каждого из профильтрованных процессов (P_j, X_j, Y_j) и значений t_n, n = 0…N–1, рассчитывался модуль вектора Умова: I_nj = |P_j X_j + iP_j Y_j|, а аргумент θ_nj вычислялся согласно (6). Число отсчетов, для которых определены значения аргумента вектора Умова, равно:

Область 0…2π разбивалась на M равных интервалов: θ_m = 2πm/M, m = 0…M – 1. Оценка плотности вероятности аргумента вектора Умова рассчитывалась по формуле:

Оценки плотностей вероятности угла φ для каждого процесса вычислялись согласно выражению: ${{\hat {w}}_{{\varphi j}}}({{\varphi }_{m}}) = {{\hat {w}}_{{{\text{U}}j}}}({{\varphi }_{m}} + {{\pi }})$, где φ_m = θ_m – π. Оценки угловой плотности модуля вектора Умова для каждого процесса рассчитывались по формуле:

Оценка угловой плотности поля по процессу (P_j, X_j, Y_j) равна: ${{\hat {G}}_{j}}({{\varphi }_{m}}) = {{\hat {U}}_{j}}({{\varphi }_{m}} + {{\pi }})$. Для сравнения результатов удобнее пользоваться нормированными оценками угловых плотностей

Результаты расчетов угловой плотности вероятности w_φ(φ) и ее оценок представлены на рис. 4. На рис. 4а сплошными гладкими линиями 1 и 2 изображены результаты расчетов плотности вероятности угла φ исходного процесса по формуле (13) и ее оценки в гауссовом приближении – по формуле (11). Ступенчатые линии – рассчитанные гистограммы оценок плотности вероятности угла φ исходного процесса (P₀, X₀, Y₀) $\hat {w}$_φ0(φ) и $\hat {w}$_φ9(φ), соответствующая частоте среза f₉ = 0.0005. Попарное сопоставление кривых показывает, что численные расчеты удовлетворительно совпадают с аналитическими результатами. Следует отметить существенное различие угловой плотности вероятности поля и ее оценки, полученной в гауссовом приближении. На рис. 4б показана эволюция оценки плотности вероятности угла $\hat {w}$_φj(φ) при изменении частоты среза фильтра f_j.

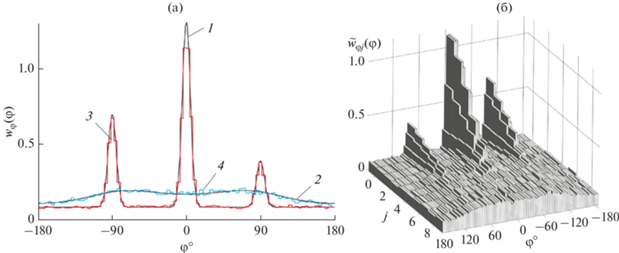
На рис. 5 представлены результаты расчета нормированной угловой плотности поля и ее оценок. На рис. 5а сплошными гладкими линиями 1 и 2 изображены результаты расчетов нормированной угловой плотности Г(φ) исходного процесса по формуле (14) и ее оценки в гауссовом приближении – по формуле (12). Ступенчатые линии – рассчитанные гистограммы оценок нормированной угловой плотности исходного процесса (P₀, X₀, Y₀) Г₀(φ) и Г₉(φ) при частоте среза фильтра f₉ = 0.0005. Сопоставление кривых показывает, что численные расчеты удовлетворительно совпадают с аналитическими. Следует также подчеркнуть существенное различие угловой плотности поля и ее оценки, полученной в гауссовом приближении. На рис. 5б показана эволюция оценки угловой плотности Г_j(φ) при изменении частоты среза фильтра f_j.

Поведение оценок угловой плотности и угловой плотности вероятности при сужении полосы анализа практически совпадает и показывает, что при снижении частоты среза фильтра f_c ниже 0.004 или f_c/(q₀ + q₁ + q₂ + q₃) < 0.03, эти характеристики близки к найденным для гауссова приближения. Напротив, для того чтобы оценки приближались к истинным характеристикам поля, необходимо использовать фильтр с частотой среза более 0.064, т.е. должно выполняться условие f_c/(q₀ + q₁ + q₂ + q₃) > 0.5. Однако, этот вывод справедлив только для фильтра рассмотренного типа и порядка. Использование фильтра иного типа и порядка повлияет на вид и длительность его импульсной характеристики, и, таким образом, изменит зависимость.

ЗАКЛЮЧЕНИЕ

При обработке сигналов ВСП могут быть получены функции, характеризующие направленные свойства поля. Такими функциями являются угловое распределение модуля вектора Умова и плотность вероятности его аргумента (фазы). Однако, для получения достоверных оценок угловой плотности и угловой плотности вероятности поля необходимо иметь возможность анализа широкополосных импульсных сигналов. Это может быть достигнуто только в том случае, когда такие сигналы, во-первых, излучаются, во-вторых, не претерпевают фатальных изменений при распространении и, в-третьих, преобразуются в форму, удобную для последующей обработки (электронные сигналы), с помощью достаточно широкополосного приемника-преобразователя.

В случае узкополосного приема оценки угловой плотности модуля и плотности вероятности аргумента вектора Умова будут близки к оценкам, которые могут быть найдены аналитически для гауссова поля. Для их вычисления достаточно знания дисперсий и функций взаимной корреляции компонент поля, которые полностью определяются только нулевой, первой и второй гармониками разложения угловой плотности поля G(φ) по углу φ. Последнее обстоятельство указывает на то, что в этом случае достоверные оценки угловой плотности поля могут быть получены в том случае, когда она формируется только перечисленными тремя гармониками разложения в ряд Фурье по углу.

Работа выполнена при поддержке государственного задания по теме “Акустика мелкого моря, нелинейная акустическая диагностика, нелинейная динамика волн” (номер гос. регистрации АААА-А18-118021390174-1).