Акустический журнал, 2022, T. 68, № 3, стр. 249-260

МОТИВИРОВКА

В статье [1] был открыт эффект “черной дыры” для упругих волн в деформируемых телах с пикообразными заострениями, которая “поглощает” энергию колебаний, не возвращая ее в массивную часть тела. Эта, ставшая уже классической, работа породила многочисленные публикации как физической направленности (см. статьи [2–7] и обзор [8]), исследующие волновые процессы в конечных объемах деформируемых сред специфической формы, так и сугубо математические (см. публикации [9–11] и др.), использующие аппарат теории самосопряженных операторов в гильбертовом пространстве и изучающие непрерывный спектр системы уравнений теории упругости.

В данной работе обсуждается феномен захвата волн, сопутствующий их распространению в утончающемся пике или замещающий волновые процессы в случае сглаженного пика. Постановка задачи теории упругости о пике с обломанным кончиком обусловлена тем обстоятельством, что в реальности изготовить идеальный пик невозможно, и в конкретных инженерных приборах пикообразное заострение всегда оказывается затупленным, а качество обработки пика соотносится с малым размером $h$ искажения идеальной формы.

Упругое тело с обломанным кончиком заострения приобретает липшицеву границу и дискретный спектр, т.е. непрерывный спектр, провоцирующий волновые процессы, отсутствует. Приведенные далее асимптотические формулы показывают, в частности, что при малом параметре $h > 0$ наблюдается высокая концентрация дискретного спектра, т.е. на “почти всех” частотах из некоторого диапазона происходит захват волн. Иными словами, найдена иная причина поглощения кинетической энергии – инициация сугубо локализованных собственных колебаний пикообразного тела.

Сначала в работе получены в значительной степени явные формулы для собственных частот колебаний балки Кирхгофа (той же одномерной модели, что и в оригинальной работе [1]) с истончающимся, но затупленным концом. На основе этих формул выявляются эффекты концентрации и “мигания” спектра при $h \to + 0$. Затем приведены известные сведения [9, 11] о непрерывном спектре задачи теории упругости для трехмерного однородного изотропного тела с идеальным пикообразным заострением, в частности, обнаружено, что при наличии богатой геометрической симметрии в спектре появляется бесконечная неограниченная последовательность собственных частот, вкрапленных в непрерывный спектр. Наконец, рассмотрена пространственная задача для тела с обломанным кончиком пика и представлена достаточно сложно устроенная асимптотика собственных частот, среди которых обнаружены группы, более разнообразные нежели в случае балки Кирхгофа, а именно, малоподвижные, планирующие и блуждающие, существенно различающиеся своим поведением при уменьшении параметра $h$.

В последнем разделе сформулированы выводы и открытые вопросы.

Результаты анонсированы в сообщениях [12, 13] и частично опубликованы в статье [14]. По существу новым является планомерное изучение дискретного спектра зауженной балки Кирхгофа, в частности, классификация его точек, а изложение фактов о трехмерном упругом пике с обломанным кончиком дополнено и согласовано с полным исследованием одномерной задачи.

СПЕКТРЫ СУЖАЮЩИХСЯ БАЛОК КИРХГОФА

После масштабирования одномерная модель балки Кирхгофа единичной длины и переменной приведенной толщины $H(z) = {{H}_{0}}{{z}^{2}}$, вырождающейся в точке $z = 0$ (рис. 1а), принимает вид

Здесь $v$ – прогиб балки, $\kappa > 0$ – частота колебаний, ${{A}^{2}} = {{\rho {{H}_{0}}} \mathord{\left/ {\vphantom {{\rho {{H}_{0}}} D}} \right. \kern-0em} D}$, а $D = {{D}_{0}}H_{0}^{3} > 0$ и $\rho > 0$ – приведенная цилиндрическая жесткость и постоянная плотность. Краевое условие в точке $z = 0$, помеченной значком $^\circ $ на рис. 1а, ставить не нужно (см., например, книгу [15; ${{\S}}$ 33]). В самом деле, при $\kappa = 0$ общее решение дифференциального уравнения (1) принимает вид

но обладает конечным интегралом энергии лишь в случае ${{c}_{3}} = {{c}_{4}} = 0$. При этом для определения коэффициентов ${{c}_{0}}$ и ${{c}_{1}}$ достаточны два краевых условия, например, (2). Аналогичная картина наблюдается и при $\kappa > 0$ (см. ниже).

Расчеты из статьи [1] показывают, что при

у уравнения (1) эйлерового типа есть четыре решения с показателями

Наличие в списке (5) трех решений, для которых расходится интеграл упругой энергии (3), означает, что замкнутый луч $[{{\kappa }_{\dag }}, + \infty )$ – непрерывный спектр задачи (1), (2), так как к тому же при $\kappa < {{\kappa }_{\dag }}$ появляются в точности два решения с конечным интегралом (3) и тем самым неоднородная задача становится однозначно разрешимой в энергетическом классе функций, которое впрочем отличается от обычного пространства Соболева ${{H}^{2}}(0,1)$. Поскольку

интеграл энергии $\mathcal{E}(v_{ \pm }^{{im}},v_{ \pm }^{{im}};{{e}^{{ - \zeta }}},{{e}^{{ - \rho \zeta }}})$ на интервалах $({{e}^{{ - \zeta }}},{{e}^{{ - \rho \zeta }}})$ при $\rho > 1$, приближающихся к точке $z = 0$, равны ${{C}_{ \pm }}(\kappa )\ln \rho $ и не зависят от параметра $\zeta \in (0,1)$. Таким образом, волны $v_{ + }^{{{\text{im}}}}$ и $v_{ - }^{{{\text{im}}}}$ переносят энергию, причем их “волновые числа” $ \pm {{b}_{ - }}(\kappa )$ показывают, что первая их них распространяется в сторону к зауженному концу балки, а вторая – в сторону от него.

В задаче об одномерной балке Кирхгофа с обломанным кончиком заострения малой длины $h > 0$ (рис. 1б)

все четыре решения (3) обладают конечной энергией $\mathcal{E}(v,v;h,1)$, энергетическое пространство совпадает с ${{H}^{2}}(0,1)$, и, в частности, поэтому спектр задачи (7)–(9) становится дискретным и представляет собой неограниченную положительную последовательность изолированных собственных частот

Отметим, что краевые условия (2) и (8) означают жесткое защемление конца $z = 1$ балки, а обломанный кончик свободен от внешних воздействий согласно равенствам (9).

АСИМПТОТИКА СОБСТВЕННЫХ ЧАСТОТ БАЛКИ С ОБЛОМАННЫМ КОНЧИКОМ

Для построения асимптотики собственных частот (10) укажем решение дифракционной задачи (1), (2)

порожденное приходящей в точку $z = 0$ волной $v_{ - }^{{{\text{im}}}}$ из списка (5) и имеющее коэффициенты в которых ${{b}_{ \pm }}(\kappa )$ – величины (6). Модуль коэффициента рассеяния $S(\kappa )$ равен единице ввиду закона сохранения энергии.

Асимптотику собственной моды задачи (7)–(9) с малым параметром $h$ ищем в виде

где многоточие заменяет младшие асимптотические члены, несущественные в предпринимаемом анализе. Подчеркнем, что в отличие от (11) в формуле (13) фигурирует решение $v_{ - }^{{{\text{re}}}}(z)$ с сильным ростом $O({{z}^{{ - {{b}_{ + }}(\kappa ) - 3/2}}})$ при $z \to + 0$, который частично компенсируется множителем ${{h}^{{{{b}_{ + }}(\kappa )}}}$. Подставим анзац (13) в краевые условия (9) и получим уравнения причем дифференциальные операторы ${{N}^{3}}(z,{{\partial }_{z}})$ и ${{N}^{2}}(z,{{\partial }_{z}})$ взяты из левых частей равенств (9). Произведем дифференцирование, исключим из системы (14) коэффициент $K(\kappa )$ и при учете выражения (12) для $S(\kappa )$ после рутинных вычислений придем к соотношению в котором

Подведем итог. Если при некотором малом $h = h_{n}^{ * } > 0$ и целом $n \in \mathbb{Z}$ какая-то частота $\kappa = \kappa (h_{n}^{ * }) > 0$ удовлетворяет вытекающему из формул (15) и (16) соотношению

то решение $(11)$ системы (7) оставляет в краевых условиях (8) и (9) незначительные невязки, приобретающие малый множитель ${{h}^{{{{b}_{ + }}(\kappa (h_{n}^{ * }))}}}$ в сравнении с самим решением. Таким образом, в силу классической леммы о “почти собственных” числах операторов (см., например, статью [16]) в $C{{h}^{{{{b}_{ + }}(\kappa (h_{n}^{ * }))}}}$-окрестности точки $\kappa (h_{n}^{ * })$ найдется настоящая собственная частота задачи (7)–(9).

ПЛАНИРУЮЩИЕ И МИГАЮЩИЕ СОБСТВЕННЫЕ ЧАСТОТЫ

Воспользуемся результатами проведенного асимптотического анализа. Процесс истончения конца балки при изготовлении заострения сымитируем посредством уменьшения размера $h$. Продифференцируем соотношение (15) для собственной частоты $\kappa (h)$ по $h$ и получим равенство

В силу формул (6) и (16) находим, что

В результате обнаруживаем, что собственные частоты (10) с большой скоростью $O((h\left| {\ln h} \right|{{)}^{{ - 1}}})$ монотонно спускаются вниз вдоль вещественной оси, но из-за множителя в правой части (18)

скорость спадает до нуля при приближении к порогу ${{\kappa }_{\dag }}$, т.е. собственные частоты останавливаются, плавно садясь на порог. Такое поведение следует охарактеризовать как планирование.

Изменим постановку вопроса и зафиксируем какую-либо частоту (4). Соотношение (15) выполнено для бесконечно малой последовательности значений длин обломков

при которых в малых окрестностях точки $\kappa > {{\kappa }_{\dag }}$ появляется собственная частота из последовательности (10). Более того, ввиду непрерывной зависимости величины $\kappa _{h}^{m}$ от $h$ для почти периодической в логарифмическом масштабе последовательности размеров ${{\{ h_{n}^{ * }\} }_{{n \in \mathbb{N}}}}$ точка $\kappa $ становится истинной собственной частотой балки длиной $1 - h_{n}^{ * }$. Такой феномен принято называть миганием спектра.

Оба обнаруженных свойства собственных частот (10) указывают на их концентрацию выше точки отсечки ${{\kappa }_{\dag }}$, которая (концентрация) усугубляется при уменьшении размера $h$. Приведем асимптотические формулы для собственных частот, приближенных к точке отсечки ${{\kappa }_{\dag }}$. Подставим асимптотический анзац

в вытекающее из формулы (15) соотношение (17) с натуральным $n$. В силу равенства (6) имеем а значит, в частности, $B(\kappa (h)) = 1 + O({{\left| {\ln h} \right|}^{{ - 2}}})$. Отсюда и из (17) и (19) выводим, что и получаем для околопороговых собственных частот окончательную асимптотическую формулу подтверждающую их концентрацию вверху от точки ${{\kappa }_{\dag }}$. Подчеркнем, что нумерация собственных частот (20) может отличаться от предписанной в последовательности (7), так как проведенный анализ устанавливает только то, что полученное асимптотическое представление выполнено при больших натуральных $n$.

РАЗНЫЕ КРАЕВЫЕ УСЛОВИЯ НА КОНЧИКЕ БАЛКИ

Результаты и способ анализа спектра сохраняются при замене краевых условий (9) условиями защемления обломанного кончика балки

Конкретные формулы для собственных частот задачи (7), (8), (21) претерпевают незначительные вариации. Например, выражение (16) упрощается следующим образом:

При этом финальное соотношение (17) остается прежним.

Аналогичные и несложные модификации нужны и при других профилях и краевых условиях, в частности, для любой из двух групп условий

в случае половины $[0,1] \mathrel\backepsilon z$ изображенной на рис. 2а балки Кирхгофа с приведенной толщиной ${{H}^{h}}(z) = \min \left\{ {1,h + {{z}^{2}}} \right\}$. Искусственные краевые условия (22) отвечают соответственно симметричному и антисимметричному изгибу балки.

Разумеется, замена краевых условий (8) какими-либо другими условиями в точке $z = 1$ не влияет cколь-нибудь существенно на поведение собственных частот при $h \to + 0$.

ТРЕХМЕРНОЕ ПИКООБРАЗНОЕ ТЕЛО

Пусть $\Omega \subset {{\mathbb{R}}^{3}}$ – пространственное однородное изотропное тело (рис. 3а), совпадающее внутри слоя $\{ x{\kern 1pt} :{{x}_{3}} \in (0,1)\} $ с пиком ${{\Pi }_{1}}$, где

и $\omega $ – область на плоскости ${{\mathbb{R}}^{2}}$, ограниченная простым кусочно-гладким контуром $\partial \omega $. Масштабированием высота пика ${{\Pi }_{1}}$ сведена к единице, т.е декартовы координаты ${{y}_{1}} = {{x}_{1}}$, ${{y}_{2}} = {{x}_{2}}$, $z = {{x}_{3}}$ и все геометрические параметры сделаны безразмерными. Собственные колебания тела $\Omega $ с частотой $\kappa > 0$ описываются краевой задачей

Здесь $k = 1,2,3$, $u = ({{u}_{1}},{{u}_{2}},{{u}_{3}}{{)}^{{\rm T}}}$ – вектор смещений, ${\rm T}$ – знак транспонирования, $n = ({{n}_{1}},{{n}_{2}},{{n}_{3}}{{)}^{{\rm T}}}$ – единичный вектор внешней нормали, определенный почти всюду на границе (разумеется, вне вершины $\mathcal{O}$ даже при гладкой поверхности $\partial \Omega {\kern 1pt} \backslash {\kern 1pt} \mathcal{O}$), а ${{\sigma }_{{jk}}}$ – декартовы компоненты тензора напряжений

Кроме того, ${{\delta }_{{j,k}}}$ – символ Кронекера, а $\lambda \geqslant 0$, $\mu > 0$ и $\rho > 0$ – постоянные Ламе и плотность материала.

Известно [9, 11], что спектр $\wp $ задачи (24), (25) имеет непрерывную компоненту ${{\wp }_{c}} = [{{\kappa }_{\dag }}, + \infty )$, а для вычисления точки отсечки ${{\kappa }_{\dag }} > 0$ достаточно изучить одномерную модель стержня с переменным сечением (см., например, [17; гл. 5]), оперирующую системой обыкновенных дифференциальных уравнений

для вектор-функции $w = ({{w}_{1}},{{w}_{2}},{{w}_{3}},{{w}_{4}}{{)}^{{\rm T}}}$, содержащей осредненные по сечениям поперечные ${{w}_{1}}$, ${{w}_{2}}$ и продольное ${{w}_{3}}$ смещения, а также поворот ${{w}_{4}}$. Кроме того, в (26) фигурируют диагональные ($4 \times 4$)-матрицы, и матрица $\mathcal{A}$ с ($2 \times 2$)-блоками ${{\mathcal{A}}_{{\# \# }}}$, ${{\mathcal{A}}_{{\# ^\circ }}} = \mathcal{A}_{{^\circ \# }}^{{\rm T}}$ и ,

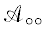При этом $E$ – модуль Юнга, $\left| \omega \right|$, $P = ({{P}_{1}},{{P}_{2}}{{)}^{{\rm T}}}$ и $I = ({{I}_{{jk}}})$ – площадь фигуры $\omega $, ее центр тяжести и тензор инерции, а $G$ – его жесткость кручения сечения [18], определенная по функции Прандтля $\Psi $,

Два последних элемента на диагонали матрицы $\mathcal{T}(z)$ из списка (27) получаются нулевыми (подробности см., например, в [17; гл. 7, ${{\S}}$ 3], [9]) потому, что поперечные колебания тонкого стержня происходят на частотах из рассматриваемого нижнего диапазона спектра, а продольные и крутильные – только на средних.

Исключим из системы (26) вектор ${{w}_{ \circ }} = ({{w}_{3}},{{w}_{4}}{{)}^{{\rm T}}}$ и получим для оставшегося вектора ${{w}_{\# }} = ({{w}_{1}},{{w}_{2}}{{)}^{{\rm T}}}$ систему двух уравнений

где – симметричная положительно определенная ($2 \times 2$)-матрица, (положительные) собственные числа которой обозначим ${{m}_{1}}$ и ${{m}_{2}}$. Считаем, что ${{m}_{2}} \geqslant {{m}_{1}}$.

Если центр тяжести $P$ совпадает с началом координат $y = ({{y}_{1}},{{y}_{2}})$ и оси ${{y}_{j}}$ направлены вдоль главных осей тензора инерции $I$, то $\mathcal{A}$ – диагональная матрица и

Решения системы дифференциальных уравнений эйлеровского типа (28) ищем в виде

где $\mathcal{W}_{\# }^{p}$ – числовой столбец, и получим характеристическое уравнение

По компонентам (30) восстанавливается вектор

Наконец, точка отсечки ${{\kappa }_{\dag }}$ – наименьшая частота, при которой среди корней биквадратного уравнения (31) имеется нуль, а именно,

В случае $\kappa = \kappa _{\dag }^{{(p)}}$ вектор ${{w}^{p}}(z) = (w_{\# }^{p}{{(z)}^{{\rm T}}},w_{^\circ }^{p}{{(z)}^{{\rm T}}}{{)}^{{\rm T}}}$ приобретает линейную зависимость от $\ln z$.

Итак, при $\kappa > \kappa _{\dag }^{{(p)}}$ у системы (28) есть решения (30) с показателями

и, например, в случае (29) соответствующие столбцы коэффициентов в представлениях (30) и (32) имеют вид

По решениям (30) и (32) в работах [11, 19] построены пространственные поля смещений $u_{{(p \pm )}}^{{{\text{im}}}}$ и $u_{{(p \pm )}}^{{{\text{re}}}}$, удовлетворяющие уравнениям (24) в укороченном пике (23) при любом $h \in (0,1)$ и краевым условиям (25) на его боковой поверхности $\partial {{\Pi }_{1}} \cap \partial {{\Pi }_{h}}$. В частности, справедливы представления

при $z \to + 0$, а также соотношения а значит, упругая и кинетическая энергии суть расходящиеся с логарифмической скоростью интегралы. Те же интегралы для полей $u_{{(p + )}}^{{{\text{re}}}}$ сходятся, но для полей $u_{{(p - )}}^{{{\text{re}}}}$ опять-таки расходятся из-за сильной степенной сингулярности в вершине пика ${{\Pi }_{1}}$. Как проверено в [9, 11], приведенная информация обеспечивает формулу для непрерывного спектра задачи (24), (25). При этом помимо основного порога – точки отсечки ${{\kappa }_{\dag }} = \kappa _{\dag }^{{(1)}}$ – в непрерывном спектре может появиться еще одна, внутренняя, точка отсечки $\kappa _{\dag }^{{(2)}}$, но в случае ${{m}_{1}} = {{m}_{2}}$ порог приобретает кратность два.

Согласно [11, 19] множители $c_{{p \pm }}^{{{\text{im}}}}$ в представлениях (36) можно выбрать так, чтобы были выполнены соотношения

в которых фигурирует симплектическая (анти-эрмитова и полуторалинейная) форма являющаяся интегралом по торцу пика (23) в формуле Грина для оператора Ламе и потому не зависящая от размера $h \in (0,1)$ для построенных полей смещений $u_{{(p \pm )}}^{{{\text{im}}}}$ и $u_{{(p \pm )}}^{{{\text{re}}}}$. Более того, благодаря условиям ортогональности и нормировки (37) у задачи (24), (25) в случае (см. формулы (33), (34) и сечения на рис. 4г и 4д) есть решение порожденное приходящей в вершину $\mathcal{O}$ волной $u_{{(p - )}}^{{{\text{im}}}}$. Трехмерное поле (40), вполне аналогичное решению (11) одномерной задачи (1), (2), имеет коэффициент рассеяния

Ситуация

(см. сечения на рис. 4а–4в) отличается от пластины Кирхгофа, а именно, появляются два ($p = 1,2$) дифракционных решения задачи (1), (2) и унитарная симметричная матрица рассеяния $S(\kappa ) = {{\left( {{{S}_{{pq}}}(\kappa )} \right)}_{{p,q = 1,2}}}$ размером $2 \times 2$. Матрица с тем же размером возникает и в ситуации (39) при $\kappa > \kappa _{\dag }^{{(2)}}$, т.е. выше второй точки отсечки непрерывного спектра ${{\wp }_{c}}$. Исчерпывающие комментарии к построению решений (40), (42), их физической интерпретации и выводу основных свойств приведены, например, в работе [19].

СОБСТВЕННЫЕ ЧАСТОТЫ ВНУТРИ НЕПРЕРЫВНОГО СПЕКТРА

Предположим, что тело $\Omega $ обладает плоскостями симметрии

Здесь $N \in \mathbb{N}$ – натуральное число, причем важно¹¹, что $N \geqslant 3$. Вырежем из $\Omega $ сектор

где $(r,\varphi ,z)$ – система цилиндрических координат, сведем на него задачу (24), (25) и поставим на образованных поверхностях ${{\Gamma }_{0}} = \{ x \in \Omega ;\varphi = 0\} $ и ${{\Gamma }_{1}} = \{ x \in \Omega ;\varphi = {\pi \mathord{\left/ {\vphantom {\pi N}} \right. \kern-0em} N}\} $ искусственные краевые условия

Эти условия обладают двумя примечательными свойствами. Во-первых, только тривиальное ($a = b = 0$) жесткое смещение²² $a + b \times x$ удовлетворяют равенствам (43), (44) при $N \geqslant 3$. Как установлено в [9; лемма 8], при выполнении трех ограничений для смещений из списка (43), (44) имеет место весовое неравенство Корна

Следовательно, спектр задачи (24), (25), (43), (44) дискретный и образует неограниченную положительную последовательность

Кроме того, соответствующие собственные моды $u_{\sphericalangle }^{m} \in {{H}^{1}}({{\Omega }_{\sphericalangle }})$ затухают при $x \to \mathcal{O}$ с экспоненциальной скоростью.

Второе нужное свойство заключается в том, что продолжения через полуплоскость $\{ x:{\kern 1pt} \varphi = 0\} $, четное для ${{u}_{\varphi }}$ и нечетное для ${{u}_{r}}$ и ${{u}_{z}}$, ввиду изотропности упругого материала сохраняют систему уравнений (24) на расширенном секторе $\{ x \in \Omega :\left| \varphi \right| < {\pi \mathord{\left/ {\vphantom {\pi N}} \right. \kern-0em} N}\} $ и краевые условия (25) на поверхности $\{ x \in \partial \Omega :{\kern 1pt} \left| \varphi \right| < {\pi \mathord{\left/ {\vphantom {\pi N}} \right. \kern-0em} N}\} $. Точно так же нечетное продолжение компоненты ${{u}_{\varphi }}$ и четное продолжение компонент ${{u}_{r}}$, ${{u}_{z}}$ через полуплоскость $\{ x:{\kern 1pt} \varphi = {\pi \mathord{\left/ {\vphantom {\pi N}} \right. \kern-0em} N}\} $ дают гладкое поле смещений в утроенном секторе $\{ x \in \Omega :\varphi \in ({{ - \pi } \mathord{\left/ {\vphantom {{ - \pi } N}} \right. \kern-0em} N},{{2\pi } \mathord{\left/ {\vphantom {{2\pi } N}} \right. \kern-0em} N})\} $. Чередуя указанные способы продолжения, получаем гладкое решение задачи (24), (25) из класса Соболева ${{H}^{1}}(\Omega )$ для всего тела $\Omega $. В итоге обнаруживаем, что каждый член $\kappa _{\sphericalangle }^{n}$ последовательности (45) – собственная частота из точечного спектра ${{\wp }_{p}}$ задачи (24), (25).

ТЕЛО С ЗАТУПЛЕННЫМ ПИКООБРАЗНЫМ ЗАОСТРЕНИЕМ

Пусть у тела $\Omega $ обломан кончик ${{\Pi }_{h}}$ малой длины $h$, а образованный торец (38) полученного таким образом тела

имеет “диаметр” $O({{h}^{2}})$. Рассмотрим спектральную краевую задачу для тела (46) со свободной поверхностью

Как и для балки Кирхгофа, при незначительной модификации представленных выше вычислений краевые условия (46) можно заменить условиями

означающими, в частности, что торец жестко защемлен. Можно сохранить идеальное пикообразное заострение, защемив боковую поверхность кончика (23) малой длины $h$, т.е. добавить к уравнениям (24) и краевым условиям (49) условия

Далее приведем исследование дискретного спектра (10) задачи (47), (49), (50) для ${{\Omega }^{h}}$ с обломанным пиком, а также мало отличающейся от нее задачи (24), (49), (51) в пикообразной области $\Omega $. Вычисления для задачи (47), (48) для тела (46) со свободной поверхностью вполне аналогичны проведенным для одномерной задачи (7)–(9). Для анизотропного тела они выполнены в [14]. Кроме того, задачу (47), (49) можно замкнуть смешанными краевыми условиями на торце

Как и для искусственных краевых условий (43) и (44), четные или нечетные продолжения компонент вектора смещений через плоскость $\{ x:{\kern 1pt} z = h\} $ позволяют перейти от задачи (47), (49), (52) на ${{\Omega }^{h}}$ к задаче для тела

имеющего свободную поверхность и изображенного на рис. 2б. Аналогичные преобразования уже обсуждались для балки Кирхгофа с глубокой вмятиной (рис. 2а).

МАЛОПОДВИЖНЫЕ, ПЛАНИРУЮЩИЕ И БЛУЖДАЮЩИЕ СОБСТВЕННЫЕ ЧАСТОТЫ

Ясно, что при $\kappa = 0$ у обеих статических задач (24), (25) и (47), (48) одинаковый набор решений (фиктивных собственных мод) – шестимерное пространство жестких смещений $a + b \times x$, три поступательных и три вращательных. Сразу же заметим, что положительные собственные частоты (если таковые имеются) из дискретного спектра ${{\wp }_{d}} \subset [0,{{\kappa }_{\dag }})$ задачи (24), (25) для исходного тела при малом его возмущении ${{\Omega }^{h}}$ также претерпевают малые возмущения. Это же относится и к собственным частотам (45) тела $\Omega $, попадающим на непрерывный спектр ${{\wp }_{c}} = [{{\kappa }_{\dag }}, + \infty )$ (при наличии указанной ранее симметрии таковые заведомо имеются), так как соответствующие моды обладают быстрым экспоненциальным затуханием при $x \to \mathcal{O}$ и потому оставляют исчезающе малые невязки в краевых условиях (48) на торце ${{\omega }_{h}}$. Следовательно, у задачи (47), (48) появляются собственные частоты, не покидающие $c_{\sphericalangle }^{n}{{e}^{{ - \delta _{\sphericalangle }^{n}/h}}}$-окрестности точки $\kappa _{\sphericalangle }^{n} \in ({{\kappa }_{\dag }}, + \infty )$, – их разумно называть малоподвижными. Такие же собственные частоты имеются и в случае постановки условий (50) или (51) для полей смещений, в которых упомянутые собственные моды в теле $\Omega $ опять оставляют экспоненциально малые невязки. Отметим, что эти условия Дирихле, а также смешанные краевые условия (52) порождают положительные возмущения нулевых собственных частот исходной задачи (24), (25). Их асимптотику построить нетрудно при помощи техники пограничного слоя (см. конец раздела).

Обратимся сначала к задаче (47), (49), (50) с условиями жесткого защемления торца (38), причем сначала для упрощения формул и рассуждений считаем, что, во-первых, выполнены геометрические условия, обеспечивающие соотношения (29) и распадение системы обыкновенных дифференциальных уравнений (28), и, во-вторых, справедливо соотношение $\kappa _{\dag }^{{(1)}} < \kappa _{\dag }^{{(2)}}$. В качестве асимптотического приближения к моде собственных колебаний тела с частотой $\kappa \in (\kappa _{\dag }^{{(1)}},\kappa _{\dag }^{{(2)}})$ (см. формулу (39)) возьмем вектор-функцию

Здесь $\chi $ – гладкая срезающая функция, равная нулю при $z > 1$ и единице при $z < {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}$. Эта функция позволяет распространить поле смещений $u_{{1 - }}^{{{\text{re}}}}$ с большой сингулярностью в вершине $\mathcal{O}$ на все тело ${{\Omega }^{h}}$, а ее введение в асимптотический анзац привносит относительно малую невязку в дифференциальные уравнения (47) и краевые условия (49). Анзац (53) вполне аналогичен асимптотической конструкции (13) для пластины Кирхгофа. Как и ранее, подставим сумму (53) в краевые условия (50) и при учете соотношений (36), (39) и (35), позволяющих выделить главные асимптотические члены, получим равенства

Исключив из этой системы ненужный коэффициент $K(\kappa )$, приходим к соотношению (15), в котором показатель ${{b}_{ \pm }}(\kappa ) = {{b}_{{1 \pm }}}(\kappa )$ взят из списка (34), а величина $B(\kappa ) = {{B}_{1}}(\kappa )$ задана формулой

Теперь превращаем соотношения (15) и (54) в следующее равенство при $p = 1$:

Видимая схожесть формул (55) и (17) обеспечивает те же выводы, что и в случае утончающейся пластины Кирхгофа. Именно, обнаруживается “мигание” спектра, т.е. каждая точка $\kappa \in (\kappa _{\dag }^{{(1)}},\kappa _{\dag }^{{(2)}})$, не являющаяся малоподвижной собственной частотой, становится истинной частотой собственных колебаний тела ${{\Omega }^{h}}$ “почти периодически” в логарифмическом масштабе ${{d}_{\kappa }}\left| {\ln h} \right|$ (далее станет понятно, что для точек $\kappa $ выше второй точки отсечки $\kappa _{\dag }^{{(2)}}$ происходит наложение двух почти периодических последовательностей). Кроме того, используя соотношения (55) и (34), находим скорость движения собственных частот вниз при уменьшении параметра $h$:

Поскольку согласно определениям (34) и (33) верны соотншения

то формулы (56) и (57) указывают на планирование собственных частот в промежутке $(\kappa _{\dag }^{{(1)}},\kappa _{\dag }^{{(2)}})$, а именно, при $h \to + 0$ они быстро ниспадают, но плавно садятся на порог $\kappa _{\dag }^{{(1)}}$.

Из первого соотношения (57) вытекает аналогичное (20) представление

которое подтверждает концентрацию собственных частот около первой точки отсечки.

В ситуации (41) (сечения на рис. 4а–4в), когда порог непрерывного спектра ${{\wp }_{c}}$ приобретает кратность два, полученные формулы (56)–(58) изменяются мало, однако для их вывода приходится решать линейные алгебраические системы размером $2 \times 2$, и поэтому они теряют явный вид. Если же вторая точка отсечки $\kappa _{\dag }^{{(2)}}$ расположена выше первой $\kappa _{\dag }^{{(1)}}$ (например, сечения на рис. 4г и 4д), то концентрация спектра наблюдается и около него. Вместе с тем поведение собственных частот $\kappa (h) > \kappa _{\dag }^{{(2)}}$ при $h \to + 0$ становится более причудливым – обсудим его.

Сначала предположим, что тело $\Omega $ обладает зеркальной симметрией относительно плоскостей $\{ x:{\kern 1pt} {{x}_{j}} = 0\} $, а значит, на поверхностях $\{ x \in \Omega :{\kern 1pt} {{x}_{j}} = 0\} $ можно назначить такие искусственные краевые условия, что у двух ($j = 1,2$) задач в областях ${{\Omega }_{{j + }}} = \{ x \in \Omega :{\kern 1pt} {{x}_{j}} > 0\} $ непрерывные спектры будут иметь единственные пороги – точки отсечки. Таким образом, для полученных задач в областях $\Omega _{{j + }}^{h}$ с обломанными заострениями для частот $\kappa (h) > \kappa _{\dag }^{{(j)}}$ верны полученные асимптотические формулы. В итоге в последовательности (10) собственных частот задачи (47), (49), (50) для тела ${{\Omega }^{h}}$ возникают две подпоследовательности ${{\{ \kappa _{{1n}}^{h}\} }_{{n \in \mathbb{N}}}}$ и ${{\{ \kappa _{{2n}}^{h}\} }_{{n \in \mathbb{N}}}}$, члены которых с разными скоростями (58) двигаются в сторону порогов $\kappa _{\dag }^{{(1)}}$ и $\kappa _{\dag }^{{(2)}}$ соответственно. Выше второй точки отсечки эти последовательности перемешиваются. Поскольку одни собственные частоты “обгоняют” другие, после их сведения в общую последовательность (10) с нумерацией единым индексом, наблюдается довольно странная картина: собственные частоты $\kappa _{N}^{h} > \kappa _{\dag }^{{(2)}}$ лавинообразно спускаются вдоль вещественной оси, однако скорость $\frac{{d\kappa _{N}^{h}}}{{dh}}$ каждой из них при $h \to + 0$ бесконечное число раз претерпевает скачки с сопутствующей флуктуацией собственной моды, причем чередование все убыстряется при приближении к порогу $\kappa _{\dag }^{{(2)}}$. Такое поведение характеризуем как блуждание собственных частот при утончении пика. Впрочем, принятые условия все-таки позволяют разделить собственные частоты на группы с регулярным поведением, которое нарушается только при “столкновениях” с малоподвижными собственными частотами.

Блуждание выше точки отсечки $\kappa _{\dag }^{{(2)}}$ наблюдается и в случае отсутствия какой-либо геометрической симметрии, однако явные асимптотические формулы становятся недоступными. Для условий (50) жесткого защемления торца принцип сравнения показывает, что собственные частоты смещаются вниз при уменьшении размера $h$, однако для условий (49) свободного торца монотонность их движения ставится под сомнение, что делает термин “блуждающие собственные частоты” еще более достоверным.

При построении младших асимптотических членов в разложениях собственных частот и соответствующих собственных мод вблизи торца ${{\omega }_{h}}$ затупленного заострения в теле ${{\Omega }^{h}}$ требуется построить пограничный слой в полубесконечном цилиндре $\omega \times ( - \infty ,0)$, полученном из области ${{\Omega }^{h}}$ в результате растяжения координат $x \mapsto {{h}^{{ - 2}}}(y,z - h)$ и формального перехода к $h = 0$. Согласно принципу Сен-Венана многие свойства решений задачи теории упругости в таком цилиндре не зависят от формы его торца, и поэтому все выкладки и рассуждения сохраняются, например, при сглаженной или наоборот неровной поверхности $\partial {{\Omega }^{h}}{\kern 1pt} \backslash {\kern 1pt} \partial \Omega $ (у тела (46) кончик “обрублен”). Кроме того, нужные свойства присущи пограничному слою в бесконечном цилиндре $\omega \times ( - \infty , + \infty )$ с условиями Дирихле на поверхности $\partial \omega \times (0, + \infty )$, т.е. представленный в данном разделе асимптотический анализ без труда приспосабливается к задаче (24), (49), (51) для тела $\Omega $ с защемленным кончиком пика. Детализированную теорию пограничных слоев, возникающих около заострений, можно найти, например, в публикации [20], где, в частности, описан способ вычисления возмущения нулевых собственных частот при постановке условий Дирихле около вершины пика.

ВЫВОДЫ И ОТКРЫТЫЕ ВОПРОСЫ

Спектр упругих тел с затупленными пикообразными заострениями является дискретным, т.е. состоит из изолированных собственных частот и потому не допускает распространения волн (в отличие от идеального пика, у которого имеется непрерывный спектр с точкой отсечки ${{\kappa }_{\dag }} > 0$). Вместе с тем при малой длине обломанного кончика $h$ наблюдается существенная, с плотностью $O({{\left| {\ln h} \right|}^{{ - 2}}})$ (см. соотношение (20)), концентрация собственных частот выше точки ${{\kappa }_{\dag }}$, способствующая захвату волн в широком диапазоне.

При утончении заострения, т.е. при уменьшении размера $h$, концентрация усугубляется, а собственные частоты приобретают ненормальное поведение, характеризующееся быстрым перемещением вдоль вещественной оси – планированием на пороги $\kappa _{\dag }^{{(j)}}$ предельного непрерывного спектра (см. формулу (33)) или хаотичным блужданием в случае $\kappa > \kappa _{\dag }^{{(2)}} > \kappa _{\dag }^{{(1)}}$. Кроме того, при $h \to + 0$ каждая точка $\kappa \in (\kappa _{\dag }^{{(1)}},\kappa _{\dag }^{{(2)}})$ становится собственной частотой “почти периодически” в логарифмическом масштабе ${{d}_{\kappa }}\left| {\ln h} \right|$, а для точек $\kappa > \kappa _{\dag }^{{(2)}}$ такое “мигание” спектра усложняется.

Именно захват волн на “почти всех” частотах выше точки отсечки ${{\kappa }_{\dag }} = \kappa _{\dag }^{{(1)}}$ предопределяет эффект “черной дыры” [1] в случае обломанного кончика пика. Математическая сторона обнаруженного феномена состоит в описании нового механизма образования непрерывного спектра из дискретных спектров сингулярно возмущенных задач.

Строение спектра трех- и двумерных упругих тел значительно более разнообразно, нежели у одномерных моделей. Это наблюдение объясняется тем, что в многомерном случае непрерывный спектр приобретает два порога (33) и в нем могут появиться собственные частоты (45). Вместе с тем примеры собственных частот внутри непрерывного спектра плоского пикообразного тела неизвестны. По построению собственные моды, отвечающие найденным частотам (45) симметричного тела $\Omega \subset {{\mathbb{R}}^{3}}$, приобретают экспоненциальное затухание при $x \to \mathcal{O}$. Собственные моды, ведущие себя как $O({{z}^{{\alpha _{ + }^{1} - 3/2}}})$, не обнаружены ни в одной из рассмотренных задач, хотя существовать они могут. До сих пор нет строгих постановок задачи теории упругости в трехмерной области с пикообразным ребром, идеальным (рис. 5а) или затупленным. Это же касается и задачи о пространственном деформируемом теле с глубокой выемкой, образующей пик вращения (рис. 5б).

Приблизительное поведение дискретного спектра при $h \to + 0$ можно усмотреть на рис. 6. Жирными линиями обозначены малоподвижные собственные частоты, которые отсутствуют в спектре зауженной балки Кирхгофа (рис. 1б), но могут появиться в спектре трехмерного тела с обломанным пиком (рис. 3б). Поскольку обыкновенное дифференциальное уравнение (1) имеет явные решения (5), а непрерывный спектр задачи (1), (2) – единственную точку отсечки (4), нетрудно заключить, что дискретный спектр задачи (7)–(9) состоит только из планирующих собственных частот. Изучение трехмерной задачи требует применения иной, гораздо более сложной техники, которая обслуживает собственные частоты с иным поведением при $h \to + 0$, например, малоподвижные и блуждающие. Весьма логично предположить, что на первом интервале $({{\kappa }^{{(1)}}},{{\kappa }^{{(2)}}})$ (см. формулы (39) и (33)) непрерывного спектра задачи (24), (25) присутствуют только планирующие и, может быть, малоподвижные собственные частоты, однако автор не знает, как подтвердить эту гипотезу строгим анализом.

Уравнение Лапласа со спектральными условиями Стеклова в области с пиком вращения, описывающими волны на поверхности тяжелой жидкости [21], изучено в работе [22]. В статьях [23–26] и др., содержащих разнообразные результаты о пространственных и плоских задачах Стеклова в пикообразных областях на рис. 3а, рис. 1а и рис. 5б, ответов на сформулированные вопросы также нет.