Акустический журнал, 2022, T. 68, № 3, стр. 261-269
О постановке задач бесконтактного поверхностного управления распространением электроакустической волны
А. С. Аветисян *
Институт Механики НАН Армении
Ереван-0019, пр. Баграмяна 24/2, Армения
* E-mail: ara.serg.avetisyan@gmail.com
Поступила в редакцию 13.10.2021
После доработки 19.01.2022
Принята к публикации 25.01.2022
- EDN: LCTWRC
- DOI: 10.31857/S0320791922030029
Аннотация
Исследована возможность постановки задач управления распространяющимися в пьезоэлектрическом полупространстве электроакустическими поперечными волнами путем неакустического воздействия на его поверхность. Наличие проводящей поверхности вблизи механически свободной поверхности пьезоэлектрического полупространства меняет в нем характер приповерхностной локализации распространяющейся электроакустической волны. Исходя из этого, предлагается постановка задачи управления процессом локализации волн. Показано, что нестационарный электрический потенциал на электрическом экране или нестационарность ширины зазора между указанными поверхностями приводят к неакустическому воздействию на пьезоэлектрическое полупространство. В задачах управления приповерхностной локализацией волновой энергии в качестве управляющей функции используются неакустические воздействия на поверхность пьезополупространства.
ВВЕДЕНИЕ
Одна из самых широко применяемых сейчас волн – это легко исследуемая волна Гуляева–Блюстейна. В 1968 г. Ю.Л. Блюстейн [1], а в 1969 г. Ю.В. Гуляев [2] теоретически подтвердили предположение М.И. Каганова, И.Л. Скловской [3] о возможной локализации волновой энергии электроактивной упругой волны сдвига на механически свободной поверхности пьезоэлектрической среды определенной симметрии, при различных граничных условиях для сопутствующего электрического поля. Существование и свойства электроупругих поверхностных волн в пьезоэлектриках тесно связаны с симметрией пьезокристалла и граничными условиями на поверхности тела.
В [4] рассмотрено влияние различных электромагнитных граничных условий на распространение поверхностных волн в пьезоэлектриках. Основой для анализа является введение электрического “поверхностного импеданса”, который связывает электрический потенциал с нормальной составляющей электрического смещения на поверхности. Для различных комбинаций граничных условий на поверхности пьезоэлектрического слоя в [5] исследованы условия локализации энергии волны в процессе распространения монохроматического сигнала электроупругого сдвига в неоднородном по толщине пьезодиэлектрическом слое.
В статьях [6–13] рассматривается распространение щелевых волн, когда поверхность другого пьезоэлектрического или электропроводящего тела находится на определенном расстоянии от поверхности пьезоэлектрической среды. В частности, в статьях [8–10] исследуется влияние идеально проводящей плоскости, находящейся на некотором расстоянии от поверхности пьезокристалла ниобата калия, на характеристики обобщенных поверхностных электроакустических волн типа Рэлея и Гуляева–Блюстейна. В статье [11] найдены условия существования, структура и дисперсия волн типа Гуляева–Блюстейна в зависимости от параметров двух разных электроупругих сред и ширины зазора между ними. В этих работах показано, как посредством сопутствующих электрических колебаний происходит просачивание энергии электроактивной упругой волны от одного тела в другое. Из этих работ также видно, что изменение расстояния между поверхностями пьезоэлектрического и электропроводящего тел или изменение электрического потенциала на поверхности одного тела изменяет импеданс на поверхности пьезоэлектрического полупространства.
Современное состояние и новые идеи приводят к некоторым тенденциям развития акустоэлектроники сверхвысоких частот [14–16]. С помощью просачивающейся через щель энергии электроакустической волны, вероятно, можно управлять скоростью объемных акустических волн, а также приповерхностной локализацией волновой энергии в базовом пьезоэлектрическом полупространстве.
Интересны задачи управления распространением электроакустической волны плоской деформации с помощью воздействия электроакустической волной антиплоской деформации, или наоборот. Такое возможно при существовании гибрида данных инородных электроактивных упругих волн (волн упругого сдвига и волн плоской деформации) в пьезоэлектрических слоистых композитах с неакустическим контактом между его слоями [18–21].
В данной работе на наглядном примере волн типа Гуляева–Блюстейна обсуждаются возможные поверхностные бесконтактные воздействия на процесс распространения электроакустической волны в пьезо-полупространстве.
1. ПРИПОВЕРХНОСТНАЯ ЛОКАЛИЗАЦИЯ ЭНЕРГИИ ЭЛЕКТРОАКУСТИЧЕСКОЙ ПОПЕРЕЧНОЙ ВОЛНЫ С ЭКРАНИРОВАННОЙ ПЬЕЗОЭЛЕКТРИЧЕСКОЙ ПОВЕРХНОСТЬЮ
Рассмотрим распространение поверхностных волн по свободной от механических нагрузок поверхности пьезоэлектрического полупространства. Электропроводящая среда (экран) расположена на некотором расстоянии $h \ne 0$ от поверхности пьезокристалла.
Координатная ось $0{{x}_{3}}$ совпадает с главной осью $\bar {p}$ симметрии пьезоэлектрического кристалла (рис. 1). Внутренняя нормаль к поверхности полупространства пьезокристалла направлена вдоль оси $0{{x}_{2}}$, а электроакустическая волна распространяется вдоль оси $0{{x}_{1}}$.
Квазистатические уравнения электроупругости антиплоской деформации ${\mathbf{U}} = [0;0;U({{x}_{1}},{{x}_{2}},t);$ $\varphi ({{x}_{1}},{{x}_{2}},t)]$ для пьезоэлектрических кристаллов классов 4mm тетрагональной и 6mm гексагональной симметрии имеют вид
(1.1)
$\begin{gathered} {{{\tilde {c}}}_{{44}}}{{\nabla }^{2}}U({{x}_{1}},{{x}_{2}},t) = \rho \ddot {U}({{x}_{1}},{{x}_{2}},t), \\ {{\nabla }^{2}}\varphi ({{x}_{1}},{{x}_{2}},t) = ({{{{e}_{{15}}}} \mathord{\left/ {\vphantom {{{{e}_{{15}}}} {{{\varepsilon }_{{11}}}}}} \right. \kern-0em} {{{\varepsilon }_{{11}}}}}){{\nabla }^{2}}U({{x}_{1}},{{x}_{2}},t). \\ \end{gathered} $В приведенных выше формулах: ${{\tilde {c}}_{{44}}} = {{c}_{{44}}}(1 + {{\chi }^{2}})$ – приведенная жесткость на сдвиг, ${{c}_{{44}}}$ – естественная жесткость на сдвиг, ${{\chi }^{2}} = {{e_{{15}}^{2}} \mathord{\left/ {\vphantom {{e_{{15}}^{2}} {({{\varepsilon }_{{11}}}{{c}_{{44}}})}}} \right. \kern-0em} {({{\varepsilon }_{{11}}}{{c}_{{44}}})}}$ – коэффициент электромеханического соединения, ${{e}_{{15}}}$ – пьезоэлектрический модуль, ${{\varepsilon }_{{11}}}$ – коэффициент диэлектрической проницаемости и $\rho $ – плотность материала.
Сопутствующий электрический потенциал ${{\varphi }_{e}}({{x}_{1}},{{x}_{2}},t)$ в вакуумном промежутке $\left\{ {\left| {{{x}_{1}}} \right| < \infty ,} \right.$ $ - h \leqslant {{x}_{2}} \leqslant 0\} $ удовлетворяет уравнению Лапласа
На механически свободной поверхности пьезоэлектрического полупространства ${{x}_{2}} = 0$ выполняются следующие граничные условия
(1.3)
${{c}_{{44}}}{{\partial }_{2}}U({{x}_{1}},{{x}_{2}},t) + {{e}_{{15}}}{{\partial }_{2}}\varphi ({{x}_{1}},{{x}_{2}},t) = 0,$(1.4)
$\begin{gathered} {{e}_{{15}}}{{\partial }_{2}}U({{x}_{1}},{{x}_{2}},t) - {{\varepsilon }_{{11}}}{{\partial }_{2}}\varphi ({{x}_{1}},{{x}_{2}},t) = \\ = - {{\varepsilon }_{0}}{{\partial }_{2}}{{\varphi }_{e}}({{x}_{1}},{{x}_{2}},t), \\ \end{gathered} $На верхней границе вакуумного промежутка ${{x}_{2}} = h$ (на заземленном экране электрического поля) выполняется граничное условие
Для исследования существования локализованных вблизи поверхности ${{x}_{2}} = 0$ электроакустических поперечных волн представлены решения сформулированной математической краевой задачи (1.1)–(1.6) в виде плоских нормальных волн
(1.7)
$\left\{ \begin{gathered} U({{x}_{1}},{{x}_{2}},t) = {{U}_{0}}({{x}_{2}})\exp [ik({{x}_{1}} - {\text{v}}t)], \hfill \\ \varphi ({{x}_{1}},{{x}_{2}},t) = {{\varphi }_{0}}({{x}_{2}})\exp [ik({{x}_{1}} - {\text{v}}t)], \hfill \\ {{\varphi }_{e}}({{x}_{1}},{{x}_{2}},t) = \varphi _{0}^{{(e)}}({{x}_{2}})\exp [ik({{x}_{1}} - {\text{v}}t)]. \hfill \\ \end{gathered} \right.$В условиях затухания на бесконечности ${{x}_{2}} \to \infty $ амплитуды характеристик электроупругой волны в пьезоэлектрическом полупространстве равны
(1.8)
$\mathop {\lim }\limits_{{{x}_{2}} \to \infty } {{U}_{0}}({{x}_{2}}) = 0,\,\,\,\,\mathop {\lim }\limits_{{{x}_{2}} \to \infty } {{\varphi }_{0}}({{x}_{2}}) = 0.$В соотношениях (1.7) для решений в виде плоских нормальных волн $k = {{2\pi } \mathord{\left/ {\vphantom {{2\pi } \lambda }} \right. \kern-0em} \lambda }$ – волновое число, $v{\text{(}}\lambda {\text{)}} = {{\omega \lambda } \mathord{\left/ {\vphantom {{\omega \lambda } {2\pi }}} \right. \kern-0em} {2\pi }}$ – фазовая скорость нормальной волны.
В соответствии с условиями на поверхности (1.5) и в случае заземленного экрана (1.6) общее решение уравнения (1.2) получается в виде
(1.9)
$\begin{gathered} {{\varphi }_{e}}({{x}_{1}},{{x}_{2}},t) = {{\varphi }_{0}}(0)\exp [ik({{x}_{1}} - vt)] \times \\ \times \,\,\left[ {\cos \left( {\frac{{2\pi {{x}_{2}}}}{{h\xi }}} \right) + \frac{{\cos ({{2\pi } \mathord{\left/ {\vphantom {{2\pi } \xi }} \right. \kern-0em} \xi })}}{{\sin ({{2\pi } \mathord{\left/ {\vphantom {{2\pi } \xi }} \right. \kern-0em} \xi })}}\sin \left( {\frac{{2\pi {{x}_{2}}}}{{h\xi }}} \right)} \right]. \\ \end{gathered} $Здесь введен параметр ξ = λ/h.
С учетом полученного решения (1.9) поверхностные условия (1.3) и (1.4) можно записать в более наглядном виде
(1.10)
$\begin{gathered} {{\partial }_{2}}U({{x}_{1}},0,t) = - \frac{{{{e}_{{15}}}}}{{{{c}_{{44}}}}}\frac{{{{\varepsilon }_{0}}}}{{{{\varepsilon }_{{11}}}(1 + {{\chi }^{2}})}}\frac{{\cos ({{2\pi } \mathord{\left/ {\vphantom {{2\pi } \xi }} \right. \kern-0em} \xi })}}{{\sin ({{2\pi } \mathord{\left/ {\vphantom {{2\pi } \xi }} \right. \kern-0em} \xi })}} \times \\ \times \,\,{{(2\pi } \mathord{\left/ {\vphantom {{(2\pi } {h\xi }}} \right. \kern-0em} {h\xi }})\varphi (0)\exp [ik({{x}_{1}} - vt)], \\ {{\partial }_{2}}\varphi ({{x}_{1}},0,t) = \frac{{{{\varepsilon }_{0}}}}{{{{\varepsilon }_{{11}}}(1 + {{\chi }^{2}})}}\frac{{\cos ({{2\pi } \mathord{\left/ {\vphantom {{2\pi } \xi }} \right. \kern-0em} \xi })}}{{\sin ({{2\pi } \mathord{\left/ {\vphantom {{2\pi } \xi }} \right. \kern-0em} \xi })}} \times \\ \times \,\,{{(2\pi } \mathord{\left/ {\vphantom {{(2\pi } {h\xi }}} \right. \kern-0em} {h\xi }})\varphi (0)\exp [ik({{x}_{1}} - vt)]. \\ \end{gathered} $Решения, удовлетворяющие условиям затухания (1.8) в пьезоэлектрическом полупространстве, записываются в виде
(1.11)
$\begin{gathered} U({{x}_{1}},{{x}_{2}},t) = {{U}_{0}}\exp \left( { - {{\alpha }_{t}}\frac{{2\pi {{x}_{2}}}}{{h\xi }}} \right)\exp [ik({{x}_{1}} - vt)], \\ \varphi ({{x}_{1}},{{x}_{2}},t) = \frac{{{{e}_{{15}}}}}{{{{\varepsilon }_{{11}}}}}U({{x}_{1}},{{x}_{2}},t) + \\ + \,\,{{\varphi }_{0}}\exp \left( { - \frac{{2\pi {{x}_{2}}}}{{h\xi }}} \right)\exp [ik({{x}_{1}} - vt)]. \\ \end{gathered} $В решениях введен коэффициент затухания несущей упругой волны ${{\alpha }_{t}} = \sqrt {1 - {{{{{(v(\xi )} \mathord{\left/ {\vphantom {{(v(\xi )} {{{{\tilde {c}}}_{t}})}}} \right. \kern-0em} {{{{\tilde {c}}}_{t}})}}}}^{2}}} $ (волновой параметр), в котором $\tilde {c}_{t}^{2} = {{{{c}_{{44}}}(1 + {{\chi }^{2}})} \mathord{\left/ {\vphantom {{{{c}_{{44}}}(1 + {{\chi }^{2}})} \rho }} \right. \kern-0em} \rho }$ – скорость поперечной волны в материале, $v(\xi )$ – фазовая скорость для всех $\lambda = {{2\pi } \mathord{\left/ {\vphantom {{2\pi } k}} \right. \kern-0em} k}$ длин распространения волн. Очевидно также, что приповерхностная локализация волновой энергии возможна только для волн с фазовой скоростью $v(\xi ) < {{\tilde {c}}_{t}}$.
Соответствующее дисперсионное уравнение получается подстановкой решений (1.11) в условия на поверхности (1.10):
(1.12)
$\sqrt {1 - {{{[{{v(\xi )} \mathord{\left/ {\vphantom {{v(\xi )} {{{c}_{t}}}}} \right. \kern-0em} {{{c}_{t}}}}]}}^{2}}} = \frac{{{{\chi }^{2}}}}{{1 + {{\chi }^{2}}}}f(\xi ).$В отличие от известного уравнения [3], правая часть уравнения содержит множитель $f(\xi )$, изменяющийся в зависимости от параметра $\xi = {\lambda \mathord{\left/ {\vphantom {\lambda h}} \right. \kern-0em} h}$. Функция
(1.13)
$f(\xi ) = \frac{{{{\varepsilon }_{0}}\left[ {1 + \exp ({{4\pi } \mathord{\left/ {\vphantom {{4\pi } \xi }} \right. \kern-0em} \xi })} \right]}}{{({{\varepsilon }_{0}} + {{\varepsilon }_{{11}}})\exp ({{4\pi } \mathord{\left/ {\vphantom {{4\pi } \xi }} \right. \kern-0em} \xi }) + ({{\varepsilon }_{0}} - {{\varepsilon }_{{11}}})}}$Очевидно, что в предельных случаях ультракоротких и инфракрасных волн в вакуумном зазоре, когда $kh = {{2\pi } \mathord{\left/ {\vphantom {{2\pi } \xi }} \right. \kern-0em} \xi } \ll 1$ и $kh = {{2\pi } \mathord{\left/ {\vphantom {{2\pi } \xi }} \right. \kern-0em} \xi } \gg 1$ соответственно, дисперсионное уравнение (1.12) имеет предельные решения, соответствующие значениям ${{f}_{\infty }}(\xi ) = 1$ и ${{f}_{0}}(\xi ) = {{\varepsilon }_{0}}{{({{\varepsilon }_{0}} + {{\varepsilon }_{{11}}})}^{{ - 1}}}$. Очевидно также, что $f(\xi )$ – монотонно возрастающая функция параметра $\xi $, значения которой лежат в интервале$\left[ {{{{{\varepsilon }_{0}}} \mathord{\left/ {\vphantom {{{{\varepsilon }_{0}}} {({{\varepsilon }_{0}} + {{\varepsilon }_{{11}}})}}} \right. \kern-0em} {({{\varepsilon }_{0}} + {{\varepsilon }_{{11}}})}};{\text{ }}1} \right]$ (рис. 2). Функция$f(\xi )$, по сути, играет роль коэффициента перехода из одного электроупругого состояния в другое.
Из уравнения дисперсии (1.12) получаем выражение для фазовой скорости
где $\chi _{1}^{2} = {{{{\chi }^{2}}} \mathord{\left/ {\vphantom {{{{\chi }^{2}}} {(1 + {{\chi }^{2}})}}} \right. \kern-0em} {(1 + {{\chi }^{2}})}}$ – приведенный коэффициент электромеханической связи пьезоэлектрического материала.В случае ультракоротких волн, когда $kh \to \infty $, или $\xi = {\lambda \mathord{\left/ {\vphantom {\lambda h}} \right. \kern-0em} h} \to 0$, получаем дисперсионное уравнение задачи Блюстейна [1]. Отсюда видно, что волна Блюстейна имеет максимальную фазовую скорость
(1.15)
${{v}_{{\text{B}}}} = v(0) = {{\tilde {с}}_{t}}\sqrt {1 - \chi _{1}^{4}{{\varepsilon _{0}^{2}} \mathord{\left/ {\vphantom {{\varepsilon _{0}^{2}} {{{{({{\varepsilon }_{0}} + {{\varepsilon }_{{11}}})}}^{2}}}}} \right. \kern-0em} {{{{({{\varepsilon }_{0}} + {{\varepsilon }_{{11}}})}}^{2}}}}} .$В случае инфрадлинных волн, когда $kh \to 0$ или $\xi = {\lambda \mathord{\left/ {\vphantom {\lambda h}} \right. \kern-0em} h} \to \infty $, получается задача о пьезоэлектрическом полупространстве с металлизированной границей без механического воздействия [2]. Из дисперсионного уравнения (1.12) получаем выражение для фазовой скорости
Поверхностные поперечные волны имеют наименьшую фазовую скорость в случае металлизированной границы пьезоэлектрического полупространства.
Из дисперсионного уравнения (1.12) и вида передаточной функции (1.13) также следует, что при наличии проводящего слоя вблизи свободной границы пьезоэлектрического полупространства поверхностные поперечные волны становятся высокодисперсными. Тогда каждой конкретной длине волнового сигнала соответствует зона допустимых частот.
(1.17)
$\sqrt {1 - \chi _{1}^{4}f_{0}^{2}(\xi )} \geqslant \frac{{\omega (\xi )}}{{{{({{{\tilde {c}}}_{t}}} \mathord{\left/ {\vphantom {{({{{\tilde {c}}}_{t}}} {h)}}} \right. \kern-0em} {h)}}\xi }} \geqslant \sqrt {1 - \chi _{1}^{4}f_{\infty }^{2}(\xi )} .$Частота $\omega (\xi )$ поверхностной волны становится монотонно возрастающей функцией параметра $\xi $ (рис. 3).
Общее решение задачи для рассматриваемого волнового движения представлено составляющими электроакустической поперечной волны в виде суперпозиции гармонических волн со всеми возможными волновыми числами [8]
(1.18)
$U({{x}_{1}},{{x}_{2}},t) = \int\limits_0^\infty {{{U}_{0}}\exp ( - k{{\alpha }_{t}}{{x}_{2}})\exp [i\theta (k)t]} \,dk,$(1.19)
$\begin{gathered} \varphi ({{x}_{1}},{{x}_{2}},t) = \left( {\frac{{{{e}_{{15}}}}}{{{{\varepsilon }_{{11}}}}}} \right)U({{x}_{1}},{{x}_{2}},t) + \\ + \,\,\int\limits_0^\infty {{{\varphi }_{0}}\exp ( - k{{x}_{2}})\exp [i\theta (k)t]dk} \,. \\ \end{gathered} $Здесь $\theta (k) = k[{{s}_{0}} - v(k)]$ – фазовая функция, амплитуды ${{U}_{0}}$ и ${{\varphi }_{0}}$ определяются из соответствующих начальных или граничных условий, ${{s}_{0}} = {{{{x}_{1}}} \mathord{\left/ {\vphantom {{{{x}_{1}}} t}} \right. \kern-0em} t}$ – фиксированный параметр.
Из (1.14), (1.18) и (1.19) следует, что наличие электропроводящего слоя у поверхности пьезоэлектрической среды приводит к уменьшению фазовой скорости и амплитуды поверхностной волны. При удалении проводящей поверхности от механически свободной поверхности пьезоэлектрика фазовая скорость поверхностной волны увеличивается, достигая своего максимума.
Изменение относительной ширины вакуумного зазора между поверхностями пьезоэлектрического полупространства и электропроводящего экрана приводит к изменению локализации энергии волны вблизи поверхности пьезоэлектрика.
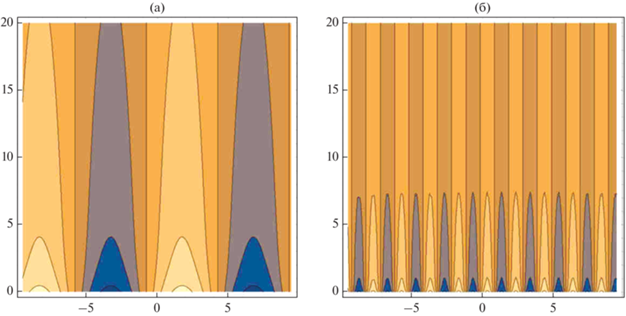
На рис. 4а и 5а показаны соответственно волновые поверхности составляющих электроакустической волны в случае узкого зазора, когда ${\lambda \mathord{\left/ {\vphantom {\lambda h}} \right. \kern-0em} h} = 10.0$. В этом случае локализация волновой энергии у поверхности мала, и волновые компоненты медленно затухают по глубине.
Рис. 4.
Эволюция подповерхностной локализации упругого сдвига в зависимости от относительной длины волны: (а) – отношение длины волны к ширине зазора ${\lambda \mathord{\left/ {\vphantom {\lambda h}} \right. \kern-0em} h} = 10$, (б) – отношение длины волны к ширине зазора ${\lambda \mathord{\left/ {\vphantom {\lambda h}} \right. \kern-0em} h} = 1.0$.

На рис. 4б и 5б показаны соответственно волновые поверхности составляющих электроакустической волны в случае широкого зазора, когда ${\lambda \mathord{\left/ {\vphantom {\lambda h}} \right. \kern-0em} h} = 1.0$. В этом случае локализация волновой энергии у поверхности сильнее, и волновые компоненты резко затухают с глубиной. Это означает, что в пьезоэлектрическом полупространстве при разной ширине вакуумного зазора возникают разные установившиеся колебания с разной приповерхностной локализацией.
Рис. 5.
Эволюция приповерхностной локализации электрического потенциала в зависимости от относительной длины волны: (а) – отношение длины волны к ширине зазора ${\lambda \mathord{\left/ {\vphantom {\lambda h}} \right. \kern-0em} h} = 10$, (б) – отношение длины волны к ширине зазора ${\lambda \mathord{\left/ {\vphantom {\lambda h}} \right. \kern-0em} h} = 1.0$.
Численные расчеты и сравнительный анализ проведены для физикомеханических характеристик пьезоэлектриков класса 6mm гексагональной симметрии PZT-4 и ZnO (Таблица 1).
Электрический экран расположен на расстоянии $h = 2.5 \times {{10}^{{ - 4}}}$ м от механически свободной поверхности пьезоэлектрического полупространства.
Принимая во внимание (1.10), можно утверждать, что поверхностные эффекты на механически свободной поверхности пьезоэлектрика (1.11) могут изменяться в случаях изменяющейся во времени ширины вакуумного зазора или изменяющейся во времени нагрузки электрического экрана.
В случае нагруженного электрического экрана с однонаправленно изменяющимся потенциалом ${{\varphi }_{e}}({{x}_{1}}, - h,t) = \phi (t)\exp (ik{{x}_{1}})$ и фиксированной шириной вакуумного зазора, когда $h = {\text{const}}$, в вакуумном зазоре можно создать сопутствующие колебания распространяющейся однонаправленной электроупругой волны:
(1.20)
$\begin{gathered} {{\varphi }_{e}}({{x}_{1}},{{x}_{2}},t) = - {{\phi }_{\varphi }}(t)\operatorname{cosec} \left( {\frac{{2\pi }}{\xi }} \right) \times \\ \times \,\,\sin \left( {\frac{{2\pi {{x}_{2}}}}{{h\xi }}} \right)\exp (ik{{x}_{1}}) + \\ + \,\,{{\varphi }_{0}}(0,t)\cos \left( {\frac{{2\pi {{x}_{2}}}}{{h\xi }}} \right)\exp (ik{{x}_{1}}) + \\ + \,\,{{\varphi }_{0}}(0,t)\operatorname{ctg} \left( {\frac{{2\pi }}{\xi }} \right)\sin \left( {\frac{{2\pi {{x}_{2}}}}{{h\xi }}} \right)\exp (ik{{x}_{1}}). \\ \end{gathered} $В случае заземленного электрического экрана и изменяющейся во времени ширины вакуумного зазора $h(t)$, в вакуумном зазоре и на поверхности пьезоэлектрика вместо (1.9) получим однонаправленно изменяющиеся сопровождающие колебания вида
(1.21)
$\begin{gathered} {{\varphi }_{e}}({{x}_{1}},{{x}_{2}},t) = {{\varphi }_{0}}(0,t){{\phi }_{h}}(t) \times \\ \times \,\,\left[ {\cos \left( {\frac{{2\pi {{x}_{2}}}}{\lambda }} \right) + \sin \left( {\frac{{2\pi {{x}_{2}}}}{\lambda }} \right)} \right]\exp (ik{{x}_{1}}). \\ \end{gathered} $В соотношениях (1.20) и (1.21) функция ${{\varphi }_{0}}(0,t)$ представляет собой гармонику установившихся электроакустических колебаний на поверхности раздела пьезоэлектрика и вакуумного зазора, ${{\phi }_{\varphi }}(t)$ и ${{\phi }_{h}}(t) = \sin \left( {{{2\pi h(t)} \mathord{\left/ {\vphantom {{2\pi h(t)} \lambda }} \right. \kern-0em} \lambda }} \right)$ – потенциалы в качестве управляющих функций.
Принимая во внимание, что вынужденные сопровождающие колебания (1.20) и (1.21) создают поверхностные воздействия на процесс распространения электроакустической поперечной волны в пьезоэлектрическом полупространстве, можно формулировать задачи бесконтактного управления локализацией волновой энергии в нем.
Таблица 1.
Модуль сдвига, плотности и скорости сдвиговых волн в некоторых пьезоэлектрических кристаллах
| PZT-4 | ZnO | |
|---|---|---|
| Модуль сдвига материала ${{c}_{{44}}}$, Па | $2.56 \times {{10}^{{10}}}$ | $4.25 \times {{10}^{{10}}}$ |
| Плотность материала $\rho {\text{, }}{{{\text{кг}}} \mathord{\left/ {\vphantom {{{\text{кг}}} {{{{\text{м}}}^{3}}}}} \right. \kern-0em} {{{{\text{м}}}^{3}}}}$ | $7.5 \times {{10}^{3}}$ | $5.68 \times {{10}^{3}}$ |
| Пьезоэлектрический модуль ${{e}_{{15}}}$, Кл/м2 | 12.7 | 0.59 |
| Диэлектрическая проницаемость ${{{{\varepsilon }_{{11}}}} \mathord{\left/ {\vphantom {{{{\varepsilon }_{{11}}}} {{{\varepsilon }_{0}}}}} \right. \kern-0em} {{{\varepsilon }_{0}}}},\;{{\text{Ф}} \mathord{\left/ {\vphantom {{\text{Ф}} {\text{м}}}} \right. \kern-0em} {\text{м}}}$ | 6.45 | 7.38 |
| ЕМ коэффициент связи ${{\chi }^{2}}$ | 0.9409 | 0.0121 |
| (SH) скорость волны ${{\tilde {C}}_{t}}{\text{, }}{{\text{м}} \mathord{\left/ {\vphantom {{\text{м}} {\text{с}}}} \right. \kern-0em} {\text{с}}}$ | $2.574 \times {{10}^{3}}$ | $2.752 \times {{10}^{3}}$ |
2. ЗАДАЧИ УПРАВЛЕНИЯ ПРИПОВЕРХНОСТНОЙ ЛОКАЛИЗАЦИЕЙ ЭНЕРГИИ ЭЛЕКТРОАКУСТИЧЕСКОЙ ПОПЕРЕЧНОЙ ВОЛНЫ ПОСРЕДСТВОМ НЕАКУСТИЧЕСКОГО ВОЗДЕЙСТВИЯ
Для однонаправленных волн вида $F({{x}_{1}},{{x}_{2}},t) = $ $ = {{F}_{{0*}}}({{x}_{{2*}}},t)\exp (ik{{x}_{1}})$ квазистатические уравнения электроупругости антиплоской деформации для пьезоэлектрической среды (1.1) можно записать в более наглядном виде
(2.1)
$\partial _{2}^{2}{{U}_{{0*}}}({{x}_{2}},t) - {{k}^{2}}{{U}_{{0*}}}({{x}_{2}},t) = \tilde {c}_{t}^{{ - 2}}{{\ddot {U}}_{{0*}}}({{x}_{2}},t),$(2.2)
$\begin{gathered} \partial _{2}^{2}{{\varphi }_{{0*}}}({{x}_{2}},t) - {{k}^{2}}{{\varphi }_{{0*}}}({{x}_{2}},t) = \\ = ({{{{e}_{{15}}}} \mathord{\left/ {\vphantom {{{{e}_{{15}}}} {{{\varepsilon }_{{11}}}}}} \right. \kern-0em} {{{\varepsilon }_{{11}}}}})\left[ {\partial _{2}^{2}{{U}_{{0*}}}({{x}_{2}},t) - {{k}^{2}}{{U}_{{0*}}}({{x}_{2}},t)} \right]. \\ \end{gathered} $Пусть в начальный момент t = 0 воздействия на установившуюся электроакустическую волну сдвига, ее волновые компоненты соответствуют значениям
(2.3)
${{U}_{{0*}}}({{x}_{2}},0) = \gamma ({{x}_{2}}),\,\,\,\,{{\dot {U}}_{{0*}}}({{x}_{2}},0) = \tilde {\gamma }({{x}_{2}}),$(2.4)
${{\varphi }_{{0*}}}({{x}_{2}},0) = \zeta ({{x}_{2}}),\,\,\,\,{{\dot {\varphi }}_{{0*}}}({{x}_{2}},0) = \tilde {\zeta }({{x}_{2}}).$Пусть необходимо за определенный промежуток времени $t \in [0;{{T}_{0}}]$ привести установившееся электроакустическое состояние и соответствующую ему приповерхностную локализацию волновой энергии в новое установившиеся состояние, со значениями волновых компонент
(2.5)
${{U}_{{0*}}}({{x}_{2}},{{T}_{0}}) = \delta ({{x}_{2}}),\,\,\,\,{{\dot {U}}_{{0*}}}({{x}_{2}},{{T}_{0}}) = \tilde {\delta }({{x}_{2}}),$(2.6)
${{\varphi }_{{0*}}}({{x}_{2}},{{T}_{0}}) = \xi ({{x}_{2}}),\,\,\,\,{{\dot {\varphi }}_{{0*}}}({{x}_{2}},{{T}_{0}}) = \tilde {\xi }({{x}_{2}}).$В квазистатической постановке задачи управления электроакустическим волновым процессом функции, описывающие начальные и финальные значения колебаний сопровождающих электрических полей $\xi ({{x}_{2}})$, $\tilde {\xi }({{x}_{2}})$, $\zeta ({{x}_{2}})$ и $\tilde {\zeta }({{x}_{2}})$, будут связаны с функциями, описывающими начальное и конечное состояния упругого смещения $\gamma ({{x}_{2}})$, $\tilde {\gamma }({{x}_{2}})$, $\delta ({{x}_{2}})$ и $\tilde {\delta }({{x}_{2}})$. Соответствующие связи между ними описываются системой уравнений (2.1) и (2.2) с условиями на поверхности.
Поэтому в квазистатической постановке задачи управления волновым процессом начальные условия в момент $t = 0$ и условия конечного состояния в момент $t = {{T}_{0}}$ для характеристик поля электроакустической волны записываются только для сдвигового упругого смещения в виде (2.3) и (2.5).
Фактически на механически свободной поверхности пьезоэлектрика неакустическое воздействие возникает как при переменной нагрузке экрана электрического поля, так и в случае, когда ширина зазора между поверхностью пьезоэлектрика и поверхностью электрического поля экрана меняется со временем. В обоих случаях поверхностные условия (1.3) и (1.4) формально могут быть записаны в единой форме
(2.7)
${{\partial }_{2}}{{U}_{{0*}}}(0,t) = - \frac{{{{e}_{{15}}}}}{{{{c}_{{44}}}}}\frac{{{{\varepsilon }_{0}}}}{{{{\varepsilon }_{{11}}}(1 + {{\chi }^{2}})}}\mu (t),$(2.8)
${{\partial }_{2}}{{\varphi }_{{0*}}}(0,t) = \frac{{{{\varepsilon }_{0}}}}{{{{\varepsilon }_{{11}}}(1 + {{\chi }^{2}})}}\mu (t).$Здесь функция поверхностного управления как функция поверхностного неакустического суммарного воздействия на поверхности пьезоэлектрика $\mu (t)$ появляется в виде свертки функции ${{\varphi }_{0}}(0,t)$ с одной из функций управления ${{\phi }_{\varphi }}(t)$ или ${{\phi }_{h}}(t) = \sin \left( {{{2\pi h(t)} \mathord{\left/ {\vphantom {{2\pi h(t)} \lambda }} \right. \kern-0em} \lambda }} \right)$.
2.1. Задача управления I типа. Задача неакустического управления приповерхностной локализацией энергии электроакустической поперечной волны посредством динамической нагрузки электрического экрана
В случае, когда экран имеет изменяющуюся по времени загрузку
общее решение уравнения (1.2) в вакуумном зазоре с учетом условий на поверхности (1.5), (2.7) и (2.8) получено в виде однонаправленных волн ${{\varphi }_{e}}({{x}_{1}},{{x}_{2}},t)$ $ = \varphi _{{0*}}^{{(e)}}({{x}_{2}},t)\exp (ik{{x}_{1}})$, где(2.10)
$\begin{gathered} \varphi _{{0*}}^{{(e)}}({{x}_{2}},t) = {{\varphi }_{0}}(0,t)\cos \left( {\frac{{2\pi {{x}_{2}}}}{{h\xi }}} \right) + \\ + \,\,{{\varphi }_{0}}(0,t){\text{ctg}}(\xi )\sin \left( {\frac{{2\pi {{x}_{2}}}}{{h\xi }}} \right) - \\ - \,\,{{\phi }_{\varphi }}(t){\text{cosec}}(\xi )\sin \left( {\frac{{2\pi {{x}_{2}}}}{{h\xi }}} \right). \\ \end{gathered} $В свертке с сопровождающими колебаниями в электроакустической волне сдвига эти вынужденные колебания создают нагрузки на поверхность пьезоэлектрика:
(2.11)
$\begin{gathered} {{\partial }_{2}}U({{x}_{1}},0,t) = \frac{{{{e}_{{15}}}}}{{{{c}_{{44}}}}}\frac{{{{\varepsilon }_{0}}}}{{{{\varepsilon }_{{11}}}(1 + {{\chi }^{2}})}}\left( {\frac{{2\pi }}{{h\xi }}} \right)\exp (ik{{x}_{1}}) \times \\ \times \,\,\left[ {{{\phi }_{\varphi }}(t)\operatorname{cosec} \left( {\frac{{2\pi }}{\xi }} \right) - {{\varphi }_{0}}(0,t)\operatorname{ctg} \left( {\frac{{2\pi }}{\xi }} \right)} \right], \\ \end{gathered} $(2.12)
$\begin{gathered} {{\partial }_{2}}\varphi ({{x}_{1}},0,t) = - \frac{{{{\varepsilon }_{0}}}}{{{{\varepsilon }_{{11}}}(1 + {{\chi }^{2}})}}\left( {\frac{{2\pi }}{{h\xi }}} \right)\exp (ik{{x}_{1}}) \times \\ \times \,\,\left[ {{{\phi }_{\varphi }}(t)\operatorname{cosec} \left( {\frac{{2\pi }}{\xi }} \right) - {{\varphi }_{0}}(0,t)\operatorname{ctg} \left( {\frac{{2\pi }}{\xi }} \right)} \right]. \\ \end{gathered} $Функция управления ${{\phi }_{\varphi }}(t)$ в суммарном воздействии появляется как слагаемое
(2.13)
$\begin{gathered} {{\mu }_{\varphi }}(t) = \left( {\frac{{2\pi }}{\lambda }} \right){{\varphi }_{0}}(t)\operatorname{ctg} \left( {\frac{{2\pi }}{\xi }} \right) - \\ - \,\,\left( {\frac{{2\pi }}{\lambda }} \right){{\phi }_{\varphi }}(t)\operatorname{cosec} \left( {\frac{{2\pi }}{\xi }} \right). \\ \end{gathered} $Следовательно, задача управления однонаправленными электроакустическими волнами с неакустическим поверхностным воздействием в пьезоэлектрическом полупространстве формулируется в виде однородных дифференциальных уравнений (2.1) и (2.2), неоднородных граничных условий (2.11) и (2.12), условий начального и конечного состояний (2.3)–(2.6) в координатной полуполосе ${{Q}_{T}} = [0 \leqslant {{x}_{2}} < \infty ) \times [0 \leqslant t \leqslant {{T}_{0}}]$.
Требуется найти такое граничное воздействие ${{\phi }_{\varphi }}(t)$, которое в течение времени ${{T}_{0}}$ переводит систему из начального состояния (2.3) и (2.4) в конечное состояние (2.5) и (2.6).
2.2. Задача управления II типа. Неакустический контроль приповерхностной локализации энергии электроакустической поперечной волны посредством динамического перемещения заземленного электрического экрана
В случае заземленного электрического экрана и изменяющейся во времени ширины вакуумного зазора $h(t)$, общее решение уравнения (1.2) в вакуумном зазоре с учетом условий (1.5) на поверхности ${{x}_{2}} = 0$ и (1.6) на поверхности ${{x}_{2}} = h(t)$ соответственно получается в виде однонаправленной волны
(2.14)
$\begin{gathered} {{\varphi }_{e}}({{x}_{1}},{{x}_{2}},t) = {{\varphi }_{0}}(0,t)\exp (ik{{x}_{1}}) \times \\ \times \,\,\left[ {\cos \left( {\frac{{2\pi {{x}_{2}}}}{\lambda }} \right) + \operatorname{ctg} \left( {\frac{{2\pi }}{{L(t)}}} \right)\sin \left( {\frac{{2\pi {{x}_{2}}}}{\lambda }} \right)} \right]. \\ \end{gathered} $С учетом вновь полученного решения (2.14), поверхностные условия (1.3) и (1.4) для однонаправленных волн можно записать в более наглядном виде
(2.15)
$\begin{gathered} {{\partial }_{2}}U({{x}_{1}},0,t) = - \frac{{{{e}_{{15}}}}}{{{{c}_{{44}}}}}\frac{{{{\varepsilon }_{0}}}}{{{{\varepsilon }_{{11}}}(1 + {{\chi }^{2}})}} \times \\ \times \,\,\frac{{2\pi }}{\lambda }\sin \left( {\frac{{2\pi h(t)}}{\lambda }} \right){{\varphi }_{0}}(0,t)\exp (ik{{x}_{1}}), \\ \end{gathered} $(2.16)
$\begin{gathered} {{\partial }_{2}}\varphi ({{x}_{1}},0,t) = \frac{{{{\varepsilon }_{0}}}}{{{{\varepsilon }_{{11}}}(1 + {{\chi }^{2}})}} \times \\ \times \,\,\frac{{2\pi }}{\lambda }\sin \left( {\frac{{2\pi h(t)}}{\lambda }} \right){{\varphi }_{0}}(0,t)\exp (ik{{x}_{1}}). \\ \end{gathered} $Функция управления ${{\phi }_{h}}(t) = \sin \left( {{{2\pi h(t)} \mathord{\left/ {\vphantom {{2\pi h(t)} \lambda }} \right. \kern-0em} \lambda }} \right)$ в суммарном воздействии появляется как множитель:
(2.17)
${{\mu }_{h}}(t) = \left( {\frac{{2\pi }}{\lambda }} \right){{\varphi }_{0}}(t)\sin \left( {\frac{{2\pi h(t)}}{\lambda }} \right).$Функция воздействия в этом случае будет равна
(2.18)
$h(t) = {{(\lambda } \mathord{\left/ {\vphantom {{(\lambda } {2\pi )}}} \right. \kern-0em} {2\pi )}}\arcsin [{{\phi }_{h}}(t)].$Соответственно, задача управления поверхностным неакустическим воздействием однонаправленных электроакустических волн в пьезоэлектрическом полупространстве формулируется в виде однородных дифференциальных уравнений (2.1) и (2.2), неоднородных граничных условий (2.15) и (2.16), условий начального и конечного состояний (2.3)–(2.6) в координатной полуполосе ${{Q}_{T}} = [0 \leqslant {{x}_{2}} < \infty ) \times [0 \leqslant t \leqslant {{T}_{0}}]$.
Требуется найти такое граничное воздействие ${{\phi }_{h}}(t)$, которое в течение времени ${{T}_{0}}$ переводит систему из начального состояния (2.3) и (2.4) в конечное состояние (2.5) и (2.6).
Решения сформулированных задач поверхностного управления методом управления собственными формами колебаний в электроакустической волне соответствующими гармониками поверхностного воздействия [18] будут представлены в следующих статьях авторов.
3. ЗАКЛЮЧЕНИЕ
Изменения электрического поля вблизи механически свободной поверхности пьезоэлектрика приводят к поверхностным воздействиям на эту поверхность. Изменения ширины зазора между механически свободной поверхностью пьезоэлектрика и заряженной плоскостью экрана также вызывают поверхностные воздействия. Воздействие на поверхность пьезоэлектрического полупространства характеризуется коэффициентом передачи воздействия.
Рассчитаны характеристики волновых составляющих электроакустического поля для коротковолнового и длинноволнового случаев. Для управления интенсивностью приповерхностной локализации волновой энергии в пьезоэлектрическом полупространстве предлагается рассматривать поверхностное воздействие как управляющую функцию.
Дана постановка задачи управления локализацией энергии поперечной электроупругой волны вблизи поверхности пьезоэлектрика.
Список литературы
Bleustein J.L. A new surface wave in piezoelectric materials // Appl. Phys. Lett. 1968. V. 13. № 12. P. 412–413. https://doi.org/10.1063/1.1652495
Гуляев Ю.В. Поверхностные электроакустические волны в твердых телах // Письма в ЖЭТФ. 1969. Т. 9. С. 37–38.
Каганов М.И., Скловская И.Л. Поверхностная волна в пьезоэлектрике // ФТТ. 1966. Т. 8. С. 2789.
Ingebrigtsen K.A. Surface waves in piezoelectrics // J. Appl. Phys. 1969. V. 40. № 7. P. 2681–2686. https://doi.org/10.1063/1.1658060
Аветисян А.С., Камалян А.А. Влияние поперечной неоднородности пьезодиэлектрического слоя и комбинации электромеханических граничных условий при распространении сдвигового электроупругого сигнала // Вестник ГИУА. Сер. “Механика, машиноведение, машиностроение”. 2014. Т. 17. № 1. С. 37–51.
Гуляев Ю.В., Плесский В.П. Щелевые акустические волны в пьезоэлектрических материалах // Акуст. журн. 1977. Т. 23. № 5. С. 716–723.
Балакирев М.К., Горчаков А.В. Проникновение упругой волны через зазор между пьезоэлектриками // ФТТ. 1977. Т. 19. № 2. С. 571–572.
Аветисян А.С. О поверхностных волнах в пьезоэлектрическом материале при наличии проводящей среды на его границе // Материалы Второй Всесоюзной научно-технической конференции “Прочность, жесткость и технологичность изделий из композиционных материалов”. ЕГУ. 1984. Т. 1. С. 27–29.
Zaitsev B.D., Kuznetsova I.E., Joshi S.G. Influence of electrical boundary conditions on structure of surface acoustic waves in potassium niobite // Electronics letters. 1999. V. 35. № 14. P. 1205–1206. https://doi.org/10.1049/el:19990799
Зайцев Б.Д., Кузнецова И.Е., Бородина И.А. Влияние электрических граничных условий на характеристики поверхностных акустических волн, распространяющихся в ниобате калия // Акуст. журн. 2004. Т. 50. № 4. С. 462–468.
Chernozatonskii L.A., Ermoshin S.N., Gramotnev D.K. Coupled Gulyayev‑Bleustein waves in a system of 2 different piezoelectrics separated by a gap // Physics Letters A. 1991. V. 154. № 9. P. 465–470. https://doi.org/10.1016/0375-601(91)90975-E
Li X.F., Yang J.S. Piezoelectric gap waves between a piezoceramic half-space and a piezoceramic plate // Sensors and Actuators. 2006. V. 132A. № 2. P. 472–479.
Yang J.S. Acoustic gap waves in piezoelectromagnetic materials // Math. and Mech. of Solids. 2006. V. 11. № 5. P. 451–458.
Гуляев Ю.В., Хикернелл Ф.С. Акустоэлектроника: история, современное состояние и новые идеи для новой эры // Акуст. журн. 2005. Т. 51. № 1. С. 101–110.
Алексеев С.Г., Гуляев Ю.В., Котелянский И.М., Мансфельд Г.Д. Некоторые тенденции развития акустоэлектроники сверхвысоких частот // Успехи физ. наук. 2005. № 8. С. 895–899. https://doi.org/10.3367/UFNr.0175.200508i.0895
Аветисян А.С., Белубекян М.В. Об учете микровращений частиц упругой среды по упрощенной теории Коссера при распространении электроупругих волн в пьезоэлектрике класса 6mm // Акуст. журн. 2019. Т. 65. № 8. С. 579–587. https://doi.org/10.1134/S1063771019050051
Бурков С.И., Зайцева М.П., Кокорин Ю.И., Сорокин Б.П., Соболев Б.В., Четвергов Н.А. Анизотропия управления скоростью объемных акустических волн электрическим полем в пьезоэлектриках со структурой селенита // Акуст. журн. 1986. Т. 32. № 5. С. 664–666.
Bergamini A.E., Zündel M., Flores Parra E.A., Delpero T., Ruzzene M., Ermanni P. Hybrid dispersive media with controllable wave propagation: A new take on smart materials // J. Appl. Phys. 2015. V. 118. https://doi.org/10.1063/1.4934202
Avetisyan A.S., Khachatryan V.M. Propagation of hybrid electroelastic waves in transversally inhomogeneous periodic piezoelectric structures // Proc. of the NAS of Armenia Mechanics. 2020. V. 73. № 1. P. 6–22. https://doi.org/10.33018/73.1.1
Avetisyan A.S., Jilavyan H.S. Hybrid of the Rayleigh and Gulyaev‑Bluestein electro-acoustic waves near the inner surface of a layered piezoelectric composite // Proc. of the NAS of Armenia Mechanics. 2021. V. 73. № 2. P. 3–21. https://doi.org/10.33018/73.2.1
Avetisyan A.S., Mkrtchyan M.H. Control of vibrations of infinite membrane tape with a moving edge in a supersonic gas flow // Proc. of the NAS of Armenia Mechanics. 2021. V. 74. № 2. P. 45–58. https://doi.org/10.33018/73.2.1
Дополнительные материалы отсутствуют.
Инструменты
Акустический журнал





