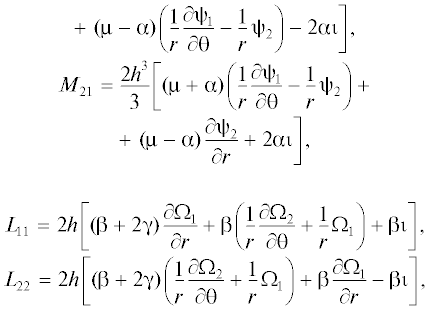Акустический журнал, 2022, T. 68, № 2, стр. 139-151
Собственные колебания микрополярных упругих гибких пластин и пологих оболочек
А. А. Саркисян a, *, **, С. О. Саркисян b, ***
a Ширакский государственный университет
3125 г. Гюмри, квартал Ани, ул. 13, дом 11, кв. 15, Армения
b Национальная академия наук Армении
3101 г. Гюмри, ул. Саят-Новы, дом 2, кв. 11, Армения
* E-mail: armenuhis@mail.ru
** E-mail: armenuhis@gmail.com
*** E-mail: s_sargsyan@yahoo.com
Поступила в редакцию 16.11.2020
После доработки 19.11.2021
Принята к публикации 24.11.2021
- EDN: QXHMIE
- DOI: 10.31857/S0320791922020083
Аннотация
Построена математическая модель динамики геометрически нелинейных (гибких) микрополярных упругих тонких пластин в декартовых и криволинейных координатах (подход обобщается также для построения модели микрополярных гибких пологих оболочек). При построении модели считается, что упругие прогибы пластинки сравнимы с их толщиной и, вместе с тем, малы по отношению к характерным размерам в плане. На основе построенной модели микрополярных упругих гибких пластин решены задачи свободных колебаний для прямоугольных и круглых пластин, а также решена задача свободных колебаний пологих оболочек. Обсуждаются эффективные стороны проявления характерных черт микрополярного материала по сравнению с соответствующим классическим материалом.
ВВЕДЕНИЕ
Проблема нелинейного динамического деформирования упругих тонкостенных конструкций является одной из фундаментальных в механике деформируемого твердого тела. В классической теории упругости широкую известность получили уравнения квадратичного варианта динамической нелинейной прикладной теории изгиба пластин Фепеля–Кармана [1] и теории изгиба пологих оболочек Маргерра [2] . В рамках этих теорий решены (см., например, [3, 4] ) многочисленные задачи нелинейного динамического деформирования упругих тонких пластин и пологих оболочек различных очертаний, под действием различных динамических внешних воздействий и при различных граничных условиях.
В настоящее время актуальна проблема построения и изучения математических прикладных теорий нелинейного динамического деформирования микрополярных упругих тонких пластин и пологих оболочек. Обзор работ по теории микрополярных упругих тонких оболочек и пластин выполнен в работе [5] . Отметим, что теоретические основания динамической микрополярной теории упругости и ее приложения к различным задачам развивались в работах [6–10] и др. Построению общей нелинейной теории микрополярных тонких оболочек посвящена работа [11] .
В работах [12–16] на основе метода гипотез, который обосновывается при анализе трехмерной теории с использованием асимптотического метода интегрирования соответствующей граничной задачи [17] , построена линейная теория динамики микрополярных упругих оболочек и пластин, и в рамках этой теории изучены различные прикладные задачи на собственные и вынужденные колебания.
В данной работе построена прикладная нелинейная теория динамического изгиба тонких упругих микрополярных пластин и пологих оболочек, которая представляет собой развитие теории Фепеля–Кармана–Маргерра применительно к микрополярной теории упругости.
ТРЕХМЕРНАЯ ГЕОМЕТРИЧЕСКИ НЕЛИНЕЙНАЯ ТЕОРИЯ МИКРОПОЛЯРНЫХ УПРУГИХ ПЛАСТИН С НЕЗАВИСИМЫМИ ПОЛЯМИ ПЕРЕМЕЩЕНИЙ И ВРАЩЕНИЙ
Рассмотрим прямоугольную тонкую пластинку постоянной толщины $2h$, считая ее трехмерным упругим микрополярным изотропным телом. Отнесем пластинку к системе декартовых координат $\left( {{{x}_{1}},{{x}_{2}},z} \right)$. Координатную плоскость ${{x}_{1}},{{x}_{2}}$ будем совмещать со срединной плоскостью пластинки. Ось $Oz$ направим вдоль нормали к срединной плоскости. Примем следующие обозначения: $\left( {{{V}_{1}},{{V}_{2}},{{V}_{3}}} \right)$ – вектор перемещения; $\left( {{{{{\omega }}}_{1}},{{{{\omega }}}_{2}},{{{{\omega }}}_{3}}} \right)$ – вектор свободного поворота.
Пусть $M({{x}_{1}},{{x}_{2}},z)$ – произвольная точка пластинки, а $N({{x}_{1}} + d{{x}_{1}},{{x}_{2}} + d{{x}_{2}},z + dz)$ – бесконечно близкая к ней соседняя точка пластинки. До деформации можно задать вектор ${\mathbf{MN}}$, проекции которого равны $\left( {d{{x}_{1}},d{{x}_{2}},dz} \right)$. После деформации точка $M$ перемещается в позицию $M{\text{*}}\left( {\xi ,\eta ,\zeta } \right)$, а точка $N$ перемещается в позицию $N{\text{*}}\left( {\xi + d\xi ,\eta + d\eta ,\zeta + d\zeta } \right)$. Новый вектор ${\mathbf{M}}{\text{*}}{\mathbf{N}}{\text{*}}$ имеет проекции $d\xi ,d\eta ,d\zeta $. В случае микрополярной теории упругости смещение элемента $d{\mathbf{r}} = \left( {d{{x}_{1}},d{{x}_{2}},dz} \right)$ обусловлено не только вектором перемещений [18]
(1)
$\begin{gathered} d\xi = \left( {1 + \frac{{\partial {{V}_{1}}}}{{\partial {{x}_{1}}}}} \right)d{{x}_{1}} + \left( {\frac{{\partial {{V}_{1}}}}{{\partial {{x}_{2}}}} + {{\omega }_{3}}} \right)d{{x}_{2}} + \left( {\frac{{\partial {{V}_{1}}}}{{\partial z}} - {{\omega }_{2}}} \right)dz, \\ d\eta = \left( {\frac{{\partial {{V}_{2}}}}{{\partial {{x}_{1}}}} - {{\omega }_{3}}} \right)d{{x}_{1}} + \\ + \,\,\left( {1 + \frac{{\partial {{V}_{2}}}}{{\partial {{x}_{2}}}}} \right)d{{x}_{2}} + \left( {\frac{{\partial {{V}_{2}}}}{{\partial z}} + {{\omega }_{1}}} \right)dz, \\ d\zeta = \left( {\frac{{\partial {{V}_{3}}}}{{\partial {{x}_{1}}}} + {{\omega }_{2}}} \right)d{{x}_{1}} + \\ + \,\,\left( {\frac{{\partial {{V}_{3}}}}{{\partial {{x}_{2}}}} - {{\omega }_{1}}} \right)d{{x}_{2}} + \left( {1 + \frac{{\partial {{V}_{3}}}}{{\partial z}}} \right)dz. \\ \end{gathered} $Далее, расстояния между соседними точками до и после деформации равны соответственно:
(3)
${{\left( {M{\text{*}}N{\text{*}}} \right)}^{2}} = ds{{{\text{*}}}^{2}} = d{{{{\xi }}}^{2}} + d{{{{\eta }}}^{2}} + d{{{{\zeta }}}^{2}}.$На основе соотношений (1)–(3) получим:
(4)
$ + \,\,2\left( {\frac{{\partial {{V}_{2}}}}{{\partial {{x}_{1}}}} - {{{{\omega }}}_{3}}} \right)\left( {\frac{{\partial {{V}_{2}}}}{{\partial z}} + {{{{\omega }}}_{1}}} \right)d{{x}_{1}}dz + $Используя компоненты тензора деформаций ${{{{\gamma }}}_{{ii}}},{{{{\gamma }}}_{{ij}}},{{{{\gamma }}}_{{33}}},{{{{\gamma }}}_{{i3}}},{{{{\gamma }}}_{{3i}}}$, разность $ds{{{\text{*}}}^{2}} - d{{s}^{2}}$ представим в виде:
(5)
$\begin{gathered} ds{{{\text{*}}}^{2}} - d{{s}^{2}} = 2{{{{\gamma }}}_{{11}}}dx_{1}^{2} + 2{{{{\gamma }}}_{{22}}}dx_{2}^{2} + 2{{{{\gamma }}}_{{33}}}d{{z}^{2}} + \\ + \,\,2\left( {{{{{\gamma }}}_{{12}}} + {{{{\gamma }}}_{{21}}}} \right)d{{x}_{1}}d{{x}_{2}} + \\ + \,\,2\left( {{{{{\gamma }}}_{{13}}} + {{{{\gamma }}}_{{31}}}} \right)d{{x}_{1}}dz + 2\left( {{{{{\gamma }}}_{{23}}} + {{{{\gamma }}}_{{32}}}} \right)d{{x}_{2}}dz, \\ \end{gathered} $(6)
$ + \,\,\frac{1}{2}\left( {\frac{{\partial {{V}_{3}}}}{{\partial {{x}_{1}}}}\frac{{\partial {{V}_{3}}}}{{\partial {{x}_{2}}}}} \right. - \left. {\frac{{\partial {{V}_{3}}}}{{\partial {{x}_{1}}}}{{{{\omega }}}_{1}} + \frac{{\partial {{V}_{3}}}}{{\partial {{x}_{2}}}}{{{{\omega }}}_{2}} - {{{{\omega }}}_{1}}{{{{\omega }}}_{2}}} \right),$Аналогично можно получить компоненты тензора изгиба‑кручения: ${{{{\chi }}}_{{ii}}},{{{{\chi }}}_{{ij}}},$${{{{\chi }}}_{{33}}},{{{{\chi }}}_{{i3}}},$${{\chi }_{{3i}}}$:
(7)
$\begin{gathered} {{{{\chi }}}_{{ii}}} = \frac{{\partial {{{{\omega }}}_{i}}}}{{\partial {{x}_{i}}}} + \frac{1}{2}\left[ {{{{\left( {\frac{{\partial {{{{\omega }}}_{1}}}}{{\partial {{x}_{i}}}}} \right)}}^{2}} + {{{\left( {\frac{{\partial {{{{\omega }}}_{2}}}}{{\partial {{x}_{i}}}}} \right)}}^{2}} + {{{\left( {\frac{{\partial {{{{\omega }}}_{3}}}}{{\partial {{x}_{i}}}}} \right)}}^{2}}} \right], \\ {{{{\chi }}}_{{33}}} = \frac{{\partial {{{{\omega }}}_{3}}}}{{\partial z}} + \frac{1}{2}\left[ {{{{\left( {\frac{{\partial {{{{\omega }}}_{1}}}}{{\partial z}}} \right)}}^{2}} + {{{\left( {\frac{{\partial {{{{\omega }}}_{2}}}}{{\partial z}}} \right)}}^{2}} + {{{\left( {\frac{{\partial {{{{\omega }}}_{3}}}}{{\partial z}}} \right)}}^{2}}} \right], \\ {{{{\chi }}}_{{ij}}} = \frac{{\partial {{{{\omega }}}_{j}}}}{{\partial {{x}_{i}}}} + \frac{{\partial {{{{\omega }}}_{j}}}}{{\partial {{x}_{i}}}}\frac{{\partial {{{{\omega }}}_{j}}}}{{\partial {{x}_{j}}}} + \frac{1}{2}\frac{{\partial {{{{\omega }}}_{3}}}}{{\partial {{x}_{i}}}}\frac{{\partial {{{{\omega }}}_{3}}}}{{\partial {{x}_{j}}}}, \\ {{{{\chi }}}_{{i3}}} = \frac{{\partial {{{{\omega }}}_{3}}}}{{\partial {{x}_{i}}}} + \frac{{\partial {{{{\omega }}}_{3}}}}{{\partial {{x}_{i}}}}\frac{{\partial {{{{\omega }}}_{3}}}}{{\partial z}} + \frac{1}{2}\frac{{\partial {{{{\omega }}}_{j}}}}{{\partial {{x}_{i}}}}\frac{{\partial {{{{\omega }}}_{j}}}}{{\partial z}}, \\ {{{{\chi }}}_{{3i}}} = \frac{{\partial {{{{\omega }}}_{i}}}}{{\partial z}} + \frac{{\partial {{{{\omega }}}_{i}}}}{{\partial {{x}_{i}}}}\frac{{\partial {{{{\omega }}}_{i}}}}{{\partial z}} + \frac{1}{2}\frac{{\partial {{{{\omega }}}_{j}}}}{{\partial {{x}_{i}}}}\frac{{\partial {{{{\omega }}}_{j}}}}{{\partial z}}. \\ \end{gathered} $Выражения (6) и (7) определяют трехмерную геометрическую модель микрополярной гибкой пластинки в декартовых координатах.
Теперь обобщим эту геометрическую модель в ортогональных криволинейных координатах ${{{{\alpha }}}_{1}},{{{{\alpha }}}_{2}},z$ (где криволинейные оси ${{{{\alpha }}}_{1}},{{{{\alpha }}}_{2}}$ расположены в срединной плоскости пластинки, а прямолинейная ось $z$ перпендикулярна к этой плоскости), а также приведем уравнения движения и соотношения упругости микрополярного материала (с независимыми полями перемещений и вращений).
Уравнения движения имеют вид [6] :
(8)
$\begin{gathered} + \,\,\frac{{\partial {{V}_{3}}}}{{\partial {{{{\alpha }}}_{1}}}}\left[ {\frac{{{{H}_{2}}}}{{{{H}_{1}}}}\frac{{\partial {{{{\sigma }}}_{{11}}}}}{{\partial {{{{\alpha }}}_{1}}}} - \frac{{{{H}_{2}}}}{{H_{1}^{2}}}\frac{{\partial {{H}_{1}}}}{{\partial {{{{\alpha }}}_{1}}}}{{{{\sigma }}}_{{11}}} + } \right. \\ \left. { + \,\,\frac{1}{{{{H}_{1}}}}\frac{{\partial {{H}_{2}}}}{{\partial {{{{\alpha }}}_{1}}}}{{{{\sigma }}}_{{11}}} + \frac{1}{2}\frac{{\partial \left( {{{{{\sigma }}}_{{12}}} + {{{{\sigma }}}_{{21}}}} \right)}}{{\partial {{{{\alpha }}}_{2}}}}} \right] + \\ + \,\,\frac{{\partial {{V}_{3}}}}{{\partial {{{{\alpha }}}_{2}}}}\left[ {\frac{{{{H}_{1}}}}{{{{H}_{2}}}}\frac{{\partial {{{{\sigma }}}_{{22}}}}}{{\partial {{{{\alpha }}}_{2}}}} - \frac{{{{H}_{1}}}}{{H_{2}^{2}}}\frac{{\partial {{H}_{2}}}}{{\partial {{{{\alpha }}}_{2}}}}{{{{\sigma }}}_{{22}}} + } \right. \\ \left. { + \,\,\frac{1}{{{{H}_{2}}}}\frac{{\partial {{H}_{1}}}}{{\partial {{{{\alpha }}}_{2}}}}{{{{\sigma }}}_{{22}}} + \frac{1}{2}\frac{{\partial \left( {{{{{\sigma }}}_{{12}}} + {{{{\sigma }}}_{{21}}}} \right)}}{{\partial {{{{\alpha }}}_{1}}}}} \right] = {{\rho }}\frac{{{{\partial }^{2}}{{V}_{3}}}}{{\partial {{t}^{2}}}}, \\ \end{gathered} $Аналогично теории Фепеля–Кармана здесь уравнения движения написаны для деформированного состояния пластин.
Физические соотношения теории упругости
(9)
${{{{\gamma }}}_{{3i}}} = \frac{{{{\mu }} + {{\alpha }}}}{{4{{\mu \alpha }}}}{{{{\sigma }}}_{{3i}}} - \frac{{{{\mu }} - {{\alpha }}}}{{4{{\mu \alpha }}}}{{{{\sigma }}}_{{i3}}},$Отметим, что физические соотношения (9) представлены в виде линейных зависимостей.
Геометрические соотношения имеют следующий вид:
(10)
$\begin{gathered} + \,\,{{( - 1)}^{j}}\frac{{\partial {{V}_{3}}}}{{\partial z}}{{{{\omega }}}_{j}} + \frac{1}{2}\left( {\frac{{\partial {{V}_{j}}}}{{\partial {{x}_{i}}}}\frac{{\partial {{V}_{j}}}}{{\partial z}} + {{{( - 1)}}^{j}}\frac{{\partial {{V}_{2}}}}{{\partial {{{{\alpha }}}_{i}}}}{{{{\omega }}}_{i}} - } \right. \\ - \,\,\left. {{{{( - 1)}}^{j}}\frac{{\partial {{V}_{j}}}}{{\partial z}}{{{{\omega }}}_{3}} - {{{{\omega }}}_{i}}{{{{\omega }}}_{3}}} \right), \\ \end{gathered} $Здесь ${{{{\sigma }}}_{{ii}}},{{{{\sigma }}}_{{ij}}},{{{{\sigma }}}_{{33}}},{{{{\sigma }}}_{{i3}}},{{{{\sigma }}}_{{3{\kern 1pt} i}}},{{{{\mu }}}_{{ii}}},{{{{\mu }}}_{{ij}}},{{{{\mu }}}_{{33}}},{{{{\mu }}}_{{i3}}},{{{{\mu }}}_{{3{\kern 1pt} i}}}$ – компоненты силового и моментного тензоров напряжений; $E,v,$ ${{\mu }} = \frac{E}{{2(1 + v)}}$, ${{\alpha }},{{\beta }},{{\gamma }},{{\varepsilon }}$ – физические константы микрополярного материала пластинки, ${{\rho }}$ – плотность материала, $J$ – момент инерции при повороте, $i,j = 1,2;\,\,i \ne j$.
Из геометрических соотношений (10) можно, в частности, получить приведенные выше соотношения (6) и (7) в декартовых координатах, если принять ${{H}_{1}} = {{H}_{2}} = 1$.
Для граничных условий на лицевых поверхностях пластинки примем граничные условия первой граничной задачи микрополярной теории упругости с независимыми полями перемещений и вращений:
(11)
${{{{\sigma }}}_{{3n}}} = p_{n}^{ \pm },\,\,\,\,{{{{\mu }}}_{{3n}}} = m_{n}^{ \pm }\,\,\,\,{\text{при}}\,\,\,\,z = \pm h{\text{ ,}}\,\,\,\,n = 1,2,3,$Граничные условия на боковой поверхности пластинки $\Sigma = {{\Sigma }_{{\text{1}}}} \cup {{\Sigma }_{{\text{2}}}}$, в зависимости от способа приложения внешней нагрузки или закрепления, запишутся либо в силовых и моментных напряжениях, либо в перемещениях и поворотах, либо в смешанном виде:
(12)
$\begin{gathered} {{\sigma }_{{mn}}}{{n}_{m}} = p_{n}^{ * },\,\,\,\,{{\mu }_{{mn}}}{{n}_{m}} = m_{n}^{*}\,\,\,\,{\text{на}}\,\,\,\,{{\Sigma }_{1}}; \\ {{V}_{n}} = V_{n}^{\centerdot },\,\,\,\,{{\omega }_{n}} = \omega _{n}^{\centerdot }\,\,\,\,{\text{на}}\,\,\,\,{{\Sigma }_{2}},\,\,\,m,n = 1,2,3, \\ \end{gathered} $При помощи начальных условий при $t = 0$ задаются значения компонентов векторов перемещения, независимого поворота, линейной и вращательной скоростей точек тела, т.е. ${{V}_{n}},\,\,{{{{\omega }}}_{n}},\,\,\frac{{\partial {{V}_{n}}}}{{\partial t}},\,\,\frac{{\partial {{{{\omega }}}_{n}}}}{{\partial t}}.$
Отметим, что, обобщая вышеприведенный подход, аналогично могут быть получены основные уравнения геометрически нелинейной трехмерной теории микрополярных упругих пологих оболочек с независимыми полями перемещений и вращений.
ГЕОМЕТРИЧЕСКИ НЕЛИНЕЙНАЯ ПРИКЛАДНАЯ МОДЕЛЬ МИКРОПОЛЯРНЫХ УПРУГИХ ПЛАСТИН ПРИ БОЛЬШИХ ПРОГИБАХ
Для приведения геометрически нелинейной трехмерной задачи микрополярной теории упругости к двумерной, будем основывать предлагаемую теорию микрополярных упругих тонких гибких пластин на следующих положениях: 1) основные гипотезы прикладной линейной теории тонких пластин (работы [12–17] ); 2) предположения нелинейной классической теории гибких пластин Кармана [1] ). Далее эти положения расписаны более подробно.
1. Нормальный элемент, первоначально перпендикулярный к срединной плоскости пластинки, остается после деформации прямолинейным, свободно поворачивается на некоторый угол, не изменяя при этом своей длины. При этом, тангенциальные компоненты вектора свободного поворота – постоянные функции по толщине пластинки, а нормальная компонента – линейная функция.
Вследствие этого имеем следующий закон изменения перемещений и свободных поворотов по толщине пластинки:
(13)
$\begin{gathered} {{V}_{i}} = {{u}_{i}}({{{{\alpha }}}_{1}},{{{{\alpha }}}_{2}},t) + z{{{{\psi }}}_{i}}({{{{\alpha }}}_{1}},{{{{\alpha }}}_{2}},t), \\ {{{{\omega }}}_{i}} = {{\Omega }_{i}}({{{{\alpha }}}_{1}},{{{{\alpha }}}_{2}},t),\,\,\,\,\left( {i = 1,2} \right), \\ \end{gathered} $(14)
${{V}_{3}} = w({{{{\alpha }}}_{1}},{{{{\alpha }}}_{2}},t),\,\,\,\,{{{{\omega }}}_{3}} = {{\Omega }_{3}}({{{{\alpha }}}_{1}},{{{{\alpha }}}_{2}},t) + z\iota ({{{{\alpha }}}_{1}},{{{{\alpha }}}_{2}},t),$2. Будем считать, что пластинка получает большие прогибы $w$, и в то же время будем считать перемещения ${{u}_{1}},{{u}_{2}}$ в срединной плоскости пластинки величинами малыми. Такое же допущение сделаем по отношению к производным $\frac{{\partial {{u}_{1}}}}{{\partial {{{{\alpha }}}_{1}}}},\,\,\frac{{\partial {{u}_{2}}}}{{\partial {{{{\alpha }}}_{1}}}},$ $\frac{{\partial {{u}_{1}}}}{{\partial {{{{\alpha }}}_{2}}}},\,\,\frac{{\partial {{u}_{2}}}}{{\partial {{{{\alpha }}}_{2}}}}$, считая их малыми по сравнению с величинами $\frac{{\partial w}}{{\partial {{\alpha }_{1}}}},\,\,\frac{{\partial w}}{{\partial {{\alpha }_{2}}}}$. Будем также считать, что квадраты производных $\frac{{\partial w}}{{\partial {{{{\alpha }}}_{1}}}},\,\,\frac{{\partial w}}{{\partial {{{{\alpha }}}_{2}}}}$ имеют тот же порядок малости, что и первая степень производных от перемещений ${{u}_{1}},{{u}_{2}}$ по ${{{{\alpha }}}_{1}}$ и ${{{{\alpha }}}_{2}}$.
Предположим также, что малы как углы поворота нормалей к срединной плоскости до деформации, так и их свободные повороты, а также в тензоре деформации учитываются нелинейные слагаемые в градиентах перемещения.
3. В физических соотношениях для ${{{{\gamma }}}_{{11}}}$ и ${{{{\gamma }}}_{{22}}}$ можно пренебрегать силовым напряжением ${{{{\sigma }}}_{{33}}}$ по сравнению с силовыми напряжениями ${{{{\sigma }}}_{{ii}}}$.
4. При определении деформаций, изгибов-кручений, силовых и моментных напряжений, для силовых напряжений ${{{{\sigma }}}_{{3i}}}$ и моментного напряжения ${{{{\mu }}}_{{33}}}$ сначала примем:
(15)
${{{{\sigma }}}_{{3i}}} = {{\mathop {{\sigma }}\limits^0 }_{{3i}}}({{{{\alpha }}}_{1}},{{{{\alpha }}}_{2}},t),\,\,\,\,{{{{\mu }}}_{{33}}} = {{\mathop {{\mu }}\limits^0 }_{{33}}}({{{{\alpha }}}_{1}},{{{{\alpha }}}_{2}},t).$После определения указанных выше величин, значения (15) для ${{{{\sigma }}}_{{3i}}}$ и ${{{{\mu }}}_{{33}}}$ уточняем, прибавляя к (15) результаты интегрирования по z уравнений движения для ${{{{\sigma }}}_{{3i}}}$ и ${{{{\mu }}}_{{33}}}$, с условием, чтобы их усредненные по толщине пластинки величины были равны нулю.
Легко показать, что компоненты тензоров деформации и изгиба-кручения будут выражаться формулами:
(16)
$\begin{gathered} {{{{\gamma }}}_{{ii}}} = {{\Gamma }_{{ii}}} + z{{K}_{{ii}}},\,\,\,\,{{{{\gamma }}}_{{ij}}} = {{\Gamma }_{{ij}}} + z{{K}_{{ij}}}, \\ {{{{\gamma }}}_{{i3}}} = {{\Gamma }_{{i3}}},\,\,\,\,{{{{\gamma }}}_{{3i}}} = {{\Gamma }_{{3i}}},\,\,\,\,{{{{\chi }}}_{{ii}}} = {{\kappa }_{{ii}}}, \\ {{{{\chi }}}_{{33}}} = \iota ,\,\,\,\,{{{{\chi }}}_{{ij}}} = {{\kappa }_{{ij}}},\,\,\,\,{{{{\chi }}}_{{i3}}} = {{\kappa }_{{i3}}} + z{{l}_{{i3}}}. \\ \end{gathered} $Здесь ${{\Gamma }_{{ii}}}$ – деформации удлинений в направлениях ${{x}_{1}},{{x}_{2}}$; ${{\Gamma }_{{ij}}},{{\Gamma }_{{i3}}},{{\Gamma }_{{3i}}}$ – деформации сдвигов в соответствующих плоскостях; ${{K}_{{ii}}}$ – изгибы срединной плоскости, обусловленные силовыми напряжениями; ${{K}_{{ij}}}$ – кручения срединной плоскости, обусловленные силовыми напряжениями; ${{\kappa }_{{ii}}},{{\kappa }_{{33}}}$ – изгибы срединной плоскости, обусловленные моментными напряжениями; ${{\kappa }_{{ij}}}$ – кручения срединной плоскости, обусловленные моментными напряжениями; ${{l}_{{i3}}}$ – гиперсдвиги срединной плоскости, обусловленные моментными напряжениями.
Как обычно принято в прикладных теориях тонких пластин, вместо компонент тензоров силовых и моментных напряжений вводим статически эквивалентные им интегральные характеристики: усилия $\left( {{{T}_{{ii}}},{{S}_{{ij}}},{{N}_{{i3}}},{{N}_{{3i}}}} \right)$, моменты $\left( {{{M}_{{ii}}},{{H}_{{ij}}},} \right.$ ${{L}_{{ii}}},{{L}_{{ij}}},\left. {{{L}_{{i3}}},{{L}_{{33}}}} \right)$ и гипермоменты $\left( {{{\Lambda }_{{i3}}}} \right)$ [12–17] :
(17)
$\begin{gathered} {{T}_{{ii}}} = \int\limits_{ - h}^h {{{{{\sigma }}}_{{ii}}}} dz,\,\,\,\,{{S}_{{ij}}} = \int\limits_{ - h}^h {{{{{\sigma }}}_{{ij}}}} dz, \\ {{N}_{{i3}}} = \int\limits_{ - h}^h {{{{{\sigma }}}_{{i3}}}} dz{\text{ }}(i \leftrightarrow 3),\,\,\,\,{{М}_{{ii}}} = \int\limits_{ - h}^h {{{{{\sigma }}}_{{ii}}}} zdz, \\ {{M}_{{ij}}} = \int\limits_{ - h}^h {{{{{\sigma }}}_{{ij}}}} zdz,\,\,\,{{L}_{{mn}}} = \int\limits_{ - h}^h {{{{{\mu }}}_{{mn}}}} dz, \\ (m,n = 1,2,3),\,\,\,\,{{\Lambda }_{{i3}}} = \int\limits_{ - h}^h {z{{{{\mu }}}_{{i3}}}} dz. \\ \end{gathered} $Основные уравнения динамики геометрически нелинейных микрополярных упругих тонких пластин со свободным вращением в криволинейных координатах срединной плоскости (${{H}_{i}} = {{A}_{i}}$ для тонких пластин) с учетом всех перечисленных выше предположений о вращательно-сдвиговых деформациях, составляют приведенную ниже систему.
Уравнения движения:
(18)
$\begin{gathered} + \,\,\frac{{\partial w}}{{\partial {{{{\alpha }}}_{2}}}}\left[ {\frac{{{{A}_{1}}}}{{{{A}_{2}}}}\frac{{\partial {{T}_{{22}}}}}{{\partial {{{{\alpha }}}_{2}}}} - \frac{{{{A}_{1}}}}{{A_{2}^{2}}}\frac{{\partial {{A}_{2}}}}{{\partial {{{{\alpha }}}_{2}}}}{{T}_{{22}}} + } \right. \\ \left. {\left. { + \,\,\frac{1}{{{{A}_{2}}}}\frac{{\partial {{A}_{1}}}}{{\partial {{{{\alpha }}}_{2}}}}{{T}_{{22}}} + \frac{1}{2}\frac{{\partial \left( {{{S}_{{12}}} + {{S}_{{21}}}} \right)}}{{\partial {{{{\alpha }}}_{1}}}}} \right]} \right\} = \\ \end{gathered} $Физические соотношения теории упругости:
Геометрические соотношения:
(20)
$\begin{gathered} {{\Gamma }_{{i3}}} = \frac{1}{{{{A}_{i}}}}\frac{{\partial w}}{{\partial {{{{\alpha }}}_{i}}}} + {{\left( { - 1} \right)}^{j}}{{\Omega }_{j}},\,\,\,\,{{\Gamma }_{{3i}}} = {{{{\psi }}}_{i}} - {{\left( { - 1} \right)}^{j}}{{\Omega }_{j}}, \\ {{K}_{{ii}}} = \frac{1}{{{{A}_{i}}}}\frac{{\partial {{\psi }_{i}}}}{{\partial {{{{\alpha }}}_{i}}}} + \frac{1}{{{{A}_{i}}{{A}_{j}}}}\frac{{\partial {{A}_{i}}}}{{\partial {{{{\alpha }}}_{j}}}}{{{{\psi }}}_{j}}, \\ \end{gathered} $Граничные условия, например, шарнирного опирания выражаются так:
(21)
$\begin{gathered} {{T}_{{ii}}} = 0,\,\,\,\,{{u}_{j}} = 0,\,\,\,\,{{M}_{{ii}}} = 0,\,\,\,\,{{{{\psi }}}_{j}} = 0, \\ w = 0,\,\,\,\,{{L}_{{ij}}} = 0,\,\,\,\,{{\Omega }_{i}} = 0, \\ {{\Lambda }_{{i3}}} = 0,\,\,\,\,{\text{при}}\,\,\,\,{{x}_{i}} = 0;a. \\ \end{gathered} $К системе основных уравнений динамики микрополярных пластин со свободным вращением (18)–(20) и граничным условиям (21) необходимо присоединить также соответствующие начальные условия для $w,{{\partial w} \mathord{\left/ {\vphantom {{\partial w} {\partial t}}} \right. \kern-0em} {\partial t}}$, ${{{{\psi }}}_{i}},{{\partial {{{{\psi }}}_{i}}} \mathord{\left/ {\vphantom {{\partial {{{{\psi }}}_{i}}} {\partial t}}} \right. \kern-0em} {\partial t}}$, ${{\Omega }_{i}},{{\partial {{\Omega }_{i}}} \mathord{\left/ {\vphantom {{\partial {{\Omega }_{i}}} {\partial t}}} \right. \kern-0em} {\partial t}}$, $\iota ,{{\partial \iota } \mathord{\left/ {\vphantom {{\partial \iota } {\partial t}}} \right. \kern-0em} {\partial t}}$.
Отметим, что аналогичный подход применен также для построения геометрически нелинейной прикладной модели микрополярных упругих тонких пологих оболочек.
СОБСТВЕННЫЕ КОЛЕБАНИЯ МИКРОПОЛЯРНЫХ УПРУГИХ ПРЯМОУГОЛЬНЫХ ПЛАСТИН ПРИ БОЛЬШИХ ПРОГИБАХ
В случае прямоугольной пластинки в основных уравнениях примем ${{A}_{1}} = {{A}_{2}} = 1$. Далее будем пренебрегать всеми инерционными членами в уравнениях движения, кроме $2{{\rho }}h\frac{{{{\partial }^{2}}w}}{{\partial {{t}^{2}}}}$.
Решение граничной задачи (18)–(21) при изучении собственных колебаний представим в виде:
(22)
$\begin{gathered} {{{{\psi }}}_{1}}({{x}_{1}},{{x}_{2}},t) = {{{{\psi }}}_{1}}(t)\cos \frac{{{{\pi }}{{x}_{1}}}}{a}\sin \frac{{{{\pi }}{{x}_{2}}}}{b}, \\ {{{{\psi }}}_{2}}({{x}_{1}},{{x}_{2}},t) = {{{{\psi }}}_{2}}(t)\sin \frac{{{{\pi }}{{x}_{1}}}}{a}\cos \frac{{{{\pi }}{{x}_{2}}}}{b}, \\ {{\Omega }_{1}}({{x}_{1}},{{x}_{2}},t) = {{\Omega }_{1}}(t)\sin \frac{{{{\pi }}{{x}_{1}}}}{a}\cos \frac{{{{\pi }}{{x}_{2}}}}{b}, \\ \end{gathered} $Решение (22) удовлетворяет граничным условиям (21). Подставим эти представления в геометрические соотношения (20). Подставляя далее получившиеся выражения для деформаций и изгибов-кручений в физические соотношения (19), найдем выражения для усилий, моментов и гипермоментов. Применяя метод Галеркина для систем уравнений движения (18), получим:
(23)
$\begin{gathered} \int\limits_0^a {\int\limits_0^b {\left( {{{N}_{{31}}} - \left( {\frac{{\partial {{M}_{{11}}}}}{{\partial {{x}_{1}}}} + \frac{{\partial {{M}_{{21}}}}}{{\partial {{x}_{2}}}}} \right)} \right)} } \times \\ \times \,\,\cos \frac{{\pi {{x}_{1}}}}{a}\sin \frac{{\pi {{x}_{2}}}}{b}d{{x}_{1}}d{{x}_{2}} = 0, \\ \int\limits_0^a {\int\limits_0^b {\left( {{{N}_{{32}}} - \left( {\frac{{\partial {{M}_{{22}}}}}{{\partial {{x}_{2}}}} + \frac{{\partial {{M}_{{12}}}}}{{\partial {{x}_{1}}}}} \right)} \right)} } \times \\ \times \,\,\sin \frac{{\pi {{x}_{1}}}}{a}\cos \frac{{\pi {{x}_{2}}}}{b}d{{x}_{1}}d{{x}_{2}} = 0, \\ \int\limits_0^a {\int\limits_0^b {\left( {\frac{{\partial {{L}_{{11}}}}}{{\partial {{x}_{1}}}} + \frac{{\partial {{L}_{{21}}}}}{{\partial {{x}_{2}}}} + \left( {{{N}_{{23}}} - {{N}_{{32}}}} \right)} \right)} } \times \\ \times \,\,\sin \frac{{\pi {{x}_{1}}}}{a}\cos \frac{{\pi {{x}_{2}}}}{b}d{{x}_{1}}d{{x}_{2}} = 0, \\ \end{gathered} $Выполним интегрирование и представим функции $w(t),\,{{u}_{1}}(t),$ ${{u}_{2}}(t),\,{{{{\psi }}}_{1}}(t),\,{{{{\psi }}}_{2}}(t),$ ${{\Omega }_{1}}(t),$${{\Omega }_{2}}(t),\,{{\Omega }_{3}}(t),\,\iota (t)$ в виде:
(24)
$\begin{gathered} w(t) = W\cos (pt),\,\,\,\,{{u}_{i}}(t) = {{U}_{i}}\cos (pt), \\ {{{{\psi }}}_{i}}(t) = {{\Psi }_{i}}\cos (pt),\,\,\,\,{{\Omega }_{i}}(t) = {{O}_{i}}\cos (pt), \\ {{\Omega }_{3}}(t) = {{O}_{3}}\cos (pt),\,\,\,\,\iota (t) = I\cos (pt). \\ \end{gathered} $Подставим эти функции в полученные уравнения, умножим их на $\cos (pt)$ и проинтегрируем по t от 0 до $\frac{{{\pi }}}{{2p}}$. В результате получим систему алгебраических уравнений относительно коэффициентов $W,\,\,{{U}_{1}},\,\,{{U}_{2}},\,\,{{\Psi }_{1}},\,\,{{\Psi }_{2}},$ ${{O}_{1}},\,\,{{O}_{2}},\,\,{{O}_{3}},\,\,I$. Из этой системы можно получить зависимость $W{\kern 1pt} - {\kern 1pt} p$.
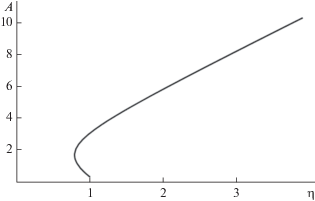
Эта задача решена также в рамках соответствующей линейной модели микрополярных упругих тонких пластин. Введем безразмерный прогиб $A = {W \mathord{\left/ {\vphantom {W h}} \right. \kern-0em} h},$ а также величину ${{\eta }} = {p \mathord{\left/ {\vphantom {p {{{p}_{0}}}}} \right. \kern-0em} {{{p}_{0}}}}$ – отношение величины $p$ к соответствующей частоте линейных колебаний ${{p}_{0}}$.
Численные расчеты выполнены для квадратной пластинки с размерами $b = a = 0.005$ м; относительная толщина принята равной $\delta = \frac{h}{a} = \frac{1}{{100}}$. Для физических постоянных приняты значения [19] ${{\alpha }} = 0.115 \times {{10}^{9}}$ Па, ${{\mu }} = 1.033 \times {{10}^{9}}$ Па, ${{\lambda }} = 2.1951 \times {{10}^{9}}$ Па, ${{\gamma }} = 4.1$ Н, ${{\varepsilon }} = 0.13$ Н, ${{\beta }} = - 2.34$ Н, ${{\rho }} = 590\,\,{{{\text{кг}}} \mathord{\left/ {\vphantom {{{\text{кг}}} {{{{\text{м}}}^{3}}}}} \right. \kern-0em} {{{{\text{м}}}^{3}}}}$, $J = 5.31 \times {{10}^{{ - 6}}}\,\,{{{\text{кг}}} \mathord{\left/ {\vphantom {{{\text{кг}}} {\text{м}}}} \right. \kern-0em} {\text{м}}}$. На рис. 1 приведена зависимость $({{\eta }},A)$, эта линия называется скелетной кривой, которая отражает основные свойства деформируемой системы [3] . Кривая $({{\eta }},A)$ представляет линию жесткого типа, т.е. с увеличением амплитуды частота возрастает. При весьма малых амплитудах имеем ${{\eta }} \to 1$. С увеличением амплитуды частота колебаний возрастает, и притом все более и более резко.
На рис. 2 приведена зависимость прогиба прямоугольной пластинки $W$от частоты $p$. Пунктирная линия соответствует классической модели, а непрерывная линия – микрополярной модели. При наличии зависимости $W{\kern 1pt} - {\kern 1pt} p$ (в размерных величинах), рис. 2 можно использовать для сравнения микрополярного и классического случаев. Видно, что при значениях частот от 3709 до 5287 с–1 в классическом случае имеются колебания, а в микрополярном – нет. Когда колебания имеют место в обоих случаях (при 5500 с–1), перемещение в микрополярном случае в $ \approx {\kern 1pt} 2.7$ раз меньше, чем в классическом случае. Это означает, что при прочих равных условиях в микрополярном случае пластинка более жесткая, чем в классическом.
СОБСТВЕННЫЕ КОЛЕБАНИЯ МИКРОПОЛЯРНЫХ УПРУГИХ КРУГЛЫХ ПЛАСТИН ПРИ БОЛЬШИХ ПРОГИБАХ
В случае круглой пластинки в основных уравнениях (18)–(20) примем ${{A}_{1}} = 1,\,\,{{A}_{2}} = r$. Тогда получим следующую, приведенную ниже систему уравнений.
Уравнения движения:
(25)
$\begin{gathered} + \,\,\frac{{\partial w}}{{\partial {{\theta }}}}\left[ {\frac{1}{{{{r}^{2}}}}\frac{{\partial {{T}_{{22}}}}}{{\partial {{\theta }}}} + \frac{1}{r}{{T}_{{11}}} + \frac{1}{{2r}}\frac{{\partial \left( {{{S}_{{12}}} + {{S}_{{21}}}} \right)}}{{\partial r}}} \right] = 2{{\rho }}h\frac{{{{\partial }^{2}}w}}{{\partial {{t}^{2}}}}{\text{,}} \\ \frac{{\partial {{L}_{{11}}}}}{{\partial r}} + \frac{1}{r}({{L}_{{11}}} - {{L}_{{22}}}) + \frac{1}{r}\frac{{\partial {{L}_{{21}}}}}{{\partial {{\theta }}}} + \\ + \,\,{{N}_{{23}}} - {{N}_{{32}}} = 2Jh\frac{{{{\partial }^{2}}{{\Omega }_{1}}}}{{\partial {{t}^{2}}}},\,\,\,\, \\ \frac{{\partial {{L}_{{12}}}}}{{\partial r}} + \frac{1}{r}\frac{{\partial {{L}_{{22}}}}}{{\partial {{\theta }}}} + \,\,\frac{1}{r}({{L}_{{12}}} + {{L}_{{21}}}) + {{N}_{{31}}} - {{N}_{{13}}} = 2Jh\frac{{{{\partial }^{2}}{{\Omega }_{2}}}}{{\partial {{t}^{2}}}}, \\ \frac{{\partial {{L}_{{13}}}}}{{\partial r}} + \frac{1}{r}{{L}_{{13}}} + \frac{1}{r}\frac{{\partial {{L}_{{23}}}}}{{\partial {{\theta }}}} + ({{S}_{{12}}} - {{S}_{{21}}}) = 2Jh\frac{{{{\partial }^{2}}{{\Omega }_{3}}}}{{\partial {{t}^{2}}}}, \\ \end{gathered} $Физико-геометрические соотношения:
(26)
$\begin{gathered} {{N}_{{31}}} = 2h\left[ {({{\mu }} + {{\alpha }}){{{{\psi }}}_{1}} + ({{\mu }} - {{\alpha }})\frac{{\partial w}}{{\partial r}} - 2{{\alpha }}{{\Omega }_{2}}} \right], \\ \\ {{N}_{{32}}} = 2h\left[ {({{\mu }} + {{\alpha }}){{{{\psi }}}_{2}} + ({{\mu }} - {{\alpha }})\frac{1}{r}\frac{{\partial w}}{{\partial {{\theta }}}} + 2{{\alpha }}{{\Omega }_{1}}} \right], \\ \\ {{M}_{{11}}} = \frac{{2E{{h}^{3}}}}{{3\left( {1 - {{v}^{2}}} \right)}}\left[ {\frac{{\partial {{{{\psi }}}_{1}}}}{{\partial r}} + v\left( {\frac{1}{r}\frac{{\partial {{{{\psi }}}_{2}}}}{{\partial {{\theta }}}} + \frac{1}{r}{{{{\psi }}}_{1}}} \right)} \right], \\ \\ {{M}_{{22}}} = \frac{{2E{{h}^{3}}}}{{3\left( {1 - {{v}^{2}}} \right)}}\left[ {\frac{1}{r}\frac{{\partial {{{{\psi }}}_{2}}}}{{\partial {{\theta }}}} + \frac{1}{r}{{{{\psi }}}_{1}} + v\frac{{\partial {{{{\psi }}}_{1}}}}{{\partial r}}} \right], \\ {{M}_{{12}}} = \frac{{2{{h}^{3}}}}{3}\left[ {({{\mu }} + {{\alpha }})\frac{{\partial {{{{\psi }}}_{2}}}}{{\partial r}} + } \right. \\ \end{gathered} $Задаются граничные условия следующего вида:
(27)
$\begin{gathered} {{T}_{{11}}} = T_{{11}}^{0},\,\,\,\,{{S}_{{12}}} = S_{{12}}^{0},\,\,\,\,{{M}_{{11}}} = M_{{11}}^{0},\,\,\,\,{{M}_{{12}}} = M_{{12}}^{0}, \\ {{T}_{{11}}}\frac{{\partial w}}{{\partial r}} + \frac{{{{S}_{{12}}} + {{S}_{{21}}}}}{2}\frac{1}{r}\frac{{\partial w}}{{\partial {{\theta }}}} + {{N}_{{13}}} = N_{{13}}^{0}, \\ {{L}_{{11}}} = L_{{11}}^{0},\,\,\,\,{{L}_{{12}}} = L_{{12}}^{0},\,\,\,\,{{\Lambda }_{{13}}} = \Lambda _{{13}}^{0}. \\ \end{gathered} $Рассмотрим осесимметричную задачу. В этом случае уравнения расщепляются на две отдельные системы уравнений: задачу изгиба и задачу кручения круглой пластинки.
В случае задачи изгиба получаем следующую систему уравнений.
Уравнения движения:
(28)
$\begin{gathered} \frac{{\partial {{N}_{{13}}}}}{{\partial r}} + \frac{1}{r}{{N}_{{13}}} + \frac{1}{r}\frac{\partial }{{\partial r}}\left( {r{{T}_{{11}}}\frac{{\partial w}}{{\partial r}}} \right) = 2{{\rho }}h\frac{{{{\partial }^{2}}w}}{{\partial {{t}^{2}}}}, \\ {{N}_{{31}}} - \left( {\frac{{\partial {{M}_{{11}}}}}{{\partial r}} + \frac{1}{r}\left( {{{M}_{{11}}} - {{M}_{{22}}}} \right)} \right) + \frac{{2{{\rho }}{{h}^{3}}}}{3}\frac{{{{\partial }^{2}}{{{{\psi }}}_{1}}}}{{\partial {{t}^{2}}}} = 0, \\ \frac{{\partial {{L}_{{12}}}}}{{\partial r}} + \frac{1}{r}\left( {{{L}_{{12}}} + {{L}_{{21}}}} \right) + {{N}_{{31}}} - {{N}_{{13}}} = 2Jh\frac{{{{\partial }^{2}}{{\Omega }_{2}}}}{{\partial {{t}^{2}}}}, \\ \frac{{\partial {{T}_{{11}}}}}{{\partial r}} + \frac{1}{r}\left( {{{T}_{{_{{11}}}}} - {{T}_{{22}}}} \right) = 2{{\rho }}h\frac{{{{\partial }^{2}}{{u}_{1}}}}{{\partial {{t}^{2}}}}. \\ \end{gathered} $Физико-геометрические соотношения:
(29)
$\begin{gathered} {{T}_{{11}}} = \frac{{2Eh}}{{1 - {{v}^{2}}}}\left[ {\frac{{\partial {{u}_{1}}}}{{\partial r}} + \frac{1}{2}{{{\left( {\frac{{\partial w}}{{\partial r}}} \right)}}^{2}} + v\frac{1}{r}{{u}_{1}}} \right], \\ {{T}_{{22}}} = \frac{{2Eh}}{{1 - {{v}^{2}}}}\left[ {\frac{1}{r}{{u}_{1}} + v\left( {\frac{{\partial {{u}_{1}}}}{{\partial r}} + \frac{1}{2}{{{\left( {\frac{{\partial w}}{{\partial r}}} \right)}}^{2}}} \right)} \right], \\ {{M}_{{11}}} = \frac{{2E{{h}^{3}}}}{{3(1 - {{v}^{2}})}}\left[ {\frac{{\partial {{{{\psi }}}_{1}}}}{{\partial r}} + v\frac{1}{r}{{{{\psi }}}_{1}}} \right], \\ {{M}_{{22}}} = \frac{{2E{{h}^{3}}}}{{3(1 - {{v}^{2}})}}\left[ {\frac{1}{r}{{{{\psi }}}_{1}} + v\frac{{\partial {{{{\psi }}}_{1}}}}{{\partial r}}} \right], \\ {{L}_{{12}}} = 2h\left[ {({{\gamma }} + {{\varepsilon }})\frac{{\partial {{\Omega }_{2}}}}{{\partial r}} - ({{\gamma }} - {{\varepsilon }})\frac{1}{r}{{\Omega }_{2}}} \right], \\ {{L}_{{21}}} = 2h\left[ { - ({{\gamma }} + {{\varepsilon }})\frac{1}{r}{{\Omega }_{2}} + ({{\gamma }} - {{\varepsilon }})\frac{{\partial {{\Omega }_{2}}}}{{\partial r}}} \right], \\ {{N}_{{13}}} = 2h\left[ {({{\mu }} + {{\alpha }})\frac{{\partial w}}{{\partial r}} + ({{\mu }} - {{\alpha }}){{{{\psi }}}_{1}} + 2{{\alpha }}{{\Omega }_{2}}} \right], \\ {{N}_{{31}}} = 2h\left[ {({{\mu }} + {{\alpha }}){{{{\psi }}}_{1}} + ({{\mu }} - {{\alpha }})\frac{{\partial w}}{{\partial r}} - 2{{\alpha }}{{\Omega }_{2}}} \right]. \\ \end{gathered} $Задаются граничные условия шарнирного опирания:
(30)
$w = 0,\,\,\,\,{{M}_{{{\text{11}}}}} = 0,\,\,\,\,{{L}_{{12}}} = 0,\,\,\,\,{\text{когда}}\,\,\,\,r = R.$В случае задачи кручения получаем следующую систему уравнений.
Уравнения движения:
(31)
$\begin{gathered} \frac{{\partial {{S}_{{12}}}}}{{\partial r}} + \frac{1}{r}\left( {{{S}_{{_{{12}}}}} + {{S}_{{21}}}} \right) = 2{{\rho }}h\frac{{{{\partial }^{2}}{{u}_{2}}}}{{\partial {{t}^{2}}}}, \\ \frac{{\partial {{L}_{{13}}}}}{{\partial r}} + \frac{1}{r}{{L}_{{13}}} + \left( {{{S}_{{_{{12}}}}} - {{S}_{{21}}}} \right) = 2Jh\frac{{{{\partial }^{2}}{{\Omega }_{3}}}}{{\partial {{t}^{2}}}}, \\ {{N}_{{32}}} - \left( {\frac{{\partial {{M}_{{12}}}}}{{\partial r}} + \frac{1}{r}\left( {{{M}_{{12}}} + {{M}_{{21}}}} \right)} \right) + \frac{{2{{\rho }}{{h}^{3}}}}{3}\frac{{{{\partial }^{2}}{{{{\psi }}}_{1}}}}{{\partial {{t}^{2}}}} = 0, \\ \frac{{\partial {{L}_{{11}}}}}{{\partial r}} + \frac{1}{r}\left( {{{L}_{{11}}} - {{L}_{{22}}}} \right) + {{N}_{{23}}} - {{N}_{{32}}} = 2Jh\frac{{{{\partial }^{2}}{{\Omega }_{1}}}}{{\partial {{t}^{2}}}}, \\ {{L}_{{33}}} - \frac{{\partial {{\Lambda }_{{13}}}}}{{\partial r}} - \left( {{{M}_{{12}}} - {{M}_{{21}}}} \right) + \frac{{2{{\rho }}{{h}^{3}}}}{3}\frac{{{{\partial }^{2}}\iota }}{{\partial {{t}^{2}}}} = 0. \\ \end{gathered} $Физико-геометрические соотношения:
Граничные условия шарнирного опирания:
(33)
${{\Omega }_{1}} = 0,\,\,\,\,{{{{\psi }}}_{2}} = 0,\,\,\,\,{{\Lambda }_{{13}}} = 0,\,\,\,\,{\text{когда}}\,\,\,\,r = R.$Далее рассмотрим задачу изгиба (28)–(30). Будем также пренебрегать всеми инерционными членами в уравнениях движения, кроме $2{{\rho }}h\frac{{{{\partial }^{2}}w}}{{\partial {{t}^{2}}}}$.
Решение граничной задачи (28)–(30) при изучении собственных колебаний представим в виде:
Решение (34) уже удовлетворяет граничным условиям (30). Подставим эти представления в геометрические соотношения (29). Получившиеся выражения для деформаций и изгибов-кручений подставим в физические соотношения и найдем выражения для усилий, моментов и гипермоментов. Применяя метод Галеркина для системы уравнений движения (28), получим:
Выполним интегрирование и затем функции $w(t),\,\,{{u}_{1}}(t),\,\,{{{{\psi }}}_{1}}(t),$ ${{\Omega }_{2}}(t)$ представим в виде:
(36)
$\begin{gathered} w(t) = W\cos (pt),\,\,\,\,{{u}_{1}}(t) = {{U}_{1}}\cos (pt){\text{,}} \\ {{{{\psi }}}_{1}}(t) = {{\Psi }_{1}}\cos (pt),\,\,\,\,{{\Omega }_{2}}(t) = {{O}_{2}}\cos (pt). \\ \end{gathered} $Подставим эти функции в полученные уравнения, умножим их на $\cos \left( {pt} \right)$ и проинтегрируем по t от 0 до $\frac{{{\pi }}}{{2p}}$. В результате получим систему алгебраических уравнений относительно коэффициентов $W,{{U}_{1}},{{\Psi }_{1}},{{O}_{2}}$, из которой можно получить зависимость $W{\kern 1pt} - {\kern 1pt} p$. Введем далее такие же обозначения, как и в случае прямоугольной пластинки.
Проведем численный анализ для вышеприведенного материала, а для геометрических размеров примем: радиус пластинки $R = 0.005$ м, относительная толщина ${{\delta }} = \frac{h}{R} = \frac{1}{{100}}$. На рис. 3 приведена зависимость $({{\eta }},A)$. Кривая $({{\eta }},A)$, как и в предыдущем случае, также представляет линию жесткого типа, т.е. с увеличением амплитуды частота возрастает. При весьма малых амплитудах имеем ${{\eta }} \to 1$. С увеличением амплитуды частота колебаний возрастает, и притом все более и более резко. При сравнении микрополярного и классического случаев зависимости $W{\kern 1pt} - {\kern 1pt} p$, можно сделать те же выводы, что имели место в случае прямоугольной пластинки.
СОБСТВЕННЫЕ КОЛЕБАНИЯ МИКРОПОЛЯРНЫХ УПРУГИХ ПОЛОГИХ ОБОЛОЧЕК ПРИ БОЛЬШИХ ПРОГИБАХ
Теперь решим также задачу свободных колебаний для микрополярных упругих тонких пологих оболочек прямоугольных в плане с шарнирно опертыми краями. Будем исходить из основных уравнений модели пологих оболочек. Здесь также будем пренебрегать всеми инерционными членами в уравнениях движения, кроме $2{{\rho }}h\frac{{{{\partial }^{2}}w}}{{\partial {{t}^{2}}}}$. Решение граничной задачи при изучении собственных колебаний также представим в виде (22).
Решение (22) уже удовлетворяет граничным условиям шарнирного опирания. Применяя метод Галеркина для систем уравнений движения, получим:
(37)
$\begin{gathered} \int\limits_0^a {\int\limits_0^b {\left( {{{N}_{{31}}} - \left( {\frac{{\partial {{M}_{{11}}}}}{{\partial {{x}_{1}}}} + \frac{{\partial {{M}_{{21}}}}}{{\partial {{x}_{2}}}}} \right)} \right)} } \times \\ \times \,\,\cos \frac{{{{\pi }}{{x}_{1}}}}{a}\sin \frac{{{{\pi }}{{x}_{2}}}}{b}d{{x}_{1}}d{{x}_{2}} = 0, \\ \int\limits_0^a {\int\limits_0^b {\left( {{{N}_{{32}}} - \left( {\frac{{\partial {{M}_{{22}}}}}{{\partial {{x}_{2}}}} + \frac{{\partial {{M}_{{12}}}}}{{\partial {{x}_{1}}}}} \right)} \right)} } \times \\ \times \,\,\sin \frac{{{{\pi }}{{x}_{1}}}}{a}\cos \frac{{{{\pi }}{{x}_{2}}}}{b}d{{x}_{1}}d{{x}_{2}} = 0, \\ \int\limits_0^a {\int\limits_0^b {\left( {\frac{{\partial {{L}_{{11}}}}}{{\partial {{x}_{1}}}} + \frac{{\partial {{L}_{{21}}}}}{{\partial {{x}_{2}}}} + \left( {{{N}_{{23}}} - {{N}_{{32}}}} \right)} \right)} } \times \\ \times \,\,\sin \frac{{{{\pi }}{{x}_{1}}}}{a}\cos \frac{{{{\pi }}{{x}_{2}}}}{b}d{{x}_{1}}d{{x}_{2}} = 0, \\ \int\limits_0^a {\int\limits_0^b {\left( {\frac{{\partial {{L}_{{22}}}}}{{\partial {{x}_{2}}}} + \frac{{\partial {{L}_{{12}}}}}{{\partial {{x}_{1}}}} - \left( {{{N}_{{13}}} - {{N}_{{31}}}} \right)} \right)} } \times \\ \end{gathered} $Здесь нужно подставить выражения для физических и геометрических соотношений, а также решение вида (22).
Выполним интегрирование и представим функции $w(t),\,\,{{u}_{1}}(t),\,\,{{u}_{2}}(t),$ ${{{{\psi }}}_{1}}(t),\,\,{{{{\psi }}}_{2}}(t),$ ${{\Omega }_{1}}(t),$ ${{\Omega }_{2}}(t),\,{{\Omega }_{3}}(t),\,\iota (t)$ в виде (24). Затем подставим их в полученные в результате интегрирования уравнения, умножим на $\cos \left( {pt} \right)$ и проинтегрируем по t от 0 до $\frac{{{\pi }}}{{2p}}$. В результате получим систему алгебраических уравнений относительно коэффициентов $W,\,{{U}_{1}},\,{{U}_{2}},$ ${{\Psi }_{1}},\,{{\Psi }_{2}},$ ${{O}_{1}},\,{{O}_{2}},\,{{O}_{3}},\,I$, из которого можно получить зависимость $W{\kern 1pt} - {\kern 1pt} p$. Численный анализ проведен для того же материала и геометрических размеров, что и в случае пластинки, кроме того $R = 0.005$ м, относительная толщина ${{\delta }} = \frac{h}{R} = \frac{1}{{100}}$. Отметим, что ${{k}_{2}} = \frac{1}{{{{R}_{2}}}} = 0$, ${{k}_{1}} = \frac{1}{R}$ (т.е. рассмотрена цилиндрическая пологая оболочка, где ${{R}_{1}},{{R}_{2}}$ – радиусы кривизны по направлениям ${{\alpha }_{1}},{{\alpha }_{2}}$), а также введена безразмерная кривизна $k* = \frac{{{{a}^{2}}}}{{{{R}_{1}}h}}$ пологой оболочки и принято $k* = 20$.
На рис. 4 приведена скелетная кривая $({{\eta }},A)$ для пологой оболочки. Кривая $({{\eta }},A)$ представляет линию мягкого типа, т.е. начальный участок здесь отклоняется к оси ординат, после этого при увеличении A амплитуда возрастает все более и более резко. Такие же качественные результаты получаются для случая круглой в плане пологой оболочки.
ЗАКЛЮЧЕНИЕ
В работе построены математические модели микрополярных гибких пластин и пологих оболочек, представляющие собой обобщение известных моделей Фепеля–Кармана–Маргерра классического случая. В рамках этих моделей численно решены задачи о свободных колебаниях прямоугольных и круглых пластин и пологих оболочек. Выявлены характерные особенности эффективных свойств микрополярного материала по сравнению с соответствующим классическим материалом.
Работа выполнена при финансовой поддержке ГКН МОН РА в рамках научных проектов 18T-2C263 и 21T-2C093.
Список литературы
Karman Th. Collected works. V. 1. London, 1956. 530 p.
Marguerre K. Die Durchschlags kraft eines schwachgekrummten Balkes // Sitzungsberichte der Berliner Mathematischen Cesellschaft. 1938. Bd. 37. S. 22–40.
Вольмир А.С. Нелинейная динамика пластинок и оболочек. М.: Наука, 1972. 432 с.
Григолюк Э.И., Мамай В.И. Нелинейное деформирование тонкостенных конструкций. М.: Физматлит, 1997. 264 с.
Altenbach J., Altenbach H., Eremeyev V.A. On generalized Cosserat-type theories of plates and shells: a short review and bibliography // Arch. Appl. Mech (Special Issue). 2010. V. 80. P. 73–92. https://doi.org/10.1007/s00419-009-0365-3
Nowacki W. Theory of Asymmetric Elasticity. Oxford, etc: Pergamon Press, 1986. 383p.
Кулеш М.А., Матвеенко В.П., Шардаков И.Н. О распространении упругих поверхностных волн в среде Коссера // Акуст. журн. 2006. Т. 52. № 2. С. 227–235.
Кулеш М.А., Матвеенко В.П., Улитин М.В., Шардаков И.Н. Анализ волнового решения уравнений эластокинетики среды Коссера в случае плоских объемных волн // Прикладная механика и техническая физика. 2008. Т. 49. № 2. С. 196–203.
Ерофеев В.И. Волновые процессы в твердых телах с микроструктурой. М.: Изд-во МГУ, 1999. 328 с.
Sadovskii V., Sadovskaya O., Varigina M. Numerical solution of dynamic problems in couple-stressed continuum of multiprocessor computer systems // Int. J. Numerical Analysis and Modeling. Series B. 2011. V. 2. № 2–3. P. 215–230.
Еремеев В.А., Зубов Л.М. Механика упругих оболочек. М.: Наука, 2008. 280 с.
Саркисян С.О. Общая динамическая теория микрополярных упругих тонких оболочек // Докл. Акад. наук России. 2011. Т. 436. № 2. С. 195–198.
Sargsyan S.H. Applied theory of dynamics of micropolar elastic thin shells ad variation principles // Advanced Structured Materials. V. 103. Dynamical Processes in Generalized Continua and Structures. Springer, 2019. P. 449–465.
Саркисян С.О., Саркисян А.А. Общая динамическая теория микрополярных упругих тонких пластин со свободным вращением и особенности их свободных колебаний // Акуст. журн. 2011. Т. 57. № 4. С. 461–469.
Саркисян С.О., Саркисян А.А. Модель колебаний микрополярных тонких оболочек // Акуст. журн. 2013. Т. 59. № 2. С. 170–181.
Sargsyan A.H., Sargsyan S.H. Dynamic model of micropolar elastic thin plates with independent fields of displacements and rotations // J. Sound Vibr. 2014. V. 333. Is. 18. P. 4354–4375.
Sargsyan S.H. asymptotically confirmed hypotheses method for the construction of micropolar and classical theories of elastic thin shells // Advances in Pure Mathematics. 2015. V. 5. № 10. P. 629–643.
Новожилов В.В. Основы нелинейной теории упругости. Л., М.: ОГИЗ. Государственное издательство технико-теоретической литературы, 1948. 213 с.
Lakes R. Experimental methods for study of Cosserat elastic solids and other generalized elastic continua // Continuum models for materials with micro-structure / Ed. By Muhlhaus H., Wiley J. N. Y.: J. Wiley and sons, Ltd., 1995. Ch. 1. P. 1–22.
Дополнительные материалы отсутствуют.
Инструменты
Акустический журнал