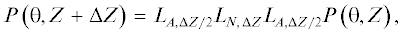1. На главную
  2. Электронные версии
  3. Акустический журнал
  4. T. 68, № 2, 2022

Акустический журнал, 2022, T. 68, № 2, стр. 152-161

Численная модель спектрального описания генерации ультразвуковой волны разностной частоты при двухчастотном взаимодействии

А. В. Тюрина a, *, П. В. Юлдашев a, **, И. Б. Есипов b, В. А. Хохлова a, ***

a Московский государственный университет им. М.В. Ломоносова, Физический факультет
119991 Москва, Ленинские горы 1, Россия

b Российский государственный университет нефти и газа им. И.М. Губкина
119991 Москва, Ленинский проспект 65, Россия

* E-mail: tiurina.av@physics.msu.ru
** E-mail: petr@acs366.phys.msu.ru
*** E-mail: vera@acs366.phys.msu.ru

Поступила в редакцию 03.11.2021
После доработки 25.11.2021
Принята к публикации 30.11.2021

Полный текст (PDF)

Аннотация

Рассматривается спектральный алгоритм описания нелинейной генерации акустической волны разностной частоты, формируемой при взаимодействии двух близких интенсивных высокочастотных волн накачки. При таком двухчастотном взаимодействии, в условиях образования ударных фронтов в профиле волны, для корректного описания ее полного спектра необходимо использовать в численном алгоритме порядка нескольких тысяч спектральных компонент. В работе предложен метод, позволяющий существенно уменьшить это число при сохранении точности расчета поля волны разностной частоты. Метод состоит в ограничении высокочастотной части спектра и прореживании комбинационных частот, расположенных между кратными исходным волнам накачки компонентами спектра. В приближении распространения плоских одномерных волн рассмотрены примеры взаимодействия близких частот, характерных для работы подводной параметрической антенны. Показано, что метод позволяет более чем в 100 раз сократить количество спектральных компонент, включенных в алгоритм описания нелинейного оператора, и тем самым уменьшить число операций на четыре порядка, что делает реализуемыми алгоритмы описания параметрических взаимодействий, в том числе и в акустических пучках.

Ключевые слова: нелинейность, спектральный метод, разностная частота

ВВЕДЕНИЕ

Исследование параметрических процессов является актуальной задачей для практических приложений нелинейной акустики [1, 2]. При нелинейном взаимодействии двух близких интенсивных высокочастотных волн накачки с частотами fpump1 и fpump2 происходит генерация кратных гармоник и комбинационных частот. Поскольку поглощение в среде растет с увеличением частоты, то высокочастотные спектральные компоненты затухают быстрее, и на достаточно большом удалении от источника распространяется только волна разностной частоты fdif = |fpump1 – fpump2| [3]. Разработка алгоритмов расчета поля волны разностной частоты не теряет своей актуальности в силу наличия ряда преимуществ нелинейного механизма генерации низкочастотного излучения и, как следствие, широкого практического применения параметрических излучателей. Особенностью такого двухчастотного взаимодействия является чрезвычайно высокая, порядка нескольких градусов, направленность низкочастотного излучения [4, 5]. Кроме того, по сравнению с обычным излучателем, работающим на той же частоте, параметрический излучатель отличается небольшими размерами, отсутствием боковых лепестков диаграммы направленности и широкой частотной полосой излучаемого сигнала.

Параметрические излучатели остаются объектом как теоретических [6], так и экспериментальных исследований в течение нескольких последних десятилетий [7–9]. Они активно используются как в гидроакустике, например, для акустической томографии морских вод, зондирования океана, профилирования донных структур [4], так и в аэроакустике [10], например, при создании звуковых прожекторов [11] для различных практических применений [12].

В теоретическом описании процесса генерации и распространения волны разностной частоты используются модели различной сложности. Наиболее общий подход при решении трехмерных задач состоит в решении конечно-разностными методами нелинейной системы уравнений для сжимаемой сплошной среды с вязкостью [13]. Однако получение решений такой системы даже для радиально симметричных источников сопряжено с большими вычислительными затратами. Более удобной моделью для практического использования является однонаправленное уравнение Вестервельта, которое учитывает эффекты нелинейности, дифракции и термовязкого поглощения [3]. В сопровождающей системе координат его можно записать в виде:

(1)
$\frac{{\partial p}}{{\partial z}} = \frac{{{\beta }}}{{c_{0}^{3}{{{{\rho }}}_{0}}}}p\frac{{\partial p}}{{\partial {{\tau }}}} + \frac{{{\delta }}}{{2c_{0}^{3}}}\frac{{{{\partial }^{2}}p}}{{\partial {{{{\tau }}}^{2}}}} + \frac{{{{c}_{0}}}}{2}\int\limits_{ - \infty }^{{\tau }} {\Delta pd{{\tau }}{\kern 1pt} {\text{'}}} .$

Здесь p – акустическое давление, z – выделенное направление вдоль оси пучка, τ = t – z/c0 – время в бегущей системе координат, Δ = ∂2/∂x2 + + ∂2/∂y2 + ∂2/∂z2 – оператор Лапласа, с0 – скорость звука, ρ0 – плотность среды, β и δ – коэффициенты нелинейности и термовязкого поглощения в среде, соответственно. При необходимости в уравнении могут быть учтены и другие механизмы поглощения, например, релаксация.

Изначально уравнение Вестервельта использовалось при описании параметрических взаимодействий для получения аналитических оценок амплитуды давления на разностной частоте в дальнем поле излучателя [3]. В современных исследованиях уравнение Вестервельта решается численно, например, конечно-разностными методами во временном представлении [14]. На основе этого уравнения также возможно получить полуаналитические решения для поля разностной частоты в квазилинейном приближении без использования параксиального приближения [15].

При численном решении уравнения Вестервельта для ультразвуковых источников медицинской акустики широкое использование получил метод расщепления по физическим факторам [16, 17]. Согласно этому методу, на каждом шаге по продольной координате распространения волны операторы в правой части уравнения, описывающие различные физические эффекты, рассчитываются отдельно. Это позволяет использовать оптимальную численную схему для того или иного оператора. Основная сложность возникает при расчете дифракционного оператора, для реализации которого часто используется метод углового спектра [18]. Для параметрических излучателей такой метод расчета был реализован в квазилинейном случае в трехмерной геометрии [19].

Более простой моделью при расчете полей параметрических излучателей является уравнение Хохлова–Заболотской–Кузнецова (ХЗК)

(2)
$\frac{{\partial p}}{{\partial z}} = \frac{{{\beta }}}{{c_{0}^{3}{{{{\rho }}}_{0}}}}p\frac{{\partial p}}{{\partial {{\tau }}}} + \frac{{{\delta }}}{{2c_{0}^{3}}}\frac{{{{\partial }^{2}}p}}{{\partial {{{{\tau }}}^{2}}}} + \frac{{{{c}_{0}}}}{2}\int\limits_{ - \infty }^{{\tau }} {{{\Delta }_{ \bot }}pd{{\tau }}{\kern 1pt} {\text{'}}} ,$
которое отличается от уравнения Вестервельта использованием параксиального приближения при расчете дифракционного оператора в правой части уравнения. Здесь Δ⊥ = ∂2/∂x2 + ∂2/∂y2 – лапласиан по поперечным координатам. Для уравнения ХЗК были разработаны конечно-разностные численные схемы как во временном [20], так и в частотном представлениях [21], которые также были основаны на методе расщепления по физическим факторам. В дальнейшем эти схемы были использованы при описании полей разностной частоты радиально симметричных [22–24] и прямоугольных излучателей [25].

Основная сложность численного моделирования параметрических взаимодействий в нелинейных пучках состоит в том, что если не ограничиваться квазилинейным приближением и принимать во внимание возможность образования разрывов в волне накачки, то количество спектральных компонент, которые формально необходимо учитывать в расчете, становится очень большим, порядка нескольких тысяч. Это становится особенно критичным при использовании спектрального подхода для расчета нелинейного оператора, так как число операций пропорционально квадрату числа гармоник [26]. В этом случае, при решении уравнений (1) и (2) методом расщепления по физическим факторам, на каждом шаге сетки вдоль координаты распространения волны фактически решается одномерная задача. Использование временного подхода также затруднительно, так как, с одной стороны, временное окно должно быть достаточно длинным, чтобы вмещать низкочастотную компоненту, а с другой стороны, шаг дискретизации по времени должен быть достаточно малым, чтобы хорошо прописывались высокочастотные компоненты и их гармоники. В результате, даже с использованием современных многоядерных компьютеров трехмерное моделирование параметрических процессов в полях, создаваемых излучателями с апертурой произвольной формы, становится сложным как с точки зрения необходимых объемов оперативной памяти, так и по времени вычислений.

Данное ограничение можно обойти, выделяя наиболее важные спектральные компоненты, которые участвуют в формировании сигнала на разностной частоте, и оперируя только ими в численной схеме. Такая идея рассматривалась ранее, но, насколько нам известно, не была реализована [24]. В нашей работе предложено оптимизировать расчет нелинейного оператора за счет прореживания спектра волны и выявления критериев, по которым гармоники исключаются либо оставляются в спектре. Представлен алгоритм решения уравнений (1) и (2) в одномерной постановке, в которых рассматриваются только операторы нелинейности и поглощения; описываются соответствующие параметрические явления. В этом случае, без учета дифракционного оператора, уравнения (1) и (2) переходят в одномерное нелинейное уравнение Бюргерса [27], а предложенный метод позволяет существенно сократить число операций в алгоритме расчета нелинейного оператора. Развитие метода в одномерной постановке направлено на его дальнейшее использование при решении полной нелинейно-дифракционной задачи, рассмотрение которой остается за рамками данной работы.

1. ТЕОРЕТИЧЕСКИЙ МЕТОД

1.1. Нелинейное уравнение Бюргерса

Для моделирования эффектов нелинейности и поглощения при взаимодействии двух близких по частоте одномерных высокочастотных плоских волн запишем уравнение Бюргерса в виде [27]:

(3)
$\frac{{\partial p}}{{\partial z}} = \frac{{{\beta }}}{{c_{0}^{3}{{{{\rho }}}_{0}}}}p\frac{{\partial p}}{{\partial {{\tau }}}} + \frac{{{\delta }}}{{2c_{0}^{3}}}\frac{{{{\partial }^{2}}p}}{{\partial {{{{\tau }}}^{2}}}},$
с граничным условием для волн накачки с частотами fpump1 и fpump2:
(4)
$p\left( {{{\tau }},z = 0} \right) = \frac{{{{p}_{0}}}}{2}\sin \left( {{{{{\omega }}}_{{{\text{pump}}1}}}{{\tau }}} \right) + \frac{{{{p}_{0}}}}{2}\sin \left( {{{{{\omega }}}_{{{\text{pump}}2}}}{{\tau }}} \right),$
где p0 – максимально достижимое акустическое давление в исходной волне накачки, а ωpump1 = = 2πfpump1 и ωpump2 = 2πfpump2 – циклические частоты.

Для удобства численного решения уравнения (3) перейдем к безразмерным переменным: P = p/p0, θ = ωdifτ, Z = z/lsh, где ωdif = 2πfdif – циклическая частота, соответствующая разностной частоте fdif = = fpump1 – fpump2 (для определенности положим fpump1 > fpump2), lsh – длина образования разрыва для периода волны с максимальной амплитудой p0 и частотой ωpump1, которая является k-той гармоникой разностной частоты (ωpump1 ≡ ωk = kωdif):

${{l}_{{{\text{sh}}}}} = \frac{{{{{{\rho }}}_{0}}c_{0}^{3}}}{{{{\beta }}{{{{\omega }}}_{{{\text{pump}}1}}}{{p}_{0}}}}.$

Вводя также обратное акустическое число Рейнольдса или число Гольдберга Γ на частоте накачки fpump1 как:

(5)
получаем уравнение Бюргерса (3) и граничное условие (4) в безразмерном виде:

(6)
$\frac{{\partial P}}{{\partial Z}} = \frac{1}{k}\left( {P\frac{{\partial P}}{{\partial {{\theta }}}} + \frac{\Gamma }{k}\frac{{{{\partial }^{2}}P}}{{\partial {{{{\theta }}}^{2}}}}} \right),$
(7)
$P\left( {{{\theta }},Z = 0} \right) = 0.5\left( {\sin \left( {k{{\theta }}} \right) + \sin \left( {\left[ {k - 1} \right]{{\theta }}} \right)} \right).$

Для уравнения (3) с граничным условием (4) можно получить аналитическое решение для амплитуды волны разностной частоты Adif,analyt(z) в квазилинейном приближении в предположении постоянства амплитуды волн накачки A1, A2 (4) [28]:

(8)
${{A}_{{{\text{dif,analyt}}}}}(z) = \frac{\beta }{{2c_{0}^{3}{{\rho }_{0}}}}{{\omega }_{{{\text{dif}}}}}{{A}_{1}}{{A}_{2}}z.$

1.2. Граничное волновое поле и параметры среды

Численное моделирование генерации и распространения волны разностной частоты проводилось на примере частот, амплитуд и параметров среды, характерных для экспериментов с недавно разработанной параметрической антенной в воде [29]. Считается, что максимальная эффективность параметрической антенны достигается при достаточно высокой интенсивности волн накачки, когда нелинейное взаимодействие компенсирует диссипативные процессы и профиль волны близок к разрывному [30, 31]. Для численного анализа в качестве граничного условия были взяты три волны накачки с частотами fpump1 = 150 кГц и fpump2 = 145, 140 и 135 кГц. Таким образом, генерировались волны разностной частоты с fdif = 5, 10 и 15 кГц, соответственно. На рис. 1 представлен один период безразмерного граничного профиля волны (7) для трех выбранных пар взаимодействующих частот накачки.

Рис. 1.

Один период безразмерного начального профиля волны при Z = 0 для трех случаев взаимодействующих пар частот накачки: (а) – fpump1 = 150 кГц и fpump2 = 145 кГц; (б) – fpump1 = 150 кГц и fpump2 = 140 кГц; (в) – fpump1 = 150 кГц и fpump2 = 135 кГц.

Для оценки относительных вкладов нелинейности и поглощения использовались данные недавних исследований с использованием подводной параметрической антенны: p0 = 0.6 МПа, c0 = = 1502.25 м/c, ρ0 = 996.81 кг/м3 [29] и характерные для морской воды величины параметров нелинейности и поглощения: β = 3.5, δ = 4.42 × 10–6 м2/c [32].

1.3. Численный алгоритм

Представим решение уравнения (6) в виде конечного ряда Фурье с Nmax временных гармоник:

$P\left( {{{\theta ,}}Z} \right) = \sum\limits_{n = - {{N}_{{\max }}}}^{{{N}_{{\max }}}} {{{P}_{n}}\left( Z \right){{e}^{{in{{\theta }}}}}} .$

Тогда уравнение (6) в частотном представлении записывается в виде конечной системы связанных нелинейных уравнений [26]:

(9)
$\frac{{\partial {{P}_{n}}}}{{\partial Z}} = \frac{{in}}{k}\left( {\sum\limits_{m = 1}^{{{N}_{{\max }}} - n} {P_{m}^{*}{{P}_{{n + m}}}} + \frac{1}{2}\sum\limits_{m = 1}^{n - 1} {{{P}_{m}}{{P}_{{n - m}}}} } \right) - \frac{\Gamma }{{{{k}^{2}}}}{{n}^{2}}{{P}_{n}},$
где 1 ≤ n ≤ Nmax, $P_{m}^{*}$ – комплексно-сопряженная амплитуда гармоники с номером m, а i – мнимая единица. При этом граничное условие (7) имеет вид: Pk–1,0 = Pk,0 = – 0.25i.

Система уравнений (9) решалaсь методом расщепления по физическим факторам [16–18], при этом каждый шаг по координате Z начинался и заканчивался оператором поглощения, рассчитываемым на половинном шаге сетки ΔZ/2. Таким образом, схема применения метода расщепления по физическим факторам выглядит так:

где действие оператора поглощения на шаге ΔZ/2 и оператора нелинейности на шаге ΔZ обозначено как LA,ΔZ/2 и LN,ΔZ, соответственно. Система нелинейных уравнений (9) без учета поглощения решалась методом Рунге–Кутты четвертого порядка [26], а для расчёта поглощения для каждой из гармоник использовалось аналитическое решение в виде затухающей экспоненты.

Для того чтобы выявить оптимальные параметры численного алгоритма для получения референсных решений, сначала рассчитывалось распространение плоской волны накачки с частотой fpump1 = 150 кГц и амплитудой p0, соответствующей максимальной амплитуде в профиле волны при двухчастотном взаимодействии (рис. 1): p(τ, z = 0) = p0sin(ωpump1τ). Расчеты проводились при учете Nmax = 250 гармоник, безразмерный шаг пространственной сетки составил ΔZ = 0.01, число Гольдберга (5) равно Γ = 10–3. Для обеспечения устойчивости численной схемы при моделировании необходимо, чтобы на разрыв приходилось около 9 точек [33], что при выбранном количестве гармоник Nmax определяется соответствующей величиной поглощения δ, поэтому физическое число Гольдберга Γ = 10–3 было увеличено примерно в 10 раз. Выбор Γmodel = 0.01 обусловлен взятым для анализа количеством гармоник Nmax = 250, соответствующим шагу сетки во времени Δθ = = π/Nmax. В этом случае заметные отличия наблюдаются только в структуре ударного фронта в его окрестности θ = 0 ± 4π/Nmax, что составляет 1.6% от длительности периода.

Сравнение результатов численного моделирования для вышеперечисленных параметров (штриховая линия) с аналитическим решением для римановой плоской волны [34] (сплошная линия) представлено на рис. 2. Как видно из рисунка, численное решение хорошо соответствует аналитическому как на расстояниях до образования разрыва (Z < 1), так и после (Z > 1). Различия проявляются только в тонкой структуре ударного фронта и обусловлены конечным значением числа Гольдберга, которое и позволяет использовать число гармоник, ограниченное сверху. На остальных участках решения практически не отличаются, и при θ = 0 ± 20π/Nmax ошибка составляет уже менее 1%. Таким образом, использование 250 гармоник для описания нелинейных процессов в высокочастотной волне представляется приемлемым.

Рис. 2.

Искажение одного периода безразмерного профиля волны накачки с частотой fpump1 = 150 кГц, амплитудой p0 и поглощением Γmodel = 0.01 на расстояниях: (а) – до образования разрыва по мере укручения фронта, Z = 0, 0.5 и 1; (б) – после образования разрыва по мере уменьшения амплитуды, Z = 1.5, 3 и 10. Профили на расстояниях Z = 3 и Z = 10 искусственно смещены вдоль временной шкалы на π/8 и π/4, соответственно. Сплошная линия – аналитическое решение, штриховая линия – численное решение в случае учета Nmax = 250 гармоник в спектре.

Далее, при моделировании двухчастотных взаимодействий, также использовалось 250 гармоник частоты накачки fpump1 и число Гольдберга Γmodel = 0.01. В прямой постановке для описания волн с выбранными частотами fpump1 = 150 кГц и fpump2 = 145, 140 и 135 кГц, необходимо учитывать Nmax = 7500, 3750 и 2500 гармоник разностной частоты, соответственно, что представляется трудно реализуемым при моделировании нелинейно-дифракционных задач на основе уравнений (1) и (2) ввиду квадратичного роста числа операций при расчете нелинейного оператора (9) в зависимости от Nmax.

1.4 Метод прореживания спектра

Идея предлагаемого в данной работе метода уменьшения числа спектральных компонент в численном решении, или прореживания спектра, состоит в следующем. Известно, что при распространении квазигармонической волны большой интенсивности каскадные процессы генерации новых частот направлены в основном в сторону перехода энергии волны вверх по спектру [27]. Эффективность обратных процессов в сторону генерации разностных частот гораздо меньше. Ясно, что основной вклад в генерацию низкочастотных компонент спектра будут вносить высокочастотные компоненты с наибольшей амплитудой, сосредоточенные вблизи кратных частот волн накачки. При этом в полном спектре нелинейной волны присутствуют частоты с достаточно малой амплитудой, которые можно отбросить без существенной потери точности решения для разностной частоты. Иллюстрация к методу прореживания спектра представлена на рис. 3 для случая fdif = 10 кГц, где слева изображен исходный спектр на расстоянии Z = 0 (два пика на частотах накачки), а справа – спектр волны на расстоянии Z = 3, рассчитанный с учетом полного числа гармоник Nmax = 3750. Отметим, что расстояние Z = 3 соответствует трем длинам образования разрыва на высокочастотном периоде с максимальной амплитудой p0, нелинейные эффекты для остальных периодов с меньшей амплитудой выражены слабее (рис. 1). Как видно, амплитуда компонент спектра максимальна вблизи кратных гармоник частот накачки, а между ними ее величина гораздо меньше.

Рис. 3.

Иллюстрация к методу прореживания спектра на примере случая fdif = 10 кГц. Слева изображен спектр исходной волны Pn, где n = f/fdif – номер гармоники разностной частоты, на расстоянии Z = 0, а справа – спектр на расстоянии Z = 3 и пороги для N = 12, 25, 50 (штриховая, штрихпунктирная и пунктирная линия, соответственно).

Чтобы определить номера гармоник с наибольшими амплитудами, вводилось безразмерное пороговое давление Pth, отсекающее гармоники с меньшей амплитудой (кроме первой) таким образом, чтобы в оптимизированном алгоритме присутствовало заранее заданное число гармоник N, меньшее, чем в эталонном решении. Здесь “эталонным” решением будем называть численное решение, полученное в моделировании с учетом всех гармоник Nmax. Пороговые значения Pth варьировались так, чтобы количество компонент спектра с амплитудой выше пороговой было N = 12, 25, 50 (штриховая, штрихпунктирная и пунктирная линия, соответственно). Также варьировалось безразмерное расстояние Z = 1, 1.5 и 3, на котором проводилась данная процедура для рассматриваемых в работе трех значений fdif. В полученном прореженном спектре с амплитудами выше порогового уровня, во-первых, ограничивалась высокочастотная часть спектра, а во-вторых, сокращалось количество комбинационных компонент, расположенных между амплитудными пиками кратных fpump1 и fpump2 частот. Далее алгоритм решения уравнения (6) модифицировался таким образом, чтобы вычисления проходили только по индексам гармоник, оставленных после прореживания.

2. РЕЗУЛЬТАТЫ И ОБСУЖДЕНИЕ

На рис. 4 представлены зависимости амплитуды Pdif волны разностной частоты от расстояния Z для трех значений fdif: 5 кГц (рис. 4а, 4г), 10 кГц (рис. 4б, 4д) и 15 кГц (рис. 4в, 4е). Эталонное решение при N = Nmax показано на всех графиках сплошной красной линией, а квазилинейное решение (8) – серой маркерной линией. Верхний ряд графиков (рис. 4а–4в) получен при прореживании спектра эталонного решения на расстоянии Z = 3 с различным количеством включенных в нелинейный алгоритм гармоник: N = 12 (штриховая линия), 25 (сплошная линия) и 50 (пунктирная линия). Нижний ряд (рис. 4г–4е) получен при прореживании спектра с фиксированным количеством включенных в нелинейный алгоритм гармоник N = 25 на различных расстояниях Z = 1 (пунктирная линия), 1.5 (штриховая линия) и 3 (сплошная линия). Зависимости Pdif(Z) на начальной стадии распространения показаны на вкладках соответствующих рисунков.

Рис. 4.

Зависимости амплитуды Pdif волны разностной частоты от расстояния Z для трех значений fdif: (а, г) 5 кГц, (б, д) 10 кГц и (в, е) 15 кГц. Графики (а)–(в) – прореживание спектра проводилось на расстоянии Z = 3 при различном количестве включенных в алгоритм гармоник: N = 12 (штриховая линия), 25 (сплошная линия) и 50 (пунктирная линия); (г)–(е) – прореживание проводилось при N = 25 на разных расстояниях: Z = 1 (пунктирная линия), 1.5 (штриховая линия) и 3 (сплошная линия). На графиках также представлено решение в квазилинейном приближении (сплошная маркерная линия) и эталонное решение (сплошная красная линия) при N = Nmax (7500, 3750 и 2500). Зависимости Pdif(Z) на начальной стадии распространения показаны на вкладках соответствующих рисунков.

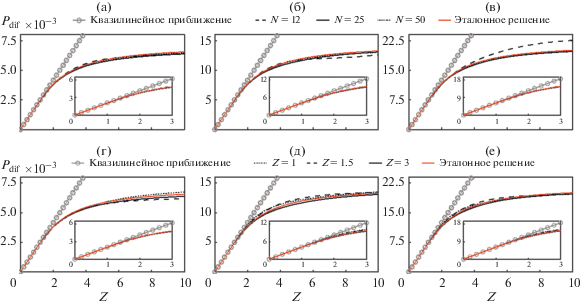
Видно, что на начальном этапе, вплоть до расстояния Z = 2, амплитуда волны разностной частоты в численном решении, как при учете всех гармоник, так и при прореживании спектра, растет линейно и практически не отличается от аналитического решения, полученного в квазилинейном приближении. Затем линейный рост замедляется и сменяется насыщением на расстояниях порядка нескольких длин образования разрыва. При этом, чем больше величина разностной частоты fdif, тем больше энергии переходит в нее от частот накачки в процессе генерации. Так, в соответствии с квазилинейным приближением (8), на расстоянии Z = 1 амплитуда волны разностной частоты пропорциональна ее величине и для fdif = = 5 кГц составляет 0.2%, для fdif = 10 кГц – 0.4% и для fdif = 15 кГц – 0.6% от максимальной амплитуды исходной волны накачки p0 или 0.01, 0.04 и 0.09% от средней по периоду низкочастотной волны начальной интенсивности $p_{0}^{2}$/(4с0ρ0). При достижении расстояний в несколько длин образования разрыва, на которых наступает насыщение амплитуды волны разностной частоты, ее амплитуда дополнительно увеличивается более чем в 2 раза, что соответствует увеличению интенсивности более чем в 4 раза.

Влияние прореживания спектра эталонного решения на расстоянии Z = 3 на точность получаемого численного решения для Pdif при различном количестве включенных в нелинейный алгоритм гармоник N = 12, 25 и 50 в сравнении с эталонным решением при N = Nmax иллюстрируется на рис. 4а–4в. Видно, что при N = 12 численное решение для волны разностной частоты сильно отличается от эталонного, начиная с расстояний порядка Z = 3. При использовании N = 25 гармоник в нелинейном алгоритме ошибка в вычислении амплитуды волны разностной частоты составляет менее 0.4% на расстоянии Z = 1, менее 1.8% на расстоянии Z = 3 и менее 2.8% на расстоянии Z = 10, при этом максимальная ошибка во всем диапазоне расстояний составляет менее 2.8%. При учете N = 50 гармоник ошибка не превышает 2% на всех расстояниях. С учетом того, что параметрические излучатели используются в основном в режимах вблизи образования ударных фронтов, выбор N = 25 гармоник представляется достаточным для дальнейшего анализа.

Влияние проведения прореживания спектра с фиксированным количеством включенных в нелинейный алгоритм гармоник N = 25 на различных расстояниях Z = 1, 1.5 и 3 в сравнении с эталонным решением при N = Nmax иллюстрируется на рис. 4г–4е. Видно, что все полученные решения достаточно близки, однако прореживание на расстоянии Z = 3 оказывается предпочтительным. При таком выборе отличие от эталонного решения на всех расстояниях для всех трех разностных частот составляет менее 2.8%.

Таким образом, для трех пар взаимодействующих волн накачки с разностными частотами fdif = 5, 10 и 15 кГц число участвующих в нелинейном алгоритме спектральных компонент возможно сократить с Nmax = 7500, 3750 и 2500 до N = 25 с ошибкой менее 3% в расчете амплитуды разностной частоты при наиболее удачном выборе расстояния, на котором выполняется прореживание спектра. Дальнейшие результаты будут представлены для N = 25 спектральных компонент, полученных при прореживании эталонного численного решения на расстоянии Z = 3.

Отметим, что на расстояниях Z < 2 аналитическое решение (8), полученное в квазилинейном приближении при условии постоянства амплитуд волн накачки (сплошная маркерная линия на рис. 4а–4е), хорошо соответствует эталонному решению и может быть использовано вместо численного расчета нелинейного оператора. На расстояниях Z > 2 ошибка при использовании квазилинейного приближения быстро возрастает.

На рис. 5 представлены характерные профили давления (рис. 5а–5г) и спектры (рис. 5д–5з) для случая fdif = 10 кГц при распространении волны на расстояния Z = 1, 1.5, 3 и 10 (тонкая красная линия) в сравнении с эталонным решением при N = Nmax (жирная серая линия) в случае прореживания спектра на расстоянии Z = 3 и выборе порога, при котором N = 25. Видно, что вследствие ограничения удерживаемых гармоник на высоких частотах, в профиле появляются осцилляции за счет эффекта отражения частот (рис. 5а–5г). Однако, как показано выше, эти артефакты в описании полного спектра волны слабо влияют на амплитуду волны разностной частоты (рис. 4). В итоговом прореженном спектре (рис. 5д–5з) остается разностная частота и группы от 1 до 5 спектральных компонент вокруг 11 пиков, кратных начальным частотам накачки. Каждая из этих групп представляет собой последовательное чередование двух и одной компонент спектра с максимальной амплитудой, по бокам которых присутствуют комбинационные частоты, число которых изменяется от 0 до 3 для первых шести групп и равно 0, начиная с седьмой.

Рис. 5.

(а)–(г) – Один период безразмерного профиля давления для fpump1 = 150 кГц и fpump2 = 140 кГц на расстояниях Z = 1, 1.5, 3 и 10, соответственно; (д)–(з) – спектр волны на тех же расстояниях Z = 1, 1.5, 3 и 10, соответственно. Жирной серой линией представлено эталонное решение, тонкой красной линией – результат прореживания спектра на расстоянии Z = 3 в случае включения в нелинейный алгоритм N = 25 гармоник.

ЗАКЛЮЧЕНИЕ

В работе численными методами исследован процесс генерации волны разностной частоты, формируемой при взаимодействии двух близких высокочастотных волн накачки в нелинейной среде. Расчеты проводились для одномерной волны на примере трех пар взаимодействующих частот, характерных для работы параметрических излучателей, используемых в подводной акустике.

Был предложен метод прореживания спектра, позволяющий сократить число включенных в нелинейный алгоритм спектральных компонент более чем на два порядка, что снижает количество операций на четыре порядка. Разработанный подход включает в себя ограничение числа высокочастотных компонент и сокращение комбинационных частот малой амплитуды, расположенных в промежутках между кратными исходным волнам гармониками. Показано, что прореживание частот в численном решении с большим числом спектральных компонент предпочтительно проводить на расстоянии, равном трем длинам образования разрыва для высокочастотного периода волны накачки с максимальной амплитудой. При таком выборе амплитуда волны разностной частоты с ошибкой менее трех процентов соответствует полученной в расчетах с учетом полного числа спектральных компонент вплоть до расстояний в десять длин образования разрыва.

Амплитуда волны разностной частоты пропорциональна величине fdif и на расстоянии, равном одной длине образования разрыва, составляет 0.2, 0.4 и 0.6% от максимальной амплитуды волны накачки или 0.01, 0.04 и 0.09% от средней по периоду низкочастотной волны интенсивности для частот fdif = 5, 10, и 15 кГц. При достижении расстояний насыщения амплитуда и интенсивность волны разностной частоты дополнительно увеличиваются более чем в 2 и в 4 раза, соответственно.

Показано также, что на расстояниях, меньших двух характерных длин образования разрыва, аналитическое выражение, полученное в квазилинейном приближении при условии постоянства амплитуд волн накачки, с хорошей точностью аппроксимирует эталонное решение для большого числа спектральных компонент. Таким образом, квазилинейное приближение может быть использовано при моделировании нелинейных пучков. Результаты, полученные в работе, в дальнейшем могут быть использованы для решения полной трехмерной нелинейно-дифракционной задачи о генерации волны разностной частоты с помощью антенной решетки [29, 31].

Работа выполнена при поддержке грантов РФФИ № 20-02-00676 и фонда “БАЗИС” 20-2-2-21-1.

Список литературы

  1. Gan W.-S., Yang J., Kamakura T. A review of parametric acoustic array in air // Applied Acoustics. 2012. V. 73. № 12. P. 1211–1219.

  2. Zhou H., Huang S.H., Li W. Parametric acoustic array and its application in underwater acoustic engineering // Sensors. 2020. V. 20. № 7. P. 2148.

  3. Westervelt P.J. Parametric acoustic array // J. Acoust. Soc. Am. 1963. V. 35. № 4. P. 535–537.

  4. Новиков Б.К., Тимошенко В.И. Параметрические антенны в гидролокации. Л.: Судостроение, 1990. 250 с.

  5. Sapozhnikov O.A., Khokhlova V.A., Cleveland R.O., Blanc-Benon P., Hamilton M.F. Nonlinear Acoustics Today // Acoustics today. 2019. V. 15. № 3. P. 55–64.

  6. Новиков Б.К., Руденко О.В., Тимошенко В.И. Нелинейная гидроакустика. Л.: Судостроение, 1981. 264 с.

  7. Зверев В.А., Калачев А.И. Измерение взаимодействия звуковых волн в жидкостях // Акуст. журн. 1958. Т. 4. № 4. С. 321–324.

  8. Зверев В.А., Калачев А.И. Измерение рассеяния звука звуком при наложении параллельных пучков // Акуст. журн. 1968. Т. 14. № 2. С. 214–220.

  9. Гурбатов С.Н., Дерябин М.С., Касьянов Д.А., Курин В.В. Об использовании вырожденного параметрического взаимодействия интенсивных акустических пучков для усиления слабых сигналов // Акуст. журн. 2017. Т. 63. № 3. С. 235–245.

  10. Bennett M.B., Blackstock D.T. Parametric array in air // J. Acoust. Soc. Am. 1975. V. 57. № 3. P. 562–568.

  11. Yoneyama M., Fujimoto J., Kawamo Y., Sasabe S. The audio spotlight: an application of nonlinear interaction of sound waves to a new type of loudspeaker design // J. Acoust. Soc. Am. 1983. V. 73. № 5. P. 1532–1536.

  12. Shi C., Gan W.-S. Development of a parametric loudspeaker: a novel directional sound generation technology // IEEE Potentials. 2010. V. 29. № 6. P. 20–24.

  13. Nomura H., Hedberg C.M., Kamakura T. Numerical simulation of parametric sound generation and its application to length-limited sound beam // Applied Acoustics. 2012. V. 73. № 12. P. 1231–1238.

  14. Zhu L., Florencio D. 3D numerical modeling of parametric speaker using finite-difference time-domain / IEEE international conference on acoustics, speech and signal processing (ICASSP). IEEE, 2015. P. 5982–5986.

  15. Cervenka M., Bednarik M. Non-paraxial model for a parametric acoustic array // J. Acoust. Soc. Am. 2013. V. 134. № 2. P. 933–938.

  16. Tavakkoli J., Cathignol D., Souchon R., Sapozhnikov O.A. Modeling of pulsed finite-amplitude focused sound beams in time domain // J. Acoust. Soc. Am. 1998. V. 104. № 4. P. 2061–2072.

  17. Юлдашев П.В., Хохлова В.А. Моделирование трехмерных нелинейных полей ультразвуковых терапевтических решеток // Акуст. журн. 2011. Т. 57. № 3. С. 337–347.

  18. Zemp R.J., Tavakkoli J., Cobbold R.S.C. Modeling of nonlinear ultrasound propagation in tissue from array transducers // J. Acoust. Soc. Am. 2003. V. 113. № 1. P. 139–152.

  19. Prieur F. 3D simulation of parametric ultrasound fields // AIP Conference Proceedings. AIP, 2012. V. 1474. № 1. P. 387–390.

  20. Lee Y.S., Hamilton M.F. Time-domain modelling of pulsed finite-amplitude sound beams // J. Acoust. Soc. Am. 1995. V. 97. № 2. P. 906–917.

  21. Aanonsen S.I. Numerical computation of the nearfield of a finite amplitude sound beam // Tech. Rep. № 73. 1983. Dept. of Math., Univ. of Bergen, Norway.

  22. Ji P., Tan E.-L., Gan W.-S., Yang J. A comparative analysis of preprocessing methods for the parametric loudspeaker based on the Khokhlov–Zabolotskaya–Kuznetsov equation for speech reproduction // IEEE transactions on audio speech and language processing. IEEE, 2011. V. 19. № 4. P. 937–946.

  23. Averkiou M.A., Lee Y.-S., Hamilton M.F. Self-demodulation of amplitude- and frequency-modulated pulses in a thermoviscous fluid // J. Acoust. Soc. Am. 1993. V. 94. № 5. P. 2876–2883.

  24. Kamakura T., Hamada N., Aoki K., Kumamoto Y. Nonlinearly generated spectral components in the nearfield of a directive sound source // J. Acoust. Soc. Am. 1989. V. 85. № 6. P. 2331–2337.

  25. Kamakura T., Nomura H., Akiyama M., Hedberg C.M. Parametric sound fields formed by phase-inversion excitation of primary waves // Acta Acustica. 2011. V. 97. № 2. P. 209–218.

  26. Кащеева С.С., Сапожников О.А., Хохлова В.А., Аверкью М.А., Крам Л.А. Нелинейное искажение и поглощение мощных акустических волн в среде со степенной зависимостью коэффициента поглощения от частоты // Акуст. журн. 2000. Т. 46. № 2. С. 211–219.

  27. Руденко О.В., Солуян С.И. Теоретические основы нелинейной акустики. М.: Наука, 1975. 288 с.

  28. Новиков Б.К., Руденко О.В., Солуян С.И. К вопросу о параметрическом излучателе ультразвука // Акуст. журн. 1975. Т. 21. № 4. С. 591–597.

  29. Есипов И.Б., Попов О.Е., Солдатов В.Г. Компрессия сигнала параметрической антенны в мелководном волноводе // Акуст. журн. 2019. Т. 65. № 4. С. 490–498.

  30. Moffett M.B., Mellen R.H., Konrad W.L. Model for parametric acoustic source of rectangular aperture // J. Acoust. Soc. Am. 1978. V. 63. № 5. C. 1326–1331.

  31. Есипов И.Б., Попов О.Е., Кенигсбергер Г.В., Сизов И.И. Параметрическая антенна для гидрофизических исследований на протяженных трассах // Известия РАН. Серия физическая. 2016. Т. 80. № 10. С. 1340–1349.

  32. Pierce A.D. Acoustics: an introduction to its physical principles and applications. Springer, 2019. 768 p.

  33. Maxwell A.D., Yuldashev P.V., Kreider W., Khokhlova T.D., Schade G.R., Hall T.L., Sapozhnikov O.A., Bailey M.R., Khokhlova V.A. A prototype therapy system for transcutaneous application of boiling histotripsy // IEEE Trans. Ultrason. Ferroelectr. Freq. Contr. IEEE, 2017. V. 64. № 10. P. 1542–1557.

  34. Гурбатов С.Н., Руденко О.В., Саичев А.И. Волны и структуры в нелинейных средах без дисперсии. М.: Физматлит, 2008. 496 с.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Акустический журнал

Архивы выпусков Информация о журнале Отправить рукопись в журнал