Акустический журнал, 2021, T. 67, № 6, стр. 617-625

ВВЕДЕНИЕ

Как известно [1], из-за высокого уровня потерь в донном грунте акустическая диагностика мелкого моря ограничена сравнительно малыми расстояниями. Даже для низкочастотного диапазона f ~ 10–10² Гц, где затухание звука сравнительно мало, акустические сигналы распространяются лишь на расстояниях от источника R ≤ 200–300 км. В этих условиях весьма актуально рассмотрение эффективности алгоритмов обработки слабых акустических сигналов на фоне помех с использованием протяженных антенных решеток (АР). Оптимальные алгоритмы обработки при этом хорошо известны (см., например, [2–5]) и требуют лишь адекватных физических моделей для корреляционных матриц сигнала и помехи на апертуре антенны. Таким образом, для оценки эффективности обнаружения (либо оценки параметров) акустических сигналов необходимы теоретические либо эмпирические модели, позволяющие прогнозировать корреляционные функции сигналов и помех в различных условиях распространения. В частности, модель сигнала при его дальнем распространении должна учитывать не только регулярные параметры мелководного канала, но и декорреляции акустического поля, обусловленные эффектами многократного его рассеяния на поверхностном волнении, случайных внутренних волнах, нерегулярном профиле дна и т.д.

На данный момент недостаточное использование таких моделей сигнала связано не столько с ограниченностью теоретических методов описания статистических характеристик акустического поля в рефракционном волноводе с нерегулярными параметрами, сколько с отсутствием апробированных гидрофизических данных о корреляционных характеристиках (либо спектрах) самих флуктуаций среды распространения. В первую очередь это относится к случайным внутренним волнам и нерегулярному рельефу дна. Вместе с тем, частотно-угловой спектр ветрового волнения изучен относительно хорошо [6], и это позволяет оценить его влияние на эффективность обработки сигналов. Результаты подобных исследований были приведены в работах [7–10], где рассматривались такие характеристики, как коэффициент усиления и угловой отклик антенны для ветрового волнения с изотропным спектром. Поскольку реальное ветровое волнение обладает высокой степенью анизотропии [6], это приводит к анизотропному характеру эффектов многократного рассеяния и, соответственно, анизотропии энергетических и корреляционных характеристик акустического поля на значительном удалении от источника. Эти вопросы были достаточно подробно рассмотрены как для поля тонального точечного источника [11], так и для динамического шума (т.е. шума ветрового происхождения) [12]. Таким образом, результаты работ [7–10], где использовалась упрощенная модель ветрового волнения с изотропным пространственным спектром, требуют уточнения в рамках более достоверной модели волнения с эмпирическим частотно-угловым спектром. Именно это является предметом данной работы.

ПОСТАНОВКА ЗАДАЧИ И ОСНОВНЫЕ УРАВНЕНИЯ

Рассмотрим акустическое поле, генерируемое тональным точечным источником с частотой f₀. Волновод предполагается плоскослоистым с профилем скорости звука c(z) и, в общем случае, многослойным дном с произвольными акустическими характеристиками. Для прикладных задач акустики мелкого моря наиболее интересен низкочастотный диапазон $f \leqslant 300$ Гц, где затухание звука относительно мало и возможно распространение акустических волн на расстояния порядка десятков и сотен километров. В этом диапазоне для описания акустического поля удобно использовать модовое представление. С учетом асимптотики функции Ханкеля при больших значениях аргумента, поле давления в дальней зоне представим в виде:

где ${{\varphi }_{p}}\left( z \right)$ – ортонормированные собственные функции мод, a_p – амплитуды мод, k_p – их волновые числа, r – расстояние от источника до точки наблюдения. В отсутствие ветрового волнения (т.е. для плоской свободной границы) коэффициенты разложения a_p с точностью до сомножителя, определяемого мощностью источника, имеют вид ${{a}_{p}} = {{\varphi }_{p}}\left( {{{z}_{{\text{И}}}}} \right)$. С учетом ветрового волнения, когда свободная поверхность становится случайной функцией горизонтальных координат и времени, коэффициенты a_p также становятся случайными величинами и в дальнейшем будут описываться функциями когерентности с горизонтальным разнесением точек наблюдения $\left\langle {{{a}_{p}}\left( {{{{\mathbf{r}}}_{1}},t} \right)a_{q}^{*}\left( {{{{\mathbf{r}}}_{2}},t} \right)} \right\rangle $. При этом функция когерентности полного поля на глубине z имеет вид

В принципе, разработанная ранее [13] теория рассеяния мод в акустическом волноводе с нерегулярной свободной границей позволяет рассчитывать эти корреляторы поля, но вследствие интерференционных эффектов они обладают сильной изменчивостью вдоль акустической трассы и плохо предсказуемы на больших удалениях от источника. Для практических приложений больший интерес представляют корреляционные характеристики поля, “сглаженные” по интерференционной структуре и плавно меняющиеся с расстоянием. В связи с этим было предложено [14] анализировать функции корреляции акустического поля, усредненные по интерференционной структуре, т.е. на пространственном масштабе ${{L}_{{{\text{инт}}}}} = {{2\pi } \mathord{\left/ {\vphantom {{2\pi } {\min \left| {{{k}_{p}} - {{k}_{q}}} \right|}}} \right. \kern-0em} {\min \left| {{{k}_{p}} - {{k}_{q}}} \right|}}$. Для описания таких усредненных по интерференционной структуре функций когерентности акустического поля достаточно анализировать автокорреляционные функции мод:

где ρ – поперечное разнесение точек наблюдения, а ось x соединяет источник и центр горизонтальной антенной решетки, где происходит прием и пространственная обработка сигнала. В формуле (2) при этом остаются лишь слагаемые с q = p.

Для расчета корреляционных функций ${{N}_{p}}\left( {\rho ,x} \right)$ в волноводе с нерегулярной границей ранее [13] было получено уравнение переноса, которое в случае ненаправленного (в горизонтальной плоскости) источника имеет вид:

Здесь ${{W}_{{pq}}}$ – вероятность перехода, описывающая взаимодействие, вследствие рассеяния, корреляционных функций мод дискретного спектра, ${{\gamma }_{p}}$ – декремент затухания модовой компоненты $\left\langle {{{a}_{p}}} \right\rangle $ когерентного поля, $\operatorname{Im} {{k}_{p}}$ – мнимая часть волнового числа k_p, обусловленная потерями в дне. Уравнение (4) получено при малых значениях параметра Рэлея, т.е. предполагает малость эффектов однократного рассеяния [15]. При этом оно позволяет описывать эффекты многократного рассеяния, приводящие к существенной декорреляции сигнала на протяженных акустических трассах. Оценки показывают, что при скорости ветра V ≤ 15 м/с и частотах $f \leqslant 300$ Гц параметр Рэлея мал в сравнении с единицей. Декремент затухания ${{\gamma }_{p}}$ и вероятность перехода ${{W}_{{pq}}}$ выражаются через частотно-угловой спектр ветрового волнения $B\left( {\Omega ,\theta } \right)$ следующим образом [11]:

где g – ускорение свободного падения, ${{k}_{0}} = {{{{\omega }_{0}}} \mathord{\left/ {\vphantom {{{{\omega }_{0}}} {c\left( 0 \right)}}} \right. \kern-0em} {c\left( 0 \right)}}$, ${{d{{\varphi }_{p}}} \mathord{\left/ {\vphantom {{d{{\varphi }_{p}}} {dz}}} \right. \kern-0em} {dz}}$ – производная собственной функции ${{\varphi }_{p}}\left( z \right)$ при z = 0.

Важно отметить, что приведенное выражение для декремента ${{\gamma }_{p}}$ учитывает рассеяние p-ой моды не только в моды дискретного спектра, но и в моды сплошного спектра, т.е. излучение энергии из волновода.

Эмпирические частотно-угловые спектры ветрового волнения имеют вид

где $S\left( \Omega \right)$ – частотный спектр, $Q\left( {\Omega ,\theta } \right)$ – нормированный на единицу угловой спектр. Для $S\left( \Omega \right)$ в дальнейшем будет использоваться спектр JONSWAP [6], который описывает наблюдаемые в экспериментах превышения спектральной плотности энергии вблизи максимума в сравнении со спектром Пирсона–Московитца: где ${{\Omega }_{m}} = {{0.9g} \mathord{\left/ {\vphantom {{0.9g} V}} \right. \kern-0em} V}$ – частота спектрального максимума (V – скорость ветра). Эмпирические константы ${{\beta }}$ и $\gamma $ имеют значения $\beta = 8 \times {{10}^{{ - 3}}}$, $1 \leqslant \gamma \leqslant 3.3$. Для углового распределения $Q\left( {\Omega ,\theta } \right)$ обычно используют выражение: где α – направление ветра, $\Gamma \left( x \right)$ – гамма-функция. Показатель анизотропии s является частотно-зависимым и определяется отношением частот ${\Omega \mathord{\left/ {\vphantom {\Omega {{{\Omega }_{m}}}}} \right. \kern-0em} {{{\Omega }_{m}}}}$. В дальнейшем будем использовать эмпирическую зависимость, предложенную в работе [16]:

Анизотропия углового спектра волнения максимальна в области частотного максимума $\Omega = {{\Omega }_{m}}$ и спадает как при $\Omega < {{\Omega }_{m}}$, так и при $\Omega > {{\Omega }_{m}}$. Следовательно, следует ожидать, что эффективная анизотропия частотно-углового спектра $B\left( {\Omega ,\theta } \right)$ зависит также и от параметра γ, при увеличении которого растет относительный вклад в эффекты рассеяния спектральных гармоник с частотами $\Omega \approx {{\Omega }_{m}}$, для которых степень анизотропии максимальна. Отметим, что в предыдущих работах [11, 12], где анализировалось влияние анизотропии волнения на статистические характеристики узкополосного сигнала и океанического шума, использовалось минимальное значение γ = 1 (то есть спектр Пирсона–Московитца) и этот эффект не обсуждался.

Уравнения (4)–(8) совместно с моделью частотно-углового спектра волнения (9)–(12) позволяют рассчитывать пространственные функции корреляции акустического поля в зависимости от направления ветра и его скорости, длины акустической трассы, ориентации приемной антенны и акустических характеристик волновода. Будем считать, что горизонтальная антенна состоит из M эквидистантных элементов с межэлементным расстоянием d, расположенных на глубине ${{z}_{{\text{A}}}}$, и ориентирована под углом β_A к направлению на источник, стандартно отсчитываемым от нормали к антенне. Расстояние между источником и центром АР обозначим R. Основной характеристикой сигнала, используемой при пространственной обработке, является его корреляционная матрица размерности (M × M). В дальнейшем будем использовать нормированную матрицу N(R), элементы которой имеют вид

где матричные элементы для каждой из мод: ${{N}_{p}}\left( {\rho ,R} \right)$ – решение уравнения (4) с начальным условиями, соответствующими точечному источнику, расположенному на глубине ${{z}_{{\text{И}}}}$. Нашей задачей является исследование эффективности пространственной обработки частично-когерентного сигнала в условиях многократного рассеяния на анизотропном волнении. Поэтому ограничимся простой моделью шума, т.е. будем предполагать, что аддитивные шумы на входе АР являются пространственно белым шумом, и нормированная корреляционная матрица шума на элементах антенны является единичной.

Для количественной оценки эффективности пространственной обработки выберем коэффициент усиления антенны G, который стандартно определяется как величина выходного отношения сигнал/шум (ОСШ), отнесенная к величине ОСШ на отдельном элементе. Естественно, величина G зависит не только от вида корреляционной матрицы N(R), но и метода пространственной обработки. Для сравнения выберем три метода пространственной обработки: стандартный метод формирования диаграммы направленности (ФАР), компенсированной в направлении на источник сигнала (величину G такой обработки обозначим G₀), метод оптимальной линейной обработки (коэффициент усиления обозначим G₁) и метод оптимальной квадратичной обработки [2–5] (коэффициент усиления обозначим G₂). Учитывая нормировку корреляционной матрицы сигнала N(R) и некоррелированность шума на всех элементах АР, для коэффициентов ${{G}_{i}}$ имеем следующие выражения:

где ${{k}_{{\text{A}}}} = {\omega \mathord{\left/ {\vphantom {\omega {c\left( {{{z}_{{\text{A}}}}} \right)}}} \right. \kern-0em} {c\left( {{{z}_{{\text{A}}}}} \right)}}$, ${{\lambda }_{i}}\left( R \right)$ – собственные значения корреляционной матрицы N(R), ${{\lambda }_{1}}\left( R \right)$ – максимальное собственное значение. Аналогичные формулы приведены в работе [10], но несколько в ином виде. Учитывая, что для нормированной матрицы сигнала $\sum\nolimits_i {{{\lambda }_{i}}\left( R \right)} = \sum\nolimits_n {{{N}_{{nn}}}\left( R \right)} = M$, нетрудно убедиться в тождественности соответствующих выражений. Что касается способа обработки, то метод ФАР не требует пояснений. Оптимальная линейная обработка состоит в скалярном умножении вектора сигнала на собственный вектор матрицы N(R), соответствующий максимальному собственному значению ${{\lambda }_{1}}\left( R \right)$. Оптимальная квадратичная обработка сигнала является многоканальной и учитывает вклад всех собственных векторов корреляционной матрицы сигнала. При этом организуется несколько каналов обработки (число их равно рангу корреляционной матрицы), в каждом канале входной сигнал умножается на один из собственных векторов, после чего квадраты полученных для всех каналов скалярных произведений с весами, равными соответствующим собственным значениям ${{\lambda }_{i}}\left( R \right)$, поступают на сумматор и выход антенны. Очевидно, что значительного увеличения коэффициента усиления G₂ в сравнении с G₁ можно ожидать, если в результате декорреляции сигнала у матрицы N(R) появятся несколько собственных значений, сопоставимых с ${{\lambda }_{1}}\left( R \right)$ (напомним, что для полностью когерентного сигнала матрица N(R) имеет лишь одно ненулевое собственное значение).

РЕЗУЛЬТАТЫ МОДЕЛИРОВАНИЯ

Ввиду сложности расчета корреляционной матрицы сигнала в многомодовом волноводе, соответствующие эффекты могут быть рассмотрены лишь путем численного моделирования. Численные расчеты выполнены для мелководного звукового канала со слабым положительным градиентом скорости звука, что, например, типично для Баренцева моря в зимний период. При этом для волновода с линейным профилем c(z) выбраны следующие параметры: c(0) = 1490 м/с, c(H) = = 1500 м/с, глубина дна H = 200 м. В качестве модели дна рассматривается жидкое полупространство со скоростью звука ${{c}_{l}} = 1800$ м/с, плотностью ρ₀ = 2 г/см³ и коэффициентом затухания δ = 0.2 дБ/км Гц. Предполагается, что источник с частотой излучения f₀ = 240 Гц расположен на глубине z_И = 197 м и на такой же глубине z_A = 197 м расположена антенна с числом элементов M = 51 и межэлементным расстоянием d = 3 м. При этом рассматривается антенна, ориентированная перпендикулярно к направлению на источник (β_A = 0) либо под углом β_A = 30°. Расчеты проводились для скоростей ветра V = 10 и V = 15 м/с, то есть согласно принятой терминологии для умеренного и сильного ветрового волнения. При этом основные результаты моделирования приведены при минимальном значении параметра γ = 1 в спектре JONSWAP, за исключением раздела, где обсуждается влияние этого параметра на коэффициенты G_i.

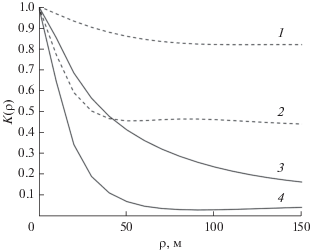
Сначала рассмотрим влияние эффектов рассеяния акустического поля анизотропным волнением на пространственную корреляцию сигнала. В качестве примера на рис. 1 приведены нормированные функции поперечной корреляции акустического поля на глубине расположения антенны

и расстоянии R = 200 км от источника. Видно, что при V = 10 м/с уровень остаточной корреляции поля (обусловленный его когерентной компонентой) остается достаточно высоким, что важно для эффективности линейной обработки сигнала. При этом важно отметить, что в случае поперечной ориентации ветра относительно акустической трассы $\left( {\alpha = \frac{\pi }{2}} \right)$ остаточные корреляции заметно меньше, чем при продольном направлении ветра ($\alpha = 0$). Этот эффект обусловлен сильной анизотропией ветрового спектра, что приводит в итоге к зависимости от угла α коэффициентов уравнения (4) и, в первую очередь, вероятности перехода между модами ${{W}_{{pq}}}\left( \rho \right)$. В случае V = 15 м/с уровень остаточных корреляций поля спадает до значений 0.2 при $\alpha = 0$ и практически до нуля при $\alpha = \frac{\pi }{2}$. От угла α зависит и эффективная ширина корреляционного максимума.

На рис. 2 приведены результаты численных расчетов коэффициентов усиления G₀, G₁ и G₂ при поперечном расположении антенны по отношению и источнику (β_A = 0) и на том же расстоянии R = 200 км. Прежде всего, отметим их симметрию относительно $\alpha = {\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-0em} 2}$. Этот результат следует из соответствующей симметрии коэффициентов уравнения (4). Как и следовало ожидать, исходя из вида функций корреляции, при умеренном ветре V = 10 м/с уменьшение коэффициентов усиления G_i по сравнению со значением G = M = 51, соответствующему коэффициенту усиления полностью когерентного по апертуре сигнала на фоне белого шума, относительно невелико и не превышает 2 дБ. При этом выигрыш оптимальной квадратичной обработки (G₂) по сравнению с оптимальной линейной (G₁) незначителен, что объясняется сохранением высокой степени когерентности сигнала на апертуре антенны. Понятна и близость значений G₁ и G₀, поскольку при поперечном расположении антенны многомодовость сигнала практически не сказывается (отсутствуют проекции модовых волновых чисел на ось АР и все моды приходят на апертуру синфазно). Тем не менее видно заметную (до 2 дБ) зависимость коэффициентов усиления G_i от направления ветра. При сильном ветре коэффициенты усиления G_i имеют существенно меньшие значения. Коэффициенты G₀ и G₁ уменьшаются в сравнении с G = M на 3–7 дБ. Угловые изменения коэффициентов усиления порядка 3 дБ. Выигрыш квадратичной обработки в сравнении с линейной достигает 3 дБ при $\alpha = {\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-0em} 2}$, что обусловлено значительной декорреляцией сигнала.

Чтобы продемонстрировать зависимость этих эффектов от расстояния R, на рис. 3 приведены коэффициенты G_i при перпендикулярной и продольной ориентациях ветра относительно акустической трассы. Видно, что и при умеренном и при сильном волнении уменьшение коэффициентов усиления G_i происходит неравномерно, наиболее заметный эффект наблюдается на R ≤ 50 км, затем изменения с расстоянием всех коэффициентов усиления существенно замедляются. Этот эффект был отмечен в работе [10] для модели изотропного ветрового волнения и объяснялся зависимостью от номера моды декремента затухания когерентной компоненты ${{\gamma }_{p}}$. На самом деле, затухание когерентной компоненты непосредственно не приводит к декорреляции сигнала, которая формируется рассеянной компонентой акустического поля и напрямую зависит от значений вероятности перехода ${{W}_{{pq}}}\left( \rho \right)$. Как видно из формулы (7), величина ${{W}_{{pq}}}\sim {{\left( {{{d{{\varphi }_{p}}} \mathord{\left/ {\vphantom {{d{{\varphi }_{p}}} {dz}}} \right. \kern-0em} {dz}}} \right)}^{2}}{{\left( {{{d{{\varphi }_{q}}} \mathord{\left/ {\vphantom {{d{{\varphi }_{q}}} {dz}}} \right. \kern-0em} {dz}}} \right)}^{2}}$, а для выбранного волновода производные собственных функций при z = 0 приблизительно пропорциональны номеру моды, за исключением нескольких низших мод. Таким образом, формирование рассеянной компоненты и спадание коэффициента корреляции поля на малых расстояниях обусловлено старшими и средними модами, для которых значения ${{W}_{{pq}}}\left( \rho \right)$ относительно велики. Но с увеличением R эти моды затухают в донном грунте (а также вследствие излучения энергии из волновода) и декорреляция определяется низшими модами, для которых эффекты рассеяния менее интенсивны. Соответственно и зависимость коэффициентов усиления G_i от направления ветра увеличивается на расстоянии R ≤ 50 км и затем плавно эволюционирует в пределах 2–3 дБ.

Рассмотрим теперь результаты численного моделирования для антенны, ориентированной под углом β_A = 30°. На рис. 4 приведены результаты расчетов коэффициентов усиления G_i в зависимости от расстояния R при $\alpha = 0$ и $\alpha = {\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-0em} 2}$. Сравнение результатов оптимальной линейной и квадратичной обработки приводит к тем же выводам: малые их отличия при умеренном ветре и заметный выигрыш квадратичной обработки при сильном ветре. Разница значений G₁ и G₂ для углов направления ветра $\alpha = 0$ и $\alpha = {\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-0em} 2}$, по-прежнему, порядка 2 дБ. Наиболее заметно отличие результатов для G₀, т.е. метода ФАР. Коэффициент усиления G₁, в отличии от случая β_A = 0, значительно растет на расстояниях R ≤ 100 км и лишь затем начинает уменьшаться с расстоянием. Это обусловлено возбуждением точечным источником широкого спектра мод и различием их волновых чисел k_p. Поскольку фазовая компенсация происходит с опорным волновым числом ${{k}_{{\text{A}}}} = {\omega \mathord{\left/ {\vphantom {\omega {c\left( {{{z}_{{\text{A}}}}} \right)}}} \right. \kern-0em} {c\left( {{{z}_{{\text{A}}}}} \right)}}$ и не учитывает индивидуальные фазовые распределения мод на апертуре, значительная часть мод “выпадает” из главного лепестка диаграммы направленности, что приводит к значительному проигрышу метода ФАР на малых расстояниях. В то же время, оптимальная линейная обработка в такой ситуации обеспечивает адаптивное, в соответствии с модовым спектром сигнала, смещение угла фазировки на максимум функции углового отклика АР и дополнительное расширение главного лепестка диаграммы направленности за счет аподизации весового вектора [10]. В результате оптимизированная диаграмма направленности “собирает” основные энергонесущие моды и увеличивает выигрыш линейной обработки сигнала в сравнении с ФАР. С увеличением дистанции R модовый спектр сигнала определяется слабозатухающими низшими модами, для которых волновые числа k_p близки к значению k_A и, соответственно, эффективность метода ФАР увеличивается. При этом G₀ приближается к значениям оптимальной линейной обработки G₁ и затем уменьшается с дистанцией, оставаясь близким к нему. На рис. 5 приведены зависимости коэффициентов усиления G_i от направления ветра для расстояния R = 200 км. Нетрудно видеть, что качественно они близки к аналогичным зависимостям для β_A = 0 (см. рис. 2), т.е. малому отличию результата для всех трех методов обработки при V = 10 м/с и заметному выигрышу оптимальной квадратичной обработки в сравнении с линейной и методом ФАР при V = 15 м/с. Угловые изменения коэффициентов усиления G_i и в этом случае порядка 2–3 дБ.

Интересно отметить, что при углах α, близких к π/4 (либо (3/4)π), результаты расчетов коэффициентов G_i мало отличаются от аналогичных результатов, полученных для упрощенной модели волнения с изотропным частотно-угловым спектром для произвольных значений дистанции R. В качестве иллюстрации на рис. 6 приведены соответствующие результаты для перпендикулярно ориентированной антенны (β_A = 0) при двух значениях скорости ветра.

В заключениe рассмотрим влияние эмпирического параметра γ в спектре JONSWAP, отражающего превышение спектрального максимума над спектром Пирсона–Московитца. Как уже отмечалось выше, значения γ > 1 усиливают вклад в эффекты рассеяния наиболее анизотропных компонент спектра волнения, что должно привести к более сильной зависимости коэффициентов усиления антенны от направления ветра. В качестве примера рассмотрим результаты расчета значений G_i при γ = 3.3 для дистанции R = 200 км и β_A = 0. Соответствующие результаты приведены на рис. 7. Сравнение их с аналогичными расчетами при γ = 1 (см. рис. 2) показывает, что при γ = 3.3 коэффициенты усиления G_i несколько уменьшились (особенно при скорости ветра V = 10 м/с) и их угловые изменения увеличились с 2 до 3 дБ, но все же эти эффекты в целом не столь значительны. Слабая зависимость от параметра γ объясняется узостью частотного интервала в спектре волнения JONSWAP, где существенно его влияние (см. (10)), и, соответственно, малым вкладом этого интервала в интегральные выражения (5) и (7).

Приведенные выше результаты численного моделирования получены для конкретного акустического волновода, хотя и с типичными характеристиками. Вместе с тем, параметры мелководных звуковых каналов обладают большим разнообразием, что, естественно, влияет на количественные зависимости коэффициентов усиления антенны. Исследовать это влияние в полном объеме не представляется возможным в рамках данной работы. Поэтому приведенные здесь численные результаты имеют скорее иллюстративный характер. Вместе с тем, полученные качественные зависимости коэффициента усиления антенны от направления ветра и дистанции, а также соотношение результатов при различных способах пространственной обработки, как нам представляется, являются типичными и для других условий распространения акустических сигналов в мелком море.

ЗАКЛЮЧЕНИЕ

В работе продолжено исследование влияния ветрового волнения на эффективность пространственной обработки низкочастотных акустических сигналов в мелком море с использованием горизонтальной антенной решетки. В отличие от предыдущих статей здесь учитывалась анизотропия эмпирического спектра ветрового волнения и, соответственно, анизотропия эффектов многократного рассеяния акустического поля на нерегулярной свободной поверхности звукового канала. Рассмотрены три метода пространственной обработки узкополосного сигнала: формирование диаграммы направленности (ФАР), оптимальная линейная обработка и оптимальная квадратичная обработка. При этом основная характеристика акустического поля – матрица пространственной корреляции на элементах АР – рассчитывалась с помощью уравнения переноса для корреляционных функций акустических мод. Ввиду сложности аналитического исследования данной задачи, основные результаты были получены путем численного моделирования для типичных условий распространения Баренцева моря в зимний период. В качестве основной характеристики пространственной обработки рассматривался коэффициент усиления антенны, который анализировался при умеренном и сильном ветровом волнении на удалении от источника до 300 км. При этом АР ориентировалась либо перпендикулярно, либо под углом к направлению на источник.

Показано, что при умеренном ветровом волнении декорреляция сигнала на элементах антенны относительно невелика и, соответственно, уменьшение коэффициента усиления не превышает 2 дБ. При этом выигрыш оптимальной квадратичной обработки по сравнению с оптимальной линейной незначителен. При сильном волнении декорреляция сигнала на апертуре АР существенно увеличивается, уменьшение коэффициента усиления достигает 5–7 дБ и выигрыш квадратичной обработки в сравнении с линейной равен 2–3 дБ. Метод ФАР сравним по эффективности с оптимальной линейной обработкой при поперечной ориентации антенны и существенно проигрывает ей при ориентации под углом к направлению на источник. Расчеты также указывают на существенную зависимость коэффициента усиления АР от направления ветра по отношению к акустической трассе. Декорреляция сигнала и снижение значения коэффициента усиления максимальны при поперечном и минимальны при продольном направлении ветра. Показано также, что полученные ранее [10] результаты с использованием модели изотропного волнения близки к результатам данной работы при направлении ветра под углом π/4 по отношению к трассе.

Данная работа выполнена при поддержке гранта РНФ № 20-19-00383.