Химия высоких энергий, 2020, T. 54, № 1, стр. 3-12
Кинетика радикально-цепной полимеризации. III. Восстановление концентрации макрорадикалов при передаче цепи
И. П. Ким a, Е. И. Кац b, В. А. Бендерский a, *
a Институт проблем химической физики РАН,
142432 Московская обл., Черноголовка, просп. Академика Семенова 1, Россия
b Институт Теоретической Физики им. Л.Д. Ландау РАН,
142432 Московская обл., Черноголовка, просп. Академика Семенова 1, Россия
* E-mail: bender@icp.ac.ru
Поступила в редакцию 25.06.2019
После доработки 25.06.2019
Принята к публикации 12.08.2019
Аннотация
Передача цепи вызывает циклы возврата–восстановления концентрации первичных радикалов в следующих поколениях и последующий повторный рост макрорадикалов. Рост цепи в отсутствие ее передачи соответствует движению по координате длины цепи волнового пакета первого поколения, а в циклах возврата возникают пакеты с запаздыванием, зависящим от длины цепи образовавшихся ранее макрорадикалов. Суперпозиция запаздывающих пакетов сравнивается с эхо Лошмидта, возникающим в квантовых системах за счет переходов между начальным состоянием и резервуаром. Предложен метод разделения концентраций макрорадикалов первого поколения и эхо и найден возраст (среднее время запаздывания) эхо, зависящий от длины цепи.
I. ВВЕДЕНИЕ
Радикально-цепная полимеризация (РЦП) является в течение многих десятилетий объектом теоретических и экспериментальных исследований. Новый интерес к этому явлению в последнем десятилетии [1–4] обусловлен возможностью создания полимеров со специальной архитектурой и молекулярно-массовым распределением, управляемым контролируемым изменением условий РЦП. Поскольку изменение этих условий учитывается в кинетических уравнениях, как изменение констант скорости роста, передачи и обрыва цепи, исследование этой возможности привело к более детальному исследованию кинетики РЦП, преимущественно на основе уравнений Смолуховского (УС) и Беккера–Деринга (УБД), описывающих кинетику агрегации и фазовых переходов первого рода [5–10]. Однако, в предыдущих статьях настоящей серии [11, 12] показано, что система кинетических уравнений, описывающих зависящие от времени концентрации реагентов (мономеров и первичных радикалов) и продуктов (олигомеров и макрорадикалов), отличается от УС и УБД тем, что в РЦП участвуют не одна, а две связанных подсистемы – превращающихся в олигомеры мономеров и превращающихся в макрорадикалы первичных радикалов, причем число частиц (мономеров и мономерных единиц в составе макрорадикалов и олигомеров и полное число радикалов) сохраняется в каждой из подсистем. Как результат взаимодействия, кинетика роста цепи макрорадикалов состоит из двух разделенных во времени составляющих. Быстрая баллистическая составляющая соответствует движению волнового пакета по длине цепи, как координате. Запаздывающая составляющая возникает, когда рост прерывается актами передачи цепи, после которых частично восстанавливается концентрация первичных радикалов и повторно растут цепи следующих поколений. В передаче цепи участвуют все образовавшиеся ранее макрорадикалы, независимо от их длины.
Наличие двух связанных подсистем (начального состояния и резервуара) характерно для широкого круга квантовых и классических динамических систем [13–17]. Эти общепринятые модели непрерывно развиваются и широко используются в различных областях химической динамики, от универсальной теории переходного состояния, передачи энергии и заряда в конденсированных средах, до стохастических превращений в больших молекулах и агрегатах [18–22]. В квантовых системах начальное состояние взаимодействует с резервуаром, обладающим плотным дискретным спектром состояний, близким по энергии к начальному [23–26]. Прямые и обратные переходы между подсистемами создают циклы возврата, в каждом из которых частично восстанавливается населенность начального состояния. Это явление, получившее название эхо Лошмидта, известно также в динамике волновых пакетов [20, 26–28]. Частота циклов возврата определяется средней разностью энергий соседних уровней, а число компонент и ширина эхо зависят от параметров взаимодействия. С ростом номера цикла эхо уширяется за счет увеличения числа состояний резервуара, участвующих в обратных переходах, и заполняет весь период цикла. Когда компоненты соседних циклов перекрываются, регулярная динамика переходит в стохастическую.
В отсутствие взаимодействия состояния резервуара взаимно ортогональны, так что переходы между ними осуществляются только через начальное состояние, как промежуточное. В результате эхо Лошмидта для начального состояния вызывает эхо и в состояниях резервуара, называемое двойными резонансами [24]. Кинетика РЦП также включает циклы возврата, обусловленные передачей цепи, частично восстанавливающей концентрацию первичных радикалов и приводящей к росту макрорадикалов, который напоминает эхо Лошмидта и двойные резонансы.
Сравним в табл. 1 характеристики процесса РЦП и обычно рассматриваемой модели АBn (начальное состояние $A$ связано с многоуровневым резервуаром взаимно ортогональных состояний $\left\{ {{{B}_{n}}} \right\}$), отождествив концентрации первичных радикалов $R$ и макрорадикалов $\left\{ {{{R}_{n}}} \right\}$ с населенностями $A$ и $\left\{ {{{B}_{n}}} \right\},$ а вероятности переходов – с константами скоростей соответственно. В обеих моделях в первом цикле происходит только переход из начального состояния в резервуар, его населенность, как и концентрация первичных радикалов монотонно уменьшается, обратные переходы из резервуара (передача цепи) отсутствуют. В модели АBn период регулярных циклов возврата определяет собственная частота (средняя разность энергий соседних состояний) в спектре резервуара. Регулярная динамика наблюдается, когда вероятности переходов $A \to {{B}_{1}}$ и ${{B}_{1}} \to A$ больше собственной частоты. В модели РЦП такого параметра нет и расположение цикла возврата во времени подлежит определению из решения кинетической задачи. В обеих моделях во втором цикле полностью восстанавливается населенность начального состояния, но в модели АBn полная населенность начального состояния и состояний резервуара сохраняется во всех циклах, а в РЦП динамика ограничена вторым циклом из-за уменьшения вероятности перехода, пропорциональной концентрации мономера. Различие моделей определяется также тем, что вероятности прямых и обратных переходов $A \Leftrightarrow {{B}_{n}}$ в АBn не зависят от времени и одинаковы для всех состояний, тогда как в РЦП происходит только зависящий от времени прямой переход $R \to {{R}_{1}}$ (бимолекулярный рост первого звена цепи, в котором участвует экспоненциально уменьшающаяся концентрация мономеров) и медленный обратный переход ${{R}_{1}} \to R$ (передача цепи). Переходы между состояниями резервуара в модели АBn, ортогональными в отсутствие взаимодействия с $A$ происходят только через него, тогда в РЦП этот канал конкурирует с более быстрым ростом цепи. В противоположность модели АBn, концентрации макрорадикалов (состояний резервуара ${{R}_{n}}$) заполняются быстрее, чем восстанавливается концентрация $R$, так, что резервуар действует на начальное состояние как единое целое. Эхо Лошмидта в концентрации макрорадикала ${{R}_{n}}$ создает совокупность каналов, в которых участвуют макрорадикалы различной длины $\left\{ {{{R}_{{n{\kern 1pt} '}}}} \right\} \to R \to {{R}_{1}} \cdots {{R}_{{n - 1}}} \to {{R}_{n}},$ причем эти каналы перемешиваются, поскольку их скорости одного порядка $k.$ Поскольку ${{k}_{n}} \ll {{K}_{n}}$ для всех $R,$ эхо преимущественно создают переходы с одним актом передачи цепи, а вклад переходов, в которых многократно образуется начальное состояние, мал. Таким образом, в модели РЦП регулярная динамика (периодичность циклов) отсутствует, поскольку все циклы, начиная со второго, перемешаны.
Таблица 1.
Сравнение динамических свойств моделей “начальное состояние–резервуар $A - {{B}_{n}}$” и РЦП $R - {{R}_{n}}$
| Характеристика | $A - {{B}_{n}}$ | $R - {{R}_{n}}$ |
|---|---|---|
| Вероятности перехода | Не зависят от времени t и номера состояния n | Зависят от t и n |
| Период цикла возврата | Период собственных колебаний резервуара T | Определяется из решения динамической задачи |
| Вероятность перехода из начального состояния в резервуар | C, одинакова для всех n, $CT \gg 1$ | Только переход $R \to {{R}_{1}}$ с константой скорости K1 |
| Вероятность обратного перехода в начальное состояние | C для всех состояний ${{B}_{n}} \to A$ | ${{k}_{n}} \ll {{K}_{n}}$ для всех состояний ${{R}_{n}} \to R$ |
| Вероятность перехода между состояниями резервуара | Только через начальное состояние: ${{B}_{n}} \to A \to {{B}_{{n{\kern 1pt} '}}}$ | Быстрый переход ${{R}_{n}} \to {{R}_{{n + 1}}}$ и медленный переход из всех состояний через начальное ${{R}_{{n{\kern 1pt} '}}} \to R \to {{R}_{1}} \cdots {{R}_{{n - 1}}} \to {{R}_{n}}$ |
| Интенсивность эхо | Одинакова во всех циклах | Уменьшается из-за экспоненциального уменьшения скорости перехода ${{R}_{n}} \to {{R}_{{n + 1}}}$ |
| Условие перехода от регулярной динамики к стохастической | Критический номер цикла ${{N}_{c}} \gg 1,$ в котором перемешиваются компоненты эхо соседних циклов | Перемешиваются все циклы, кроме первого |
| Эхо Лошмидта в начальном состоянии и в состояниях резервуара | В каждом регулярном цикле, $N \leqslant {{N}_{c}}$ | Только во втором цикле, если для всех состояний ${{k}_{n}} \ll {{K}_{n}}$ |
Модель АBn не описывает процессы возврата в RRn. Насколько мы сумели установить, адекватная модель этого процесса еще не рассматривалась, хотя именно свойства эхо Лошмидта во многом определяют возможности создания РЦП с управляемыми характеристиками. Решение этой задачи и представлено в статье.
Во втором разделе статьи представлено аналитическое решение кинетической задачи, когда константы скорости роста и передачи цепи не зависят от ее длины. В третьем разделе описан метод разделения составляющих концентрации макрорадикалов, обусловленных баллистическим ростом в первом и диффузионным ростом цепи во втором цикле, и рассмотрены характеристики эхо Лошмидта. Четвертый раздел посвящен зависимости возраста цепи макрорадикалов первого и второго поколений. Результаты суммированы в пятом разделе.
Компьютерные расчеты выполнены в кодах MATLAB-R-2018 по программе ODE113. Число кинетических уравнений обычно составляло N = 100, а в контрольных расчетах, где проверялось, что результаты не зависят от N, увеличивалось до 200.
II. РОСТ МАКРОРАДИКАЛОВ В УСЛОВИЯХ ПЕРЕДАЧИ ЦЕПИ
В принятой схеме РЦП [11, 12], где константы скорости роста kg и передачи цепи kt не зависят от ее длины, концентрация мономеров экспоненциально уменьшается во времени
и концентрации первичных радикалов подчиняются уравнению(2)
$\dot {R} + \left( {{\text{exp}}\left( { - at} \right) + k} \right) = ka,\,\,\,\,R\left( 0 \right) = a,$(4)
$\begin{gathered} {{R}_{b}}\left( t \right) = a{\text{exp}}\left( { - \Phi \left( t \right) - kt} \right), \\ ~{{R}_{d}}\left( t \right) = ka{\text{exp}}\left( { - \Phi \left( t \right) - kt} \right) \times \\ \times \,\,\int\limits_0^t {{\text{exp}}\left( { - \Phi \left( {t{\kern 1pt} '} \right) - kt{\kern 1pt} '} \right)} dt{\kern 1pt} ', \\ \end{gathered} $(6)
$\begin{gathered} R\left( t \right) \approx {{R}_{b}}\left( t \right) \approx a{{(1 + k)}^{{ - 1}}}\left( {{\text{exp}}\left( { - \left( {1 + k} \right)t} \right) + k} \right), \\ \Phi \approx t \gg kt,~\,\,\,\,at \ll 1. \\ \end{gathered} $Диффузионная составляющая преобладает в заключительной стадии РЦП, когда из-за уменьшения концентрации мономеров (1) скорость роста цепи становится одного порядка, а затем и меньше, чем ее передачи, что и приводит к восстановлению начальной концентрации $R\left( t \right)$
(7)
$\begin{gathered} R\left( t \right) \approx {{R}_{d}}\left( t \right) \approx a\left( {1 - \exp \left( { - kt} \right)} \right), \\ \Phi \sim {1 \mathord{\left/ {\vphantom {1 a}} \right. \kern-0em} a} \ll kt. \\ \end{gathered} $Согласно (6) и (7), спад и рост $R\left( t \right)$ происходят в различных масштабах времени, поскольку $k,$ $a \ll 1.$ Между ними расположена широкая промежуточная область, в которой происходит основной рост цепи макрорадикалов при малой и приблизительно постоянной концентрации первичных радикалов, причем продолжительность этой области уменьшается, а концентрация первичных радикалов возрастает с ростом $k$(рис. 1). Как показано в [11], подстановка
(8)
$u = {{a}^{{ - 1}}}{\text{exp}}\left( { - at} \right),\,\,\,\,\nu = {k \mathord{\left/ {\vphantom {k a}} \right. \kern-0em} a},$(9)
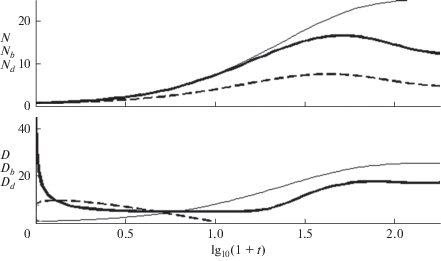
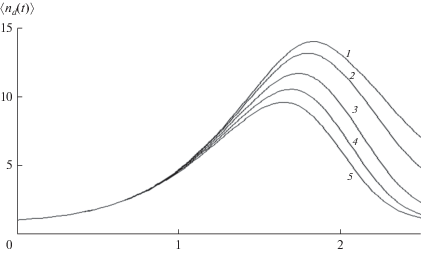
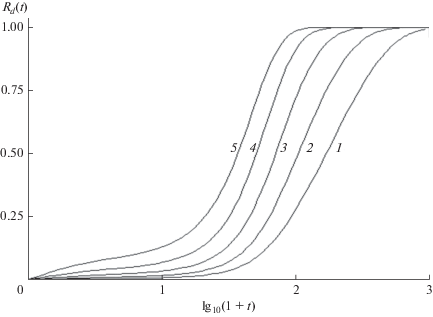
${{R}_{d}}\left( u \right) = k{{e}^{u}}{{u}^{\nu }}\left( {\Gamma \left( {u, - \nu } \right) - \Gamma \left( {{1 \mathord{\left/ {\vphantom {1 a}} \right. \kern-0em} a}, - \nu } \right)} \right).$Рис. 1.
Восстановление концентрации (эхо Лошмидта) в концентрации первичных радикалов. a = 0.02, k = 0.005, 0.01, 0.02, 0.04, 0.08 (кривые 1–5 соответственно).
Поскольку начальная концентрация первичных радикалов на несколько порядков меньше, чем мономеров $\left( {a \ll 1} \right),$ $\Gamma \left( {{1 \mathord{\left/ {\vphantom {1 a}} \right. \kern-0em} a}, - \nu } \right)$ можно заменить первым членом асимптотического разложения
(10)
$\Gamma \left( {1{\text{/}}a, - \nu } \right) \approx {{a}^{{1 + \nu }}}{\text{exp}}\left( { - 1{\text{/}}a} \right),$(11)
$\begin{gathered} \Gamma \left( {u, - \nu } \right) = {{u}^{{ - \left( {1 + \nu } \right)}}}{{e}^{{ - u}}}\left( {1 - \mathop \sum \limits_{n = 1} {{{( - 1)}}^{n}}{{{(1 + \nu )}}_{n}}{{u}^{{ - n}}}} \right), \\ {{(1 + \nu )}_{n}} = \left( {1 + \nu } \right) \cdots \left( {n - 1 + \nu } \right), \\ \end{gathered} $(12)
$\begin{gathered} \Gamma \left( {u, - \nu } \right) \approx \Gamma \left( { - \nu } \right) - {{e}^{{ - u}}}{{u}^{{ - \nu }}}\sum\limits_{n = 0} {\frac{{{{u}^{n}}}}{{{{{\left( { - \nu } \right)}}_{{n + 1~}}}}}} , \\ {{\left( { - \nu } \right)}_{{n = 1}}} = - \nu \left( {1 - \nu } \right) \cdots \left( {n - \nu } \right). \\ \end{gathered} $Уравнения (9)–(13) описывают восстановление $R\left( t \right)$ при $at \gg 1.$Чтобы в компьютерных расчетах избежать операций с многозначными гамма функциями с отрицательным индексом, используются рекуррентные соотношения, увеличивающие индекс. Например, для $0 < {v} < 1$
(13)
$\begin{gathered} {{R}_{d}}\left( u \right) = a\left( {1 - {{R}_{b}}\left( u \right) - {{e}^{u}}{{u}^{{v}}}} \right. \times \\ \times \,\,\left. {\left( {\Gamma \left( {u,1 - {v}} \right) - \Gamma \left( {{{a}^{{ - 1}}},1 - {v}} \right)} \right)} \right). \\ \end{gathered} $Из (13) следует, что кинетика ${{R}_{d}}\left( t \right)$ включает начальный участок медленного роста в области $u > 1,$ т.е. $1 < t < {{a}^{{ - 1}}}{\text{ln}}\left( {{{a}^{{ - 1}}}} \right),$ где, в согласие с (6), концентрация первичных радикалов пропорциональна $k$ и мала по сравнению с начальной, и последующее увеличение до начального значения при $u < 1.$ Начальный участок соответствуют росту длины цепи макрорадикалов, когда их суммарная концентрация почти постоянна, медленно уменьшаясь за счет передачи цепи, что и приводит к незначительному начальному росту ${{R}_{d}}\left( t \right).$ Последующее восстановление начальной концентрации первичных радикалов происходит из-за уменьшения концентрации мономера (1), когда скорость роста цепи становится меньше скорости ее передачи, т.е. $u < {v}\sim 1,$ ${\text{exp}}\left( { - at} \right) < k.$ Таким образом, два участка изменения ${{R}_{d}}\left( t \right)$ cоответствуют областям $u > 1$ и $u < 1,$ в которых (13) можно переписать, пользуясь разложением неполных гамма-функций в асимптотический и степенной ряд соответственно:
(14)
$\Gamma \left( { - {v},u} \right) \approx \left\{ {\begin{array}{*{20}{c}} { - {{{v}}^{{ - 1}}}\Gamma \left( {1 - {v}} \right) + {{u}^{{ - {v}}}}\left( {{{{v}}^{{ - 1}}} + {{{(1 - {v})}}^{{ - 1}}}u - {{{(2 - {v})}}^{{ - 1}}}{{{{u}^{2}}} \mathord{\left/ {\vphantom {{{{u}^{2}}} 2}} \right. \kern-0em} 2}!\, + \cdots } \right)~,~\,\,u < 1} \\ {{{e}^{{ - u}}}{{u}^{{ - \left( {1 + {v}} \right)}}}\left( {1 - \frac{{\Gamma \left( {2 + {v}} \right)}}{{\Gamma \left( {1 + {v}} \right)}}{{u}^{{ - 1}}} + \frac{{\Gamma \left( {3 + {v}} \right)}}{{\Gamma \left( {1 + {v}} \right)}}{{u}^{{ - 2}}} - \cdots } \right)~,~\,\,u > 1} \end{array}} \right..$Поскольку разложения (14) удовлетворительно совпадают в области $u\sim 1,$ ими можно воспользоваться для расчета составляющих концентраций макрорадикалов с длиной цепи $n \geqslant 1,$ решая кинетические уравнения последовательно
(15)
$\begin{gathered} {{{\dot {R}}}_{n}} + \left( {{\text{exp}}\left( { - at} \right) + k} \right){{R}_{n}} = {\text{exp}}\left( { - at} \right){{R}_{{n - 1}}}, \\ {{R}_{n}}\left( 0 \right) = 0. \\ \end{gathered} $Из (15) следует, что ${{R}_{n}}\left( t \right),$ как и $R\left( t \right),$ состоят из быстрой баллистической и последующей медленной составляющих
(16)
$\begin{gathered} {{R}_{n}}\left( t \right) = {{R}_{{nb}}}\left( t \right) + {{R}_{{nd}}}\left( t \right), \\ {{R}_{{nb}}}\left( t \right) = \exp \left( { - \Phi \left( t \right) - kt} \right)~{{\Phi }^{n}}(t){\text{/}}n!, \\ ~{{R}_{{nd}}}\left( t \right) = ~\exp \left( { - \Phi \left( t \right) - kt} \right) \times \\ \times \,\,\int\limits_0^t {\exp } \left( {\Phi \left( {t{\kern 1pt} '} \right) + \left( {k - a} \right)t{\kern 1pt} '} \right){{R}_{{n - 1}}}\left( {t{\kern 1pt} '} \right)dt{\kern 1pt} '. \\ \end{gathered} $Быстрая составляющая ${{R}_{{nb}}}\left( t \right),$ относящаяся к баллистическому росту цепи первого поколения, описывается, как и при $k = 0,$ распределением Пуассона [12]. Уменьшение концентрации, обусловленное передачей цепи, учитывает дополнительный сомножитель ${\text{exp}}\left( { - kt} \right).$ Максимум ${{R}_{{nb}}}\left( {{{T}_{n}}} \right)$ определяет уравнение
(17)
$\left( {1 + {v}{\text{/}}u\left( {{{T}_{n}}} \right)} \right)\Phi \left( {{{T}_{n}}} \right) = n,$III. ЭХО ЛОШМИДТА ДЛЯ МАКРОРАДИКАЛОВ
Поскольку (16) определяет ${{R}_{{nb}}}\left( t \right)$ аналитически, ${{R}_{n}}\left( t \right)$ можно разделить на составляющие и найти ${{R}_{{nd}}}\left( t \right)$ из компьютерного решения кинетических уравнений (15). Метод разделения иллюстрирует рис. 2. Достоинство метода состоит в том, что его точность не зависит от формы перекрывающихся составляющих и их изменений с длиной цепи (рис. 3). Короткие цепи образуются с наибольшим запаздыванием, когда максимумы эхо ${{R}_{{nd}}}\left( {T_{n}^{{{\text{**}}}}} \right)$ расположены в области $u\left( {T_{n}^{{{\text{**}}}}} \right) \leqslant 1$ и на несколько порядков больше, чем для баллистического роста, $T_{n}^{{{\text{**}}}} \gg {{T}_{n}},$ так что баллистический рост и эхо значительно разделены (рис. 2 и верхняя панель рис. 3). С ростом nTn увеличивается в согласие с (17), а $T_{n}^{{{\text{**}}}}$ уменьшается, и ширина эхо, определяемая интервалом $T_{n}^{{{\text{**}}}} - {{T}_{n}},$ падает. Уменьшение $T_{n}^{{{\text{**}}}}$ с ростом n связано с тем, что после акта передачи цепь второго поколения растет при более низкой концентрации мономеров и, как следствие, оказывается короче цепи первого поколения. Для достаточно длинных цепей основной вклад в эхо вносят короткие цепи, и его максимум смещается в сторону меньших времен. При дальнейшем росте $n$ эхо сужается и его максимум смещается в область $u\left( {T_{n}^{{{\text{**}}}}} \right)\sim 1$ (средняя панель на рис. 3). При $u\left( {T_{n}^{{{\text{**}}}}} \right) \gg 1{{R}_{{nb}}}\left( t \right)$ и ${{R}_{{nd}}}\left( t \right)$ почти полностью перекрываются, и $T_{n}^{{{\text{**}}}} - {{T}_{n}} \to 0,$ как и относительный вклад эхо (нижняя панель рис. 3). Сужение и уменьшение эхо, определяемые запаздыванием, вызванным уменьшением скорости роста цепи из-за расхода мономера, являются характерными особенностями РЦП, отмеченными в табл. 1.
Рис. 2.
Баллистическая и диффузионная составляющие концентрации макрорадикалов с длиной цепи n = 5, 12 и 30 (кривые 1–3, сплошные и пунктирные линии соответственно). a = 0.02, k = 0.01.
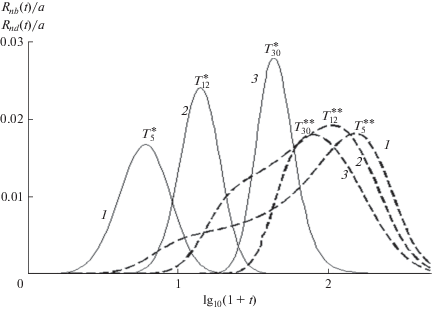
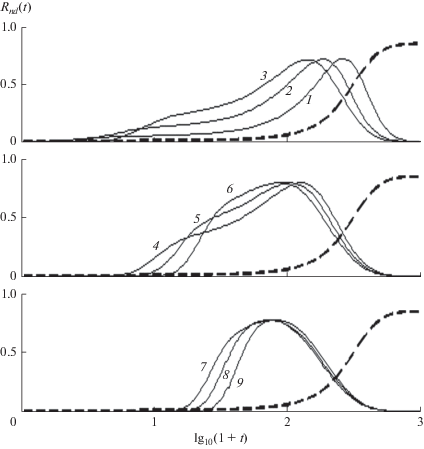
Рис. 3.
Эхо Лошмидта в концентрациях макрорадикалов с длиной цепи n. Панели сверху вниз: n = 1, 3, 6, 9, 12, 17, 20, 24, 29, кривые 1–9 соответственно. a = 0.02, k = 0.01. Пунктиром показана концентрация первичных радикалов. Амплитуды эхо увеличены до 1.
Зависящие от времени нулевой и первый моменты распределения макрорадикалов первого поколения и их отношение, равное среднечисловой длине цепи, имеют вид
(18)
$\begin{gathered} {{S}_{{0b}}}\left( t \right) = \sum\limits_{n = 1}^\infty {{{R}_{{nb}}}} \left( t \right) = \exp \left( { - kt} \right)\left( {1 - \exp ( - \Phi \left( t \right)} \right), \\ ~{{S}_{{1b}}}\left( t \right) = \sum\limits_{n = 1}^\infty {n{{R}_{{nb}}}} \left( t \right) = \exp \left( { - kt} \right)\Phi , \\ {{N}_{b}}\left( t \right) = {{S}_{{1b}}}\left( t \right){\text{/}}{{S}_{{0b}}}\left( t \right) = \Phi {\text{/}}(1 - \exp \left( { - \Phi } \right)). \\ \end{gathered} $Выражение (18) показывает, что ${{N}_{b}}\left( t \right) \ll a$ и не зависит от k. Из (16) следует, что моменты распределения ${{R}_{{nd}}}\left( t \right),$ средне-числовая длина цепи и дисперсия распределения макрорадикалов в эхо равны
(19)
$\begin{gathered} {{S}_{{\alpha d}}} = \sum\limits_{n = 1}^\infty {{{n}^{\alpha }}} {{R}_{{nb}}}\left( t \right),\,\,\,\,\alpha = 0,1,2, \\ {{N}_{d}}\left( t \right) = {{S}_{{1d}}}\left( t \right){\text{/}}{{S}_{{0d}}}\left( t \right),\,\,\,\,{{D}_{d}} = {{\left( {{{S}_{{2d}}}\left( t \right){\text{/}}{{S}_{{0d}}}\left( t \right)} \right)}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}. \\ \end{gathered} $Среднечисловая длина цепи макрорадикалов с учетом обеих составляющих равна
(20)
$N\left( t \right) = \frac{{\Phi \left( t \right){\text{exp}}\left( { - kt} \right) + {{S}_{{1d}}}\left( t \right)}}{{\left( {1 - {\text{exp}}\left( { - \Phi \times 9t} \right)} \right){\text{exp}}\left( { - kt} \right) + {{S}_{{{\text{01}}}}}\left( t \right)}}.$Метод, рассмотренный выше, позволяет определить характеристики (19). Их сравнение с теми же характеристиками распределений макрорадикалов в целом и макрорадикалов первого поколения представлено на рис. 4. Моменты распределений и средние длины цепи в эхо меньше, чем при баллистическом росте и уменьшаются с увеличением k. Максимумы N(t) расположены в окрестности Tn, когда доминирует баллистическая составляющая. Последующее уменьшение средней длины происходит в цикле возврата. Как показано в [4], узкая дисперсия распределения является отличительным свойством олигомеров с регулируемой длиной цепи и архитектурой. На нижней панели рис. 4 показано, что изменение дисперсии во времени так же, как и концентрации первичных радикалов, состоит из начального участка быстрого уменьшения, связанного как с уширением распределения при баллистическом росте [12], так и вкладом эхо, области приблизительно постоянной дисперсии и последующего роста, когда эхо подавлено. В согласие с рис. 2, средняя длины цепи в эхо уменьшается с ростом константы скорости передачи цепи k (рис. 5).
IV. ВОЗРАСТ МАКРОРАДИКАЛОВ
Различие баллистического и диффузионного роста макрорадикалов, рассмотренное в предыдущих разделах, показывает, что средняя длина цепи и ее дисперсия не дают полного представления о кинетике РЦП. Причина того, что трех моментов недостаточно, заключается в том, что оба распределения зависят от времени и изменения их моментов соизмеримы.
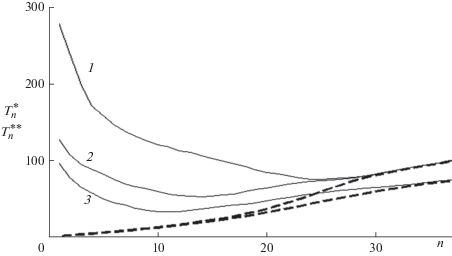
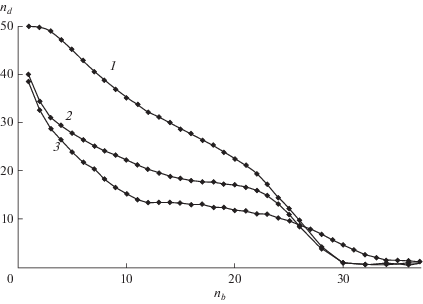
В подобных случаях целесообразно ввести дополнительные характеристики РЦП. Поскольку $k \ll 1,$ передача цепи незначительно влияет на последующий баллистический рост цепи второго поколения, подходящими характеристиками являются время роста, принятое равным $T_{n}^{{{\text{**}}}} - {{T}_{n}},$ которое можно назвать возрастом, и длина цепи второго поколения $\left\langle {{{n}_{d}}} \right\rangle .$ Обе характеристики усредняются по совокупности всех состояний $1 \leqslant s \leqslant {\text{max}}\left( n \right),$ в которых возможен акт передачи с учетом населенностей этих состояний. Следует отметить, что эти характеристики не сводятся к отношениям моментов, поскольку связаны только с временами баллистического роста цепей двух поколений (рис. 2). Зависимости этих характеристик от длины цепи представлены на рис. 6 и 7. Значения $T_{n}^{{{\text{**}}}}$ уменьшаются с ростом $n$ до тех пор, пока не исчезает вклад эхо в концентрацию макрорадикалов и составляющие полностью перекрываются, $T_{n}^{{{\text{**}}}} \approx {{T}_{n}},$ после чего остается только баллистический рост. При малых n время роста цепи второго поколения намного больше, чем баллистического роста (17), поскольку в передаче цепи участвуют цепи, длина которых превышает 1/a. Поскольку цепи второго поколения также растут баллистически, возраст $T_{n}^{{{\text{**}}}}$ зависит от значений параметров a и ${v}{\text{:}}$ с ростом начальной концентрации первичных радикалов и константы скорости передачи цепи возраст (т.е. время роста цепи второго поколения) сокращается. Средняя длина цепи второго поколения, найденная из данных рис. 6 и (17), уменьшается с ростом длины цепи (рис. 7).
V. ВЫВОДЫ
1. Показано, что концентрации макрорадикалов в процессе РЦП являются суммами двух составляющих с различной зависимостью формы и амплитуды от времени. Быстрая составляющая обусловлена баллистическим ростом цепей первого поколения, а вторая – ростом цепей второго поколения, инициируемым актом передачи цепи, в котором погибают с не зависящей от их длины вероятностью все ранее образовавшиеся макрорадикалы и зарождается новая баллистическая цепь. Вторая составляющая, в которой участвует совокупность макрорадикалов первого поколения с различной длиной, запаздывает во времени и уширяется по сравнению с первой. Поскольку она частично восстанавливает концентрации макрорадикалов с задержкой по времени по сравнению с первой, она названа эхо.
2. Предложен метод разделения первой составляющей и эхо, не зависящий от изменения их формы и ширины, включающий компьютерное решение кинетических уравнений и аналитическое определение концентраций макрорадикалов первого поколения.
3. Показано, что вклад эхо существенен при росте коротких цепей, не ограниченном уменьшением концентрации мономера. Когда образуются длинные цепи первого поколения, гибель мономера в процессе их образования подавляет эхо.
4. Разделение составляющих позволяет не только определить моменты их распределений, но ввести две дополнительных характеристики эхо: среднее время его задержки (возраст) и среднюю длину цепи второго поколения.
5. Моменты молекулярно-массовых распределений в сочетании с дополнительными характеристиками обеспечивает детальное описание кинетики РЦП при произвольных зависимостях констант скорости роста и передачи цепи от ее длины.
Список литературы
Lynd N.A., Hillmayer M.A., Matsen M.W. // Macromolecules. 2008. V. 41. P. 4531.
Listak J., Jacubovski W., Mueller L., Plichta A., Matyjaszewski K., Bockstaller M.R. // Macromolecules. 2008. V. 41. P. 5919.
Zhao T., Zheng Y., Poly J., Wang W. // Nature Comm. 2013. V. 4. P. 1873.
Gentekos D.T., Dupuis L.N., Fors B.P. // J. Am. Chem. Soc. 2016. V. 138. P. 1848.
Leyvraz F. // Phys. Reps. 2003. V. 383. P. 95.
Kuchanov S.I., Slot H., Stroeks A. // Progr. Polym. Sci. 2004. V. 29. P. 513.
Wattis J.A.D., Bolton C.D., Coveney P.V. // J. Phys. A. 2004. V. 37. P. 2895.
Wattis J.A.D. // J. Phys. A. 2006. V. 39. P. 7283.
Wattis J.A.D. // Physica D. 2006. V. 222. P. 1.
Leyvraz F. // Phys. Reps. 2003. V. 383. P. 95.
Ким И.П., Кац Е.И., Бендерский В.А. // Химия высоких энергий. 2019. Т. 53. № 4. С. 255.
Ким И.П., Бендерский В.А. // Химия высоких энергий. 2019. Т. 53. № 5. С. 339.
Заславский Г.М. Стохастичность динамических систем. М.: Наука, 1984.
Leggett A.J., Chakravarty S., Dorsey A.T., Fisher M.P.A., Garg A., Zwerger M. // Rev. Mod. Phys. 1987. V. 59. P. 1.
Hanggi P., Talkner P., Borcovek M. // Rev. Mod. Phys. 1990. V. 62. P. 251.
Benderskii V.A., Makarov D.E., Wight C.A. Chemical Dynamics at Low Temperatures. 1994. Wiley. N.Y.
Weiss U. // Quantum Dissipative Systems. 1999. World Scientific. Singapore.
Lee H.M., Kim J., Kim C.-J., Kim K.S. // J. Chem. Phys. 2002. V. 116. P. 6549.
Giese K., Petkovic M., Naundorf H., Kuhn O. // Phys. Reps. 2006. V. 430. P. 211.
Benderskii V.A., Kotkin A.S., Kats E.I. // Phys. Lett. A. 2013. V. 377. P. 737.
Oliver T.A.A., Lewis N.H.C., Fleming G.R. // Proc. Nat. Acad. Sci. USA 2014. V. 111. P. 10061.
Medders G.R., Alguire E.C., Jain A., Subotnik J.E. // J. Phys. Chem. A 2017. V. 121. P. 1425.
Бендерский В.А., Фальковский Л.А., Кац Е.И. // Письма в ЖЭТФ. 2007. Т. 86. С. 249.
Бендерский В.А., Гак Л.Н., Кац Е.И. // ЖЭТФ. 2009. Т. 135. С. 176.
Бендерский В.А., Гак Л.Н., Кац Е.И. // ЖЭТФ. 2009. Т. 136. С. 589.
Бендерский В.А., Кац Е.И. // ЖЭТФ. 20011. Т. 140. С. 647.
Robinet R.W. // Phys. Reps. 2004. V. 392. P. 1.
Ohmori K. // Annu. Rev. Phys. Chem.2009. 60. 487.
Бейтмен Г., Эрдейи А. // Высшие трансцендентные функции. Т. 2. М.: Наука, 1965.
Дополнительные материалы отсутствуют.
Инструменты
Химия высоких энергий