Вестник Военного инновационного технополиса «ЭРА», 2023, T. 4, № 3, стр. 276-283

Автономный контроль целостности навигационных данных в вертикальном канале

А. П. Удалова^1, *

¹ Военный инновационный технополис “ЭРА”
Анапа, Россия

Поступила в редакцию 09.10.2023
После доработки 09.11.2023
Принята к публикации 09.11.2023

DOI: 10.56304/S2782375X23030191

Аннотация

Обоснована необходимость осуществления автономного контроля целостности навигационных данных спутниковых радионавигационных систем в навигационных комплексах наземных подвижных объектов. Рассмотрены комплексные оптимальные алгоритмы оценивания координат и параметров движения наземных подвижных объектов в вертикальной плоскости. Разработана структурная схема устройства вычисления оценки вектора состояния наземных подвижных объектов в вертикальной плоскости с автономной подсистемой контроля целостности навигационных данных спутниковых радионавигационных систем. Методом статистического компьютерного моделирования определены фактические и потенциальные характеристики точности приведенных комплексных оптимальных алгоритмов.

ВВЕДЕНИЕ

При решении задач навигации наземных подвижных объектов (НПО) главным критерием работы навигационных систем является точность определения координат местоположения и параметров движения НПО. Требования к точности местоопределения транспортных средств напрямую зависят от предназначения навигационного комплекса. В [1] приведены требования к точности местоопределения НПО. Например, при общегородских и пригородных перевозках среднее квадратическое отклонение (СКО) должно составлять 15–65 м. В настоящее время актуальным направлением развития транспортной техники являются высокоавтоматизированные транспортные средства (ВАТС). В понятие ВАТС включены автономные или беспилотные транспортные средства, требования к точности (СКО) навигации которых для системы управления городским автотранспортом в центре составляет 2.5 м, на трассе – 15 м, для системы управления региональными перевозками – 10 м [1].

Для обеспечения высокой точности определения координат местоположения и параметров движения НПО в составе навигационного комплекса используется аппаратура приема сигналов спутниковых радионавигационных систем (СРНС) [2, 3]. Однако при решении задач навигации с использованием данных СРНС существует проблема возникновения помех в аппаратуре потребителя сигналов СРНС [4]. По происхождению помехи разделяют на непреднамеренные (естественные, неумышленные) и преднамеренные (искусственные, организованные).

Непреднамеренными помехами являются ионосферная рефракция, ошибки эфемеридных данных, тропосферная рефракция, ошибки спутниковых часов, отраженный сигнал (многолучевость) и собственные шумы приемника.

К преднамеренным (организованным) помехам относят помехи, создаваемые специальными средствами, предназначенными для подавления радиоэлектронных средств [5]. Кроме того, в условиях военных действий возможны попытки как постановки преднамеренных помех с целью подавления сигнала СРНС, так и попытки навязывания, т.е. подмены сигнала и ввода в приемную аппаратуру противника заведомо ложной информации при помощи сторонних передатчиков. В это понятие включают и применение помехоустойчивых кодов, так как в условиях радиоэлектронной войны попытки навязывания начинаются с постановки активных помех с целью прервать нормальную работу и дезориентировать противника [6, 7].

Поэтому наряду с обеспечением высокой точности местоопределения НПО возникает необходимость параллельно решать задачу обеспечения целостности навигационных данных. Под целостностью здесь понимают способность навигационного комплекса обеспечить своевременное предупреждение о том, что данные на входе аппаратуры приема сигнала СРНС являются недостоверными, и изолировать навигационное решение от этих аномалий [8]. Внешне нарушение целостности радиосигналов навигационных спутников проявляется в виде наличия резко выделяющихся из ряда измерений параметров этих сигналов.

Очевидно, что обнаружение этих аномалий требует наличия информационной избыточности в системе. Целостность навигационных данных СРНС обеспечивается, как правило, автономными системами контроля целостности ввиду их независимости от внешнего канала передачи данных и оперативности [9–11]. Среди систем, обеспечивающих автономный контроль целостности, преимуществом обладают системы, использующие фильтрационные методы, называемые также методами усреднения. Они учитывают измерения радионавигационных параметров, предшествующих моменту контроля целостности, поэтому позволяют обнаружить факт аномальной работы аппаратуры приема сигналов СРНС в момент его возникновения и имеют меньшую вероятность ложных срабатываний.

Однако они не в полной мере отвечают перспективным требованиям обеспечения точности навигационных данных. Поэтому разработка методов автономного контроля целостности навигационных данных СРНС является своевременной и актуальной задачей.

ЭКСПЕРИМЕНТАЛЬНАЯ ЧАСТЬ

Каждый отдельный измеритель, входящий в состав навигационной системы, не удовлетворяет всем требованиям, предъявляемым к измерению соответствующего параметра. Поэтому требуется одновременное измерение одинаковых параметров с помощью устройств и систем, работающих на различных физических принципах. Для этого в современных навигационных комплексах осуществляется совместная обработка информации нескольких измерителей, т.е. комплексирование измерителей [12–14].

Комплексирование заключается в использовании информации об одних и тех же или функционально связанных параметрах от различных измерителей. Таким образом повышаются точность и надежность определения навигационных параметров. Для получения максимального результата от комплексирования необходимо решить задачу синтеза, определяющего оптимальную структуру системы комплексной обработки информации [15].

Для решения задачи обеспечения целостности навигационных данных СРНС рассмотрим комплексирование таких радиотехнических и нерадиотехнических измерителей, как аппаратура приема сигналов СРНС и барометрический высотомер (БВ). Таким образом, контроль целостности будет осуществляться в вертикальном канале.

В [16] получены комплексные оптимальные алгоритмы обработки информации. Подлежащий оцениванию вектор состояния имеет вид [16]:

(1)

${\mathbf{X}}({{t}_{k}}) = {{[{{H}_{{{\text{ОТН}}}}}({{t}_{k}}),{{V}_{Z}}({{t}_{k}}),\Delta H({{t}_{k}}),{{\Delta }_{{aZ}}}({{t}_{k}})]}^{T}},$

где ${{H}_{{{\text{ОТН}}}}}({{t}_{k}})$ – измеренное значение высоты объекта, ${{V}_{Z}}({{t}_{k}})$ – вертикальная скорость движения объекта, $\Delta H({{t}_{k}})$ – постоянная составляющая погрешности измерения высоты объекта, ${{\Delta }_{{aZ}}}({{t}_{k}})$ – постоянная составляющая погрешности измерения ускорения.

Вектор состояния описывается разностным векторно-матричным стохастическим уравнением [16]:

(2)

$\begin{gathered} {\mathbf{X}}({{t}_{{k + 1}}}) = {{{\mathbf{\Phi }}}_{{xx}}}({{t}_{{k + 1}}},{{t}_{k}}){\mathbf{X}}({{t}_{k}}) + {\mathbf{\Psi }}({{t}_{{k + 1}}},{{t}_{k}}){\mathbf{W}}({{t}_{k}}) + \\ + \;{{{\mathbf{\Gamma }}}_{x}}({{t}_{{k + 1}}},{{t}_{k}}){{N}_{x}}({{t}_{k}}), \\ \end{gathered} $

где ${\mathbf{W}}({{t}_{k}})$ – известный вектор управления, имеющий вид ${\mathbf{W}} = {{[a_{Z}^{{{\text{ИНС}}}},g]}^{T}}$, ${{N}_{x}}({{t}_{k}})$ – формирующие стандартные гауссовские случайные величины, имеющие вид ${{N}_{x}}({{t}_{k}}) = {{n}_{{aZ}}}({{t}_{k}})$, где ${{n}_{{aZ}}}({{t}_{k}})$ – взаимонезависимые выборки гауссовского процесса с нулевым математическим ожиданием и единичной дисперсией, ${{{\mathbf{\Phi }}}_{{xx}}}$ – фундаментальная матрица размером 4 × 4 с ненулевыми элементами ${{ф}_{{x{{x}_{{11}}}}}} = {{ф}_{{x{{x}_{{22}}}}}} = {{ф}_{{x{{x}_{{33}}}}}} = {{ф}_{{x{{x}_{{44}}}}}} = 1$, ${{ф}_{{x{{x}_{{12}}}}}} = T$, ${{ф}_{{x{{x}_{{14}}}}}}$ = = ‒0.5T², ${{ф}_{{x{{x}_{{24}}}}}} = - T$, T – интервал дискретизации, ${\mathbf{\Psi }}$ – переходная матрица управления размером 4 × 2 с ненулевыми элементами ${{\psi }_{{_{{11}}}}}$ = 0.5T², ${{\psi }_{{_{{12}}}}}$ = = –0.5T², ${{\psi }_{{_{{21}}}}} = T$, ${{\psi }_{{_{{22}}}}} = - T$; ${{{\mathbf{\Gamma }}}_{x}}$ – переходной вектор возмущения размером 4 × 1 с ненулевыми элементами, ${{г}_{{{{x}_{{11}}}}}} = - 0.5{{T}^{2}}{{\sigma }_{a}}{{(2T{\text{/}}{{\alpha }_{a}})}^{{0.5}}}$, ${{г}_{{{{x}_{{21}}}}}} = $ $ = - T{{\sigma }_{a}}{{(2T{\text{/}}{{\alpha }_{a}})}^{{0.5}}}$, где $\sigma _{a}^{2}$ – дисперсия флуктуационной погрешности, α_a – коэффициент, характеризующий ширину спектра погрешности.

Вектор наблюдения, определяемый по формуле [16]:

(3)

${\mathbf{\Xi }}({{t}_{k}}) = {{[{{\xi }_{1}}({{t}_{k}}),{{\xi }_{2}}({{t}_{k}})]}^{T}},$

включает в себя наблюдения на выходе БВ ${{\xi }_{1}}({{t}_{k}}) = H_{{{\text{ОТН}}}}^{{{\text{БВ}}}}({{t}_{k}})$ и аппаратуры приема сигналов СРНС ${{\xi }_{2}}({{t}_{k}}) = {{H}^{{{\text{СРНС}}}}}({{t}_{k}})$, которые описываются выражениями

(4)

${{\xi }_{1}}({{t}_{k}}) = {{{\mathbf{H}}}_{1}}({{t}_{k}}){\mathbf{X}}({{t}_{k}}) + {{u}_{{{\text{БВ}}}}}({{t}_{k}}),$

(5)

${{\xi }_{2}}({{t}_{k}}) = {{{\mathbf{H}}}_{2}}({{t}_{k}}){\mathbf{X}}({{t}_{k}}) + {{V}_{2}} + {{Г}_{2}}({{t}_{k}}){{N}_{2}}({{t}_{k}}),$

где ${{{\mathbf{H}}}_{1}}$ – вектор наблюдения размером 1 × 4 с ненулевыми элементами ${{h}_{{{{1}_{{11}}}}}} = {{h}_{{{{1}_{{13}}}}}} = 1$, ${{{\mathbf{H}}}_{2}}$ – вектор наблюдения размером 1 × 4 с ненулевым элементом ${{h}_{{{{2}_{{11}}}}}} = 1$, V₂ = R₀ – расстояние от центра Земли до уровня моря, ${{u}_{{{\text{БB}}}}}$ – флуктуационная погрешность, Γ₂ = σ_z – известная величина, равная среднеквадратической ошибке флуктуационной погрешности измерения, ${{N}_{2}}({{t}_{k}}) = {{n}_{z}}({{t}_{k}})$ – шум наблюдения.

Уравнения наблюдения (4, 5) и модель изменения вектора состояния (2) являются линейными. Оценка вектора состояния в соответствии с методами оптимальной линейной фильтрации определяется выражением [17]:

$\begin{gathered} {\mathbf{X}}{{{\kern 1pt} }^{*}}({{t}_{{k + 1}}}) = {{{\mathbf{\Phi }}}_{{xx}}}({{t}_{{k + 1}}},{{t}_{k}}){{{\mathbf{X}}}^{*}}({{t}_{k}}) + {\mathbf{\Psi }}({{t}_{{k + 1}}},{{t}_{k}}){\mathbf{W}}({{t}_{k}}) + \\ + \;{{{\mathbf{K}}}_{1}}({{t}_{{k + 1}}})[{{\xi }_{1}}({{t}_{{k + 1}}}) - {{\varphi }_{{uu}}}({{t}_{{k + 1}}},{{t}_{k}}){{\xi }_{1}}({{t}_{k}}) - \\ \end{gathered} $

(6)

$\begin{gathered} - \;{{{\mathbf{H}}}_{1}}({{t}_{{k + 1}}}){\mathbf{\Psi }}({{t}_{{k + 1}}},{{t}_{k}}){\mathbf{W}}({{t}_{k}}) + {{\varphi }_{{uu}}}({{t}_{{k + 1}}},{{t}_{k}}){{{\mathbf{H}}}_{1}}({{t}_{k}}){{{\mathbf{X}}}^{*}}({{t}_{k}}) - \\ - \;{{{\mathbf{H}}}_{1}}({{t}_{{k + 1}}}){{{\mathbf{\Phi }}}_{{xx}}}({{t}_{{k + 1}}},{{t}_{k}}){{{\mathbf{X}}}^{*}}({{t}_{k}})] + {{{\mathbf{K}}}_{2}}({{t}_{{k + 1}}})[{{\xi }_{2}}({{t}_{{k + 1}}}) - \\ \end{gathered} $

$\begin{gathered} - \;{{{\mathbf{H}}}_{2}}({{t}_{{k + 1}}}){\mathbf{\Psi }}({{t}_{{k + 1}}},{{t}_{k}}){\mathbf{W}}({{t}_{k}}) - {{V}_{2}} - \\ - \;{{{\mathbf{H}}}_{2}}({{t}_{{k + 1}}}){{{\mathbf{\Phi }}}_{{xx}}}({{t}_{{k + 1}}},{{t}_{k}}){{{\mathbf{X}}}^{*}}({{t}_{k}})], \\ \end{gathered} $

где ${{\varphi }_{{uu}}}({{t}_{{k + 1}}},{{t}_{k}})$ – постоянная величина, зависящая от интервала дискретизации, ${{{\mathbf{K}}}_{1}}({{t}_{{k + 1}}})$ и ${{{\mathbf{K}}}_{2}}({{t}_{{k + 1}}})$ – вектор-столбцы размером 4 × 1 матрицы оптимальных коэффициентов передачи ${\mathbf{K}}({{t}_{{k + 1}}}) = $ $ = [{{{\mathbf{K}}}_{1}}({{t}_{{k + 1}}}) \vdots {{{\mathbf{K}}}_{2}}({{t}_{{k + 1}}})]$, определяемой соотношениями [17]:

(7)

$\begin{gathered} {\mathbf{K}}({{t}_{{k + 1}}}) = [{{{\mathbf{\Phi }}}_{{xx}}}({{t}_{{k + 1}}},{{t}_{k}}){\mathbf{P}}({{t}_{k}}){\mathbf{\Phi }}_{{yx}}^{T}({{t}_{{k + 1}}},{{t}_{k}}) + {{{\mathbf{B}}}_{{xy}}}] \times \\ \times \;{{[{\mathbf{B}}_{{yy}}^{{ - 1}} + {{{\mathbf{\Phi }}}_{{yx}}}({{t}_{{k + 1}}},{{t}_{k}}){\mathbf{P}}({{t}_{k}}){\mathbf{\Phi }}_{{yx}}^{T}({{t}_{{k + 1}}},{{t}_{k}})]}^{{ - 1}}}, \\ \end{gathered} $

(8)

$\begin{gathered} {\mathbf{P}}({{t}_{{k + 1}}}) = {{{\mathbf{\Phi }}}_{{xx}}}({{t}_{{k + 1}}},{{t}_{k}}){\mathbf{P}}({{t}_{k}}){\mathbf{\Phi }}_{{xx}}^{T}({{t}_{{k + 1}}},{{t}_{k}}) - \\ - \;{\mathbf{K}}({{t}_{{k + 1}}}){{[{{{\mathbf{B}}}_{{xy}}} + {{{\mathbf{\Phi }}}_{{xx}}}({{t}_{{k + 1}}},{{t}_{k}}){\mathbf{P}}({{t}_{k}}){\mathbf{\Phi }}_{{yx}}^{T}({{t}_{{k + 1}}},{{t}_{k}})]}^{T}}, \\ \end{gathered} $

где ${\mathbf{P}}({{t}_{{k + 1}}})$ – матрица вторых центральных моментов (ковариаций) ошибок оценивания размером 4 × 4, ${\mathbf{\Phi }}_{{yx}}^{{}}({{t}_{{k + 1}}},{{t}_{k}})$, ${\mathbf{B}}_{{xy}}^{{}}$,${\mathbf{B}}_{{yy}}^{{}}$– блочные матрицы вида [17]:

(9)

$\begin{gathered} {{{\mathbf{\Phi }}}_{{yx}}}({{t}_{{k + 1}}},{{t}_{k}}) = \\ = \left[ {\frac{{{{{\mathbf{H}}}_{1}}({{t}_{{k + 1}}}){{{\mathbf{\Phi }}}_{{xx}}}({{t}_{{k + 1}}},{{t}_{k}}) - {{\varphi }_{{uu}}}({{t}_{{k + 1}}},{{t}_{k}}){{{\mathbf{H}}}_{1}}({{t}_{k}})}}{{{{{\mathbf{H}}}_{2}}({{t}_{{k + 1}}}){{{\mathbf{\Phi }}}_{{xx}}}({{t}_{{k + 1}}},{{t}_{k}})}}} \right], \\ \end{gathered} $

(10)

$\begin{gathered} {{{\mathbf{B}}}_{{xy}}} = [{{{\mathbf{\Gamma }}}_{x}}({{t}_{{k + 1}}},{{t}_{k}}){\mathbf{\Gamma }}_{x}^{T}({{t}_{{k + 1}}},{{t}_{k}}){\mathbf{H}}_{1}^{T}({{t}_{{k + 1}}})|{{{\mathbf{\Gamma }}}_{x}}({{t}_{{k + 1}}},{{t}_{k}}) \times \\ \times \;{\mathbf{\Gamma }}_{x}^{T}({{t}_{{k + 1}}},{{t}_{k}}){\mathbf{H}}_{2}^{T}({{t}_{{k + 1}}}), \\ \end{gathered} $

(11)

$\begin{array}{*{20}{c}} {{{{\mathbf{B}}}_{{yy}}} = \left[ {\frac{{{{{\mathbf{H}}}_{1}}({{t}_{{k + 1}}}){{{\mathbf{\Gamma }}}_{x}}({{t}_{{k + 1}}},{{t}_{k}}){\mathbf{\Gamma }}_{x}^{T}({{t}_{{k + 1}}},{{t}_{k}}){\mathbf{H}}_{1}^{T}({{t}_{{k + 1}}}) - \varphi _{{uu}}^{2}({{t}_{{k + 1}}},{{t}_{k}})}}{{{{{\mathbf{H}}}_{2}}({{t}_{{k + 1}}}){{{\mathbf{\Gamma }}}_{x}}({{t}_{{k + 1}}},{{t}_{k}}){\mathbf{\Gamma }}_{x}^{T}({{t}_{{k + 1}}},{{t}_{k}}){\mathbf{H}}_{1}^{T}({{t}_{{k + 1}}})}}\begin{array}{*{20}{c}} | \\ | \end{array}} \right.} \\ {\left. {\begin{array}{*{20}{c}} | \\ | \end{array}\frac{{{{{\mathbf{H}}}_{1}}({{t}_{{k + 1}}}){{{\mathbf{\Gamma }}}_{x}}({{t}_{{k + 1}}},{{t}_{k}}){\mathbf{\Gamma }}_{x}^{T}({{t}_{{k + 1}}},{{t}_{k}}){\mathbf{H}}_{2}^{T}({{t}_{{k + 1}}})}}{{{{{\mathbf{H}}}_{2}}({{t}_{{k + 1}}}){{{\mathbf{\Gamma }}}_{x}}({{t}_{{k + 1}}},{{t}_{k}}){\mathbf{\Gamma }}_{x}^{T}({{t}_{{k + 1}}},{{t}_{k}}){\mathbf{H}}_{2}^{T}({{t}_{{k + 1}}}) + Г_{2}^{2}({{t}_{k}})}}} \right]} \end{array}.$

Векторно-матричному разностному уравнению вида [17]:

(12)

${\mathbf{X}}{\kern 1pt} *({{t}_{{k + 1}}}) = \left[ {\begin{array}{*{20}{c}} {H_{{ОТН}}^{*}({{t}_{{k + 1}}})} \\ {V_{Z}^{*}({{t}_{{k + 1}}})} \\ {\Delta {{H}^{*}}({{t}_{{k + 1}}})} \\ {\Delta _{{aZ}}^{*}({{t}_{{k + 1}}})} \end{array}} \right]$

для оценки вектора состояния соответствует система разностных уравнений:

$\begin{gathered} H_{{{\text{ОТН}}}}^{*}({{t}_{{k + 1}}}) = H_{{{\text{ОТН}}}}^{*}({{t}_{k}}) + T \cdot V_{Z}^{*}({{t}_{k}}) - \\ - \;0.5 \cdot {{T}^{2}} \cdot \Delta _{{aZ}}^{*}({{t}_{k}}) + 0.5 \cdot {{T}^{2}} \cdot a_{Z}^{{{\text{ИНС}}}}({{t}_{k}}) - \\ - \;0.5 \cdot {{T}^{2}} \cdot g + {{k}_{{11}}} \cdot [H_{{{\text{ОТН}}}}^{{{\text{БВ}}}}({{t}_{{k + 1}}}) - {{\varphi }_{{uu}}} \cdot H_{{{\text{ОТН}}}}^{{{\text{БВ}}}}({{t}_{k}}) - \\ \end{gathered} $

(13)

$\begin{gathered} - 0.5 \cdot {{T}^{2}} \cdot a_{Z}^{{{\text{ИНС}}}}({{t}_{k}}) + 0.5 \cdot {{T}^{2}} \cdot g + {{\varphi }_{{uu}}} \cdot H_{{{\text{ОТН}}}}^{*}({{t}_{k}}) + \\ + \;{{\varphi }_{{uu}}} \cdot \Delta {{{\rm H}}^{*}}({{t}_{k}}) - H_{{{\text{ОТН}}}}^{*}({{t}_{k}}) - T \cdot V_{Z}^{*}({{t}_{k}}) - \\ - \;\Delta {{H}^{*}}({{t}_{k}}) + 0.5 \cdot {{T}^{2}} \cdot \Delta _{{aZ}}^{*}({{t}_{k}})] + \\ \end{gathered} $

$\begin{gathered} + \;{{k}_{{12}}} \cdot [{{H}^{{{\text{СРНС}}}}}({{t}_{{k + 1}}}) - 0.5 \cdot {{T}^{2}} \cdot a_{Z}^{{{\text{ИНС}}}}({{t}_{k}}) + \\ + \;0.5 \cdot {{T}^{2}} \cdot g - {{R}_{0}} - H_{{ОТН}}^{*}({{t}_{k}}) - \\ - \;T \cdot V_{Z}^{*}({{t}_{k}}) + 0.5 \cdot {{T}^{2}} \cdot \Delta _{{aZ}}^{*}({{t}_{k}})], \\ \end{gathered} $

$\begin{gathered} V_{Z}^{*}({{t}_{{k + 1}}}) = V_{Z}^{*}({{t}_{k}}) - T \cdot \Delta _{{aZ}}^{*}({{t}_{k}}) + T \cdot a_{Z}^{{{\text{ИНС}}}}({{t}_{k}}) - \\ - \;T \cdot g + {{k}_{{21}}} \cdot [H_{{{\text{ОТН}}}}^{{{\text{БВ}}}}({{t}_{{k + 1}}}) - {{\varphi }_{{uu}}} \cdot H_{{{\text{ОТН}}}}^{{{\text{БВ}}}}({{t}_{k}}) - \\ \end{gathered} $

(14)

$\begin{gathered} - \;0.5 \cdot {{T}^{2}} \cdot a_{Z}^{{{\text{ИНС}}}}({{t}_{k}}) + 0.5 \cdot {{T}^{2}} \cdot g + {{\varphi }_{{uu}}} \cdot H_{{{\text{ОТН}}}}^{*}({{t}_{k}}) + \\ + \;{{\varphi }_{{uu}}} \cdot \Delta {{H}^{*}}({{t}_{k}}) - H_{{{\text{ОТН}}}}^{*}({{t}_{k}}) - T \cdot V_{Z}^{*}({{t}_{k}}) - \\ - \;\Delta {{H}^{*}}({{t}_{k}}) + 0.5 \cdot {{T}^{2}} \cdot \Delta _{{aZ}}^{*}({{t}_{k}})] + {{k}_{{22}}} \cdot [{{H}^{{{\text{СРНС}}}}}({{t}_{{k + 1}}}) - \\ \end{gathered} $

$\begin{gathered} - \;0.5 \cdot {{T}^{2}} \cdot a_{Z}^{{{\text{ИНС}}}}({{t}_{k}}) + 0.5 \cdot {{T}^{2}} \cdot g - {{R}_{0}} - H_{{{\text{ОТН}}}}^{*}({{t}_{k}}) - \\ - \;T \cdot V_{Z}^{*}({{t}_{k}}) + 0.5 \cdot {{T}^{2}} \cdot \Delta _{{aZ}}^{*}({{t}_{k}})], \\ \end{gathered} $

$\begin{gathered} \Delta {{H}^{*}}({{t}_{{k + 1}}}) = \Delta {{H}^{*}}({{t}_{k}}) + {{k}_{{31}}} \cdot \left[ {H_{{{\text{ОТН}}}}^{{{\text{БВ}}}}({{t}_{{k + 1}}}) - } \right. \\ - \;{{\varphi }_{{uu}}} \cdot H_{{{\text{ОТН}}}}^{{{\text{БВ}}}}({{t}_{k}}) - 0.5 \cdot {{T}^{2}} \cdot a_{Z}^{{{\text{ИНС}}}}({{t}_{k}}) + 0.5 \cdot {{T}^{2}} \cdot g + \\ \end{gathered} $

(15)

$\begin{gathered} + \;{{\varphi }_{{uu}}} \cdot H_{{{\text{ОТН}}}}^{*}({{t}_{k}}) + {{\varphi }_{{uu}}} \cdot \Delta {{H}^{*}}({{t}_{k}}) - H_{{{\text{ОТН}}}}^{*}({{t}_{k}}) - \\ - \;T \cdot V_{Z}^{*}({{t}_{k}}) - \Delta {{H}^{*}}({{t}_{k}}) + 0.5 \cdot {{T}^{2}} \cdot \Delta _{{aZ}}^{*}({{t}_{k}})] + \\ \end{gathered} $

$\begin{gathered} + \;{{k}_{{32}}} \cdot \left[ {{{H}^{{{\text{СРНС}}}}}({{t}_{{k + 1}}})} \right. - 0.5 \cdot {{T}^{2}} \cdot a_{Z}^{{{\text{ИНС}}}}({{t}_{k}}) + \\ + \;0.5 \cdot {{T}^{2}} \cdot g - {{R}_{0}} - H_{{{\text{ОТН}}}}^{*}({{t}_{k}}) - T \cdot V_{Z}^{*}({{t}_{k}}) + \\ + \;0.5 \cdot {{T}^{2}} \cdot \Delta _{{aZ}}^{*}({{t}_{k}})], \\ \end{gathered} $

$\begin{gathered} \Delta _{{aZ}}^{*}({{t}_{{k + 1}}}) = \Delta _{{aZ}}^{*}({{t}_{k}}) + {{k}_{{41}}} \cdot [H_{{{\text{ОТН}}}}^{{{\text{БВ}}}}({{t}_{{k + 1}}}) - \\ - \;{{\varphi }_{{uu}}} \cdot H_{{{\text{ОТН}}}}^{{{\text{БВ}}}}({{t}_{k}}) - 0.5 \cdot {{T}^{2}} \cdot a_{Z}^{{{\text{ИНС}}}}({{t}_{k}}) + \\ + \;0.5 \cdot {{T}^{2}} \cdot g + {{\varphi }_{{uu}}} \cdot H_{{{\text{ОТН}}}}^{*}({{t}_{k}}) + \\ \end{gathered} $

(16)

$\begin{gathered} + \;{{\varphi }_{{uu}}} \cdot \Delta {{H}^{*}}({{t}_{k}}) - H_{{{\text{ОТН}}}}^{*}({{t}_{k}}) - T \cdot V_{Z}^{*}({{t}_{k}}) - \\ - \;\Delta {{H}^{*}}({{t}_{k}}) + 0.5 \cdot {{T}^{2}} \cdot \Delta _{{aZ}}^{*}({{t}_{k}})] + \\ + \;{{k}_{{42}}} \cdot [{{H}^{{{\text{СРНС}}}}}({{t}_{{k + 1}}}) - \\ \end{gathered} $

где $Н_{{{\text{ОТН}}}}^{*}$ – оценка постоянной составляющей погрешности измерения высоты объекта, $V_{Z}^{*}$ – оценка вертикальной скорости движения объекта, $\Delta Н{\kern 1pt} *$ – оценка постоянной составляющей погрешности измерения высоты объекта; $\Delta _{{aZ}}^{*}$ – оценка постоянной составляющей погрешности измерения ускорения, $a_{Z}^{{{\text{ИНС}}}}$– измеренное значение ускорения на выходе вертикального канала инерциальной навигационной системы (ИНС) в дискретные моменты времени, $g$ – ускорение свободного падения.

РЕЗУЛЬТАТЫ И ИХ ОБСУЖДЕНИЕ

В соответствии с алгоритмом (6) разработана структурная схема устройства вычисления оценки вектора состояния наземных подвижных объектов в вертикальной плоскости с автономной подсистемой контроля целостности навигационных данных спутниковых радионавигационных систем, представленная на рис. 1.

Рис. 1.

Структурная схема устройства вычисления оценки вектора состояния наземных подвижных объектов в вертикальной плоскости с автономной подсистемой контроля целостности навигационных данных спутниковых радионавигационных систем.

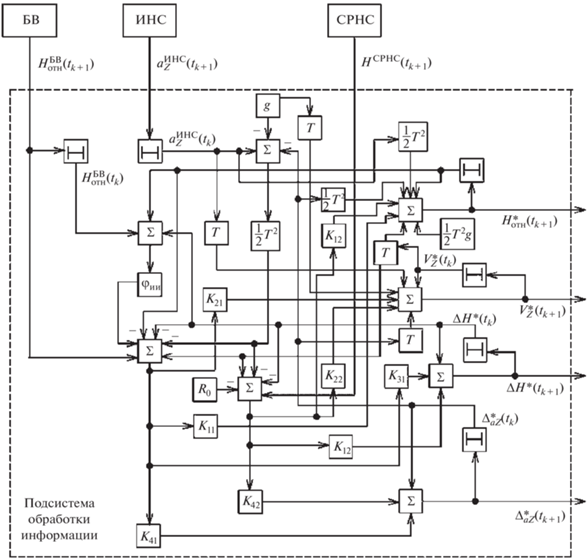
В состав схемы входят сумматоры, линии задержки, усилители с переменными коэффициентами усиления k₁₁(t_k+1), k₂₁(t_k+1), k₃₁(t_k+1), k₄₁(t_k+1), k₁₂(t_k+1), k₂₂(t_k+1), k₃₂(t_k+1), k₄₂(t_k+1), усилитель с коэффициентом усиления ${{\phi }_{{uu}}}({{t}_{{k + 1}}},{{t}_{k}})$, ключевое устройство. Автономная система контроля анализирует значения оценок ошибок измерений $\Delta H{\kern 1pt} *({{t}_{{k + 1}}})$ и $\Delta _{{aZ}}^{*}({{t}_{{k + 1}}})$. По результатам анализа принимается решение на использование информации о координатах НПО (широта, долгота, высота) с выхода приемной аппаратуры СРНС для решения задач навигации. Если использовать данные СРНС нельзя, то сигнал, поступающий на ключевое устройство от автономной системы контроля целостности, запрещает прохождение данных СРНС для их дальнейшей обработки.

Для приведенных выше алгоритмов обработки информации важным является нахождение их потенциальных и фактических характеристик точности. Для получения потенциальных характеристик точности решали систему векторно-матричных разностных уравнений (7, 8). Потенциальная дисперсия ошибки оценивания относительной высоты является элементом P(1,1), а потенциальная дисперсия ошибки оценивания вертикальной скорости – элементом P(2,2) матрицы вторых центральных моментов ошибок, определяемой выражением (8).

С целью определения фактических характеристик точности было проведено статистическое компьютерное моделирование синтезированных алгоритмов при следующих исходных данных: $\Delta H\left( {{{t}_{k}}} \right)$ = 5 м, k = 0, 1, 2, …, T = 0.02 с, γ_БВ = 10 с^–1, σ_БВ = 1 м, ${{R}_{0}}$ = 6371110 м, ${{Н}_{{{\text{ОТН}}}}}({{t}_{k}})$ = 1000 м, k = = 0, 1, 2, …, σ_z = 3 м, ${{a}_{Z}}$ = 0 м, ${{\Delta }_{{aZ}}}$ = 0.2, σ_a = 0.03, α_a = 50, g = 9.8 м.

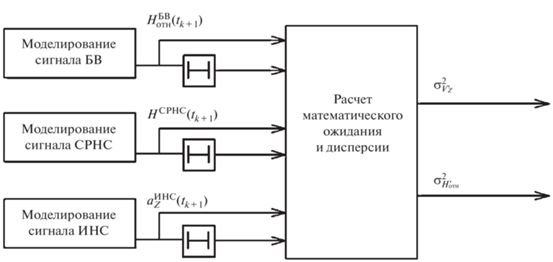
Для получения реализаций оценок относительной высоты и вертикальной скорости объекта моделировали выходные сигналы СРНС, БВ и датчика линейных ускорений, которые далее обрабатывали в соответствии с приведенными выше алгоритмами. Статистические характеристики (математическое ожидание и дисперсия) получали методом статистической обработки данных, компьютерное моделирование проводили в соответствии со схемой, приведенной на рис. 2.

Рис. 2.

Схема статистического компьютерного моделирования.

В ходе компьютерного моделирования были получены 100 реализаций оценок относительной высоты (рис. 3а) и вертикальной скорости (рис. 3б). Затем рассчитали математическое ожидание и дисперсию оценки. Полученные результаты показали, что потенциальная дисперсия ошибки оценивания относительной высоты составляет 0.0016 м² (рис. 4а), фактическая дисперсия ошибки оценивания – 1.8463 м² (рис. 5а), потенциальная дисперсия ошибки оценивания вертикальной скорости – 9.4499 × 10^–7 м²/с² (рис. 4б), а фактическая дисперсия ошибки оценивания – 1.1364 × 10^–6 м²/с² (рис. 5б).

Рис. 3.

Реализации оценок: а – относительной высоты $H_{{{\text{OTH}}}}^{*}$, б – вертикальной скорости $V_{Z}^{*}$.

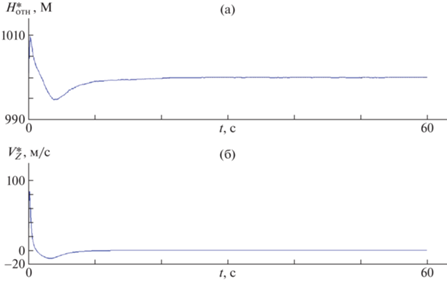
Рис. 4.

Потенциальные характеристики точности: а – дисперсия ошибки оценивания относительной высоты, б – дисперсия ошибки оценивания вертикальной скорости.

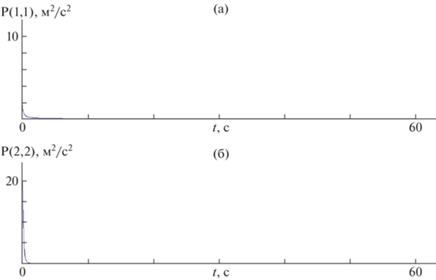
Рис. 5.

Фактические характеристики точности: а – дисперсия ошибки оценивания относительной высоты; б – дисперсия ошибки оценивания вертикальной скорости.

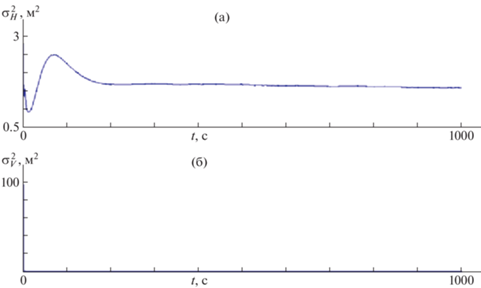
Полученные результаты показывают большую разницу между потенциальными и фактическими характеристиками. Это обусловлено тем, что при получении потенциальных характеристик не учитываются многие факторы воздействия на систему, ухудшающие ее точность.

ЗАКЛЮЧЕНИЕ

Разработана структурная схема вычисления оценки вектора состояния наземных подвижных объектов в вертикальной плоскости с автономной подсистемой контроля целостности навигационных данных спутниковых радионавигационных систем.

Проведен расчет потенциальных характеристик точности оптимальных алгоритмов оценивания координат и параметров движения НПО. Методом статистического компьютерного моделирования проведен расчет фактических характеристик точности. Полученные результаты позволяют сделать вывод о целесообразности применения в навигационных комплексах НПО описанных оптимальных алгоритмов оценивания координат и параметров движения НПО в вертикальной плоскости для осуществления автономного контроля целостности данных СРНС.

Список литературы

Радионавигационный план Российской Федерации. Утвержден приказом Минпромторга России от 4 октября 2019 г. № 3296. www.internavigation.ru/documents/RNP2011.doc
Бакитько Р.В., Болденков Е.Н., Булавский Н.Т. и др. ГЛОНАСС. Принципы построения и функционирования / Под общ. ред. Перова А.И., Харисо-ва В.И. 4-е изд., перераб. и доп. М.: Радиотехника, 2010. 800 с.
Ориентация и навигация подвижных объектов: современные информационные технологии / Под ред. Алешина Б.С. и др. М.: ФИЗМАТЛИТ, 2006. 424 с.
Зализнюк А.Н., Флегонтов А.В., Волков А.А. // Военная мысль. 2022. № 9. С. 65.
Гладышев А.Б., Фомин А.Н., Ермоленко Д.С. // Космические аппараты и технологии. 2022. Т. 6. № 1 (39). С. 38.
Federal Radionavigation Plan. 2019. https://rosap.ntl.bts.gov/view/dot/63024
Якушенко С.А., Забело А.Н., Егрушев В.Е. и др. // Int. J. Human. Nat. Sci. 2022. V. 9–1 (72). P. 80. https://doi.org/10.24412/2500-1000-2022-9-1-80-86
ГОСТ Р 54460-2011. Глобальные навигационные спутниковые системы. Система мониторинга и контроля целостности. Общие технические требования и методы испытаний. Введ. 2012-07-01. М.: Стандартинформ, 2012. 8 с.
Торгашев Б.В. // Экономика и качество систем связи. 2022. № 4. С. 62.
Исаев М.А., Линец Г.И. // Системы управления, связи и безопасности. 2021. № 4. С. 72.
Леонидов Н.В. // Космические аппараты и технологии. 2021. Т. 5. № 1 (35). https://doi.org/10.26732/j.st.2021.1.05
Ярлыков М.С. Статистическая теория радионавигации. М.: Радио и связь, 1985. 344 с.
Богданов М.Б., Прохорцов А.В., Савельев В.В. и др. // Изв. ТулГУ. Технические науки. 2020. № 5. С. 118.
Ермаков П.Г., Гоголев А.А. // East Europ. Sci. J. 2021. № 12 (76). P. 25.
Корнилов А.В., Корчагин К.С., Лосев В.В. // Труды МАИ. 2021. № 117. https://doi.org/10.34759/TRD-2021-117-09
Иванов А.В. // Радиотехника. 2011. № 5. С. 6.
Иванов А.В., Комраков Д.В., Сурков В.О. // Вопр. соврем. науки и практики. Университет им. В.И. Вернадского. 2014. № 52. С. 53.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Вестник Военного инновационного технополиса «ЭРА»

Архивы выпусков Информация о журнале Отправить рукопись в журнал