Вестник Военного инновационного технополиса «ЭРА», 2023, T. 4, № 2, стр. 208-213

ВВЕДЕНИЕ

Коммерческие суда относительно медленно используют потенциал полной интегрированной автоматизации в отрасли по сравнению с военными. Повышение уровня судовой автоматизации и систем интеграционной мобильности позволяет привести к существенной экономии и снижению затрат [1, 2].

Военные суда достаточно давно внедряют интегрированные системы, способные создавать связь с различными судовыми компонентами и сводить системы – в основном защитные и оружейные платформы – в один контрольный и наблюдательный пункт.

Сегодня системы автоматизации судна позволяют различным географически разрозненным компонентам соединиться и взаимодействовать, что позволяет оборудованию и системам управляться и функционировать дистанционно.

На торговых судах и военных кораблях во всем мире используются судовые системы управления и автоматизации для оптимизации работы корабельных двигателей, поворотных движителей, балласта, двигательных установок, рулевых устройств и т.д. Единая судовая архитектура должна обеспечивать управление и визуализацию в масштабах всего судна.

Разделим методы оптимизации дискретно-цифровых регуляторов САР непрерывными объектами на:

– методы замены оптимального непрерывного регулятора дискретно-цифровым в соответствии с выбранным критерием совпадения свойств САР с непрерывным и квазинепрерывным управлением;

– методы непосредственной оптимизации дискретно-цифрового регулятора с непрерывным объектом в контуре в соответствии с критерием близости оптимизированной САР к инвариантной или в соответствии с другим критерием [1–4].

Цель исследования – оптимизация цифрового регулятора системы автоматического регулирования непрерывного объекта.

ЭКСПЕРИМЕНТАЛЬНАЯ ЧАСТЬ

Пусть дана непрерывная САР, регулятор которой уже оптимизирован одним из методов.

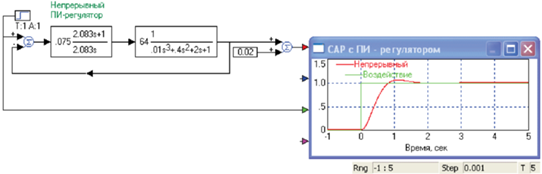
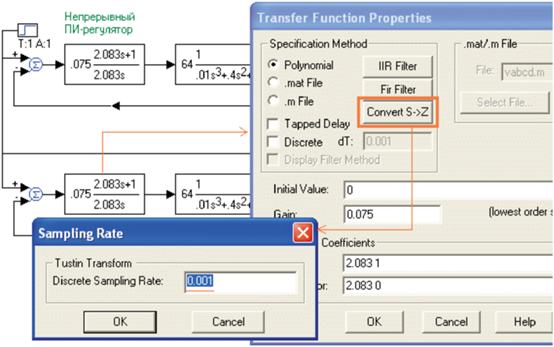
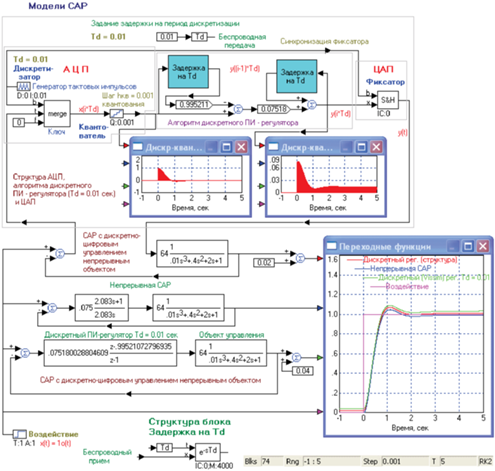
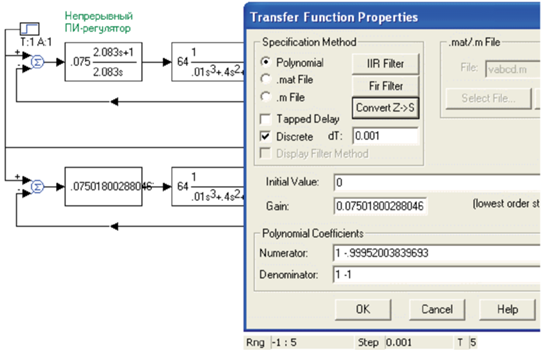
Замена непрерывного ПИ-регулятора осуществляется в соответствии с указаниями, приведенными в [5–8]. Для этого нужно скопировать оптимизированную САР, поместить ее ниже на рабочем поле для сравнения результатов и подключить ее к генератору ступеньки и осциллографу. Далее следует щелкнуть правой кнопкой по блоку ПИ-регулятора в копии САР, а в появившемся окне щелкнуть по кнопке Convert S → Z. В появившемся окне задать значение периода дискретизации. VisSim предлагает наименьший возможный при заданном шаге моделирования период дискретизации, равный этой величине. Для выбора периода дискретизации нужно обратиться к постоянным времени объекта управления. Как видно на рис. 1, наибольшая постоянная времени объекта равна 2 с, следующая по величине равна 0.4/2 = 0.2 с и последняя равна 0.01/(2 × × 0.4) = 0.0125 с. Таким образом, период дискретизации следует выбрать меньшим, чем наименьшая постоянная времени, например равным шагу моделирования 0.001 с.

Рис. 1.

Исходная непрерывная оптимизированная САР.

Щелкнув по кнопке “ОК”, получаем пересчитанные значения коэффициентов, т.е. значения коэффициентов Z-передаточной функции.Рис.2

Рис. 2.

Задание периода дискретизации дискретной модели ПИ-регулятора равным 0.001 с.

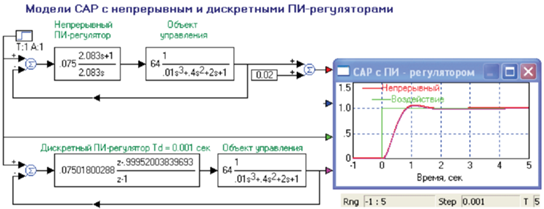
Щелкнув по кнопке “ОК”, получаем модель САР с цифровым управлением непрерывным объектом с периодом дискретизации, равным 0.001 с, которую можно запустить для расчета для сравнения переходных характеристик моделей [6, 9–11]. Рис.3

Рис. 3.

Окно с коэффициентами Z-передаточной функции цифрового ПИ-регулятора, эквивалентного непрерывному регулятору.

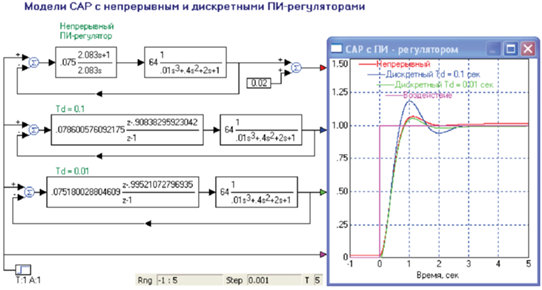
Для удобства сравнения переходная функция непрерывной САР приподнята на 0.02 единицы. Тем не менее полезно посмотреть на поведение САР и при больших значениях периода дискретизации, что позволит снизить вычислительную нагрузку на цифровой процессор компьютера, который будет осуществлять функции регулятора в производственных условиях. Увеличим в 10, а затем и в 100 раз период дискретизации. Если период дискретизации, равный 0.01 с, еще обеспечивает соответствие свойств непрерывной САР и САР с дискретным управлением, то дискретизация с периодом 0.1 с для заданного объекта приводит к существенным отличиям от оптимизированной непрерывной САР. Тем не менее САР с цифровым управлением с периодом дискретизации, равным 0.1 с, обеспечивает слежение, хотя и с несколько завышенным значением перерегулирования, равным 20%.Рис.4

Рис. 4.

Выбранный период дискретизации с цифровым управлением непрерывной.

РЕЗУЛЬТАТЫ И ИХ ОБСУЖДЕНИЕ

Определим алгоритм работы цифрового регулятора. На цифровой регулятор подается непрерывный сигнал ошибки с устройства сравнения (сумматора). Поэтому сигнал ошибки необходимо предварительно дискредитизировать и квантовать, т.е. преобразовать в последовательность числовых значений ошибки, следующих с периодом дискретизации, а затем уже подавать на цифровой процессор [11–15]. Эту функцию в реальной системе выполняет АЦП (аналогово-цифровой преобразователь). Собственно алгоритм работы с дискретизированным сигналом определяется Z-передаточной функцией ПИ-регулятора, которая уже получена (рис. 5). Построим цифровой алгоритм обработки для ПИ-регулятора с периодом дискретизации, равным 0.01 с.

Рис. 5.

Модель с непрерывным и дискретным регулятором.

Исходное выражение Z-передаточной функции дискретного ПИ-регулятора:

Числитель и знаменатель разделены на старшую степень знаменателя, т.е. на z и домножены на –1:

Z-изображение выходного сигнала ПИ-регулятора:

Переход к оригиналам, к решетчатым функциям, во временную область:

Полученная формула указывает алгоритм преобразования решетчатой функции, подаваемой с АЦП на цифровой ПИ-регулятор, параметры которого определены для периода дискретизации, равного 0.01 с. Алгоритм состоит в следующем (рис. 6).

Рис. 6.

Получение формулы вычисления значений решетчатой функции выходного сигнала дискретного регулятора.

Как видно из последней формулы, очередное на текущем такте значение выходного сигнала ПИ-регулятора определяется как сумма предыдущего его выходного значения и взвешенной с коэффициентом 0.07518 разности текущего и предыдущего, умноженного на 0.99 5211, значения входного сигнала (ошибки регулирования). Этот алгоритм легко может быть реализован на любом языке программирования, поддерживаемом тем компьютером, на который подается дискретизированный и квантованный сигнал, в том числе на языках Ассемблер, С++, Delphi и др., а также в виде структурной схемы в программах объектно-ориентированного моделирования, например Vissim, Simulink.

На вход цифрового процессора, реализующего алгоритм работы регулятора, подается цифровая решетчатая функция ошибки регулирования, а на выходе получается цифровая решетчатая функция управляющего сигнала объекта управления, которую следует преобразовать в непрерывный сигнал специальным фильтром, например ФНЧ или фильтром-защелкой (фиксатором значений на период дискретизации). Предлагается пример реализации цифрового алгоритма ПИ-регулятора в программе Vissim.

В соответствии со сформулированным выше алгоритмом в Vissim может быть построена структурная схема, выполняющая его.

Отметим, что в этой схеме модель дискретизатора построена на управляемом ключе merge, в то время как в схеме рис. 7 использована эквивалентная в математическом смысле операция перемножения стробирующих импульсов и входного сигнала.

Рис. 7.

Модели с дискретно-цифровым управлением при правильном подборе параметров дискретных ПИ-регуляторов.

ЗАКЛЮЧЕНИЕ

Некоторые или все элементы непрерывной САР, а также непрерывная САР целиком могут быть промоделированы дискретными моделями, описываемыми разностными, а не дифференциальными, как это делается в случае непрерывных моделей, уравнениями. Практическое значение в теории управления имеет представление дискретной моделью регулятора, что позволяет получить алгоритм цифрового преобразования, осуществляемого регулятором над ошибкой регулирования, и в конечном итоге организовать дискретно-цифровое управление непрерывным объектом с помощью цифрового процессора. Дискретизацию и квантование сигнала ошибки, а также восстановление сигнала управления следует осуществлять с должной точностью, обеспечивающей требуемую точность регулирования. Так, период дискретизации должен быть значительно меньше, по крайней мере, наибольшей постоянной времени объекта управления, а шаг квантования должен быть, по крайней мере, меньше максимально допустимой ошибки регулирования. Уменьшение периода дискретизации и шага квантования существенно повышает требования к быстродействию процессора.